Super-Shuffle Product and Cut-Box Coproduct on (0,1)-Matrices

Sifan Song, Huilan Li^*

School of Mathematics and Statistics, Shandong Normal University, Jinan, China.

DOI: 10.4236/ojapps.2023.138105                

Abstract

In 2014, Vargas first defined a super-shuffle product and a cut-box coproduct on permutations. In 2020, Aval, Bergeron and Machacek introduced the super-shuffle product and the cut-box coproduct on labeled simple graphs. In this paper, we generalize the super-shuffle product and the cut-box coproduct from labeled simple graphs to (0,1)-matrices. Then we prove that the vector space spanned by (0,1)-matrices with the super-shuffle product is a graded algebra and with the cut-box coproduct is a graded coalgebra.

Keywords

(0, 1)-Matrix, Super-Shuffle Product, Cut-Box Coproduct, Graded Algebra, Graded Coalgebra

1. Introduction

In 1941, Hopf [1] first put forward the concept of both algebra structure and coalgebra structure in the study of cohomology algebra $H^{\mathrm{<mo>\; *\; </mo>}}\left(G\mathrm{,}K\right)$ of Lie group G. After that, more and more interesting questions about algebras and coalgebras have attracted many mathematicians to work and study on them continuously. Among those questions, it is a hot topic how to construct algebras and coalgebras on combinatorial objects.

In 2014, Vargas [2] defined a super-shuffle product $\underset{\_}{ш}$ and a coproduct ${\Delta }_{\diamond }$ , called cut-box coproduct by Liu and Li [3] on permutations. In 2005, Aguiar and Sottile introduced the global descents of permutations in symmetric groups [4] . On this basis, Zhao and Li derived another shuffle product and deconcatenation coproduct from the classical one on permutations. Then they proved the vector space spanned by permutations with the shuffle product that is a graded algebra and with the deconcatenation coproduct that is a graded coalgebra [5] in 2020. In the same year, Aval, Bergeron and Machacek introduced the super-shuffle product and the cut-box coproduct on labeled simple graphs without proof [6] . In 2023, Dong [7] proved the vector space spanned by labeled graphs with the super-shuffle product is a graded algebra and with the cut-box coproduct is a graded coalgebra.

In fact, matrices are related to permutations and graphs closely. A (0,1)-matrix is a matrix whose entries are all 0 or 1, also called a binary matrix. It is widely used in graph theory [8] [9] , combinatorics [10] , linear programming [11] [12] [13] and computer science [14] . In this paper, we first generalize the super-shuffle product and the cut-box coproduct from labeled simple graphs to (0,1)-matrices, then we prove that the vector space with the super-shuffle product that is a graded algebra and with the cut-box coproduct that is a graded coalgebra.

This paper is organized as follows. We start by recalling some notations on (0,1)-matrices and defining the vector space $\mathcal{M}$ spanned by (0,1)-matrices in Section 2. In Section 3, we define the cut-box coproduct $\Delta$ on $\mathcal{M}$ and prove $\mathcal{M}$ with coproduct $\Delta$ that is a graded coalgebra. In Section 4, we define the super-shuffle product $\ast$ on $\mathcal{M}$ and prove $\mathcal{M}$ with product $\ast$ that is a graded algebra. Lastly, we summarize our main conclusions in Section 5.

2. Basic Definitions

An $s\times n$ matrix $A={\left(a_{ij}\right)}_{s\times n}$ is called a (0,1)-matrix if

$A={\left(\begin{array}{cc}\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}& \begin{array}{cc}\cdots & a_{1n}\\ \cdots & a_{2n}\end{array}\\ \begin{array}{cc}⋮& ⋮\\ a_{s1}& a_{s2}\end{array}& \begin{array}{cc}\ddots & ⋮\\ \cdots & a_{sn}\end{array}\end{array}\right)}_{s\times n}\mathrm{,}$

where $a_{ij}$ is either 0 or 1. In particular, the empty matrix is the matrix with no entries, denoted by $\epsilon$ .

Define

$\left[n\right]=(\begin{array}{ll}\left\{1,2,\cdots ,n\right\},\hfill & n>0,\hfill \\ \varnothing ,\hfill & n=0,\hfill \end{array}$

and

$\left[i,j\right]=(\begin{array}{ll}\left\{i,i+1,\cdots ,j\right\},\hfill & i\le j,\hfill \\ \varnothing ,\hfill & i>j.\hfill \end{array}$

Let $I=\left\{i_1\mathrm{,}{i}_2\mathrm{,}\cdots \mathrm{,}{i}_k\right\}\subseteq \left[s\right]$ and $J=\left\{j_1\mathrm{,}{j}_2\mathrm{,}\cdots \mathrm{,}{j}_q\right\}\subseteq \left[n\right]$ , where $i_1<i_2<\cdots <i_k\le s$ and $j_1<j_2<\cdots <j_q\le n$ . For an $s\times n$ (0,1)-matrix A, the restriction of A on $I\times J$ is the submatrix formed by the entries, in the same relative positions, in both rows indexed by I and columns indexed by J, denoted by $A_{I\times J}$ . In particular, if $I=\left[s\right]$ and $J=\left[n\right]$ , $A_{I\times J}=A$ and if I or J is empty, $A_{I\times J}=\epsilon$ . For convenience, let $A_I$ denote $A_{I\times I}$ and call $A_I$ the restriction of A on I.

Example 1. The matrix

$A=\left(\begin{array}{ccccccc}0& 1& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 1& 0& 0\\ 0& 1& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 1& 0\end{array}\right)$

is a 4 × 7 (0,1)-matrix. We have

$A_{\left\{\mathrm{1,2}\right\}\times \left\{\mathrm{1,2,7}\right\}}=\left(\begin{array}{ccc}0& 1& 1\\ 0& 0& 0\end{array}\right)$

and

$A_{\left[3\right]}=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 0\\ 0& 1& 0\end{array}\right)\mathrm{.}$

Let $M_n=\left\{A\mathrm{<mo>\; |\; </mo>}A=\left(a_{ij}\right)\text{is}\text{an}n\times n\left(\mathrm{0,1}\right)\text{-matrix}\right\}$ and ${\mathcal{M}}_n$ be the vector space spanned by $M_n$ over field $\mathbb{K}$ , for any non-negative integer n. For example,

$\begin{array}{l}{M}_2=\{\left[\begin{array}{cc}0& 0\\ 0& 0\end{array}\right]\mathrm{,}\left[\begin{array}{cc}1& 0\\ 0& 0\end{array}\right]\mathrm{,}\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]\mathrm{,}\left[\begin{array}{cc}0& 0\\ 1& 0\end{array}\right]\mathrm{,}\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]\mathrm{,}\left[\begin{array}{cc}1& 1\\ 0& 0\end{array}\right]\mathrm{,}\left[\begin{array}{cc}1& 0\\ 1& 0\end{array}\right]\mathrm{,}\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\mathrm{,}\\ \mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]\mathrm{,}\left[\begin{array}{cc}0& 1\\ 0& 1\end{array}\right]\mathrm{,}\left[\begin{array}{cc}0& 0\\ 1& 1\end{array}\right]\mathrm{,}\left[\begin{array}{cc}1& 1\\ 1& 0\end{array}\right]\mathrm{,}\left[\begin{array}{cc}1& 1\\ 0& 1\end{array}\right]\mathrm{,}\left[\begin{array}{cc}1& 0\\ 1& 1\end{array}\right]\mathrm{,}\left[\begin{array}{cc}0& 1\\ 1& 1\end{array}\right]\mathrm{,}\left[\begin{array}{cc}1& 1\\ 1& 1\end{array}\right]\}.\end{array}$

In particular, $M_0=\left\{\epsilon \right\}$ and ${\mathcal{M}}_0=\mathbb{K}{M}_0$ . Denote

$M={\displaystyle \underset{n=0}{\overset{\infty }{\cup }}}{M}_n\text{and}\mathcal{M}=\underset{n=0}{\overset{\infty }{{\displaystyle \oplus }}}{\mathcal{M}}_n\mathrm{.}$

If A and B are both non-empty matrices, then we denote $A\diamond B=\left[\begin{array}{cc}A& O\\ O& B\end{array}\right]$ , where O’s are zero matrices. In particular, $\epsilon \diamond A=A\diamond \epsilon =A$ for any (0,1)-matrix A.

Example 2. For $A=\left(\begin{array}{cc}0& 0\\ 1& 1\end{array}\right)$ and $B=\left(\begin{array}{ccc}1& 0& 0\\ 1& 0& 1\\ 0& 1& 1\end{array}\right)$ , we have

$A\diamond B=\left(\begin{array}{ccccc}0& 0& 0& 0& 0\\ 1& 1& 0& 0& 0\\ 0& 0& 1& 0& 0\\ 0& 0& 1& 0& 1\\ 0& 0& 0& 1& 1\end{array}\right).$

For A in $M_n$ , we call i a spilt of A, if $A_{\left[i\right]}\diamond A_{\left[n\right]\mathrm{<mo\; stretchy="false">\; ]\; </mo>}\backslash \left[i\right]}=A\mathrm{,}$ where $0\le i\le n$ . By the definition, 0 and n are always splits of a (0,1)-matrix in $M_n$ when $n\ge 1$ , called trivial splits. Obviously, $A_{\left[i\right]\times \left(\left[n\right]\backslash \left[i\right]\right)}=A_{\left(\left[n\right]\backslash \left[i\right]\right)\times \left[i\right]}=\epsilon$ when i is a trivial spilt of A; $A_{\left[i\right]\times \left(\left[n\right]\backslash \left[i\right]\right)}=O_{i\times \left(n-i\right)}$ and $A_{\left(\left[n\right]\backslash \left[i\right]\right)\times \left[i\right]}=O_{\left(n-i\right)\times i}$ when i is a non-trivial spilt of A. We call A indecomposible if it is non-empty and only has trivial splits.

For A in $M_n$ , $n\ge 1$ , suppose that $\left\{i_0\mathrm{,}{i}_1\mathrm{,}\cdots \mathrm{,}{i}_s\right\}$ is the set of all splits of A, where $0=i_0<i_1<\cdots <i_s=n$ . We call $A_{\left[i_{k-1}+\mathrm{1,}{i}_k\right]}$ an atom of A, $1\le k\le s$ . Obviously, there is no non-trivial split of $A_{\left[i_{k-1}+\mathrm{1,}{i}_k\right]}$ for $1\le k\le s$ . Let $A_k=A_{\left[i_{k-1}+1,i_k\right]},$ for $1\le k\le s$ . We define the decomposition of A by $A=A_1\diamond A_2\diamond \cdots \diamond A_s\mathrm{.}$

In particular, when A is indecomposable or empty, its decomposition is itself.

Example 3. 1) The set of splits of

$\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 1& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 1& 1& 1\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 1& 0& 0\end{array}\right]$

is $\left\{\mathrm{0,1,3,6}\right\}$ and its decomposition is

$\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 1& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 1& 1& 1\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 1& 0& 0\end{array}\right]=\left[\begin{array}{c}1\end{array}\right]\diamond \left[\begin{array}{cc}1& 1\\ 0& 1\end{array}\right]\diamond \left[\begin{array}{ccc}1& 1& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right]\mathrm{.}$

Its atoms are

$\left[\begin{array}{c}1\end{array}\right]\mathrm{,\; <mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}\left[\begin{array}{cc}1& 1\\ 0& 1\end{array}\right]\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}\text{and}\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>\; <mtext>\; \hspace{0.17em}\; </mtext>}\left[\begin{array}{ccc}1& 1& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right]\mathrm{.}$

2) The set of splits of $\left[\begin{array}{ccc}1& 0& 1\\ 0& 1& 0\\ 1& 0& 1\end{array}\right]$ is $\left\{\mathrm{0,3}\right\}$ , so it is indecomposable. Its decomposition is itself, and so is its atom.

3. Cut-Box Coproduct and Coalgebra

In this section, we define the cut-box coproduct on the vector space $\mathcal{M}$ . Then we prove the space with the cut-box coproduct is a graded coalgebra.

Define the cut-box coproduct $\Delta$ on $\mathcal{M}$ by $\Delta \left(A\right)={\displaystyle \underset{j=0}{\overset{s}{\sum }}}{A}_1\diamond \cdots \diamond A_j\otimes A_{j+1}\diamond \cdots \diamond A_s$ for non-empty matrix A in $M_n$ with decomposition $A=A_1\diamond A_2\diamond \cdots \diamond A_s$ , where $A_1\diamond \cdots \diamond A_0=A_{s+1}\diamond \cdots \diamond A_s=\epsilon$ . In particular, define $\Delta \left(\epsilon \right)=\epsilon \otimes \epsilon$ .

Define the counit $\nu$ from $\mathcal{M}$ to $\mathbb{K}$ by

$\nu \left(A\right)=(\begin{array}{cc}\mathrm{1,}& A=\epsilon \mathrm{,}\\ \mathrm{0,}& \text{otherwise}\mathrm{,}\end{array}$

for A in M.

Example 4. From Example 3 and the definition of the cut-box coproduct, we have

$\begin{array}{l}\Delta \left(\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 1& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 1& 1& 1\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 1& 0& 0\end{array}\right]\right)=\Delta \left(\left[\begin{array}{c}1\end{array}\right]\diamond \left[\begin{array}{cc}1& 1\\ 0& 1\end{array}\right]\diamond \left[\begin{array}{ccc}1& 1& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right]\right)\\ =\epsilon \otimes \left[\begin{array}{c}1\end{array}\right]\diamond \left[\begin{array}{cc}1& 1\\ 0& 1\end{array}\right]\diamond \left[\begin{array}{ccc}1& 1& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right]+\left[\begin{array}{c}1\end{array}\right]\otimes \left[\begin{array}{cc}1& 1\\ 0& 1\end{array}\right]\diamond \left[\begin{array}{ccc}1& 1& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right]\\ +\left[\begin{array}{c}1\end{array}\right]\diamond \left[\begin{array}{cc}1& 1\\ 0& 1\end{array}\right]\otimes \left[\begin{array}{ccc}1& 1& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right]+\left[\begin{array}{c}1\end{array}\right]\diamond \left[\begin{array}{cc}1& 1\\ 0& 1\end{array}\right]\diamond \left[\begin{array}{ccc}1& 1& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right]\otimes \epsilon \\ =\epsilon \otimes \left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 1& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 1& 1& 1\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 1& 0& 0\end{array}\right]+\left[\begin{array}{c}1\end{array}\right]\otimes \left[\begin{array}{ccccc}1& 1& 0& 0& 0\\ 0& 1& 0& 0& 0\\ 0& 0& 1& 1& 1\\ 0& 0& 0& 1& 0\\ 0& 0& 1& 0& 0\end{array}\right]\\ +\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 1\\ 0& 0& 1\end{array}\right]\otimes \left[\begin{array}{ccc}1& 1& 1\\ 0& 1& 0\\ 1& 0& 0\end{array}\right]+\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 1& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 1& 1& 1\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 1& 0& 0\end{array}\right]\otimes \epsilon \end{array}$

and

$\Delta \left(\left[\begin{array}{ccc}1& 0& 1\\ 0& 1& 0\\ 1& 0& 1\end{array}\right]\right)=\epsilon \otimes \left[\begin{array}{ccc}1& 0& 1\\ 0& 1& 0\\ 1& 0& 1\end{array}\right]+\left[\begin{array}{ccc}1& 0& 1\\ 0& 1& 0\\ 1& 0& 1\end{array}\right]\otimes \epsilon \mathrm{.}$

Theorem 1. $\left(\mathcal{M}\mathrm{,}\Delta \mathrm{,}\nu \right)$ is a graded coalgebra.

Proof. It is easy to verify that $\nu$ is a counit. Obviously, $\left(\text{id}\otimes \Delta \right)\circ \Delta \left(\epsilon \right)=\epsilon \otimes \epsilon \otimes \epsilon =\left(\Delta \otimes \text{id}\right)\circ \Delta \left(\epsilon \right)\mathrm{.}$

Suppose A in $M_n$ with $n\ge 1$ and its decomposition is $A=A_1\diamond A_2\diamond \cdots \diamond A_s\mathrm{.}$

Then

$\begin{array}{l}\left(\text{id}\otimes \Delta \right)\circ \Delta \left(A\right)\\ =\left(\text{id}\otimes \Delta \right)\circ \Delta \left(A_1\diamond A_2\diamond \cdots \diamond A_s\right)\\ =\left(\text{id}\otimes \Delta \right)\left({\displaystyle \underset{j=0}{\overset{s}{\sum }}}{A}_1\diamond \cdots \diamond A_j\otimes A_{j+1}\diamond \cdots \diamond A_s\right)\\ ={\displaystyle \underset{j=0}{\overset{s}{\sum }}}{A}_1\diamond \cdots \diamond A_j\otimes \left({\displaystyle \underset{k=j}{\overset{s}{\sum }}}{A}_{j+1}\diamond \cdots \diamond A_k\otimes A_{k+1}\diamond \cdots \diamond A_s\right)\end{array}$

$\begin{array}{l}={\displaystyle \underset{0\le j\le k\le s}{\sum }}{A}_1\diamond \cdots \diamond A_j\otimes A_{j+1}\diamond \cdots \diamond A_k\otimes A_{k+1}\diamond \cdots \diamond A_s\\ ={\displaystyle \underset{k=0}{\overset{s}{\sum }}}\left({\displaystyle \underset{j=0}{\overset{k}{\sum }}}{A}_1\diamond \cdots \diamond A_j\otimes A_{j+1}\diamond \cdots \diamond A_k\right)\otimes A_{k+1}\diamond \cdots \diamond A_s\\ =\left(\Delta \otimes \text{id}\right)\left({\displaystyle \underset{k=0}{\overset{s}{\sum }}}{A}_1\diamond \cdots \diamond A_k\otimes A_{k+1}\diamond \cdots \diamond A_s\right)\\ =\left(\Delta \otimes \text{id}\right)\circ \Delta \left(A\right)\mathrm{,}\end{array}$

where $A_{j+1}\diamond \cdots \diamond A_j=\epsilon$ for $0\le j\le s$ . So $\Delta$ satisfies the coassociative law.

Obviously, by the definitions of $\Delta$ and $\nu$ , we have $\Delta \left({\mathcal{M}}_n\right)\subseteq \underset{}{{\displaystyle {{\displaystyle \oplus }}_{}}}{\mathcal{M}}_i\otimes {\mathcal{M}}_{n-i}$ and $\nu \left({\mathcal{M}}_n\right)=0$ for $n>0$ . Hence $\left(\mathcal{M}\mathrm{,}\Delta \mathrm{,}\nu \right)$ is a graded coalgebra.

□

4. Super-Shuffle Product and Algebra

In this section, we define the super-shuffle product on the vector space $\mathcal{M}$ . Then we prove the space with the super-shuffle product is a graded algebra.

Define the super-shuffle product $\ast$ on $\mathcal{M}$ by

$A\ast B={\displaystyle \underset{\begin{array}{c}C\in M_{m+n}\\ I\mathrm{,}J\mathrm{<mo>\; :\; </mo>}I\cup J=\left[m+n\right]\\ C_I=A,C_J=B\end{array}}{\sum }}C$ (1)

for A in $M_m$ and B in $M_n$ , where C traverses all matrices in $M_{m+n}$ with the restriction on I is A, on J is B, on $I\times J$ and $J\times I$ are arbitrary (0,1)-matrices. Obviously, the product $\ast$ is commutative and $\epsilon \ast A=A\ast \epsilon =A$ , for any A in M. Define the unit $\mu$ from $\mathbb{K}$ to $\mathcal{M}$ by $\mu \left(1\right)=\epsilon$ .

Example 5. For $A=\left[\begin{array}{cc}1& 1\\ 1& 0\end{array}\right],\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}B=\left[\begin{array}{c}1\end{array}\right]$ we have

$\begin{array}{c}+\left[\begin{array}{ccc}1& 0& 1\\ 1& 1& 0\\ 1& 1& 0\end{array}\right]+\left[\begin{array}{ccc}1& 0& 1\\ 0& 1& 1\\ 1& 1& 0\end{array}\right]+\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 0& 0\end{array}\right]+\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 0\\ 1& 1& 0\end{array}\right]+\left[\begin{array}{ccc}1& 1& 1\\ 0& 1& 1\\ 1& 1& 0\end{array}\right]\\ +\left[\begin{array}{ccc}1& 0& 1\\ 1& 1& 1\\ 1& 1& 0\end{array}\right]+\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 0\end{array}\right]+\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 1\\ 0& 1& 0\end{array}\right]+\left[\begin{array}{ccc}1& 1& 0\\ 0& 1& 1\\ 0& 1& 0\end{array}\right]+\left[\begin{array}{ccc}1& 0& 1\\ 0& 1& 1\\ 0& 1& 0\end{array}\right]\\ +\left[\begin{array}{ccc}1& 0& 0\\ 1& 1& 1\\ 0& 1& 0\end{array}\right]+\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 1\\ 1& 1& 0\end{array}\right]+\left[\begin{array}{ccc}1& 1& 1\\ 0& 1& 1\\ 0& 1& 0\end{array}\right]+\left[\begin{array}{ccc}1& 1& 0\\ 1& 1& 1\\ 0& 1& 0\end{array}\right]+\left[\begin{array}{ccc}1& 1& 0\\ 0& 1& 1\\ 1& 1& 0\end{array}\right]\\ +\left[\begin{array}{ccc}1& 0& 1\\ 1& 1& 1\\ 0& 1& 0\end{array}\right]+\left[\begin{array}{ccc}1& 0& 1\\ 0& 1& 1\\ 1& 1& 0\end{array}\right]+\left[\begin{array}{ccc}1& 0& 0\\ 1& 1& 1\\ 1& 1& 0\end{array}\right]+\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 0& 1& 0\end{array}\right]+\left[\begin{array}{ccc}1& 1& 1\\ 0& 1& 1\\ 1& 1& 0\end{array}\right]\\ +\left[\begin{array}{ccc}1& 1& 0\\ 1& 1& 1\\ 1& 1& 0\end{array}\right]+\left[\begin{array}{ccc}1& 0& 1\\ 1& 1& 1\\ 1& 1& 0\end{array}\right]+\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 0\end{array}\right]\mathrm{.}\end{array}$

Here, we color the entries of C in $A\ast B$ restricted to A red and to B blue, respectively. Although $\left[\begin{array}{ccc}1& 0& 1\\ 0& 1& 1\\ 1& 1& 0\end{array}\right]$ and $\left[\begin{array}{ccc}1& 0& 1\\ 0& 1& 1\\ 1& 1& 0\end{array}\right]$ are same matrices, we consider they are different. Then each term in $A\ast B$ is unique.

Let $W=\left\{i_1\mathrm{,}{i}_2\mathrm{,}\cdots \mathrm{,}{i}_n\right\}$ be a set of positive integers where $i_1<i_2<\cdots <i_n$ . Define a mapping ${\text{st}}_W$ from W to $\left[\left|W\right|\right]$ by ${\text{st}}_W\left(i_a\right)=a$ for $1\le a\le n$ , and call it the standardization of W [6] . For a subset T of W, denote ${\text{st}}_W\left(T\right)=\left\{{\text{st}}_W\left(i\right)\mathrm{<mo>\; |\; </mo>}i\in T\right\}$ . Obviously, ${\text{st}}_W$ is a 1-1 mapping from the set of subsets of W to the set of subsets of $\left[\left|W\right|\right]$ . Therefore, for any subset H of $\left[\left|W\right|\right]$ , there must exist a unique subset P of W such that $H={\text{st}}_W\left(P\right)$ .

Remark 1. ( [15] ) Let W be a set of positive integers and P be a subset of W. Then there exists a unique subset H in $\left[\left|W\right|\right]$ such that

${\text{st}}_P\left(i\right)={\text{st}}_H\left({\text{st}}_W\left(i\right)\right)\mathrm{,}$

for any i in P. Actually, $H={\text{st}}_W\left(P\right)$ .

Example 6. For $W=\left\{\mathrm{3,5,7,8,9}\right\}$ and $P=\left\{\mathrm{3,7,8}\right\}$ , ${\text{st}}_P\left(3\right)=1$ , ${\text{st}}_P\left(7\right)=2$ , ${\text{st}}_P\left(8\right)=3$ , ${\text{st}}_W\left(3\right)=1$ , ${\text{st}}_W\left(7\right)=3$ and ${\text{st}}_W\left(8\right)=4$ . Take $H={\text{st}}_W\left(P\right)={\text{st}}_W\left(\left\{\mathrm{3,7,8}\right\}\right)=\left\{\mathrm{1,3,4}\right\}$ . Furthermore, ${\text{st}}_H\left({\text{st}}_W\left(3\right)\right)=1$ , ${\text{st}}_H\left({\text{st}}_W\left(7\right)\right)=2$ , ${\text{st}}_H\left({\text{st}}_W\left(8\right)\right)=3$ .

Next, in order to prove $\left(\mathcal{M}\mathrm{,}\ast \mathrm{,}\mu \right)$ is a graded algebra, we give one lemma.

Lemma 2. Assume $A={\left(a_{ij}\right)}_{n\times n}$ is a (0,1)-matrix, $W\subseteq \left[n\right]$ and $H\subseteq \left[\left|W\right|\right]$ . Then there exists a subset P of W such that $A_P={\left(A_W\right)}_H$ .

Proof. By the definition of ${\text{st}}_W$ , there must exist a subset P of W such that ${\text{st}}_W\left(P\right)=H$ . Next, we prove $A_P={\left(A_W\right)}_H$ .

Let $A_P$ be $B=\left(b_{ij}\right)$ , $A_W$ be $C=\left(c_{ij}\right)$ and ${\left(A_W\right)}_H$ be $D=\left(d_{ij}\right)$ . Obviously, B and D are both (0,1)-matrices. We just need to show that $b_{ij}=d_{ij}$ for each $i\mathrm{,}j$ in $\left[\left|P\right|\right]$ . For $b_{ij}$ in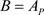, there must exist $i^{\prime }$ and $j^{\prime }$ in P such that ${\text{st}}_P\left(i^{\prime }\right)=i$ , ${\text{st}}_P\left(j^{\prime }\right)=j$ and. Since P is a subset of W, there must exist ${i^{\prime }}^{\prime }$ and ${j^{\prime }}^{\prime }$ in $\left[\left|W\right|\right]$ such that ${\text{st}}_W\left(i^{\prime }\right)={i^{\prime }}^{\prime }$ , ${\text{st}}_W\left(j^{\prime }\right)={j^{\prime }}^{\prime }$ and $a_{i^{\prime }{j}^{\prime }}=c_{{i^{\prime }}^{\prime }{j^{\prime }}^{\prime }}$ . On the other hand, we have ${\text{st}}_W\left(P\right)=H$ and ${\text{st}}_W$ is a 1-1 mapping from the set of subsets of W to the set of subsets of $\left[\left|W\right|\right]$ , therefore ${i^{\prime }}^{\prime }$ and ${j^{\prime }}^{\prime }$ are in H. Then there must exist ${{i^{\prime }}^{\prime }}^{\prime }$ and in $\left[\left|H\right|\right]$ such that ${\text{st}}_H\left({i^{\prime }}^{\prime }\right)={{i^{\prime }}^{\prime }}^{\prime }$ , ${\text{st}}_H\left({j^{\prime }}^{\prime }\right)={{j^{\prime }}^{\prime }}^{\prime }$ and $c_{{i^{\prime }}^{\prime }{j^{\prime }}^{\prime }}=d_{{{i^{\prime }}^{\prime }}^{\prime }{{j^{\prime }}^{\prime }}^{\prime }}$ . Hence, $b_{ij}=d_{{{i^{\prime }}^{\prime }}^{\prime }{{j^{\prime }}^{\prime }}^{\prime }}$ . By Remark 1, we have $i={\text{st}}_P\left(i^{\prime }\right)={\text{st}}_H\left({\text{st}}_W\left(i^{\prime }\right)\right)={\text{st}}_H\left({i^{\prime }}^{\prime }\right)={{i^{\prime }}^{\prime }}^{\prime }$ and $j={\text{st}}_P\left(j^{\prime }\right)={\text{st}}_H\left({\text{st}}_W\left(j^{\prime }\right)\right)={\text{st}}_H\left({j^{\prime }}^{\prime }\right)={{j^{\prime }}^{\prime }}^{\prime }\mathrm{.}$

Thus, for each $i\mathrm{,}j$ in $\left[\left|P\right|\right]$ , $b_{ij}=d_{ij}$ , i.e., $A_P={\left(A_W\right)}_H$ . □

Theorem 3. $\left(\mathcal{M}\mathrm{,}\ast \mathrm{,}\mu \right)$ is a graded algebra.

Proof. It is easy to verify that $\mu$ is a unit. For A in $M_h$ , B in $M_k$ and C in $M_l$ , we have

$A\ast B={\displaystyle \underset{\begin{array}{c}X\in M_{h+k}\\ H,K:H\cup K=\left[h+k\right]\\ X_H=A,X_K=B\end{array}}{\sum }}X.$

Then for any term Y in $\left(A\ast B\right)\ast C$ , there exist two disjoint subsets W and L of $\left[h+k+l\right]$ with $\left|W\right|=h+k$ and $\left|L\right|=l$ such that $Y_W$ is a term in $A\ast B$ and $Y_L=C$ . It means

$\left(A\ast B\right)\ast C={\displaystyle \underset{\begin{array}{c}X\in M_{h+k}\\ H,K:H\cup K=\left[h+k\right]\\ X_H=A,X_K=B\end{array}}{\sum }}{\displaystyle \underset{\begin{array}{c}Y\in M_{h+k+l}\\ W,L:W\cup L=\left[h+k+l\right]\\ Y_W=X,Y_L=C\end{array}}{\sum }}Y.$ (2)

For a fixed W in $\left[h+k+l\right]$ with cardinality $h+k$ , there exist two disjoint subsets H and K of $\left[h+k\right]$ with $\left|H\right|=h$ and $\left|K\right|=k$ such that

${\left(Y_W\right)}_H=A\text{and}{\left(Y_W\right)}_K=B\mathrm{.}$

Since H is a subset of $\left[\left|W\right|\right]=\left[h+k\right]$ , due to the Lemma 2, there exists a subset P of W corresponding to H with $\left|P\right|=h$ such that $H={\text{st}}_W\left(P\right)$ and

$Y_P={\left(Y_W\right)}_H=A.$

Similarly, there exists a subset Q of W with $\left|Q\right|=k$ corresponding to K such that $K={\text{st}}_W\left(Q\right)$ and

$Y_Q={\left(Y_W\right)}_K=B.$

In (2), for a fixed subset W in $\left[h+k+l\right]$ with cardinality $h+k$ , H traverses all subsets with cardinality h in $\left[h+k\right]$ , since $Y_W$ traverses all terms in $A\ast B$ . Meanwhile, P traverses all subsets with cardinality h in W. Therefore, P traverses all subsets with cardinality h in $\left[h+k+l\right]$ when W traverses all subsets with cardinality $h+k$ in $\left[h+k+l\right]$ . Similarly, Q traverses all subsets with candinality k in $\left[h+k+l\right]$ when W traverses all subsets with cardinality $h+k$ in $\left[h+k+l\right]$ from $W=P\cup Q$ . Thus (2) can be rewritten as

$\left(A\ast B\right)\ast C={\displaystyle \underset{\begin{array}{c}Y\in M_{h+k+l}\\ P,Q,L:P\cup Q\cup L=\left[h+k+l\right]\\ Y_P=A,Y_Q=B,Y_L=C\end{array}}{\sum }}Y.$ (3)

Similarly, $A\ast \left(B\ast C\right)$ can be rewritten as (3). Hence, $\ast$ satisfies the associative law and $\left(\mathcal{M}\mathrm{,}\ast \mathrm{,}\mu \right)$ is an algebra.

By the definitions of the product $\ast$ and $\mu$ , we have ${\mathcal{M}}_r\ast {\mathcal{M}}_s\subseteq {\mathcal{M}}_{r+s}$ and $\mu \left(\mathbb{K}\right)\subseteq {\mathcal{M}}_0$ . So $\left(\mathcal{M}\mathrm{,}\ast \mathrm{,}\mu \right)$ is a graded algebra. □

5. Conclusion and Suggestion

Let $\mathcal{M}$ be the vector space spanned by (0,1)-matrices. Firstly, we introduce splits and the decomposition of a (0,1)-matrix. Then we define the cut-box coproduct $\Delta$ and the super-shuffle product $\ast$ on $\mathcal{M}$ . We prove the cut-box coproduct $\Delta$ satisfies coassociativity and the super-shuffle product $\ast$ satisfies associativity, i.e., $\left(\mathcal{M}\mathrm{,}\Delta \mathrm{,}\nu \right)$ is a graded coalgebra and $\left(\mathcal{M}\mathrm{,}\ast \mathrm{,}\mu \right)$ is a graded algebra.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Nos. 11701339 and 12071265).

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Hopf, H. (1964) über die Topologie der Gruppen-Mannigfaltigkeiten und Ihrer Verallgemeinerungen. In: Selecta Heinz Hopf, Springer, Berlin, 119-151. https://doi.org/10.1007/978-3-662-25046-4_9
[2]	Vargas, Y. (2014) Hopf Algebra of Permutation Pattern Functions. 26th International Conference on Formal Power Series and Algebraic Combinatorics (FPSAC 2014), Chicago, 29 June-3 July 2014. https://doi.org/10.46298/dmtcs.2446
[3]	Liu, M. and Li, H. (2021) A Hopf Algebra on Permutations Arising from Super-Shuffle Product. Symmetry, 13, Article No. 1010. https://doi.org/10.3390/sym13061010
[4]	Aguiar, M. and Sottile, F. (2005) Structure of the Malvenuto-Reutenauer Hopf Algebra of Permutations. Advances in Mathematics, 191, 225-275. https://doi.org/10.1016/j.aim.2004.03.007
[5]	Zhao, M. and Li, H. (2021) A Pair of Dual Hopf Algebras on Permutations. AIMS Mathematics, 6, 5106-5123. https://doi.org/10.3934/math.2021302
[6]	Aval, J.C., Bergeron, N. and Machacek, J. (2020) New Invariants for Permutations, Orders and Graphs. Advances in Applied Mathematics, 121, Article ID: 102080. https://doi.org/10.1016/j.aam.2020.102080
[7]	Dong, J. (2023) Hopf Algebras on Simple Graphs. Shandong Normal University, Jinan.
[8]	Huang, X. and Huang, Q. (2017) On Regular Graphs with Four Distinct Eigenvalues. Linear Algebra and Its Applications, 512, 219-233. https://doi.org/10.1016/j.laa.2016.09.043
[9]	Cardoso, D. and Rojo, O. (2017) Edge Perturbations on Graphs with Cluster: Adjacency, Laplacian and Signless Laplacian Eigenvalues. Linear Algebra and Its Applications, 512, 113-128. https://doi.org/10.1016/j.laa.2016.09.031
[10]	Constantin, P. (1991) Combinatorial Matrix Theory. Cambridge University Press, Cambridge.
[11]	Borrero, J.S., Gillen, C. and Prokopyev, O.A. (2016) A Simple Technique to Improve Linearized Reformulations of Fractical (Hyperbolic) 0-1 Programming Problems. Operations Research Letters, 44, 479-486. https://doi.org/10.1016/j.orl.2016.03.015
[12]	Punnen, A.P., Sripratak, P. and Karapetyan, D. (2015) The Bipartite Unconstrained 0-1 Quadratic Programming Problem: Polynomially Solvable Cases. Discrete Applied Mathematics, 193, 1-10. https://doi.org/10.1016/j.dam.2015.04.004
[13]	Soylu, B. (2015) Heuristic Approaches for Biobjective Mixed 0-1 Integer Linear Programming Problems. European Journal of Operational Research, 245, 690-703. https://doi.org/10.1016/j.ejor.2015.04.010
[14]	Zhang, S., Lin, P., Wang, K. and Wu, G. (2016) Construction of Binary Shift Dual Codes. Journal of Jiangxi University of Science and Technology, 37, 74-79. (In Chinese) https://doi.org/10.13265/j.cnki.jxlgdxxb.2016.01.014
[15]	Dong, J. and Li, H. (2023) A Hopf Algebra of Labeled Simple Graphs. Open Journal of Applied Sciences, 13, 120-135. https://doi.org/10.4236/ojapps.2023.131011