Actuator Fault Diagnosis for a Class of One-Dimensional Nonlinear Heat Equations via Backstepping Method

Lei Chen

School of Mathematics and Statistics, Shandong Normal University, Jinan, China.

DOI: 10.4236/ojapps.2023.138099                

Abstract

In this paper, an actuator fault diagnosis scheme based on the backstepping method is proposed for a class of nonlinear heat equations. The fault diagnosis scheme includes fault detection, fault estimation and time to failure (TTF) prediction. Firstly, we achieve fault detection by comparing the detection residual with a predetermined threshold, where the detection residual is defined as the difference between the observer output and the system measurement output. Then, we estimate the fault function through the fault parameter update law and calculate the TTF using only limited measurements. Finally, the numerical simulation is performed on a nonlinear heat equation to verify the effectiveness of the proposed fault diagnosis scheme.

Keywords

Fault Detection, Fault Estimation, Time to Failure (TTF), Nonlinear Heat Equations, Backstepping

1. Introduction

As the production and life of mechanization and intelligence, the partial differential equation (PDE) control systems are widely used in the chemical industry [1] [2] , transportation systems [3] , aerospace [4] and other fields [5] [6] [7] . With the expansion of system scale and the increase of system complexity, once the system fails, it will cause incalculable losses and seriously threaten the safety of people’s lives and property. Therefore, how to effectively improve the security and stability of the system is particularly important. The design of the fault diagnosis (FD) scheme is the key to improving the system’s stability and reliability [8] - [12] .

Considering the characteristic of the system state changing with time and space, the ordinary differential equation (ODE) model based on the lumped parameter representation of the distributed parameter system (DPS) is not suitable for simulating the dynamic behavior of the actual system [13] - [18] . On the contrary, the dynamic behavior of DPS is more suitable to be described by PDE. The existing fault diagnosis method of DPS is mainly divided into two categories. The first kind is to approximate DPS using finite dimensional ODE, which is known as the early lumped design. However, due to the model reduction in the modeling process, this diagnosis scheme may produce false alarms and missed alarms [19] [20] . Feng, Li and Yang provided estimates for the parabolic DPS distributed fault problem [21] through the tedious early lumped design. Another kind of fault diagnosis is to design directly on the basis of the original PDE system, which is called the later lumped design. In recent years, significant achievements have been made in fault diagnosis based on DPS. Ghantasala and El-Farra studied the actuator fault diagnosis of a parabolic PDE system [22] . Ferdowsi et al. designed a fault detection observer using the PDE direct representation of the original system [23] . Similarly, the fault detection method by designing observers in linear DPS systems has been widely used [24] [25] [26] . Dey, Perez and Moura studied the problem of robust fault detection in a linear parabolic system with uncertainties [27] . Cai, Ferdowsi and Sarangapani proposed a fault parameter update law and the display expression of TTF [28] . Feng et al. [29] utilized the backstepping method [30] [31] to achieve the distribution anomaly localization of linear parabolic DPS through a limited number of measurements. Kwan et al. [32] approximated the fault by building a stochastic model and proposed the remaining useful life (RUL) or failure time (TTF).

The existing research results mentioned above are mainly aimed at linear systems, but most practical systems are complex nonlinear systems. Compared with the research results of linear DPSs fault diagnosis, the research results in the field of nonlinear DPSs are relatively insufficient. Ferdowsi, Cai and Jagannathan realized the fault diagnosis of nonlinear DPS by making reasonable assumptions about the nonlinear terms in the system [33] .

Inspired by this, we propose a new backstepping-based fault detection, fault estimation and TTF prediction scheme for a class of nonlinear heat equations. Based on the effectiveness of the backstepping method in observer design [30] [31] [34] [35] [36] , we apply this method to observer design as well. Firstly, we design an observer to estimate the state and output of the system in the absence of a system fault. The estimated system output is compared with the measured output to obtain the detection residual. The detection residual is bounded when there is a bounded uncertainty or disturbance in the system. In particular, the detection residual converges to zero exponentially when the nonlinear term satisfies some conditions and there is no disturbance or uncertainty in the system. However, once a system fault occurs, the actual measured output will deviate from the estimated output, resulting in an increase in the residual. If the detection residual of the system exceeds the predefined threshold, we determine that the system has detected a fault. Once a fault is detected in the system, we add an adaptive term estimation term to the original observer to learn the dynamic behavior of the fault. Next, we give the estimation of the fault by the parameter update law and the error of the fault estimation is bounded. Finally, with only a limited number of measurements, we propose an explicit expression for the estimation of TTF.

Compared with the traditional early lumped design that utilizes finite dimensional ODE to approximate DPS, the fault diagnosis scheme proposed in this paper is directly based on DPS modeling, avoiding false alarms and missed alarms in the fault diagnosis process caused by model reduction during the modeling process. In addition, we use the Lyapunov function method instead of the operator theory, which effectively reduces the amount of computation and is more conducive to the application of practical engineering production.

In summary, this paper proposes a backstepping-based nonlinear heat equations fault diagnosis scheme. The main contributions of this paper are as follows:

1) A nonlinear heat equation fault diagnosis scheme is proposed by making rational assumptions about the nonlinear term;

2) The fault parameters are estimated through the designed fault parameter updating law;

3) Once a fault is detected in the system, an adaptive term is added to the existing observer to provide an online estimate of the TTF of the system.

The remaining sections of this paper are arranged as follows. We introduce the relevant preparatory knowledge and give a brief description of the system in Section 2. In Section 3, fault detection, fault estimation and TTF prediction schemes are proposed. To verify the effectiveness of the proposed scheme, we conduct numerical simulations in Section 4. In the end, we briefly conclude this paper in Section 5.

2. Preliminary Knowledge and Problem Statement

In this paper, the mathematical symbols we used are standard. $\left|\nu \right|$ is the absolute value of $\nu$ for any $\nu \in ℝ$ , where $ℝ$ represents the set of all real numbers. The function $\nu \left(s\right)$ is square integrable on the Hilbert space ${\mathcal{L}}^2\left(\left[\mathrm{0,1}\right]\right)={\mathcal{L}}^2\left(\left[\mathrm{0,1}\right]\mathrm{<mo>\; ;\; </mo>}ℝ\right)$ with the ${\mathcal{L}}^2$ norm

${\Vert \nu (\cdot )\Vert }_2=\sqrt{{\displaystyle {\int }_0^1}{\nu }^2\left(s\right)\text{d}s}\mathrm{.}$

At the beginning, we will briefly review several common inequalities that may be used in this paper.

· Young’s inequality:

$ab\le \frac{\eta }{2}{a}^2+\frac{1}{2\eta }{b}^2,ab\ge -\frac{\eta }{2}{a}^2-\frac{1}{2\eta }{b}^2,$

where $a,b,\eta \in ℝ$ and $\eta >0$ .

· Cauchy-Schwarz inequality:

${\displaystyle {\int }_0^1}{\vartheta }_1\left(s\right){\vartheta }_2\left(s\right)\text{d}s\le {\Vert {\vartheta }_1\left(s\right)\Vert }_2{\Vert {\vartheta }_2\left(s\right)\Vert }_2\mathrm{,}$

where ${\vartheta }_1\left(s\right)\mathrm{,}{\vartheta }_2\left(s\right)\in {\mathcal{L}}^2\left(\left[\mathrm{0,1}\right]\right)$ .

· Agmon’s inequality:

$\underset{s\in \left[\mathrm{0,1}\right]}{\max }{\left|\upsilon \left(s\right)\right|}^2\le {\upsilon }^2\left(0\right)+2{\Vert \upsilon \Vert }_2{\Vert {\upsilon }_s\Vert }_2\mathrm{,}$

$\underset{s\in \left[\mathrm{0,1}\right]}{\max }{\left|\upsilon \left(s\right)\right|}^2\le {\upsilon }^2\left(1\right)+2{\Vert \upsilon \Vert }_2{\Vert {\upsilon }_s\Vert }_2\mathrm{,}$

where $\upsilon \left(s\right)\in {\mathcal{L}}^2\left(\left[\mathrm{0,1}\right]\right)$ .

In this paper, we consider a class of one-dimensional nonlinear heat equations that can be described by

$\{\begin{array}{ll}{\nu }_t\left(s,t\right)={\nu }_{ss}\left(s,t\right)+\varphi \left(\nu ,s\right)+\psi \left(s,t\right),\hfill & s\in \left[0,1\right],t>0,\hfill \\ y=\nu \left(0,t\right),\hfill & t\ge 0\hfill \end{array}$ (2.1)

with the boundary conditions

$\{\begin{array}{ll}{\nu }_s\left(0,t\right)=0,\hfill & t\ge 0,\hfill \\ \nu \left(1,t\right)=\theta U\left(t\right),\hfill & t\ge 0,\hfill \end{array}$ (2.2)

and initial condition

$\nu \left(s\mathrm{,0}\right)={\nu }_0\left(s\right)\mathrm{,}s\in \left[\mathrm{0,1}\right]\mathrm{,}$ (2.3)

where $\nu \left(\cdot \mathrm{,}t\right)\in {\mathcal{L}}^2\left(\left[\mathrm{0,1}\right]\right)$ is the state variable; $\varphi \left(\nu \mathrm{,}s\right)\in {\mathcal{L}}^2\left(\left[\mathrm{0,1}\right]\right)$ is Lipschitz continuous function; $\psi \left(s\mathrm{,}t\right)$ indicates the system uncertainty or disturbance; $\theta$ represents an actuator fault which is bounded by ${\theta }_{\min }\le \left|\theta \right|\le {\theta }_{\max }$ ; $U\left(t\right)$ is the boundary control input. y represents the output of the system, which can be obtained by measurement.

Assumption 2.1. For the nonlinear function $\varphi \left(\nu \mathrm{,}s\right)$ , we make the following assumptions:

· $\varphi \left(\nu \mathrm{,}s\right)$ is Lipschitz continuous with respect to $\nu$ and $\nu \left(s\right)\in {\mathcal{L}}^2\left(\left[\mathrm{0,1}\right]\right)$ , $s\in \left[\mathrm{0,1}\right]$ , $t\ge 0$ .

· $\varphi \left(\nu \mathrm{,}s\right)$ satisfies

$\varphi \left(\nu +\Delta \nu \mathrm{,}s\right)-\varphi \left(\nu \mathrm{,}s\right)=\frac{\partial \varphi \left(\nu \mathrm{,}s\right)}{\partial \nu }\Delta \nu +{\epsilon }_{\varphi }\left(s\mathrm{,}t\right)\mathrm{,}$ (2.4)

where $\Delta \nu$ denotes a small variation of $\nu$ , ${\epsilon }_{\varphi }\left(s\mathrm{,}t\right)$ is the approximation error satisfying ${\Vert {\epsilon }_{\varphi }\Vert }_{\mathrm{2,}n}\le {\bar{\epsilon }}_{\varphi }$ and ${\bar{\epsilon }}_{\varphi }$ is a positive constant.

In particular, when the approximation error ${\epsilon }_{\varphi }\left(s\mathrm{,}t\right)=0$ , for the nonlinear function $\varphi \left(\nu \mathrm{,}s\right)$ we can get

$\varphi \left(\nu +\Delta \nu \mathrm{,}s\right)-\varphi \left(\nu \mathrm{,}s\right)=\frac{\partial \varphi \left(\nu \mathrm{,}s\right)}{\partial \nu }\Delta \nu \mathrm{.}$ (2.5)

Assumption 2.2. The distributed uncertainty or disturbance $\psi \left(s\mathrm{,}t\right)$ in the system is bounded, i.e.

${\Vert \psi \left(\cdot \mathrm{,}t\right)\Vert }_2\le \bar{\psi }\mathrm{,}$

where $\bar{\psi }>0$ is a known constant.

Assumption 2.3. In this article, we assume that there is a stable control such that the system under the condition of the healthy state is bounded.

3. Fault Diagnosis Scheme

In this section, we first consider the case where there is no disturbance or uncertainty in the system, i.e. $\psi \left(s\mathrm{,}t\right)=0$ . On this basis, an observer is designed in the healthy state of the system. The estimated output of the system obtained through the observer will converge to the actual measured value under the healthy condition when there is no disturbance or uncertainty in the system through selecting the observer gain reasonably. We define the detection residual as the difference between the estimated output and the measured output. However, once a system fault occurs, the actual measured output will deviate from the estimated output given by the observer, resulting in an increase in the residual error. Thus, we can compare the detection residual with the predefined threshold to complete the fault detection.

Remark 3.1. In this paper, we consider that the required measurement results are noise-free. Moreover, the detection residuals are bounded rather than converging to zero due to bounded uncertainties and disturbances in the system.

3.1. Fault Detection Observer

First of all, we design an observer for system (2.1) as follows

$\{\begin{array}{ll}{\hat{\nu }}_t\left(s,t\right)={\hat{\nu }}_{ss}\left(s,t\right)+\varphi \left(\hat{\nu },s\right)+p_1\left(s\right)\left(\nu \left(0,t\right)-\hat{\nu }\left(0,t\right)\right),\hfill & s\in \left[0,1\right],t>0,\hfill \\ {\hat{\nu }}_s\left(0,t\right)=p_{10}\left(\nu \left(0,t\right)-\hat{\nu }\left(0,t\right)\right),\hfill & t\ge 0,\hfill \\ \hat{\nu }\left(1,t\right)=U\left(t\right),\hfill & t\ge 0,\hfill \end{array}$ (3.1)

where $\hat{\nu }\left(s\mathrm{,}t\right)$ represents the estimated system state, $\hat{y}\left(t\right)=\hat{\nu }\left(\mathrm{0,}t\right)$ is estimated output of the system, $p_1\left(s\right)$ and $p_{10}$ denote the observer gains that we need to determine in the following. The detection residual $r\left(t\right)$ is defined by

$r\left(t\right)=\nu \left(\mathrm{0,}t\right)-\hat{\nu }\left(\mathrm{0,}t\right)\mathrm{,}t\ge 0.$ (3.2)

Next, we define the system state residual or system state estimation error as $\tilde{\nu }\left(s\mathrm{,}t\right)=\nu \left(s\mathrm{,}t\right)-\hat{\nu }\left(s\mathrm{,}t\right)\mathrm{,}$ from which the observer performance can be analyzed. If the state residual is used for fault detection, the availability of the entire state of the system is required, which is relatively difficult. However, that is unnecessary because the PDE in (2.1) transfers the influence of faults in the system to the output. Therefore, we can complete the fault detection with the aid of the output residual error $r\left(t\right)$ .

When there is no fault in the system, i.e. $\theta =1$ , the state residual dynamical system can be expressed as

$\{\begin{array}{ll}{\tilde{\nu }}_t\left(s,t\right)={\tilde{\nu }}_{ss}\left(s,t\right)+\varphi \left(\nu ,s\right)-\varphi \left(\hat{\nu },s\right)+\psi \left(s,t\right)-p_1\left(s\right)\tilde{\nu }\left(0,t\right),\hfill & s\in \left[0,1\right],t>0,\hfill \\ {\tilde{\nu }}_s\left(0,t\right)=-p_{10}\tilde{\nu }\left(0,t\right),\hfill & t\ge 0,\hfill \\ \tilde{\nu }\left(1,t\right)=0,\hfill & t\ge 0,\hfill \end{array}$ (3.3)

combined with (2.1), (2.2) and (3.1).

From Assumption 2.2, we can get $A\left(s\mathrm{,}t\right)={\frac{\partial \varphi \left(\nu \mathrm{,}s\right)}{\partial \nu }|}_{\nu =\hat{\nu }}$ through $\varphi \left(\nu ,s\right)-\varphi \left(\hat{\nu },s\right)={\frac{\partial \varphi \left(\nu ,s\right)}{\partial \nu }|}_{\nu =\hat{\nu }}\tilde{\nu }\left(s,t\right)+{\epsilon }_{\varphi }\left(s,t\right)$ . So we can write the error system (3.3) as

$\{\begin{array}{ll}{\tilde{\nu }}_t\left(s,t\right)={\tilde{\nu }}_{ss}\left(s,t\right)+A\left(s,t\right)\tilde{\nu }\left(s,t\right)+{\epsilon }_{\varphi }\left(s,t\right)+\psi \left(s,t\right)-p_1\left(s\right)\tilde{\nu }\left(0,t\right),\hfill & s\in \left[0,1\right],t>0,\hfill \\ {\tilde{\nu }}_s\left(0,t\right)=-p_{10}\tilde{\nu }\left(0,t\right),\hfill & t\ge 0,\hfill \\ \tilde{\nu }\left(1,t\right)=0,\hfill & t\ge 0.\hfill \end{array}$ (3.4)

It should be noted that when the term $A\left(s,t\right)\tilde{\nu }\left(s,t\right)$ in (3.4) is sufficiently large, the system will become unstable.

For the above problem, we can eliminate the influence of $A\left(s,t\right)\tilde{\nu }\left(s,t\right)$ through the Volterra integral transformation [34] , and the observer gain can be obtained through the following Lemma 3.1.

Lemma 3.1. ( [34] ) With the help of the following integral transformation

$\tilde{\nu }\left(s\mathrm{,}t\right)=\xi \left(s\mathrm{,}t\right)-{\displaystyle {\int }_0^s}\Gamma \left(s\mathrm{,}\sigma \mathrm{,}t\right)\xi \left(\sigma \mathrm{,}t\right)\text{d}\sigma \mathrm{,}$ (3.5)

where $\Gamma \left(s\mathrm{,}\sigma \mathrm{,}t\right)$ is the unique solution of (3.7), we can convert the original error system (3.4) to the target $\xi$ system

$\{\begin{array}{ll}{\xi }_t\left(s,t\right)={\xi }_{ss}\left(s,t\right)-d\xi \left(s,t\right)+{\psi }_M\left(s,t\right)+{\epsilon }_{\varphi }{}_M\left(s,t\right),\hfill & s\in \left[0,1\right],t>0,\hfill \\ {\xi }_s\left(0,t\right)=0,\hfill & t\ge 0,\hfill \\ \xi \left(1,t\right)=0,\hfill & t\ge 0,\hfill \end{array}$ (3.6)

where d is a positive constant; $\psi \left(s\mathrm{,}t\right)$ and ${\epsilon }_{\varphi }\left(s\mathrm{,}t\right)$ satisfy

$\psi \left(s\mathrm{,}t\right)={\psi }_M\left(s\mathrm{,}t\right)-{\displaystyle {\int }_0^s}\Gamma \left(s,\sigma ,t\right){\psi }_M\left(\sigma ,t\right)\text{d}\sigma ,$

${\epsilon }_{\varphi }\left(s\mathrm{,}t\right)={\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)-{\displaystyle {\int }_0^s}\Gamma \left(s,\sigma ,t\right){\epsilon }_{\varphi }{}_M\left(\sigma ,t\right)\text{d}\sigma .$

Lemma 3.2. ( [34] ) The gain kernel function $\Gamma \left(s\mathrm{,}\sigma \mathrm{,}t\right)$ satisfies

$\{\begin{array}{l}\frac{\partial \Gamma \left(s,\sigma ,t\right)}{\partial t}=\left[A\left(s,t\right)+d\right]\Gamma \left(s,\sigma ,t\right)+\frac{{\partial }^2\Gamma \left(s,\sigma ,t\right)}{\partial {\sigma }^2}-\frac{{\partial }^2\Gamma \left(s,\sigma ,t\right)}{\partial s^2},\\ \Gamma \left(1,\sigma ,t\right)=0,\\ \Gamma \left(s,s,t\right)=\frac{s-1}{2}\left[A\left(s,t\right)+d\right],\end{array}$ (3.7)

where d is a positive constant and $A\left(s,t\right)={\frac{\partial \varphi \left(\nu ,s\right)}{\partial \nu }|}_{\nu =\hat{\nu }}$ . The observer gains are given by

$\{\begin{array}{l}{p}_1\left(s,t\right)=\frac{\partial \Gamma \left(s,0,t\right)}{\partial \sigma },\\ p_{10}\left(t\right)=\Gamma \left(0,0,t\right).\end{array}$ (3.8)

Lemma 3.3. ( [34] ) The kernel function $M\left(s\mathrm{,}\eta \mathrm{,}t\right)$ of the inverse transformation of $\Gamma \left(s\mathrm{,}x\mathrm{,}t\right)$ satisfies

$\xi \left(s,t\right)=\tilde{\nu }\left(s,t\right)+{\displaystyle {\int }_0^s}M\left(s,\eta ,t\right)\tilde{\nu }\left(\eta ,t\right)\text{d}\eta .$

Remark 3.2. Through the Lemma 3.3, we can get ${\psi }_M$ and ${\epsilon }_{\varphi }{}_M$ as follows:

${\psi }_M\left(s\mathrm{,}t\right)=\psi \left(s\mathrm{,}t\right)+{\displaystyle {\int }_0^s}M\left(s\mathrm{,}\eta \mathrm{,}t\right)\psi \left(\eta \mathrm{,}t\right)\text{d}\eta \mathrm{,}$

${\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)={\epsilon }_{\varphi }\left(s\mathrm{,}t\right)+{\displaystyle {\int }_0^s}M\left(s\mathrm{,}\eta \mathrm{,}t\right){\epsilon }_{\varphi }\left(\eta \mathrm{,}t\right)\text{d}\eta \mathrm{.}$

With the aid of the trigonometric inequality, we have estimations of ${\psi }_M\left(s\mathrm{,}t\right)$ and ${\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)$ as

${\Vert {\psi }_M\left(s\mathrm{,}t\right)\Vert }_2\le {\Vert \psi \left(s\mathrm{,}t\right)\Vert }_2+{\Vert {\displaystyle {\int }_0^s}M\left(s\mathrm{,}\eta \mathrm{,}t\right)\psi \left(\eta \mathrm{,}t\right)\text{d}\eta \Vert }_2\le \left(\bar{M}+1\right)\bar{\psi }\mathrm{,}$

${\Vert {\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)\Vert }_2\le {\Vert {\epsilon }_{\varphi }\left(s\mathrm{,}t\right)\Vert }_2+{\Vert {\displaystyle {\int }_0^s}M\left(s\mathrm{,}\eta \mathrm{,}t\right){\epsilon }_{\varphi }\left(\eta \mathrm{,}t\right)\text{d}\eta \Vert }_2\le \left(\bar{M}+1\right){\bar{\epsilon }}_{\varphi }\mathrm{,}$

where $\bar{M}=\underset{0\le s\le 1}{\max }{\Vert M\left(s\mathrm{,}\eta \mathrm{,}t\right)\Vert }_2$ , $\bar{\psi }=\underset{0\le s\le 1}{\max }{\Vert \psi \left(s\mathrm{,}t\right)\Vert }_2$ , ${\bar{\epsilon }}_{\varphi }=\underset{0\le s\le 1}{\max }{\Vert {\epsilon }_{\varphi }\left(s\mathrm{,}t\right)\Vert }_2$ .

Lemma 3.4. ( [37] ) For real functions $G\left(t\right)$ and $f\left(t\right)$ , if $\stackrel{\dot{}}{G}\left(t\right)\le -\alpha G\left(t\right)+f\left(t\right)\mathrm{,}\forall t\ge \mathrm{0,}$ then $G\left(t\right)\le {\text{e}}^{-\alpha t}G\left(0\right)+{\displaystyle {\int }_0^t}{\text{e}}^{-\alpha \left(t-\eta \right)}f\left(\eta \right)\text{d}\eta ,\forall t\ge 0,$ where $\alpha >0$ is a constant.

Through the following two theorems, we respectively provide the stability proof of the detection residual under the condition of healthy operation of the system and the criteria for the fault detection.

Theorem 3.1. For the error dynamics system (3.6), we have the following stability analysis:

1) the error system $\xi$ is bounded when there is no disturbance or uncertainty, i.e. ${\psi }_M\left(s\mathrm{,}t\right)=0$ . In particular, the error system $\xi$ converges exponentially to zero when the nonlinear term $\varphi \left(\upsilon \mathrm{,}s\right)$ satisfies (2.5), i.e. ${\epsilon }_{\varphi }\left(s\mathrm{,}t\right)=0$ ;

2) the error system $\xi$ is bounded when there is a disturbance or uncertainty in the system, i.e. ${\psi }_M\left(s\mathrm{,}t\right)\ne 0$ .

The bound of $\xi \left(s\mathrm{,}t\right)$ can be written as ${\Vert \xi \left(s\mathrm{,}t\right)\Vert }_{\infty }\le {\xi }_m\left(t\right)\mathrm{,}$ where

$\{\begin{array}{l}{\xi }_m\left(t\right)=\sqrt{2{\text{e}}^{-2\left(d-1\right)t}{W}_1\left(0\right)+\frac{1}{\alpha \left(d-1\right)}{\left(\bar{M}+1\right)}^2{D}^2},\\ W_1\left(0\right)=\frac{1}{2}\left({\Vert {\xi }_0\Vert }_2^2+{\Vert {\xi }_{s0}\Vert }_2^2\right)\end{array}$ (3.9)

with $0\le \alpha \le 1$ and

$D=\{\begin{array}{ll}{\bar{\epsilon }}_{\varphi },\hfill & {\psi }_M\left(s,t\right)=0,\hfill \\ \bar{\psi }+{\bar{\epsilon }}_{\varphi },\hfill & {\psi }_M\left(s,t\right)\ne 0.\hfill \end{array}$ (3.10)

Proof. First of all, we choose the following Lyapunov function for system (3.6),

$W_1\left(t\right)=\frac{1}{2}{\displaystyle {\int }_0^1}{\xi }^2\left(s\mathrm{,}t\right)\text{d}s+\frac{1}{2}{\displaystyle {\int }_0^1}{\xi }_s^2\left(s\mathrm{,}t\right)\text{d}s\mathrm{.}$ (3.11)

Then, taking the derivative of $W_1\left(t\right)$ yields

$\begin{array}{c}\stackrel{\dot{}}{W}\left(t\right)=-\left(1+d\right){\displaystyle {\int }_0^1}{\xi }_s^2\left(s\mathrm{,}t\right)\text{d}s-d{\displaystyle {\int }_0^1}{\xi }^2\left(s\mathrm{,}t\right)\text{d}s-{\displaystyle {\int }_0^1}{\xi }_{ss}^2\left(s\mathrm{,}t\right)\text{d}s\\ +{\displaystyle {\int }_0^1}\left({\psi }_M\left(s\mathrm{,}t\right)+{\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)\right)\xi \left(s\mathrm{,}t\right)\text{d}s-{\displaystyle {\int }_0^1}\left({\psi }_M\left(s\mathrm{,}t\right)+{\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)\right){\xi }_{ss}\left(s\mathrm{,}t\right)\text{d}s\end{array}$ (3.12)

through the integration by parts and the error dynamic system (3.6).

We can see that the fourth and fifth terms in the right of (3.12) both contain ${\psi }_M+{\epsilon }_{\varphi }{}_M$ which is bounded. Considering that ${\psi }_M\left(s\mathrm{,}t\right)$ is not always zero, we first consider the existence of the uncertainty and disturbance in the system, i.e. ${\psi }_M\left(s\mathrm{,}t\right)\ne 0$ .

With the aid of the Cauchy-Schwarz inequality and Young’s inequality, we can get an upper bound of the fourth term in the right of (3.12),

$\begin{array}{l}{\displaystyle {\int }_0^1}\left({\psi }_M\left(s\mathrm{,}t\right)+{\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)\right)\xi \left(s\mathrm{,}t\right)\text{d}s\\ ={\displaystyle {\int }_0^1}{\psi }_M\left(s\mathrm{,}t\right)\xi \left(s\mathrm{,}t\right)\text{d}s+{\displaystyle {\int }_0^1}{\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)\xi \left(s\mathrm{,}t\right)\text{d}s\\ \le {\left({\displaystyle {\int }_0^1}{\psi }_M^2\left(s\mathrm{,}t\right)\text{d}s\right)}^{\frac{1}{2}}{\left({\displaystyle {\int }_0^1}{\xi }^2\left(s\mathrm{,}t\right)\text{d}s\right)}^{\frac{1}{2}}+{\left({\displaystyle {\int }_0^1}{\epsilon }_{\varphi }{}_M^2\left(s\mathrm{,}t\right)\text{d}s\right)}^{\frac{1}{2}}{\left({\displaystyle {\int }_0^1}{\xi }^2\left(s\mathrm{,}t\right)\text{d}s\right)}^{\frac{1}{2}}\\ ={\Vert {\psi }_M\left(s\mathrm{,}t\right)\Vert }_2{\Vert \xi \left(s\mathrm{,}t\right)\Vert }_2+{\Vert {\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)\Vert }_2{\Vert \xi \left(s\mathrm{,}t\right)\Vert }_2\\ \le \frac{1}{2\alpha }\left[{\Vert {\psi }_M\left(s\mathrm{,}t\right)\Vert }_2^2+{\Vert {\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)\Vert }_2^2\right]+\alpha {\Vert \xi \left(s\mathrm{,}t\right)\Vert }_2^2\mathrm{,}\end{array}$ (3.13)

where $\alpha$ is a positive constant. Using the same method for the fifth item in the right of (3.12), we can get

$\begin{array}{l}{\displaystyle {\int }_0^1}\left({\psi }_M\left(s\mathrm{,}t\right)+{\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)\right){\xi }_{ss}\left(s\mathrm{,}t\right)\text{d}s\\ \le \frac{1}{2\alpha }\left[{\Vert {\psi }_M\left(s\mathrm{,}t\right)\Vert }_2^2+{\Vert {\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)\Vert }_2^2\right]+\alpha {\Vert {\xi }_{ss}\left(s\mathrm{,}t\right)\Vert }_2^2\mathrm{.}\end{array}$ (3.14)

By substituting (3.13) and (3.14) into (3.12), the upper bound of ${\stackrel{\dot{}}{W}}_1\left(t\right)$ can be expressed as

$\begin{array}{c}{\stackrel{\dot{}}{W}}_1\left(t\right)\le -\left(1+d\right){\Vert {\xi }_s\left(s\mathrm{,}t\right)\Vert }_2^2+\left(\alpha -d\right){\Vert \xi \left(s\mathrm{,}t\right)\Vert }_2^2+\left(\alpha -1\right){\Vert {\xi }_{ss}\left(s\mathrm{,}t\right)\Vert }_2^2\\ +\frac{1}{\alpha }\left[{\Vert {\psi }_M\left(s\mathrm{,}t\right)\Vert }_2^2+{\Vert {\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)\Vert }_2^2\right]\mathrm{.}\end{array}$ (3.15)

Let $\alpha$ satisfy $0<\alpha \le 1$ , then the upper bound of ${\stackrel{\dot{}}{W}}_1\left(t\right)$ is further represented as

$\begin{array}{c}{\stackrel{\dot{}}{W}}_1\left(t\right)\le -\left(1+d\right){\Vert {\xi }_s\left(s\mathrm{,}t\right)\Vert }_2^2+\left(1-d\right){\Vert \xi \left(s\mathrm{,}t\right)\Vert }_2^2+\frac{1}{\alpha }\left[{\Vert {\psi }_M\left(s\mathrm{,}t\right)\Vert }_2^2+{\Vert {\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)\Vert }_2^2\right]\\ \le \left(1-d\right){\Vert {\xi }_s\left(s\mathrm{,}t\right)\Vert }_2^2+\left(1-d\right){\Vert \xi \left(s\mathrm{,}t\right)\Vert }_2^2+\frac{1}{\alpha }\left[{\Vert {\psi }_M\left(s\mathrm{,}t\right)\Vert }_2^2+{\Vert {\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)\Vert }_2^2\right]\\ \le 2\left(1-d\right)W_1\mathrm{<mo\; stretchy="false">\; (\; </mo>}t\mathrm{<mo\; stretchy="false">\; )\; </mo>}+\frac{1}{\alpha }\left[{\Vert {\psi }_M\left(s\mathrm{,}t\right)\Vert }_2^2+{\Vert {\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)\Vert }_2^2\right]\mathrm{.}\end{array}$ (3.16)

Considering $d>1$ and combining the Remark 3.1 and Lemma 3.4, we get

$W_1\left(t\right)\le {\text{e}}^{-2\left(d-1\right)t}{W}_1\left(0\right)+\frac{1}{2\alpha \left(d-1\right)}{\left(\bar{M}+1\right)}^2{D}^2,$ (3.17)

where $D=\bar{\psi }+{\bar{\epsilon }}_{\varphi }$ .

Moreover, for the state of system (3.6) we have

$\begin{array}{c}{\Vert \xi \left(s\mathrm{,}t\right)\Vert }_{\infty }^2\le 2{\Vert \xi \left(s\mathrm{,}t\right)\Vert }_2{\Vert {\xi }_s\left(s\mathrm{,}t\right)\Vert }_2\le {\Vert \xi \left(s\mathrm{,}t\right)\Vert }_2^2+{\Vert {\xi }_s\left(s\mathrm{,}t\right)\Vert }_2^2\\ =2W_1\left(t\right)\le 2{\text{e}}^{-2\left(d-1\right)t}{W}_1\left(0\right)+\frac{1}{\alpha \left(d-1\right)}{\left(\bar{M}+1\right)}^2{D}^2\end{array}$ (3.18)

by applying the Young’s inequality and Agmon’s inequality and combining (3.17).

Finally, combining (3.17) and (3.18), we can get the upper bound of $\xi$ ,

${\Vert \xi \left(s,t\right)\Vert }_{\infty }\le \sqrt{2{\text{e}}^{-2\left(d-1\right)t}{W}_1\left(0\right)+\frac{1}{\alpha \left(d-1\right)}{\left(\bar{M}+1\right)}^2{D}^2},$ (3.19)

where $D=\bar{\psi }+{\bar{\epsilon }}_{\varphi }$ . From this, it can be seen that (2) holds.

In the other case, when there is no uncertainty or disturbance in the system, i.e. ${\psi }_M\left(s\mathrm{,}t\right)=0$ , the same conclusion can be obtained, except that $D=\bar{\psi }+{\bar{\epsilon }}_{\varphi }$ is replaced by $D={\bar{\epsilon }}_{\varphi }$ in (3.19). In particular, when the nonlinear term in the system satisfies (2.1), i.e. ${\bar{\epsilon }}_{\varphi }=0$ , we can obtain that $\xi$ exponential converges to zero. Thus, (1) is also proved.

Remark 3.3. According to (3.2) and (3.5), $r\left(t\right)=\xi \left(\mathrm{0,}t\right)$ . Therefore, based on the above discussion, we can define the upper bound of the residual system obtained in the healthy state as the threshold $R\left(t\right)$ for fault detection, i.e.

$R\left(t\right)=\sqrt{2{\text{e}}^{-2\left(d-1\right)t}{W}_1\left(0\right)+\frac{1}{\alpha \left(d-1\right)}{\left(\bar{M}+1\right)}^2{D}^2}.$ (3.20)

Note that the predefined threshold is “time-varying” and the “time-varying” is determined by the exponential term ${\text{e}}^{-2\left(d-1\right)t}{W}_1\left(0\right)$ of (3.20).

Considering the above, we can give the fault detection logic as follows.

Theorem 3.2. Comparing the residual function $r\left(t\right)$ with the threshold function $R\left(t\right)$ , we present the following fault detection logic,

$\{\begin{array}{l}r\left(t\right)>R\left(t\right)\Rightarrow \text{faultattime}t\mathrm{,}\\ r\left(t\right)\le R\left(t\right)\Rightarrow \text{fault-freeattime}t.\end{array}$ (3.21)

3.2. Fault Estimation

Once the system is detected to have a fault, it is necessary to further estimate the fault parameters. For the better fault estimation, an adaptive estimation term $\hat{\theta }$ which is activated only when the fault in the system is detected is added to the original observer.

Thus, the original observer (3.1) becomes the following observer

$\{\begin{array}{ll}{\hat{\nu }}_t\left(s,t\right)={\hat{\nu }}_{ss}\left(s,t\right)+\varphi \left(\hat{\nu },s\right)+p_1\left(s\right)\left(\nu \left(0,t\right)-\hat{\nu }\left(0,t\right)\right),\hfill & s\in \left[0,1\right],t>0,\hfill \\ {\hat{\nu }}_s\left(0,t\right)=p_{10}\left(\nu \left(0,t\right)-\hat{\nu }\left(0,t\right)\right),\hfill & t\ge 0,\hfill \\ \hat{\nu }\left(1,t\right)=\hat{\theta }U\left(t\right),\hfill & t\ge 0,\hfill \\ \hat{y}\left(t\right)=\hat{\nu }\left(0,t\right),\hfill & t\ge 0.\hfill \end{array}$ (3.22)

By making the difference between the original system (2.1)-(2.3) and the newly constructed observer (3.22), a new system state residual dynamic system can be written as

$\{\begin{array}{ll}{\tilde{\nu }}_t\left(s,t\right)={\tilde{\nu }}_{ss}\left(s,t\right)+\varphi \left(\nu ,s\right)-\varphi \left(\hat{\nu },s\right)+\psi \left(s,t\right)-p_1\left(s\right)\tilde{\nu }\left(0,t\right),\hfill & s\in \left[0,1\right],t>0,\hfill \\ {\tilde{\nu }}_s\left(0,t\right)=-p_{10}\tilde{\nu }\left(0,t\right),\hfill & t\ge 0,\hfill \\ \tilde{\nu }\left(1,t\right)=\tilde{\theta }\left(t\right)U\left(t\right),\hfill & t\ge 0,\hfill \\ \tilde{y}\left(t\right)=\tilde{\nu }\left(0,t\right),\hfill & t\ge 0,\hfill \end{array}$ (3.23)

where $\tilde{\theta }\left(t\right)=\theta -\hat{\theta }$ is defined as the fault parameter estimation error.

Next, the performance of the newly designed observer is analyzed and the fault estimation is given by the following theorem.

Theorem 3.3. (Fault Estimation) Once the fault is detected in the system, the parameter update law,

$\stackrel{\dot{}}{\hat{\theta }}\left(t\right)=\gamma U\left(t\right)\left({\tilde{\nu }}_s\left(\mathrm{1,}t\right)+{\displaystyle {\int }_0^1}{M}_s\left(\mathrm{1,}\eta \mathrm{,}t\right)\tilde{\nu }\left(\eta \mathrm{,}t\right)\text{d}\eta \right)-\rho \hat{\theta }\left(t\right)$ (3.24)

will be activated to provide an estimate of the fault parameter, where $\gamma >0$ is the adaptation rate, $\rho >0$ , $d>\eta >0$ and $M\left(s\mathrm{,}\eta \mathrm{,}t\right)$ is given by Lemma 3.3.

Proof. The proof and derivation process of the above theorem is roughly similar to the previous Theorem 3.2. First of all, we apply the transformation (3.5) to the residual system (3.22) to get the new target $\xi$ system,

$\{\begin{array}{ll}{\xi }_t\left(s,t\right)={\xi }_{ss}\left(s,t\right)-d\xi \left(s,t\right)+{\psi }_M\left(s,t\right)+{\epsilon }_{\varphi }{}_M\left(s,t\right),\hfill & s\in \left[0,1\right],t>0,\hfill \\ {\xi }_s\left(0,t\right)=0,\hfill & t\ge 0,\hfill \\ \xi \left(1,t\right)=\tilde{\theta }\left(t\right)U\left(t\right),\hfill & t\ge 0,\hfill \end{array}$ (3.25)

where d is a positive constant and the specific expression of ${\psi }_M\left(s\mathrm{,}t\right)$ and ${\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)$ can be found in Remark 3.2. It is noted that the boundary condition $\xi \left(\mathrm{1,}t\right)$ is changed between the (3.6) and the original system (3.25).

Then, we choose the following Lyapunov function for system (3.25),

$W_2\left(t\right)=\frac{1}{2}{\displaystyle {\int }_0^1}{\xi }^2\left(s,t\right)\text{d}s+\frac{1}{2\gamma }{\tilde{\theta }}^2\left(t\right).$ (3.26)

Similarly, by taking the derivative of $W_2\left(t\right)$ , we can get

$\begin{array}{c}{\stackrel{\dot{}}{W}}_2\left(t\right)=-{\displaystyle {\int }_0^1}{\xi }_s^2\left(s,t\right)\text{d}s-d{\displaystyle {\int }_0^1}{\xi }^2\left(s,t\right)\text{d}s+{\displaystyle {\int }_0^1}\left({\psi }_M\left(s,t\right)+{\epsilon }_{\varphi }{}_M\left(s,t\right)\right)\xi \left(s,t\right)\text{d}s\\ +{\xi }_s\left(1,t\right)\tilde{\theta }\left(t\right)U\left(t\right)+\frac{\tilde{\theta }\left(t\right)\stackrel{\dot{}}{\tilde{\theta }}\left(t\right)}{\gamma }\end{array}$ (3.27)

through the integration by parts and (3.25). Note that $\stackrel{\dot{}}{\tilde{\theta }}\left(t\right)={\left(\theta -\hat{\theta }\left(t\right)\right)}^{\prime }=-\stackrel{\dot{}}{\hat{\theta }}\left(t\right)$ , so (3.27) can be further written as

$\begin{array}{c}{\stackrel{\dot{}}{W}}_2\left(t\right)=-{\displaystyle {\int }_0^1}{\xi }_s^2\left(s,t\right)\text{d}s-d{\displaystyle {\int }_0^1}{\xi }^2\left(s,t\right)\text{d}s+{\displaystyle {\int }_0^1}\left({\psi }_M\left(s,t\right)+{\epsilon }_{\varphi }{}_M\left(s,t\right)\right)\xi \left(s,t\right)\text{d}s\\ +{\xi }_s\left(1,t\right)\tilde{\theta }\left(t\right)U\left(t\right)-\frac{\tilde{\theta }\left(t\right)\stackrel{\dot{}}{\hat{\theta }}\left(t\right)}{\gamma }.\end{array}$ (3.28)

Then, we can take

$\stackrel{\dot{}}{\hat{\theta }}\left(t\right)=\gamma U\left(t\right){\xi }_s\left(\mathrm{1,}t\right)-\rho \hat{\theta }\left(t\right)$ (3.29)

to eliminate the effect of the positive term ${\xi }_s\left(\mathrm{1,}t\right)\tilde{\theta }\left(t\right)U\left(t\right)$ in the right of (3.28).

Substituting the above parameter updating law (3.29) into (3.28), we have

$\begin{array}{c}{\stackrel{\dot{}}{W}}_2\left(t\right)=-{\displaystyle {\int }_0^1}{\xi }_s^2\left(s\mathrm{,}t\right)\text{d}s-d{\displaystyle {\int }_0^1}{\xi }^2\left(s\mathrm{,}t\right)\text{d}s+{\displaystyle {\int }_0^1}\left({\psi }_M\left(s\mathrm{,}t\right)+{\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)\right)\xi \left(s\mathrm{,}t\right)\text{d}s\\ +\frac{\rho \tilde{\theta }\left(t\right)\hat{\theta }\left(t\right)}{\gamma }\mathrm{.}\end{array}$ (3.30)

Considering the boundedness of ${\psi }_M$ and ${\epsilon }_{\varphi }{}_M$ , we can adopt a similar procedure as the derivation of (3.13) for the third term in the right of (3.27) to get

$\begin{array}{l}{\displaystyle {\int }_0^1}\left({\psi }_M\left(s\mathrm{,}t\right)+{\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)\right)\xi \left(s\mathrm{,}t\right)\text{d}s\\ \le \frac{1}{2\eta }\left[{\Vert {\psi }_M\left(s\mathrm{,}t\right)\Vert }_2^2+{\Vert {\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)\Vert }_2^2\right]+\eta {\Vert \xi \left(s\mathrm{,}t\right)\Vert }_2^2\mathrm{,}\end{array}$ (3.31)

where $\eta$ is a positive constant. For the term with the fault parameter, we have

$\begin{array}{c}\tilde{\theta }\left(t\right)\hat{\theta }\left(t\right)=\tilde{\theta }\left(t\right)\left(\theta -\tilde{\theta }\left(t\right)\right)=-{\tilde{\theta }}^2\left(t\right)+\theta \tilde{\theta }\left(t\right)\\ \le -{\tilde{\theta }}^2\left(t\right)+\frac{{\tilde{\theta }}^2\left(t\right)+{\theta }^2}{2}=-\frac{{\tilde{\theta }}^2\left(t\right)-{\theta }^2}{2}.\end{array}$ (3.32)

Next, applying the Poincare inequality ${\displaystyle {\int }_0^1}{\xi }^2\left(s\mathrm{,}t\right)\text{d}s\le \frac{4}{{\pi }^2}{\displaystyle {\int }_0^1}{\xi }_s^2\left(s\mathrm{,}t\right)\text{d}s$ to the first term of the right of (3.30) and combining (3.31) and (3.32), we can obtain the upper bound of ${\stackrel{\dot{}}{W}}_2\left(t\right)$ as

$\begin{array}{c}{\stackrel{\dot{}}{W}}_2\left(t\right)\le -\left(d-\eta +\frac{{\pi }^2}{4}\right){\Vert \xi \left(s\mathrm{,}t\right)\Vert }_2^2-\frac{\rho }{2\gamma }{\tilde{\theta }}^2\left(t\right)+\frac{\rho {\theta }_{\max }^2}{2\gamma }\\ +\frac{1}{2\eta }\left[{\Vert {\psi }_M\left(s\mathrm{,}t\right)\Vert }_2^2+{\Vert {\epsilon }_{\varphi }{}_M\left(s\mathrm{,}t\right)\Vert }_2^2\right]\\ \le -AW\left(t\right)+B\mathrm{,}\end{array}$ (3.33)

where $A=\min \left\{2\left(d+\frac{{\pi }^2}{4}-\eta \right)\mathrm{,}\rho \right\}$ , $B=\frac{\rho {\theta }_{\max }^2}{2\gamma }+\frac{1}{2\eta }{\left(\bar{M}+1\right)}^2{D}^2$ , D is defined in (3.10) and $\bar{M}$ is defined in Remark 3.2.

Since $\rho >0$ and $d>\eta >0$ , (3.33) can be further written as

$W_2\left(t\right)\le {\text{e}}^{-At}{W}_2\left(0\right)+\frac{B}{A}.$ (3.34)

Thus, by combining the Lyapunov function $W_2\left(t\right)$ and $\gamma >0$ , we have

${\Vert \xi \left(s\mathrm{,}t\right)\Vert }_2\le \sqrt{2{\text{e}}^{-At}{W}_2\left(0\right)+\frac{2B}{A}}\mathrm{,}$ (3.35)

${\Vert \tilde{\theta }\left(t\right)\Vert }_2\le \sqrt{2\gamma {\text{e}}^{-At}{W}_2\left(0\right)+\frac{2\gamma B}{A}}\mathrm{,}$ (3.36)

where $A=\min \left\{2\left(d+\frac{{\pi }^2}{4}-\eta \right)\mathrm{,}\rho \right\}$ , $B=\frac{\rho {\theta }_{\max }^2}{2\gamma }+\frac{1}{2\eta }{\left(\bar{M}+1\right)}^2{D}^2$ , $D=\bar{\psi }+{\bar{\epsilon }}_{\varphi }$ .

$\square$

Remark 3.4. For the convergence and boundedness of ${\Vert \xi \left(\cdot \mathrm{,}t\right)\Vert }_2$ and ${\Vert \theta \left(t\right)\Vert }_2$ , we give the following explanations:

1) When no disturbance or uncertainty in the system, i.e. ${\psi }_M\left(s\mathrm{,}t\right)=0$ , and the nonlinear function $\varphi \left(\upsilon \mathrm{,}s\right)$ satisfies (2.5), i.e. ${\bar{\epsilon }}_{\varphi }=0$ , by adjusting parameter $\gamma$ , $\rho$ , it can be obtained that for $t\to \infty$ , ${\Vert \xi \left(\cdot \mathrm{,}t\right)\Vert }_2$ is asymptotically stable and ${\Vert \theta \left(t\right)\Vert }_2$ is bounded.

2) When there is a disturbance or uncertainty in the system, i.e. $\psi \left(s\mathrm{,}t\right)\ne 0$ , it can be seen from (3.35) and (3.36) that ${\Vert \xi \left(\cdot \mathrm{,}t\right)\Vert }_2$ and ${\Vert \theta \left(t\right)\Vert }_2$ are bounded.

3.3. Fault Prediction

The system can maintain normal operation for a short period of time after a fault occurs. However, the system cannot always maintain normal operation after a failure, so it is necessary to estimate how long the system can remain operational after a system fault is detected. In this section, we use the fault estimation parameter update law to propose the TTF scheme, which is used to predict the time that the system can still maintain normal operation after a fault has been detected. The TTF is defined as the difference between the current time t and the system failure time $t_f$ , i.e. $\text{TTF}\left(t\right)=t_f-t$ . In the following, we will give an explicit expression of TTF with the help of the parameter update law.

Theorem 3.4. (TTF Prediction) When a fault is detected in the system, we can obtain the TTF as

$\text{TTF}\left(t\right)=\frac{1}{\rho }\ln \frac{\rho \hat{\theta }\left(t\right)-\gamma U\left(t\right)Q\left(t\right)}{\rho {\theta }_f\left(t\right)-\gamma U\left(t\right)Q\left(t\right)},$ (3.37)

where ${\theta }_f$ is the falt limit for $\theta$ , $Q\left(t\right)={\tilde{\nu }}_s\left(\mathrm{1,}t\right)+{\displaystyle {\int }_0^1}{M}_s\left(\mathrm{1,}\eta \mathrm{,}t\right)\tilde{\nu }\left(\eta \mathrm{,}t\right)\text{d}\eta$ .

Proof. We consider ${\tilde{\upsilon }}_s\left(\mathrm{1,}t\right)$ and ${\displaystyle {\int }_0^1}\tilde{\upsilon }\left(\eta \mathrm{,}t\right)\text{d}\eta$ as known measurement signals that remain in the interval $\left[t\mathrm{,}{t}_f\right]$ . The following estimate of the fault parameters can be obtained by solving the parameter update law (3.24),

$\hat{\theta }\left(t_f\right)={\text{e}}^{-\rho \left(t_f-t\right)}\hat{\theta }\left(t\right)+{\displaystyle {\int }_t^{t_f}}{\text{e}}^{-\rho \left(t_f-x\right)}\gamma U\left(x\right)\left({\tilde{\nu }}_s\left(1,x\right)+{\displaystyle {\int }_0^1}{M}_s\left(1,\eta ,\tau \right)\tilde{\nu }\left(\eta ,\tau \right)\text{d}\eta \right)\text{d}x,t_f>t,$ (3.38)

where t is the current time after the system detected the fault and $t_f$ is the time of system breakdown or failure. We assume that the criterion for discriminating a system breakdown or failure is that the estimated fault parameter $\hat{\theta }\left(t\right)$ reaches an artificially imposed upper bound on the fault parameter.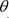

Next, we set $t_f$ as the time for the fault estimate $\hat{\theta }$ reaches the fault limit ${\theta }_f$ , from which we can obtain

$\begin{array}{l}\hat{\theta }\left(t_f\right)={\theta }_f\\ ={\text{e}}^{-\rho \left(t_f-t\right)}\hat{\theta }\left(t\right)+\frac{\gamma U\left(t\right)\left(1-{\text{e}}^{-\rho \left(t_f-t\right)}\right)\left({\tilde{\nu }}_s\left(1,t\right)+{\displaystyle {\int }_0^1}{M}_s\left(1,\eta ,t\right)\tilde{\nu }\left(\eta ,t\right)\text{d}\eta \right)}{\rho }\\ ={\text{e}}^{-\rho \left(t_f-t\right)}\hat{\theta }\left(t\right)+\frac{\gamma U\left(t\right)\left(1-{\text{e}}^{-\rho \left(t_f-t\right)}\right)Q\left(t\right)}{\rho },\end{array}$ (3.39)

where $Q\left(t\right)={\tilde{\nu }}_s\left(1,t\right)+{\displaystyle {\int }_0^1}{M}_s\left(1,\eta ,t\right)\tilde{\nu }\left(\eta ,t\right)\text{d}\eta$ . Finally, substituting $\text{TTF}=t_f-t$ into (3.39) and solving it, we can obtain the explicit expression (3.37) of TTF.

$\square$

4. Numerical Simulations

To verify the effectiveness of the fault diagnosis scheme proposed in this paper, we conduct numerical simulations on the original system (2.1) and (2.2).

The functions in the original system and parameters in the numerical simulation process are defined as $\varphi \left(\upsilon \mathrm{,}s\right)=s\sin t$ , $\psi \left(s,t\right)=0.05{\text{e}}^{-0.5{\left(s-0.3\right)}^2}\sin t$ , $d=2$ and $\alpha =\frac{1}{2}$ .

The fault parameter $\theta$ is selected as the piecewise function $\theta =1-0.5\Theta \left(t-18\right),\Theta =\{\begin{array}{ll}0,\hfill & t<18,\hfill \\ 1-{\text{e}}^{-0.3\left(t-18\right)},\hfill & t\ge 18,\hfill \end{array}$ and from the piecewise function $\Theta$ , we can observe that the system is subjected to a fault at 18 seconds.

We used the finite element method (FDM) to numerically simulate the scheme studied in this paper. It can be seen from Figure 1(a) that in a healthy state where there is no fault in the system, error system $\xi \left(s\mathrm{,}t\right)$ is bounded without disturbance or uncertainty in the system. In particular, when the nonlinear term in the system satisfies ${\bar{\epsilon }}_{\varphi }=0$ , it can be seen from Figure 1(b) that the error system $\xi \left(s\mathrm{,}t\right)$ in Figure 1(c) can exponentially converge to zero. When there is a disturbance or uncertainty in the system, the error system $\xi \left(s\mathrm{,}t\right)$ is also bounded in the healthy state, as shown in Figure 0. However, when we impose a fault in the system, the error system $\xi \left(s\mathrm{,}t\right)$ is also ultimately bounded as shown in Figure 1(d).

From Figure 2(a), it can be seen that when $t=18\text{s}$ , the detection residual $r\left(t\right)$ exceeds the threshold $R\left(t\right)$ , which means that a fault has been detected. Special attention should be paid to that the fault detection scheme proposed in this paper adopts a time-varying threshold. To better illustrate its advantages, we compared the detection residual $r\left(t\right)$ with the constant threshold $R_c$ used in traditional fault detection methods. From Figure 2(b), it can be seen that when $t>18\text{s}$ , the detection residual $r\left(t\right)$ exceeds the constant threshold $R_c$ , which means that the system is detected to have a fault. However, it can be observed from Figure 2(b) that there are still some cases where the detection residual $r\left(t\right)$ exceeds the constant threshold $R_c$ before the actual time of the fault

Figure 1. The performance of the error system $\xi \left(s\mathrm{,}t\right)$ .

Figure 2. Fault detection results.

occurrence, i.e. $t\le 18\text{s}$ , and these situations will lead to false alarms of the fault detection.

The fault parameter update law (3.24) proposed in this paper is used to estimate the fault parameters, where the parameters are set as $\gamma =0.05$ and $\rho =0.15$ . The actual fault parameter $\theta$ and the estimated fault parameter $\hat{\theta }$ are shown in Figure 3.

Finally, we can further obtain the estimated TTF through the estimated fault parameters and the explicit expression (3.37) of TTF, where the failure limit of the the fault parameter we choose as ${\theta }_f=0.5$ . It can be seen from Figure 4 that

Figure 3. Estimated fault $\hat{\theta }$ and actual fault $\theta$ .

Figure 4. Estimated TTF.

when the system is at time $t=21.5\text{s}$ , TTF = 0, indicating that the system crashes and cannot operate normally anymore.

5. Conclusion

In this paper, we propose an actuator fault diagnosis scheme for a class of nonlinear heat equations. The fault detection is completed by comparing the detection residual with the time-varying threshold. Once a fault is detected in the system, the updated law of the estimated fault parameters is given by adding an adaptive estimation term to the original observer. In addition, we use limited measurements to predict TTF. Finally, the effectiveness and feasibility of the proposed scheme are verified through numerical simulation results. The future research will extend to the fields of fault isolation and other partial differential equations.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Dong, J., Wang, Q., Wang, M. and Peng, K. (2018) Data-Driven Quality Monitoring Techniques for Distributed Parameter Systems with Application to Hot-Rolled Strip Laminar Cooling Process. IEEE Access, 6, 16646-16654. https://doi.org/10.1109/ACCESS.2018.2812919
[2]	Hong, W., Lee, Y.T. and Gong, H. (2004) Thermal Analysis of Layer Formation in a Stepless Rapid Prototyping Process. Applied Thermal Engineering, 24, 255-268. https://doi.org/10.1016/j.applthermaleng.2003.08.015
[3]	Khan, F.A., Imran, M., Abbas, H. and Durad, M.H. (2017) A Detection and Prevention System against Collaborative Attacks in Mobile ad Hoc Networks. Future Generation Computer Systems, 68, 416-427. https://doi.org/10.1016/j.future.2016.07.010
[4]	Song, X., Zhang, Q., Wang, M. and Song, S. (2021) Distributed Estimation for Nonlinear PDE Systems Using Space-Sampling Approach: Applications to High-Speed Aerospace Vehicle. Nonlinear Dynamics, 106, 3183-3198. https://doi.org/10.1007/s11071-021-06725-4
[5]	Song, X., Wang, M., Park, J.H. and Song, S. (2020) Spatial-L∞-Norm-Based Finite-Time Bounded Control for Semilinear Parabolic PDE Systems with Applications to Chemical-Reaction Processes. IEEE Transactions on Cybernetics, 52, 178-191. https://doi.org/10.1109/TCYB.2020.2972634
[6]	Perthame, B. (2004) PDE Models for Chemotactic Movements: Parabolic, Hyperbolic and Kinetic. Applications of Mathematics, 49, 539-564. https://doi.org/10.1007/s10492-004-6431-9
[7]	Ren, Y., Wang, A. and Hong, W. (2017) Fault Diagnosis and Tolerant Control for Discrete Stochastic Distribution Collaborative Control Systems. IEEE Transactions on Systems Man and Cybernetics Systems, 45, 462-471. https://doi.org/10.1109/TSMC.2014.2358635
[8]	Jiang, B., Marcel, S. and Vincent, C. (2006) Fault Accommodation for Nonlinear Dynamic Systems. IEEE Transactions on Automatic Control, 51, 1578-1583. https://doi.org/10.1109/TAC.2006.878732
[9]	Gao, Z., Cecati, C. and Ding, S.X. (2015) A Survey of Fault Diagnosis and Fault-Tolerant Techniques-Part I: Fault Diagnosis with Model-Based and Signal-Based Approaches. IEEE Transactions on Industrial Electronics, 62, 3757-3767. https://doi.org/10.1109/TIE.2015.2417501
[10]	Balogh, A. and Krstic, M. (2002) Infinite Dimensional Backstepping-Style Feedback Transformations for a Heat Equation with an Arbitrary Level of Instability. European Journal of Control, 8, 165-175. https://doi.org/10.3166/ejc.8.165-175
[11]	Cao, F. and Liu, J. (2018) Adaptive Actuator Fault Compensation Control for a Rigid-Flexible Manipulator with ODEs-PDEs Model. International Journal of Systems Science, 49, 1748-1759. https://doi.org/10.1080/00207721.2018.1479002
[12]	Peng, W. and Vachtsevanos, G. (2001) Fault Prognostics Using Dynamic Wavelet Neural Networks. 2001 IEEE Autotestcon Proceedings. IEEE Systems Readiness Technology Conference. (Cat. No.01CH37237), Valley Forge, 20-23 August 2001, 857-870.
[13]	Patan, M. and Uciński, D. (2005) Optimal Activation Strategy of Discrete Scanning Sensors for Fault Detection in Distributed-Parameter Systems. IFAC Proceedings Volumes, 38, 209-214. https://doi.org/10.3182/20050703-6-CZ-1902.01837
[14]	Alonso, A.A. and Ydstie, B.E. (2001) Stabilization of Distributed Systems Using Irreversible Thermodynamics. Automatica, 37, 1739-1755. https://doi.org/10.1016/S0005-1098(01)00140-6
[15]	Demetriou, M.A. and Kazantzis, N. (2004) A New Actuator Activation Policy for Performance Enhancement of Controlled Diffusion Processes. Automatica, 40, 415-421. https://doi.org/10.1016/j.automatica.2003.10.023
[16]	Wang, Z., Zhang, B., Yuan, J. and Che, D. (2018) Robust Adaptive Fault Tolerant Control for a Class of Linearly Parameterized Uncertain Nonlinear Systems: An Integrated Method. Transactions of the Institute of Measurement and Control, 40, 2129-2140. https://doi.org/10.1177/0142331217696142
[17]	Ferdowsi, H., Cai, J. and Sarangapani, J. (2022) Actuator and Sensor Fault Detection and Failure Prediction for Systems with Multi-Dimensional Nonlinear Partial Differential Equations. International Journal of Control, Automation and Systems, 20, 789-802. https://doi.org/10.1007/s12555-019-0622-3
[18]	Baniamerian, A. and Khorasani, K. (2012) Fault Detection and Isolation of Dissipative Parabolic PDEs: Finite-Dimensional Geometric Approach. 2012 American Control Conference, Montreal, 27-29 June 2012, 5894-5899. https://doi.org/10.1109/ACC.2012.6315006
[19]	Demetriou, M.A., Ackleh, A.S. and Reich, S. (1998) Detection and Accommodation of Second Order Distributed Parameter Systems with Abrupt Changes in Input Term: Existence and Approximation. Theory and Practice of Control and Systems, 34, 720-725. https://doi.org/10.1142/9789814447317_0119
[20]	Armaou, A. and Demetriou, M.A. (2008) Robust Detection and Accommodation of Incipient Component and Actuator Faults in Nonlinear Distributed Processes. AIChE Journal, 54, 2651-2662. https://doi.org/10.1002/aic.11539
[21]	Feng, Y., Li, H.X. and Yang, H.D. (2019) Abnormal Source Identification for Parabolic Distributed Parameter Systems. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 51, 5698-5707. https://doi.org/10.1109/TSMC.2019.2956985
[22]	Ghantasala, S. and El-Farra, N.H. (2009) Robust Actuator Fault Isolation and Management in Constrained Uncertain Parabolic PDE Systems. Automatica, 45, 2368-2373. https://doi.org/10.1016/j.automatica.2009.06.024
[23]	Ferdowsi, H. and Jagannathan, S. (2014) Fault Diagnosis of a Class of Distributed Parameter Systems Modeled by Parabolic Partial Differential Equations. 2014 American Control Conference, Portland, 4-6 June 2014, 5434-5439. https://doi.org/10.1109/ACC.2014.6858836
[24]	Du, D.S. (2017) Fault Detection for Discrete-Time Linear Systems Based on Descriptor Observer Approach. Applied Mathematics and Computation, 293, 575-585. https://doi.org/10.1016/j.amc.2016.08.052
[25]	Li, S., Chen, Y. and Zhan, J. (2021) Simultaneous Observer-Based Fault Detection and Event-Triggered Consensus Control for Multi-Agent Systems. Journal of the Franklin Institute, 358, 3276-3301. https://doi.org/10.1016/j.jfranklin.2021.02.009
[26]	Zhao, Z., Yang, Y., Ding, S.X. and Li, L. (2018) Robust Fault Detection for Observer-Based Feedback Control Systems. Circuits, Systems, and Signal Processing, 37, 3364-3382. https://doi.org/10.1007/s00034-017-0726-z
[27]	Dey, S., Perez, H.E. and Moura, S.J. (2019) Robust Fault Detection of a Class of Uncertain Linear Parabolic PDEs. Automatica, 107, 502-510. https://doi.org/10.1016/j.automatica.2019.06.014
[28]	Cai, J., Ferdowsi, H. and Sarangapani, J. (2016) Model-Based Fault Detection, Estimation, and Prediction for a Class of Linear Distributed Parameter Systems. Automatica, 66, 122-131. https://doi.org/10.1016/j.automatica.2015.12.028
[29]	Feng, Y., Wang, Y., Wang, J.W. and Li, H.X. (2022) Backstepping-Based Distributed Abnormality Localization for Linear Parabolic Distributed Parameter Systems. Automatica, 135, Article ID: 109930. https://doi.org/10.1016/j.automatica.2021.109930
[30]	Smyshlyaev, A. and Krstic, M. (2004) Closed-Form Boundary State Feedbacks for a Class of 1-D Partial Integro-Differential Equations. IEEE Transactions on Automatic Control, 49, 2185-2202. https://doi.org/10.1109/TAC.2004.838495
[31]	Smyshlyaev, A. and Krstic, M. (2005) Backstepping Observers for a Class of Parabolic PDEs. Systems and Control Letters, 54, 613-625. https://doi.org/10.1016/j.sysconle.2004.11.001
[32]	Kwan, C., Zhang, X., Xu, R. and Haynes, L. (2003) A Novel Approach to Fault Diagnostics and Prognostics. IEEE International Conference on Robotics and Automation, Taipei, 14-19 September 2003, 604-609. https://doi.org/10.1109/ROBOT.2003.1241660
[33]	Ferdowsi, H., Cai, J. and Jagannathan, S. (2019) Fault Detection and Estimation for a Class of Nonlinear Distributed Parameter Systems. 2019 IEEE International Conference on Prognostics and Health Management, San Francisco, 17-20 June 2019, 1-8. https://doi.org/10.1109/ICPHM.2019.8819432
[34]	Meurer, T. (2013) On the Extended Luenberger-Type Observer for Semilinear Distributed-Parameter Systems. IEEE Transactions on Automatic Control, 58, 1732-1743. https://doi.org/10.1109/TAC.2013.2243312
[35]	Chen, L. (2022) Backstepping-Based Distributed Abnormality Detection for Nolinear Parabolic Distributed Prameter Systems. Engineering, 14, 285-299. https://doi.org/10.4236/eng.2022.147023
[36]	Tarammim, A. and Akter, M. (2022) A Comparative Study of Synchronization Methods of Rucklidge Chaotic Systems with Design of Active Control and Backstepping Methods. International Journal of Modern Nonlinear Theory and Application, 11, 31-51. https://doi.org/10.4236/ijmnta.2022.112003
[37]	Lavretsky, E. and Wise, K.A. (2012) Robust Adaptive Control. In: Lavretsky, E. and Wise, K.A., Eds., Robust and Adaptive Control: With Aerospace Applications, Springer, London, 317-353. https://doi.org/10.1007/978-1-4471-4396-3_11