Dirichlet-to-Neumann Map for a Hyperbolic Equation

Fagueye Ndiaye¹, Mouhamadou Ngom², Diaraf Seck³

¹Department of Mathematics, Cheikh Anta Diop University, Dakar-Fann, Senegal.
²Alioune Diop University, Bambey, Senegal.
³Cheikh Anta Diop University of Dakar, Dakar Fann, Senegal.

DOI: 10.4236/jamp.2023.118145                

Abstract

In this paper, we provide an explicit expression for the full Dirichlet-to-Neumann map corresponding to a radial potential for a hyperbolic differential equation in 3-dimensional. We show that the Dirichlet-Neumann operators corresponding to a potential radial have the same properties for hyperbolic differential equations as for elliptic differential equations. We numerically implement the coefficients of the explicit formulas. Moreover, a Lipschitz type stability is established near the edge of the domain by an estimation constant. That is necessary for the reconstruction of the potential from Dirichlet-to-Neumann map in the inverse problem for a hyperbolic differential equation.

Keywords

Hyperbolic Differential Equation, Calderón’s Problem, Schrödinger Operator, Potential, Inverse Potential Problem, Dirichlet-to-Neumann Map, Numerical Simulations, Lipschitz Stability

1. Introduction

Let us consider a bounded domain $\Omega \subset {ℝ}^3$ with smooth boundary and the parameters w and T in ${ℝ}_{+}^{\mathrm{<mo>\; *\; </mo>}}$ . The boundary value problem for a hyperbolic differential equation in $\Omega \times \left(\mathrm{0,}T\right)$ is given as follows.

$\{\begin{array}{ll}\frac{{\partial }^{2}v}{\partial t^2}-\Delta v+p\left(x\right)v=0\hfill & \text{in}\Omega \times \left(\mathrm{0,}T\right)\hfill \\ v\left(x\mathrm{,}t\right)=f{\text{e}}^{iwt}\hfill & \text{on}\partial \Omega \times \left(\mathrm{0,}T\right)\hfill \\ v\left(x\mathrm{,0}\right)=v_0\left(x\right)\hfill & \text{in}\Omega \hfill \\ \frac{\partial }{\partial t}v\left(x\mathrm{,0}\right)=v_1\left(x\right)\hfill & \text{in}\Omega \hfill \end{array}$ (1)

Assuming that $f\in H^{1/2}\left(\partial \Omega \right)$ , $v_0\in H^1\left(\Omega \right)$ and $v_1\in L^2\left(\Omega \right)$ are given, verified the compatibility condition $v_0\left(x\right)=f\left(x\right)$ , $v_1\left(x\right)=iwf\left(x\right)$ for all $x\in \partial \Omega$ . The potential p is a given real-valued function satisfying $p\in {\text{L}}^{\infty }\left(\Omega \right)$ .

• Let us suppose that the solution v has a fixed temporal frequency, then $v=u{\text{e}}^{iwt}$ and the problem (1) is equivalent to the Schrödinger equation with w² energy.

$\{\begin{array}{ll}-\Delta u+p\left(x\right)u=w^{2}u\hfill & \text{in}\Omega \hfill \\ u=f\hfill & \text{on}\partial \Omega \hfill \end{array}$ (2)

with $p\in {\text{L}}^{\infty }\left(\Omega \right)$ is the potential and $w\in ℝ$ fixed, the pulsations.

• The problem (2) is equivalent to the Schrödinger equation

$\{\begin{array}{ll}\left(-\Delta +\left(p-w^2\right)\right)u=0\hfill & \text{in}\Omega \hfill \\ u=f\hfill & \text{on}\partial \Omega \hfill \end{array}$ (3)

with the function p satisfying $p\in {\text{L}}^{\infty }\left(\Omega \right)$ .

• This problem direct is analogous to the problem studied by Ndiaye in [1] in the case where $w=0$ .

• Our aim is to show that the Dirichlet-Neumann operators corresponding to a potential radial have the same properties for hyperbolic differential equations as for elliptic differential equations.

• Our contribution in this paper is to determine an explicit formula for the Dirichlet-to-Neumann map for a piecewise constant radial potential for the Schrödinger equation with w² energy in dimension three in a ball, using the method developed in [1] for the stationary case. A Lipschitz type stability is established near the edge of the domain by giving an estimation constant. In this paper, the results obtained in [1] are generalised.

• Our motivation of this paper is to know the Dirichlet-to-Neumann map ${\Lambda }_p\left(w\right)$ , for a piecewise constant radial potential p in dimension three in a ball,

for a fixed maximal time, from the knowledge of the Cauchy data $\left(f\mathrm{,}\frac{\partial u}{\partial \nu }\right)$ to

be able to solve the inverse problem of the hyperbolic differential Equation (1) in dimension three. The good knowledge of the characteristic properties of the Dirichlet-to-Neumann map ${\Lambda }_p\left(w\right)$ allows to solve the inverse problem which consists to determine the potential p from the knowledge of $\left(f\mathrm{,}{\Lambda }_p\left(w\right)\right)$ for a hyperbolic differential equation. And the study of this inverse problem also motivated us to study the Lipschitz type stability which will allow us to obtain a result at least at the edge of $\Omega$ with an estimate constant to be determined for a hyperbolic differential equation.

The paper is organized as follows. In Section 2, we define the Dirichlet-to-Neumann map for the Schrödinger equation with w² energy, and then present the radial solutions of this equation in Section 3. In Section 4, we give an explicit formula for DDirichlet-to-Neumann map when the potential is radial, followed by some simulations. In Section 4, we study the stability of the map that associates a Dirichlet-to-Neumann map to any potential. In Section 5, we present conclusions and perspectives.

2. Definition of the Dirichlet-to-Neumann Map for Schrödinger Equation with w² Energy

First, in this section, we define the Dirichlet-to-Neumann map ${\Lambda }_p$ , for the hyperbolic differential equation, formally as

$\begin{array}{l}{\Lambda }_p\mathrm{<mo>\; :\; </mo>}{H}^{1/2}\left(\partial \Omega \right)\to H^{-1/2}\left(\partial \Omega \right)\\ f{\text{e}}^{iwt}\mapsto {\Lambda }_p\left(f{\text{e}}^{iwt}\right)={\frac{\partial v}{\partial \nu }|}_{\partial \Omega }\mathrm{,}\end{array}$ (4)

with $v=u{\text{e}}^{iwt}$ and where $\nu$ is the outer unit normal vector to $\partial \Omega$ .

The map $f{\text{e}}^{iwt}\mapsto {\Lambda }_p\left(f{\text{e}}^{iwt}\right)$ depends linearly on f for any fixed time t. Then, we have

${\Lambda }_p\left(f{\text{e}}^{iwt}\right)={\text{e}}^{iwt}{\Lambda }_p\left(f\right)={{\text{e}}^{iwt}\frac{\partial u}{\partial \nu }|}_{\partial \Omega }\mathrm{.}$

This allows us to define the Dirichlet-to-Neumann map ${\Lambda }_p\left(w\right)$ , for the Schrödinger Equation (2) with w² energy, formally as

$\begin{array}{l}{\Lambda }_p\left(w\right)\mathrm{<mo>\; :\; </mo>}{H}^{1/2}\left(\partial \Omega \right)\to H^{-1/2}\left(\partial \Omega \right)\\ f\mapsto {\Lambda }_p\left(w\right)f={\frac{\partial u}{\partial \nu }|}_{\partial \Omega }\mathrm{,}\end{array}$ (5)

where $\nu$ is the outer unit normal vector to $\partial \Omega$ .

The map $f\mapsto {\Lambda }_p\left(w\right)f$ depends linearly on f. ${\Lambda }_p\left(w\right)$ encodes the measurements of $\frac{\partial u}{\partial \nu }$ for all possible functions f on the boundary of $\Omega$ .

Now, we have to determine an explicit formula for the Dirichlet-to-Neumann map ${\Lambda }_p\left(w\right)$ for a piecewise constant radial potential for the Schrödinger Equation (2) with w² energy in dimension three in a ball, using the method developed in [1] . We need to assume that 0 is not a Dirichlet eigenvalue of $\left(-\Delta +p-w^2\right)$ in $\Omega$ .

Now, we look more closely at the direct problem with the potential p. Let the unit ball $B=\left\{x\in {ℝ}^3\mathrm{<mo>\; :\; </mo>}\left|x\right|\le 1\right\}$ in ${ℝ}^3$ .

We focus on $p\in {\text{L}}^{\infty }\left(B\right)$ with $p\left(x\right)=p\left(\left|x\right|\right)$ is being radial, $f\in H^{\frac{1}{2}}\left(\partial B\right)$ given and assuming that 0 is not eigenvalue of

$\{\begin{array}{ll}\left(-\Delta +p-w^2\right)u=0\hfill & \text{in}\left|x\right|<1,\hfill \\ u=f\hfill & \text{on}\left|x\right|=1.\hfill \end{array}$ (6)

These choices guarantee the existence of a solution of (6) by the Fourier method and 0 is not an eigenvalue ensuring the uniqueness of the solution.

Then the map $f\mapsto {\Lambda }_p\left(w\right)f$ is well defined. To obtain an explicit formula for the Dirichlet-to-Neumann map ${\Lambda }_p\left(w\right)$ , defined in (5), we will consider that it verifies the following results (see [2] ), which we’ll prove numerically:

1) If $p\left(x\right)\ne w^2$ , then ${\Lambda }_p\left(w\right)$ is diagonalisable in the sense that the spectrum is discrete, $\left\{{\lambda }_k\left[p-w^2\right]\mathrm{,}k\in {\mathbb{N}}_0\right\}$ .

In this case, if ${\mathcal{N}}_k$ is the subspace of spherical harmonics of degree k, then

${{\Lambda }_p\left(w\right)|}_{{\mathcal{N}}_k}={\lambda }_k\left[p-w^2\right]I_{{\mathcal{N}}_k}\mathrm{.}$

2) If $p\left(x\right)=w^2$ and ${\varphi }_k\in {\mathcal{N}}_k$ then ${\Lambda }_{w^2}\left({\varphi }_k\right)=k{\varphi }_k,k=0,1,2,\cdots$

3) ${\lambda }_k\left[p-w^2\right]-k\to 0$ if $k\to \infty$ .

Then in the following, we give a recurrence relation for the explicit calculation of the spectrum in the case where $p\left(x\right)$ is a step potential, to give an approximation of the spectrum of a general potential. For all this, we need to recall some properties that will be useful.

3. Radial Solutions for the Schrödinger Equation with w² Energy

In this section, we present some results obtained from writing the problem (6) in polar coordinates $r>0$ , $\theta \in {\mathbb{S}}^2$ . We want to obtain “complex geometrical optics” solutions or solutions of Faddeev type, see [3] .

Lemma 3.1: If u is the solution of (6) and $X\left(r\mathrm{,}\theta \right)=u\left(r\theta \right)$ in terms of spherical harmonics, then the function X satisfies the problem

$\{\begin{array}{l}{r}^2{X}^{″}+2r{X}^{\prime }+{\Delta }_{S}X-\left[p\left(r\right)-w^2\right]r^{2}X=0,\\ \underset{r>0,r\to 0}{\lim }X\left(r,\theta \right)<\infty ,X\left(1,\theta \right)=f\left(\theta \right),\end{array}$ (7)

where $-{\Delta }_S{Y}_{\mathcal{l}}^k=\mathcal{l}\left(\mathcal{l}+1\right)Y_{\mathcal{l}}^k$ , $Y_{\mathcal{l}}^k\in {\mathcal{N}}_{\mathcal{l}}$ .

For the proof of Lemma 3.1, see [1] .

Lemma 3.2: If $f\left(\theta \right)={\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}{f}_{\mathcal{l}k}{Y}_{\mathcal{l}}^k\left(\theta \right)$ in $H^{1/2}\left({\mathbb{S}}^2\right)$ , then Equation (6) admits a unique solution of the form

$X\left(r,\theta \right)={\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}{X}_{\mathcal{l}k}\left(r\right)Y_{\mathcal{l}}^k\left(\theta \right),$ (8)

where $X_{\mathcal{l}k}$ satisfies the problem

$\{\begin{array}{l}{r}^2{X^{″}}_{\mathcal{l}k}+2r{X^{\prime }}_{\mathcal{l}k}-\mathcal{l}\left(\mathcal{l}+1\right)X_{\mathcal{l}k}-\left[p\left(r\right)-w^2\right]r^2{X}_{\mathcal{l}k}=0,r\in \left(0,1\right),\\ \underset{r>0,r\to 0}{\lim }{X}_{\mathcal{l}k}\left(r\right)<\infty ,X_{\mathcal{l}k}\left(1\right)=f_{\mathcal{l}k}.\end{array}$ (9)

For the proof of Lemma 3.2, see [1] .

Lemma 3.3: If $X_{\mathcal{l}k}$ is the solution of (9), then we have

${\Lambda }_p\left(w\right)f={\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}{X^{\prime }}_{\mathcal{l}k}\left(1\right)Y_{\mathcal{l}}^k\left(\theta \right).$ (10)

For the proof of Lemma 3.3, see [1] .

We note that the differential Equation in (9) does not depend on k, so we will eliminate the dependence on k. Then

Lemma 3.4: If in (9) we take $f=Y_{\mathcal{l}}$ , that is, the spherical harmonic of degree $\mathcal{l}$ , it follows that

${\Lambda }_p\left(w\right)Y_{\mathcal{l}}={X^{\prime }}_{\mathcal{l}}\left(1\right)Y_{\mathcal{l}}\mathrm{.}$ (11)

Then ${X^{\prime }}_l\left(1\right)$ is an eigenvalue of ${\Lambda }_q$ with multiplicity $2\mathcal{l}+1$ and its eigenfunctions are ${\left\{Y_{\mathcal{l}}^k\right\}}_{k=-\mathcal{l},-\mathcal{l}+1,\cdots ,\mathcal{l}-1,\mathcal{l}}$ .

For the proof of Lemma 3.4, see [1] .

In the next section, we will use these results to give an explicit formula for the Dirichlet-to-Neumann map when the potential is a radial function.

4. Explicit Formula for the Dirichlet to Neumann Map

4.1. The Case Where p Is a Piecewise Constant Radial Potential

Let us introduce the theorem where the expression of the Dirichlet-to-Neumann map is presented when p is a piecewise constant radial potential, based on the results of the previous section.

• In the following, for all $\mathcal{l}\in \mathbb{N}$ , $p_{\mathcal{l}}^m\left(r\right)$ denotes the Bessel function of the first type $j_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m-w^2\right|}r\right)$ or the Bessel function of the second type $i_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m-w^2\right|}r\right)$ , and $q_{\mathcal{l}}^m\left(r\right)$ denotes the modified Bessel function of the first type $y_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m-w^2\right|}r\right)$ or the modified Bessel function of the second type ${\left(-1\right)}^{\mathcal{l}+1}{k}_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m-w^2\right|}r\right)$ , see Equations (29) and (30).

• Theorem 4.1: Let the unit ball B in ${ℝ}^3$ and the scaled potential $p\in {\text{L}}^{\infty }\left(B\right)$ with

$p\left(r\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}}{\gamma }_m{\chi }_{\left(r_{m-1},r_m\right)},r=\left|x\right|,$ (12)

where $n\ge 1$ , ${\gamma }_m\mathrm{,}{r}_m\in ℝ$ , with $m=1,2,\cdots ,n$ and $0=r_0<r_1<\cdots <r_{n-1}<r_n=1$ , such that the Dirichlet problem for $\left(-\Delta +p-w^2\right)$ is well-posed.

Then there is an explicit formula for the Dirichlet-to-Neumann map defined as follows:

${\Lambda }_p\left(w\right)Y_{\mathcal{l}}^k=\left[C_w\left(k_n{p}_{\mathcal{l}-1}^n\left(1\right)-\frac{k_n{p}_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{q}_{\mathcal{l}-1}^n\left(1\right)\right)+\frac{k_n{q}_{\mathcal{l}-1}^n\left(1\right)-\mathcal{l}{q}_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}\right]Y_{\mathcal{l}}^k\mathrm{,}$ (13)

$\mathcal{l}=1,2,\cdots$ with $k_n,p_{\mathcal{l}-1}^n,p_{\mathcal{l}}^n,q_{\mathcal{l}-1}^n,q_{\mathcal{l}}^n$ and $C_w$ depending on $w,n$ and $\mathcal{l}$ .

Remark 4.1 We assume that ${\gamma }_m\ne w^2$ to simplify the calculations. If we want to consider this case in the simulations, we approximate it by $\gamma =w^2-0.01$ .

Proof of Theorem 4.1. p is a piecewise constant radial function, $p\left(r\right)=p\left(\left|x\right|\right)$ , defined by

$p\left(r\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}}{\gamma }_m{\chi }_{\left(r_{m-1},r_m\right)},r=\left|x\right|,$

with $0=r_0<r_1<\cdots <r_{n-1}<r_n=1$ , ${\gamma }_m\in ℝ$ , and there is no case where ${\gamma }_m={\gamma }_{m+1}$ for all $m\in \left\{\mathrm{1,2,}\cdots \mathrm{,}n-1\right\}$ .

We solve the Schrödinger Equation (2) with w² energy, with $f=Y_{\mathcal{l}}^k$ for a fixed $\mathcal{l}$ . Thus in Equation (9) we have $f_{\mathcal{l}k}=1$ .

We look for a solution y of (9), of type

$y\left(r\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}}{y}_m\left(r\right),$ (14)

where $y_1$ is the solution of

$\{\begin{array}{l}{r}^2{y}^{″}+2r{y}^{\prime }-\mathcal{l}\left(\mathcal{l}+1\right)y-\left({\gamma }_1-w^2\right)r^{2}y=0,r\in \left(0,r_1\right),\\ \underset{r>0,r\to 0}{\lim }y\left(r\right)<\infty .\end{array}$ (15)

For $m=\mathrm{2,3,}\cdots \mathrm{,}n-1$ , we have a $y_m$ which satisfies

$r^2{y}^{″}+2r{y}^{\prime }-\mathcal{l}\left(\mathcal{l}+1\right)y-\left({\gamma }_m-w^2\right)r^{2}y=\mathrm{0,}r\in \left(r_{m-1}\mathrm{,}{r}_m\right)\mathrm{,}$ (16)

and $y_n$ in this equation

$\{\begin{array}{l}{r}^2{y}^{″}+2r{y}^{\prime }-\mathcal{l}\left(\mathcal{l}+1\right)y-\left({\gamma }_n-w^2\right)r^{2}y=0,r\in \left(r_{n-1},1\right),\\ y\left(1\right)=1,\end{array}$ (17)

and the following compatibility conditions are satisfied

$\{\begin{array}{l}{y}_1\left(r_1\right)=y_2\left(r_1\right)\hfill \\ {y^{\prime }}_1\left(r_1\right)={y^{\prime }}_2\left(r_1\right)\hfill \\ y_2\left(r_2\right)=y_3\left(r_2\right)\hfill \\ {y^{\prime }}_2\left(r_2\right)={y^{\prime }}_3\left(r_2\right)\hfill \\ ⋮\hfill \\ y_{n-2}\left(r_{n-2}\right)=y_{n-1}\left(r_{n-2}\right)\hfill \\ {y^{\prime }}_{n-2}\left(r_{n-2}\right)={y^{\prime }}_{n-1}\left(r_{n-2}\right)\hfill \\ y_{n-1}\left(r_{n-1}\right)=y_n\left(r_{n-1}\right)\hfill \\ {y^{\prime }}_{n-1}\left(r_{n-1}\right)={y^{\prime }}_n\left(r_{n-1}\right)\hfill \end{array}$ (18)

• The general solution of the equation

$r^2{y}^{″}+2r{y}^{\prime }-\mathcal{l}\left(\mathcal{l}+1\right)y-\left({\gamma }_m-w^2\right)r^{2}y=\mathrm{0,}r\in \left(r_{m-1}\mathrm{,}{r}_m\right)\mathrm{,}m=\mathrm{1,2,}\cdots \mathrm{,}n\mathrm{,}$

• is

$y_m\left(r\right)=A_m^{\mathcal{l}}{j}_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m-w^2\right|}r\right)+B_m^{\mathcal{l}}{y}_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m-w^2\right|}r\right)$ , if ${\gamma }_m<w^2$ , with $A_m^{\mathcal{l}},B_m^{\mathcal{l}}\in ℝ$ ,

where $j_{\mathcal{l}}$ and $y_{\mathcal{l}}$ are the Bessel functions of the first and second type, respectively,

$y_m\left(r\right)=A_m^{\mathcal{l}}{r}^{\mathcal{l}}+B_m^{\mathcal{l}}{r}^{-\left(\mathcal{l}+1\right)}$ , if ${\gamma }_m=w^2$ , with $A_m^{\mathcal{l}},B_m^{\mathcal{l}}\in ℝ$ ,

• and

$y_m\left(r\right)=A_m^{\mathcal{l}}{i}_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m-w^2\right|}r\right)+B_m^{\mathcal{l}}{\left(-1\right)}^{\mathcal{l}+1}{k}_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m-w^2\right|}r\right)$ , if ${\gamma }_m>w^2$ ,

with $A_m^{\mathcal{l}}\mathrm{,}{B}_m^{\mathcal{l}}\in ℝ$ , where $i_{\mathcal{l}}$ and $k_{\mathcal{l}}$ are the modified Bessel functions of the first and second type, respectively,

For $m=1,2,\cdots ,n$ , let us introduce the functions $z_{\mathcal{l}}^m\mathrm{,}{p}_{\mathcal{l}}^m\mathrm{,}{s}_{\mathcal{l}}^m$ , and $q_{\mathcal{l}}^m$ such that

• $z_{\mathcal{l}}^m\left(r\right)$ and $p_{\mathcal{l}}^m\left(r\right)$ will be denoted by $j_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m-w^2\right|}r\right)$ or $i_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m-w^2\right|}r\right)$ depending on whether ${\gamma }_m<w^2$ or ${\gamma }_m>w^2$ .

• $s_{\mathcal{l}}^m\left(r\right)$ and $q_{\mathcal{l}}^m\left(r\right)$ will be denoted by $y_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m-w^2\right|}r\right)$ or ${\left(-1\right)}^{\mathcal{l}+1}{k}_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m-w^2\right|}r\right)$ depending on whether ${\gamma }_m<w^2$ or ${\gamma }_m>w^2$ .

• Let pose $k_m=\sqrt{\left|{\gamma }_m-w^2\right|}$ , $m=1,2,\cdots ,n$ .

As the functions $y_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_1-w^2\right|}r\right)$ or ${\left(-1\right)}^{\mathcal{l}+1}{k}_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_1-w^2\right|}r\right)$ go to $-\infty$ when $r\to 0$ , we have

$y_1\left(r\right)=A_1^{\mathcal{l}}{z}_{\mathcal{l}}^1\left(r\right)\mathrm{,}\text{or}\left(A_1^{\mathcal{l}}{p}_{\mathcal{l}}^1\left(r\right)\right)\mathrm{.}$

For $m=\mathrm{1,2,}\cdots \mathrm{,}n-1$ , we have

$y_m\left(r\right)=A_m^{\mathcal{l}}{z}_{\mathcal{l}}^m\left(r\right)+B_m^{\mathcal{l}}{s}_{\mathcal{l}}^m\left(r\right)\left(\text{or}{A}_m^{\mathcal{l}}{p}_{\mathcal{l}}^m\left(r\right)+B_m^{\mathcal{l}}{q}_{\mathcal{l}}^m\left(r\right)\right)\mathrm{,}$

and

$y_n\left(r\right)=A_n^{\mathcal{l}}{z}_{\mathcal{l}}^n\left(r\right)+B_n^{\mathcal{l}}{s}_{\mathcal{l}}^n\left(r\right)\left(\text{or}{A}_n^{\mathcal{l}}{p}_{\mathcal{l}}^n\left(r\right)+B_n^{\mathcal{l}}{q}_{\mathcal{l}}^n\left(r\right)\right)\mathrm{,}\text{with}{A}_n^{\mathcal{l}}+B_n^{\mathcal{l}}=1.$

We will need the following derivative formulas.

If $f_{\mathcal{l}}^m$ denotes $j_{\mathcal{l}}^m$ , $y_{\mathcal{l}}^m$ , $i_{\mathcal{l}}^m$ , or ${\left(-1\right)}^{\mathcal{l}+1}{k}_{\mathcal{l}}^m$ with $f_{\mathcal{l}}^m\left(r\right)=f_{\mathcal{l}}\left(k_{m}r\right)$ , then

${\left(f_{\mathcal{l}}^m\right)}^{\prime }\left(r\right)=k_m{f^{\prime }}_{\mathcal{l}}\left(k_{m}r\right)$ , where ${f^{\prime }}_{\mathcal{l}}$ satisfies 31

${f^{\prime }}_{\mathcal{l}}\left(z\right)=f_{\mathcal{l}-1}\left(z\right)-\frac{\mathcal{l}+1}{z}{f}_{\mathcal{l}}\left(z\right)\mathrm{.}$

From 18 and 4.1, we have the following system of $\left(2n-2\right)\times \left(2n-2\right)$ equations

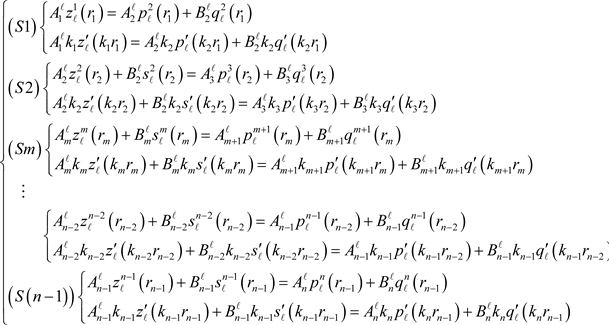(19)

where $A_n^{\mathcal{l}}$ and $B_n^{\mathcal{l}}$ are related by

$A_n^{\mathcal{l}}{p}_{\mathcal{l}}^n\left(1\right)+B_n^{\mathcal{l}}{q}_{\mathcal{l}}^n\left(1\right)=1.$ (20)

We recall (see 11) that our aim is to calculate $y^{\prime }\left(1\right)$ or ${y^{\prime }}_n\left(1\right)$ . By condition 20, we are only interesting in finding the unknown $A_n^{\mathcal{l}}$ of system 19.

Our strategy is the same in see [1] . It will be to find the unknowns $A_2^{\mathcal{l}}$ and $B_2^{\mathcal{l}}$ in terms of $A_1^{\mathcal{l}}$ by solving $\left(S1\right)$ . And for $m=\mathrm{2,3,}\cdots \mathrm{,}n-2$ , solve $S\left(m\right)$ to obtain $A_{m+1}^{\mathcal{l}}$ and $B_{m+1}^{\mathcal{l}}$ in terms of $A_1^{\mathcal{l}}$ . Then transform the system $S\left(n-1\right)$ into a system of two unknowns $A_1^{\mathcal{l}}$ and $A_n^{\mathcal{l}}$ and two equations. At this point we solve $S\left(n-1\right)$ .

For this purpose, we will need the following formulas of the Wronskians W, see [4] .

$\begin{array}{l}W\left\{j_{\mathcal{l}}\left(z\right),y_{\mathcal{l}}\left(z\right)\right\}=z^{-2},\\ W\left\{i_{\mathcal{l}}\left(z\right),{\left(-1\right)}^{\mathcal{l}+1}{k}_{\mathcal{l}}\left(z\right)\right\}=\frac{{\left(-1\right)}^{\mathcal{l}}\pi }{2}{z}^{-2}.\end{array}$ (21)

The problem with including the ${\gamma }_m=w^2$ case is that the functions $r^{\mathcal{l}}$ and $r^{-\left(\mathcal{l}+1\right)}$ do not satisfy our system. Perhaps a linear combination of different types of functions would make it easy to take into account the case ${\gamma }_m=w^2$ in the general scheme.

Then, according [1] , we have to solve

$\{\begin{array}{l}{M}_{11}{A}_1^{\mathcal{l}}+M_{12}{A}_n^{\mathcal{l}}=\frac{q_{\mathcal{l}}^n\left(r_{n-1}\right)}{q_{\mathcal{l}}^n\left(1\right)}\\ M_{21}{A}_1^{\mathcal{l}}+M_{22}{A}_n^{\mathcal{l}}=\frac{k_n{q^{\prime }}_{\mathcal{l}}\left(k_n{r}_{n-1}\right)}{q_{\mathcal{l}}^n\left(1\right)},\end{array}$ (22)

where

$\{\begin{array}{l}{M}_{11}=C_{n-2}\left(\mathcal{l}\right)z_{\mathcal{l}}^{n-1}\left(r_{n-1}\right)+D_{n-2}\left(\mathcal{l}\right)s_{\mathcal{l}}^{n-1}\left(r_{n-1}\right),\\ M_{12}=-\left(p_{\mathcal{l}}^n\left(r_{n-1}\right)-\frac{p_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{q}_{\mathcal{l}}^n\left(r_{n-1}\right)\right),\\ M_{21}=C_{n-2}\left(\mathcal{l}\right)k_{n-1}{z^{\prime }}_{\mathcal{l}}\left(k_{n-1}{r}_{n-1}\right)+D_{n-2}\left(\mathcal{l}\right)k_{n-1}{s^{\prime }}_{\mathcal{l}}\left(k_{n-1}{r}_{n-1}\right),\\ M_{22}=-\left(k_n{p^{\prime }}_{\mathcal{l}}\left(k_n{r}_{n-1}\right)-\frac{p_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{k}_n{q^{\prime }}_{\mathcal{l}}\left(k_n{r}_{n-1}\right)\right).\end{array}$ (23)

If the solution of this system is $\left(\begin{array}{c}{A}_1^{\mathcal{l}}\\ A_n^{\mathcal{l}}\end{array}\right)$ , the $\mathcal{l}-1$ eigenvalue is

${\lambda }_{\mathcal{l}-1}\left(w\right)=A_n^{\mathcal{l}}\left(k_n{p^{\prime }}_{\mathcal{l}}\left(k_n\right)-\frac{p_{\mathcal{l}}^n(1)}{q_{\mathcal{l}}^n(1)}{k}_n{q^{\prime }}_{\mathcal{l}}\left(k_n\right)\right)+\frac{k_n{q^{\prime }}_{\mathcal{l}}\left(k_n\right)}{q_{\mathcal{l}}^n\left(1\right)},\text{with}\mathcal{l}=1,2,\cdots$

Or

${\lambda }_{\mathcal{l}-1}\left(w\right)=A_n^{\mathcal{l}}\left(k_n{p}_{\mathcal{l}-1}^n\left(1\right)-\frac{k_n{p}_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{q}_{\mathcal{l}-1}^n\left(1\right)\right)+\frac{k_n{q}_{\mathcal{l}-1}^n\left(1\right)-\mathcal{l}{q}_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)},\mathcal{l}=1,2,\cdots$ (24)

where $A_n^{\mathcal{l}}$ depends on $n\mathrm{,}w$ and $\mathcal{l}$ , for all pulsations fixed w.

Taking $C_w=A_n^{\mathcal{l}}$ , we have the result. $\square$

Finally, we have obtained an explicit expression of the Dirichlet-to-Neumann map ${\Lambda }_p\left(w\right)$ , for all pulsations fixed w.

We will illustrate that ${\lambda }_{\mathcal{l}-1}\left(w\right)\mathrm{,}\mathcal{l}\ge 1$ in (24) verify the proprieties 1 and 3 in Section 2 with various examples, for all pulsations fixed w. We will do some numerical simulations for this.

4.2. The Case Where the Potential p Is a Continuous Radial Function

• In this section, we assume that the potential p is a continuous function with $p\left(r\right)>w^2$ or $p\left(r\right)<w^2$ in the interval $\left[\mathrm{0,1}\right]$ .

Let introduce the theorems which gives us the expression of the Dirichlet-to-Neumann map when the potential p is a continuous function, based on the results of a piecewise constant radial potential.

For all $\mathcal{l}\in \mathbb{N}$ , $p_{\mathcal{l}}^m\left(r\right)$ denotes the Bessel function of the first type $j_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m-w^2\right|}r\right)$ or the Bessel function of the second type $i_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m-w^2\right|}r\right)$ , and $q_{\mathcal{l}}^m\left(r\right)$ denotes the modified Bessel function of the first type $y_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m-w^2\right|}r\right)$ or the modified Bessel function of the second type ${\left(-1\right)}^{\mathcal{l}+1}{k}_{\mathcal{l}}\left(\sqrt{\left|{\gamma }_m-w^2\right|}r\right)$ .

• Theorem 4.2: Let the unit ball B in ${ℝ}^3$ and a continuous radial potential function $p\in {\text{L}}^{\infty }\left(B\right)$ with $p\left(r\right)=p\left(\left|x\right|\right)$ , where $p\left(r\right)>w^2$ or $p\left(r\right)<w^2$ , such that the Dirichlet problem for $\left(-\Delta +p-w^2\right)$ is well posed.

Let n be a large integer number such that $\left[0,1\right]={\displaystyle \underset{1}{\overset{n}{\cup }}}\left[r_{m-1},r_m\right]$ with $m=1,\cdots ,n$ and where $r_0=0$ , $r_n=1$ and $r_m-r_{m-1}=\frac{1}{n}$ .

Let a denote $k_m=\sqrt{\left|p\left(r_m\right)-w^2\right|}$ .

There is, for n enough large integer numbers and $\mathcal{l}=1,2,\cdots$ , an explicit formula for the Dirichlet-to-Neumann map is defined as follows:

${\Lambda }_p\left(w\right)Y_{\mathcal{l}}^k=\left[{\tilde{C}}_w\left(k_1{p}_{\mathcal{l}-1}^{*}\left(1\right)-\frac{k_1{p}_{\mathcal{l}}^{*}\left(1\right)}{q_{\mathcal{l}}^{*}\left(1\right)}{q}_{\mathcal{l}-1}^{*}\left(1\right)\right)+\frac{k_1{q}_{\mathcal{l}-1}^{*}\left(1\right)-\mathcal{l}{q}_{\mathcal{l}}^{*}\left(1\right)}{q_{\mathcal{l}}^{*}\left(1\right)}\right]Y_{\mathcal{l}}^k.$ (25)

With $k_1\mathrm{,}{p}_{\mathcal{l}-1}^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{p}_{\mathcal{l}}^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{q}_{\mathcal{l}-1}^{\mathrm{<mo>\; *\; </mo>}}\mathrm{,}{q}_{\mathcal{l}}^{\mathrm{<mo>\; *\; </mo>}}$ and ${\tilde{C}}_w$ depending on w

${\tilde{C}}_w$ depending $\mathcal{l}$ , $p_{\mathcal{l}}^{\mathrm{<mo>\; *\; </mo>}}\left(1\right)=p_{\mathcal{l}}\left(\sqrt{\left|p\left(1\right)-w^2\right|}\right)$ , $p_{\mathcal{l}-1}^{\mathrm{<mo>\; *\; </mo>}}\left(1\right)=p_{\mathcal{l}-1}\left(\sqrt{\left|p\left(1\right)-w^2\right|}\right)$ , $q_{\mathcal{l}}^{\mathrm{<mo>\; *\; </mo>}}\left(1\right)=q_{\mathcal{l}}\left(\sqrt{\left|p\left(1\right)-w^2\right|}\right)$ and $q_{\mathcal{l}-1}^{\mathrm{<mo>\; *\; </mo>}}\left(1\right)=q_{\mathcal{l}-1}\left(\sqrt{\left|p\left(1\right)-w^2\right|}\right)$ .

Proof of theorem 4.2. Let introduce $p_i,i=1,2$ be piecewise constant radial functions, $p_i\left(r\right)=p\left(\left|x\right|\right)$ , defined by

$p_1\left(r\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}}\left[p\left(r_{m-1}\right)-w^2\right]{\chi }_{\left(r_{m-1},r_m\right)},p_2\left(r\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}}\left[p\left(r_m\right)-w^2\right]{\chi }_{\left(r_{m-1},r_m\right)},r=\left|x\right|.$

Then from theorem 4.1,

${\Lambda }_{p_1}\left(w\right)Y_{\mathcal{l}}^k=\left[C_w^1\left(k_{n-1}^1{p}_{\mathcal{l}-1}^n\left(1\right)-\frac{k_{n-1}^1{p}_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{q}_{\mathcal{l}-1}^n\left(1\right)\right)+\frac{k_{n-1}^1{q}_{\mathcal{l}-1}^n\left(1\right)-\mathcal{l}{q}_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}\right]Y_{\mathcal{l}}^k,$

and

${\Lambda }_{p_2}\left(w\right)Y_{\mathcal{l}}^k=\left[C_w^2\left(k_n^2{p}_{\mathcal{l}-1}^n\left(1\right)-\frac{k_n^2{p}_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{q}_{\mathcal{l}-1}^n\left(1\right)\right)+\frac{k_n^2{q}_{\mathcal{l}-1}^n\left(1\right)-\mathcal{l}{q}_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}\right]Y_{\mathcal{l}}^k,$

for all $\mathcal{l}=1,2,\cdots$ with $C_w^1$ and $C_w^2$ depending on $w\mathrm{,}n$ and $\mathcal{l}$ , for all pulsations fixed w.

If p is increasing, then $p_1\left(r\right)\le p\left(r\right)\le p_2\left(r\right)$ ; if not, $p_1\left(r\right)\le p\left(r\right)\le p_2\left(r\right)$ .

We have $\underset{n\to \infty }{\lim }{p}_2\left(r\right)=\underset{n\to \infty }{\lim }{p}_1\left(r\right)=p\left(r\right)$ , and then there is ${\tilde{C}}_w\left(\mathcal{l}\right)$ such that

$\underset{n\to \infty }{\lim }{C}_w^1\left(n,\mathcal{l}\right)=\underset{n\to \infty }{\lim }{C}_w^2\left(n,\mathcal{l}\right)={\tilde{C}}_w\left(\mathcal{l}\right)$ .

We know that $p_{\mathcal{l}}^n\left(1\right)=p_{\mathcal{l}}\left(k_n\right)$ , $p_{\mathcal{l}-1}^n\left(1\right)=p_{\mathcal{l}-1}\left(k_n\right)$ , $q_{\mathcal{l}}^n\left(1\right)=q_{\mathcal{l}}\left(k_n\right)$ , $q_{\mathcal{l}-1}^n\left(1\right)=q_{\mathcal{l}-1}\left(k_n\right)$ , and $k_n=\sqrt{\left|p\left(1\right)-w^2\right|}$ , then $p_{\mathcal{l}}^{\mathrm{<mo>\; *\; </mo>}}\left(1\right)=p_{\mathcal{l}}\left(\sqrt{\left|p\left(1\right)-w^2\right|}\right)$ , $p_{\mathcal{l}-1}^{\mathrm{<mo>\; *\; </mo>}}\left(1\right)=p_{\mathcal{l}-1}\left(\sqrt{\left|p\left(1\right)-w^2\right|}\right)$ , $q_{\mathcal{l}}^{\mathrm{<mo>\; *\; </mo>}}\left(1\right)=q_{\mathcal{l}}\left(\sqrt{\left|p\left(1\right)-w^2\right|}\right)$ and $q_{\mathcal{l}-1}^{\mathrm{<mo>\; *\; </mo>}}\left(1\right)=q_{\mathcal{l}-1}\left(\sqrt{\left|p\left(1\right)-w^2\right|}\right)$ .

Taking n going to $\infty$ in ${\Lambda }_{p_1}\left(w\right)$ and ${\Lambda }_{p_2}\left(w\right)$ and using theorem 4.1, we have result 25. $\square$

4.3. Numerical Simulations

In this section, we denote $k=\mathcal{l}-1$, and then $k=0,1,2,\cdots$ when $\mathcal{l}=1,2,\cdots$ , and then we write ${\lambda }_k$ in the simulations. We will numerically compute the potential p, ${\lambda }_k$ , $k-{\lambda }_k$ , and $\log \left(\left|k-{\lambda }_k\right|\right)$ , $k=\mathrm{0,1,2,}\cdots$ . We will check numerically if the eigenvalues found in theorems (4.1) and (4.2) verify the properties 1 to 3 introduced in section 2. We will use the Matlab trial version [2021b] for it and vary the pulsations w.

We consider the case where the radial potential is defined by a piecewise constant function

$p\left(r\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}}{\gamma }_m{\chi }_{\left(r_{m-1},r_m\right)},r=\left|x\right|,$

where $n\ge 1$ , ${\gamma }_m\mathrm{,}{r}_m\in ℝ$ , with $m=1,2,\cdots ,n$ , $0=r_0<r_1<\cdot \cdot \cdot <r_{n-1}<r_n=1$ .

And the case where the radial potential is defined by a continuous function

$p\left(r\right),r=\left|x\right|,$

with $\left[0,1\right]={\displaystyle \underset{1}{\overset{n}{\cup }}}\left[r_{m-1},r_m\right],m=1,\cdots ,n$ where n is a large integer number,

$r_0=0$ , $r_n=1$ and $r_m-r_{m-1}=\frac{1}{n}$ , such that the Dirichlet problem for $-\Delta +p-w^2$ is well-posed.

We will choose potentials in different cases, such that when we take $w=0$ , we find the results found in [1] .

For first, we consider two examples of piecewise constant radial potential functions where the length of the interval $\left[r_{m-1}\mathrm{,}{r}_m\right]$ is arbitrary.

• We denote Case 1 the case where the potential value at each interval is a random value between $-2+w^2$ and $2+w^2$ with w arbitrary choisen.

Secondly, we consider an example of radial continuous potential function in $\left[0,1\right]={\displaystyle \underset{1}{\overset{n}{\cup }}}\left[r_{m-1},r_m\right],m=1,\cdots ,n$ where the length of the interval $\left[r_{m-1}\mathrm{,}{r}_m\right]$ is constant and equal to $\frac{1}{n}$ .

• We denote this example Case 2 taking $p\left(r\right)=r^2+w^2$ . We approximate it by two piecewise constant radial potential functions $p_1\left(r\right)$ and $p_2\left(r\right)$ such that $p_1\left(r\right)\le p\left(r\right)\le p_2\left(r\right)$ .

Using the results of the above section for these cases, we obtain the following results.

4.3.1. Case 1

First, we take $T=5$ in this case then, $w=\frac{2\pi }{T}$ . In Figure 1 there is an example of the potential p and in Figure 2 we see the corresponding eigenvalues. As excepted, we confirm in Figure 3 and Figure 4.

Secondly, we take $T=10$ in this case then, $w=\frac{2\pi }{T}$ . We have the results from Figures 5-8.

4.3.2. Case 2

First, we take $T=5$ in this case then, $w=\frac{2\pi }{T}$ . In Figure 9 we have the potential curve $p\left(r\right)=r^2+w^2$ in red and this with its approximation by a piecewise constant radial potential in black. In Figure 10 we see the corresponding eigenvalues. As excepted, we confirm in Figure 11 and Figure 12.

Figure 1. Radial potential in Case 1 for T = 5.

Figure 2. Eigenvalues associated with potential in Case 1 for T = 5.

Figure 3. (Eigenvalues-order)-limit in Case 1 for T = 5.

Figure 4. Confirmation eigenvalues limit in Case 1 for T = 5.

Figure 5. Radial potential in Case 1 for T = 10.

Figure 6. Eigenvalues associated with potential in Case 1 for T = 10.

Figure 7. (Eigenvalues-order)-limit in Case 1 for T = 10.

Figure 8. Confirmation eigenvalues limit in Case 1 for T = 10.

Figure 9. Continuous radial potential in Case 2 for T = 5.

Figure 10. Eigenvalues associated with Continuous radial potential in Case 2 for T = 5.

Figure 11. (Eigenvalues-order)-limit in Case 2 for T = 5.

Figure 12. Confirmation eigenvalues limit in Case 2 for T = 5.

Secondly, we take $T=10$ in this case then, $w=\frac{2\pi }{T}$ . We make the same simulations and have the results from Figures 13-16.

Remark 4.2 All these figures, in these different cases and for all $T>0$ , show that the eigenvalues defining the Dirichlet-to-Neumann map in theorem (4.2) verify the 1 to 3 properties considered in Section 2. Theorems are essential tools to determine the explicit expression of the DN map when f, defined in ${\mathbb{S}}^2$ , is

usually written as Fourier series $f\left(\theta \right)={\displaystyle \underset{\mathcal{l}=0}{\overset{\infty }{\sum }}}{\displaystyle \underset{k=-\mathcal{l}}{\overset{\mathcal{l}}{\sum }}}{\hat{f}}_{\mathcal{l}k}{Y}_{\mathcal{l}}^k\left(\theta \right)$ .

These results are very essential for studying the inverse problem for our hyperbolic differential equation transformed into a Schrödinger equation with energy w². We are interesting by the stability of the map that associates a Dirichlet-to-Neumann map to any potential. That is the purpose of the following section.

4.4. Stability

In this section, we are interested in the map

$\begin{array}{l}{\Lambda }_w\mathrm{<mo>\; :\; </mo>}{L}^{\infty }\left({\mathbb{S}}^2\right)\to \mathcal{L}\left(H^{1/2}\left({\mathbb{S}}^2\right)\mathrm{,}{H}^{-1/2}\left({\mathbb{S}}^2\right)\right)\\ p\mapsto {\Lambda }_p\left(w\right)\mathrm{,}\end{array}$ (26)

where the Dirichlet-to-Neumann map ${\Lambda }_p\left(w\right)$ is defined in theorem (4.1), see [1] . This is an important role in the inverse potential problem, which consists to study its inversion. In the mathematical literature, the Dirichlet to Neumann map is invertible on its range. Take into account how the measurements for the inverse problem for our Schrödinger equation with energy w², are made at ${\mathbb{S}}^2$ , we know that there may be some noise in the measured Dirichlet-to-Neumann map and that the noisy version of the real Dirichlet-to-Neumann map may not be a Dirichlet-to-Neumann map corresponding to piecewise constant potentials. Therefore, the stability analysis of ${\Lambda }_w$ , possibly including a regularization strategy useful for the numerical algorithm, would be interesting.

Figure 13. Continuous radial potential in Case 2 for T = 10.

Figure 14. Eigenvalues associated with Continuous radial potential in Case 2 for T = 10.

Figure 15. (Eigenvalues-order)-limit in Case 2 for T = 10.

Figure 16. Confirmation eigenvalues limit in Case 2 for T = 10.

Let us consider the following map ${\Lambda }_w\mathrm{<mo>\; :\; </mo>}p\mapsto {\Lambda }_p\left(w\right)$ . We are interested in a quantification of the difference of two potentials in the $L^{\infty }$ topology in terms of the distance of their associated Dirichlet-to-Neumann maps. This stability is necessary for all reconstruction algorithms to recover the potential from the Dirichlet-to-Neumann map, see [3] [5] . Then we would like to estimate $p_1-p_2$ in a certain norm defined by

${\Vert {\Lambda }_{p_1}\left(w\right)-{\Lambda }_{p_2}\left(w\right)\Vert }_{H^{1/2}\to H^{-1/2}}=\underset{f\in H^{1/2}\left({\mathbb{S}}^2\right)\mathrm{,}f\ne 0}{\sup }\frac{{\Vert \left({\Lambda }_{p_1}\left(w\right)-{\Lambda }_{p_2}\left(w\right)\right)f\Vert }_{H^{-1/2}\left({\mathbb{S}}^2\right)}}{{\Vert f\Vert }_{H^{1/2}(\; S\; 2\; )}}$

There are stability results when the potential $q_i$ , in a Schrödinger equation without energy w², has some smoothness.

In [6] , Joel and al. estimate the difference $q_1-q_2$ in a lower norm in terms of the difference of the Dirichlet-to-Neumann data maps for $\frac{d}{2}<s\in \mathbb{N}$ , $d\ge 3$ and ${\Vert q_i\Vert }_{s\mathrm{,}\Omega }\le M$ , with d the space dimension.

In [7] , for any $d\ge 3$ and $m>0$ , Mandache proved that there is $\alpha >0$ such that for every $M>0$ there is $C\left(M\right)>0$ , so that ${\Vert q_i\Vert }_{C^m}\le M,i=1,2$ implies

${\Vert q_1-q_2\Vert }_{L^{\infty }\left(\Omega \right)}\le C\left(M\right){\left(\log \left(1+{\Vert {\Lambda }_{q_1}-{\Lambda }_{q_2}\Vert }_{H^{1/2}\to H^{-1/2}}^{-1}\right)\right)}^{-\alpha }.$ (27)

He shows that (27) is optimal, in the sense that it cannot hold with $\alpha >m\left(2d-1\right)/d$ .

According [7] , for arbitrary potential q, the Lipschitz stability cannot be hold.

In [3] , M. Salo proved for $q_i\in {\text{L}}^{\infty }\left(\Omega \right)$ that a log-stability estimate holds when $q_1-q_2\in H^{-1}\left(\Omega \right)$ , $\Omega \subseteq {ℝ}^n$ is a bounded open set with ${\mathcal{C}}^{\infty }$ boundary, and dimension $d\ge 3$ .

We work in the case of piecewise constant arbitrary potentials p. Let us introduce for $n\ge 1$ and finite, $m=\mathrm{1,2,}\cdots \mathrm{,}n$ and $0=r_0<r_1<\cdots <r_{n-1}<r_n=1$ , the space

$\mathcal{Q}=\left\{p\in {\text{L}}^{\infty }\left(B\right)\mathrm{<mo>\; :\; </mo>}p\left(r\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}}{\gamma }_m{\chi }_{\left(r_{m-1}\mathrm{,}{r}_m\right)}\mathrm{,}r=\left|x\right|\mathrm{,}{r}_m\in \left[\mathrm{0,1}\right]\mathrm{,}{\gamma }_m\in ℝ\right\}$

In the case where ${\gamma }_m=w^2$ , $m=\mathrm{1,2,}\cdots \mathrm{,}n$ , we approximate it by $w^2-0.01$ .

Here, we establish Lipschitz stability by giving a constant, which depends on n and $\mathcal{l}$ on the dimension n of the potential space.

Our method follows the ideas in [1] [8] [9] , where Alessandrini and al. considered special classes of piecewise constant conductivities, and the method of Bereta and al. in [10] , for $n\ge 2$ .

The Lipschitz stability of an inverse boundary value problem for a Schrödinger type equation is proved by Bereta and al. in [10] , for $n\ge 2$ .

Here, we study the Lipschitz stability of the map that associates a Dirichlet-to-Neumann map to any piecewise constant potential p, our approach is analogous with the ideas in [1] .

• Theorem 4.3 Let the unit ball B in ${ℝ}^3$ and the scaled potential $q_i,i=1,2$ verifes

$p_i\left(r\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}}{\gamma }_m^i{\chi }_{\left(r_{m-1},r_m\right)},i=1,2,r=\left|x\right|,$

where $n\ge 1$ , ${\gamma }_m^i\mathrm{,}{r}_m\in ℝ$ , with $m=\mathrm{1,2,}\cdots \mathrm{,}n$ and $0=r_0<r_1<\cdots <r_{n-1}<r_n=1$ , and $k_m^i=\sqrt{\left|{\gamma }_m^i-w^2\right|}$ , such that the Dirichlet problems for $\left(-\Delta +p_i-w^2\right)$ is well-posed. Assume that $\left({\gamma }_n^1-w^2\right)\times \left({\gamma }_n^2-w^2\right)>0$ and there is a positive constant M such that

${\Vert p_i\Vert }_{L^{\infty }\left(B\right)}\le M\mathrm{.}$

Then there is a constant $C=C\left(n\mathrm{,}w\mathrm{,}M\mathrm{,}\mathcal{l}\right)$ for all w, such that:

$\left|{\gamma }_n^1-{\gamma }_n^2\right|\le C\left({\Vert {\Lambda }_{p_1}\left(w\right)-{\Lambda }_{p_2}\left(w\right)\Vert }_{H^{1/2}\to H^{-1/2}}\right)\mathrm{.}$ (28)

The result gives us the Lipschitz stability near to the edge ${\mathbb{S}}^2$ .

Proof of theorem 4.3. $q_i\in \mathcal{Q},i=1,2$ , then we can write

$p_1\left(r\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}}{\gamma }_m^1{\chi }_{\left(r_{m-1}^1,r_m^1\right)}$ and $p_2\left(r\right)={\displaystyle \underset{m=1}{\overset{n}{\sum }}}{\gamma }_m^2{\chi }_{\left(r_{m-1}^2,r_m^2\right)}$ , $r=\left|x\right|$ ,

for $n\ge 1$ , $m=1,2,\cdots ,n$ , ${\gamma }_m^1,r_m^1,{\gamma }_m^2,r_m^2\in ℝ$ , $0=r_0^1<r_1^1<\cdots <r_{n-1}^1<r_n^1=1$ and $0=r_0^2<r_1^2<\cdots <r_{n-1}^2<r_n^2=1$ . We assume that $r_m^1=r_m^2=r_m$ for all $m=0,1,2,\cdots$

We have for all $Y_{\mathcal{l}}^k\in H^{1/2}\left({\mathbb{S}}^2\right)\mathrm{,}\mathcal{l}\ge 1$ ,

${\Vert {\Lambda }_{p_1}-{\Lambda }_{p_2}\Vert }_{H^{1/2}\to H^{-1/2}}=\underset{Y_{\mathcal{l}}^k\in H^{1/2}\left({\mathbb{S}}^2\right)\mathrm{,}\mathcal{l}\ge 1}{\sup }{\Vert \left({\Lambda }_{p_1}\left(w\right)-{\Lambda }_{p_2}\left(w\right)\right)Y_{\mathcal{l}}^k\Vert }_{H^{-1/2}(\; S\; 2\; )}$

From theorem (4.1), we obtain

${\Vert \left({\Lambda }_{p_1}\left(w\right)-{\Lambda }_{p_2}\left(w\right)\right)Y_{\mathcal{l}}^k\Vert }_{H^{-1/2}\left({\mathbb{S}}^2\right)}={\left|{\lambda }_{\mathcal{l}-1}^1\left(w\right)-{\lambda }_{\mathcal{l}-1}^2\left(w\right)\right|}^2{\Vert Y_{\mathcal{l}}^k\Vert }^2\text{for}\text{all}\mathcal{l}\ge 1$

where ${\lambda }_{\mathcal{l}-1}^1\left(w\right)\mathrm{,}{\lambda }_{\mathcal{l}-1}^2\left(w\right)$ verify the relation (24) for all $n\ge 1$ and finite, $\mathcal{l}\ge 1$ . Then

${\Vert {\Lambda }_{p_1}-{\Lambda }_{p_2}\Vert }_{H^{1/2}\to H^{-1/2}}=\underset{\mathcal{l}\ge 1}{\sup }\left|{\lambda }_{\mathcal{l}-1}^1\left(w\right)-{\lambda }_{\mathcal{l}-1}^2\left(w\right)\right|$

Let denote $P_{n,\mathcal{l}}^1\left[p_1\right]=k_n^1\left({\left[A1\right]}_n^{\mathcal{l}}\left({p^{\prime }}_{\mathcal{l}}\left(k_n^1\right)-\frac{p_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{q^{\prime }}_{\mathcal{l}}\left(k_n^1\right)\right)+\frac{{q^{\prime }}_{\mathcal{l}}\left(k_n^1\right)}{q_{\mathcal{l}}^n\left(1\right)}\right)$ where $\left(\begin{array}{c}{\left[A1\right]}_1^{\mathcal{l}}\\ {\left[A1\right]}_n^{\mathcal{l}}\end{array}\right)$ is the solution of 22 associated to $p_1$ and $P_{n\mathrm{,}\mathcal{l}}^1\left[p_1\right]$ the $\mathcal{l}-1$ eingenvalue associated to $p_1$ .

And $P_{n,\mathcal{l}}^2\left[p_2\right]=k_n^2\left({\left[A2\right]}_n^{\mathcal{l}}\left({p^{\prime }}_{\mathcal{l}}\left(k_n^2\right)-\frac{p_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{q^{\prime }}_{\mathcal{l}}\left(k_n^2\right)\right)+\frac{{q^{\prime }}_{\mathcal{l}}\left(k_n^2\right)}{q_{\mathcal{l}}^n\left(1\right)}\right)$ where $\left(\begin{array}{c}{\left[A2\right]}_1^{\mathcal{l}}\\ {\left[A2\right]}_n^{\mathcal{l}}\end{array}\right)$ is the solution of 22 associated to $p_2$ and $P_{n\mathrm{,}\mathcal{l}}^2\left[p_2\right]$ the $\mathcal{l}-1$ eingenvalue associated to $p_2$ .

We have

${\lambda }_{\mathcal{l}-1}^1\left(w\right)-{\lambda }_{\mathcal{l}-1}^2\left(w\right)=P_{n,\mathcal{l}}^1\left[p_1\right]-P_{n,\mathcal{l}}^2\left[p_2\right]$

Then

${\Vert {\Lambda }_{p_1}-{\Lambda }_{p_2}\Vert }_{H^{1/2}\to H^{-1/2}}\ge \left|P_{n\mathrm{,}\mathcal{l}}^1\left[p_1\right]-P_{n\mathrm{,}\mathcal{l}}^2\left[p_2\right]\right|$

Let denote $A={\left[A1\right]}_n^{\mathcal{l}}\left({p^{\prime }}_{\mathcal{l}}\left(k_n^1\right)-\frac{p_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{q^{\prime }}_{\mathcal{l}}\left(k_n^1\right)\right)+\frac{{q^{\prime }}_{\mathcal{l}}\left(k_n^1\right)}{q_{\mathcal{l}}^n\left(1\right)}$ , $B={\left[A2\right]}_n^{\mathcal{l}}\left({p^{\prime }}_{\mathcal{l}}\left(k_n^2\right)-\frac{p_{\mathcal{l}}^n\left(1\right)}{q_{\mathcal{l}}^n\left(1\right)}{q^{\prime }}_{\mathcal{l}}\left(k_n^2\right)\right)+\frac{{q^{\prime }}_{\mathcal{l}}\left(k_n^2\right)}{q_{\mathcal{l}}^n\left(1\right)}$ and $D=\inf \left(A,B\right)$ .

We have $\left|P_{n\mathrm{,}\mathcal{l}}^1\left[p_1\right]-P_{n\mathrm{,}\mathcal{l}}^2\left[p_2\right]\right|\ge \left|k_n^1-k_n^2\right|D\ge \frac{\left|\left|{\gamma }_n^1-w^2\right|-\left|{\gamma }_n^2-w^2\right|\right|}{2\sqrt{M}}D$ for all $n\ge 1$ finite, $\mathcal{l}\ge 1$ and $M>0$ .

We have D is positive real depending on $n\mathrm{,}w\mathrm{,}\mathcal{l}$ and $\left({\gamma }_n^1-w^2\right)\times \left({\gamma }_n^2-w^2\right)>0$ . Then for all $M>0$

${\Vert {\Lambda }_{p_1}\left(w\right)-{\Lambda }_{p_2}\left(w\right)\Vert }_{H^{1/2}\to H^{-1/2}}\ge \frac{D\left(\mathcal{l}\mathrm{,}n\right)}{2\sqrt{M}}\left|{\gamma }_n^1-{\gamma }_n^2\right|\mathrm{.}$

If we take $C\left(\mathcal{l}\mathrm{,}n\mathrm{,}w\mathrm{,}M\right)=\frac{2\sqrt{M}}{D\left(\mathcal{l}\mathrm{,}w\mathrm{,}n\right)}$ , then we have the result. $\square$

Remark 4.3 The study of stability for a continuous radial potential function would follow from the study of stability in the case where the potential is a piecewise radial function. It is sufficient to approximate this continuous function by two piecewise radial functions.

5. Conclusion

We can conclude that when we consider that the potential $p\left(r\right)$ is radial function for the Schrödinger equation with energy w² defined in the unit ball which has no zero on the interval $\left(\mathrm{0,1}\right)$ , there exists an explicit formula for the Dirichlet-to-Neumann map given in theorem (4.1) for all piecewise constant radial potential function, and in theorem (4.2) for all continuous radial potential function. We have established a Lipschitz stability result near the edge of the domain with a constant depending on the dimension of the potential space and the order of the eigenvalues. The Lipschitz stability result of the map that associates a Dirichlet-to-Neumann map to any radial potential p is essential for the study of its inversion. This explicit formula of the Dirichlet-to-Neumann map ${\Lambda }_p\left(w\right)f$ in dimension 3 is a generalization of the results obtained in [1] . They are very important results which allow to study an inverse inverse for a hyperbolic differential equation ; they will open the way to the development of important research on the type of inverse problems. In the perspective, we will consider, among other things, the numerical study of the Dirichlet-to-Neumann map in the unit ball in ${ℝ}^3$ , the reconstructing of the potential from the Dirichlet-to-Neumann map both theoretically and numerically, and then the analytical study of the Dirichlet-to-Neumann map in the case where the potential has one or more zeros on the interval $\left(\mathrm{0,1}\right)$ . In addition, a Lipschitz type stability in the depth of the domain will be studied by giving an estimation constant.

Data Availability Statement

The data used to support the findings of this study are included within the article.

Appendix

We consider the spherical Bessel functions

$j_{\mathcal{l}}\left(r\right)=\sqrt{\frac{\pi }{2r}}{J}_{\mathcal{l}+\frac{1}{2}}\left(r\right),y_{\mathcal{l}}\left(r\right)=\sqrt{\frac{\pi }{2r}}{Y}_{\mathcal{l}+\frac{1}{2}}\left(r\right),$ (29)

that satisfies the equation

$r^2{y}^{″}+2r{y}^{\prime }+\left(r^2-\mathcal{l}\left(\mathcal{l}+1\right)\right)y=0.$

The modified spherical Bessel functions

$i_{\mathcal{l}}\left(r\right)=\sqrt{\frac{\pi }{2r}}{I}_{\mathcal{l}+\frac{1}{2}}\left(r\right),k_{\mathcal{l}}\left(r\right)=\sqrt{\frac{\pi }{2r}}{K}_{\mathcal{l}+\frac{1}{2}}\left(r\right),$ (30)

that satisfies the equation.

If $f_{\mathcal{l}}=j_{\mathcal{l}},y_{\mathcal{l}},i_{\mathcal{l}},{\left(-1\right)}^{\mathcal{l}+1}{k}_{\mathcal{l}}$ then

${f^{\prime }}_{\mathcal{l}}\left(r\right)=f_{\mathcal{l}-1}-\frac{\mathcal{l}+1}{r}{f}_{\mathcal{l}}\left(r\right)\mathrm{.}$ (31)

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Ndiaye, F. (2022) An Explicit Formula of the Dirichlet-to-Neumann Map for a Radial Potential in Dimension 3. Journal of Applied Mathematics and Physics, 10, 379-404. https://doi.org/10.4236/jamp.2022.102030
[2]	Mueller, J.L. and Siltanen, S. (2012) Linear and Nonlinear Inverse Problems with Practical Applications. SIAM, Society for Industrial and Applied Mathematics, Philadelphia. https://doi.org/10.1137/1.9781611972344
[3]	Faddeev, L.D. (1965) Growing Solutions of the Schrödinger Equation. Doklady Akademii Nauk SSSR, 165, 514-517.
[4]	Abramowitz, M. and Stregun, I.A. (1954) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. National Science Foundation and the Massachusetts Institute of Technology, Cambridge, 15-16.
[5]	Choudhury, A.P. and Heck, H. (2017) Increasing Stability for the Inverse Problem for the Schrödinger Equation. Mathematics. Mathematical Methods in the Applied Sciences, 41, 606-614.
[6]	Joel, F., Mikko, S. and Gunther, U. (2001) The Calderón Problem—An Introduction to Inverse Problems. Measurement Science and Technology, 12, 1061-1068.
[7]	Mandache, N. (2001) Exponential Instability in an Inverse Problem for Schrödinger Equation. Inverse Problem, 17, 1435-1444. https://doi.org/10.1088/0266-5611/17/5/313
[8]	Alessandrini, G. and Vessella, S. (2005) Lipschitz Stability for the Inverse Conductivity Problem. Advances in Applied Mathematics, 35, 207-241. https://doi.org/10.1016/j.aam.2004.12.002
[9]	Alessandrini, G., De Hoop, M.V., Graburro, R. and Sincich, E. (2017) Lipschitz Stability for the Electrostatic Inverse Boundary Value Problem with Piecewise Linear Conductivities. Journal de mathématiques pures et appliquées, 107, 638-664. https://doi.org/10.1016/j.matpur.2016.10.001
[10]	Beretta, E. and Francini, E. (2011) Lipschitz Stability for the Electrical Impedance Tomography Problem: The Complex Case. Communications in Partial Differential Equations, 36, 1723-1749. https://doi.org/10.1080/03605302.2011.552930