Existence and Uniqueness Results for a Fully Third-Order Boundary Value Problem

Xiaoming Liu, Yongxiang Li^*

Department of Mathematics, Northwest Normal University, Lanzhou, China.

DOI: 10.4236/apm.2023.138033                

Abstract

The boundary value problems of the third-order ordinary differential equation have many practical application backgrounds and their some special cases have been studied by many authors. However, few scholars have studied the boundary value problems of the complete third-order differential equations u′′′(t) = f (t,u(t),u′(t),u′′(t)). In this paper, we discuss the existence and uniqueness of solutions and positive solutions of the fully third-order ordinary differential equation on [0,1] with the boundary condition u(0) = u′(1) = u′′(1) = 0. Under some inequality conditions on nonlinearity f some new existence and uniqueness results of solutions and positive solutions are obtained.

Keywords

Fully Third-Order BVP, Solution, Positive Solution, Existence and Uniqueness, Inequality Conditions

1. Introduction and Main Results

In this paper we discuss existence of solutions for third-order boundary value problem (BVP) with fully nonlinear term

$\{\begin{array}{l}{{u^{\prime }}^{\prime }}^{\prime }\left(t\right)=f\left(t,u\left(t\right),u^{\prime }\left(t\right),{u^{\prime }}^{\prime }\left(t\right)\right),t\in I,\\ u\left(0\right)=u^{\prime }\left(1\right)={u^{\prime }}^{\prime }\left(1\right)=0,\end{array}$ (1.1)

where $I=\left[\mathrm{0,1}\right]$ , $f\mathrm{<mo>\; :\; </mo>}I\times {ℝ}^3\to ℝ$ is a continuous nonlinearity.

The boundary value problems of the third-order ordinary differential equation have many practical application backgrounds. They appear in many different areas of applied mathematics and physics, such as the deflection of the curved beam with constant or variable cross section, the three-layer beam, electromagnetic wave or gravity driven flows, etc. [1] [2] . These problems have attracted the attention of many authors, and some theorems and methods of nonlinear functional analysis have been applied to research the solvability of these problems, such as the topological transversality [3] , the monotone iterative technique [4] [5] [6] , the method of upper and lower solutions [7] [8] [9] , Leray-Schauder degree [10] [11] [12] [13] , the fixed point theory of increasing operator [14] [15] , the fixed-point theorem of Guo-Krasnoselskii’s cone expansion or compression type [16] [17] [18] [19] .

However, most of the above work is about the special case of that nonlinearity f that does not contain derivative term $u^{\prime }$ or ${u^{\prime }}^{\prime }$ , only a few authors consider the case with fully nonlinear term. Recently, the authors of Reference [20] considered the fully third-order BVP (1.1) and they showed when nonlinearity $f\left(t\mathrm{,}x\mathrm{,}y\mathrm{,}z\right)$ is nonnegative and superlinear or sublinear growth on $\left(x\mathrm{,}y\mathrm{,}z\right)$ at origin and infinity, BVP (1.1) has at least one positive solution by using the fixed point index theory in cones. In this paper, we will use different methods to establish the existence and uniqueness results of solution and positive solution for general BVP (1.1) under some simple inequality conditions without restriction of the growth of nonlinearity.

Let $r>0$ be a constant. We define two domains of ${ℝ}^3$ by

$D_r=\left\{\left(x\mathrm{,}y\mathrm{,}z\right)\mathrm{<mo>\; |\; </mo>}\left|x\right|\le \frac{r}{6}\mathrm{,}\left|y\right|\le \frac{r}{2}\mathrm{,}\left|z\right|\le r\right\}\mathrm{,}$ (1.2)

$D_r^{+}=\left\{\left(x\mathrm{,}y\mathrm{,}z\right)\mathrm{<mo>\; |\; </mo>0}\le x\le \frac{r}{6}\mathrm{,}0\le y\le \frac{r}{2}\mathrm{,}-r\le z\le 0\right\}\mathrm{.}$ (1.3)

Let $f\mathrm{<mo>\; :\; </mo>}I\times {ℝ}^3\to ℝ$ be continuous and set

$f_r=\max \left\{\left|f\left(t\mathrm{,}x\mathrm{,}y\mathrm{,}z\right)\right|\mathrm{<mo>\; |\; </mo>}t\in I\mathrm{,}\left(x\mathrm{,}y\mathrm{,}z\right)\in D_r\right\}\mathrm{,}$ (1.4)

$f_r^{+}=\max \left\{f\left(t\mathrm{,}x\mathrm{,}y\mathrm{,}z\right)\mathrm{<mo>\; |\; </mo>}t\in I\mathrm{,}\left(x\mathrm{,}y\mathrm{,}z\right)\in D_r^{+}\right\}\mathrm{.}$ (1.5)

Our main results are as follows:

Theorem 1.1. Let $f\mathrm{<mo>\; :\; </mo>}I\times {ℝ}^3\to ℝ$ be continuous. If there exists a constant $r>0$ such that $f_r\le r$ , then BVP (1.1) has a solution u satisfies

$\left(u\left(t\right)\mathrm{,}{u}^{\prime }\left(t\right)\mathrm{,}{u^{\prime }}^{\prime }\left(t\right)\right)\in D_r\mathrm{,}t\in I\mathrm{.}$ (1.6)

Theorem 1.2. Under the assumptions of Theorem 1.1, if f satisfies the following Lipschtz type condition in $D_r$

(H1) there exist constants $a_0\mathrm{,}{a}_1\mathrm{,}{a}_2\ge 0$ restricted by

$\frac{a_0}{6}+\frac{a_1}{2}+a_2<1,$ (1.7)

such that

$\left|f\left(t\mathrm{,}{x}_2\mathrm{,}{y}_2\mathrm{,}{z}_2\right)-f\left(t\mathrm{,}{x}_1\mathrm{,}{y}_1\mathrm{,}{z}_1\right)\right|\le a_0\left|x_2-x_1\right|+a_1\left|y_2-y_1\right|+a_2\left|z_2-z_1\right|\mathrm{,}$ (1.8)

for any $t\in I$ and $\left(x_1\mathrm{,}{y}_1\mathrm{,}{z}_1\right)\mathrm{,}\left(x_2\mathrm{,}{y}_2\mathrm{,}{z}_2\right)\in D_r$ , then BVP (1.1) has a unique solution satisfies (1.6).

Let 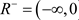$R^{+}=\left[\mathrm{0,}\infty \right)$ ,. When nonlinearity f is nonnegative, we have the following existence theorems of positive solution:

Theorem 1.3. Let $f\mathrm{<mo>\; :\; </mo>}I\times {ℝ}^{+}\times {ℝ}^{+}\times {ℝ}^{-}\to {ℝ}^{+}$ be continuous. If there exists a constant $r>0$ such that $f_r^{+}\le r$ , then BVP (1.1) has a solution u satisfies

$\left(u\left(t\right)\mathrm{,}{u}^{\prime }\left(t\right)\mathrm{,}{u^{\prime }}^{\prime }\left(t\right)\right)\in D_r^{+}\mathrm{,}t\in I\mathrm{.}$ (1.9)

Theorem 1.4. Under the assumptions of Theorem 1.3, if there exist constants $a_0\mathrm{,}{a}_1\mathrm{,}{a}_2\ge 0$ restricted by (1.7) such that f satisfies the Lipschtz condition (1.8) in $D_r^{+}$ , then BVP (1.1) has a unique solution satisfies (1.9).

Note that (1.9) implies $u\left(t\right)\ge 0$ for every $t\in I$ , and hence it is a positive solution of BVP (1.1).

If f satisfies that

$\underset{r\to \infty }{\lim \inf }\frac{f_r}{r}<1,$ (1.10)

we easily verify that for any $R>0$ , there exists $r>R$ such that $f_r<r$ . Hence by Theorem 1.1, we have:

Corollary 1.5. If $f\mathrm{<mo>\; :\; </mo>}I\times {ℝ}^3\to ℝ$ be continuous and satisfies (1.10), BVP (1.1) has at least one solution.

Similarly, by Theorem 1.3, we have:

Corollary 1.6. Let $f\mathrm{<mo>\; :\; </mo>}I\times {ℝ}^{+}\times {ℝ}^{+}\times {ℝ}^{-}\to {ℝ}^{+}$ be continuous and satisfy

$\underset{r\to \infty }{\lim \inf }\frac{f_r^{+}}{r}<1.$ (1.11)

Then BVP (1.1) has at least one positive solution.

The proof of Theorems 1.1 - 1.4 will be given in next section. Some applications and examples are presented in Section 3 to illustrate the applicability of our results.

2. Proof of the Main Results

Let $C\left(I\right)$ denote the Banach space of all continuous function $u\left(t\right)$ on I with norm ${\Vert u\Vert }_C={\max }_{t\in I}\left|u\left(t\right)\right|$ . Generally for $n\in \mathbb{N}$ , we use $C^n\left(I\right)$ to denote the Banach space of all nth-order continuous differentiable function on I with the norm ${\Vert u\Vert }_{C^n}=\max \left\{{\Vert u\Vert }_C\mathrm{,}{\Vert u^{\prime }\Vert }_C\mathrm{,}\cdots ,{\Vert u^{\left(n\right)}\Vert }_C\right\}$ . Let $C^{+}\left(I\right)$ be the cone of nonnegative functions in $C\left(I\right)$ .

To discuss BVP (1.1), we first consider the corresponding linear boundary value problem (LBVP)

$\{\begin{array}{l}{{u^{\prime }}^{\prime }}^{\prime }\left(t\right)=h\left(t\right),t\in I,\\ u\left(0\right)=u^{\prime }\left(1\right)={u^{\prime }}^{\prime }\left(1\right)=0.\end{array}$ (2.1)

where $h\in C\left(I\right)$ is a given function.

Lemma 2.1. For every $h\in C\left(I\right)$ , LBVP (2.1) has a unique solution $u:=Sh\in C^3\left(I\right)$ , which satisfies

${\Vert u\Vert }_C\le \frac{1}{6}{\Vert h\Vert }_C\mathrm{,}{\Vert u^{\prime }\Vert }_C\le \frac{1}{2}{\Vert h\Vert }_C\mathrm{,}{\Vert {u^{\prime }}^{\prime }\Vert }_C\le {\Vert h\Vert }_C\mathrm{.}$ (2.2)

Moreover, the solution operator $S\mathrm{<mo>\; :\; </mo>}C\left(I\right)\to C^3\left(I\right)$ is a bounded linear operator. When $h\in C^{+}\left(I\right)$ , the solution of LBVP (2.1) satisfies

$u\left(t\right)\ge \mathrm{0,}{u}^{\prime }\left(t\right)\ge \mathrm{0,}{u^{\prime }}^{\prime }\left(t\right)\le \mathrm{0,}t\in I\mathrm{.}$ (2.3)

Proof. Let. Integrating the Equation (2.1), we obtain that

$u\left(t\right)={\displaystyle {\int }_0^t}\tau \text{d}\tau {\displaystyle {\int }_{\tau }^1}h\left(s\right)\text{d}s+{\displaystyle {\int }_t^1}t\text{d}\tau {\displaystyle {\int }_{\tau }^1}h\left(s\right)\text{d}s:=Sh\left(t\right),t\in I.$ (2.4)

by this expression we have

$\begin{array}{l}{u}^{\prime }\left(t\right)={\displaystyle {\int }_t^1}\text{d}\tau {\displaystyle {\int }_{\tau }^1}h\left(s\right)\text{d}s,t\in I,\\ {u^{\prime }}^{\prime }\left(t\right)=-{\displaystyle {\int }_t^1}h\left(s\right)\text{d}s,t\in I,\\ {{u^{\prime }}^{\prime }}^{\prime }\left(t\right)=h\left(t\right),t\in I.\end{array}$ (2.5)

Hence $u\in C^3\left(I\right)$ is a unique solution of LBVP (2.1). For every $t\in I$ , by (2.4) and (2.5), we have

$\begin{array}{c}\left|u\left(t\right)\right|\le {\displaystyle {\int }_0^t}\tau \text{d}\tau {\displaystyle {\int }_{\tau }^1}\left|h\left(s\right)\right|\text{d}s+{\displaystyle {\int }_t^1}t\text{d}\tau {\displaystyle {\int }_{\tau }^1}\left|h\left(s\right)\right|\text{d}s\\ \le {\displaystyle {\int }_0^t}\tau \left(1-\tau \right)\text{d}\tau {\Vert h\Vert }_C+{\displaystyle {\int }_t^1}t\left(1-\tau \right)\text{d}\tau {\Vert h\Vert }_C\\ =\frac{1}{6}\left(1-{\left(1-t\right)}^3\right){\Vert h\Vert }_C\le \frac{1}{6}{\Vert h\Vert }_C,\end{array}$

$\begin{array}{c}\left|u^{\prime }\left(t\right)\right|\le {\displaystyle {\int }_t^1}\text{d}\tau {\displaystyle {\int }_{\tau }^1}\left|h\left(s\right)\right|\text{d}s\le {\displaystyle {\int }_t^1}\left(1-\tau \right)\text{d}\tau {\Vert h\Vert }_C\\ \le \frac{1}{2}{\left(1-t\right)}^2{\Vert h\Vert }_C\le \frac{1}{2}{\Vert h\Vert }_C\mathrm{,}\end{array}$

$\left|{u^{\prime }}^{\prime }\left(t\right)\right|\le {\displaystyle {\int }_t^1}\left|h\left(s\right)\right|\text{d}s\le \left(1-t\right){\Vert h\Vert }_C\le {\Vert h\Vert }_C\mathrm{,}$

$\left|{{u^{\prime }}^{\prime }}^{\prime }\left(t\right)\right|\le \left|h\left(t\right)\right|\le {\Vert h\Vert }_C\mathrm{.}$

This means that (2.2) holds and

${\Vert Sh\Vert }_{C^3}={\Vert u\Vert }_{C^3}\le {\Vert h\Vert }_C\mathrm{.}$

Hence $S\mathrm{<mo>\; :\; </mo>}C\left(I\right)\to C^3\left(I\right)$ is bounded. When $h\in C^{+}\left(I\right)$ , by (2.4) and (2.5), (2.3) holds. $\square$

Proof of Theorem 1.1. Define a mapping $F\mathrm{<mo>\; :\; </mo>}{C}^2\left(I\right)\to C\left(I\right)$ by

$F\left(u\right)\left(t\right)\mathrm{<mo>\; :\; </mo>}=f\left(t\mathrm{,}u\left(t\right)\mathrm{,}{u}^{\prime }\left(t\right)\mathrm{,}{u^{\prime }}^{\prime }\left(t\right)\right)\mathrm{,}t\in I\mathrm{.}$ (2.6)

Then by the continuity of f, $F\mathrm{<mo>\; :\; </mo>}{C}^2\left(I\right)\to C\left(I\right)$ is continuous and it maps every bounded in $C^2\left(I\right)$ into a bounded set in $C\left(I\right)$ . By the compactness of the embedding $C^3\left(I\right)$ ↪ $C^2\left(I\right)$ , the solution operator of LBVP (2.1) $S\mathrm{<mo>\; :\; </mo>}C\left(I\right)\to C^2\left(I\right)$ is completely continuous. Hence, the composition operator of S and F

$A\mathrm{<mo>\; :\; </mo>}=S\circ F\mathrm{<mo>\; :\; </mo>}{C}^2\left(I\right)\to C^2\left(I\right)$ (2.7)

is completely continuous. By the definitions of S and F, the solution of BVP (1.1) is equivalent to the fixed point of A. We use the Schauder fixed point theorem to show A has a fixed u satisfied (1.6).

For the positive constant r in Theorem 1.1, define a bounded subset of $C^2\left(I\right)$ by

${\Omega }_r=\left\{u\in C^2\left(I\right)|{\Vert u\Vert }_C\le \frac{r}{6},{\Vert u^{\prime }\Vert }_C\le \frac{r}{2},{\Vert {u^{\prime }}^{\prime }\Vert }_C\le r\right\}.$ (2.8)

Clearly, 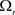is convex and closed in $C^2\left(I\right)$ . We show that

$A\left({\Omega }_r\right)=S\left(F\left({\Omega }_r\right)\right)\subset {\Omega }_r\mathrm{.}$ (2.9)

For any $u\in {\Omega }_r$ , set $h=F\left(u\right)$ . Then $h\in C\left(I\right)$ and $Au=S\left(F\left(u\right)\right)=Sh$ . By the definitions of ${\Omega }_r$ and $D_r$ , u satisfies

$\left(u\left(t\right)\mathrm{,}{u}^{\prime }\left(t\right)\mathrm{,}{u^{\prime }}^{\prime }\left(t\right)\right)\in D_r\mathrm{,}t\in I\mathrm{.}$

For every $t\in I$ , by the definition of $f_r$ , we obtain that

$\left|h\left(t\right)\right|=\left|F\left(u\right)\left(t\right)\right|=\left|f\left(t,u\left(t\right),u^{\prime }\left(t\right),{u^{\prime }}^{\prime }\left(t\right)\right)\right|\le f_r\le r,$ (2.10)

and hence ${\Vert h\Vert }_C\le r$ . By this and (2.2) of Lemma 2.1, $Au=Sh\in {\Omega }_r$ . Thus (2.9) holds. By the Schauder fixed point theorem, A has a fixed u in ${\Omega }_r$ . By the definition of ${\Omega }_r$ , u satisfies (1.6) and it is a solution of BVP (1.1). $\square$

Proof of Theorem 1.2. By Theorem 1.1, BVP (1.1) has at least one solution satisfies (1.6). Let $u_1\mathrm{,}{u}_2\in C^3\left(I\right)$ be two solutions of BVP (1) satisfied (1.6). Then $u_1=S\left(F\left(u_1\right)\right)$ , $u_2=S\left(F\left(u_2\right)\right)$ . Set $u=u_2-u_1$ and $h=F\left(u_2\right)-F\left(u_1\right)$ . Then

$u=S\left(F\left(u_2\right)\right)-S\left(F\left(u_2\right)\right)=S\left(F\left(u_2\right)-F\left(u_2\right)\right)=Sh.$

By the definition of the operator S, u is the solution of LBVP (2.1). Hence, $u=Sh$ satisfies (2.2). By the assumption (H1) and (2.2), for every $t\in I$ , we have

$\begin{array}{c}\left|h\left(t\right)\right|=\left|F\left(u_2\right)\left(t\right)-F\left(u_1\right)\left(t\right)\right|\\ =\left|f\left(t,u_2\left(t\right),{u^{\prime }}_2\left(t\right),{u^{″}}_2\left(t\right)\right)-f\left(t,u_1\left(t\right),{u^{\prime }}_1\left(t\right),{u^{″}}_1\left(t\right)\right)\right|\\ \le a_0\left|u_2\left(t\right)-u_1\left(t\right)\right|+a_1\left|{u^{\prime }}_2\left(t\right)-{u^{\prime }}_1\left(t\right)\right|+a_2\left|{u^{″}}_2\left(t\right)-{u^{″}}_1\left(t\right)\right|\\ \le a_0{\Vert u_2-u_1\Vert }_C+a_1{\Vert {u^{\prime }}_2-{u^{\prime }}_1\Vert }_C+a_2{\Vert {u^{″}}_2-{u^{″}}_1\Vert }_C\\ =a_0{\Vert u\Vert }_C+a_1{\Vert u^{\prime }\Vert }_C+a_2{\Vert u^{″}\Vert }_C\\ =\left(\frac{a_0}{6}+\frac{a_1}{2}+a_2\right){\Vert h\Vert }_C.\end{array}$

From this it follows that

${\Vert h\Vert }_C\le \left(\frac{a_0}{6}+\frac{a_1}{2}+a_2\right){\Vert h\Vert }_C\mathrm{.}$ (2.11)

This implies that ${\Vert h\Vert }_C=0$ , so that $u=Sh=0$ . Hence $u_2=u_1$ . This means BVP (1.1) has only one solution satisfied (1.6). $\square$

Proof of Theorem 1.3. Define a closed convex cone of $C^2\left(I\right)$ by

$K=\left\{u\in C^2\left(I\right)|u\left(t\right)\ge 0,u^{\prime }\left(t\right)\ge 0,{u^{\prime }}^{\prime }\left(t\right)\le 0,t\in I\right\}.$ (2.12)

By the continuity of $f\mathrm{<mo>\; :\; </mo>}I\times {ℝ}^{+}\times {ℝ}^{+}\times {ℝ}^{-}\to {ℝ}^{+}$ , the mapping $F\mathrm{<mo>\; :\; </mo>}K\to C^{+}\left(I\right)$ defined by (2.6) is continuous and it maps every bounded in K into a bounded set in $C^{+}\left(I\right)$ . By (2.3), the solution operator S of BVP (2.1) satisfies

$S\left(C^{+}\left(I\right)\right)\subset K\mathrm{.}$ (2.13)

Hence, the composition operator $A=S\circ F:K\to K$ is completely continuous. Set

${\Omega }_r^{+}={\Omega }_r\cap K\mathrm{.}$ (2.14)

Then ${\Omega }_r^{+}$ is a bounded closed convex set in $C^2\left(I\right)$ . Similar to the proof of (2.9), we can obtain that

$A\left({\Omega }_r^{+}\right)=S\left(F\left({\Omega }_r^{+}\right)\right)\subset {\Omega }_r^{+}\mathrm{.}$ (2.15)

Therefore, by the Schauder fixed point theorem, A has a fixed u in ${\Omega }_r^{+}$ . By the definition of ${\Omega }_r^{+}$ , u satisfies (1.9) and is a solution of BVP (1.1). $\square$

Proof of Theorem 1.4. The existence of a solution satisfied (1.9) is guaranteed by Theorem 1.3. Let $u_1\mathrm{,}{u}_2\in C^3\left(I\right)$ be two solutions of BVP (1) satisfied (1.9). Then $u_1\mathrm{,}{u}_2\in {\Omega }_r^{+}$ and $u_1=S\left(F\left(u_1\right)\right)$ , $u_2=S\left(F\left(u_2\right)\right)$ . Set $u=u_2-u_1$ and $h=F\left(u_2\right)-F\left(u_1\right)$ . Then $h\in C\left(I\right)$ and $u=Sh$ . Similar to the argument in Theorem 1.2, we can prove that h satisfies (2.11). From (2.11) it follows that $h=0$ . So we have $u=Sh=0$ , that is $u_1=u_2$ . Hence BVP (1.1) has a unique solution satisfied (1.9).

3. Applications

In this section, we use the main results obtained in Section 1 to deduce some concrete existence and uniqueness theorems for some third-order boundary value problems.

Firstly, our main results can be applied to BVP (1.1) under the nonlinearity $f\left(t\mathrm{,}x\mathrm{,}y\mathrm{,}z\right)$ is linear growth on x, y and z.

Theorem 3.1. Let $f\mathrm{<mo>\; :\; </mo>}I\times {ℝ}^3\to ℝ$ be continuous and satisfy the following linear growth condition.

(H2) there exist constants $a_0\mathrm{,}{a}_1\mathrm{,}{a}_2\ge 0$ restricted by (1.7) and $c>0$ , such that

$\left|f\left(t\mathrm{,}x\mathrm{,}y\mathrm{,}z\right)\right|\le a_0\left|x\right|+a_1\left|y\right|+a_2\left|z\right|+c\mathrm{,}\left(t\mathrm{,}x\mathrm{,}y\mathrm{,}z\right)\in I\times {ℝ}^3\mathrm{.}$ (3.1)

Then BVP (1.1) has at least one solution.

Proof. For $r>0$ , when $t\in I$ and $\left(x\mathrm{,}y\mathrm{,}z\right)\in D_r$ , by (3.1) and the definition of $D_r$ , we have

$\left|f\left(t\mathrm{,}x\mathrm{,}y\mathrm{,}z\right)\right|\le a_0\left|x\right|+a_1\left|y\right|+a_2\left|z\right|+c\le \left(\frac{a_0}{6}+\frac{a_1}{2}+a_2\right)r+c\mathrm{.}$

Hence, by (1.4) and (1.7) we have

$\frac{f_r}{r}\le \frac{a_0}{6}+\frac{a_1}{2}+a_2+\frac{c}{r}\to \frac{a_0}{6}+\frac{a_1}{2}+a_2<1,r\to \infty .$ (3.2)

Hence when r large enough, $\frac{f_r}{r}<1$ , and the assumption of Theorem 1.1 is satisfied. By Theorem 1.1, BVP (1.1) has at least one solution. $\square$

In Theorem 3.1, when f is nonnegative, any solution u of BVP (1.1) is positive. In fact, since $h=F\left(u\right)\in C^{+}\left(I\right)$ , by Lemma 2.1, $u=S\left(F\left(u\right)\right)=Sh$ satisfies (2.2), and u is a positive solution of BVP(1.1). That is:

Corollary 3.2. Let $f\mathrm{<mo>\; :\; </mo>}I\times {ℝ}^3\to {ℝ}^{+}$ be continuous and satisfy the assumption (H2). Then BVP (1.1) has at least one positive solution.

Strengthening the condition of Theorem 3.1, we have the following uniqueness result:

Theorem 3.3. Let $f\mathrm{<mo>\; :\; </mo>}I\times {ℝ}^3\to ℝ$ be continuous and satisfy the following global Lipschitz condition.

(H3) there exist constants $a_0\mathrm{,}{a}_1\mathrm{,}{a}_2\ge 0$ restricted by (1.7) such that

$\left|f\left(t\mathrm{,}{x}_2\mathrm{,}{y}_2\mathrm{,}{z}_2\right)-f\left(t\mathrm{,}{x}_1\mathrm{,}{y}_1\mathrm{,}{z}_1\right)\right|\le a_0\left|x_2-x_1\right|+a_1\left|y_2-y_1\right|+a_2\left|z_2-z_1\right|\mathrm{,}$ (3.3)

for any $t\in I$ and $\left(x_1\mathrm{,}{y}_1\mathrm{,}{z}_1\right)\mathrm{,}\left(x_2\mathrm{,}{y}_2\mathrm{,}{z}_2\right)\in {ℝ}^3$ , Then BVP (1.1) has a unique solution.

Proof. For any $t\in I$ and $\left(x\mathrm{,}y\mathrm{,}z\right)\in {ℝ}^3$ , in Condition (H3) choosing $\left(x_2\mathrm{,}{y}_2\mathrm{,}{z}_2\right)=\left(x\mathrm{,}y\mathrm{,}z\right)$ , $\left(x_1\mathrm{,}{y}_1\mathrm{,}{z}_1\right)=\left(\mathrm{0,0,0}\right)$ , and setting $c={\max }_{t\in I}\left|f\left(t\mathrm{,0,0,0}\right)\right|+1$ , we obtain that (H1) holds. By Theorem 1.1, BVP (1.1) has at least one solution.

By (3.2), there exists $R_0>0$ such that $f_r<r$ for $r>R_0$ . Let $u_1\mathrm{,}{u}_2\in C^3\left(I\right)$ be two solutions of BVP (1). Setting

$\begin{array}{l}{r}_1=\max \left\{6{\Vert u_1\Vert }_C,2{\Vert {u^{\prime }}_1\Vert }_C,{\Vert {u^{″}}_1\Vert }_C\right\},\\ r_2=\max \left\{6{\Vert u_2\Vert }_C,2{\Vert {u^{\prime }}_2\Vert }_C,{\Vert {u^{″}}_2\Vert }_C\right\},\end{array}$ (3.4)

and choosing $r>\max \left\{R_0,r_1,r_2\right\}$ , we have

$f_r<r\text{and}{\Vert u_i\Vert }_C\le \frac{r}{6},{\Vert {u^{\prime }}_i\Vert }_C\le \frac{r}{2},{\Vert {u^{″}}_i\Vert }_C\le r,i=1,2.$ (3.5)

Hence $u_1$ and $u_2$ satisfy (1.6). By the uniqueness conclusion of Theorem 1.2, $u_1=u_2$ . Hence BVP (1.1) has a unique solution. $\square$

By Theorem 3.3 and Corollary 3.2, we have:

Corollary 3.4. Let $f\mathrm{<mo>\; :\; </mo>}I\times {ℝ}^3\to {ℝ}^{+}$ be continuous and satisfy the assumption (H3). Then BVP (1.1) has a unique positive solution.

Secondly, our main results can be also applied to BVP (1.1) with superlinear growth nonlinearity f.

Example 3.1. Consider the following superlinear third-order boundary value problem

$\{\begin{array}{l}{{u^{\prime }}^{\prime }}^{\prime }\left(t\right)=u^2\left(t\right)+{u^{\prime }}^2\left(t\right)+u\left(t\right){{u^{\prime }}^{\prime }}^2\left(t\right)+\frac{1}{6}\sin \pi t,t\in \left[0,1\right],\\ u\left(0\right)=u^{\prime }\left(1\right)={u^{\prime }}^{\prime }\left(1\right)=0.\end{array}$ (3.6)

Corresponding to BVP (1.1), the nonlinearity is

$f\left(t,x,y,z\right)=x^2+y^2+x{z}^2+\frac{1}{6}\sin \pi t,$ (3.7)

which is superlinear on x, y and z. We verify that f satisfies the condition of Theorem 1.3 for $r=1$ .

For every $t\in I$ and $\left(x\mathrm{,}y\mathrm{,}z\right)\in D_1^{+}$ , by (3.7)

$0\le f\left(t,x,y,z\right)\le \frac{1}{36}+\frac{1}{4}+\frac{1}{2}+\frac{1}{6}=\frac{17}{18}<1.$ (3.8)

Hence $f_1^{+}\le 1$ . That is, f satisfies the condition of Theorem 1.3 for $r=1$ . By Theorem 1.3, BVP (3.6) has at least one positive solution.

It should be noted that this existence result of BVP (3.6) can not be obtained from ( [20] , Theorem 1.1), since the corresponding nonlinearity f does not satisfy the Condition (F1) of ( [20] , Theorem 1.1).

Funding

This research is supported by NNSFs of China (12061062, 11661071).

Conflicts of Interest

The authors declare that they have no conflicts of interest.

References

[1]	Greguš, M. (1987) Third Order Linear Differential Equations. Reidel, Dordrecht.
[2]	Greguš, M. (1994) Two Sorts of Boundary-Value Problems of Nonlinear Third Order Differential Equations. Archivum Mathematicum, 30, 285-292. http://dml.cz/dmlcz/107515
[3]	O’Regan, D.J. (1987) Topological Transversality: Application to Third-Order Boundary Value Problems. SIAM Journal on Mathematical Analysis, 18, 630-641. https://doi.org/10.1137/0518048
[4]	Omari, P. and Trombetta, M. (1992) Remarks on the Lower and Upper Solutions Method for Second and Third-Order Periodic Boundary Value Problems. Applied Mathematics and Computation, 50, 1-21. https://doi.org/10.1016/0096-3003(92)90007-N
[5]	Cabada, A. (1994) The Method of Lower and Upper Solutions for Second, Third, Forth, and Higher Order Boundary Value Problems. Journal of Mathematical Analysis and Applications, 185, 302-320. https://doi.org/10.1006/jmaa.1994.1250
[6]	Cabada, A. (1995) The Method of Lower and Upper Solutions for Third-Order Periodic Boundary Value Problems. Journal of Mathematical Analysis and Applications, 195, 568-589. https://doi.org/10.1006/jmaa.1995.1375
[7]	Cabada, A. and Lois, S. (1999) Existence of Solution for Discontinuous Third Order Boundary Value Problems. Journal of Computational and Applied Mathematics, 110, 105-114. https://doi.org/10.1016/S0377-0427(99)00199-5
[8]	Cabada, A., Grossinho, M.R. and Minhos, F. (2003) On the Solvability of Some Discontinuous Third Order Nonlinear Differential Equations with Two Point Boundary Conditions. Journal of Mathematical Analysis and Applications, 285, 174-190. https://doi.org/10.1016/S0022-247X(03)00388-3
[9]	Grossinho, M.R. and Minhós, F.M. (2001) Existence Result for Some Third Order Separated Boundary Value Problems. Nonlinear Analysis: Theory, Methods & Applications, 47, 2407-2418. https://doi.org/10.1016/S0362-546X(01)00364-9
[10]	Grossinho, M.R., Minhos, F.M. and Santos, A.I. (2005) Solvability of Some Third-Order Boundary Value Problems with Asymmetric Unbounded Nonlinearities. Nonlinear Analysis: Theory, Methods & Applications, 62, 1235-1250. https://doi.org/10.1016/j.na.2005.04.029
[11]	Grossinho, M.R., Minhos, F.M. and Santos, A.I. (2005) Existence Result for a Third-Order ODE with Nonlinear Boundary Conditions in Presence of a Sign-Type Nagumo Control. Journal of Mathematical Analysis and Applications, 309, 271-283. https://doi.org/10.1016/j.jmaa.2005.01.030
[12]	Du, Z., Ge, W. and Lin, X. (2004) Existence of Solutions for a Class of Third-Order Nonlinear Boundary Value Problems. Journal of Mathematical Analysis and Applications, 294, 104-112. https://doi.org/10.1016/j.jmaa.2004.02.001
[13]	Benmezai, A., Henderson, J. and Meziani, M. (2013) A Third Order Boundary Value Problem with Jumping Nonlinearities. Nonlinear Analysis: Theory, Methods & Applications, 77, 33-44. https://doi.org/10.1016/j.na.2012.08.018
[14]	Yao, Q. and Feng, Y. (2002) The Existence of Solutions for a Third Order Two-Point Boundary Value Problem. Applied Mathematics Letters, 15, 227-232. https://doi.org/10.1016/S0893-9659(01)00122-7
[15]	Feng, Y. and Liu, S. (2005) Solvability of a Third-Order Two-Point Boundary Value Problem. Applied Mathematics Letters, 18, 1034-1040. https://doi.org/10.1016/j.aml.2004.04.016
[16]	Li, S.H. (2006) Positive Solutions of Nonlinear Singular Third-Order Two-Point Boundary Value Problem. Journal of Mathematical Analysis and Applications, 323, 413-425. https://doi.org/10.1016/j.jmaa.2005.10.037
[17]	Sun, Y.P. (2005) Positive Solutions of Singular Third-Order Three-Point Boundary Value Problem. Journal of Mathematical Analysis and Applications, 306, 589-603. https://doi.org/10.1016/j.jmaa.2004.10.029
[18]	Liu, Z., Ume, J.S. and Kang, S.M. (2007) Positive Solutions of a Singular Nonlinear Third Order Two-Point Boundary Value Problem. Journal of Mathematical Analysis and Applications, 326, 589-601. https://doi.org/10.1016/j.jmaa.2006.03.030
[19]	Feng, X. and Feng, H. (2022) Existence and Multiplicity of Positive Solutions for a Singular Third-Order Three-Point Boundary Value Problem with a Parameter. Journal of Applied Mathematics and Physics, 10, 1146-1157. https://doi.org/10.4236/jamp.2022.104080
[20]	Li, Y.X. and Li, Y.H. (2017) Positive Solutions of a Third-Order Boundary Value Problem with Full Nonlinearity. Mediterranean Journal of Mathematics, 14, Article No. 128. https://doi.org/10.1007/s00009-017-0928-4