Inequalities for Scalar Curvature and Shape Operator of an R-Lightlike Submanifold in Semi-Riemannian Manifold

Menedore Karimumuryango¹, Domitien Ndayirukiye², Hans-Fotsing Tetsing³, Gilbert Nibaruta², Aboubacar Nibirantiza⁴

¹Institut de Statistique Appliquée, Université du Burundi, Bujumbura, Burundi.
²Section des Mathématiques, Ecole Normale Supérieure, Bujumbura, Burundi.
³University of Douala, Douala, Cameroon.
⁴Institute of Applied Pedagogy, University of Burundi, Bujumbura, Burundi.

DOI: 10.4236/jamp.2023.117123                

Abstract

We establish the links between the lightlike geometry and basics invariants of the associated semi-Riemannian geometry on r-lightlike submanifold and semi-Riemannian constructed from a semi-Riemannian ambient. Then we establish some basic inequalities, involving the scalar curvature and shape operator on r-lightlike coisotropic submanifold in semi-Riemannian manifold. Equality cases are also discussed.

Keywords

Semi-Riemannian Submanifold, Submanifold, Rigging, Closed Normalization, Associated Semi-Riemannian Metric

1. Introduction

One of the most fundamental problems in submanifold theory is the problem of isometric immersibility. The embedding problem had been around since Riemann in 1854. Soon after Riemann introduced the notion of a manifold, Schläfli conjectured that every Riemannian manifold could be locally considered as a

submanifold of an Euclidean space with dimension $\frac{1}{2}n\left(n+1\right)$ in 1873. This

was later proved in different steps by Janet (1926), E. Cartan revised Janet’s paper with the same title in 1927.

This result of Cartan-Janet implies that every Einstein n-manifold ( $n\ge 3$ ) can

be locally isometrically embedded in ${\mathbb{E}}^{\frac{n\left(n+1\right)}{2}}$ . In 1956 J. Nash proved that every

closed Riemannian n-manifold can be isometrically embedded in a Euclidean

m-space ${\mathbb{E}}^m$ with $m=\frac{1}{2}n\left(3n+11\right)$ and he proved also that every non-closed

Riemannian n-manifold can be isometrically embedded in ${\mathbb{E}}^m$ with

$m=\frac{1}{2}n\left(n+1\right)\left(3n+11\right)$ .

R. E. Greene improved Nash’s result in (1970) and proved that every non-compact Riemannian n-manifold can be isometrically embedded in the Euclidean m-space ${\mathbb{E}}^m$ with $m=2\left(2n+1\right)\left(3n+7\right)$ .

In 1970, Clarke and Greene proved that any semi-Riemannian n-manifold $M_q^n$ with index q can be isometrically embedded in a semi-Euclidean m-space ${\mathbb{E}}_{\bar{q}}^m$ , for m and $\bar{q}$ large enough. Moreover, this embedding may be taken inside any given open set in ${\mathbb{E}}_{\bar{q}}^m$ . The problem of discovering simple sharp relationships between intrinsic and extrinsic invariants of a Riemannian submanifold becomes one of the most fundamental problems in submanifold theory. The main extrinsic invariant is the squared mean curvature and the main intrinsic invariants include the classical curvature invariants namely the scalar curvature and the Ricci curvature. The conformal screen notion on lightlike hypersurface introduced in [1] .

In [2] , B.-Y. Chen recalled that one of the basic interests of submanifold theory is to establish simple relationships between the main extrinsic invariants and the main intrinsic invariants of a submanifold. Many famous results in differential geometry can be regarded as results in this respect. In this regard, B. Y. Chen [3] proved a basic inequality involving the Ricci curvature and the squared mean curvature of submanifolds in a real space form. In [4] introduced the notion of screen distribution which provides a direct sum decomposition of $T\bar{M}$ with certain nice properties.

In [5] , the author immersed a lightlike hypersurface equipped with the Riemannian metric (induced on it by the rigging) into a Riemannian manifold suitably constructed on the Lorentzian manifold and she established the basic relationships between the main extrinsic invariants and the main intrinsic invariants named Chen-Ricci inequality of the lightlike hypersurface in the Lorentzian manifold. Inequalities between extrinsic and intrinsic are explored to give some characterizations of isometric immersions. Since the Riemann curvature tensor is one of the central concepts in differential geometry that allows us to get relationships between geometric objects, it is difficult to hundle it in case of lightlike geometry because the algebraic properties are not verified in general case. We have to ensure the algebraicity of Riemann curvature tensor in degenerate case. In 1965, A. Friedman proved that any n-dimensional semi-Riemannian manifold of index q can be isometrically embedded in a semi-Euclidean space of

dimension $\frac{1}{2}n\left(n+1\right)$ and index $\ge q$ [6] .

In [7] the autors established some remarkable geometric roperties to ensure algebraicity of the induced Riemannian curvature tensor on lightlike Warped Product Manifolds. The same approach has been explored in [8] to present osserman conditions for lightlike warped product manifolds. Using rigging technical, the authors showed the nonexistence of stable currents in lightlike hypersurface of Lorentzian manifold and they has established some inequalities between the main extrinsic and intrinsic invariants on lightlike hypersurface in the Lorentzian manifold in [9] [10] .

In this paper, we establish inequalities for a submanifold of a semi-Riemannian manifold. In our approach, to deal with the problem concerning the algebraicity properties of the Riemannian curvature tensor induced on a submanifold, we induce a semi-Riemannian metric on the lightlike submanifold and we immersed isometrically the lightlike submanifold endowed with semi-Riemmannian metric in semi-Riemmannian manifold. We then establish links between the lightlike geometry and basics invariants of the associated nondegenerate geometry such as linear connection, the curvature tensor, Ricci curvature such that is symmetric and sectional curvature and we established some inequalities between scalar curvature and shape operator of lightlike submanifold in semi-Riemannian manifold with the a spacelike, timelike mean curvature, timelike geodesic, spacelike geodesic and timelike mixed geodesic. We give the following diagram illustrates the situation:

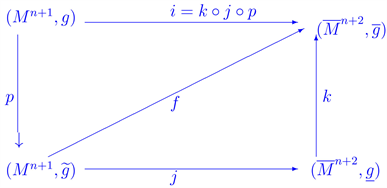
The remaining of this paper is organized as follows:

Section 2 contains most of the prerequisites material of lightlike submanifolds in semi-Riemannian Manifold. The normalization and the associated semi-Riemannian structure on a normalized null submanifold using Rigging techniques are introduced and discussed in Section 3. The relashionship between the lightlike and the associated semi-Riemannian geometry is considered in Section 4. In the last section, we give the inequalities between the scalar curvature of lightlike submanifold in semi-Riemannian manifold.

2. Preliminaries

Let $\left(\bar{M}\mathrm{,}\bar{g}\right)$ be a real $\left(n+k\right)$ -dimensional semi-Riemannian manifold of constant index $q\in \left\{\mathrm{1,}\cdots \mathrm{,}n+k-1\right\}$ where $n>1,k\ge 1$ . Suppose M is a n-dimensional submanifold of $\bar{M}$ . In case ${\bar{g}}_x$ is non-degenerate on $T_{x}M$ , then $T_{x}M$ and $T_x{M}^{\perp }$ are complementary orthogonal vector subspaces of $T_x\bar{M}$ , a part of the normal vector bundle $T{M}^{\perp }$ (the radical distribution) lies in the tangent bundle $TM$ of a submanifold M of a semi-Riemannian manifold $\bar{M}$ . Otherwise, $T_{x}M$ and $T_x{M}^{\perp }$ are degenerate orthogonal subspaces but no longer complementary subspaces, that is $TM\cap T{M}^{\perp }\ne \left\{0\right\}$ . Thus a basic problem of the lightlike submanifolds is to replace the intersecting part by a vector subbundle whose sections are nowhere tangent to M. To overcome with this problem posed by lightlike submanifolds, the authors Bejancu and Duggal introduced the notion of screen distribution which provides a direct sum decomposition of $T\bar{M}$ with certain nice properties. Used a screen distribution $S\left(TM\right)$ on M and a screen vector bundle $S\left(T{M}^{\perp }\right)$ over M to construct a transversal bundle $tr\left(TM\right)$ . They obtained the structure equations of M that relate the curvature tensor of $\bar{M}$ with the curvature tensor of the linear connections induced on the vector bundles involved in the study. If the mapping $Rad\left(TM\right)$ is a smooth distribution with constant rank $r>0$ , then, it is said the radical (lightlike) distribution on M. Also, g is called r-null (r-lightlike, r-degenerate) metric on M the submanifold M is said to be r-lightlike (r-lightlike, r-degenerate) submanifold of $\bar{M}$ , with nullity degree r and is simply called null (lightlike) submanifold. Any complementary (and hence orthogonal) distribution $S\left(TM\right)$ of $Rad\left(TM\right)$ in $TM$ is called a screen distribution. For a fixed screen distribution $S\left(TM\right)$ on M, the tangent bundle splits as

$TM=RadTM{\oplus }_{orth}S\left(TM\right).$ (1)

Certainly, $S\left(TM\right)$ is not unique, however it is canonically isomorphic to the factor vector bundle $T{M}^{\mathrm{<mo>\; *\; </mo>}}=TM/RadTM$ considered by Kupeli [11] . $S\left(TM\right)$ can be constructed by using the local equations of the submanifold and therefore it enables us to obtain the main induced geometrical objects: induced connection, second fundamental form, shap operator, $\cdots$ A screen transversal vector bundle $S\left(T{M}^{\perp }\right)$ on M is any (semi-Riemannian) complementary vector bundle of $Rad\left(TM\right)$ in $T{M}^{\perp }$ . It is obvious that $S\left(T{M}^{\perp }\right)$ is non-degenerate with respect to $\bar{g}$ and $T{M}^{\perp }$ has the following orthogonal direct decomposition

$T{M}^{\perp }=RadTM{\oplus }_{orth}S\left(T{M}^{\perp }\right)\mathrm{.}$ (2)

$S\left(TM\right)$ and $S\left(T{M}^{\perp }\right)$ are called a screen distibution and a screen transversal vector bundle of M respectively. As $S\left(TM\right)$ is not degenerate let $S\left(T{M}^{\perp }\right)$ be its complementary orthogonal in ${T\bar{M}|}_M$ . Then we have the following decomposition

${T\bar{M}|}_M=S\left(TM\right){\oplus }_{orth}S{\left(TM\right)}^{\perp }\mathrm{.}$ (3)

Note that $S\left(T{M}^{\perp }\right)$ is a vector subbundle of $S{\left(TM\right)}^{\perp }$ and since both are non-degenerate we have the following orthogonal direct decomposition

$S{\left(TM\right)}^{\perp }=S\left(T{M}^{\perp }\right){\oplus }_{orth}S{\left(T{M}^{\perp }\right)}^{\perp }\mathrm{.}$

Since the theory of null submanifold M is mainly based on both $S\left(TM\right)$ and $S\left(T{M}^{\perp }\right)$ , a null submanifold is denoted by $\left(M\mathrm{,}g\mathrm{,}S\left(TM\right)\mathrm{,}S\left(T{M}^{\perp }\right)\right)$ and we have four sub-cases with respect to the dimension and codimension of M and rank of $RadTM$ :

1) r-null(lightlike) if $r<\min \left(n,k\right)$ ;

2) Coisotropic if $r=k<n$ (hence $S\left(T{M}^{\perp }\right)=\left\{0\right\}$ );

3) Isotropic if $r=n<k$ , (hence $S\left(TM\right)=\left\{0\right\}$ );

4) Totally null if $r=n=k$ , (hence $S\left(TM\right)=\left\{0\right\}=S\left(T{M}^{\perp }\right)$ ).

We have seen from the above that the normal bundle $T{M}^{\perp }$ is orthogonal but not a complement to $TM$ , since it intersects the null tangent bundle $RadTM$ . This creates a problem as a vector of $T_x\bar{M}$ cannot be decomposed uniquely into a component tangent of $T_{x}M$ and a component of $T_x{M}^{\perp }$ . Therefore, the standard definition of second fundamental forms and the Gauss-Weingarten formulae do not work, To deal with this anomaly, one of the techniques used consists to split the tangent bundle $T\bar{M}$ into four non-intersecting complementary (but not orthogonal) vectors bundle.

Theorem 2.1 Let $\left(M\mathrm{,}g\mathrm{,}S\left(TM\right)\mathrm{,}S\left(T{M}^{\perp }\right)\right)$ be an r-lightlike submanifold of $\left(\bar{M}\mathrm{,}\bar{g}\right)$ with $r>1$ . Suppose $\mathcal{U}$ is a coordinate neighbourhood of M and $\left\{{\xi }_i\right\}\mathrm{<mo>\; ;\; </mo>}i\in \left\{\mathrm{1,}\cdots \mathrm{,}r\right\}$ a basis of ${\Gamma \left(RadTM\right)|}_{\mathcal{U}}$ . Then there exist smooth sections

$\left\{N_i\right\}$ of ${S{\left(T{M}^{\perp }\right)}^{\perp }|}_{\mathcal{U}}$ such that

$\bar{g}\left(N_i\mathrm{,}{\xi }_i\right)={\delta }_{ij}\mathrm{,}$ (4)

and

$\bar{g}\left(N_i\mathrm{,}{N}_j\right)=0$ (5)

for any $i\mathrm{,}j\in \left\{\mathrm{1,}\cdots \mathrm{,}r\right\}$ .

It follows that there exists a null transversal vector bundle $ltr\left(TM\right)$ locally spanned by $\left\{N_i\right\}$ . By using (4) and (2) it is easy to check that $B=\left\{{\xi }_1\mathrm{,}\cdots \mathrm{,}{\xi }_r\mathrm{,}{N}_1\mathrm{,}\cdots \mathrm{,}{N}_r\right\}$ is a basis of $\Gamma S{\left(T{M}^{\perp }\right)}_{\mathrm{<mo>\; |\; </mo>}U}^{\perp }$ . The set of local sections $\left\{N_i\right\}$ is not unique even if one use the same vector bundle in general. Let $tr\left(TM\right)$ be complementary called (but not orthogonal) vector bundle to $TM$ in ${T\bar{M}|}_M$ . Then the following hold

$tr\left(TM\right)=ltr\left(TM\right){\oplus }_{Orth}S\left(T{M}^{\perp }\right)\mathrm{,}$ (6)

${T\bar{M}|}_M=S\left(TM\right){\oplus }_{Orth}\left(RadTM\oplus ltr\left(TM\right)\right){\oplus }_{Orth}S\left(T{M}^{\perp }\right)=TM\oplus tr\left(TM\right)\mathrm{.}$ (7)

Let $\bar{\nabla }$ be the Levi-Civita connection on $\bar{M}$ . As TM and $tr\left(TM\right)$ are complementary sub-bundles of ${T\bar{M}|}_M$ , the Gauss and Weingarten formulae are

${\bar{\nabla }}_{X}Y={\nabla }_{X}Y+h\left(X\mathrm{,}Y\right)\mathrm{,}$ (8)

${\bar{\nabla }}_{X}V=-A_{V}X+{\nabla }_X^{t}V,$ (9)

$\forall X\mathrm{,}Y\in \Gamma \left(TM\right)\mathrm{,}V\in \Gamma \left(tr\left(TM\right)\right)$ . $\nabla$ and ${\nabla }^t$ are linear connections on TM and the vector bundle $tr\left(TM\right)$ called the induced linear connection and the transversal linear connection on M respectively.

$\nabla$ is torsion-free linear connection. The components ${\nabla }_{X}Y$ and $-A_{V}X$ belong to $\Gamma \left(TM\right)$ , $h\left(X\mathrm{,}Y\right)$ and ${\nabla }_X^{t}V$ to $\Gamma \left(tr\left(TM\right)\right)$ . Also h is a $\Gamma \left(tr\left(TM\right)\right)$ -valued symmetric bilinear form on $\Gamma \left(TM\right)$ called the second fundamental form of M with respect to $tr\left(TM\right)$ . A is a $\Gamma \left(TM\right)$ -valued bilinear form defined on $\Gamma \left(tr\left(TM\right)\right)\times \Gamma \left(TM\right)$ called shape operator of M. From the geometry of non-degenerate submanifolds [12] , it is known that the induced connection on a non-degenerate submanifold is a Levi-Civita connection. Unfortunately, in general, this is not true for a null submanifold.

$\left({\nabla }_{X}g\right)\left(X\mathrm{,}Y\right)=\bar{g}\left(h^l\left(X\mathrm{,}Y\right)\right)+\bar{g}\left(h^l\left(X\mathrm{,}Z\right)\mathrm{,}Y\right)$ (10)

$\left({\nabla }_X^t\bar{g}\right)\left(V\mathrm{,}{V}^{\prime }\right)=-\left\{\bar{g}\left(A_{V}X\mathrm{,}{V}^{\prime }\right)+\bar{g}\left(A_{V^{\prime }}X\mathrm{,}V\right)\right\}$ (11)

for all $X\mathrm{,}Y\mathrm{,}Z\in \Gamma \left(TM\right)\mathrm{<mo>\; ;\; </mo>}V\mathrm{,}{V}^{\prime }\in \Gamma \left(tr\left(TM\right)\right)$ . Thus, it follows that the induced connection $\nabla$ is not a Levi-Civita connection.

According to the decomposition (6), let L and S denote the projection morphisms of $tr\left(TM\right)$ onto $ltr\left(TM\right)$ and $S\left(T{M}^{\perp }\right)$ respectively, $h^l=L\circ h$ , $h^s=S\circ h$ , $D_X^{l}V=L\left({\nabla }_X^{t}V\right)$ , $D_X^{s}V=S\left({\nabla }_X^{t}V\right)$ . The transformations $D^l$ and $D^s$ do not define linear connections but Otsuki connections on $tr\left(TM\right)$ with respect to the vector bundle morphisms L and S. Then we have

${\bar{\nabla }}_{X}Y={\nabla }_{X}Y+h^l\left(X\mathrm{,}Y\right)+h^s\left(X\mathrm{,}Y\right)$ (12)

${\bar{\nabla }}_{X}N=-A_{N}X+D_X^{l}N+D^s\left(X\mathrm{,}N\right)$ (13)

${\bar{\nabla }}_{X}W=-A_{W}X+D^l\left(X\mathrm{,}W\right)+{\nabla }_X^{s}W$ (14)

$\forall X\mathrm{,}Y\in \Gamma \left(TM\right)\mathrm{,}N\in \Gamma \left(ltr\left(M\right)\right)$ and $W\in \Gamma \left(S\left(T{M}^{\perp }\right)\right)$ . Since $\bar{\nabla }$ is a metric connection, using (12) - (14) we have

$\bar{g}\left(h^s\left(X\mathrm{,}Y\right)\mathrm{,}W\right)+\bar{g}\left(Y\mathrm{,}{D}^l\left(X\mathrm{,}W\right)\right)=g\left(A_{W}X\mathrm{,}Y\right)$ (15)

$\bar{g}\left(D^s\left(X\mathrm{,}N\right)\mathrm{,}W\right)=\bar{g}\left(N\mathrm{,}{A}_{W}X\right)\mathrm{.}$ (16)

As $h^l$ and $h^s$ are $\Gamma \left(ltr\left(TM\right)\right)$ -valued and $\Gamma \left(S\left(T{M}^{\perp }\right)\right)$ -valued respectively, we call them the null second fundamental form and the screen second fundamental form of M.

Suppose M is either with $r<\min \left\{m,k\right\}$ or coisotropic. Then, using the decomposition (1) we get

${\nabla }_{X}Y={\nabla }_X^{\mathrm{<mo>\; *\; </mo>}}PY+h^{\mathrm{<mo>\; *\; </mo>}}\left(X\mathrm{,}PY\right)$ (17)

${\nabla }_X\xi =-A_{\xi }^{\mathrm{<mo>\; *\; </mo>}}X+{\nabla }_X^{\mathrm{<mo>\; *\; </mo>}t}\xi$ (18)

for any $X\mathrm{,}Y\in \Gamma \left(TM\right)$ and $\xi \in \Gamma \left(RadTM\right)$ , where $\left\{{\nabla }_X^{\mathrm{<mo>\; *\; </mo>}}PY\mathrm{,}{A}_{\xi }^{\mathrm{<mo>\; *\; </mo>}}X\right\}$ and $\left\{h^{\mathrm{<mo>\; *\; </mo>}}\left(X\mathrm{,}PY\right)\mathrm{,}{\nabla }_X^{\mathrm{<mo>\; *\; </mo>}t}\xi \right\}$ belong to $\Gamma \left(S\left(TM\right)\right)$ and $\Gamma \left(Rad\left(TM\right)\right)$ respectively. It follows that ${\nabla }^{\mathrm{<mo>\; *\; </mo>}}$ and ${\nabla }^{\mathrm{<mo>\; *\; </mo>}t}$ are linear connections on $S\left(TM\right)$ and $RadTM$ respectively. On the other hand, $h^{\mathrm{<mo>\; *\; </mo>}}$ and $A^{\mathrm{<mo>\; *\; </mo>}}$ are $\Gamma \left(RadTM\right)$ -valued and $\Gamma \left(S\left(TM\right)\right)$ -valued bilinear forms on $\Gamma \left(TM\right)\times \Gamma \left(S\left(TM\right)\right)$ and $\Gamma \left(RadTM\right)\times \Gamma \left(TM\right)$ Called the second fundamental forms of distributions $S\left(TM\right)$ and $Rad\left(TM\right)$ respectively.

For any $\xi \in \Gamma \left(RadTM\right)$ consider the linear operator

$A_{\xi }\mathrm{<mo>\; :\; </mo>}\Gamma \left(TM\right)\to \Gamma \left(S\left(TM\right)\right)\mathrm{<mo>\; ;\; </mo>}{A}_{\xi }^{\mathrm{<mo>\; *\; </mo>}}X=A^{\mathrm{<mo>\; *\; </mo>}}\left(\xi \mathrm{,}X\right)\mathrm{,}\forall X\in \Gamma <span\; class="bracketMark">(\; T\; M\; )</span>$

and call it the shape operator of $S\left(TM\right)$ with respect to $\xi$ . Also, call ${\nabla }^{\mathrm{<mo>\; *\; </mo>}}$ and ${\nabla }^{\mathrm{<mo>\; *\; </mo>}t}$ the induced connections on $S\left(TM\right)$ and $RadTM$ respectively.

The second fundamental form and shape operator of non-degenerate submanifold of a semi-Riemannian manifold are related by means of the metric tensor field. Contrary in case of null submanifolds there are interrelations between geometric objects induced by $tr\left(TM\right)$ on one side and geometric objects induced by $S\left(TM\right)$ on the other side. More precisely,

$\begin{array}{l}\bar{g}\left(h^l\left(X,PY\right)\right)=g\left(A_{\xi }^{*}X,PY\right),\bar{g}\left(h^{*}\left(X,PY\right),N\right)=g\left(A_{N}X,PY\right),\\ \bar{g}\left(h^l\left(X,\xi \right),\xi \right)=0,A_{\xi }^{*}\xi =0.\end{array}$ (19)

From (19) as $h^l$ is symetric, it follows that the shape operator of $S\left(TM\right)$ is a self-adjoint operator on $S\left(TM\right)$ .

Next, consider a coordinate neighbourhood $U$ of M and let $\left\{N_i\mathrm{,}{W}_{\alpha }\right\}$ be a basis of $\Gamma \left({tr\left(TM\right)|}_M\right)$ where $N_i\in \Gamma \left({ltr\left(TM\right)|}_M\right)\mathrm{,}i\in \left\{\mathrm{1,}\cdots \mathrm{,}r\right\}$ and $W_{\alpha }\in \Gamma \left({S\left(T{M}^{\perp }\right)|}_{\mathcal{U}}\right)\mathrm{,}\alpha \in \left\{r+\mathrm{1,}\cdots \mathrm{,}k\right\}$ . Then (12) becomes

${\bar{\nabla }}_{X}Y={\nabla }_{X}Y+{\displaystyle \underset{i=1}{\overset{r}{\sum }}}{h}_i^l\left(X,Y\right)N_i+{\displaystyle \underset{\alpha =r}{\overset{k}{\sum }}}{h}_i^s\left(X,Y\right)W_{\alpha }.$ (20)

We call $\left\{h_i^l\right\}$ and $\left\{h_{\alpha }^s\right\}$ the local null second fundamental forms and the local screen second fundamental forms of M on $U$ .

We recall the equations of Gauss, Codazzi and Ricci with play an important role in studying differential geometry of non-degenerate submanifolds Let $\bar{R}$ and R denote the Riemannian curvature tensors of $\bar{\nabla }$ and $\nabla$ on $\bar{M}$ and M respectively. The Gauss equation are given by

$\begin{array}{c}\bar{R}\left(X,Y\right)Z=R\left(X,Y\right)Z+A_{h^l\left(X,Z\right)}Y-A_{h^l\left(Y,Z\right)}X+A_{h^s\left(X,Z\right)}Y-A_{h^s\left(Y,Z\right)}X\\ +\left({\nabla }_X{h}^l\right)\left(Y,Z\right)-\left({\nabla }_Y{h}^l\right)\left(X,Z\right)+D^l\left(X,h^s\left(Y,Z\right)\right)\\ -D^l\left(Y,h^s\left(X,Z\right)\right)+\left({\nabla }_X{h}^s\right)\left(Y,Z\right)-\left({\nabla }_Y{h}^s\right)\left(X,Z\right)\\ +D^s\left(X,h^l\left(Y,Z\right)\right)-D^s\left(Y,h^s\left(X,Z\right)\right)\end{array}$

$\forall X\mathrm{,}Y\mathrm{,}Z\mathrm{,}U\in \Gamma \left(TM\right)$ . Therefore

$\begin{array}{c}\bar{R}\left(X,Y,PZ,PU\right)=R\left(X,Y,Z,PU\right)+\bar{g}\left(h^{*}\left(Y,PU\right),h^l\left(X,Z\right)\right)\\ -\bar{g}\left(h^{*}\left(X,PU\right),h^l\left(Y,Z\right)\right)+\bar{g}\left(h^s\left(Y,PU\right),h^s\left(X,Z\right)\right)\\ -\bar{g}\left(h^s\left(X,PU\right),h^s\left(Y,Z\right)\right),\end{array}$ (21)

Throughout, we consider that the submanifold is coisotropic that is $h^s=0$ . Let the differential 1-forms ${\omega }_i,i=1,\cdots ,r\left(0<r<\min \left\{m,n\right\}\right)$ defined by:

${\omega }_i\left(X\right)=\bar{g}\left(X\mathrm{,}{N}_i\right)\mathrm{,}\forall X\in \Gamma \left({TM|}_{\mathcal{U}}\right)\mathrm{,}i\in \left\{\mathrm{1,}\cdots \mathrm{,}r\right\}\mathrm{.}$ (22)

Then any vector X on M is expressed on $U$ as follows

$X=PX+{\displaystyle \underset{i=1}{\overset{r}{\sum }}}{\omega }_i\left(X\right){\xi }_i$ (23)

where P is the projection morphism of $\Gamma \left(TM\right)$ onto $\Gamma \left(S\left(TM\right)\right)$ .

Lemma 2.1 [13] If $a_1\mathrm{,}\cdots \mathrm{,}{a}_n$ are real numbers then

$\frac{1}{n}{\left({\displaystyle \underset{i=1}{\overset{n}{\sum }}}{a}_i\right)}^2\le {\displaystyle \underset{i=1}{\overset{n}{\sum }}}{a}_i^2,$ (24)

with equality if and only if $a_1=\cdots =a_n$ .

3. Normalization and Induced Semi-Riemannian Metric

Let $\varpi$ denote the 1-form which satisfying $\varpi \left(\mathrm{.}\right)=\bar{g}\left(N\mathrm{,.}\right)$ . Then, take

$\omega =f^{\star }\varpi$ (25)

to be its restriction to M, the map $f\mathrm{<mo>\; :\; </mo>}M\to \bar{M}$ being the inclusion map. Throughout, a screen distribution on M is denote by $S\left(N\right)$ .

We define the associated semi-Riemannian metric on $\bar{M}$ as

$\underset{\_}{g}=\bar{g}-\varpi \otimes \varpi \text{and}\tilde{g}=i^{\star }\underset{\_}{g}=g-{\omega }_{i=1}^r\otimes {\omega }_{i=1}^r\mathrm{.}$ (26)

Lemma 3.1 [14] Let $\left(M^n\mathrm{,}g\right)$ be a submanifold in semi-Riemannian manifold $\left({\bar{M}}^{n+1}\mathrm{,}\bar{g}\right)$ . Then, $\tilde{g}$ is nondegenerate.

Let $\left(M\mathrm{,}g\mathrm{,}S\left(N\right)\right)$ be a normalized null submanifold of a semi-Riemannian manifold, then the integral curves of the rigged vector field $\xi$ are pregeodesic but not geodesic in general. The following lemma shows that in case the normalization is a conformal vector field, then $\xi$ is $\bar{g}$ -geodesic.

Lemma 3.2 Let $\left(M\mathrm{,}g\mathrm{,}S\left(N\right)\right)$ be a conformal normalized null submanifold of a semi-Riemannian manifold such, then ${\xi }_i$ is $\bar{g}$ -geodesic and ${\displaystyle {\sum }_{i=1}^r}\tau \left({\xi }_i\right)=0$ .

Definition 3.1 A normalized null submanifold $\left(M\mathrm{,}g\mathrm{,}N\right)$ of a semi-Riemannian manifold $\left(\bar{M}\mathrm{,}\bar{g}\right)$ is said to have a conformal screen if there exists a non vanishing smooth function $\phi$ on M such that $A_N=\phi A_{\xi }^{\star }$ holds.

This is equivalent to saying that $g\left(A_{N}X\mathrm{,}PY\right)=\phi g\left(A_{\xi }^{\star }X\mathrm{,}Y\right)$ for all tangent vector fields X and Y. The function $\phi$ is called the conformal factor.

4. Relation between the Null and the Associated Semi-Riemannian Geometry

The main focus of this section lies on deriving jump formulas for the various curvature quantities, that is, how the Riemann and Ricci tensor and scalar curvature of course the reason why this is of a particular interest lies in physics, mainly general relativity, where such formulas might find an application due to the Einstein field equations.

Theorem 4.1 [14] Let $\left(M\mathrm{,}{g}^n\mathrm{,}N\right)$ be a r-closed coisotropic normalized null submanifold with rigged vector field $\xi$ in a $\left(n+k\right)$ semi-Riemannian manifold. Then $\forall X\mathrm{,}Y\in \Gamma \left(TM\right)$ , we have the following:

$\begin{array}{c}\tilde{R}ic\left(X,Y\right)=Ric\left(X,Y\right)-{\displaystyle \underset{i=1}{\overset{r}{\sum }}}[\langle A_{{\xi }_i}^{*}X,Y\rangle -{\displaystyle \underset{i=1}{\overset{r}{\sum }}}\langle A_{N_i}X,Y\rangle \\ +{\displaystyle \underset{i=1}{\overset{r}{\sum }}}{\tau }^{N_i}\left(X\right){\displaystyle \underset{i=1}{\overset{r}{\sum }}}{\omega }_i\left(Y\right)]tr{A}_{{\xi }_i}^{*}\\ +{\displaystyle \underset{i=1}{\overset{r}{\sum }}}\langle \left({\nabla }_{\xi }{A}_{{\xi }_i}^{*}\right)\left(X\right),Y\rangle -{\displaystyle \underset{i=1}{\overset{r}{\sum }}}\langle \left({\nabla }_{\xi }{A}_{N_i}\right)\left(X\right),Y\rangle \\ +{\displaystyle \underset{i=1}{\overset{r}{\sum }}}\left({\nabla }_{{\xi }_i}{\tau }^{N_i}\right)\left(X\right){\displaystyle \underset{i=1}{\overset{r}{\sum }}}{\omega }_i\left(Y\right)-\left({\nabla }_X{\tau }^N\right)\left(Y\right).\end{array}$ (27)

where $\tilde{R}ic$ and $Ric$ denote the Ricci curvature of $\tilde{\nabla }$ and $\nabla$ respectively.

Lemma 4.1 [14] Let $\left(M^n\mathrm{,}g\right)$ be a r-closed and conformal (with factor $\phi$ ) coisotropic normalized null submanifold with rigged vector field $\xi$ in a $\left(n+k\right)$ semi-Riemannian manifold. Then

$\begin{array}{c}\tilde{R}ic\left(X,Y\right)=Ric\left(X,Y\right)-{\displaystyle \underset{i=1}{\overset{r}{\sum }}}[\left(1-\phi \right)\langle A_{{\xi }_i}^{*}X,Y\rangle tr{A}_{{\xi }_i}^{*}\begin{array}{c}\\ \end{array}\\ -\left(1-\phi \right){\displaystyle \underset{i=1}{\overset{r}{\sum }}}\langle \left({\nabla }_{{\xi }_i}{A}_{{\xi }_i}^{*}\right)\left(X\right),Y\rangle ].\end{array}$ (28)

Theorem 4.2 [14] Let $\left(M^n\mathrm{,}g\right)$ be a r-closed coisotropic normalized null sub-manifold with rigged vector field $\xi$ and ${\tau }^N\left(\xi \right)=0$ in a semi-Riemannian manifold. Then

$\begin{array}{c}\tilde{\Upsilon }=r^0-{\displaystyle \underset{i=1}{\overset{r}{\sum }}}\left[tr{A}_{{\xi }_i}^{*}-tr{A}_{N_i}\right]tr{A}_{{\xi }_i}^{*}\\ +{\displaystyle \underset{i=1}{\overset{r}{\sum }}}\left[tr\left({\nabla }_{{\xi }_i}{A}_{{\xi }_i}^{*}\right)-tr\left({\nabla }_{{\xi }_i}{A}_{N_i}\right)+{\tau }^N\left({\tau }^{{\#}_{\eta }}\right)-di{v}^g{\tau }^{N_i{}^{\#}}\right].\end{array}$ (29)

Corollary 4.1 Let $\left(M^n\mathrm{,}g\right)$ be a closed and conformal (with factor $\phi$ ) normalized null submanifold with rigged vector field $\xi$ in a $\left(n+k\right)$ semi-Riemannian manifold. Then

$\tilde{\Upsilon }=r^0+\left(\phi -1\right){\displaystyle \underset{i=1}{\overset{r}{\sum }}}\left[{\left(tr{A}_{{\xi }_i}^{*}\right)}^2-tr\left({\nabla }_{{\xi }_i}{A}_{{\xi }_i}^{*}\right)\right].$ (30)

Since the sectional curvature of null submanifold equipped with associated Riemannian metric is symmetric, we can denote the scalar curvature by $\tilde{r}$ with respect $\tilde{g}$ as follows:

$\tilde{r}={\displaystyle \underset{1\le i<j\le n}{\sum }}\tilde{K}\left(e_i,e_j\right)=\frac{1}{2}\tilde{\Upsilon }.$ (31)

By (31), (29) and (30) become

$\begin{array}{c}\tilde{r}=r^0-\frac{1}{2}{\displaystyle \underset{i=1}{\overset{r}{\sum }}}\{\left[tr{A}_{{\xi }_i}^{*}-tr{A}_{N_i}\right]tr{A}_{{\xi }_i}^{*}-tr\left({\nabla }_{{\xi }_i}{A}_{{\xi }_i}^{*}\right)+tr\left({\nabla }_{{\xi }_i}{A}_{N_i}\right)\\ +di{v}^g{\tau }^{N_i}{}^{{\#}_{\omega }}+{\tau }^N\left({\tau }^{{\#}_{\eta }}\right)\}.\end{array}$ (32)

$\tilde{r}=r^0+\frac{1}{2}\left(\phi -1\right)\left[{\left(tr{A}_{{\xi }_i}^{*}\right)}^2-tr\left({\nabla }_{{\xi }_i}{A}_{{\xi }_i}^{*}\right)\right].$ (33)

5. Link between Geometry of $\tilde{g}$ and $\underset{\_}{g}$

Let $\left(M\mathrm{,}\tilde{g}\right)$ be an n-dimensional semi-Riemannian submanifold of index $q-1$ of an $\left(n+k\right)$ -dimensional semi-Riemannian manifold $\left(\bar{M}\mathrm{,}{\bar{g}}_{\alpha }\right)$ . We shall use the inner product notation $\langle \mathrm{,}\rangle$ for both the metrics of M and the induced metric g on the null submanifold M. The semi-Riemannian submanifold M is spacelike if $q=0$ ; and it is timelike if $q=n$ . The Gauss and Weingarten formulas are given, respectively, by

${\bar{\nabla }}_{\alpha X}Y={\tilde{\nabla }}_{X}Y+\delta \left(X\mathrm{,}Y\right)$ (34)

${\bar{\nabla }}_{\alpha X}\xi =-A_{\alpha X}^{\star }\xi +D_{\alpha X}\xi \mathrm{.}$ (35)

where $A_{\xi }X$ and $D_X\xi$ are the tangential and normal components of ${\bar{\nabla }}_{\alpha X}\xi$ for all $X\mathrm{,}Y\in TM$ and $\xi \in T^{\perp }M$ , where ${\bar{\nabla }}_{\alpha }\mathrm{,}\tilde{\nabla }$ are the semi-Riemannian connections with respect $\underset{\_}{g}$ and $\tilde{g}$ respectively. The second fundamental form $\delta$ related to the shape operator A by

$\langle \delta \left(X\mathrm{,}Y\right)\mathrm{,}\xi \rangle =\langle A_{\xi }^{\star }X\mathrm{,}Y\rangle$ (36)

The second fundamental form can be used to determine a relationship between the curvature of $\bar{M}$ and of M with respect to ${\bar{g}}_{\alpha }$ and $\tilde{g}$ respectively. More precisely we have the following

${\bar{g}}_{\alpha }\left({\bar{R}}_{\alpha }\left(X\mathrm{,}Y\right)Z\mathrm{,}W\right)=\tilde{g}\left(\tilde{R}\left(X\mathrm{,}Y\right)Z\mathrm{,}W\right)+\delta \left(X\mathrm{,}Z\right)\delta \left(Y\mathrm{,}W\right)-\delta \left(Y\mathrm{,}Z\right)\delta \left(X\mathrm{,}W\right)\mathrm{.}$ (37)

for all $X\mathrm{,}Y\mathrm{,}Z\mathrm{,}W\in TM$ , where $\bar{R}$ and $\tilde{R}$ are the curvature tensors of $\bar{M}$ and M respectively of $\bar{g}$ and $\tilde{g}$ .

Let $\left\{e_1\mathrm{,}\cdots \mathrm{,}{e}_n\right\}$ be any orthonormal basis for $T_{x}M$ . The mean curvature vector $H\left(x\right)$ at $x\in M$ is defined by

$H\left(x\right)=\frac{1}{n}{\displaystyle \underset{i=r+1}{\overset{n}{\sum }}}{\epsilon }_i\delta \left(e_i,e_i\right)={\displaystyle \underset{i=r+1}{\overset{n}{\sum }}}\bar{g}\left(e_i,e_i\right)\bar{g}\left(A_{\xi }^{*}\left(e_i\right),e_i\right),$ (38)

being $\left(e_{r+1}\mathrm{,}\cdots \mathrm{,}{e}_n\right)$ an orthonormal basis of $S\left(N\right)$ at x. A submanifold is said to be minimal if and only if its mean curvature vector vanishes. Minimal submanifolds appear in a natural way as the critical points of the volume functional and they are a topic of current interest in differential geometry. We say that a submanifold is totally geodesic if its second fundamental form vanishes, $\delta =0$ . This is equivalent to saying that every geodesic in M is also a geodesic in $\bar{M}$ . If $\delta \left(X\mathrm{,}Y\right)=\langle X\mathrm{,}Y\rangle H$ for all $X\mathrm{,}Y\in TM$ , then M is totally umbilical.

Let $\left(M\mathrm{,}\tilde{g}\right)$ be an n-dimensional semi-Riemannian submanifold of index $q-1$ of an $\left(n+k\right)$ -dimensional semi-Riemannian manifold $\left(\bar{M}\mathrm{,}{\bar{g}}_{\alpha }\right)$ . Let $\left\{e_r\mathrm{,}{e}_1\mathrm{,}\cdots \mathrm{,}{e}_n\right\}$ be an orthogonal basis of the tangent space $T_{x}M$ and $e_r$ with $r\in \left\{\mathrm{1,}\cdots \mathrm{,}k\right\}$ , be an orthonormal basis of the normal space $T^{\perp }M$ with respect $\tilde{g}$ . We put

${\delta }_{ij}^r=\langle \delta \left(e_i\mathrm{,}{e}_j\right)\mathrm{,}{e}_r\rangle$ (39)

so that

$\delta \left(e_i\mathrm{,}{e}_j\right)={\epsilon }_r\langle \delta \left(e_i\mathrm{,}{e}_j\right)\mathrm{,}{e}_r\rangle e_r={\epsilon }_r{\delta }_{ij}^r{e}_r\mathrm{,\; <mtext>\; \hspace{0.17em}\; </mtext>}{\epsilon }_r=\langle e_r\mathrm{,}{e}_r\rangle \mathrm{.}$ (40)

where the quantities ${\delta }_{ij}^r$ are called the coefficients of the second fundamental form $\delta$ . We put also

${\Vert \delta \Vert }_{\tilde{g}}^2={\displaystyle \underset{i,j=1}{\overset{n}{\sum }}}{\Vert \langle \delta \left(e_i,e_j\right),\delta \left(e_i,e_j\right)\rangle \Vert }_{\tilde{g}}^2={\displaystyle \underset{i,j=1}{\overset{n}{\sum }}}{\delta }_{ij}^r$ (41)

Let ${\tilde{K}}_{\alpha ij}$ and ${\bar{K}}_{\alpha ij}$ denote the sectional curvature of the plane section spanned by $e_i$ and $e_j$ at x in the submanifold $\left(M\mathrm{,}\tilde{g}\right)$ and in the semi-Riemannian manifold $\left(\bar{M}\mathrm{,}{\bar{g}}_{\alpha }\right)$ . Thus, ${\tilde{K}}_{\alpha ij}$ and ${\bar{k}}_{\alpha ij}$ are the intrinsic and the extrinsic sectional curvatures of the Span $\pi =\left\{e_i\mathrm{,}{e}_j\right\}$ . From (37), we get

${\bar{K}}_{\alpha }\left(\pi \right)={\tilde{K}}_{\alpha }\left(\pi \right)+{\epsilon }_i{\epsilon }_j\langle \delta \left(e_i\mathrm{,}{e}_j\right)\mathrm{,}\delta \left(e_j\mathrm{,}{e}_i\right)\rangle -{\epsilon }_i{\epsilon }_j\langle \delta \left(e_i\mathrm{,}{e}_i\right)\mathrm{,}\delta \left(e_j\mathrm{,}{e}_j\right)\rangle$ (42)

which turns out to be

${\bar{K}}_{\alpha }\left(\pi \right)={\tilde{K}}_{\alpha }\left(\pi \right)+{\displaystyle \underset{r=1}{\overset{k}{\sum }}}{\epsilon }_i{\epsilon }_j{\left({\delta }_{ij}^r\right)}^2-{\displaystyle \underset{r=1}{\overset{k}{\sum }}}{\epsilon }_i{\epsilon }_j{\delta }_{ii}^r{\delta }_{jj}^r.$ (43)

The scalar curvature ${\tilde{r}}_{\alpha }$ of M at x with respect $\tilde{g}$ in the ambient semi-Riemannian manifold $\left(\bar{M}\mathrm{,}{\bar{g}}_{\alpha }\right)$ is defined by

${\tilde{r}}_{\alpha }\left(x\right)={\displaystyle \underset{0\le i<j\le n}{\sum }}{\tilde{K}}_{\alpha ij}=\frac{1}{2}{\displaystyle \underset{i=1}{\overset{n}{\sum }}}\tilde{R}i{c}_{\alpha }\left(e_i\right).$ (44)

If $D$ is any distribution on M, then the g-orthogonal distribution of $D$ , denoted by $D^{\perp }$ , is the distribution whose fibre over each point $p\in M$ is $\left\{D=X\in T_{x}M\mathrm{<mo>\; :\; </mo>}g\left(X\mathrm{,}Y\right)=\mathrm{0\; <mtext>\; \hspace{0.17em}\; </mtext>}\forall Y{D}_x\right\}$ . Where $D_x$ denotes the fibre of $D$ over x.

Now we consider the following maximally timelike and maximally spacelike distribution on M $D_{\mu }$ and $D$ , we write a g-orthogonal decomposition

$TM=D_{\mu }{\oplus }_{ort}{D}_{\nu }\mathrm{.}$ (45)

Thus there is an orthonormal frame $\left\{e_1\mathrm{,}\cdots \mathrm{,}{e}_q\mathrm{,}{e}_{q+1}\mathrm{,}\cdots \mathrm{,}{e}_n\right\}$ , where $D_{\mu }=\left\{e_1\mathrm{,}\cdots \mathrm{,}{e}_q\right\}$ is the maximally timelike and $D_{\nu }=\left\{e_{q+1}\mathrm{,}\cdots \mathrm{,}{e}_n\right\}$ is the maximally spacelike. If $\tilde{D}$ is any subbundle of $T^{\perp }M$ , then the $\bar{g}$ -orthogonal subbundle of $\tilde{D}$ , denoted by ${\tilde{D}}^{\perp }$ , is the subbundle of $T^{\perp }M$ such that ${\tilde{D}}^{\perp }=\left\{V\in T_x{M}^{\perp }\mathrm{<mo>\; :\; </mo>}\bar{g}\left(V\mathrm{,}W\right)=0\forall W\in {\tilde{D}}^{\perp }\mathrm{,}x\in M\right\}$

Now, there is always a $\bar{g}$ -orthogonal decomposition of the normal bundle $T^{\perp }M$ as

$T^{\perp }M={\tilde{D}}_{\mu }{\oplus }_{ort}{\tilde{D}}_{\nu }$ (46)

where ${\tilde{D}}_{\mu }={\tilde{e}}_1\mathrm{,}\cdots \mathrm{,}{\tilde{e}}_q$ is the maximally timelike and ${\tilde{D}}_{\nu }={\tilde{e}}_{q+1}\mathrm{,}\cdots \mathrm{,}{\tilde{e}}_n$ is the maximally spacelike. Let $\left(M\mathrm{,}\tilde{g}\right)$ be an (n)-dimensional semi-Riemannian submanifold of index q of an $\left(n+\bar{n}\right)$ -dimensional semi-Riemannian $\left(\bar{M}\mathrm{,}{\bar{g}}_{\alpha }\right)$ .

A normal subbundle of $T{M}^{\perp }$ will be called maximally timelike if it is timelike and has rank ${\tilde{q}}_{\alpha }$ . Similarly, a normal subbundle of $T{M}^{\perp }$ will be called maximally spacelike if it is spacelike and has rank $\left(\bar{n}-{\tilde{q}}_{\alpha }\right)$ . we can write now

$\delta \left(X\mathrm{,}Y\right)={\delta }^{{\tilde{D}}_{\mu }}\left(X\mathrm{,}Y\right)+{\delta }^{{\tilde{D}}_{\nu }}\left(X\mathrm{,}Y\right)$ (47)

where ${\delta }^{{\tilde{D}}_{\mu }}\left(X\mathrm{,}Y\right)\in {\tilde{D}}_{\mu }$ and ${\delta }^{{\tilde{D}}_{\nu }}\left(X\mathrm{,}Y\right)\in {\tilde{D}}_{\nu }$ .

6. Relationships between the $\underset{\_}{g}$ and $\bar{g}$ Geometry

In this section, we give the links between to geometric objects of $g_{\omega }$ and $\bar{g}$ using rigging techniques.

Lemma 6.1 [14] Let $\left(M\mathrm{,}g\mathrm{,}N\right)$ be a normalized null submanifold in semi-Riemmannian manifold $\left(\bar{M}\mathrm{,}\bar{g}\right)$ and ${\bar{\nabla }}_{\alpha }$ , $\bar{\nabla }$ be the Levi-Civita connections of $\underset{\_}{g}$ and $\bar{g}$ respectively. Let $\left(\bar{M}\mathrm{,}{\bar{g}}_{\alpha }\right)$ be a semi-Riemannian manifold of index $\left(q+{\tilde{q}}_{\alpha }\right)$ constructed in a semi-Riemannian manifold $\left(\bar{M}\mathrm{,}\bar{g}\right)$ . Then forall $X\mathrm{,}Y\in \Gamma \left(T\bar{M}\right)$ , we prove the following:

$\begin{array}{c}{\bar{\nabla }}_{\alpha X}Y={\bar{\nabla }}_{X}Y+\frac{1}{2}\{\left[-2\bar{g}\left(A_{N_i}X,Y\right)+2{\tau }^{N_i}\left(X\right)\varpi \left(Y\right)-d\varpi \left(X,Y\right)\right]N_i\\ +{\left(i_{X}d\varpi \right)}^{\#}\varpi \left(Y\right)+{\left(i_{Y}d\varpi \right)}^{\#}\varpi \left(X\right)\}.\end{array}$ (48)

In particular, for a closed normalization, we have this

${\bar{\nabla }}_{\alpha X}Y={\bar{\nabla }}_{X}Y+\frac{1}{2}\left[-2\bar{g}\left(A_{N_i}X\mathrm{,}Y\right)+2{\tau }^{N_i}\left(X\right)\varpi \left(Y\right)\right]N_i\mathrm{.}$ (49)

Lemma 6.2 [14] Let $\left(M\mathrm{,}g\mathrm{,}{N}_i\right)$ be a normalized null submanifold in semi-Riemmannian manifold $\left(\bar{M}\mathrm{,}\bar{g}\right)$ . Let $\left(\bar{M}\mathrm{,}{\bar{g}}_{\alpha }\right)$ be a semi-Riemannian manifold constructed in a semi-Riemannian manifold $\left(\bar{M}\mathrm{,}\bar{g}\right)$ , $\bar{R}$ and ${\bar{R}}_{\alpha }$ the curvatures tensors of $\bar{\nabla }$ and ${\bar{\nabla }}_{\alpha }$ respectively. Then

$\begin{array}{l}{\bar{g}}_{\alpha }\left({\bar{R}}_{\alpha }\left(X,Y\right)Z,W\right)\\ =\bar{g}\left(\bar{R}\left(X,Y\right)Z,W\right)+\bar{g}\left(A_{N_i}Y,Z\right)\bar{g}\left(A_{N_i}X,W\right)-{\tau }^{N_i}\left(Y\right)\varpi \left(Z\right)\bar{g}\left(A_{N_i}X,W\right)\\ -\bar{g}\left(A_{N_i}X,Z\right)\bar{g}\left(A_{N_i}Y,W\right)+{\tau }^{N_i}\left(X\right)\varpi \left(Z\right)\bar{g}\left(A_{N_i}Y,W\right)+\{\bar{g}\left(\left({\bar{\nabla }}_Y{A}_{N_i}\right)\left(X\right),Z\right)\\ +d{\tau }^{N_i}\left(X,Y\right)\varpi \left(Z\right)-{\tau }^{N_i}\left(X\right)\bar{g}\left(A_{N_i}Y,Z\right)-\bar{g}\left(\left({\bar{\nabla }}_X{A}_{N_i}\right)\left(Y\right),Z\right)\\ +{\tau }^{N_i}\left(Y\right)\bar{g}\left(A_{N_i}X,Z\right)\}\varpi \left(W\right),\mathrm{<mtext>\; \hspace{0.17em}\; </mtext>}\forall X,Y,Z,W\in \Gamma \left(T\bar{M}\right).\end{array}$ (50)

In the following, by using a quasiorthonormal basis $B=\left\{e_0=\xi ,e_1,\cdots ,e_n,e_{n+1}=N\right\}$ for $\left(T_x\bar{M}\mathrm{,}{\bar{g}}_x\right)$ we can prove the the relashionship between the Ricci curvature of $\bar{R}i{c}_{\alpha }$ and the corresponding $\bar{R}ic$ by contracting (50) with ${\bar{g}}_{\alpha }$ .

Theorem 6.1 [14] Let $\left(M\mathrm{,}g\mathrm{,}N\right)$ be a closed normalized r-null submanifold in semi-Riemmannian manifold $\left(\bar{M}\mathrm{,}\bar{g}\right)$ . Let $\left(\bar{M}\mathrm{,}{\bar{g}}_{\alpha }\right)$ be a semi-Riemannian manifold constructed in a semi-Riemannian manifold the curvatures tensors of $\bar{g}$ and $\underset{\_}{g}$ $\left(\bar{M}\mathrm{,}\bar{g}\right)$ , $\bar{R}i{c}_{\alpha }$ and $\bar{R}ic$ are respectively related on $\bar{M}$ by

$\begin{array}{c}\bar{R}i{c}_{\alpha }\left(X\mathrm{,}Y\right)=\bar{R}ic\left(X\mathrm{,}Y\right)+\left\{\bar{g}\left(A_{N}X\mathrm{,}Y\right)+\bar{g}\left(A_N\xi \mathrm{,}X\right)\varpi \left(Y\right)\right\}tr{A}_N\\ -\bar{g}\left(A_{N}X\mathrm{,}{A}_{N}Y\right)+\bar{g}\left(\left({\bar{\nabla }}_X{A}_N\right)\left(\xi \right)\mathrm{,}Y\right)-\left({\bar{\nabla }}_{\xi }{A}_N\xi \mathrm{,}X\right)\\ +\bar{g}\left(A_N\xi \mathrm{,}{A}_{\xi }^{\star }\mathrm{,}X\right)-\bar{g}\left(\left({\bar{\nabla }}_{\xi }{A}_N\right)\left(X\right)\mathrm{,}Y\right)-\bar{g}\left(A_N\xi \mathrm{,}X\right)\bar{g}\left(A_N\xi \mathrm{,}Y\right)\end{array}$ (51)

Theorem 6.2 [14] Let $\left(M\mathrm{,}g\mathrm{,}\zeta \right)$ be a normalized null submanifold in semi-Riemmannian manifold $\left(\bar{M}\mathrm{,}\bar{g}\right)$ . Let $\left(\bar{M}\mathrm{,}{\bar{g}}_{\alpha }\right)$ be a semi-Riemannian manifold constructed in a semi-Riemannian manifold the scalar curvatures of $\bar{g}$ and $\underset{\_}{g}$ $\left(\bar{M}\mathrm{,}\bar{g}\right)$ , ${\bar{r}}_{\alpha }$ and $\bar{r}$ are respectively related on $\bar{M}$ by

$\begin{array}{c}{\bar{\Upsilon }}_{\alpha }=\bar{r}+\frac{1}{2}\{{\left(tr\left(A_N\right)\right)}^2-tr{\left(A_N\right)}^2-{\Vert A_N\xi \Vert }_{\bar{g}}^2+\langle A_N\xi \mathrm{,}{A}_{\xi }^{\star }{e}_a\rangle \\ -tr\left({\bar{\nabla }}_{\xi }{A}_N\right)-div{\tau }^{N^{\#}{}^{{\bar{g}}_{\alpha }}}\}\mathrm{.}\end{array}$ (52)

7. Inequalities of Scalar Curvature of Null Submanifold in Semi-Riemannian Manifold

Now, to establish inequality between the extrinsic scalar curvature of M and the scalar curvature of $\left(\bar{M}\mathrm{,}{\bar{g}}_{\alpha }\right)$ , we shall need the followings définitions and lemma.

Definition 7.1 Let $\left(M\mathrm{,}{\tilde{g}}_{\alpha }\right)$ be an n-dimensional semi-Riemannian submanifold of index $\left(q+{\tilde{q}}_{\alpha }\right)$ of an $\left(n+k\right)$ -dimensional semi-Riemannian manifold $\left(\bar{M}\mathrm{,}{\bar{g}}_{\alpha }\right)$ of index q. The submanifold will be called

1) Timelike $D_{\mu }$ -geodesic if ${\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\mu }}=0$ ,

2) Timelike $D_{\nu }$ -geodesic if ${\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\mu }}=0$ ,

3) Spacelike $D_{\mu }$ -geodesic if ${\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\nu }}=0$ ,

4) Spacelike $D_{\mu }$ -geodesic if ${\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\nu }}=0$ ,

5) Timelike mixed geodesic if ${\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\mu }}=0$ ,

6) Spacelike mixed geodesic if ${\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\nu }}=0$ .

Theorem 7.1 Let $\left(M^n\mathrm{,}g\mathrm{,}\zeta \right)$ be a normalized r-null submanifold in semi-Riemmannian manifold $\left({\bar{M}}^{n+k}\mathrm{,}\bar{g}\right)$ . Let the isometrical immersion $\left(M^n\mathrm{,}\tilde{g}\right)$ in $\left({\bar{M}}^{n+k}\mathrm{,}{\bar{g}}_{\alpha }\right)$ of null submanifold equipped with a semi-Riemannian manifold of index $\left(q+{\tilde{q}}_{\alpha }\right)$ in sem-Riemannian constructed in a semi-Riemannian manifold of index q. If the mean curvature is spacelike-geodesic, then

$\begin{array}{c}{r}^0\le \bar{r}+\frac{1}{2}\left\{n^2\langle H\mathrm{,}H\rangle +{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\mu }}\Vert }^2+{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2\right\}+{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2+\frac{1}{2}\{{\left(tr{A}_N\right)}^2-tr{\left(A_N\right)}^2\\ -{\Vert A_N\xi \Vert }_{\bar{g}}^2+\langle A_N\xi \mathrm{,}{A}_{\xi }^{\star }\rangle +\left[tr{A}_{\xi }^{\star }-tr{A}_N\right]tr{A}_{\xi }^{\star }-tr\left({\nabla }_{\xi }{A}_{\xi }^{\star }\right)+{\tau }^N\left({\tau }^{{\#}_{\eta }}\right)\}\mathrm{.}\end{array}$ (53)

Also, if the mean curvature is timelike, then

$\begin{array}{c}{r}^0\ge \bar{r}+\frac{1}{2}\left[n^2\langle H\mathrm{,}H\rangle -{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2-{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2\right]-{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2+\frac{1}{2}\{{\left(tr{A}_N\right)}^2-tr{\left(A_N\right)}^2\\ -{\Vert A_N\xi \Vert }_{\bar{g}}^2+\langle A_N\xi \mathrm{,}{A}_{\xi }^{\star }\rangle +\left[tr{A}_{\xi }^{\star }-tr{A}_N\right]tr{A}_{\xi }^{\star }-tr\mathrm{<mo\; stretchy="false">\; (\; </mo>}{\nabla }_{\xi }{A}_{\xi }^{\star }\mathrm{<mo\; stretchy="false">\; )\; </mo>}+{\tau }^N\left({\tau }^{{\#}_{\eta }}\right)\}\mathrm{.}\end{array}$ (54)

If the equality case of (53) is satisfied at each point $x\in M$ , then the mean curvature is timelike and M is timelike mixed geodesic. If the equality case of (54) is satisfied at each point $x\in M$ , then the mean curvature is spacelike and M is spacelike mixed geodesic. The equalities in both the cases (53) and (54) are true simultaneously if and only if M is totally geodesic.

Let $D_{\mu }$ be a maximally timelike, $D_{\nu }$ be a maximally spacelike distribution on TM and ${\tilde{D}}_{\mu }$ be a maximally timelike distribution, ${\tilde{D}}_{\nu }$ be a maximal spacelike distribution on $T^{\perp }M$ . If we put (40) in (38), then we get

$nH={\displaystyle \underset{r=1}{\overset{{\tilde{q}}_{\alpha }}{\sum }}}{\displaystyle \underset{j=1}{\overset{q}{\sum }}}{\delta }_{jj}^r{e}_r-{\displaystyle \underset{r={\tilde{q}}_{\alpha }+1}{\overset{k}{\sum }}}{\displaystyle \underset{j=1}{\overset{q}{\sum }}}{\delta }_{jj}^r{e}_r-{\displaystyle \underset{r=1}{\overset{{\tilde{q}}_{\alpha }}{\sum }}}{\displaystyle \underset{j=q+1}{\overset{n}{\sum }}}{\delta }_{jj}^r{e}_r+{\displaystyle \underset{r={\tilde{q}}_{\alpha }+1}{\overset{k}{\sum }}}{\displaystyle \underset{j=q+1}{\overset{n}{\sum }}}{\delta }_{jj}^r{e}_r.$ (55)

$n^2\Vert H\Vert ={\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\nu }}\Vert }^2+{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2-{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\mu }}\Vert }^2-{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2$ (56)

which is equivalent to say that the mean curvature is timelike if the submanifold is spacelike $D_{\mu }$ -geodesic and spacelike $D_{\nu }$ -geodesic, and the mean curvature is spacelike if the submanifold is timelike $D_{\mu }$ -geodesic and timelike $D_{\nu }$ -geodesic. The lightlike submanifold equipped with a semi-Riemannian metric $\tilde{g}$ is a semi-Riemannian submanifold of index $\bar{q}$ .

Using the equality (44) and stanard techniques as [3] , we have

$\begin{array}{c}{\tilde{r}}_{\alpha }={\bar{r}}_{\alpha }+\frac{1}{2}\left[n^2\langle H\mathrm{,}H\rangle +{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\mu }}\Vert }^2+{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2-{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\nu }}\Vert }^2-{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2\right]\\ -{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2+{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2\mathrm{.}\end{array}$ (57)

Which lead to the following inequality

${\tilde{r}}_{\alpha }\le {\bar{r}}_{\alpha }+\frac{1}{2}\left[n^2\langle H\mathrm{,}H\rangle +{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\mu }}\Vert }^2+{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2\right]+{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2\mathrm{.}$ (58)

Putting (32) in (58), we have the inequality

$\begin{array}{c}{r}^0\le {\bar{r}}_{\alpha }+\frac{1}{2}\left[n^2\langle H\mathrm{,}H\rangle +{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\mu }}\Vert }^2+{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2\right]+{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2\\ +\frac{1}{2}\left\{\left[tr{A}_{\xi }^{\star }-tr{A}_N\right]tr{A}_{\xi }^{\star }-tr\left({\nabla }_{\xi }{A}_{\xi }^{\star }\right)+tr\left({\nabla }_{\xi }{A}_N\right)+div{\tau }^{N^{\#}}+{\tau }^N\left({\tau }^{{\#}_{\eta }}\right)\right\}\mathrm{.}\end{array}$ (59)

Putting (52) in (59), we obtain the announced result. If the equality case of (53 is true, then ${\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2={\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}\tilde{H}}^{{\tilde{D}}_{\nu }}\Vert }^2={\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2=0$ . We can prove the rest part follows from

${\tilde{r}}_{\alpha }\ge {\bar{r}}_{\alpha }+\frac{1}{2}\left[n^2\langle H\mathrm{,}H\rangle -{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\mu }}\Vert }^2-{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2\right]-{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2\mathrm{.}$ (60)

If the equality case of (53), then ${\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2={\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2={\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2=0$ .

Corollary 7.1 Let $\left(M^n\mathrm{,}g\mathrm{,}\zeta \right)$ be a conformally closed normalized r-null submanifold with the mean curvature is spacelike in semi-Riemmannian manifold $\left({\bar{M}}^{n+k}\mathrm{,}\bar{g}\right)$ with conformal factor $\phi$ and the isometrical immersion $\left(M^n\mathrm{,}\tilde{g}\right)$ in $\left(\bar{M}\mathrm{,}{\bar{g}}_{\alpha }\right)$ of null submanifold equipped with a semi-Riemannian manifold $\tilde{g}$ in sem-Riemannian constructed in a semi-Riemannian manifold of index q. If the mean curvature is spacelike-geodesic, then

$\begin{array}{c}{r}^0\le \bar{r}+\frac{1}{2}\left[n^2\langle H\mathrm{,}H\rangle +{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\mu }}\Vert }^2+{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2\right]+{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2\\ +\frac{1}{2}{\phi }^2\left\{{\left(tr{A}_{\xi }^{\star }\right)}^2-tr{\left(A_{\xi }^{\star }\right)}^2\right\}+\frac{1}{2}\left\{\left(1-\phi \right){\left(tr{A}_{\xi }^{\star }\right)}^2-tr\left({\nabla }_{\xi }{A}_{\xi }^{\star }\right)+{\tau }^N\left({\tau }^{{\#}_{\eta }}\right)\right\}\mathrm{.}\end{array}$ (61)

If the equality case of (61) is satisfied at each point $x\in M$ , then the mean curvature is timelike and M is timelike mixed geodesic. Also, If the mean curvature is timelike, then

$\begin{array}{c}{r}^0\ge \bar{r}+\frac{1}{2}\left[n^2\langle H\mathrm{,}H\rangle -{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2-{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2\right]-{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2\\ +\frac{1}{2}{\phi }^2\left\{{\left(tr{A}_{\xi }^{\star }\right)}^2-tr{\left(A_{\xi }^{\star }\right)}^2\right\}+\frac{1}{2}\left\{\left(1-\phi \right){\left(tr{A}_{\xi }^{\star }\right)}^2-tr\left({\nabla }_{\xi }{A}_{\xi }^{\star }\right)+{\tau }^N\left({\tau }^{{\#}_{\eta }}\right)\right\}\mathrm{.}\end{array}$ (62)

If the equality case of (62) is satisfied at each point $x\in M$ , then the mean curvature is spacelike and M is spacelike mixed geodesic. The equalities in both the cases (61) and (62) are true simultaneously if and only if M is totally geodesic.

Theorem 7.2 Let $\left(M^n\mathrm{,}{\tilde{g}}_{\alpha }\mathrm{,}\zeta \right)$ be a normalized r-null submanifold equipped with a associated semi-Riemannian ${\tilde{g}}_{\alpha }$ in semi-Riemmannian manifold $\left({\bar{M}}^{n+k}\mathrm{,}{\bar{g}}_{\alpha }\right)$ . If $\left(M\mathrm{,}{\tilde{g}}_{\alpha }\right)$ is timelike geodesic, then

$\begin{array}{c}{r}^0\ge \bar{r}+\frac{1}{2}\left(n^2\langle H\mathrm{,}H\rangle -{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\nu }}\Vert }^2-{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2\right)+\frac{1}{2}\{{\left(tr{A}_N\right)}^2-tr{\left(A_N\right)}^2\\ -{\Vert A_N\xi \Vert }_{\bar{g}}^2+\langle A_N\xi \mathrm{,}{A}_{\xi }^{\star }\rangle +\left[tr{A}_{\xi }^{\star }-tr{A}_N\right]tr{A}_{\xi }^{\star }-tr\left({\nabla }_{\xi }{A}_{\xi }^{\star }\right)+{\tau }^N\left({\tau }^{{\#}_{\eta }}\right)\}\mathrm{.}\end{array}$ (63)

If the equality case of (63) is satisfied at each point $x\in M$ , then M is mixed geodesic.

From (57) and under the assumption that the submanifold is timelike geodesic, we have:

${\tilde{r}}_{\alpha }={\bar{r}}_{\alpha }+\frac{1}{2}\left[n^2\langle H\mathrm{,}H\rangle -{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\nu }}\Vert }^2-{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2\right]+{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2\mathrm{,}$ (64)

which implies the inequality

${\tilde{r}}_{\alpha }\ge {\bar{r}}_{\alpha }+\frac{1}{2}\left[n^2\langle H\mathrm{,}H\rangle -{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\nu }}\Vert }^2-{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2\right]\mathrm{.}$ (65)

Putting (32) in (65), we have the inequality

$\begin{array}{c}{r}^0\ge {\bar{r}}_{\alpha }+\frac{1}{2}\left(n^2\langle H\mathrm{,}H\rangle -{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\nu }}\Vert }^2-{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2\right)\\ +\frac{1}{2}\left\{\left[tr{A}_{\xi }^{\star }-tr{A}_N\right]tr{A}_{\xi }^{\star }-tr\left({\nabla }_{\xi }{A}_{\xi }^{\star }\right)+tr\left({\nabla }_{\xi }{A}_N\right)+div{\tau }^{N^{\#}}+{\tau }^N\left({\tau }^{{\#}_{\eta }}\right)\right\}\mathrm{.}\end{array}$ (66)

and putting (52) in (66), we obtain (63) the equality case of (63) is satisfied if ${\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2=0$ , which is equivalent to say that M is mixed geodesic.

In the conformally case with conformal factor $\phi$ , we can prove the following

Corollary 7.2

$\begin{array}{c}{r}^0\ge {\bar{r}}_{\alpha }+\frac{1}{2}\left(n^2\langle H\mathrm{,}H\rangle -{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\nu }}\Vert }^2-{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2\right)+\frac{1}{2}{\phi }^2\left\{{\left(tr{A}_{\xi }^{\star }\right)}^2-tr{\left(A_{\xi }^{\star }\right)}^2\right\}\\ +\frac{1}{2}\left\{\left(1-\phi \right){\left(tr{A}_{\xi }^{\star }\right)}^2-tr\left({\nabla }_{\xi }{A}_{\xi }^{\star }\right)+{\tau }^N\left({\tau }^{{\#}_{\eta }}\right)\right\}\mathrm{.}\end{array}$ (67)

If the equality case of (67) is satisfied at each point $x\in M$ , then M is mixed geodesic.

Theorem 7.3 Let $\left(M^n\mathrm{,}g\mathrm{,}\zeta \right)$ be a normalized r-null submanifold in semi-Riemmannian manifold $\left(\bar{M}\mathrm{,}\bar{g}\right)$ and the isometrical immersion $\left(M^n\mathrm{,}\tilde{g}\right)$ in $\left(\bar{M}\mathrm{,}{\bar{g}}_{\alpha }\right)$ of null submanifold equipped with a semi-Riemannian manifold $\tilde{g}$ in semi-Riemannian constructed in a semi-Riemannian manifold of index q. If $\left(M\mathrm{,}\tilde{g}\right)$ is timelike geodesics, then

$\begin{array}{c}{r}^0\le \bar{r}+\frac{1}{2}{n}^2\langle H\mathrm{,}H\rangle +{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2+\frac{1}{2}\{{\left(tr{A}_N\right)}^2-tr{\left(A_N\right)}^2-{\Vert A_N\xi \Vert }_{\bar{g}}^2\\ +\langle A_N\xi \mathrm{,}{A}_{\xi }^{\star }\rangle +\left[tr{A}_{\xi }^{\star }-tr{A}_N\right]tr{A}_{\xi }^{\star }-tr\left({\nabla }_{\xi }{A}_{\xi }^{\star }\right)+{\tau }^N\left({\tau }^{{\#}_{\eta }}\right)\}\mathrm{.}\end{array}$ (68)

If the equality case of (68) is true, then M is minimal

The submanifold equipped with associated semi-Riemannian $\left(M^n\mathrm{,}\tilde{g}\right)$ is isometrically immersed in a Riemannian manifold $\left(\bar{M}\mathrm{,}{\bar{g}}_{\alpha }\right)$ is semi-riemannian submanifold. Under the assumption that the submanifold is timelike geodesic, from (57) and using semi-Riemannian technical, we have the following inequality

${\tilde{r}}_{\alpha }\le {\bar{r}}_{\alpha }+\frac{1}{2}{n}^2\langle H\mathrm{,}H\rangle +{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2\mathrm{,}$ (69)

Putting (32) in (65), we have

$\begin{array}{c}{r}^0\le {\bar{r}}_{\alpha }+\frac{1}{2}{n}^2\langle H\mathrm{,}H\rangle +{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2+\frac{1}{2}\{\left[tr{A}_{\xi }^{\star }-tr{A}_N\right]tr{A}_{\xi }^{\star }\\ -tr\left({\nabla }_{\xi }{A}_{\xi }^{\star }\right)+tr\left({\nabla }_{\xi }{A}_N\right)+div{\tau }^{N^{\#}}+{\tau }^N\left({\tau }^{{\#}_{\eta }}\right)\}\mathrm{.}\end{array}$ (70)

and putting (52) in (70), the desired result hold. If the equality case of (68) is true, then ${\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\nu }}\Vert }^2={\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2=0$ , which is equivalent to say that M is minimal.

Corollary 7.3 Let $\left(M^n\mathrm{,}g\mathrm{,}\zeta \right)$ be a closed conformally normalized r-null submanifold in semi-Riemmannian manifold $\left(\bar{M}\mathrm{,}\bar{g}\right)$ with conformal factor $\phi$ and the isometrical immersion $\left(M\mathrm{,}\tilde{g}\right)$ in $\left(\bar{M}\mathrm{,}{\bar{g}}_{\alpha }\right)$ of null submanifold equipped with a semi-Riemannian manifold $\tilde{g}$ in sem-Riemannian constructed in a semi-Riemannian manifold of index q. If $\left(M^n\mathrm{,}\tilde{g}\right)$ is timelike geodesic, then

$\begin{array}{c}{r}^0\le \bar{r}+\frac{1}{2}{n}^2\langle H\mathrm{,}H\rangle +{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\nu }}\Vert }^2+\frac{1}{2}{\phi }^2\left\{{\left(tr{A}_{\xi }^{\star }\right)}^2-tr{\left(A_{\xi }^{\star }\right)}^2\right\}\\ +\frac{1}{2}\left\{\left(1-\phi \right){\left(tr{A}_{\xi }^{\star }\right)}^2-tr\left({\nabla }_{\xi }{A}_{\xi }^{\star }\right)+{\tau }^N\left({\tau }^{{\#}_{\eta }}\right)\right\}\mathrm{.}\end{array}$ (71)

If the equality case of (71) is true, then M is minimal

Theorem 7.4 Let $\left(M^n\mathrm{,}g\mathrm{,}\zeta \right)$ be a closed normalized r-null submanifold in semi-Riemmannian manifold $\left(\bar{M}\mathrm{,}\bar{g}\right)$ and the isometrical immersion $\left(M\mathrm{,}\tilde{g}\right)$ in $\left(\bar{M}\mathrm{,}{\bar{g}}_{\alpha }\right)$ of null submanifold equipped with a semi-Riemannian manifold $\tilde{g}$ in sem-Riemannian constructed in a semi-Riemannian manifold of index q. If $\left(M^n\mathrm{,}\tilde{g}\right)$ is spacelike geodesic, then

$\begin{array}{c}{r}^0\le \bar{r}+\frac{1}{2}\left(n^2\langle H\mathrm{,}H\rangle +{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\mu }}\Vert }^2+{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2\right)+\frac{1}{2}\{{\left(tr{A}_N\right)}^2-tr{\left(A_N\right)}^2\\ -{\Vert A_N\xi \Vert }_{\bar{g}}^2+\langle A_N\xi \mathrm{,}{A}_{\xi }^{\star }\rangle +\left[tr{A}_{\xi }^{\star }-tr{A}_N\right]tr{A}_{\xi }^{\star }-tr\left({\nabla }_{\xi }{A}_{\xi }^{\star }\right)+{\tau }^N\left({\tau }^{{\#}_{\eta }}\right)\}\mathrm{.}\end{array}$ (72)

The equality case of (72) is satisfied at each point $p\in M$ if and only if M is mixed geodesic.

From (57) and under the assumption of theorem, we have

${\tilde{r}}_{\alpha }\le {\bar{r}}_{\alpha }+\frac{1}{2}\left[n^2\langle H\mathrm{,}H\rangle +{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\mu }}\Vert }^2+{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2\right]-{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2\mathrm{.}$ (73)

Putting (32) in (73), we have

$\begin{array}{c}{r}^0\le {\bar{r}}_{\alpha }+\frac{1}{2}\left(n^2\langle H\mathrm{,}H\rangle +{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\mu }}\Vert }^2+{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2\right)\\ +\frac{1}{2}\left\{\left[tr{A}_{\xi }^{\star }-tr{A}_N\right]tr{A}_{\xi }^{\star }-tr\left({\nabla }_{\xi }{A}_{\xi }^{\star }\right)+tr\left({\nabla }_{\xi }{A}_N\right)+div{\tau }^{N^{\#}}+{\tau }^N\left({\tau }^{{\#}_{\eta }}\right)\right\}\mathrm{.}\end{array}$ (74)

and putting (52), (74), on obtain (72). With the equality if and only if ${\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2=0$ . which is equivalent to say that M is mixed geodesic.

Corollary 7.4

$\begin{array}{c}{r}^0\le \bar{r}+\frac{1}{2}\left(n^2\langle H\mathrm{,}H\rangle +{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\mu }}\Vert }^2+{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2\right)+\frac{1}{2}{\phi }^2\left\{{\left(tr{A}_{\xi }^{\star }\right)}^2-tr{\left(A_{\xi }^{\star }\right)}^2\right\}\\ +\frac{1}{2}\left\{\left(1-\phi \right){\left(tr{A}_{\xi }^{\star }\right)}^2-tr\left({\nabla }_{\xi }{A}_{\xi }^{\star }\right)+{\tau }^N\left({\tau }^{{\#}_{\eta }}\right)\right\}\mathrm{.}\end{array}$ (75)

The equality case of (75) is satisfied at each point $p\in M$ if and only if M is mixed geodesic.

Theorem 7.5 Let $\left(M^n\mathrm{,}g\mathrm{,}\zeta \right)$ be a closed normalized r-null submanifold in semi-Riemmannian manifold $\left(\bar{M}\mathrm{,}\bar{g}\right)$ and the isometrical immersion $\left(M\mathrm{,}\tilde{g}\right)$ in $\left(\bar{M}\mathrm{,}{\bar{g}}_{\alpha }\right)$ of null submanifold equipped with a semi-Riemannian manifold $\tilde{g}$ in sem-Riemannian constructed in a semi-Riemannian manifold of index q. If $\left(M^n\mathrm{,}\tilde{g}\right)$ is spacelike geodesic, then

$\begin{array}{c}{r}^0\ge \bar{r}+\frac{1}{2}{n}^2\langle H\mathrm{,}H\rangle -{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2+\frac{1}{2}\{{\left(tr{A}_N\right)}^2-tr{\left(A_N\right)}^2-{\Vert A_N\xi \Vert }_{\bar{g}}^2\\ +\langle A_N\xi \mathrm{,}{A}_{\xi }^{\star }\rangle +\left[tr{A}_{\xi }^{\star }-tr{A}_N\right]tr{A}_{\xi }^{\star }-tr\left({\nabla }_{\xi }{A}_{\xi }^{\star }\right)+{\tau }^N\left({\tau }^{{\#}_{\eta }}\right)\}\mathrm{.}\end{array}$ (76)

The equality case of (76) is satisfied at each point $p\in M$ if and only if M is minimal.

Under the assumption of theorem, from (57) and substituting (32), and (52) in (57), we prof (76). With the equality if and only if ${\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }}^{{\tilde{D}}_{\mu }}\Vert }^2={\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2=0$

Corollary 7.5 Let $\left(M^n\mathrm{,}g\mathrm{,}\zeta \right)$ be a conformally normalized r-null submanifold in semi-Riemmannian manifold $\left(\bar{M}\mathrm{,}\bar{g}\right)$ with conformal factor $\phi$ and the isometrical immersion $\left(M\mathrm{,}\tilde{g}\right)$ in $\left(\bar{M}\mathrm{,}{\bar{g}}_{\alpha }\right)$ of null submanifold equipped with a semi-Riemannian manifold $\tilde{g}$ in sem-Riemannian constructed in a semi-Riemannian manifold of index q. Then

$\begin{array}{c}{r}^0\ge \bar{r}+\frac{1}{2}{n}^2\langle H\mathrm{,}H\rangle -{\Vert {\sigma }_{\mathrm{<mo>\; |\; </mo>}{D}_{\mu }\times D_{\nu }}^{{\tilde{D}}_{\mu }}\Vert }^2+\frac{1}{2}{\phi }^2\left\{{\left(tr{A}_{\xi }^{\star }\right)}^2-tr{\left(A_{\xi }^{\star }\right)}^2\right\}\\ +\frac{1}{2}\left\{\left(1-\phi \right){\left(tr{A}_{\xi }^{\star }\right)}^2-tr\left({\nabla }_{\xi }{A}_{\xi }^{\star }\right)+{\tau }^N\left({\tau }^{{\#}_{\eta }}\right)\right\}.\end{array}$ (77)

The equality case of (77) is satisfied at each point $p\in M$ if and only if M is minimal.

8. Conclusion

In this paper, some basic inequalities, involving the scalar curvature and the mean curvature, for a lightlike submanifold of a semi-Riemannian manifold are obtained. We established some inequalities between scalar curvature and shape operator of lightlike submanifold in semi-Riemannian manifold with the spacelike, timelike mean curvature, timelike geodesic, spacelike geodesic and timelike mixed geodesic. Equality cases are also discussed. For the rest of the work, we will establish other inequalities with an example for understand the methodology and its potential applications.

Acknowledgements

The authors are thankful to the reviewer for his/her valuable comments towards the improvement of the paper.

Conflicts of Interest

The authors declare that no competing interests regarding the publication of this paper.

References

[1]	Atindogbe, C. and Duggal, K.L. (2004) Conformal Sreen on Lightlike Submanifolds. International Journal of Pure and Applied Mathematics, 11, 421-442.
[2]	Chen, B.-Y. (1993) Some Pinching and Classification Theorems for Minimal Submani-Folds. Archiv der Mathematik (Basel), 60, 568-578. https://doi.org/10.1007/BF01236084
[3]	Chen, B.-Y. (1999) Relations between Ricci Curvature and Shape Operator for Sub-Manifolds with Arbitrary Codimensions. Glasgow Mathematical Journal, 41, 33-41. https://doi.org/10.1017/S0017089599970271
[4]	Duggal, K.L. and Bejancu, A. (1996) Lightlike Submanifolds of Semi-Riemannian Manifolds and Applications. Kluwer Academic, 364. https://doi.org/10.1007/978-94-017-2089-2
[5]	Gutiérrez, M. and Olea, B. (2015) Induced Riemannian Structures on Null Submanifolds. Mathematische Nachrichten, 289, 1219-1236. https://doi.org/10.1002/mana.201400355
[6]	Friedman, A. (1965) Isometric Embedding of Semi-Riemannian Manifolds into Euclidean Spaces. Reviews of Modern Physics, 37, 201-203. https://doi.org/10.1103/RevModPhys.37.201.2
[7]	Ndayirukiye, D., Nibaruta, G., Karimumuryango, M. and Nibirantiza, A. (2019) Algebraicity of Induced Riemannian Curvature Tensor on Lightlike Warped Product Manifolds. Journal of Applied Mathematics and Physics, 7, 3132-3139. https://doi.org/10.4236/jamp.2019.712220
[8]	Ndayirukiye, D., Nibirantiza, A., Nibaruta, G. and Karimumuryango, M. (2020) Osserman Conditions in Lightlike Warped Product Geometry. Journal of Applied Mathematics and Physics, 8, 585-596. https://doi.org/10.4236/jamp.2020.84045
[9]	Karimumuryango, M. (2021) Hans Fotsing Tetsing: Rigging and Nonexistence of Stable Currents in Null Hypersurface of Lorentzian Manifold. Differential Geometry-Dynamical Systems, 23, 74-89.
[10]	Karimumuryango, M. (2018) Chen’s Ricci Inequalities and Topological Obstructions on Null Submanifolds of a Lorentzian Manifold. Journal of Inequalities and Applications, 2018, 126.
[11]	Kupeli, D.N. (1987) On Null Submanifolds in Spacetimes. Geometry Dedicata, 23, 33-51. https://doi.org/10.1007/BF00147389
[12]	O. Neill, B. (1983) Semi-Riemannian Geometry with Applications to Relativity. Academic Press.
[13]	Tripathi, M.M. (2003) Certain Basic Inequalities for Submanifolds in (K, μ) Space. Recent Advances in Riemannian and Lorentzian Geometries Baltimore, 187-202. https://doi.org/10.1090/conm/337/06061
[14]	Karimumuryango, M., Nibaruta, G., Ndayishimiye, D. and Nibirantiza, A. (2021) On Structure Semi-Riemmannian of Lightlike Hypersurface of Semi-Riemannian Manifold.