1. Introduction
The theory of operator spaces is a natural non-commutative quantization of Banach space theory. Many problems in operator spaces are naturally motivated by both Banach space theory and operator algebra theory. Some local properties such as injectivity, nuclearity, local reflexivity and exactness have been intensively studied in [1] [2] [3] . In particular, we have for any operator space V,
(1)
The first implication of (1) was proved in [3] and the second in [2] . In [2] , Effros, Ozawa and Ruan showed that an operator space V is nuclear if and only if V is locally reflexive and
is injective. As pointed out in [2] , local reflexivity is an essential condition in this result since Kirchberg [4] has constructed a separable non-nuclear operator space V for which
. Turning to
-algebra theory, using Conne’s deep work in [5] , Choi and Effros proved the following result in [6] [7] :
In [8] , Dong and Ruan showed that an operator space V is exact if and only if V is locally reflexive and
is weak* exact.
For the convenience of the readers, we recall some basic notations and results in operator spaces, the details of which can be found in [9] [10] . Given abstract operator spaces V and W and a linear mapping
, for each
there is a corresponding linear mapping
defined by
for all
. We define the completely bounded norm of
by
(this might be infinite). It is evident that the norms
form an increasing sequence
We say that
is completely bounded (respectively, completely contractive) if
(respectively,
). It is a simple matter to verify that
is a norm on the linear space
of completely bounded linear mappings
. We say that
is a complete quotient mapping if each
is a quotient mapping (i.e.
maps
onto
), and that
is an exact complete quotient mapping if each
is an exact quotient mapping (i.e.
maps
onto
).
We use the notations
and
for the injective, projective operator space tensor products (see [11] [12] ). In the following, we give some definitions of local properties in the system
for operator spaces. Given an operator space V, we define:
(a) Injectivity (see [9] ). If for any operator space
and a complete contraction
, there is a completely contractive extension
.
(b) Local reflexivity (see [9] ). If for any finite dimensional operator space L, every complete contraction
is the point-weak* limit of a net of complete contractions
. It follows from Theorem 14.3.1 in [9] that an operator space V is locally reflexive if and only if
for any finite dimensional operator space L.
(c) Exactness (see [9] or [10] ). If for any finite dimensional subspace L of V and every
, there exists an integer n and a subspace
such that
. This is equivalent to the following definition: there exists a diagram of complete contractions.
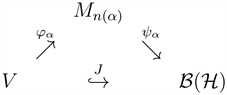
which approximately commute in the point-norm topology.
(d) Nuclearity (see [9] ). There exists a diagram of complete contractions
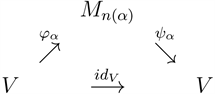
which approximately commute in the point-norm topology.
(e) Finitely representable in
(see [1] [3] ). Given operator spaces E and F, we define the completely bounded Banach-Mazur distance introduced in [3] :
(2)
Given a family of operator spaces
and the distance (2), for every finite-dimensional subspace L of V and
, there exists a subspace S of some
such that
.
(f) The weak expectation property (or simply, WEP) (see [9] ). Given an operator space V, for any completely isometric inclusion
↪
, there exists a completely contractive mapping
such that
, where
↪
is the canonical inclusion.
Mapping spaces naturally arise in both the theory and applications of functional analysis. Grothendieck introduced the theory of nuclear mapping spaces
, integral mapping spaces
and 1-summing mapping spaces
in [13] . Nuclear mappings play an important part in the theory of Schwartz spaces and their applications to differential equations and quantum field theory. Grothendieck also used 1-summing mappings to investigate the Dvoretzky-Rogers theorem. It has been said that Grothendieck’s theory of 1-summing mappings is in some sense at the heart of Banach space theory.
With the results in [14] [15] [16] , it is now evident that major components of Grothendieck’s program make sense in the context of operator spaces. An operator space mapping space O is an assignment to each pair of operator spaces
of a linear space
of completely bounded mapping
, together with an operator space matrix norm
, such that for each
,
(a)
;
(b) for any linear mapping
and
,
We define the completely nuclear mapping space
to be the image of the canonical mapping
, with the quotient operator space structure determined by the identification
We let
be the corresponding norm on
.
Given operator spaces V and W, we define a mapping
to be completely integral if
We let
denote the set of all completely integral mappings from V into W. It is known from Lemma 12.3.1 in [9] that the following assertions are equivalent:
(a)
;
(b) for all finite dimensional operator spaces L,
(c) for all operator spaces U,
if
is a linear mapping of operator spaces, then we define
in
by
(3)
If
, we say that
is a completely 1-summing mapping from V into W and we refer to (3) as the completely 1-summing norm of
. We let
denote the space of all completely 1-summing mappings from V into W.
For given operator spaces V and W, analogues of four of the most important Banach mapping spaces (nuclear mapping spaces, integral mapping spaces, absolutely summing mapping spaces and bounded mapping spaces) are the completely nuclear mapping spaces
, the completely integral mapping spaces
, the completely 1-summing mapping spaces
and the completely bounded mapping spaces
. We have the following contractive inclusions:
As we know, mapping spaces provide a fundamental tool for studying Banach spaces and operator spaces. In this note, we are interested in the local properties in the system of completely 1-summing mapping spaces
. As we have seen, the local theory in the system of completely 1-summing mapping spaces is quite different from the original local theory of completely bounded mapping spaces.
2. Completely 1-Summing Mapping Space
We let
denote the space of all completely 1-summing mappings from V into W. This is again an operator space since we may use the embedding
↪
For any matrix
,
Let
,
We have
.
Hahn-Banach theorem is the key initial ingredient of classical functional analysis. So we first investigate its analogue in the system of completely 1-summing mapping spaces.
Definition 2.1. We say an operator space V is injective in the system
if for any operator spaces
, every completely 1-summing mapping
has a linear extension
satisfying
.
Lemma 2.2. A nuclear operator space V is injective in the system
if and only if for any inclusion of operator spaces
, the restriction mapping
is an exact completely quotient mapping.
Proof. From Corollary 15.5.3 in [9] , if V is a nuclear operator space, then we have the isometry
for all operator space W. By the Lemma 2.2 in [17] , we get the conclusion.¨
Proposition 2.3. If an operator space U is injective in the system
and
is a completely contractive projection, then
is again injective in the system
.
Proof. Let
and
with
.
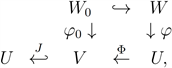
where J is the inclusion mapping. It follows from the completely 1-summing injectivity of U that there exists an extension
with
and
Since for any
,
. Thus we have
and this implies that
is an extension of
with
Therefore
is again injective in the system
.¨
Definition 2.4. (Definition 2.1 in [18] ) An operator space V is nuclear in the system
if there exists a diagram of linear mappings with
,
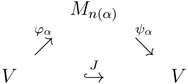
which approximately commute in the point-norm topology.
Theorem 2.5. An operator space V is nuclear in the system
if and only if V is nuclear and
.
Proof. From Corollary 13.2.2 in [9] , we have
. If an operator space
is nuclear in the system
, it is nuclear in the system
. By Theorem 3.4 in [17] , we have V is nuclear and
. We get
. Conversely, suppose that V is nuclear and
. By nuclearity of V, there exists a diagram of complete contractions
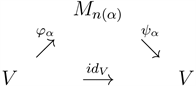
which approximately commute in the point-norm topology. Thus we have
and
Therefore V is nuclear in the system
.¨
Definition 2.6. (Definition 3.1 in [18] ) An operator space V is
-nuclear in the system
if there exists a diagram of linear mappings with
,
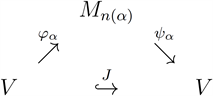
which approximately commute in the point-norm topology.
Theorem 2.7. An operator space V is
-nuclear in the system
if and only if V is nuclear and
.
Proof. The proof is similar to that of Theorem 2.5.¨
Definition 2.8. An operator space V is locally reflexive in the system
if for any finite dimensional operator space L,
Proposition 2.9. If V has WEP, V is locally reflexive in the system
if and only if it is locally reflexive in the system
.
Proof. From Corollary 15.5.2 in [9] , if V has WEP, we have the isometry
for all operator spaces L.¨
Proposition 2.10. If
is an injective
-algebra,
is locally reflexive in the system
if and only if it is locally reflexive in the system
.
Proof. From Proposition 15.5.1 in [9] ,
is an injective
-algebra, we have the isometry
for all operator spaces L.¨
Definition 2.11. An operator space
is exact in the system
if there exists a diagram of linear mappings with
,
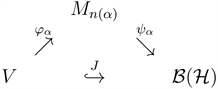
which approximately commute in the point-norm topology.
Proposition 2.12. An operator space V is nuclear in the system
, then it is nuclear in the system
.
Proof. From Corollary 13.2.2 in [9] , we have
.¨
Proposition 2.13. An operator space V is exact in the system
, then it is nuclear in the system
.
Proof. From Corollary 13.2.2 in [9] , we have
.¨
Corollary 2.14. An operator space V is nuclear in the system
if and only if
.
Proof. From Proposition 2.12, the operator space V is also nuclear in the system
. From Theorem 3.11 in [17] , we have
. The converse is obvious.¨
From the work of Kirchberg and Pisier ( [3] [19] ) we see that an operator space V is exact if and only if it is finitely representable in
. In this note, we will consider the analogue in the system of completely 1-summing mapping spaces. Given operator spaces
, we define
Definition 2.15. Given a family of operator spaces
. We say that an operator space V is finitely representable in
in the system
if for every finite-dimensional subspace L of V and
, there exists a subspace S of some
such that
.
In this paper, we are mainly interested in the finite-representability in
in the system
.
Theorem 2.16. An operator space
is exact in the system
if and only if V is finitely representable in
in the system
.
Proof. Suppose that
is exact in the system
. By Definition 2.11, there exists a diagram of linear mappings with
,
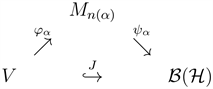
which approximately commute in the point-norm topology. Thus for any
and any finite dimensional subspace
, we choose Auerbach basis
and
. It follows from the exactness of V in the system
that we can find linear mappings

and
such that
and
,
. Lemma 15.3.3 in [9] implies that there is a complete isomorphism
such that
, where
and
. Thus
is a linear isomorphism with inverse
satisfying
So V is finitely representable in
in the system
.
Conversely, suppose that V is finitely representable in
in the system
. By Definition 2.15, for any
and any finite dimensional subspace
, there exist an integer n, a subspace
and a linear isomorphism
such that
. Since
it follows from the injectivity of
in the system
that there exists an extension
with
Similarly, since
the injectivity of
in the system
implies that we have an extension
with
Thus we have the following diagram
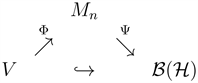
with
and
. It is routine to show that V is exact in the system
.¨
Proposition 2.17. An operator space V is finitely representable in
in the system
, then it is nuclear in the system
.
Proof. From Corollary 13.2.2 in [9] , we have
.¨
Corollary 2.18. An operator space V is finitely representable in
in the system
if and only if
.
Proof. From the above proposition, the operator space V is also finitely representable in
in the system
. From Theorem 4.3 in [17] , we have
. The converse is obvious.¨
3. Conclusion
In this paper, we have investigated local properties in the system of completely 1-summing mapping spaces. Combined with the work of [17] [18] , we have provided a very complete characterization of the local properties of completely 1-summing mapping spaces, completely nuclear mapping spaces and completely Integral Mapping Spaces. We have found if an operator is WEP, the locally reflexive property is equivalent in completely 1-summing mapping space and completely nuclear mapping spaces. And if an operator is exact, the finitely representable property is equivalent in completely 1-summing mapping space and completely nuclear mapping spaces.
In future work, we will apply the theories of completely 1-summing mapping spaces to the category of C*-algebras. For example, we will study Kirchberg’s conjecture and QWEP conjecture in the system of completely 1-summing mapping spaces. In addition, we will intensively study the relationship between various mapping spaces.
Fund
Project partially supported by Zhejiang Provincial Natural Science Foundation of China (Grant No. LQ21A010015).