The Infinity Tree: Representing Infinities of Real Numbers with Countably Infinite Tree Structures ()
1. Introduction
In 1891, Georg F. L. P. Cantor published a diagonalization argument to contend that the set of real numbers is not countably infinite [1] . He started by positing that the set of reals had been put into a countably infinite list and then used diagonalization to argue that there is a real number that is not included in such a list. His argument, that the real numbers have a higher order of infinity than the natural numbers, has been the foundation of much work on “transfinite numbers” since then.
This paper presents a counter-argument, discussing how the infinite set of real numbers between 0 and 1 could be represented by a countably infinite tree structure (called an “infinity tree”) that would avoid Cantor’s diagonalization. This idea is then extended, to discuss how all the real numbers could be represented by a countable collection of infinity trees, and how infinity trees could represent all imaginary and complex numbers, and all points in any number of dimensions in multi-dimensional spaces. The cardinality of the nodes in this more elaborate combination of infinity trees would still be the countable infinityא 0.
The objective of this paper is not to overturn previous research based on Cantor’s argument, but to suggest that this situation may be treated as a definitional choice: If we define “countably infinite cardinality” as a property that can be represented by a countably infinite list of individual elements, each of countably infinite length, then within this branch of cardinality theory we could preserve and continue to develop the mathematics about different cardinalities of infinity that has been built on top of Cantor’s argument.
On the other hand, if we define countably infinite cardinality as a property that can be represented by a data structure with a countably infinite number of elements, such as an infinity tree, then we have an opportunity to develop a non-Cantorian theory of infinity.
2. A Thought Experiment
Suppose we perform a thought experiment and construct an infinite tree structure as follows:
· The root node has the label ●, representing a decimal point, implicitly preceded by 0.
· Each node in the tree has pointers to 10 different nodes below it, labeled with the digits 0 through 9. The 10 nodes are unique to the node above them. No other node points to any of them.
· The tree is not reentrant. No two nodes point to the same another node. There is no circular path between nodes. No node points to itself.
This is just a simple infinite tree, with a branching factor of 10. Just a few of the nodes and branches of the first few levels of the “infinity tree” are shown in Figure 1.
For the infinite tree, the following assertions hold:
1) Every finite path from the root node to a descendant corresponds to a finite decimal number between 0 and 1. Therefore, every node below the root node also corresponds to a finite decimal number between 0.0 and 1.0, indicated by the path reaching it from the root node.
2) The nodes in the tree are countably infinite, i.e., each node can be counted by a distinct, sequential natural number (1, 2, 3, …). This can be done by navigating the tree breadth-first: The root node is counted 1. Its descendants are counted 2 through 11. The nodes at the next level down are counted 12 through 111, and so forth, counting nodes breadth-first throughout the tree. Therefore,
![]()
Figure 1. A simple infinity tree diagram.
the set of all nodes in the infinite tree is countably infinite.
3) The arcs in the tree are also countably infinite, in the same breadth-first manner since each node has exactly ten arcs going from it.
4) For each non-root node N, there is a unique, finite path from the root node to node N. So, the number of finite paths to nodes in the tree is also countably infinite.
5) Every infinite path descending from the root node of the tree corresponds to an infinite decimal fraction, from zero up to but not including 1. The tree can at most represent .99999999…and get infinitesimally close to 1.
6) Every infinite decimal from 0 up to but not including 1 corresponds to an infinite path in the tree descending from the root node.
7) So, a countably infinite set of nodes and arcs represents the infinite set of infinite paths from 0 downward through the tree.
8) So, a countably infinite set of nodes and arcs in a tree represents the set of infinite decimals from 0 up to but not including 1.
9) Therefore, the set of infinite decimals between 0 and 1.0 can be mapped to and represented by a countably infinite set of nodes and arcs. Any number between 0 and 1 can be reached to any desired degree of precision, with countably many nodes and arcs.
To consider Cantor’s diagonalization in this context: The paths through the first n levels of the tree below its root node (which contains the decimal point) correspond to a list of all the decimals of length n, which would contain 10n rows. If we go through the first n rows of the list and diagonally choose a different digit in each row, then the new sequence of digits that we have specified are somewhere in the remaining (10n − n) rows of the list. In effect, this jumps to a different row of the list. Cantor’s diagonalization does not show that a finite countable list does not contain all sequences of length n. It only shows that the first n rows of such a list cannot contain all sequences of length n.
Cantor’s diagonalization does show that a hypothetical countably infinite list cannot contain every real number in the interval [0, 1) specified with all its digits completely. Even so, a countably infinite tree structure can contain every real number in the interval [0, 1) specified with all its digits completely.
One might argue that since the set of real numbers in this range is contained in the countably infinite set of nodes of the infinity tree, the set of real numbers in this range must therefore be countably infinite.
If this argument cannot be proved or disproved, then we could treat this as a definitional choice, in different branches of cardinality theory: If we define countable cardinality as what can be represented by a countable list of individual elements, each element of perhaps infinite length, then within this branch of cardinality theory we would preserve and continue to develop the mathematics for different cardinalities of infinity that have been built on top of Cantor’s argument.
If we define countably infinite cardinality as what can be represented by a data structure with a countably infinite number of elements, such as an infinity tree, then we have an opportunity to develop a non-Cantorian theory of infinity.
Perhaps equivalently, we might treat this choice of definitions for countable cardinality as an axiomatic choice.
3. Infinities of All Real Numbers and Multi-Dimensional Spaces
The previous section focused on the interval [0, 1). Let us next consider the infinity of all real numbers, and the infinity of different multi-dimensional spaces. To begin, we suppose that the cardinality of the set of real numbers in the range [0, 1) is that of the natural numbers, which is conventionally represented byא 0. Symbolically, we would write:
|[0,1)| =א 0
More generally, for n ≥ 0:
|[n, n + 1)| =א 0
|(−n − 1, −n]| =א 0
That is, we can envision a forest of infinity trees, with an infinity tree between each integer and its successor, and with each infinity tree being countably infinite. Each tree in the forest can be uniquely indicated by the integer at the open boundary of the interval for the tree. For example, the tree representing the interval [22, 23) can be indicated by 23. The tree representing the interval (−47, −46] can be indicated by −47. Since the number of nonzero integers is countably infinite, they together indicate a countably infinite forest of countably infinite trees. This forest of trees effectively represents the set of all real numbers.
One might think that the cardinality of the forest must be greater than the cardinality of each infinity tree. Yet we could represent the forest with a combination of infinity trees, each containing a countably infinite number of nodes. And we could have another infinity tree to represent the possible axes for a multi-dimensional space of numbers, that could represent real numbers, imaginary numbers, complex numbers, etc. The cardinality of the nodes in this more elaborate, combination of infinity trees would still be the countable infinityא 0.
Figure 2 below illustrates this idea. Page space permits diagramming only two levels for each tree, though each infinity tree has as many levels as there are natural numbers.
Let D be the number of dimensions for a multi-dimensional space. We first choose a number D ≥ 1 from an infinity tree for the countably infinite set of natural numbers. This involves taking any finite number of steps in the top infinity tree labeled Ω in Figure 2 to choose a value for D. For each dimension d such that 1 ≤ d ≤ D, we choose a specific, arbitrary integer coordinate value nd from either the infinity tree for the positive integers n ≥ 1 or the infinity tree for the negative integers n ≤ −1. This chooses an integer at the open boundary of an interval for the dimension d, i.e., either [nd − 1, nd ) or (nd, nd + 1], respectively. This also involves taking any finite number of steps in an infinity tree. These choices are illustrated by the tree labeled I in the middle of Figure 2.
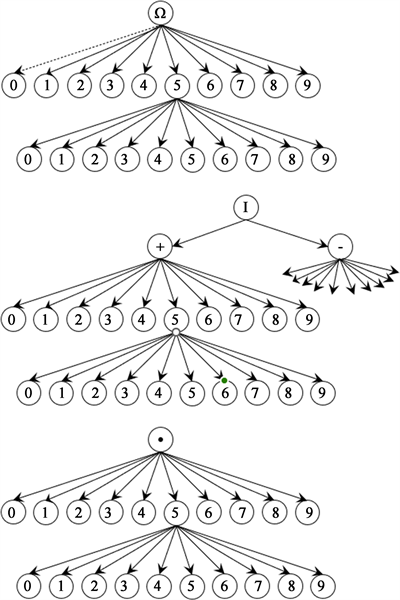
The above diagram shows infinity trees for representing spaces with any finite number of dimensions. The diagram uses a dashed line to show an option for choosing a space with 0 dimensions. Similarly, the diagram could be altered to support specifying spaces with a negative number of dimensions, or a fractional number of dimensions. These are much less intuitive, yet might be useful in some contexts, e.g., considering ideas for dimensions of space within black holes or negative universes.
Figure 2. Compound infinity tree diagram.
Finally, for each dimension d such that 1 ≤ d ≤ D, we choose a specific, arbitrary fractional coordinate value fd such that 0 ≤ fd < 1, from the infinity tree for the real numbers in the range [0, 1). This again involves taking any finite number of steps in an infinity tree. This choice is illustrated by the infinity tree labeled ● at the bottom of Figure 2.
If nd ≥ 1, then we have effectively specified (nd −1 + fd) for dimension d. If nd ≤ −1, then we have effectively specified (nd + 1 − fd) for dimension d. The combination of finite paths that we have chosen through these infinity trees effectively specifies any point in any multi-dimensional space, to any finite desired degree of precision, using a finite number of steps.
Since any location in these multi-dimensional spaces can be reached by navigating an unlimited yet countable number of dimensions, and an unlimited yet countable number of locations in each dimension, the set of spatial locations in these multi-dimensional spaces is countably infinite.
4. Relation to the Continuum Hypothesis
Cantor advanced the Continuum Hypothesis in 1878, which states that “there is no set whose cardinality is strictly between that of the integers and the real numbers” [2] . Establishing the truth or falsity of the hypothesis was the first of Hilbert’s 23 problems [3] . Cantor was unable to prove or disprove the hypothesis during his lifetime, and it remains unproven to this date. In 1940, Gödel showed that the hypothesis is consistent with the axioms of set theory, including the Axiom of Choice [4] . In 1963, Cohen showed that the hypothesis “cannot be derived from the other axioms of set theory, including the Axiom of Choice” [5] .
The approach of this paper, which holds that the infinite cardinality of the real numbers can be represented by countably infinite tree structures, is actually consistent with the Continuum Hypothesis: there cannot be a set with cardinality between that of the integers and the real numbers if the set of integers and the set of real numbers have the same cardinality.
5. Relation to Cantor’s 1874 Proof of Non-Denumerability
In 1874, Cantor published a different proof [6] that the set of real numbers is not countably infinite, which did not use the diagonalization argument he published in 1891. He considered the set of all real algebraic numbers ω that are solutions to polynomial equations of the standard form
, where the coefficients are integers, the numbers n and a0 are positive, the coefficients ai do not have any common factors, and the equation is irreducible.
Cantor showed that if the solutions to all these algebraic equations were put into an infinite ordered sequence, in one-to-one correspondence with the natural numbers, then the sequence would omit infinitely many transcendental real numbers that are not solutions of any algebraic equation.
Cantor’s 1874 proof does not address or defeat this paper’s discussion regarding an infinity tree providing a data structure with a countably infinite number of nodes that includes all the real numbers between 0 and 1. Nor does his 1874 proof address or defeat this paper’s discussion in section 3 above, showing that a countably infinite collection of infinity trees each with a countably infinite number of nodes could include all the real numbers: The infinity tree for the range [0, 1) has the property that any node n at a level l of the tree has a countable infinity of nodes below it which represent all possible continuations of fractions from node n.
6. Historical Notes
Some mathematicians (e.g., Kronecker, Poincare) resisted Cantor’s theory of transfinite numbers [7] . However, others (e.g., Hilbert) accepted Cantor’s theory [8] , and by now it is widely accepted by mathematicians.
I learned about Cantor’s diagonalization over 50 years ago and accepted it at the time. However, after watching a television program [9] one evening in 2022, I went to sleep and awoke in the middle of the night with the idea that a tree structure might be a possible way to avoid Cantor’s diagonalization.
7. Conclusions
The countably infinite set of nodes of an infinity tree can represent all the digits of all the decimal numbers between any integer and its successor, and a countably infinite collection of infinity trees can represent all the real numbers. So, it would be reasonable to have a “non-Cantorian” branch of cardinality theory with a definition of countability allowing the set of real numbers to be considered as countably infinite.
This would be consistent with Cantor’s Continuum Hypothesis, which holds that “there is no set whose cardinality is strictly between that of the integers and the real numbers.”
A higher-level infinity tree can provide a countably infinite representation for any number of dimensions in a multi-dimensional space.
It does not appear that this paper’s non-Cantorian theory of infinity would have any consequences for the natural sciences or other branches of mathematics, even though concepts of infinity may play a role in theoretical physics and cosmology [10] [11] . It does not affect how calculations are performed, nor what results are obtained.