Verification of the Landau Equation and Hardy’s Inequality

Salih Yousuf Mohamed Salih

Department of Mathematics, Faculty of Science, Bakht Al-Ruda University, Duwaym, Sudan.

DOI: 10.4236/am.2023.143013                

Abstract

We prove the L estimate for the isotropic version of the homogeneous landau problem, which was explored by M. Gualdani and N. Guillen. As shown in a region of the smooth potentials range under values of the interaction exponent (2), a weighted Poincaré inequality is a natural consequence of the traditional weighted Hardy inequality, which in turn implies that the norms of solutions propagate in the L1 space. Now, the L estimate is based on the work of De Giorgi, Nash, and Moser, as well as a few weighted Sobolev inequalities.

Keywords

Hardy’s Inequality, Sobolev Inequalities, the Landau Equation, L-Estimate

1. Introduction and Main Result

Given the equation

${\partial }_t{f}_j=c_{d,ϵ-2}\text{div}{{\displaystyle \sum }}^{\text{}}\left({\displaystyle {\int }_{{ℝ}^d}\frac{1}{{\left|v-v_{\text{*}}\right|}^{-ϵ}}}\left[f_j\left(v_{\text{*}},t\right)\nabla f_j\left(v,t\right)-f_j\left(v,t\right){\nabla }_{\text{*}}{f}_j\left(v_{\text{*}},t\right)\right]\text{d}{v}_{\text{*}}\right),$ (1.1)

If $f_j\left(v,t\right)$ is a positive function and the constant $c_{d,ϵ-2}$ is positive and solely relies on the dimension and $\left(ϵ-2\right)$ . A extremely soft potential has a constant of $\left(ϵ-2\right)\in \left[-d,-2\right]$ , $d\ge 3$ . Similarity to the homogeneous Landau equation is what piques our curiosity in (1.1).

${\partial }_t{f}_j=c_{d,ϵ-2}{\displaystyle \sum \text{div}}\left({\displaystyle {\int }_{{ℝ}^d}\frac{\mathbb{P}\left(v-v_{\text{*}}\right)}{{\left|v-v_{\text{*}}\right|}^{-ϵ}}}\left[f_j\left(v_{\text{*}},t\right)\nabla f_j\left(v,t\right)-f_j\left(v,t\right){\nabla }_{\text{*}}{f}_j\left(v_{\text{*}},t\right)\right]\text{d}{v}_{\text{*}}\right),$ (1.2)

where the projection into z orthonormal complement yields a matrix kernel denoted by $\mathbb{P}(\; z\; )$

$\mathbb{P}\left(z\right)=\mathbb{I}-\frac{z\otimes z}{{\left|z\right|}^2},z\in {ℝ}^d\backslash \left\{0\right\}\text{.}$

The phrase $\mathbb{P}\left(z\right)$ in (1.2) is an anisotropy that is absent from (1.1). (1.1). Consequently, (1.1) might be seen as an isotropic variant of the Landau Equation (1.2). Motivated by this link, Krieger and Strain presented Equation (1.1) in [1], with the expectation that comprehending (1.1) may lead to new insights on (1.2). [1] suggested a revision to (1.1) in light of $\left(ϵ-2\right)=-d=-3$ ,

${\partial }_t{f}_j=a{{\displaystyle \sum }}^{\text{}}\left[f_j\right]\text{Δ}{f}_j+\left(1+ϵ\right){\displaystyle \sum f_j^2},\left(1+ϵ\right)\in \left[0,1\right],$ (1.3)

where $a\left[f_j\right]:=f_j\ast {\left|v\right|}^{-1}$ . Here, (1.3) with $ϵ=0$ corresponds to (1.1). It is shown by [1] that solutions to (1.3) that are spherically symmetric and radially decreasing become smooth in limited time for $ϵ<-1/4$ . Later, in [2], using a novel nonlocal inequality for $d=2-ϵ$ , Gressman, Krieger, and Strain extended this finding to the range $ϵ<1/75$ .

${\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum f_j^{2+ϵ}}}\text{d}v\le \frac{{\left(2+ϵ\right)}^2}{1+{ϵ}^2}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a\left[f_j\right]}}\left|\nabla f_j^{\frac{1+ϵ}{2}}\right|\text{d}v\text{.}$

[3] demonstrates that for $ϵ=0$ , spherically solutions symmetric to (1.3) immediately regularize and always stay smooth. The method described in [3] encompasses (1.3) for every $-1\le ϵ\le 0$ and offers a $L^{\infty }$ , (1.2) solved under the condition that a certain spectral constraint holds. Later, in [4], we use the knowledge that $a\left[f_j\right]$ is an A 1 weight to establish an $L^{\infty }$ -estimate for weak solutions of (1.1) and (1.2) for $\left(ϵ-2\right)\ge -2$ and solution of the equation for 0. We provide a novel $L^{\infty }$ -estimated for (1.1) where $\left(ϵ-2\right)\in \left({\left(ϵ-2\right)}_{\text{*}},-2\right]$ , ${\left(ϵ-2\right)}_{\text{*}}$ is defined as below.

Theorem 1.1. Let $f_j:{ℝ}^d\times \left[0,T\right]\to ℝ$ be a non-negative classical solution of (1.1) with $\left(ϵ-2\right)\in \left[-1-\frac{d}{2},-2\right]$ and initial data ${\left(f_j\right)}_{in}$ that belongs to $L_2^1\cap L^1\left({ℝ}^d\right)$ .

1) For any $\left(1+ϵ\right)$ with $1+ϵ\le \frac{d+\left(ϵ-2\right)}{-ϵ}$ , the norm ${\Vert f_j\left(t\right)\Vert }_{L^{1+ϵ}\left({ℝ}^d\right)}$ is non-increasing in time.

2) Let ${\left(ϵ-2\right)}_{\text{*}}\in \left(-1-\frac{d}{2},-2\right)$ be the unique solution to

$\frac{d}{d+ϵ}=\frac{d+\left(ϵ-2\right)}{-ϵ}\text{.}$

If ${\left(f_j\right)}_{\text{in}}$ also belongs to $L^{1+ϵ}\left({ℝ}^d\right)$ for some $1+ϵ>\frac{d}{d+ϵ}$ , any solution to (1.1) for $\left(ϵ-2\right)\in \left({\left(ϵ-2\right)}_{\text{*}},-2\right]$ is uniformly bounded for times away from zero, and

$\underset{B_R\times \left[\tau ,T\right]}{\sup }{\displaystyle \sum f_j\left(v,t\right)}\le \left(1+ϵ\right){{\displaystyle \sum }}^{\text{}}\left(d,\left(ϵ-2\right),{\left(f_j\right)}_{\text{in}},R,\tau ,T\right)\text{.}$

In particular, for $\left(ϵ-2\right)\in \left({\left(ϵ-2\right)}_{\text{*}},-2\right]$ , its classical solutions of (1.1) is smoothing.

For $d=3$ we have ${\left(ϵ-2\right)}_{\text{*}}\approx -2.458$ while for $d=4$ we have ${\left(ϵ-2\right)}_{\text{*}}\approx -2.87$ . The value ${\left(ϵ-2\right)}_{\text{*}}$ is uniquely defined in the range $\left(-d,-2\right)$ .

The proof of Theorem 1.1 is relatively straightforward. For that, let $h\left[f_j\right]$ be the Riesz potential of $f_j$ ,

$h\left[f_j\right]:={{\displaystyle \sum }}^{\text{}}{\left(-\text{Δ}\right)}^{-\frac{d+\left(ϵ-2\right)}{2}}{f}_j=\left(1+ϵ\right)\left(d,d+\left(ϵ-2\right)\right){\displaystyle {\int }_{{ℝ}^d}{{\displaystyle \sum }}^{\text{}}}\frac{f_j\left(v_{\text{*}}\right)}{{\left|v-v_{\text{*}}\right|}^{\left(2-ϵ\right)}}\text{d}{v}_{\text{*}},$

where the normalization $\left(1+ϵ\right)\left(d,d+\left(ϵ-2\right)\right)$ constant arising in the operator ${\left(-\text{Δ}\right)}^{-\frac{d+\left(ϵ-2\right)}{2}}$ , namely

$\left(1+ϵ\right)\left(d,1+ϵ\right)={\pi }^{-\frac{d}{2}}{2}^{-\left(1+ϵ\right)}\frac{\text{Γ}\left(\frac{d-\left(1+ϵ\right)}{2}\right)}{\text{Γ}\left(\frac{1+ϵ}{2}\right)},ϵ\ge 0.$

In particular, $h\left[f_j\right]\to f_j$ as $\left(ϵ-2\right)\to -d$ . Next, we shall denote by $a\left[f_j\right]$ the convolution

$a\left[f_j\right]:=c_{d,ϵ-2}{\displaystyle {\int }_{{ℝ}^d}{{\displaystyle \sum }}^{\text{}}}\frac{f_j\left(v_{\text{*}}\right)}{{\left|v-v_{\text{*}}\right|}^{-ϵ}}\text{d}{v}_{\text{*}}\text{.}$

We rewrite (1.1) as

${\partial }_t{f}_j={\displaystyle \sum \text{div}}\left(a\left[f_j\right]\nabla f_j-f_j\nabla a\left[f_j\right]\right),$

or, in a non-divergence form,

${\partial }_t{f}_j={\displaystyle \sum a\left[f_j\right]\text{Δ}{f}_j}+ϵ{\displaystyle \sum f_{j}h}\left[f_j\right],$

provided $c_{d,ϵ-2}$ is chosen as

$c_{d,ϵ-2}:=\frac{\left(1+ϵ\right)\left(d,d+\left(ϵ-2\right)\right)}{d+\left(ϵ-2\right)},\text{or}\text{equivalently}{c}_{d,ϵ-2}:=\left(ϵ\right)\left(1+ϵ\right)\left(d,d+ϵ\right),$

so that

$\text{Δ}a\left[f_j\right]=c_{d,ϵ-2}\left(d+\left(ϵ-2\right)\right)\left(ϵ\right){\displaystyle {\int }_{{ℝ}^d}{{\displaystyle \sum }}^{\text{}}}\frac{f_j\left(v_{\text{*}}\right)}{{\left|v-v_{\text{*}}\right|}^{-\left(ϵ-2\right)}}\text{d}{v}_{\text{*}}=\left(ϵ\right){\displaystyle \sum h}\left[f_j\right]\text{.}$ (1.4)

Note that our choice of $c_{d,ϵ-2}$ (which is well defined for any $2\le ϵ\le 0$ ), and We define $a\left[f_j\right]$ to be the operator $\left(ϵ\right){\left(-\text{Δ}\right)}^{-\frac{d+ϵ}{2}}{f}_j$ , not disrupt the internal logic of (1.1) A simple rescaling of time may do away with this constant.

For $ϵ=0$ , Equation (1.1) reduces substantially: for sufficiently smooth functions $f_j$ , it simplifies to a heat equation,

${\partial }_t{f}_j=c_{d,-2}{\displaystyle \sum \text{div}}\left({\displaystyle {\int }_{{ℝ}^d}{f}_j}\left(v_{\text{*}},t\right)\nabla f_j\left(v,t\right)\text{d}{v}_{\text{*}}\right)=c_{d,-2}{{\displaystyle \sum }}^{\text{}}{\Vert {\left(f_j\right)}_{\text{in}}\Vert }_{L^1}\text{Δ}{f}_j$

Since the $L^1$ norm is preserved, that is why. When $ϵ=0$ , the reaction term arises from the derivatives of $\mathbb{P}\left(v\right)$ , which is absent in the traditional Landau Equation (1.2).

Now we explain the basic idea of the proof. For a classical solution of (1.1) we have

$\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum f_j^{1+ϵ}}}\text{d}v=-\frac{4ϵ}{1+ϵ}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a\left[f_j\right]}}{\left|\nabla f_j^{1+ϵ/2}\right|}^2\text{d}v+{ϵ}^2{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum h}}\left[f_j\right]f_j^{1+ϵ}\text{d}v$

We make an estimate of the second integral by using the previous one as a basis. This allows us to put a limit on the right hand side. This is the most important aspect of Theorem 1.1, and it can be accomplished with the help of the weighted Hardy inequality [5].

${\left(d+\left(ϵ-2\right)\right)}^2{\displaystyle {\int }_{{ℝ}^d}{{\displaystyle \sum }}^{\text{}}}{\left|v\right|}^{ϵ-2}{\varphi }_j^2\text{d}v\le 4{\displaystyle {\int }_{{ℝ}^d}{{\displaystyle \sum }}^{\text{}}}{\left|v\right|}^{ϵ}{\left|\nabla {\varphi }_j\right|}^2\text{d}v,ϵ>2-d\text{.}$

This inequality implies, via convolution, the following weighted Poincare’s inequality

$\left(d+\left(ϵ-2\right)\right){\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum h}}\left[f_j\right]{\varphi }_j^2\text{d}v\le 4{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}\left[f_j\right]{\left|\nabla {\varphi }_j\right|}^2\text{d}v\text{.}$ (1.5)

For $\left(ϵ-2\right)$ belonging to the interval $\left({\left(ϵ-2\right)}_{\text{*}},-2\right]$ , thanks to (1.5), we can show that

$\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum f_j^{1+ϵ}}}\text{d}v\le 0,$

This is sufficient evidence to establish that $f_j$ is a member of $L^{\infty }$ for positive times.

There is evidence in the published works to support the previous claim. As an example, check out Theorem 3.8 in [6] or Theorem 2.9 in [4]. Following the procedure described in [4], we give the evidence here for the sake of completeness. For any $ϵ>-\left(1+d\right)$ , we shall demonstrate that a-Poincare’s inequality of the form is obtained by imposing a constraint on $f_j$ in $L^{\infty }\left(0,T,L^{1+ϵ}\left({ℝ}^d\right)\right)$ :

$\begin{array}{c}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum h}}\left[f_j\right]{\varphi }_j^2\text{d}v\le \epsilon {\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}\left[f_j\right]{\left|\nabla {\varphi }_j\right|}^2\text{d}v\\ +\left(1+ϵ\right){{\displaystyle \sum }}^{\text{}}\left({\left(f_j\right)}_{in},R\right){\epsilon }^{-\frac{2}{\eta }}{\displaystyle {\int }_{{ℝ}^d}a}\left[f_j\right]{\varphi }_j^2\text{d}v\text{.}\end{array}$ (1.6)

This above inequality, combined with a Moser’s iteration, yields the desired $L^{\infty }$ -bound for $f_j$ .

A Background on the Homogeneous Landau Equation

As the major finding, we find that for the isotropic Equation (1.1), there exists a nontrivial region of the extremely soft potentials range, $-d\le ϵ\le 0$ for which one may rule out the production of singularities in limited time. Given the similarities between (1.1) and the homogeneous Landau Equation (1.2), and the open subject of L estimates for the latter equation when $-d\le ϵ\le 0$ , this is of interest. We address a small portion of the Landau equation to demonstrate the current state of knowledge about (1.2), as well as to highlight the factors that make analyzing the equation in the extremely soft potentials region so challenging.

For the Landau Equation (1.2), the issue of $L^{\infty }$ -estimates for solutions remains a challenging open subject when $ϵ<0$ . In fact, the singularity of the kernel in $h\left[f_j\right]$ increases as $\left(ϵ-2\right)$ decreases, necessitating more integrability in order for $f_j$ to exert control over $h\left[f_j\right]$ . The regularity hypothesis is well established in the 0 range. Works by Desvillettes and Villani [4] [6] not only address the presence and long-time convergence to equilibrium of solutions, but also the subject of regularity of solutions, for the case of hard potentials (2). Alexandre, Liao, and Lin [7] achieve the propagation of L² estimates for solutions (possibly expanding with time) for soft potentials 02 and d = 3, from which larger L estimates and greater regularity may be acquired. Refer to [8] if you want to know what happens when you set to 0. When 00, Silvestre [6] calculates the solution’s mass, energy, and entropy a priori to get an estimate for L. (and accordingly are not growing with time). Once the $L^{1+ϵ}$ -norm of $f_j$ , with $ϵ>-\left(1+d\right)$ , is constrained uniformly in time, the L norm is under control for $0<ϵ<0$ , according to the conclusions in [6]. Similar findings, however shown using a different approach, may be found in [4]. Although the estimates in [4] make advantage of the divergence structure of the equation and are proven for weak solutions, the estimate for $h\left[f_j\right]$ that they provide deteriorates as v increases. In order to get global boundaries in space, [6] use non-divergence methods.

Recent discoveries on the nature of potential singularities have reduced the possible explosion scenarios for extremely soft potentials. The weak solutions to (1.2) (with d = 3) have a set of unique times with Hausdorff dimension at most 1/2, as shown by Golse, Gualdani, Imbert, and Vasseur in [9]. New insights on the behavior of solutions to (1.2) (with d = 3) in H 1-norm towards the blow-up time were recently reported in [5] by Desvillettes, He, and Jiang. Most significantly, they demonstrate that solutions may become smooth again after a blow-up and continue to be so in the future, see [10] [11] [12] [13]. In [14], Bedrossian, Gualdani and Snelson rule out type I self-similar blow-up for solutions to (1.2). There is an important connection between $L^{\infty }$ bounds and uniqueness. Fournier and Guerin proved a uniqueness result for bounded weak solutions in [1], this being for $\gamma \in \left(-d,-2\right)$ . In fact, the work [11] guarantees uniqueness of solutions with $f\in L^{\infty }$ and in particular to bounded solutions.

The work [11] was followed by Fournier’s work in [15] with a corresponding uniqueness result for $\gamma =-d$ . Later in [16], Chern and Gualdani proved a uniqueness result for sufficiently integrable solutions for the Landau equation with Coulomb interactions.

2. Hardy’s Inequality

Given the classical Hardy inequality,

${\left(d+\left(ϵ-2\right)\right)}^2{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\left|v\right|}^{ϵ-2}}}{\varphi }_j^2\text{d}v\le 4{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\left|v\right|}^{ϵ}}}{\left|\nabla {\varphi }_j\right|}^2\text{d}v,ϵ>2-d\text{.}$ (2.1)

We review one elementary way of proving (2.1), a deeper and broader discussion on Hardy’s inequality can be found in the book by Ghoussoub and Moradifam [5]. First notice that

$-\text{Δ}{\left|v\right|}^{ϵ}=\left(d+\left(ϵ-2\right)\right)\left(-ϵ\right){\left|v\right|}^{ϵ-2}\text{.}$

Multiply both sides of this equation by ${\varphi }_j$ . Integration by parts and Cauchy-Schwarz yield

$\begin{array}{l}\left(d+\left(ϵ-2\right)\right)\left(-ϵ\right){\displaystyle \int {\varphi }_j^2{\left|v\right|}^{ϵ-2}\text{d}v}=2{\displaystyle \int \nabla {\left|v\right|}^{ϵ}{\varphi }_j\nabla {\varphi }_j\text{d}v}\\ \le 2{\left({{\displaystyle \int }}^{\text{}}{\left(1+ϵ\right)}^2\left(v\right){\left|\nabla {\left|v\right|}^{ϵ}\right|}^2{\varphi }_j^2\text{d}v\right)}^{\frac{1}{2}}{\left({{\displaystyle \int }}^{\text{}}\frac{{\left|\nabla {\varphi }_j\right|}^2}{{\left(1+ϵ\right)}^2\left(v\right)}\text{d}v\right)}^{\frac{1}{2}}\text{.}\end{array}$

We pick now the best weight $\left(1+ϵ\right)\left(v\right)$ such that

${\left(1+ϵ\right)}^2\left(v\right){\left|\nabla {\left|v\right|}^{ϵ}\right|}^2\le {\left|v\right|}^{ϵ-2}\text{.}$

or equivalently

${\left(1+ϵ\right)}^2\left(v\right)=\frac{1}{{\left|v\right|}^{ϵ}{ϵ}^2}\text{.}$

With this choice of ${\left(1+ϵ\right)}^2\left(v\right)$ , we obtain (2.1) (see [8] ).

Lemma 2.1. Let $2-d<ϵ<0$ . Fix a non-negative $f_j\in L^1\left({ℝ}^d\right)$ and let $a\left[f_j\right]$ and $h\left[f_j\right]$ be as in Section 1, then the following inequality holds for all ${\varphi }_j\in {\left(1+ϵ\right)}_c^1\left({ℝ}^d\right)$ (and limits of such functions)

$\left(d+\left(ϵ-2\right)\right){\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum h\left[f_j\right]{\varphi }_j^2\text{d}v}}\le 4{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}\left[f_j\right]{\left|\nabla {\varphi }_j\right|}^2\text{d}v\text{.}$ (2.2)

Proof. Fix ${\varphi }_j\in {\left(1+ϵ\right)}_c^1\left({ℝ}^d\right)$ . By a change of variables, we see that (2.1) is equivalent to the inequalities (with $\in {ℝ}^d$ )

${\left(d+\left(ϵ-2\right)\right)}^2{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\left|v-w\right|}^{ϵ-2}{\varphi }_j^2\text{d}v}}\le 4{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\left|v-w\right|}^{ϵ}}}{\left|\nabla {\varphi }_j\right|}^2\text{d}v$ (2.3)

Let us multiply (2.3) by $f_j\left(w\right)\ge 0$ and integrate the resulting expression in w, we obtain

${\left(d+\left(ϵ-2\right)\right)}^2{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum \left(f_j\ast {\left|v\right|}^{ϵ-2}\right){\varphi }_j^2\text{d}v}}\le 4{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum \left(f_j\ast {\left|v\right|}^{ϵ}\right)}}{\left|\nabla {\varphi }_j\right|}^2\text{d}v\text{.}$ (2.4)

Substituting in (2.4) the expression for $\text{Δ}a\left[f_j\right]$ and making use of (1.4), the lemma is proved.

Lemma 2.1 is key, as it leads to the propagation of $L^{1+ϵ}$ bounds for solutions to (1.1), proven in the next section. The range of $\left(1+ϵ\right)$ ’s is limited by the constants appearing in (2.2), and this is the sole limitation on the range of $\left(ϵ-2\right)$ ’s covered by Theorem 1.1. This motivates the following (admittedly open ended) eigenvalue problem.

Problem. Fix d and $\left(ϵ-2\right)\in \left[-d,-2\right]$ . Let $f_j\in L^1\left({ℝ}^d\right)$ be non-negative, and let

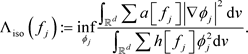(2.5)

Determine under what circumstances can we say that

${\text{Λ}}_{\text{iso}}\left(f_j\right)>\frac{d+\left(ϵ-2\right)}{4}\text{.}$

If $f_j$ is just a generic function in $L^1$ , then one cannot do better than inequality (2.2). To see this, take a sequence of functions ${\left(f_j\right)}_n$ which are converging as $n\to \infty$ to a Dirac delta at 0. For this sequence, (2.2) converges to (2.1), which is known to be sharp ( [17] Section 4.3).

The corresponding problem for the Landau equation would be,

${\text{Λ}}_{\text{Landau}}\left(f_j\right):=\underset{{\varphi }_j}{\inf }\frac{{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum \left(A\left[f_j\right]\nabla {\varphi }_j,\nabla {\varphi }_j\right)\text{d}v}}}{{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum h}}\left[f_j\right]{\varphi }^2\text{d}v},$ (2.6)

where $A\left[f_j\right]:={\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum \frac{\mathbb{P}\left(v-v_{\text{*}}\right)}{{\left|v-v_{\text{*}}\right|}^{-ϵ}}{f}_j\left(v_{\text{*}}\right)\text{d}{v}_{\text{*}}}}$ . The significance of this eigenvalue problem is well known in the Landau and Boltzmann literature. We do not know whether an elementary argument as in Lemma 2.1 yields a similar bound for (2.6). If one argues by direct analogy with Lemma 2.1 one would have to contend with the projection term $\mathbb{P}\left(v\right)$ appearing in $A\left[f_j\right]$ , and it is not immediately clear how this can be done.

The theory of weighted normed inequalities can yield certain estimates for ${\text{Λ}}_{\text{iso}}$ , or ${\text{Λ}}_{\text{Landau}}$ . The value in (2.5) is directly related to the quantity

$\underset{B}{\sup }{\left|B\right|}^{\frac{2}{d}}\frac{{\displaystyle \sum {\displaystyle {\int }_{B}h}}\left[f_j\right]\text{d}v}{{\displaystyle {\int }_B{\displaystyle \sum a}}\left[f_j\right]\text{d}v},$ (2.7)

above for all non-negative $f_j\in L^1\left({ℝ}^d\right)$ is bounded by a universal constant (see [4] ). Finally, it is worth mentioning that decreasing $f_j$ for any spherically symmetric and radially, solving (1.2) $\left(ϵ=2-d\right)$ , the $L^{\infty }$ norm of $f_j$ cannot blow up at a finite time T if, for this $f_j$ , the quantity (2.7) remains bounded by 1/96 (this is likely a non-sharp estimate). See [16].

3. Propagation of $L^{1+ϵ}$ Bounds

We shall make use of Lemma 2.1 to show that various $L^{1+ϵ}$ norms propagate forward in time, at least for some range of $\left(ϵ-2\right)$ ’s (see [8] ).

Lemma 3.1. (Propagation of integrability.) Let $f_j$ be a nonnegative solution to (1.1) with initial data $f_j\left(v,0\right)={\left(f_j\right)}_{in}$ . For every $\left(1+ϵ\right)$ such that

$1\le \left(1+ϵ\right)\le \frac{d+\left(ϵ-2\right)}{-ϵ}$

the norm ${\Vert f_j\left(t\right)\Vert }_{L^{1+ϵ}}$ is non-increasing in t. In particular, for every $t\in \left[0,T\right]$ we have

${\Vert {\displaystyle \sum f_j\left(t\right)}\Vert }_{L^{1+ϵ}}\le {{\displaystyle \sum }}^{\text{}}{\Vert {\left(f_j\right)}_{\text{in}}\Vert }_{L^{1+ϵ}}$

Proof. Multiply (1.1) by $f_j^{ϵ}$ for some $ϵ\ge 0$ and integrate over ${ℝ}^d$ . We obtain

$\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum f_j^{1+ϵ}\text{d}v}}=-\frac{4ϵ}{1+ϵ}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}\left[f_j\right]{\left|\nabla f_j^{1+ϵ/2}\right|}^2\text{d}v+{ϵ}^2{\displaystyle \sum {\displaystyle {\int }_{{ℝ}^d}h}}\left[f_j\right]f_j^{1+ϵ}\text{d}v$

To estimate the last term ${\displaystyle {\int }_{{ℝ}^d}h}\left[f_j\right]f_j^{1+ϵ}\text{d}v$ we use Lemma 2.1 with ${\varphi }_j=f_j^{1+ϵ/2}$ . One gets

$\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum f_j^{1+ϵ}\text{d}v}}\le -4ϵ\left[\frac{1}{1+ϵ}+\frac{ϵ}{d+\left(ϵ-2\right)}\right]{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}\left[f_j\right]{\left|\nabla f_j^{1+ϵ/2}\right|}^2\text{d}v$

It follows that ${\Vert f_j\left(t\right)\Vert }_{1+ϵ}^{1+ϵ}$ is non-increasing whenever the expression in the brackets is non-positive, which is the case given the assumption on $\left(1+ϵ\right)$ . This concludes the proof of the lemma, and of the first part of Theorem 1.1.

Remark 3.2. For there to be any $\left(1+ϵ\right)$ such that $1\le \left(1+ϵ\right)\le \left(d+\left(ϵ-2\right)\right)/\left(-ϵ\right)$ it must be that $ϵ\ge 1-\frac{d}{2}.$

It follows that Lemma 3.1 is of no use for values of $\left(ϵ-2\right)$ close to $-d$ .

4. Controlling the Second Moment

Solutions to (1.1) conserve mass and first moment, but not second moment. We show that second moments grow linearly in time, provided $a\left[f_j\right]$ is uniformly bounded (see [8] ).

Lemma 4.1. The second moment of $f_j$ , solution to (1.1), evolves according to the formula

$\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum f_j}}\left(v,t\right){\left|v\right|}^2\text{d}v=2\left(d+ϵ\right){\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum f_j}}\left(v,t\right)a\left[f_j\right]\left(v,t\right)\text{d}v\text{.}$

In particular, for all $t\in \left[0,T\right]$ and $ϵ>-\left(1+d\right)$ we have

$\begin{array}{c}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum f_j}}\left(T,v\right){\left|v\right|}^2\text{d}v\le {\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\left(f_j\right)}_{\text{in}}}}\left(v\right){\left|v\right|}^2\text{d}v\\ +T{\left(1+ϵ\right)}_{d,\left(ϵ-2\right),\left(1+ϵ\right)}{{\displaystyle \sum }}^{\text{}}{\Vert f_j\Vert }_{L^{\infty }\left(0,T,L^{1+ϵ}\right)}^{1-\theta }{\Vert {\left(f_j\right)}_{\text{in}}\Vert }_{L^1}^{1+\theta },\end{array}$

where $\theta :=\frac{\left|ϵ\right|{\left(1+ϵ\right)}^{\prime }}{d}$ .

Proof. Integration by parts yields

$\frac{1}{2}\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum f_j}}\left(t,v\right){\left|v\right|}^2\text{d}v=-{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum \left(v,a\left[f_j\right]\nabla f_j-f_j\nabla a\left[f_j\right]\right)\text{d}v}}\text{.}$

Using the integral form for $a\left[f_j\right]$ we rewrite the expression on the right, leading to

$\begin{array}{l}\frac{1}{2}\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum f_j}}\left(t,v\right){\left|v\right|}^2\text{d}v\\ =-c_{d,ϵ-2}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle {\int }_{{ℝ}^d}v}}{{\displaystyle \sum }}^{\text{}}\cdot \frac{f_j\left(w\right)\nabla f_j\left(v\right)-f_j\left(v\right)\nabla f_j\left(w\right)}{{\left|v-w\right|}^{-ϵ}}\text{d}w\text{d}v\\ -\frac{c_{d,ϵ-2}}{2}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum v}}}-w\cdot \frac{f_j\left(w\right)\nabla f_j\left(v\right)-f_j\left(v\right)\nabla f_j\left(w\right)}{{\left|v-w\right|}^{-ϵ}}\text{d}w\text{d}v.\end{array}$

Integration by parts in both v and w yields

$\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum f_j}}\left(t,v\right){\left|v\right|}^2\text{d}v=2\left(d+ϵ\right){\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum f_{j}a}}\left[f_j\right]\text{d}v,$

since

$\text{div}\left(\frac{z}{{\left|z\right|}^{-ϵ}}\right)=\frac{d+ϵ}{{\left|z\right|}^{-ϵ}}\text{.}$

This proves the first part of the lemma. For the second part, it is clear that

$\frac{1}{2}\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum f_j}}\left(t,v\right){\left|v\right|}^2\text{d}v\le \left(d+ϵ\right){{\displaystyle \sum }}^{\text{}}{\Vert f_j\left(t\right)\Vert }_{L^1}{\Vert a\left(t\right)\Vert }_{L^{\infty }}\text{.}$

Then, integrating the resulting inequality in time, the estimate follows thanks to an elementary interpolation argument (see Remark 4.2)

${\Vert a\Vert }_{L^{\infty }\left(0,T,L^{\infty }\left({ℝ}^d\right)\right)}\le {\left(1+ϵ\right)}_{d,ϵ-2,1+ϵ}{{\displaystyle \sum }}^{\text{}}{\Vert f_j\left(t\right)\Vert }_{L^{\infty }\left(0,T,L^{1+ϵ}\left({ℝ}^d\right)\right)}^{\theta }{\Vert {\left(f_j\right)}_{\text{in}}\Vert }_{L^1}^{1-\theta }\text{.}$

Remark 4.2. The following estimate is well known and we recall it here for completeness: let $ϵ>-\left(1+d\right)$ , for every $ϵ>-1$ we have that

$\begin{array}{c}a\left[f_j\right]=c_{d,ϵ-2}{\displaystyle {\int }_{B_{1+ϵ}\left(v\right)}{\displaystyle \sum f_j}}\left(w\right){\left|v-w\right|}^{ϵ}\text{d}w+c_{d,ϵ-2}{\displaystyle {\int }_{{ℝ}^d\backslash B_{1+ϵ}\left(v\right)}{\displaystyle \sum f_j}}\left(w\right){\left|v-w\right|}^{ϵ}\text{d}w\\ \le c_{d,ϵ-2}{{\displaystyle \sum }}^{\text{}}{\Vert f_j\Vert }_{L^{1+ϵ}}{\left({\displaystyle {\int }_{B_{1+ϵ}}{\left|w\right|}^{\left(ϵ\right){\left(1+ϵ\right)}^{\prime }}\text{d}w}\right)}^{\frac{1}{1+{ϵ}^{\prime }}}+c_{d,ϵ-2}{\left(1+ϵ\right)}^{ϵ}{{\displaystyle \sum }}^{\text{}}{\Vert f_j\Vert }_{L^1}\end{array}$

Optimizing the right hand side with respect to $\left(1+ϵ\right)$ , the following estimate follows

${\Vert {\displaystyle \sum a}\left[f_j\right]\Vert }_{L^{\infty }}\le {\left(1+ϵ\right)}_{d,\left(ϵ-2\right),1+ϵ}{{\displaystyle \sum }}^{\text{}}{\Vert f_j\Vert }_{L^{1+ϵ}}^{\theta }{\Vert f_j\Vert }_{L^1}^{1-\theta },\text{where}\theta =\frac{\left|ϵ\right|{\left(1+ϵ\right)}^{\prime }}{d}\text{.}$

Corollary 4.3. Let $ϵ>-\left(1+d\right)$ . For all $v\in {ℝ}^d$ and $t\in \left[0,T\right]$ , the following inequality holds

$a\left[f_j\right]\left(v,t\right)\ge \mathcal{l}{\langle v\rangle }^{ϵ}$

where

$\mathcal{l}:=c_{d,ϵ-2}{{\displaystyle \sum }}^{\text{}}\frac{{\Vert {\left(f_j\right)}_{\text{in}}\Vert }_{L^1}^{\left(1-ϵ\right)}}{{\left(c_1+c_{2}T{\Vert f_j\Vert }_{L^{\infty }\left(0,T,L^{1+ϵ}\left({ℝ}^d\right)\right)}^{1-\theta }{\Vert {\left(f_j\right)}_{\text{in}}\Vert }_{L^1}^{1+\theta }\right)}^{-ϵ}}$

Proof. For any $ϵ\ge 0$ we have

${\displaystyle {\int }_{{ℝ}^d\backslash B_{1+ϵ}}{\displaystyle \sum f_j}}\left(v,t\right)\text{d}v\le {\left(1+ϵ\right)}^{-2}{\displaystyle {\int }_{{ℝ}^d\backslash B_{1+ϵ}}{\displaystyle \sum f_j}}\left(v,t\right){\left|v\right|}^2\text{d}v\le {\left(1+ϵ\right)}^{-2}{{\displaystyle \sum }}^{\text{}}{\Vert f_j\left(t\right)\Vert }_{L_2^1}\text{.}$

From here, taking $\left(1+ϵ\right)=\frac{2{\Vert f\left(t\right)\Vert }_{L_2^1}}{{\Vert f\left(t\right)\Vert }_{L^1}}$ , we get

${\displaystyle {\int }_{B_{1+ϵ}}{\displaystyle \sum f_j}}\left(v,t\right)\text{d}v\ge \frac{1}{2}{{\displaystyle \sum }}^{\text{}}{\Vert {\left(f_j\right)}_{\text{in}}\Vert }_{L^1}$

Then, since $\left|v-w\right|\le \left|v\right|+\left(1+ϵ\right)$ whenever $w\in B_{1+ϵ}$ ,

$\begin{array}{c}a\left(v,t\right)\ge c_{d,ϵ-2}{\displaystyle {\int }_{B_{1+ϵ}}{\displaystyle \sum f_j}}\left(w,t\right){\left(\left|v\right|+\left(1+ϵ\right)\right)}^{ϵ}\text{d}w\\ \ge \frac{1}{2}{c}_{d,ϵ-2}{{\displaystyle \sum }}^{\text{}}{\Vert {\left(f_j\right)}_{\text{in}}\Vert }_{L^1}{\left(\left|v\right|+\left(1+ϵ\right)\right)}^{ϵ}\text{.}\end{array}$

In particular

$\begin{array}{c}a\left(v,t\right)\ge \frac{1}{2}{c}_{d,ϵ-2}{{\displaystyle \sum }}^{\text{}}{\Vert {\left(f_j\right)}_{\text{in}}\Vert }_{L^1}{\left(1+ϵ\right)}^{ϵ}{\langle v\rangle }^{ϵ}\\ \ge c_{d,ϵ-2}{{\displaystyle \sum }}^{\text{}}\frac{{\Vert {\left(f_j\right)}_{\text{in}}\Vert }_{L^1}^{1-ϵ}}{{\left(c_1+c_{2}T{\Vert f_j\left(t\right)\Vert }_{L^{1+ϵ}}^{1-\theta }{\Vert {\left(f_j\right)}_{\text{in}}\Vert }_{L^1}^{1+\theta }\right)}^{-ϵ}}{\langle v\rangle }^{ϵ}\end{array}$

using Lemma 4.1 to bound ${\left(1+ϵ\right)}^{ϵ}$ from below.

5. Some Weighted Inequalities

The result will be integral inequalities of the form

${\left({\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\omega }_1}}{\left|{\varphi }_j\right|}^{1+ϵ}\text{d}v\right)}^{\frac{1}{1+ϵ}}\le \left(1+ϵ\right){\left({\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\omega }_2}}{\left|\nabla {\varphi }_j\right|}^2\text{d}v\right)}^{\frac{1}{2}}$

for various choices of the exponent $\left(1+ϵ\right)$ , weights ${\omega }_i$ , and constant $\left(1+ϵ\right)$ which are pertinent to obtaining estimates a la De Giorgi-Nash-Moser for solutions of (1.1). For a more complete discussion, see ( [4], Section 3.2).

A central object in these inequalities is the following product of averages of the weights, taken over an arbitrary cube $Q\subset {ℝ}^d$ , (here, “ $f_j$ ” denotes average over the set of integration)

$\begin{array}{l}{\sigma }_{\left(1+ϵ\right),\left(1+ϵ\right)}\left(Q,{\omega }_1,{\omega }_2\right)\\ :={\left|Q\right|}^{\frac{1}{d}-\frac{1}{2}+\frac{1}{1+ϵ}}{{\displaystyle \sum }}^{\text{}}{\left({\left(f_j\right)}_Q{\omega }_1^{1+ϵ}\text{d}v\right)}^{\frac{1}{{\left(1+ϵ\right)}^2}}{\left({\left(f_j\right)}_Q{\omega }_2^{-\left(1+ϵ\right)}\text{d}v\right)}^{\frac{1}{2\left(1+ϵ\right)}}\text{.}\end{array}$

The significance of ${\sigma }_{\left(1+ϵ\right),\left(1+ϵ\right)}\left(Q,{\omega }_1,{\omega }_2\right)$ is captured by the following theorem (see [18], Theorem 1]). (Also see [8] ).

Theorem 5.1. Let $Q\subset {ℝ}^d,ϵ\ge 0$ , and let ${\omega }_1,{\omega }_2$ be two weights. Define, for some $\left(1+ϵ\right)\left(d,\left(1+ϵ\right),\left(1+ϵ\right)\right)$ ,

${\mathcal{C}}_{\left(1+ϵ\right),\left(1+ϵ\right)}\left(Q,{\omega }_1,{\omega }_2\right):=\left(1+ϵ\right)\left(d,\left(1+ϵ\right),\left(1+ϵ\right)\right)\underset{Q^{\prime }\subset 8Q}{\sup }{\sigma }_{\left(1+ϵ\right),\left(1+ϵ\right)}\left(Q^{\prime },{\omega }_1,{\omega }_2\right)\text{.}$

Then, for any ${\varphi }_j$ supported in Q or any ${\varphi }_j$ such that ${\left(f_j\right)}_Q{\varphi }_j\text{d}v=0$ , we have

${\left({\displaystyle {\int }_Q{\displaystyle \sum {\omega }_1}}{\left|{\varphi }_j\right|}^{1+ϵ}\text{d}v\right)}^{\frac{1}{1+ϵ}}\le {\mathcal{C}}_{\left(1+ϵ\right),\left(1+ϵ\right)}\left(Q,{\omega }_1,{\omega }_2\right){\left({\displaystyle {\int }_Q{\displaystyle \sum {\omega }_2}}{\left|\nabla {\varphi }_j\right|}^2\text{d}v\right)}^{\frac{1}{2}}$

The next two propositions give estimates on ${\sigma }_{\left(1+ϵ\right),\left(1+ϵ\right)}\left(Q,{\omega }_1,{\omega }_2\right)$ for two combination of weights, namely ${\omega }_1=a{\left[f_j\right]}^m$ , ${\omega }_2=a\left[f_j\right]$ and ${\omega }_1=h\left[f_j\right]$ , ${\omega }_2=a\left[f_j\right]$ .

There are two exponents that will be appearing repeatedly in what follows (see [8] ):

$m:=\frac{d}{d-2},2\left(1+\frac{2}{d}\right):=2\left(1+\frac{2}{d}\right)\text{.}$ (5.1)

Proposition 5.2. There exists $ϵ\ge 0$ depending only on d and $\left(ϵ-2\right)$ such that for non-negative $f_j\in L^1\left({ℝ}^d\right)$ and any cube $Q\subset {ℝ}^d$ ,

${\sigma }_{2m,\left(1+ϵ\right)}{{\displaystyle \sum }}^{\text{}}\left(Q,a{\left[f_j\right]}^m,a\left[f_j\right]\right)\le \left(1+ϵ\right)\text{.}$

Proof. For $ϵ>2-d$ , Lemma 3.5 from ( [14], Section 3) says there is some $ϵ>0$ such that

${{\displaystyle \sum }}^{\text{}}{\left({\displaystyle {\int }_{Q}a}{\left[f_j\right]}^{m\left(1+ϵ\right)}\text{d}v\right)}^{\frac{1}{m\left(1+ϵ\right)}}\le \left(1+ϵ\right){\displaystyle {\int }_Q{\displaystyle \sum a}}\left[f_j\right]\text{d}v,$

$1=\left(d,ϵ-2,m\left(1+ϵ\right)\right)$

As it was also noted in ( [4], Section 3), there is a universal constant such that

${\displaystyle {\int }_Q{\displaystyle \sum a}}\left[f_j\right]\text{d}v\le \left(1+ϵ\right)\underset{Q}{\inf }{\displaystyle \sum a}\left[f_j\right],$

which means also that

$\underset{Q}{\sup }{\displaystyle \sum a}{\left[f_j\right]}^{-1}\le \left(1+ϵ\right){{\displaystyle \sum }}^{\text{}}{\left({\displaystyle {\int }_{Q}a}\left[f_j\right]\text{d}v\right)}^{-1}$

Putting these two observations together it follows that

${{\displaystyle \sum }}^{\text{}}{\left({\displaystyle {\int }_{Q^{\prime }}a}{\left[f\right]}^{m\left(1+ϵ\right)}\text{d}v\right)}^{\frac{1}{2m\left(1+ϵ\right)}}{\left({\left(f_j\right)}_{Q^{\prime }}{\displaystyle {\int }_{Q^{\prime }}{\left(a\left[f_j\right]\right)}^{-\left(1+ϵ\right)}\text{d}v}\right)}^{\frac{1}{2\left(1+ϵ\right)}}\le \left(1+ϵ\right)\text{.}$

Lastly, m solves $\frac{1}{d}-\frac{1}{2}+\frac{1}{2m}=0$ (it is its determining property), and the proposition is proved.

The next one if the key proposition for the proof of (1.6) (see [8] ):

Proposition 5.3. There is $ϵ>\frac{d+2}{2}$ such that given a cube $Q\subset B_R$ with $\left|Q\right|\le 1$ we have

$\begin{array}{l}{{\displaystyle \sum }}^{\text{}}{\left[{\sigma }_{2,\left(1+ϵ\right)}\left(Q,h\left[f_j\right],a\left[f_j\right]\right)\right]}^2\\ \le \theta \left({\left|Q\right|}^{\frac{1}{d}}\right):=\left(1+ϵ\right){{\displaystyle \sum }}^{\text{}}\left({\Vert f_j\Vert }_{L^{\infty }\left(L^{\left(1+ϵ\right)\left(\left(ϵ-2\right),d,\left(1+ϵ\right)\right)}\right)},{\Vert f_j\Vert }_{L^{\infty }\left(L^1\right)}\right){\langle R\rangle }^{\left|ϵ\right|}{\left|Q\right|}^{\frac{\eta }{d}}\text{.}\end{array}$

Here $\eta :=2-\frac{d}{1+ϵ}>0$ and $\left(1+ϵ\right)\left(\left(ϵ-2\right),d,\left(1+ϵ\right)\right):=\frac{d\left(1+ϵ\right)}{d+\left(1+ϵ\right)\left(d+\left(ϵ-2\right)\right)}$ .

In particular, one can chose $\left(1+ϵ\right)$ infinitesimally close to $\frac{d}{2}$ , resulting in $\left(1+ϵ\right)\left(ϵ-2,d,\left(1+ϵ\right)\right)$ to be greater, but as close as one wishes to $\frac{d}{d+ϵ}$ .

Proof. Classical fractional integral estimates say that

${\Vert {\displaystyle \sum h}\left[f_j\right]\Vert }_{L^{d-\left(1+ϵ\right)\left(d+\left(ϵ-2\right)\right)}}\le {\left(1+ϵ\right)}_{d,d+\left(ϵ-2\right)}{{\displaystyle \sum }}^{\text{}}{\Vert f_j\Vert }_{L^{1+ϵ}},\text{provided}\left(1+ϵ\right)<\frac{d}{d+\left(ϵ-2\right)}\text{.}$

We want to choose $\left(1+ϵ\right)$ so that $\left(1+ϵ\right)=\frac{d\left(1+ϵ\right)}{d-\left(1+ϵ\right)\left(d+\left(ϵ-2\right)\right)}$ , which results in $\left(1+ϵ\right)\left(ϵ-2,d,\left(1+ϵ\right)\right)=\frac{d\left(1+ϵ\right)}{d+\left(1+ϵ\right)\left(d+\left(ϵ-2\right)\right)}$ . Therefore,

${\left|Q^{\prime }\right|}^{\frac{2}{d}}{{\displaystyle \sum }}^{\text{}}{\left({\displaystyle {\int }_{Q^{\prime }}h}{\left[f_j\right]}^{1+ϵ}\text{d}v\right)}^{\frac{1}{1+ϵ}}\le \left(1+ϵ\right){\left|Q^{\prime }\right|}^{\frac{2}{d}-\frac{1}{1+ϵ}}{{\displaystyle \sum }}^{\text{}}{\Vert f_j\Vert }_{L^{\left(1+ϵ\right)\left(ϵ-2,d,\left(1+ϵ\right)\right)}}\text{.}$

We can take $\left(1+ϵ\right)$ larger but arbitrarily close to $\frac{d}{2}$ (to have $\frac{2}{d}-\frac{1}{1+ϵ}$ positive) which results in $\left(1+ϵ\right)\left(ϵ-2,d,\left(1+ϵ\right)\right)$ be strictly greater, but arbitrarily close to, $d/\left(d+2+\left(ϵ-2\right)\right)$ . Hence,

${\left|Q\right|}^{\frac{2}{d}}{{\displaystyle \sum }}^{\text{}}{\left({\displaystyle {\int }_{Q^{\prime }}h}{\left[f_j\right]}^{1+ϵ}\text{d}v\right)}^{\frac{1}{1+ϵ}}\le \left(1+ϵ\right){\left|Q^{\prime }\right|}^{\frac{\eta }{d}}{{\displaystyle \sum }}^{\text{}}{\Vert f_j\Vert }_{L^{\left(1+ϵ\right)\left(ϵ-2,d,\left(1+ϵ\right)\right)}}\text{.}$

Thanks to the bound from below for $a\left[f_j\right]$ from Corollary 4.3, we have

${{\displaystyle \sum }}^{\text{}}{\left({\displaystyle {\int }_{Q^{\prime }}a}{\left[f_j\right]}^{-\left(1+ϵ\right)}\text{d}v\right)}^{\frac{1}{1+ϵ}}\le \left(1+ϵ\right){\langle R\rangle }^{\left|ϵ\right|},\forall Q^{\prime }\subset 8Q\text{.}$

We work towards estimating the other factor.

It follows that

$\begin{array}{l}{{\displaystyle \sum }}^{\text{}}{\left|Q^{\prime }\right|}^{\frac{2}{d}}{\left({\displaystyle {\int }_{Q^{\prime }}h}{\left[f_j\right]}^{1+ϵ}\text{d}v\right)}^{\frac{1}{1+ϵ}}{\left({\displaystyle {\int }_{Q^{\prime }}a}{\left[f_j\right]}^{-\left(1+ϵ\right)}\text{d}v\right)}^{\frac{1}{1+ϵ}}\\ \le \left(1+ϵ\right){\langle R\rangle }^{\left|ϵ\right|}{\left|Q^{\prime }\right|}^{\frac{\eta }{d}}{{\displaystyle \sum }}^{\text{}}{\Vert f_j\Vert }_{L^{\left(1+ϵ\right)\left(ϵ-2,\left(1+ϵ\right)\right)}}\text{.}\end{array}$

This estimate is for all cubes $Q^{\prime }$ such that $Q^{\prime }\subset 8Q$ , which proves the proposition.

An immediate consequence of Theorem 5.1 and Proposition 5.2 is the following inequality.

Corollary 5.4. There is a universal constant $\left(1+ϵ\right)$ such that for all ${\varphi }_j$ we have

${\left({\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a^m}}\left[f_j\right]{\varphi }_j^{2m}\text{d}v\right)}^{\frac{1}{m}}\le \left(1+ϵ\right){\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}\left[f_j\right]{\left|\nabla {\varphi }_j\right|}^2\text{d}v\text{.}$ (5.2)

Corollary 5.4 implies, via an elementary interpolation argument, a space-time integral inequality for functions ${\varphi }_j:{ℝ}^d\times \left[0,T\right]\to ℝ$ (see [8] ).

Corollary 5.5. There is a universal constant $\left(1+ϵ\right)$ such that

$\begin{array}{l}{\displaystyle {\int }_0^T{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}}\left[f_j\right]{\varphi }_j^{2\left(1+\frac{2}{d}\right)}\text{d}v\text{d}t\\ \le \left(1+ϵ\right){{\displaystyle \sum }}^{\text{}}{\left({\displaystyle {\int }_0^T{\displaystyle {\int }_{{ℝ}^d}a}}\left[f_j\right]{\left|\nabla {\varphi }_j\right|}^2\text{d}v\text{d}t+\underset{\left(0,T\right)}{\sup }{\displaystyle {\int }_{{ℝ}^d}{\varphi }_j^2\text{d}v}\right)}^{2\left(1+\frac{2}{d}\right)/2}\text{.}\end{array}$

Proof. We follow the standard proof of this space-time inequality (see proof of Theorem 2.12 and 2.13 in [19]. First, we estimate the integral of ${\left|{\varphi }_j\right|}^{2\left(1+\frac{2}{d}\right)}$ with weight $a\left[f_j\right]$ by interpolation

$\begin{array}{l}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}\left[f_j\right]{\left|{\varphi }_j\right|}^{2\left(1+\frac{2}{d}\right)}\text{d}v\\ ={\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}\left[f_j\right]{\varphi }_j^{\left(2\left(1+\frac{2}{d}\right)\right)\theta +\left(2\left(1+\frac{2}{d}\right)\right)\left(1-\theta \right)}dv\\ \le {{\displaystyle \sum }}^{\text{}}{\left({\displaystyle {\int }_{{ℝ}^d}}a{\left[f_j\right]}^{\frac{2m}{\left(1-\theta \right)\left(2\left(1+\frac{2}{d}\right)\right)}}{\left|{\varphi }_j\right|}^{2m}\text{d}v\right)}^{\frac{\left(1-\theta \right)\left(2\left(1+\frac{2}{d}\right)\right)}{2m}}{\left({\displaystyle {\int }_{{ℝ}^d}{\varphi }_j^2\text{d}v}\right)}^{\frac{\left(2\left(1+\frac{2}{d}\right)\right)\theta }{2}}.\end{array}$

The exponent $\theta \in \left(0,1\right)$ is determined from the relation $\frac{1}{2\left(1+\frac{2}{d}\right)}=\frac{1-\theta }{2m}+\frac{\theta }{2}$ . Simplifying, we obtain

${\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}\left[f_j\right]{\left|{\varphi }_j\right|}^{2\left(1+\frac{2}{d}\right)}\text{d}v\le {{\displaystyle \sum }}^{\text{}}{\left({\displaystyle {\int }_{{ℝ}^d}a}{\left[f_j\right]}^m{\left|{\varphi }_j\right|}^{2m}\text{d}v\right)}^{\frac{1}{m}}{\left({\displaystyle {\int }_{{ℝ}^d}{\varphi }_j^2\text{d}v}\right)}^{\frac{m-1}{m}}\text{.}$

Now, by Corollary 5.4

${\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}\left[f_j\right]{\left|{\varphi }_j\right|}^{2\left(1+\frac{2}{d}\right)}\text{d}v\le \left(1+ϵ\right){{\displaystyle \sum }}^{\text{}}\left({\displaystyle {\int }_{{ℝ}^d}a}\left[f_j\right]{\left|\nabla {\varphi }_j\right|}^2\text{d}v\right){\left({\displaystyle {\int }_{{ℝ}^d}{\varphi }_j^2\text{d}v}\right)}^{\frac{m-1}{m}}\text{.}$

Integrating this over time we have

$\begin{array}{l}{\displaystyle {\int }_0^T{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}}\left[f_j\right]{\left|{\varphi }_j\right|}^{2\left(1+\frac{2}{d}\right)}\text{d}v\text{d}t\\ \le \left(1+ϵ\right){{\displaystyle \sum }}^{\text{}}\left({\displaystyle {\int }_0^T{\displaystyle {\int }_{{ℝ}^d}a}}\left[f_j\right]{\left|\nabla {\varphi }_j\right|}^2\text{d}v\text{d}t\right){\left(\underset{\left(0,T\right)}{\sup }{\displaystyle {\int }_{{ℝ}^d}{\varphi }_j^2\text{d}v}\right)}^{\frac{m-1}{m}}\text{.}\end{array}$

From this last inequality it follows trivially that

$\begin{array}{l}{\displaystyle {\int }_0^T{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}}\left[f_j\right]{\left|{\varphi }_j\right|}^{2\left(1+\frac{2}{d}\right)}\text{d}v\text{d}t\\ \le \left(1+ϵ\right){{\displaystyle \sum }}^{\text{}}{\left({\displaystyle {\int }_0^T{\displaystyle {\int }_{{ℝ}^d}a}}\left[f_j\right]{\left|\nabla {\varphi }_j\right|}^2\text{d}v\text{d}t+\underset{\left(0,T\right)}{\sup }{\displaystyle {\int }_{{ℝ}^d}{\varphi }_j^2\text{d}v}\right)}^{2-\frac{1}{m}}\text{.}\end{array}$

Noting that $2-\frac{1}{m}=2-\frac{d-2}{d}=1+\frac{2}{d}=\frac{2\left(1+\frac{2}{d}\right)}{2}$ , the corollary is proved.

The other important use of Theorem 5.1 is in proving a ε-Poincaré inequality, which also relies crucially on Proposition 5.3 and the $L^{1+ϵ}$ bound on $f_j$ (see [8] ).

Corollary 5.6. Let $R>0$ and $\epsilon \in \left(0,{\epsilon }_0\right)$ . For any ${\varphi }_j$ supported in $B_R\left(0\right)$ we have

$\begin{array}{l}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum h}}\left[f_j\right]{\varphi }_j^2\text{d}v\\ \le \epsilon {\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}\left[f_j\right]{\left|\nabla {\varphi }_j\right|}^2\text{d}v+\left(1+ϵ\right){{\displaystyle \sum }}^{\text{}}\left({\left(f_j\right)}_{\text{in}},R\right){\epsilon }^{-\frac{2}{\eta }}{\displaystyle {\int }_{{ℝ}^d}a}\left[f_j\right]{\varphi }_j^2\text{d}v\end{array}$

Here, ${\epsilon }_0:=\theta \left(1\right)/\left(1+ϵ\right)\left(d,ϵ-2\right),\theta \left(1+ϵ\right)$ and $\eta$ are as in Proposition 5.3 and

$\left(1+ϵ\right)\left({\left(f_j\right)}_{\text{in}},R\right)={\left(4\left(1+ϵ\right)\right)}^{\frac{2}{\eta }}{\langle R\rangle }^{\frac{2\left|ϵ\right|}{\eta }}{\Vert {{\displaystyle \sum }}^{\text{}}{\left(f_j\right)}_{\text{in}}\Vert }_{L^{\left(1+ϵ\right)\left(\left(ϵ-2\right),d,\left(1+ϵ\right)\right)}}^{\frac{2}{\eta }}\text{.}$

Proof. Let Q be any cube in ${ℝ}^d$ with $\left|Q\right|\le 1$ . Since ${\varphi }_j={\varphi }_j-{\left({\varphi }_j\right)}_Q+{\left({\varphi }_j\right)}_Q$ it is elementary that

${\displaystyle {\int }_Q{\displaystyle \sum h}}\left[f_j\right]{\varphi }_j^2\text{d}v\le 4{\displaystyle {\int }_Q{\displaystyle \sum h}}\left[f_j\right]{\left({\varphi }_j-{\left({\varphi }_j\right)}_Q\right)}^2\text{d}v+{\displaystyle \sum 4}{\left({\varphi }_j\right)}_Q^2{\displaystyle {\int }_{Q}h}\left[f_j\right]\text{d}v,$ (5.3)

where ${\left({\varphi }_j\right)}_Q$ denotes the average over Q,

${\left({\varphi }_j\right)}_Q={\displaystyle {\int }_Q{\displaystyle \sum {\varphi }_j\text{d}v}}\text{.}$

Applying Hölder’s inequality to ${\displaystyle {\int }_Q{\displaystyle \sum a^{-\frac{1}{2}}}}\left(a^{\frac{1}{2}}\left|{\varphi }_j\right|\right)\text{d}v$ , it follows that

${\left({\varphi }_j\right)}_Q^2\le {\left({\displaystyle {\int }_Q{\displaystyle \sum \left|{\varphi }_j\right|\text{d}v}}\right)}^2\le {{\displaystyle \sum }}^{\text{}}\left({\displaystyle {\int }_{Q}a{\varphi }_j^2\text{d}v}\right)\left({\displaystyle {\int }_Q{a}^{-1}\text{d}v}\right)\text{.}$

Therefore,

$\begin{array}{c}{\displaystyle \sum 4}{\left({\varphi }_j\right)}_Q^2{\displaystyle {\int }_{Q}h\text{d}v}\le 4\left({\displaystyle {\int }_{Q}h\text{d}v}\right)\left({\displaystyle {\int }_Q{a}^{-1}\text{d}v}\right)\left({\displaystyle {\int }_Q{\displaystyle \sum a{\varphi }_j^2\text{d}v}}\right)\\ \le 4\left(1+ϵ\right){\left|Q\right|}^{-\frac{2}{d}}{\displaystyle {\int }_Q{\displaystyle \sum a{\varphi }_j^2\text{d}v}}\end{array}$

Now, we bound the first term on the right of (5.3) by means of Theorem 5.1, so

${\displaystyle {\int }_Q{\displaystyle \sum h{\varphi }_j^2\text{d}v}}\le 4{\mathcal{C}}_{2,2}\left(Q,h,a\right){\displaystyle {\int }_Q{\displaystyle \sum a}}{\left|\nabla {\varphi }_j\right|}^2\text{d}v+4\left(1+ϵ\right){\left|Q\right|}^{-\frac{2}{d}}{\displaystyle {\int }_Q{\displaystyle \sum a{\varphi }_j^2\text{d}v}}$

Then, by Proposition 5.3, we conclude that

$\begin{array}{l}{\displaystyle {\int }_Q{\displaystyle \sum h{\varphi }_j^2\text{d}v}}\le 4\left(1+ϵ\right)\theta \left(\left(1+ϵ\right)\right){\displaystyle {\int }_Q{\displaystyle \sum a}}{\left|\nabla {\varphi }_j\right|}^2\text{d}v\\ +4\left(1+ϵ\right){\left|Q\right|}^{-\frac{2}{d}}{\displaystyle {\int }_Q{\displaystyle \sum a{\varphi }_j^2\text{d}v}},\left(1+ϵ\right):={\left|Q\right|}^{\frac{1}{d}}\text{.}\end{array}$

where $1=\left(d,ϵ-2\right)$ and $\theta$ is as in Proposition 5.3. Adding up these inequalities for each Q of the form $\left(1+ϵ\right){\left[0,1\right]}^d+\left(1+ϵ\right)z,z\in {\mathbb{Z}}^d$

${\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum h{\varphi }_j^2\text{d}v}}\le 4\theta \left(1+ϵ\right){\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}{\left|\nabla {\varphi }_j\right|}^2\text{d}v+4{\left(1+ϵ\right)}^{-1}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a{\varphi }_j^2\text{d}v}}\text{.}$

Let $\epsilon \in \left(0,\eta \left(1\right)/\left(4\left(1+ϵ\right)\right)\right)$ , then there is some $-1<ϵ<0$ such that $4\theta \left(1+ϵ\right)=\epsilon$ , namely

$\epsilon =4\left(1+ϵ\right){\langle R\rangle }^{\left|ϵ\right|}{{\displaystyle \sum }}^{\text{}}{\Vert {\left(f_j\right)}_{\text{in}}\Vert }_{L^{\left(1+ϵ\right)\left(ϵ-2,d,\left(1+ϵ\right)\right)}}{\left(1+ϵ\right)}^{\eta }\text{.}$

Indeed, this $\left(1+ϵ\right)=\left(1+ϵ\right)\left(\epsilon \right)$ is such that

${\left(1+ϵ\right)}^{-2}={\left(4\left(1+ϵ\right)\right)}^{\frac{2}{\eta }}{\langle R\rangle }^{\frac{2\left|ϵ\right|}{\eta }}{{\displaystyle \sum }}^{\text{}}{\Vert {\left(f_j\right)}_{\text{in}}\Vert }_{L^{\left(1+ϵ\right)\left(ϵ-2,d,\left(1+ϵ\right)\right)}}^{\frac{2}{\eta }}{\epsilon }^{-\frac{2}{\eta }}\text{.}$

Thus,

${\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum h{\varphi }_j^2\text{d}v}}\le \epsilon {\displaystyle {\int }_{{ℝ}^d}a}{{\displaystyle \sum }}^{\text{}}{\left|\nabla {\varphi }_j\right|}^2\text{d}v+\left(1+ϵ\right){{\displaystyle \sum }}^{\text{}}\left({\left(f_j\right)}_{\text{in}},R\right){\epsilon }^{-\frac{2}{\eta }}{\displaystyle {\int }_{{ℝ}^d}a{\varphi }_j^2\text{d}v}$

and the corollary is proved.

6. Moser’s Iteration

A ε-Poincare, The solution $f_j$ of (1.1) its estimate because inequality like the one obtained in Corollary 5.6 when valid, see [19].

In Proposition 5.3 and Corollary 5.6 we have proved that the ε-Poincaré inequality holds if $f_j\in L^{\infty }\left(0,T,L^{1+ϵ}\left({ℝ}^d\right)\right)$ for $ϵ>-\left(1+d\right)$ . In view of Lemma 3.1 solutions to (1.1) belong to $L^{1+ϵ}\left({ℝ}^d\right)$ with $ϵ>-\left(1+d\right)$ if the initial data belong to the same $L^{1+ϵ}\left({ℝ}^d\right)$ space and, most importantly, if $\frac{d}{d+ϵ}\le \frac{d+\left(ϵ-2\right)}{-ϵ}$ . This last inequality holds true for $ϵ-2\in \left({\left(ϵ-2\right)}_{\text{*}},-2\right]$ , with ${\left(ϵ-2\right)}_{\text{*}}$ the unique solution to

$\frac{d}{d+ϵ}=\frac{d+\left(ϵ-2\right)}{-ϵ}.$

Observe that for $2-d<ϵ<0$ the function $ϵ-2\mapsto d/\left(d+\left(ϵ-2\right)+2\right)$ is strictly decreasing, while $ϵ-2\mapsto \left(d+\left(ϵ-2\right)\right)/\left(-ϵ\right)$ is strictly increasing. At $ϵ-2=-d$ they are equal to $\frac{d}{2}$ and 0, respectively and at $ϵ=0$ they are equal to 1 and $+\infty$ , respectively. It follows there is exactly one ${\left(ϵ-2\right)}_{\text{*}}\in \left(-d,-2\right)$ where they agree. Alternatively, after solving the respective quadratic equation one can see that ${\left(ϵ-2\right)}_{\text{*}}$ is given by the formula

${\left(ϵ-2\right)}_{\text{*}}=-1-\frac{3}{2}d+\frac{1}{2}\sqrt{5d^2-4d+4}\text{.}$

So, if $\left(ϵ-2\right)\in \left({\left(ϵ-2\right)}_{\text{*}},-2\right]$ , it should be no surprise that the $L^{\infty }$ estimate for $f_j$ follows. As mentioned earlier, there are several ways how to show that. We will follow the Moser’s approach introduced in [19], with consists on estimating the norms

${\left({\displaystyle {\int }_0^T{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}}\left[f_j\right]{\rho }^2{f}_j^{1+ϵ}\text{d}v\text{d}t\right)}^{\frac{1}{1+ϵ}},$

For rising powers of $\left(1+ϵ\right)$ and different cutoff functions $\rho$ . Although the reasons are identical to [20], we describe their derivation here. This proves Theorem 1.1.

After obtaining an energy identity, we will utilize the-Poincaré inequality to restrict the most troublesome component (the integral involving a $h\left[f_j\right]f_j^{1+ϵ}$ term) and get an energy inequality. The $L^{1+ϵ}$ norms will be periodically limited as $ϵ\to \infty$ . By this energy inequality and the space-time weighted inequality (5.2). Here’s (see [21] ).

Proposition 6.1. Let $ϵ>0$ and let $\rho \in {\left(1+ϵ\right)}_c^2\left({ℝ}^d\right)$ , then

$\begin{array}{c}\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\rho }^2{f}_j^{1+ϵ}\text{d}v}}=-\frac{4ϵ}{1+ϵ}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}\left[f_j\right]{\left|\nabla \left(\rho f_j^{1+ϵ/2}\right)\right|}^2\text{d}v\\ +{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum \left(c_1\left(1+ϵ\right){\left|\nabla \rho \right|}^2-\text{Δ}{\rho }^2\right)a\left[f_j\right]f_j^{1+ϵ}\text{d}v}}\\ +\left(ϵ\right){\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum \left(-\text{Δ}a\left[f_j\right]\right){\rho }^2{f}_j^{1+ϵ}\text{d}v}}\\ -c_2\left(1+ϵ\right){\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}\left[f_j\right]f_j^{1+ϵ/2}\left(\nabla \left(\rho f_j^{1+ϵ/2}\right),\nabla \rho \right)\text{d}v\end{array}$

where $c_1\left(1+ϵ\right)=4\left(\frac{1+ϵ+{ϵ}^2}{1+ϵ}\right),c_2\left(1+ϵ\right)=4\left(\frac{1+{ϵ}^2}{1+ϵ}\right)$ .

Proof. For simplicity we shall write a instead of $a\left[f_j\right]$ . From the equation and integration by parts, we have

$\begin{array}{c}\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\rho }^2{f}_j^{1+ϵ}\text{d}v}}=\left(1+ϵ\right){\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\rho }^2{f}_j^{ϵ}{\partial }_t{f}_j\text{d}v}}\\ =-\left(1+ϵ\right){\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum \left(\nabla \left({\rho }^2{f}_j^{ϵ}\right),a\nabla f_j-f_j\nabla a\right)\text{d}v}}\text{.}\end{array}$

The integral on the right is equal to the sum of four terms, which we denote (I), (II), (III), and (IV), and which we now analyze one by one.

First, note that ${{\displaystyle \sum }}^{\text{}}\left(\nabla f_j^{ϵ},\nabla f_j\right)=\left(ϵ\right){\displaystyle \sum f_j^{ϵ-1}}{\left|\nabla f_j\right|}^2=\left(ϵ\right)\left(4/{\left(1+ϵ\right)}^2\right){{\displaystyle \sum }}^{\text{}}\left|\nabla f_j^{\frac{1+ϵ}{2}}\right|$ , therefore

$\left(\text{I}\right)={\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\rho }^2}}\left(\nabla f_j^{ϵ},a\nabla f_j\right)\text{d}v=\frac{4ϵ}{{\left(1+ϵ\right)}^2}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\rho }^{2}a}}{\left|\nabla f_j^{\frac{1+ϵ}{2}}\right|}^2\text{d}v\text{.}$

Next, we rewrite each of the other three terms using integration by parts, as follows

$\begin{array}{c}\left(\text{II}\right)={\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum f_j^{ϵ}}}\left(\nabla {\rho }^2,a\nabla f_j\right)\text{d}v=\frac{ϵ}{1+ϵ}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum \left(\nabla {\rho }^2,a\nabla f_j^{1+ϵ}\right)\text{d}v}}\\ =-\frac{ϵ}{1+ϵ}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum \left(f_j^{1+ϵ}\left(\nabla {\rho }^2,\nabla a\right)+f_j^{1+ϵ}a\text{Δ}{\rho }^2\right)\text{d}v}},\end{array}$

$\begin{array}{c}\left(\text{III}\right)={\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\rho }^2}}\left(\nabla f_j^{ϵ},-f_j\nabla a\right)\text{d}v=\frac{ϵ}{1+ϵ}{\displaystyle {\int }_{{ℝ}^d}{\rho }^2}\left(\nabla f_j^{1+ϵ},-\nabla a\right)\text{d}v\\ =\frac{ϵ}{1+ϵ}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum \left({\rho }^2{f}_j^{1+ϵ}\text{Δ}a+f_j^{1+ϵ}\left(\nabla {\rho }^2,\nabla a\right)\right)\text{d}v}},\end{array}$

$\begin{array}{c}\left(\text{IV}\right)={\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum f_j^{ϵ}}}\left(\nabla {\rho }^2,-f_j\nabla a\right)\text{d}v=-{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum f_j^{1+ϵ}}}\left(\nabla {\rho }^2,\nabla a\right)\text{d}v\\ =2{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a{f}_j^{1+ϵ/2}}}\left(\nabla f_j^{1+ϵ/2},\nabla {\rho }^2\right)\text{d}v+{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a{f}_j^{1+ϵ}\text{Δ}{\rho }^2\text{d}v}}\text{.}\end{array}$

Adding these identities up, we have

$\begin{array}{l}\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\rho }^2{f}_j^{1+ϵ}\text{d}v}}\\ =-\frac{4\left(ϵ\right)}{1+ϵ}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\rho }^{2}a}}{\left|\nabla f_j^{1+ϵ/2}\right|}^2\text{d}v-{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum \left(\text{Δ}{\rho }^2\right)a{f}_j^{1+ϵ}\text{d}v}}\\ +\left(ϵ\right){\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum \left(-\text{Δ}a\right){\rho }^2{f}_j^{1+ϵ}\text{d}v}}-2\left(1+ϵ\right){\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a{f}_j^{1+ϵ/2}}}\left(\nabla f_j^{1+ϵ/2},\nabla {\rho }^2\right)\text{d}v.\end{array}$

We use the elementary identity ${\displaystyle \sum \rho \nabla f_j^{1+ϵ/2}}={\displaystyle \sum \nabla }\left(\rho f_j^{1+ϵ/2}\right)-{\displaystyle \sum f_j^{1+ϵ/2}\nabla \rho }$ and rewrite further,

$\begin{array}{c}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\rho }^{2}a}}{\left|\nabla f_j^{1+ϵ/2}\right|}^2\text{d}v={\displaystyle \int {\displaystyle \sum a}}{\left|\nabla \left(\rho f_j^{1+ϵ/2}\right)\right|}^2\text{d}v+{\displaystyle \int {\displaystyle \sum f_j^{1+ϵ}a}}{\left|\nabla \rho \right|}^2\text{d}v\\ -2{\displaystyle \int {\displaystyle \sum f_j^{1+ϵ/2}a}}\left(\nabla \left(\rho f_j^{1+ϵ/2}\right),\nabla \rho \right)\text{d}v\end{array}$

$\begin{array}{c}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a{f}_j^{1+ϵ/2}}}\left(\nabla f_j^{1+ϵ/2},\nabla {\rho }^2\right)\text{d}v=2{\displaystyle {\int }_{{ℝ}^d}a}{\displaystyle \sum f_j^{1+ϵ/2}}\left(\nabla \left(\rho f_j^{1+ϵ/2}\right),\nabla \rho \right)\text{d}v\\ -2{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a{f}_j^{1+ϵ}}}{\left|\nabla \rho \right|}^2\text{d}v\text{.}\end{array}$

In conclusion,

$\begin{array}{c}\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\rho }^2{f}_j^{1+ϵ}\text{d}v}}=-\frac{4ϵ}{1+ϵ}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}{\left|\nabla \left(\rho f_j^{1+ϵ/2}\right)\right|}^2\text{d}v\\ +{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum \left(4\left(\frac{1+ϵ+{ϵ}^2}{1+ϵ}\right){\left|\nabla \rho \right|}^2-\text{Δ}{\rho }^2\right)a{f}_j^{1+ϵ}\text{d}v}}\\ +\left(ϵ\right){\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum \left(-\text{Δ}a\right){\rho }^2{f}_j^{1+ϵ}\text{d}v}}\\ -4\left(\frac{1+{ϵ}^2}{1+ϵ}\right){\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a{f}_j^{1+ϵ/2}}}\left(\nabla \left(\rho f^{1+ϵ/2}\right),\nabla \rho \right)\text{d}v\text{.}\end{array}$

Since for Theorem 1.1 we only consider $\left(1+ϵ\right)$ ’s with $ϵ>-\left(1+d\right)$ , we will always assume that with $ϵ>-\left(1+d\right)$ , is true for the rest of this section. Since we are now bounded away from $\left(1+ϵ\right)$ (we have $ϵ<0$ ), this also makes some of the constants easier to understand (see [8] ).

Proposition 6.2. Let $\rho \in {\left(1+ϵ\right)}_c^2\left(B_R\right)$ . Given any three times $T_1<T_2<T_3$ in $\left[0,T\right]$ the quantity

$\underset{\left(T_2,T_3\right)}{\sup }{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\rho }^2{f}_j^{1+ϵ}\text{d}v}}+\frac{ϵ}{1+ϵ}{\displaystyle {\int }_{T_2}^{T_3}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}}\left[f_j\right]{\left|\nabla \left(\rho f_j^{1+ϵ/2}\right)\right|}^2\text{d}v\text{d}t$

is not greater than

$\left(\frac{1}{T_2-T_1}+{\left(1+ϵ\right)}_1\right){\displaystyle {\int }_{T_1}^{T_3}{\displaystyle \int {\displaystyle \sum {\rho }^2{f}_j^{1+ϵ}\text{d}v\text{d}t}}}+\left(1+ϵ\right)\left(d,ϵ-2\right)$

$1+{ϵ}^2{\displaystyle {\int }_{T_1}^{T_3}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}}\left[f_j\right]f_j^{1+ϵ}\left({\left|\nabla \rho \right|}^2+\left|\text{Δ}{\rho }^2\right|\right)\text{d}v\text{d}t,$ (6.1)

where ${\left(1+ϵ\right)}_1={\left(1+ϵ\right)}_1\left({\left(f_j\right)}_{\text{in}},R,\left(1+ϵ\right)\right)$ .

Proof. Take the identity in Proposition 6.1 Per Young’s inequality, for every $\epsilon >0$ we have

$2{\displaystyle \sum a{f}_j^{1+ϵ/2}}\left|\left(\nabla \left(\rho f_j^{1+ϵ/2}\right),\nabla \rho \right)\right|\le \epsilon {\displaystyle \sum a}{\left|\nabla \left(\rho f_j^{1+ϵ/2}\right)\right|}^2+{\epsilon }^{-1}{\displaystyle \sum a{f}_j^{1+ϵ}}{\left|\nabla \rho \right|}^2\text{.}$

For $\epsilon =0$ in particular, it follows that

$\begin{array}{l}-4{{\displaystyle \sum }}^{\text{}}\left(\frac{1+{ϵ}^2}{1+ϵ}\right)a{f}_j^{1+ϵ/2}\left(\nabla \left(\rho f_j^{1+ϵ/2}\right),\nabla \rho \right)\\ \le \frac{2ϵ}{1+ϵ}{\displaystyle \sum a}{\left|\nabla \left(\rho f_j^{1+ϵ/2}\right)\right|}^2+2{\left(\frac{1+{ϵ}^2}{1+ϵ}\right)}^2\frac{ϵ}{1+ϵ}{\displaystyle \sum a{f}_j^{1+ϵ}}{\left|\nabla \rho \right|}^2\text{.}\end{array}$

Therefore,

$\begin{array}{c}\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\rho }^2{f}_j^{1+ϵ}\text{d}v}}\le -\frac{2ϵ}{1+ϵ}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}{\left|\nabla \left(\rho f_j^{1+ϵ/2}\right)\right|}^2\text{d}v\\ +{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum \left(4\left(\frac{1+ϵ+{ϵ}^2}{1+ϵ}\right){\left|\nabla \rho \right|}^2-\text{Δ}{\rho }^2\right)a{f}_j^{1+ϵ}\text{d}v}}\\ +\left(ϵ\right){\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum \left(-\text{Δ}a\right){\rho }^2{f}_j^{1+ϵ}\text{d}v}}\\ +{\left(\frac{1+{ϵ}^2}{1+ϵ}\right)}^2\frac{1+ϵ}{ϵ}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a{f}_j^{1+ϵ}}}{\left|\nabla \rho \right|}^2\text{d}v\text{.}\end{array}$

By combining we get:

$\begin{array}{l}\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\rho }^2{f}_j^{1+ϵ}\text{d}v}}+\frac{2ϵ}{1+ϵ}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}{\left|\nabla \left(\rho f_j^{1+ϵ/2}\right)\right|}^2\text{d}v\\ \le {\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum \left({\left(1+ϵ\right)}^2{\left|\nabla \rho \right|}^2-\text{Δ}{\rho }^2\right)a{f}_j^{1+ϵ}\text{d}v}}+\left(ϵ\right){\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum \left(-\text{Δ}a\right){\rho }^2{f}_j^{1+ϵ}\text{d}v}},\end{array}$

where ${\left(1+ϵ\right)}^2={\left(\frac{1+{ϵ}^2}{1+ϵ}\right)}^2\frac{1+ϵ}{ϵ}+4\left(\frac{1+ϵ+{ϵ}^2}{1+ϵ}\right)$ . Since $\left(1+ϵ\right)\ge \frac{d}{d+ϵ}>2$ , it is elementary that

$1\le \left(1+ϵ\right)\left(d,ϵ-2\right)\text{.}$

Now we apply Corollary 5.6 with $\epsilon =\min \left\{\frac{1}{1+ϵ},\eta \left(1\right)\right\}$ . This yields

$\begin{array}{l}\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\rho }^2{f}_j^{1+ϵ}\text{d}v}}+\frac{ϵ}{1+ϵ}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}{\left|\nabla \left(\rho f_j^{1+ϵ/2}\right)\right|}^2\text{d}v\\ \le {\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum \left(\left(1+ϵ\right)\left(d,ϵ-2\right){\left(1+ϵ\right)}^2{\left|\nabla \rho \right|}^2-\text{Δ}{\rho }^2\right)a{f}_j^{1+ϵ}\text{d}v}}\\ +\left(1+ϵ\right){{\displaystyle \sum }}^{\text{}}\left({\left(f_j\right)}_{\text{in}},ϵ-2,{\left(1+ϵ\right)}_0,R\right){\left(1+ϵ\right)}^m{\displaystyle {\int }_{{ℝ}^d}{\rho }^2{f}_j^{1+ϵ}\text{d}v}\end{array}$

Integrate now in $t\in \left(t_1,t_2\right)$ and obtain the sup and average with regard to $\left(T_2,T_3\right)$ , respectively. Hence,

$\underset{\left(T_2,T_3\right)}{\sup }{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\rho }^2{f}_j^{1+ϵ}\text{d}v}}+\frac{ϵ}{1+ϵ}{\displaystyle {\int }_{T_2}^{T_3}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}}{\left|\nabla \left(\rho f_j^{1+ϵ/2}\right)\right|}^2\text{d}v\text{d}t$

is no larger than

$\begin{array}{l}{{\displaystyle \sum }}^{\text{}}\left(\frac{1}{T_2-T_1}+\left(1+ϵ\right)\left({\left(f_j\right)}_{\text{in}},ϵ-2,{\left(1+ϵ\right)}_0,R\right){\left(1+ϵ\right)}^m\right){\displaystyle {\int }_{T_1}^{T_3}{\displaystyle {\int }_{{ℝ}^d}{\rho }^2{f}_j^{1+ϵ}\text{d}v\text{d}t}}\\ +\left(1+ϵ\right)\left(d,ϵ-2\right){\left(1+ϵ\right)}^2{\displaystyle {\int }_{T_1}^{T_3}{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a{f}_j^{1+ϵ}}}}\left({\left|\nabla \rho \right|}^2+\left|\text{Δ}{\rho }^2\right|\right)\text{d}v\text{d}t\text{.}\end{array}$

All that remains of the proof of Theorem 1.1 is covered by the following lemma. This lemma

The following lemma takes care of the rest of the proof of Theorem 1.1. This theorem can be thought of as an estimate of the form $L^{1+ϵ}\to L^{\infty }$ in the spirit of the De Giorgi-Nash-Moser theory, using Moser’s method. In what comes next, keep in mind that the exponent $2\left(1+\frac{2}{d}\right)=2\left(1+\frac{2}{d}\right)$ was defined in (5.1), and that $ϵ>-\left(1+d\right)$ was shown to be true (see [8] )

Lemma 6.3. Let $R\ge 1$ and $T>0$ , then for any $v\in B_R$ and $t\in \left(T/2,T\right)$ we have

$\begin{array}{c}{\displaystyle \sum f_j}\left(v,t\right)\le {{\displaystyle \sum }}^{\text{}}\left(1+ϵ\right)\left({\left(f_j\right)}_{\text{in}},1+ϵ,ϵ-2,R,T\right){\left(1+\frac{1}{T}\right)}^{\frac{1}{1+ϵ}\frac{2\left(1+\frac{2}{d}\right)}{\left(2\left(1+\frac{2}{d}\right)\right)-2}}\\ \times {\left({\displaystyle {\int }_{T/4}^T{\displaystyle {\int }_{B_{2R}}a}}\left[f_j\right]f_j^{1+ϵ}\text{d}v\text{d}t\right)}^{\frac{1}{1+ϵ}}\text{.}\end{array}$

Proof. We introduce the sequences

$T_n:=\frac{1}{4}\left(2-\frac{1}{2^n}\right)T,R_n:=\left(1+\frac{1}{2^n}\right)R,{\left(1+ϵ\right)}_n:=\left(1+ϵ\right){\left(\frac{2\left(1+\frac{2}{d}\right)}{2}\right)}^n,\forall n\in \mathbb{N}\text{.}$

We also pick a sequence of functions ${\rho }_n\in {\left(1+ϵ\right)}_c^2\left(B_{R_n}\left(0\right)\right)$ such that

$\{\begin{array}{l}0\le {\rho }_n\le 1\text{in}{B}_{R_n}\left(0\right)\backslash B_{R_{n+1}}\left(0\right),{\rho }_n\equiv 1\text{in}{B}_{R_{n+1}}\left(0\right),\\ \left|\nabla {\rho }_{n+1}\right|\le \left(1+ϵ\right)\left(d\right)R^{-1}{2}^n\\ \left|\text{Δ}{\rho }_{n+1}^2\right|\le \left(1+ϵ\right)\left(d\right)R^{-2}{4}^n\end{array}$ (6.2)

Now, for each n ≥ 0, let E_n denote the quantity,

$E_n:={\left({\displaystyle {\int }_{T_n}^T{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\rho }_n^{1+2ϵ}a}}}\left[f_j\right]f_j^{{\left(1+ϵ\right)}_n}\text{d}v\text{d}t\right)}^{\frac{1}{{\left(1+ϵ\right)}_n}}\text{.}$

We will develop a recursive relation for $E_n$ , as is customary for divergence elliptic equations. First, keep in mind that $E_{n+1}$ may also be expressed as,

$E_{n+1}^{{\left(1+ϵ\right)}_n}={\left({\displaystyle {\int }_{T_{n+1}}^T{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}}\left[f_j\right]{\left({\rho }_{n+1}{f}^{\frac{{\left(1+ϵ\right)}_n}{2}}\right)}^{2\left(1+\frac{2}{d}\right)}\text{d}v\text{d}t\right)}^{\frac{2}{2\left(1+\frac{2}{d}\right)}}\text{.}$

Thanks to the space-time inequality (5.2) we have

$\begin{array}{l}\left(1+ϵ\right){\left(d,ϵ-2\right)}^{-1}{E}_{n+1}^{{\left(1+ϵ\right)}_n}\\ \le \underset{\left(T_{n+1},T\right)}{\sup }\left\{{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum {\rho }_{n+1}^2{f}_j^{{\left(1+ϵ\right)}_n}\left(t\right)\text{d}v}}\right\}\\ +\frac{\left({\left(1+ϵ\right)}_n-1\right)}{{\left(1+ϵ\right)}_n}{\displaystyle {\int }_{T_{n+1}}^T{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}}\left[f_j\right]{\left|\nabla \left({\rho }_{n+1}{f}_j^{\frac{{\left(1+ϵ\right)}_n}{2}}\right)\right|}^2\text{d}v\text{d}t\text{.}\end{array}$

Then, the energy inequality from Proposition 6.2 says that $\left(1+ϵ\right){\left(d,ϵ-2\right)}^{-1}{E}_{n+1}^{{\left(1+ϵ\right)}_n}$ is no larger than

$\begin{array}{l}{{\displaystyle \sum }}^{\text{}}\left(\frac{2^{n+2}}{T}+\left(1+ϵ\right)\left({\left(f_j\right)}_{\text{in}},ϵ-2,R\right){\left(1+ϵ\right)}_n^m\right){\displaystyle {\int }_{T_n}^T{\displaystyle {\int }_{{ℝ}^d}}}{\rho }_{n+1}^2{f}_j^{{\left(1+ϵ\right)}_n}\text{d}v\text{d}t\\ +\left(1+ϵ\right)\left(d,ϵ-2\right){\left(1+ϵ\right)}_n^2{\displaystyle {\int }_{T_n}^T{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}}\left[f_j\right]f_j^{{\left(1+ϵ\right)}_n}\left({\left|\nabla {\rho }_{n+1}\right|}^2+\left|\text{Δ}{\rho }_{n+1}^2\right|\right)\text{d}v\text{d}t.\end{array}$

Keep in mind that the first sum can’t be bigger than

$\begin{array}{l}{{\displaystyle \sum }}^{\text{}}\left(\frac{2^{n+2}}{T}+\left(1+ϵ\right)\left({\left(f_j\right)}_{\text{in}},\left(ϵ-2\right),{\left(1+ϵ\right)}_0,R\right){\left(1+ϵ\right)}_n^m\right)\\ \frac{1}{\underset{B_R\times \left(0,T\right)}{\min }a\left[f_j\right]}{\displaystyle {\int }_{T_n}^T{\displaystyle {\int }_{{ℝ}^d}{\rho }_n^{2\left(1+\frac{2}{d}\right)}a{f}_j^{{\left(1+ϵ\right)}_n}\text{d}v}}\text{.}\end{array}$

Next, again thanks to ${\rho }_n\equiv 1$ in the support of ${\rho }_{n+1}$ , and in particular

${\left|\nabla {\rho }_{n+1}\right|}^2\le \left(1+ϵ\right)R^{-2}{4}^n{\rho }_n^{2\left(1+\frac{2}{d}\right)},\left|\text{Δ}{\rho }_{n+1}^2\right|\le \left(1+ϵ\right)R^{-2}{4}^n{\rho }_n^{2\left(1+\frac{2}{d}\right)},$

so the second integral above is no larger than

$\left(1+ϵ\right)\left(d,ϵ-2\right){\left(1+ϵ\right)}_n^2{R}^{-2}{4}^n{\displaystyle {\int }_{T_n}^T{\displaystyle {\int }_{{ℝ}^d}{\displaystyle \sum a}}}\left[f_j\right]{\rho }_n^{2\left(1+\frac{2}{d}\right)}{f}_j^{{\left(1+ϵ\right)}_n}\text{d}v\text{d}t$

In conclusion,

$\begin{array}{l}{E}_{n+1}\le \left(1+ϵ\right){{\displaystyle \sum }}^{\text{}}[\left(\frac{2^{n+2}}{T}+\left(1+ϵ\right)\left({\left(f_j\right)}_{in},ϵ-2,R\right){\left(1+ϵ\right)}_n^m\right)\left(1+ϵ\right)\left({\left(f_j\right)}_{in},T\right)R^{-ϵ}\\ {\begin{array}{c}\\ \end{array}+\left(1+ϵ\right)\left(d,ϵ-2\right){\left(1+ϵ\right)}_n^2{R}^{-2}{4}^n]}^{\frac{1}{{\left(1+ϵ\right)}_n}}{E}_n\end{array}$

Set

$b=\max \left\{4\left(2\left(1+\frac{2}{d}\right)\right),{\left(2\left(1+\frac{2}{d}\right)/2\right)}^m\right\},$

$\begin{array}{l}m=\left(1+ϵ\right){{\displaystyle \sum }}^{\text{}}[\left(T^{-1}+\left(1+ϵ\right)\left({\left(f_j\right)}_{in},\left(ϵ-2\right),R\right){\left(1+ϵ\right)}^m\right)\left(1+ϵ\right)\left({\left(f_j\right)}_{\text{in}},R^{\left|ϵ\right|}\right)\\ {{\displaystyle }}_{}^{}+\left(d,ϵ-2\right){\left(1+ϵ\right)}^3{R}^{-2}]\text{.}\end{array}$

Then

$E_{n+1}\le b^{\frac{n}{{\left(1+ϵ\right)}_n}}{m}^{\frac{1}{{\left(1+ϵ\right)}_n}}{E}_n\text{.}$

This recursive relationship and a simple argument from induction show that

$E_n\le b^{{\displaystyle {\sum }_{k=0}^{n-1}\frac{k}{{\left(1+ϵ\right)}_k}}}{m}^{{\displaystyle {\sum }_{k=0}^{n-1}\frac{1}{{\left(1+ϵ\right)}_k}}}{E}_0\text{.}$

Since

$\begin{array}{c}{\displaystyle {\sum }_{k=0}^{n-1}\frac{k}{{\left(1+ϵ\right)}_k}}=\frac{1}{1+ϵ}{\displaystyle {\sum }_{k=0}^{n-1}k}{\left(\frac{2}{2\left(1+\frac{2}{d}\right)}\right)}^k\le \frac{1}{1+ϵ}{\displaystyle {\sum }_{k=0}^{\infty }k}{\left(\frac{2}{2\left(1+\frac{2}{d}\right)}\right)}^k\\ =\frac{1}{1+ϵ}\frac{2\left(2\left(1+\frac{2}{d}\right)\right)}{{\left(\left(2\left(1+\frac{2}{d}\right)\right)-2\right)}^2}\end{array}$

$\begin{array}{c}{\displaystyle {\sum }_{k=0}^{n-1}\frac{1}{{\left(1+ϵ\right)}_k}}=\frac{1}{1+ϵ}{\displaystyle {\sum }_{k=0}^{n-1}{\left(\frac{2}{2\left(1+\frac{2}{d}\right)}\right)}^k}\le \frac{1}{1+ϵ}{\displaystyle {\sum }_{k=0}^{\infty }{\left(\frac{2}{2\left(1+\frac{2}{d}\right)}\right)}^k}\\ =\frac{1}{1+ϵ}\frac{2\left(1+\frac{2}{d}\right)}{\left(2\left(1+\frac{2}{d}\right)\right)-2},\end{array}$

we conclude that

$E_n\le b^{\frac{1}{1+ϵ}\frac{2\left(2\left(1+\frac{2}{d}\right)\right)}{{\left(\left(2\left(1+\frac{2}{d}\right)\right)-2\right)}^2}}{m}^{\frac{1}{1+ϵ}\frac{2\left(1+\frac{2}{d}\right)}{\left(2\left(1+\frac{2}{d}\right)\right)-2}}{E}_0\text{.}$ (6.3)

Observe that

$E_0\le {\left({\displaystyle {\int }_{T/4}^T{\displaystyle {\int }_{B_{2R}\left(0\right)}{\displaystyle \sum a}}}\left[f_j\right]f_j^{1+ϵ}\text{d}v\text{d}t\right)}^{1/1+ϵ}$

Now, since $T_n\le T/2$ and ${\eta }_n\ge 1$ in $B_R$ for all n, it follows that

$E_n\ge {\left({\displaystyle {\int }_{T/2}^T{\displaystyle {\int }_{B_{2R}}{\displaystyle \sum a}}}\left[f_j\right]f_j^{{\left(1+ϵ\right)}_n}\text{d}v\text{d}t\right)}^{\frac{1}{{\left(1+ϵ\right)}_n}}\text{.}$

Considering that $a>0$ everywhere, it follows that

$\underset{n\to \infty }{\lim \sup }{E}_n\ge {{\displaystyle \sum }}^{\text{}}{\Vert f_j\Vert }_{L^{\infty }\left(B_R\times \left(T/2,T\right)\right)}.$

Theorem 1.1, the proof of the lemma and with (6.3).

7. Conclusion

We compute an $L^{\infty }$ approximation for the isotropic counterpart of the homogeneous Landau equation in this publication. This is carried out for interaction exponent values in (some of) the extremely soft potentials range. Our major insight is that certain $L^P$ norms of solutions propagate from the traditional weighted Hardy inequality. Certain weighted Sobolev inequalities and De Giorgi-Nash-Moser theory provide a logical foundation for the $L^{\infty }$ estimate.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Krieger, J. and Strain, R. (2012) Global Solutions to a Non-Local Diffusion Equation with Quadratic Non-Linearity. Communications in Partial Differential Equations, 37, 647-689. https://doi.org/10.1080/03605302.2011.643437
[2]	Gressman, P., Krieger, J. and Strain, R. (2012) A Non-Local Inequality and Global Existence. Advances in Mathematics, 230, 642-648. https://doi.org/10.1016/j.aim.2012.02.017
[3]	Gualdani, M.P. and Guillen, N. (2016) Estimates for Radial Solutions of the Homogeneous Landau Equation with Coulomb Potential. Analysis and PDE, 9, 1772-1809. https://doi.org/10.2140/apde.2016.9.1772
[4]	Gualdani, M. and Guillen, N. (2019) On Ap Weights and the Landau Equation. Calculus of Variations and Partial Differential Equations, 58, Article No. 17. https://doi.org/10.1007/s00526-018-1451-6
[5]	Ghoussoub, N. and Moradifam, A. (2013) Functional Inequalities: New Perspectives and New Applications. In: Mathematical Surveys and Monographs, Vol. 187, American Mathematical Society, Rhode Island. https://doi.org/10.1090/surv/187
[6]	Silvestre, L. (2017) Upper Bounds for Parabolic Equations and the Landau Equation. Journal of Differential Equations, 262, 3034-3055. https://doi.org/10.1016/j.jde.2016.11.010
[7]	Alexandre, R., Liao, J. and Lin, C. (2015) Some a Priori Estimates for the Homogeneous Landau Equation with Soft Potentials. Kinetic and Related Models, 8, 617-650. https://doi.org/10.3934/krm.2015.8.617
[8]	Gualdani, M. and Guillen, N. (2021) Hardy’s Inequality and (Almost) the Landau Equation. ArXiv: 2106.13363v1.
[9]	Golse, F., Gualdani, M., Imbert, C. and Vasseur, A. (2019) Partial Regularity in Time for the Space Homogeneous Landau Equation with Coulomb Potential. Annales Scientifiques de l’école Normale Supérieure, In Press. ArXiv.1906.02841.
[10]	Sagadeeva, M.A. and Hasan, F.L. (2015) Existence of Invariant Spaces and Exponential Dichotomies of Solutions for Dynamical Sobolev Type Equations in Quasi-Banach Spaces. Bulletin of the South Ural State University, Series: Mathematics, Mechanics, Physics, 7, 46-53. https://doi.org/10.14529/mmph150406
[11]	Gu, Y. (2022) Conceptual Problems in Bell’s Inequality and Quantum Entanglement. Journal of Applied Mathematics and Physics, 10, 2216-2231. https://doi.org/10.4236/jamp.2022.107152
[12]	Sagadeeva, M.A. and Hasan, F.L. (2015) Bounded Solutions of Barenblatt-Zheltov-Kochina Model in Quasi-Sobolev Spaces. Bulletin of the South Ural State University, Series: Mathematical Modelling, Programming and Computer Software, 8, 138-144. https://doi.org/10.14529/mmp150414
[13]	Noori, M. and Mahmood, A. (2020) On a Nonlinear Volterra-Fredholm Integrodifferential Equation on Time Scales. Open Access Library Journal, 7, e6103. https://doi.org/10.4236/oalib.1106103
[14]	Bedrossian, J., Gualdani, M. and Snelson, S. (2021) Non-Existence of Some Approximately Self-Similar Singularities for the Landau, Vlasov-Poisson-Landau, and Boltzmann Equations. ArXiv: 2105.03942.
[15]	Fournier, N. (2010) Uniqueness of Bounded Solutions for the Homogeneous Landau Equation with a Coulomb Potential. Communications in Mathematical Physics, 299, 765-782. https://doi.org/10.1007/s00220-010-1113-9
[16]	Chern, J.-L. and Gualdani, M. (2022) Uniqueness of Higher Integrable Solution to the Landau Equation with Coulomb Interactions. Mathematical Research Letters, 29, 945-960. https://doi.org/10.4310/MRL.2022.v29.n4.a2
[17]	Desvillettes, L., He, L.-B. and Jiang, J.-C. (2020) A New Monotonicity Formula for the Spatially Homogeneous Landau Equation with Coulomb Potential and Its Applications. ArXiv: 2011.00386.
[18]	Sawyer, E. and Wheeden, R. (1992) Weighted Inequalities for Fractional Integrals on Euclidean and Homogeneous Spaces. American Journal of Mathematics, 114, 813-874. https://doi.org/10.2307/2374799
[19]	Desvillettes, L. and Villani, C. (2000) On the Spatially Homogeneous Landau Equation for Hard Potentials Part II: H-Theorem and Applications. Communications in Partial Differential Equations, 25, 261-298. https://doi.org/10.1080/03605300008821513
[20]	Baras, P. and Goldstein, J.A. (1984) The Heat Equation with a Singular Potential. Transactions of the American Mathematical Society, 284, 121-139. https://doi.org/10.1090/S0002-9947-1984-0742415-3
[21]	Wu, K.-C. (2014) Global in Time Estimates for the Spatially Homogeneous Landau Equation with Soft Potentials. Journal of Functional Analysis, 266, 3134-3155. https://doi.org/10.1016/j.jfa.2013.11.005