Developing Mathematical Proof: Back to the Future with Vieta Extended Theorem

Lea Dorel, Esther Openhaim

Beit Berl Post Office, Math Department, Beit Berl College, Kfar Saba, Israel.

DOI: 10.4236/ce.2022.1310211                

Abstract

The education system is in a constant search for ways to improve the quality of its daily educational work in the classroom, in response to the increasing demand that its graduates reach achievements appropriate for the 21^stcentury. The current mathematics curriculum for middle schools in Israel introduces students mainly to proofs in geometry, and seems unaware of the need for algebraic proofs and the insights rooted in proving theorems. This paper suggests interesting and challenging research activity for 8^th and 9^th grade students, who are taking their first steps in algebra. This activity would require them to go back in time to the 16^th century, and follow the work of François Viète, a French mathematician who was one of the fathers of modern algebra. Algebraic knowledge required to prove Vieta’s extended theorem corresponds to the algebraic knowledge of middle school students. The activity suggested in this historic context could be an intellectual experience for the students because it encourages searching for relationships and constancy, understanding the need for proof in algebra, and applying the theorem through solving varied questions and creating new questions. Mathematics teachers who choose this topic and place the students at the center as independent learners, could cultivate and promote mathematical thinking among their students.

Keywords

Mathematical Thinking, High-Order Thinking, History of Algebra, Theorems and Proof in Algebra

1. Introduction

Developing mathematical thinking is one of the main goals of the outline of the mathematics curriculum in the scientific track (5 units). Mathematical thinking includes logical thinking, scientific and critical thinking, algorithmic thinking, and understanding basic concepts such as definition, argument, theorem, reverse theorem, and, obviously, proof (as opposed to explanations or examples) (Laikin & Livne, 2015). Developing mathematical thinking is a process acquired through active learning and experience over years. Research has shown that even students in academic institutions find it difficult to understand formal mathematical texts and to write precise proof (Bills & Tall, 1998). The main experience of high school students in Israel in deductive logical thinking is in geometry. In algebra, algebraic manipulations are not considered conducive of mathematical thinking, but rather to practice technical skills. Tall (1998) claimed that an algebraic argument, which is a formal version of an arithmetic phenomenon (constancy), could be a fitting basis for developing mathematical thinking if it is eventually proven.

Cognitive theories argue that significant learning occurs when the student is an active participant in structuring the knowledge in a social interaction that provides meaning (Tzelermeir & Kozolin, 2019). Therefore, a student’s reflective thinking about the meaning of the proof and its structure is a crucial component of meaningful learning.

The aim of this work is to promote mathematical thinking and student self-efficacy through a research task.

2. Historic and Pedagogic Background

François Viète was one of the great mathematicians of the 16^th century. Viète was born at Fontenay-le-Comte in the south of France in 1540. He was a lawyer by training but spent most of his time on mathematics and astronomy. His main work was published in “Introduction to the Art of Analysis”, also known as “New Algebra”, in 1591. Viète’s main idea was to make algebra a powerful mathematical tool, and he was the first to use letters as parameters in equations to express algebraic ideas and generalizations. Among other topics, he studied homogenous equations, and is known to future generations as the man who formulated and proved Vieta’s formula.

Viète claimed that the value of two numbers could be found if their sum and product are known. He also proved that if the sum and product of two numbers are known, then, by algebraic manipulations, their difference could be found, and thus the value of each separately (Strick, 2013). Strick (2013) noted that Viète formulated the following theorem for a second-order polynomial:

If a variable A satisfies the following quadratic equation $\left(B+D\right)A-A^2=BD$ , then B and D are its solutions. The corresponding theorem for a third-order polynomial is:

If a variable A satisfies the cubic equation

$A^3-\left(B+C+D\right)A^2+\left(BC+BD+CD\right)A=BCD$

then B, C and D are its solutions.

Following is the general form of the extended Vieta formula in modern-day mathematical symbols:

Theorem 1: Let $P_n\left(x\right)=x^n+a_1{x}^{n-1}+a_2{x}^{n-2}+\cdots +{\left(-1\right)}^n{a}_n$ be n-order polynomial with n different roots $x_1,x_2,x_3,\cdots ,x_n$ . Then the polynomial coefficients hold the following n equations

$\{\begin{array}{l}{x}_1+x_2+\cdots +x_n=-a_1\\ x_1{x}_2+x_1{x}_3+\cdots +x_1{x}_n+x_2{x}_3+x_2{x}_4+\cdots +x_{n-1}{x}_n=a_2\\ x_1{x}_2{x}_3+x_1{x}_2{x}_4+\cdots +x_1{x}_2{x}_n+x_2{x}_3{x}_4+x_2{x}_3{x}_n+\cdots +x_{n-2}{x}_{n-1}{x}_n=-a_3\\ ⋮\\ x_1{x}_2{x}_3\cdots x_n={\left(-1\right)}^n{a}_n\end{array}$

We propose research activity surrounding this theorem that could interest and challenge 8^th and 9^th grade math-loving students, and perhaps beyond. As stated, the mathematical knowledge required to prove the Vieta theorem in cases of second- and third-order polynomials fits the mathematical knowledge of these age groups: short multiplication formulas, extended factorization, solving algebraic equations, and divisibility rules. This experiential activity invites them to step into the shoes of the inventor and developer of modern algebra, and follow his work processes, culminating in their coping with the general form of the Vieta theorem. The suggested activity could contribute to the students’ development as researchers, by encouraging them to look for relationships, constancy, and generalizations, which require creativity and high-level thinking, and provide answers to intellectual curiosity.

According to Vygotsky’s cognitive development theory (Tzelermeir & Kozolin, 2019) developmental activity must be built on control of cognitive functions in the individual’s Zone of Proximal Development (ZPD). However, the activity must expand the ZPD of those students whose ZPD is not deep enough. Learning should take into account the basic knowledge from which to start out and expand it through developing mathematical group discourse and/or self-reflection by means of learning metacognitive strategies and collaborative learning (Sfard, 2014).

Finding an assignment that encourages math-loving students is not a trivial task for teachers. In this activity, the students rely on rudimentary mathematical knowledge (basic 9^th grade mathematics), and delve into it by examining individual cases, discovering constancy, making assumptions and hypotheses, formulating theorems, and proving and applying them.

3. Goals

Research activity on the Vieta theorem is suggested as extracurricular activity that could be offered as alternative evaluation, self-study, group study of pairs or foursomes, for advanced students who are curious, math lovers, and excellence classes. The proposed activity aspires to the following goals:

• To develop the ability to read and understand texts that include mathematical expressions (for students that are not deterred by reading and deciphering such texts).

• To learn how to disassemble difficulties, and approach a mathematical issue methodically: analyze, understand, generalize, prove, and apply.

• To experience the process of researching and solving mathematical problems (the extended Vieta theorem).

• To discover an important chapter in the history of mathematics, which is the foundation of modern-day mathematical knowledge.

• To face challenges, and develop self-efficacy, tenacity, and intellectual and social collaboration.

As mentioned, we are going “back to the future” with the Vieta theorem—back to the 16^th century and his work but looking to the future—to deciphering the theorem and the elements of the language of mathematics, and to developing mathematical thinking with which to face the challenges of the 21^st century.

Activity Stages

The journey back to the future is a modular journey.

Stage 1—Vieta’s theorem—formulating the extended theorem, understanding the mathematical language, and understanding the meaning of the theorem in depth. We, hence, suggest two different approaches to developing the research work: 1) Induction from the specific to the general; 2) Deduction from the general to the specific.

Stage 2—Formal proof of the general Vieta’s theorem for an n^th polynomial through mathematical induction.

Stage 3—Discussion of the insights and use of Vieta’s theorem as a strategy to solving various questions.

It is possible to move from Stage 1 to the assignments in Stage 3, and then go back to Stage 2 while learning and following the students’ questions and the processes they experience when solving the problems. The ability to think creatively is the key to achieving good performance in mathematics. Discovery and proof of new theorems can be considered the peak of mathematical experience (Tall et al., 2012).

Stage 1: Two approaches to learning

Induction from the specific to the general. The starting point of the inductive approach is the ZPD. Middle school students in Israel learn to factorize trinomials $x^2-ax+b=0$ by means of a mathematical “trick”: They are told to guess two numbers whose product is b and sum is a, and then they are taught to factorize a trinomial. The trick is presented without an explanation or proof (middle school curriculum). We propose showing the students what is behind the trick, and delving into the relationships, including proof for a 2^nd order polynomial.

1) Vieta’s theorem for second-order polynomials is:

If second order polynomial coefficients satisfy the relationship $x^2-\left(x_1+x_2\right)x+x_1\cdot x_2=0$ , then x₁ and x₂ are the equation’s roots.

We suggest to students to prove this theorem, giving the hint: to factorize the equation $x^2-\left(x_1+x_2\right)x+x_1\cdot x_2=0$ .

Then the following questions arise:

2) Do you think the theorem is correct for every 2^nd order polynomial that satisfies these relationships? Are there cases when the theorem is incorrect?

3) Try to formulate the inverse theorem:

If x₁ and x₂ are the roots of the polynomial $P\left(x\right)=x^2+a_{1}x+a_2=0$ then holds the following $x_1{x}_2=a_2$ , $x_1+x_2=-a_1$ .

We suggest students to prove the inverse theorem, giving a hint: If x₁, x₂ are the equation’s roots, then $\left(x-x_1\right)\left(x-x_2\right)=0$ .

4) What is the difference between the theorem and the inverse theorem?

5) Write 2^nd order polynomials that have: two roots, one root, no roots—examine.

Now the teacher can encourage the students to ask questions and search for answers and prove them, the teacher can make sure that the students understand the significance of the theorem and its proof, and to conclude with the mathematical formulation of Vieta’s theorem in both directions which is as follows:

Theorem 2. Let $P\left(x\right)=x^2+a_{1}x+a_2$ be the 2^nd order polynomial. x₁ and x₂ are its roots if and only if they satisfy: $x_1+x_2=-a_1$ , $x_1{x}_2=a_2$ .

Research of Vieta’s theorem for polynomials higher than 2^nd order could be given as individual work, while presenting questions that stimulate interest and motivation. We give the students the opportunity to continue the work independently:

1) Relate to Vieta’s historical story, present the formulation of the theorem for n = 3, examine it, and prove it. If the third order equation with variable A is:

$A^3-\left(B+C+D\right)A^2+\left(BC+BD+CD\right)A=BCD$ then B, C, and D are its solutions.

2) Continue to investigate for n = 3, and search for constancy out of curiosity. Use the “what if not?” strategy and ask whether such relationships exist between coefficients in 3^rd, 4^th and 5^th order polynomials. Finally, reach a generalization for an n-order polynomial.

Deduction from the general to the specific. The starting point of the deductive approach is to present Vieta’s theorem in its precise mathematical formulation, to give the students a chance to decipher a mathematical text and understand it, through a process that imitates the work of the famous mathematician. This is a complex task, especially for students who have no idea how to deal with deciphering a mathematical text. However, this is an opportunity to allow students to enter a process that imitates the mathematician’s work. The teacher’s goal is to mediate, to soften if necessary, and to provoke the students to ask questions about the number of coefficients in each polynomial, the characterization of the series of sums of each coefficient, the products series of each sum, the signs of each coefficient, and how the constancy develops from an n order polynomial to an n + 1 order polynomial.

The natural strategy is to examine the theorem for specific cases of n, and to observe the resultant items and the constancy in the transition from n to n + 1, and vice versa.

Following is the proof of Vieta’s inverse theorem from n = 3 to n = 2.

Theorem 3 (Inverse theorem): Let $P\left(x\right)=x^3+a_1{x}^2+a_{2}x+a_3$ be the 3^rd order polynomial. $x_1,x_2,x_3$ are its roots if and only if the polynomial coefficients $a_1,a_2,a_3$ satisfy the follows: $x_1+x_2+x_3=-a_1$ , $x_1{x}_2+x_1{x}_3+x_2{x}_3=a_2$ , $x_1{x}_2{x}_3=-a_3$ .

Proof:

$x^3-\left(x_1+x_2+x_3\right)x^2+\left(x_1{x}_2+x_1{x}_3+x_2{x}_3\right)x-x_1{x}_2{x}_3=0$

$x^3-x_1{x}^2-x_2{x}^2-x_3{x}^2+x_1{x}_{2}x+x_1{x}_{3}x+x_2{x}_{3}x-x_1{x}_2{x}_3=0$

Extracting the common factor in pairs we get:

$x^2\left(x-x_1\right)-x_{2}x\left(x-x_1\right)-x_{3}x\left(x-x_1\right)+x_2{x}_3\left(x-x_1\right)=0$

$\left(x-x_1\right)\left(x^2-\left(x_2+x_3\right)x+x_2{x}_3\right)=0$

Thus, by extracting the common factor (x − x₁), we get the 2^nd order polynomial whose coefficients satisfy Vieta’s theorem. Therefore, x₂ and x₃ are the roots of the 2^nd order polynomial. Hence, we get:

$0=\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)$

It is very important to prove Vieta’s theorem and inverse theorem for n = 3 and n = 4 order polynomials. In the first proof process, when you open the parentheses and combine like terms, it is important to discover the constancy in the transition from an n order polynomial to an n + 1 order polynomial. When proving the inverse theorem, factorization should be performed to move from an n + 1 order polynomial to an n order polynomial.

The proof of specific cases is a good foundation for understanding how to use mathematical induction to build the general proof of Vieta’s theorem generalized for every natural n.

Stage 2: Formal proof of Vieta’s extended theorem through mathematical induction

Proof of Vieta’s extended theorem through mathematical induction.

Step I: Examine the theorem for n = 2:

$P_2\left(x\right)=x^2+a_{1}x+a_2=0$ ,

x₁ and x₂ are the solution of the given equation if and only if $x_1+x_2=-a_1$ , $x_1{x}_2={\left(-1\right)}^2{a}_2$ . It was proven (see Theorem 2).

Step II: The hypothesis stage for a n − 1 order polynomial

Consider that $x_2,\cdots ,x_n$ are roots of the n − 1 order polynomial:

$P_{n-1}\left(x\right)=x^{n-1}+a_1{x}^{n-1}+a_2{x}^{n-2}+\cdots +{\left(-1\right)}^n{a}_{n-1}$

And:

$\{\begin{array}{l}{x}_2+\cdots +x_n=-a_1\\ x_2{x}_3+\cdots +x_2{x}_n+x_3{x}_4+\cdots +x_{n-1}{x}_n=a_2\\ x_2{x}_3{x}_4+\cdots +x_2{x}_3{x}_n+x_3{x}_4{x}_5+\cdots +x_{n-3}{x}_{n-2}{x}_{n-1}=-a_3\\ ⋮\\ x_2{x}_3\cdots x_n={\left(-1\right)}^{n-1}{a}_{n-1}\end{array}$

Step III: The transition stage based on the hypothesis that $x_2,\cdots ,x_n$ are roots of the n − 1 order polynomial: We prove that $x_1,x_2,\cdots ,x_n$ which satisfies:

$\{\begin{array}{l}{x}_1+x_2+\cdots +x_n=-b_1\\ x_1{x}_2+x_1{x}_3+\cdots +x_1{x}_n+x_2{x}_3+\cdots +x_2{x}_n+x_3{x}_4+\cdots +x_{n-1}{x}_n=b_2\\ x_2{x}_3{x}_4+\cdots +x_2{x}_3{x}_n+x_3{x}_4{x}_5+\cdots +x_{n-3}{x}_{n-2}{x}_{n-1}=-b_3\\ ⋮\\ x_1{x}_2{x}_3\cdots x_n={\left(-1\right)}^n{b}_n\end{array}$

are the roots of the n-order polynomial:

$P_n\left(x\right)=x^n-b_1{x}^{n-1}+b_2{x}^{n-2}+\cdots +{\left(-1\right)}^n{b}_n$

Proof:

$\begin{array}{l}{P}_n\left(x\right)=x^n-\left(x_1+x_2+\cdots +x_n\right)x^{n-1}+(x_1{x}_2+x_1{x}_3+\cdots +x_1{x}_n+x_2{x}_3+\cdots \\ +x_2{x}_n+x_3{x}_4+\cdots +x_{n-1}{x}_n)x^{n-2}+\cdots +{\left(-1\right)}^n{x}_1{x}_2{x}_3\cdots x_n=0\end{array}$

$\begin{array}{l}=x^{n-1}\left(x-x_1\right)-\left(x_2{x}^{n-2}\left(x-x_1\right)+x_3{x}^{n-2}\left(x-x_1\right)+\cdots +x_n{x}^{n-2}\left(x-x_1\right)\right)\\ +(x_2{x}_3{x}^{n-3}\left(x-x_1\right)+x_2{x}_4{x}^{n-3}\left(x-x_1\right)+\cdots +x_2{x}_n{x}^{n-3}\left(x-x_1\right)\\ +x_3{x}_4{x}^{n-3}\left(x-x_1\right)+\cdots +x_{n-1}{x}_n{x}^{n-3}\left(x-x_1\right))+\cdots \\ +{\left(-1\right)}^n{x}_2{x}_3\cdots x_n\left(x-x_1\right)=0\end{array}$

$P_n\left(x\right)=\left(x-x_1\right)\left(x^{n-1}-a_1{x}^{n-1}+a_2{x}^{n-2}+\cdots +{\left(-1\right)}^{n-1}{a}_{n-1}\right)=0$

Based on the hypothesis that $x_2,\cdots ,x_n$ are roots of the n − 1 order polynomial, we get that $x_1,x_2,\cdots ,x_n$ are the roots of the n order polynomial.

$P_n\left(x\right)=\left(x-x_1\right)\left(x^{n-1}-a_1{x}^{n-1}+a_2{x}^{n-2}+\cdots +{\left(-1\right)}^{n-1}{a}_{n-1}\right)$

Stage 3: Discussion of the insights and uses of Vieta’s theorem as a problem-solving strategy

The third stage consists of two parts: First, discussion of the issues that stem directly from dealing with the theorem and its components, and insights that stem from the theorem and are expressed in the solutions of appropriate questions. Second, applying Vieta’s extended theorem as a strategy to solve problems in algebra and geometry.

Part 1—Issues that stem from the theorem and its components

As mentioned, it is important to develop group discourse and discussions and/or personal reflection on the significance of the theorems and proofs, through cooperation between the students and the teacher. The teacher’s role is to elicit questions and issues for thought, and discuss them in class, in order to deepen the students’ understanding of the theorem and its significance.

1) Check whether the students understand the difference between the theorem and the inverse theorem, and how it is proven in each situation.

2) Check the students’ understanding of the term “if and only if”.

3) Check correct application of algebraic manipulations in proof of Vieta’s theorem for a general case of n-order polynomials versus specific cases when n = 2 and n = 3.

4) Check application of Vieta’s extended theorem in new situations and solving unusual problems that require high-order thinking.

Following are number of issues for thinking and classroom discussion within this activity:

• Is Vieta’s extended theorem for an n-order polynomial true for every natural n?

• Are there solutions for an n-order polynomial whose coefficients do not confirm the relationships of Vieta’s extended theorem?

• Does Vieta’s extended theorem indicate an algorithm to finding the roots of polynomials?

• Given 2^nd and 3^rd order polynomials, suggest an algorithm for finding their roots (if they exist).

• Given n different real numbers, how can you build an equation that they are its roots?

Next, we present examples of questions that examine insights and comprehension performance of Vieta’s theorem, followed by didactic analyses:

Question 1: Given three roots of a 3^rd order polynomial $x_1=1,x_2=-1,x_3=3$

1) Find the polynomial coefficients.

2) Are the roots the polynomial roots $p\left(x\right)=x^3+3x^2-x-3$

Didactic analysis of Question 1:

• Use of Vieta’s theorem and in the relationship between coefficients and roots in a 3^rd order polynomial.

• Use of algebraic manipulations and presentation units to find the roots.

• Applying the meaning of the term if and only if in both directions.

Question 2: Given the following system of equations:

$\{\begin{array}{l}a+b+c=20\\ ab+bc+ac=121\\ abc=200\end{array}$

1) Can this equation be solved? Yes/No. Explain your answer.

2) If yes, develop an algorithm to find the solutions.

Didactic analysis and solution of Question 2:

1) Based on Vieta’s theorem, the given system of equations fits a 3^rd order polynomial, and a, b, c are roots of the equation: $x^3-20x^2+121x-200=0$ .

2) Developing the algorithm to a 3^rd order polynomial is based on several hypotheses:

An odd-numbered polynomial has at least one real root;

By finding one real root, the polynomial can be divided and produce a 2^nd order polynomial;

One of the roots must be one of the divisors of the coefficient $abc=200=2^3\cdot 5^2$ ;

The divisors of 200 are: 1, 2, 4, 5, 8, 10, 20, 25, 40, 50, 100, 200;

The fitting root is $\left(x-8\right)\left(x^2-12x+25\right)=0$ , $x=8$ ;

The solutions of the system are: $a=8$ , $b=6+\sqrt{11}$ , $c=6-\sqrt{11}$ .

Question 3: Given is the following system of equations:

$\begin{array}{l}a+b=6\\ a^2+b^2=6\end{array}$

1) Does this system of equations have real roots?

2) If yes, find the solutions. If no, explain your answer.

Didactic analysis and solution of Question 3:

Through algebraic manipulations, we can obtain the product $ab=15$ , and the sum $a+b=6$ . This gives us the equation $x^2-6x+15=0$ . Since $\Delta <0$ , the equation does not have real roots.

Question 4:

When proving Vieta’s extended theorem, we extract the common factor $\left(x-x_1\right)$ from pairs of expressions so that we get factorization of an n-order polynomial to the product of multiplication of an n-1 order polynomial by the factor $\left(x-x_1\right)$ (see formal extended proof). How can we make sure that there is a common factor of all terms of partial sums?

Didactic analysis and solution of Question 4:

To solve this question, students should be guided to perform algebraic manipulations for concrete cases of 2^nd, 3^rd and 4^th order polynomials, focusing on the number of coefficients and the partial sums. In the transition from line n to its

sequential line n + 1, the binomial formula $\left(\begin{array}{c}n+1\\ k\end{array}\right)=\left(\begin{array}{c}n\\ k-1\end{array}\right)+\left(\begin{array}{c}n\\ k\end{array}\right)$ assures that no member in the partial sums of the polynomial is left out.

4. Applications of the Theorem in Algebra and Geometry

Question 5: Solve the following system of equations:

$\{\begin{array}{l}\frac{x}{y}+\frac{y}{z}+\frac{z}{x}=3\\ \frac{y}{x}+\frac{z}{y}+\frac{x}{z}=3\\ x+y+z=3\end{array}$

Didactic analysis and solution of Question 5:

Given is a system of three equations and three unknowns. We can convert the equations to a different system of equations as follows: $\frac{x}{y}=u,\frac{y}{z}=v,\frac{z}{x}=w$ .

The system is consequently written as: $\{\begin{array}{l}u+v+w=3\\ \frac{1}{u}+\frac{1}{v}+\frac{1}{w}=3\\ uvw=1\end{array}$ .

Through mathematical manipulations we get: $\{\begin{array}{l}u+v+w=3\\ uv+vu+vw=3\\ uvw=1\end{array}$ .

The system conforms with Vieta’s theorem for a 3^rd order polynomial. The polynomial is: $t^3-3t^2+3t-1=0$ . u, v, w are the roots of the system. The roots product is 1, and the roots sum is 3. The roots are: $u=v=w=1$ .

Question 6:

Given is a triangle ABC. The radius of the incircle is r = 1. The radius of the circumcircle is R = 5. The triangle circumference is 20 cm. Find the sides of the triangle.

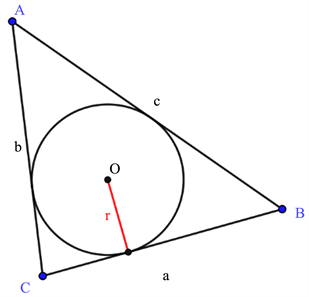
Didactic analysis and solution of Question 6:

This is a complex geometrical question. Finding the equations requires thorough knowledge of geometry and use of triangle area strategies. The area of a triangle can be calculated in three different ways according to three different geometric theorems. The resulting system of equations indicates that there is a solution, because the system corresponds with Vieta’s theorem. Thus, the way to finding the solutions is challenging in itself.

We mark the triangle sides as a, b, c. It is known that $a+b+c=20$ . We use the three equations to calculate the triangle area:

• Calculating the triangle area by incircle radius and sum of the three sides

$S=\frac{a+b+c}{2}r=10$

• Calculating the triangle area by the three sides and circumcircle radius

$S=\frac{abc}{4R}\Rightarrow abc=4\times 5\times 10=200$

• Calculating the triangle area by the three sides and circle radius (Heron’s formula)

$S^2=p\left(p-a\right)\cdot \left(p-b\right)\cdot \left(p-c\right),p=\frac{a+b+c}{2}=10$

When we substitute all the values, we get a system of equations:

$\{\begin{array}{l}a+b+c=20\\ ab+bc+ac=121\\ abc=200\end{array}$

a, b, c uphold Vieta’s theorem, and they are the roots of the polynomial:

$x^3-20x^2+121x-200=0$

The triangle’s sides are: $a=8,b=6+\sqrt{11},c=6-\sqrt{11}$ .

5. Summary

Learning to think mathematically means learning to create a point of view on mathematics, which is to appreciate the process of abstraction in mathematics and try to apply it to problem solving (Schoenfeld, 2016). Mathematical competencies (math problem solving, communication, literacy, presentation) are especially dependent on the level of thinking (decisive, critical, creative, metacognitive thinking) (Maslihah et al., 2020). Mathematical thinking can provide the ability to solve mathematical problems and the skills needed in independent learning (Lee, Ng, & Bull, 2018). The thinking skills are also associated with mathematical literacy (Zetriuslita et al., 2020). Many scholars share the view that thinking skills play a critical role in modern learning and education. Development of mathematical thinking is the main goal in teaching mathematics. Teachers should focus on development mathematical thinking skills through learning activities that can improve mathematics achievements (Nepal, 2016).

The “back to the future” activity with Vieta’s extended theorem is research work that provides an opening for 8^th and 9^th graders to the world of algebraic concepts, understanding and skills, and insights of mathematical research in algebra, which fits their ZPD (Kozolin, 2004).

We have shown how it is possible to lead students, through Vieta’s theorem, to read and understand what an algebraic theorem is, what the theorem means, what direct and reverse theorems are, and the differences between proof in either direction. We presented two approaches to introducing Vieta’s theorem—the inductive approach that focuses on developing the theorem through specific cases and generalizing from them; and the deductive approach that starts with presenting the general theorem in symbolic mathematical language, and deciphering Vieta’s extended theorem from the general to the specific. We have shown how Vieta’s theorem can be factorized and formulated for specific cases. We have also shown how proof can be structured and formulated through mathematical induction.

The journey culminated in introducing different and varied questions that require high-order thinking, and examine the students’ comprehension performance regarding various aspects of the theorem.

The “back to the future” journey with Vieta’s extended theorem is an appropriate solution for methodically cultivating the culture of mathematical thinking, provided that the individual learner or group of students are put at the center of the learning. The teacher’s role is to mediate and guide the students in their endeavors. The mathematics teacher helps students to develop as independent researchers, and encourages them to seek relationships, constancy, and generalizations. This experience can develop among the students a deep acquaintance with the essence of mathematical thinking, resilience, and confidence to cope with problem-solving, to boost their achievements, and to nurture higher mathematical skills (Bsharaa, 2016; Mani & Emanuel, 2006).

Research activity on the Vieta theorem is proposed as extracurricular activity that could be offered as an alternative evaluation project, for self-directed learning, for group study of pairs or larger groups, for advanced students who are curious, math-lovers, and other forms of excellence classes.

We hope that mathematics teachers choose this topic to cultivate their students’ mathematical thinking.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Bills, E., & Tall, D. O. (1998). Operable Definitions in Advanced Mathematics: The Case of the Least Upper Bound. In Proceedings of P.M.E. 22 (pp. 104-111).
[2]	Bsharaa, S. (2016). Cultivating Self-Guidance in Learning and Teaching Mathematics. Rav Gvanim, 2, 211-234. (In Hebrew) https://www.gordon.ac.il/sites/gordon/UserContent/files/bsharaa.pdf
[3]	Kozolin, A. (2004). The Social-Cultural Psychology of Lev Vygotsky. In Learning in a Social Context—Development of Higher Psychological Processes (pp. 20-22). Mofet Institue. (In Hebrew)
[4]	Laikin, R., & Livne, R. (2015). Mathematics Curriculum for Middle School—Structure and Principles. Aleh, 51, 5-13. (In Hebrew)
[5]	Lee, K., Ng, S. F., & Bull, R. (2018). Learning and Solving Algebra Word Problems: The Roles of Relational Skills, Arithmetic, and Executive Functioning. Developmental Psychology, 54, 1758-1772. https://doi.org/10.1037/dev0000561
[6]	Mani, A., & Emanuel, D. (2006). Socio-Mathematical Norms in Mathematical Teaching-Learning Environments, and Their Affinity to Creating Self-Directed Learning among 3rd Grade Students. In Conference on Planning Learning in an Era of Standards (pp. 213-234). Mofet Institute. (In Hebrew)
[7]	Maslihah, S., Waluya, S. B., & Suyitno, A. (2020). The Role of Mathematical Literacy to Improve High Order Thinking Skills. Journal of Physics: Conference Series, 1539, Article ID: 012085. https://doi.org/10.1088/1742-6596/1539/1/012085
[8]	Nepal, B. (2016). Relationship between Mathematical Thinking and Mathematics Achievement. IOSR Journal of Research Method in Education, 6, 46-49.
[9]	Schoenfeld, A. H. (2016). Learning to Think Mathematically: Problem Solving, Metacognition, and Sense Making in Mathematics (Reprint). Journal of Education, 196, 1-38. https://doi.org/10.1177/002205741619600202
[10]	Sfard, A. (2014). University Mathematics as a Discourse—Why, How, and What for? Research in Mathematics Education, 16, 199-203. https://doi.org/10.1080/14794802.2014.918339
[11]	Strick, H. (2013). Francois Vieta. Spektrum der Wissenschaft Verlagsgesellschaft Heidelberg. https://www.spektrum.de/wissen/francois-viete-im-nebenberuf-schoepfer-der-modernen-algebra/1214470
[12]	Tall, D. O. (1998). The Cognitive Development of Proof: Is Mathematical Proof for All or for Some? In Proceedings of Conference of the University of Chicago School Mathematics Project (pp. 1-19).
[13]	Tall, D., Yevdokimov, O., Koichu, B., Whiteley, W., Kondratieva, M., & Cheng, Y. (2012). Cognitive Development of Proof. In Proof and Proving in Mathematics Education (pp. 13-49). Springer. https://doi.org/10.1007/978-94-007-2129-6_2
[14]	Tzelermeir, M., & Kozolin, A. (2019). Lev Vygotsky and Social-Cultural Theory—Challe- nges in Education—Then and Now. Mofet Institute. (In Hebrew)
[15]	Zetriuslita, Z., Wahyudin, W., & Jarnawi, J. (2020). The Correlation among Students’ Response in Apply Problem Based Learning and Cognitive Conflict Strategy to Improve Critical Thinking Skills and Curiosity Attitude Based on Academic Level. Journal of Physics: Conference Series, 1521, 32-34. https://doi.org/10.1088/1742-6596/1521/3/032034