Linear MMSE Channel Estimation for Underlay Cognitive Radio Networks ()
1. Introduction
The wireless network has taken a great turnover when MIMO architectures were introduced, which brought a whole new scenario for development of transmissions strategies being able to make efficient use of spatial diversity and/or multiplexing. The emerging cognitive radio technologies also aim to develop transmission methods able to adapt each link of a MIMO channel in order to achieve better overall performance. This efficient use is usually employed if accurate channel state information (CSI) is available at the transmitter, which is obtained via channel estimation procedures.
A popular and recent example of application of channel estimation is the introduction of IEEE 802.11n network standard [1] , which is known to achieve much greater transmission rate and make efficient use of unlicensed spectrum bands. Even though this protocol is destined for indoor scenarios, it is a very popular and simple example for explaining the main functionality of training and channel estimation timings. This high throughput standard offers several enhancements to medium access control (MAC) layer and plays an important role in popularization of MIMO technologies. The 802.11n employs high throughput orthogonal frequency division multiplexing (HT-OFDM) by using technologies such as MIMO, channel biding, beamforming and space-time block coding (STBC).
In order to provide means for accurate channel estimation, the IEEE 802.11n has two operation modes: mixed and green field modes. As illustrated in Figure 1, there is basically one structural difference between these modes: the time period destined for training and channel estimation, and the data transmission event.
Even though training periods bring possibility of performance enhancement, it also causes spectral/power efficiency loss. Spectral efficiency is defined as the net bit rate over the channel bandwidth. The longer preamble is used, the lower net bit rate is achieved. Consequently, it is desired to keep the training period as low as possible.
The high throughput mesh network is a promising scenario for cognitive radios [2] . Also, our previous analysis [3] has demonstrated that accurate (virtually perfect) CSI estimations bring significant improvements in capacity, once correct interference cancellation and power allocation can be applied together. Indeed, the optimization techniques are deployed in [3] to design CR precoding strategies aiming at maximizing the sum capacity of multiple input-single-output cognitive radio networks (MISO-CRNs). The chosen technique is zero-forcing water-filling (ZFWF). To maximize the sum capacity, the number of secondary users to be supported in a certain CRN is optimally determined. The choice of 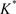 is based only on the number of base station (BS) antennas and SINR. This might be very useful when designing and controlling the network, once the BS can select the best quality links and discard the poor ones.
is based only on the number of base station (BS) antennas and SINR. This might be very useful when designing and controlling the network, once the BS can select the best quality links and discard the poor ones.
Other studies have proved that different beamforming techniques may cause improvements on the spectral efficiency [4] and also SINR maximization [5] . Therefore, the following facts are enough reasons to motivate the study of channel estimation techniques and their impact on the performance of CR networks: 1) Accuracy in the CSI estimations brings huge improvements to wireless transmissions; 2) Accurate CSI estimations allow CR devices to successfully explore powerful interference cancellation techniques; 3) The imperfections of the CSI estimations are due to the miss-detection of signals; 4) Study of imperfect CSI effects brings means of analysing possible errors and extrapolation of interference thresholds; 5) Current communication protocols allow transmission periods dedicated to training and channel estimation; 6) Use of known pilot sequences allows SUs to estimate both SU’s and PU’s channel matrix.
In [6] , the authors deal with the joint problem of channel estimation and pilot assignment, addressing its impact on DL transmissions in an underlay cognitive radio scenario (uCRN). Primary networks suffer from the cognitive interference, which can be mitigated by deploying beamforming at the cognitive systems to
![]()
Figure 1. IEEE 802.11n HT-PLCP (Physical Layer Convergence Protocol) frame formats.
spatially direct the transmissions away from the primary receivers. The accuracy of the CSI plays an important role in the beamformer designs, since the channel estimate is affected by interference. Hence, [6] propose joint procedures for channel estimation and pilot allocation while reducing the impact of pilot contamination at the primary and cognitive systems. For that, the authors exploit the information embedded in the covariance matrices to separate the channel estimate from other users’ channels in correlated cognitive single input multiple input (SIMO) channels.
A cooperative hybrid underlay-overlay cognitive radio combined with non-orthogonal multiple access (CHCR-NOMA) system, where a secondary source and a primary source share a secondary decode-and-forward relay by using NOMA principles is proposed recently in [7] . The authors provide closed-form expressions for the outage probability of both PUs and SUs, assuming imperfect CSI and imperfect successive interference cancellation (SIC). Moreover, the authors tackle the power allocation problem for various transmit powers and different distances of the primary destination from the relay to ensure priority to the primary user or to satisfy the fairness requirements of both the destinations.
Contributions. CRN is a recent and promising field of study that needs a closer look and some special analysis. As a consequence of its topology, cognitive transceivers must always be working under high interference. The knowledge of channel characteristics or statistics is essential for precoding design and performance optimization. Hence, this work contributes to the literature on the following CRN aspects:
• Mathematical determination of Linear MMSE (LMMSE) channel estimation for underlay CRN mode with simultaneous transmission of PUs and SUs;
• Proof that knowledge of both primary and secondary pilot sequences is necessary to apply LMMSE channel estimation;
• Simultaneous estimation of both PU and SU channels for underlay CRN, where all users are transmitting over the entire period of time;
• Analysis of impact of imperfect channel estimation on capacity of secondary users;
• Quantification of capacity loss of the underlay CRNs due to imperfect channel estimations.
The remainder of this work is organized into four sections. Section 1 presents the adopted underlay MU-MISO-CRN system model, evidencing the channel estimation problem in underlay CRNs. In Section 3 the linear MMSE MU-MISO CRN channel estimator is derived for synchronous scenarios. Numerical results in Section 3 demonstrate the effectiveness of the proposed LMMSE channel estimation method for underlay MU-MISO-CRNs in both asynchronous and synchronous scenarios. Conclusions remarks are offered in Section 7.
2. System Model
A single-cell underlay multiuser (MU) MISO-CRN will be considered, where a CR-BS with nBS antennas is communicating with K SUs and M PUs. The secondary transmission is established via a full-duplex link where the CR-BS has means of properly estimating all necessary channel characteristics and making the best use of it to enhance its transmission.
This work consists of separately analyzing uplink (UL) and downlink (DL) of a single cell underlay MU-MISO-CRN. The channel training occurs at uplink, while the data transmission is analyzed at the downlink (DL). During UL, the CR-BS simultaneously receives PUs and SUs pilot sequences and estimates both channel matrices. After receiving and processing the data, the CR-BS makes the best use of such a information to design efficient precoders according to the strategy developed in [3] .
A possible time-slot structure is depicted in Figure 2, where the channel estimation is composed of two stages that must be no longer than N symbols. Firstly, the CR-BS receives all transmitted pilot sequences and then processes it to estimate the channel matrix and design efficient transmission precoders according to theory of [3] . Subsequently, the CR-BS transmits the estimated channel to allow the CR node to properly decode the following message; finally, the CR-BS transmits all desired data. An essential condition is that the period T must be smaller than the channel’s coherence time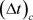 . This constraint guarantees that all estimated channel parameters at the uplink can be reasonably used on the following downlink data transmission.
. This constraint guarantees that all estimated channel parameters at the uplink can be reasonably used on the following downlink data transmission.
For sake of simplicity and compactness, the system model presented in this work relies on synchronous transmission and assumes orthogonal training sequences, which is not the most realistic case in the uplink direction, once it is impractical to synchronize all PUs and SUs such that its transmitted pilot sequences will be simultaneously received at CR-BS and without overlapping of two or more consecutive symbols. However, some asynchronous practical cases will be analyzed numerically in Section 3, where the pilot sequence is quasi-orthogonal and some overlapping is accepted at the CR-BS.
Next, uplink channel estimation and downlink data transmission will be described. The uplink underlay CRN is used for training and channel estimation, and a few estimation techniques will be studied and hereafter compared. In this case, research of LMMSE technique adapted to MISO-CRN came up with a novelty to prove that knowledge of primary and secondary pilot sequence and
noise variances are strictly necessary. Moreover, the downlink data transmission subsection explains how the channel estimative will be used to efficiently design optimal precoders according to the analytical findings in [3] .
2.1. Uplink—Training and Channel Estimation
The considered uplink configuration is depicted in Figure 3(a), where vectors , with
, with  and
and 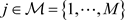 aresecondary and primary channel vectors, respectively.
aresecondary and primary channel vectors, respectively.
Observe that, even though both primary and secondary signals may be interfering on other users signals, our interest herein is to collect the received signal at CR-BS, which is composed by PUs’ and SU’s pilot sequences. Once an underlay CR transmission is considered, both PUs and SUs are simultaneously transmitting their training sequence and the CR-BS receives a signal  as follows:
as follows:
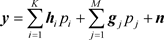 (1)
(1)
where 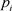 is an arbitrary pilot symbol and
is an arbitrary pilot symbol and  is the complex Additive White Gaussian Noise (AWGN).
is the complex Additive White Gaussian Noise (AWGN).
Alternatively, Equation (1) can be re-written with the channel matrix ,
,  and the pilot sequences
and the pilot sequences 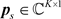 and
and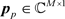 :
:
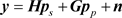 (2)
(2)
A certain number of training realizations is usually required to properly estimate the channel in MIMO systems [8] . The lower bound of training symbols is known to be the number of receiving antennas. In this work, the training length N will be larger than nBS, such as , in order to avoid possible channel estimation uncertainties. However, as explained before, training sequence length directly affects energy/spectral efficiency. Also, as mentioned before, the total frame length must be smaller than the coherence time of the channel.
, in order to avoid possible channel estimation uncertainties. However, as explained before, training sequence length directly affects energy/spectral efficiency. Also, as mentioned before, the total frame length must be smaller than the coherence time of the channel.
As a consequence, the pilot symbol vectors  and
and ![]() can be substituted by its respective matrix form
can be substituted by its respective matrix form ![]() and
and![]() , which results in the following received signal:
, which results in the following received signal:
![]() (3)
(3)
where ![]() is the received signal, the wireless channels
is the received signal, the wireless channels ![]() and
and ![]() are complex Gaussian variables and Rayleigh flat fading assumed to be constant for
are complex Gaussian variables and Rayleigh flat fading assumed to be constant for ![]() symbols.
symbols.
![]() a) UL
a) UL ![]() b) DL
b) DL
Figure 3. Uplink and downlink underlay MU-MISO-CRN scenarios.
2.2. Estimating PU’s and SU’s Channel Matrices in Underlay CRNs
The main idea is to make use of one training period to simultaneously estimate both primary and secondary channel matrix. However, the problem herein is that, for underlay CRN scenarios, PUs are constantly transmitting (and usually SUs are also aiming to do so). As a consequence, the estimators ![]() and
and ![]() have to deal with a constant interference: when estimating
have to deal with a constant interference: when estimating![]() , there is the primary term
, there is the primary term ![]() and, when estimating
and, when estimating![]() , there is an interference referent to
, there is an interference referent to![]() .
.
All researches until now focus on estimating ![]() and
and ![]() separately or only one of them. However, the precoder studied in [3] relies on knowledge of both
separately or only one of them. However, the precoder studied in [3] relies on knowledge of both ![]() and
and![]() , and the fastest way of doing such estimation is to only one received signal of length N to estimate both channel matrix.
, and the fastest way of doing such estimation is to only one received signal of length N to estimate both channel matrix.
Underlay CRNs do not need a spectrum sensing stage, which allows all SUs to make use of the training period only to estimate the channel; consequently, the proposed frame structure of Figure 2 still valid for the underlay MU-MISO CRN scenario.
It is known that some estimation techniques present better results for certain network configuration or are less computationally complex. Indeed, in the following, the least squares (LS) and the minimum mean squares error (MMSE) estimation techniques will be briefly presented, in order to allow a future analysis of the impact of the use of such estimators on sum capacity and error performance. The classical LS estimator will be firstly introduced and can be straightforwardly adapted to MU-MISO CRN channel estimation application scenarios. However, the LMMSE case can not be easily adapted and some new inferences are presented.
2.3. Least Squares MU-MISO CRN Channel Estimator
The LS channel estimator is intended to find a parameter ![]() to minimize the function
to minimize the function![]() :
:
![]() (4)
(4)
The gradient of ![]() is then calculated and set to zero as:
is then calculated and set to zero as:
![]()
![]()
![]() (5)
(5)
where the training matrix ![]() can be referent to SUs (
can be referent to SUs (![]() ) or PUs (
) or PUs (![]() ); the pseudo-inverse matrix of
); the pseudo-inverse matrix of ![]() is given by
is given by![]() .
.
It is important to remember that, differently from other traditional MIMO architectures, an underlay CR has to use the same received signal ![]() to estimate two distinct channel matrices, which may result in poor performance. Consequently, estimative of
to estimate two distinct channel matrices, which may result in poor performance. Consequently, estimative of ![]() has to lead with interference from PUs and vice-versa. From (5), each LS estimator (secondary and primary) can be written as [9] :
has to lead with interference from PUs and vice-versa. From (5), each LS estimator (secondary and primary) can be written as [9] :
![]() (6)
(6)
![]() (7)
(7)
3. Linear MMSE MU-MISO CRN Channel Estimator
The LMMSE estimator has a general form![]() , where the matrix
, where the matrix ![]() is responsible for minimizing the difference between
is responsible for minimizing the difference between ![]() and
and ![]() as follows:
as follows:
![]() (8)
(8)
This approach is named Linear MMSE because the estimated channel matrix is a linear weighted combination of received signals.
The classical solution for problem (8) is applicable for SISO, SIMO and MIMO scenarios. In these cases, an arbitrary estimated channel matrix ![]() is calculated based on the cross-correlation between
is calculated based on the cross-correlation between ![]() and the received signal Y, namely matrix
and the received signal Y, namely matrix![]() , the inverse of the autocorrelation of
, the inverse of the autocorrelation of![]() , i.e.,
, i.e., ![]() , and the proper received signal
, and the proper received signal ![]() [10] :
[10] :
![]() (9)
(9)
A more detailed description of the classic LMMSE definition is written on Appendix A.
The novelty regarding the CRN channel estimation is the adaptation of Equation (9) to MU-MISO-CRN scenarios. Such analysis presents some peculiarities that must be properly unveiled. Considering the ideal synchronized received signal with orthogonal training sequences1, Equation (3), it is necessary to adapt the classic cross-correlation2 and autocorrelation matrix from (9) for the MISO-CRN, where there exists two major series of pilot sequences and channel matrix. Indeed, the following has to be calculated:
![]() (10)
(10)
![]() (11)
(11)
where the correlation matrix![]() ,
, ![]() ,
, ![]() and
and ![]() have the following specific forms:
have the following specific forms:
![]() (12)
(12)
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
The above result, even though obtained for a synchronous case, describes that for underlay CRN it is strictly necessary knowledge of both primary and secondary pilot sequences and channel variances. This interesting result puts some serious constraints regarding possible standards to regulate the CR transmission scheme: primary users, apart from allowing secondary users to transmit over a specific bandwidth, must at least share its pilot sequence indexes in order to allow SUs to efficiently design precoders/decoders while avoiding (or smartly reducing) possible interferences.
Until now, two estimation methods have been studied: the classic LS and LMMSE. The LS can be straight forwardly applied to MISO-CRN; however, the above research unveiled that LMMSE needs some special care regarding knowledge of pilot sequences and signals statistics. The next step is to apply these results to precoder ZFWF studied in [3] , which requires knowledge of ![]() and
and ![]() to optimally design a precoder to maximize the sum capacity of a CRNs.
to optimally design a precoder to maximize the sum capacity of a CRNs.
Data Transmission in DL
This work has already revealed that SUs must know the primary pilot sequence and channel variance, apart from its pilot sequence, to accurately estimate the channel matrix via LMMSE estimation. Additionally, this Section intended to study the effect of channel estimation error on the CR transmissions. Notice that two estimation algorithms can be derived for UL channel estimation from the previous section 2, which results in four CR channel estimation matrices, ![]() ,
, ![]() ,
, ![]() and
and![]() . These results will now be used to design efficient precoders according to [3] , which is summarized by the optimization problems in ( [3] , Equations (15)-(17)). Even though the channel estimation is proceeded during the uplink transmission, all collected data and estimated channel matrix can be used for a downlink transmission, once the coherence time has been considered greater than a frame transmission period. This is known as the uplink-downlink duality, which says the channel matrix estimations obtained during uplink can be transposed and deployed for a downlink transmission purpose, with sum power constraint modification [12] [13] .
. These results will now be used to design efficient precoders according to [3] , which is summarized by the optimization problems in ( [3] , Equations (15)-(17)). Even though the channel estimation is proceeded during the uplink transmission, all collected data and estimated channel matrix can be used for a downlink transmission, once the coherence time has been considered greater than a frame transmission period. This is known as the uplink-downlink duality, which says the channel matrix estimations obtained during uplink can be transposed and deployed for a downlink transmission purpose, with sum power constraint modification [12] [13] .
In the DL transmission, for the purpose of data transmission, the nBS antenna CR-BS broadcasts the signal to K SUs, while M PUs are constantly transmitting, as described in Figure 3(b). With the purpose of maximizing the sum capacity, the CR-BS employs a ZFWF precoder ![]() based on the previous obtained channel matrix estimations
based on the previous obtained channel matrix estimations ![]() and
and ![]() in a same way of ( [3] , Equation (13)), having the following form:
in a same way of ( [3] , Equation (13)), having the following form:
![]() (16)
(16)
where the pseudo-inverse matrix ![]() is the ZF solution given as:
is the ZF solution given as:
![]() (17)
(17)
and ![]() is based on the estimated PU’s and SU’s channel matrices. Besides, the vector
is based on the estimated PU’s and SU’s channel matrices. Besides, the vector ![]() is an optimal power allocation resultant from the WF algorithm, which has been described by [3] , Equation (17)].
is an optimal power allocation resultant from the WF algorithm, which has been described by [3] , Equation (17)].
The above precoder is a sub-optimal solution for the sum capacity problem. Once the optimal one is based on perfect channel state information at the transmitter, if an estimated version of ![]() or
or ![]() is used, the ZF does not completely forces inter users interferences and, consequently, the WF algorithm is erroneously applied to non-parallel channels. Hence, the received signal at k-th SU when the ZFWF precoder is not perfectly designed presents interference from others SUs and PUs and is given by:
is used, the ZF does not completely forces inter users interferences and, consequently, the WF algorithm is erroneously applied to non-parallel channels. Hence, the received signal at k-th SU when the ZFWF precoder is not perfectly designed presents interference from others SUs and PUs and is given by:
![]() (18)
(18)
where ![]() a transmitted symbol destined to SU k,
a transmitted symbol destined to SU k, ![]() is the associated sub-optimal precoder,
is the associated sub-optimal precoder, ![]() is the j-th PU transmitted symbol,
is the j-th PU transmitted symbol, ![]() is the complex channel gain relating PU j and SU k and
is the complex channel gain relating PU j and SU k and ![]() is the AWGN. All information symbols are normalized, i.e.,
is the AWGN. All information symbols are normalized, i.e.,![]() ; hence, the kth transmitted power is determined only by the precoder
; hence, the kth transmitted power is determined only by the precoder![]() .
.
An important point to be considered in CRN is the absence of knowledge about primary transmission information. Indeed, SUs have to lead with a constant interference coming from PUs. For sake of simplicity, once PUs are considered to be always transmitting, an average constant interference power ![]() can be used instead of determining
can be used instead of determining![]() . For a large number of PU’s or antennas, the interference can be considered Gaussian distributed. Even though this assumption is not so accurate for fewer antennas/users, it will be used to model the interference power, which will be incorporated into the noise term in (18), such that the noise variance is increased,
. For a large number of PU’s or antennas, the interference can be considered Gaussian distributed. Even though this assumption is not so accurate for fewer antennas/users, it will be used to model the interference power, which will be incorporated into the noise term in (18), such that the noise variance is increased,![]() . Consequently, the received signal at k-th SU can be simplified as:
. Consequently, the received signal at k-th SU can be simplified as:
![]() (19)
(19)
As seen in (19), every k-th SU link is subject to interference from SU’s and additive noise. Hence, the signal to interference plus noise ratio (SINR) of SU k is ready defined as:
![]() (20)
(20)
where the notation ![]() comes from the channel error estimation impact on the precoder vector calculation. Consequently, the sum capacity of the K active SUs is written as:
comes from the channel error estimation impact on the precoder vector calculation. Consequently, the sum capacity of the K active SUs is written as:
![]() (21)
(21)
Notice that, when perfect channel state information is attained at the transmitter side, ![]() ,
, ![]() and the precoder is optimally designed (
and the precoder is optimally designed (![]() ). As a consequence, the ZF stage will perfectly force interferences to zero and (20) will be reduced to:
). As a consequence, the ZF stage will perfectly force interferences to zero and (20) will be reduced to:
![]() (22)
(22)
The impact of imperfect channel estimation will be quantized and compared to the ideal case in the next section. As mentioned before, all mathematical discussion was based on synchronous transmission at the uplink and use of orthogonal pilot sequences, which eases the process of finding a closed solution for all channel estimators. However, this is not a realistic scenario. In order to corroborate our theoretical findings and verify how harmful the imperfect channel estimation actually is, the presented numerical results considering asynchronous reception and non-orthogonal pilot sequences are analyzed in the sequel and compared to the ideal case.
4. Numerical Results
All numerical results presented in this section aim to analyze and quantify the effect of imperfect channel estimation on the sum capacity optimization problem. In order to do so, a block fading channel model will be considered, where the channel coefficients remain static for a period of at least T + 1 symbols [14] . Indeed, results from channel estimation during N symbols can be fairly used on downlink transmission.
Basically two scenarios will be analyzed in this Section. Firstly, a potential market for CR technologies, which is the use of white spaces to offer reliable bandwidth to emergency and public safety communications [15] . In such scenario, there exists few users allocated around the city, but they need a reliable and constant link to communicate in case of an emergency. Secondly, a network with greater spatial diversity will be considered, which illustrates, for example, a sensor network with many sensors and one central multi antenna CR-BS.
Apart from considering two potential markets for CRN, this section will also analyze the effect of asynchronous transmitter, where the received pilot sequences at CR-BS arrive delayed and overlapped. A comparison between the classical LS and the adapted LMMSE for synchronous and asynchronous transmitter with two different pilot sequences sets, Walsh-Hadamard (W-H) and Gold codes will be employed to simulate the results in terms of sum capacity and capacity loss. For all synchronous cases, the Walsh-Hadamard code sequences have been used, once it was proved in [11] to present the better performance. However, for the asynchronous situation, W-H codes actually degrade the transmission. As a consequence, for all asynchronous CRNs scenarios simulations the Gold sequences were deployed.
4.1. White Spaces—Sparse Scenarios
The first simulation makes use of the ideal case with synchronous transmission and orthogonal pilot sequence in low-density user scenarios. The chosen pilot sequence set is the W-H with ![]() symbols for a configuration with
symbols for a configuration with![]() ,
, ![]() and
and ![]() with varying uplink SINR (estimation). It is expected that higher uplink SINR scenarios lead to more accurate channel estimative; consequently, the precoder matrix is more efficiently designed and higher capacity is achieved. In order to analyze this effect, Figure 4(a) presents the sum capacity for a MU-MISO CRN, where the channel estimation has been proceeded with LS or LMMSE methods. For this simulation, the capacity curves were averaged over 1000 Monte Carlo trials.
with varying uplink SINR (estimation). It is expected that higher uplink SINR scenarios lead to more accurate channel estimative; consequently, the precoder matrix is more efficiently designed and higher capacity is achieved. In order to analyze this effect, Figure 4(a) presents the sum capacity for a MU-MISO CRN, where the channel estimation has been proceeded with LS or LMMSE methods. For this simulation, the capacity curves were averaged over 1000 Monte Carlo trials.
The perfect CSI case in Figure 4 (blue solid line) consists of designing the precoder matrix ![]() assuming
assuming![]() . As expected, a channel estimation in lower uplink SINR scenarios leads to poorer capacity for the downlink transmission. It is firstly observed that channel estimation causes a great decrease in the sum capacity. As expected, the lower uplink SINR is used, the poorer capacity. Usually, transmission systems seek to operate at high SINRs to estimate the channel, which imposes less interference and, consequently, a more accurate estimative.
. As expected, a channel estimation in lower uplink SINR scenarios leads to poorer capacity for the downlink transmission. It is firstly observed that channel estimation causes a great decrease in the sum capacity. As expected, the lower uplink SINR is used, the poorer capacity. Usually, transmission systems seek to operate at high SINRs to estimate the channel, which imposes less interference and, consequently, a more accurate estimative.
The asynchronous case presented in Figure 4(b) considers 10% delayed received signals and non-orthogonal pilot sequences. Comparison of both solid and dotted lines of Figure 4(b) corroborates, as expected, de-synchronization and correlated sequences significantly negatively impact the sum capacity.
Considering the perfect CSI capacity as ![]() and that capacity
and that capacity ![]() achieved using precorders with imperfect channel estimations
achieved using precorders with imperfect channel estimations![]() ; hence, the capacity loss is expressed simply by:
; hence, the capacity loss is expressed simply by:
![]() (23)
(23)
![]()
Figure 4. Sum capacity for different values of ![]() at the uplink channel estimation process for a MU-MISO CRN with
at the uplink channel estimation process for a MU-MISO CRN with![]() .
.
Figure 5 expresses the capacity loss for every CRN system configuration previously analyzed. It is observed that, the more accurate channel estimator is used, the higher capacity is achieved (Figure 4), and the higher capacity loss is resultant. However, once all cases with use of estimated channels limit the maximum system capacity, for high downlink SINR values the capacity loss increases significantly. Figure 5(a) shoes that there is not a significant improvement from LS to LMMSE in therms of capacity loss. In addition, comparing the capacity losses in Figure 5(a) and Figure 5(b), one can conclude that for high quality SINR scenarios the de-synchronization does not poses great harm; however, it significantly impacts on the capacity loss when the CRN system operates under low SINR scenarios. Indeed, under low γ’s the capacity losses in Figure 5(b) are significant when compared with the synchronous case of Figure 5(a).
Analysis of both figures shows that the uplink SINR imposes a capacity limit on downlink transmissions. In all cases, for higher downlink SINR values, the capacity loss increases significantly. Even though the estimation is done with![]() , the capacity loss overcomes 10%. This comes from the fact that, with perfect channel estimation, the precoder optimally allocates power for all users; however, LS and LMMSE estimators necessary imply in imperfect PU’s and SU’s channel matrix estimations, and consequently, they are not optimal.
, the capacity loss overcomes 10%. This comes from the fact that, with perfect channel estimation, the precoder optimally allocates power for all users; however, LS and LMMSE estimators necessary imply in imperfect PU’s and SU’s channel matrix estimations, and consequently, they are not optimal.
Previous analyses of Figure 4 and Figure 5 prove that channel estimation poses a very important point on CRN, once it significantly impacts the results of precoder design; consequently, performance and capacity will also be affected. Once, in real scenarios, the synchronization is impossible to be achieved, transceivers and CR-BS must design robust precoders and decoders able to tackle with such unavoidable interference.
![]()
Figure 5. Capacity loss for different values of ![]() at the uplink channel estimation process for a MU-MISO CRN with
at the uplink channel estimation process for a MU-MISO CRN with![]() .
.
4.2. Sensor Network—High Spatial Diversity
Similar to previous results, in this subsection, the effect of channel estimation under a few different circumstances will be analyzed, i.e., under massive number of CR-BS antennas and a high number of SU’s nodes. However, we will explore a greater diversity scenario, where the asynchronous transmission condition has chances of lowering even more the sum capacity.
Firstly, from Figure 6, it is observed that not only the overall DL capacity increases remarkably, but also the difference between the curves resultant from LS and LMMSE. Previously, both techniques had similar impact on sum capacity![]() . However, in this scenario the LMMSE algorithm shows a significant decrease in capacity performance compared to LS estimator. Such LMSE difference in performance is even more pronounced for low SINR’s.
. However, in this scenario the LMMSE algorithm shows a significant decrease in capacity performance compared to LS estimator. Such LMSE difference in performance is even more pronounced for low SINR’s.
Also, observation of Figure 7 reinforce that, for CRN systems with greater spatial diversity the use of Gold sequence sets, which has been proven to be better than W-H sets for asynchronous transmission system [11] , result in similar sum capacity for MU-MISO CRN. Simulations proved that, for this scenario configuration, the LMMSE has been presented better results in terms of sum capacity. As consequence, if only sum capacity is desired to be maximized, LMMSE showed to be the best option due its greater resultant sum capacity. Its However, the tradeoff capacity and complexity has to be analyzed, once the LMMSE algorithm needs some extra knowledge about pilot sequence and channel statistics if compared to LS technique.
![]()
Figure 6. Sum capacity for different values of ![]() at the uplink channel estimation process for a MU-MISO CRN with
at the uplink channel estimation process for a MU-MISO CRN with![]() .
.
![]()
Figure 7. Capacity loss for different values of ![]() at the uplink channel estimation process for a MU-MISO CRN with
at the uplink channel estimation process for a MU-MISO CRN with![]() .
.
5. Conclusions
A full duplex MISO-CRN wireless transmission has been studied, where channel estimation has proceeded at the uplink in order to offer means for accurate precoding design at the downlink side. As observed, the precoder performance is directly related to the channel estimative accuracy; this makes a reliable channel estimation process indispensable for CR communications.
This work has proposed and analyzed two CRN channel estimation techniques based on LS and MMSE methods, and the impact on the precoder design has been quantified. Numerical simulation results demonstrated that the estimation process must be done under high values of uplink SINR in order to offer means for an accurate estimation. This is seen from the difference in capacity loss for cases with ![]() and
and![]() , where the lower SINR case resulted in over 20% of capacity loss.
, where the lower SINR case resulted in over 20% of capacity loss.
The theory beyond LMMSE has been firstly adapted in such a way to show that any cognitive device that wishes to make use of ZFWF precoder proposed in [3] must know primary and secondary pilot sequences and its statistics. This finding has been proved to happen when orthogonal code sequences and synchronous transmitters are deployed; however, numerical results proved that case with asynchronous transmitters and Gold sequence sets do not offer great deterioration on the sum capacity.
To sum up, this work has analyzed the impact of channel estimation errors on the MISO-CRN system in order to demonstrate that an accurate training process is essential to designing suitable precoders.
Acknowledgements
This work was supported in part by the National Council for Scientific and Technological Development (CNPq) of Brazil under Grants 310681/2019-7, and in part by Coordenação de Aperfeiçoamento de Pessoal de Nível Superior, Brazil (scholarship), and by the Londrina State University-Paraná State Government (UEL).
Appendix A. Linear Minimum Mean Squared Error Channel Estimator Derivation
Consider a SISO transmission where N pilot symbols are transmitted. The received signal is![]() . The LMMSE estimator
. The LMMSE estimator![]() , whith
, whith![]() , is a weighted linear combination of received signals and the vector
, is a weighted linear combination of received signals and the vector ![]() is such that minimizes the mean squared error
is such that minimizes the mean squared error![]() .
.
The MSE is written as:
![]()
The vector ![]() that minimizes the MSE is found when setting
that minimizes the MSE is found when setting ![]() to zero:
to zero:
![]()
![]()
Hence, the LMMSE for a SISO scenario is finally written as:
![]()
NOTES
1Note that this case is specific for synchronized SU’s and/or PU’s transmitters, once no overlapping between consecutive samples is considered in such received signal expression. Even though this characterizes a not completely realistic configuration, it makes simpler the process of developing mathematic expressions for both estimated channels. The numerical results in Section 3 will present some analysis regarding non-synchronized transmitters and also non-orthogonal training sequences.
2The analysis of effect of non-orthogonal training sequences will be done with help of Gold sequences, which has already been proved to offer better performance results in realistic asynchronous scenarios if compared to other non-orthogonal sequences [11] .