Backstepping-Based Distributed Abnormality Detection for Nolinear Parabolic Distributed Prameter Systems

Lei Chen

School of Mathematics and Statistics, Shandong Normal University, Jinan, China.

DOI: 10.4236/eng.2022.147023                

Abstract

In this paper, we proposed a model-based abnormality detection scheme for a class of nonlinear parabolic distributed parameter systems (DPSs). The proposed methodology consists of the design of an observer and an abnormality detection filter (ADF) based on the backstepping technique and a limited number of in-domain measurements plus one boundary measurement. By taking the difference between the measured and estimated outputs from observer, a residual signal is generated for fault detection. For the detection purpose, the residual is evaluated in a lumped manner and we propose an explicit expression for the time-varying threshold. The convergence properties of the PDE observer and the residual are analyzed by Lyapunov stability theory. Eventually, the proposed abnormality detection scheme is demonstrated on a nonlinear DPS.

Keywords

Abnormality Detection, Backstepping, Nonlinear Parabolic Systems, Distributed Parameter Systems, Lyapunov Function

1. Introduction

With the mechanization and intellectualization of production and life, complex nonlinear control system is widely used in chemical industry [1], transportation system [2] and other fields [3]. To improve the reliability and availability of complex dynamic system in industrial assembly line, abnormality detection in industrial process described by distributed parameter system (DPS) is of vital importance [4]. The DPSs are usually modeled by partial differential equation (PDE). The most unique characteristic of DPS is that the state variables change in both time and space domains, which makes the traditional ordinary differential equation (ODE) unable to accurately describe its dynamic behavior. Distribution abnormalities have been extensively studied in the literature. For example, the distributed thermal failure of lithium-ion batteries studied by Dey et al. in [5] [6] may lead to battery degradation and failure, which belongs to distribution abnormality.

For actuator failures in the domain, this is a special case of abnormal distribution. El-Farra and Ghantasala discussed in [7] that the actuator failures in the diffusion reaction process widely exist in chemical processes. Abnormal behavior or events in DPS can lead to controller failures or unexpected system responses, which are detrimental to the safe and reliable operation of the system. Without loss of generality, according to the research results of Dey, Perez and Moura in [5] [6], the fault of the dynamic system in the model can be classified as the abnormal term $s\left(x,t\right)$ in the equation. Considering the spatial distribution characteristics of state variables in DPS, we can regard the distributed abnormalities discussed in the above literature as general distribution faults in fault diagnosis (FD).

In recent years, Dey et al. in [6] and Ghantasala et al. in [8] have made remarkable research results on FD problems of DPS. Ferdowsi and Jagannathan constructed the fault diagnosis observer of DPS by using the direct representation of PDE of the system, and realized the fault diagnosis of DPS of a class of parabolic PDE [9]. At the same time, observer-based fault detection methods have been widely used in linear systems and some important studies have been made in [10] [11] [12]. For example, Cai, Ferdowsi and Sarangapani constructed a new model-based fault detection method in [13], in which a state observer was constructed based on the boundary measurements of the original PDE system. Later, through the unremitting efforts of scientific researchers, the observer-based fault detection method was introduced into the study of nonlinear system fault detection, and many remarkable research results were obtained in [14] [15] [16]. In [16], a comprehensive design scheme of observer-based fault detection system is proposed for a nonlinear system. The above mentioned fault diagnosis work is put forward under model-based. The existing model-based DPS fault detection and diagnosis methods can be roughly divided into two categories: one is the finite-dimensional ODE representation of DPS, that is, the early lumped design; the other is based on the original PDE system, that is, the late lumped design. However, the DPS fault detection and adjustment scheme using finite-dimensional ODE to approximate PDE model may lead to missed detection and false alarms due to the model reduction [17] [18]. In [19], Lei et al. studied the spatial-temporal fault detection problem of a class of nonlinear reaction-diffusion equations by using the linear matrix inequalities (LIMs) method. Feng, Li and Yang studied the distributed fault estimation problem of parabolic DPS in [20] through cumbersome early lumped design. However, due to the neglect of the remaining infinite-dimensional dynamical system in the design stage, observation overflow will occur, which will seriously affect the estimation performance. Although we need a large number of in-domain measurements to achieve satisfactory performance, it is almost impossible to achieve full-state measurements in industrial processes. Recently, Ferdowsi and Cai studied the problem of fault detection and estimation for a class of nonlinear DPS in [21], in which the method of parameter updating law is adopted to estimate the fault function. Feng, Wang et al. in [22] studied a class of distributed anomaly location for linear DPS through a limited number of measurements. On this basis, the nonlinear term is introduced to further discuss the problem of abnormality detection in DPS.

Based on the works aforementioned, the nonlinear term is introduced into the system discussed in this paper, and the anomaly detection problem of the system is further discussed. This paper constructs an ADF for the detection of distribution abnormalities by using a finite number of in-domain measurements plus one boundary measurement. The distribution abnormality term $s\left(x,t\right)$ is defined as the unknown distribution term containing all functions of unknown form in the space. When there is an abnormality in the system, the dynamics of nonlinear DPS will change, resulting in the system output deviation from the estimated state given by the observer, and thus the detection residual will increase. Once the detection residuals exceed the predefined detection threshold, the system is considered to be abnormal. According to the effectiveness of backstepping method in observer design in [23] [24] [25], this paper applies it to the design of ADF. Moreover, since early lumping technique is not used, there is no observation overflow problem at the design stage. Combined with the treatment of nonlinear term in the research of nonlinear DPS in [21], this method is extended to the system studied in this paper.

In summary, this paper provides an abnormality detection scheme for a class of nonlinear parabolic DPSs. The main contributions of this paper are as follows:

1) Abnormality detection of nonlinear DPS is realized by the assumption processing of the nonlinear function in the system;

2) Based on backstepping method and finite measured values, an ADF with time-varying threshold is designed to avoid false alarms in abnormality detection;

3) By Lyapunov function method instead of operator theory, the amount of computation is reduced effectively, which is more conducive to the application of practical engineering production.

The rest of this paper is summarized as follows. In Section 2, relevant preparatory knowledge and the system problem statement are introduced. The ADF design and lumped residual evaluation are proposed in Section 3. In Section 4, a nonlinear DPS example is given to illustrate the effectiveness of the proposed scheme. Finally, we summarize this paper in Section 5.

2. Problem Statement

The notations used in this paper are standard. $ℝ$ and $ℝ$ represent the set of all real numbers and n dimensional Euclidean spaces, respectively, and their norm is expressed as $\Vert \cdot \Vert$. $\left|u\right|$ denotes the absolute value of u for any $u\in ℝ$. The function1 $u\left(x\right)$ is square integrable on the Hilbert space $L^2\left(\left[0,1\right]\right)\triangleq L^2\left(\left[0,1\right];ℝ\right)$ with the corresponding norm

${\Vert u(\cdot )\Vert }_2=\sqrt{{\displaystyle {\int }_0^1{u}^2\left(x\right)\text{d}x}}$

The spatial $L^{\infty }$ norm is defined as ${\Vert u(\cdot )\Vert }_2=\underset{x\in \left[0,1\right]}{\max }\left|u\left(x\right)\right|$. $u_t=\partial u/\partial t$,

$u_x=\partial u/\partial x$, $u_{xx}={\partial }^{2}u/\partial x^2$.

Now we recall some useful inequalities we will use in the following sections.

· Young’s inequality: For $a,b,\lambda \in ℝ$ with $\lambda >0$, then

$ab\le \frac{\lambda }{2}{a}^2+\frac{1}{2\lambda }{b}^2$, $ab\le -\frac{\lambda }{2}{a}^2-\frac{1}{2\lambda }{b}^2$.

· Cauchy-Schwarz inequality:

${\displaystyle {\int }_0^1{f}_1\left(x\right)f_2\left(x\right)\text{d}x}\le {\Vert f_1\left(x\right)\Vert }_2{\Vert f_2\left(x\right)\Vert }_2$,

where $f_1\left(x\right),f_2\left(x\right)\in L^2\left(\left[0,1\right]\right)$.

· Agmon’s inequality:

$\underset{x\in [0,1]}{\max }{\left|u\left(x\right)\right|}^2\le u^2\left(0\right)+2{\Vert u\Vert }_2{\Vert u_x\Vert }_2$,

$\underset{x\in [0,1]}{\max }{\left|u\left(x\right)\right|}^2\le u^2\left(1\right)+2{\Vert u\Vert }_2{\Vert u_x\Vert }_2$,

where $u\left(x\right)\in L^2\left(\left[0,1\right]\right)$.

In this paper, we consider a class of nolinear DPSs described by the following parabolic PDE in one spatial dimension:

$\{\begin{array}{l}{u}_t\left(x,t\right)=u_x\left(x,t\right)+Q\left(x,t\right)+f\left(u,x\right)+d\left(x,t\right)+s\left(x,t\right),\text{}x\in \left[0,1\right],t>0\text{}\\ y\left(t\right)={\displaystyle {\int }_0^{1}c\left(x\right)u\left(x,t\right)\text{d}x},t\ge 0,\\ c\left(x\right)={\left[\delta \left(x-0\right),\delta \left(x-x_1\right),\cdots ,\delta \left(x-x_N\right)\right]}^{\text{T}},\end{array}$ (2.1)

subject to the following boundary conditions

$\{\begin{array}{l}{u}_x\left(0,t\right)=0,t\ge 0,\\ u\left(1,t\right)=0,t\ge 0,\end{array}$ (2.2)

and initial condition

$u\left(x,0\right)=u_0\left(x\right),x\in \left[0,1\right]$, (2.3)

where $u\left(\cdot ,t\right)\in L^2\left(\left[0,1\right]\right)$ denotes the state variable; $f\left(u,x\right)\in L^2\left(\left[0,1\right]\right)$ is Lipschitz continuous function. $Q\left(x,t\right)$, $d\left(x,t\right)$ and $s\left(x,t\right)$ denote a continuous distributed input, an unknown continuous distributed disturbance and an unknown continuous distributed abnormality. $\delta (\cdot )$ is a Dirac distribution [26]; $y\left(t\right)\in {ℝ}^{N+1}\left(N\ge 1\right)$ is N in-domain pointwise measurements ( $0<x_1<\cdots <x_N<1$ ) plus one boundary measurement $u\left(0,t\right)$.

Assumption 2.1. The distributed disturbance $d\left(x,t\right)$ in the system is bounded in the sense of $L^2$ norm, i.e.

${\Vert d\left(\cdot ,t\right)\Vert }_2\le \bar{d}$,

where $\bar{d}>0$ is a known constant.

Assumption 2.2. The nonlinear function $f\left(u,x\right)$ satisfies the following conditions:

· $f\left(u,x\right)$ is Lipschitz continuous in u and $x\in \left[0,1\right]$, $t\ge 0$, $u\left(x\right)\in L^2\left(\left[0,1\right]\right)$.

· $f\left(u,x\right)$ should satisfy

$f\left(u+\Delta u,x\right)-f\left(u,x\right)=\frac{\partial f\left(u,x\right)}{\partial u}\Delta u+{\epsilon }_f\left(\Delta u,x\right)$ (2.4)

where Δu represents a small change in u and ${\epsilon }_f\left(\Delta u,x\right)$ is the approximation error satisfying ${\Vert {\epsilon }_f\Vert }_{2,n}\le {\bar{\epsilon }}_f$, and note that ${\bar{\epsilon }}_f$ is a constant.

In particular, when the nonlinear function $f\left(u,x\right)$ satisfies

$f\left(u+\Delta u,x\right)-f\left(u,x\right)=\frac{\partial f\left(u,x\right)}{\partial u}\Delta u$ (2.5)

i.e. ${\epsilon }_f\left(\Delta u,x\right)=0$, and from that ${\bar{\epsilon }}_f=0$ can be obtained.

Assumption 2.3. The system (2.1) is controllable, and there is a control $Q\left(t\right)$, which can guarantee system stability before and after abnormality.

3. Abnormality Detection Scheme

In this paper, we design an ADF for abnormality detection in time domain by using a limited number of measurements (including a boundary measurement) on system (2.1) with boundary condition (2.2) and initial value (2.3). This section mainly includes two parts, one is the design of observer, the other is the design of ADF and lumped residual evaluation.

3.1. Observer Design

We construct the following observer for system (2.1):

$\{\begin{array}{l}{\hat{u}}_t\left(x,t\right)={\hat{u}}_{xx}\left(x,t\right)+Q\left(x,t\right)+p_1\left(x\right)\left(u\left(0,t\right)-\hat{u}\left(0,t\right)\right)+f\left(\hat{u},x\right),x\in \left[0,1\right],t>0,\\ \hat{y}\left(t\right)={\displaystyle {\int }_0^{1}c\left(x\right)\hat{u}\left(x,t\right)\text{d}x},t>0,\\ {\hat{u}}_x\left(0,t\right)=p_{10}\left(u\left(0,t\right)-\hat{u}\left(0,t\right)\right),t>0,\\ \hat{u}\left(1,t\right)=0,t>0,\end{array}$ (3.1)

where $p_1\left(x\right)$ and $p_{10}$ denote the observer gains to be determined. Then we can design an ADF for time domain detection first by constructing the following residual $r\left(t\right)$ :

$r\left(t\right)\triangleq y\left(t\right)-\hat{y}\left(t\right),t\ge 0$. (3.2)

By introducing the error variables

$\tilde{u}\left(x,t\right)=u\left(x,t\right)-\hat{u}\left(x,t\right)$,

and combining (2.1), (2.2), (3.1), we can obtain the following error system $\tilde{u}\left(x,t\right)$ :

$\begin{array}{l}{\tilde{u}}_t\left(x,t\right)={\tilde{u}}_{xx}\left(x,t\right)-p_1\left(x\right)\tilde{u}\left(0,t\right)+s\left(x,t\right)+d\left(x,t\right)+f\left(u,x\right)-f\left(\tilde{u},x\right),x\in \left[0,1\right],t>0,\\ r\left(t\right)={\displaystyle {\int }_0^{1}c\left(x\right)\tilde{u}\left(x,t\right)\text{d}x},t>0,\\ {\tilde{u}}_x\left(0,t\right)=-p_{10}\tilde{u}\left(0,t\right),t>0,\\ \tilde{u}\left(1,t\right)=0,t>0.\end{array}$ (3.3)

It should be noted that from Assumption 2.2, we can have $A\left(x,t\right)={\frac{\partial f\left(u,x\right)}{\partial u}|}_{u=\hat{u}}$ through $f\left(u,x\right)-f\left(\hat{u},x\right)={\frac{\partial f\left(u,x\right)}{\partial u}|}_{u=\hat{u}}\tilde{u}\left(x,t\right)+{\epsilon }_f\left(\tilde{u},x\right)$. So the above error system (3.3) can be rewritten as

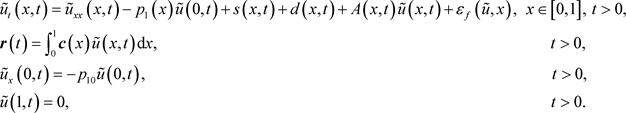(3.4)

Note that the term $A\left(x,t\right)\tilde{u}\left(x,t\right)$ in the observer error dynamics described by (3.4) can make the system to be unstable when $A\left(x,t\right)\tilde{u}\left(x,t\right)$ become positively large.

We can eliminate $A\left(x,t\right)\tilde{u}\left(x,t\right)$ by the Volterra integral transformation [25] and obtain the observer gain by the following lemma.

Lemma 3.1. ( [25]) By the following Volterra integral transformation:

$\tilde{u}\left(x,t\right)=\tilde{\omega }\left(x,t\right)-{\displaystyle {\int }_0^{1}L\left(x,\tau ,t\right)\tilde{\omega }\left(\tau ,t\right)\text{d}\tau },$ (3.5)

where $L\left(x,\tau ,t\right)$ is the unique solution of (3.7), the error system (3.4) is transformed into the following target $\tilde{\omega }$ system

$\{\begin{array}{l}{\tilde{\omega }}_t\left(x,t\right)={\tilde{\omega }}_{xx}\left(x,t\right)-b\tilde{\omega }\left(x,t\right)+d_M\left(x,t\right)+s_M\left(x,t\right)+{\epsilon }_{f_M}\left(\tilde{u},x\right),\\ {\tilde{\omega }}_x\left(0,t\right)=0,\\ \tilde{\omega }\left(1,t\right)=0,\end{array}$ (3.6)

where $b>0$ is an constant; $x\in \left[0,1\right]$ is the spatial coordinate; $t\in \left[0,\infty \right]$ is the time and

$\begin{array}{l}s\left(x,t\right)=s_M\left(x,t\right)-{\displaystyle {\int }_0^{x}L\left(x,\tau ,t\right)s_M\left(\tau ,t\right)\text{d}\tau },\\ d\left(x,t\right)=d_M\left(x,t\right)-{\displaystyle {\int }_0^{x}L\left(x,\tau ,t\right)d_M\left(\tau ,t\right)\text{d}\tau },\\ {\epsilon }_f\left(x,t\right)={\epsilon }_{f_M}\left(x,t\right)-{\displaystyle {\int }_0^{x}L\left(x,\tau ,t\right){\epsilon }_{f_M}\left(\tau ,t\right)\text{d}\tau }.\end{array}$

Lemma 3.2. ( [25]) The gain kernel $L\left(x,\tau ,t\right)$ is the solution to the well-posed PDE given by

$\{\begin{array}{l}\frac{\partial L\left(x,\tau ,t\right)}{\partial t}=A\left(x,t\right)L\left(x,\tau ,t\right)+bL\left(x,\tau ,t\right)+\frac{{\partial }^{2}L\left(x,\tau ,t\right)}{\partial {\tau }^2}-\frac{{\partial }^{2}L\left(x,\tau ,t\right)}{\partial x^2},\\ L\left(1,\tau ,t\right)=0,\\ L\left(x,x,t\right)=\frac{x-1}{2}\left[A\left(x,t\right)+b\right],\end{array}$ (3.7)

where $b>0$ is an constant and $A\left(x,t\right)$ is defined in (2.4). The observer gains can be obtained as obtained

$\{\begin{array}{l}{p}_1\left(x,t\right)=\frac{\partial L\left(x,0,t\right)}{\partial \tau },\\ p_{10}\left(t\right)=L\left(0,0,t\right).\end{array}$ (3.8)

Lemma 3.3. ( [25]) $M\left(x,\eta ,t\right)$ is the gain kernel of the following inverse transformation

$\tilde{\omega }\left(x,t\right)=\tilde{u}\left(x,t\right)+{\displaystyle {\int }_0^{x}M\left(x,\eta ,t\right)\tilde{u}\left(\eta ,t\right)\text{d}\eta }.$

Remark 3.1. By the inverse transformation in Lemma 3.3, we can deduce the explicit representation of $d_M$, ${\epsilon }_{f_M}$

$\begin{array}{l}{d}_M\left(x,t\right)=d\left(x,t\right)+{\displaystyle {\int }_0^{x}M\left(x,\eta ,t\right)d\left(\eta ,t\right)\text{d}\eta },\\ {\epsilon }_{f_M}\left(x,t\right)={\epsilon }_f\left(x,t\right)+{\displaystyle {\int }_0^{x}M\left(x,\eta ,t\right){\epsilon }_f\left(\eta ,t\right)\text{d}\eta }.\end{array}$

By trigonometric inequality, we have

$\begin{array}{l}{\Vert d_M\left(x,t\right)\Vert }_2\le {\Vert d\left(x,t\right)\Vert }_2+{\Vert {\displaystyle {\int }_0^{x}M\left(x,\eta ,t\right)d\left(\eta ,t\right)\text{d}\eta }\Vert }_2,\\ {\Vert {\epsilon }_{f_M}\left(x,t\right)\Vert }_2\le {\Vert {\epsilon }_f\left(x,t\right)\Vert }_2+{\Vert {\displaystyle {\int }_0^{x}M\left(x,\eta ,t\right){\epsilon }_f\left(\eta ,t\right)\text{d}\eta }\Vert }_2.\end{array}$

Moreover, it can be derived that

${\Vert {\displaystyle {\int }_0^{x}M\left(x,\eta ,t\right){\epsilon }_f\left(\eta ,t\right)\text{d}\eta }\Vert }_2\le \bar{M}\bar{d}$,

where $\bar{M}=\underset{0\le x\le 1}{\max }{\Vert M\left(x,\eta ,t\right)\Vert }_2$. Hence we can have

${\Vert d_M\left(x,t\right)\Vert }_2\le \left(\bar{M}+1\right)\bar{d},{\Vert {\epsilon }_{f_M}\left(x,t\right)\Vert }_2\le \left(\bar{M}+1\right){\bar{\epsilon }}_f.$

Lemma 3.4. ( [27]) Suppose V(t) and g(t) are real functions. If

$\stackrel{\dot{}}{V}\left(t\right)\le -\beta V\left(t\right)+g\left(t\right),\forall t\ge 0,$

then

$\stackrel{\dot{}}{V}\left(t\right)\le {\text{e}}^{-\beta t}V\left(0\right)+{\displaystyle {\int }_0^1{\text{e}}^{-\beta \left(t-\tau \right)}g\left(\tau \right)\text{d}\tau },\forall t\ge 0,$

where β is a finite constant.

Theorem 3.1. Considering the error dynamics (3.6), we have

1) In the presence of no disturbance and no abnormality, i.e. $d_M\left(x,t\right)=0$ and $s_M\left(x,t\right)=0$, $\tilde{\omega }$ is bounded. In particular, when the nonlinear function $f\left(u,x\right)$ satisfies (2.5), then error dynamics (3.6) can be exponentially stable.

2) In the presence of disturbance, i.e. $d_M\left(x,t\right)\ne 0$ and $s_M\left(x,t\right)=0$, $\tilde{\omega }$ is bounded.

The bounds on $\tilde{\omega }$ discussed above can be written as the following expression:

${\Vert \tilde{\omega }\left(x,t\right)\Vert }_{\infty }\le {\tilde{\omega }}_m\left(t\right)$,

where

$\{\begin{array}{l}{\tilde{\omega }}_m\left(t\right)=\sqrt{2{\text{e}}^{-2\left(b-1\right)t}V\left(0\right)+\frac{1}{\gamma \left(b-1\right)}{\left(\bar{M}+1\right)}^2{D}^2},\\ V\left(0\right)=\frac{1}{2}\left({\Vert {\tilde{\omega }}_0\Vert }_2^2+{\Vert {\tilde{\omega }}_{x0}\Vert }_2^2\right),\end{array}$ (3.9)

with $0\le \gamma \le 1$ and

$D=\{\begin{array}{l}\bar{d},d_M\left(x,t\right)=0,s_M\left(x,t\right)=0\\ \bar{d}+{\bar{\epsilon }}_f,d_M\left(x,t\right)\ne 0,s_M\left(x,t\right)=0\end{array}$ (3.10)

Proof. We consider the following Lyapunov function to analyze the error dynamics (3.6)

$V\left(t\right)=\frac{1}{2}{\displaystyle {\int }_0^1\left({\tilde{\omega }}^2\left(x,t\right)+{\tilde{\omega }}_x^2\left(x,t\right)\right)\text{d}x.}$ (3.11)

In general, from the aspects of physical meaning, Lyapunov function (3.11) represents the energy of the system we are studying. In addition, from the point of view of the mathematical calculation process, the function in the form of (3.11) can be selected to eliminate or avoid some unexpected items in the specific calculation, making the result more concise and clear.

By the integration by parts and (3.6), the derivative of V(t) can be written as

$\begin{array}{c}\stackrel{\dot{}}{V}\left(t\right)=-\left(1+b\right){\Vert {\tilde{\omega }}_x\left(x,t\right)\Vert }_2^2-b{\Vert \tilde{\omega }\left(x,t\right)\Vert }_2^2-{\Vert {\tilde{\omega }}_{xx}\left(x,t\right)\Vert }_2^2\\ +{\displaystyle {\int }_0^1\left(d_M\left(x,t\right)+{\epsilon }_{f_M}\left(x,t\right)\right)\tilde{\omega }\left(x,t\right)\text{d}x}\\ -{\displaystyle {\int }_0^1\left(d_M\left(x,t\right)+{\epsilon }_{f_M}\left(x,t\right)\right){\tilde{\omega }}_{xx}\left(x,t\right)\text{d}x}\end{array}$ (3.12)

Note that both the fourth and fifth items of (3.12) contain $d_M+{\epsilon }_{f_M}$, which is not always zero. Considering the boundness of $d_M$ and ${\epsilon }_{f_M}$, we first discuss the case when there exist disturbances, i.e. $d_M\left(x,t\right)\ne 0$ and $s_M\left(x,t\right)=0$.

Applying the Cauchy-Schwarz inequality and Young’s inequality on the fourth term of (3.12), we have

$\begin{array}{l}{\displaystyle {\int }_0^1\left(d_M\left(x,t\right)+{\epsilon }_{f_M}\left(x,t\right)\right)\tilde{\omega }\left(x,t\right)\text{d}x}\\ ={\displaystyle {\int }_0^1{d}_M\left(x,t\right)\tilde{\omega }\left(x,t\right)\text{d}x}+{\displaystyle {\int }_0^1{\epsilon }_{f_M}\left(x,t\right)\tilde{\omega }\left(x,t\right)\text{d}x}\\ \le {\left({\displaystyle {\int }_0^1{d}_M^2\left(x,t\right)\text{d}x}\right)}^{\frac{1}{2}}{\left({\displaystyle {\int }_0^1{\tilde{\omega }}^2\left(x,t\right)\text{d}x}\right)}^{\frac{1}{2}}+{\left({\displaystyle {\int }_0^1{\epsilon }_{f_M}^2\left(x,t\right)\text{d}x}\right)}^{\frac{1}{2}}{\left({\displaystyle {\int }_0^1{\tilde{\omega }}^2\left(x,t\right)\text{d}x}\right)}^{\frac{1}{2}}\\ ={\Vert d_M\left(x,t\right)\Vert }_2{\Vert \tilde{\omega }\left(x,t\right)\Vert }_2+{\Vert {\epsilon }_{f_M}\left(x,t\right)\Vert }_2{\Vert \tilde{\omega }\left(x,t\right)\Vert }_2\\ \le \frac{1}{2\gamma }\left[{\Vert d_M\left(x,t\right)\Vert }_2^2+{\Vert {\epsilon }_{f_M}\left(x,t\right)\Vert }_2^2\right]+\gamma {\Vert \tilde{\omega }\left(x,t\right)\Vert }_2^2,\end{array}$ (3.13)

where $\gamma >0$ is a positive constant. Similarly, it can be obtained that

$\begin{array}{l}{\displaystyle {\int }_0^1\left(d_M\left(x,t\right)+{\epsilon }_{f_M}\left(x,t\right)\right){\tilde{\omega }}_{xx}\left(x,t\right)\text{d}x}\\ \le \frac{1}{2\gamma }\left[{\Vert d_M\left(x,t\right)\Vert }_2^2+{\Vert {\epsilon }_{f_M}\left(x,t\right)\Vert }_2^2\right]+\gamma {\Vert {\tilde{\omega }}_{xx}\left(x,t\right)\Vert }_2^2.\end{array}$ (3.14)

Next, considering (3.13) and (3.14), we can write an upper bound for $\stackrel{\dot{}}{V}\left(t\right)$ from (3.12)

$\begin{array}{l}\stackrel{\dot{}}{V}\left(t\right)=-\left(1+b\right){\Vert {\tilde{\omega }}_x\left(x,t\right)\Vert }_2^2+\left(\gamma -b\right){\Vert \tilde{\omega }\left(x,t\right)\Vert }_2^2-\left(\gamma -1\right){\Vert {\tilde{\omega }}_{xx}\left(x,t\right)\Vert }_2^2\\ +\frac{1}{\gamma }\left[{\Vert d_M\left(x,t\right)\Vert }_2^2+{\Vert {\epsilon }_{f_M}\left(x,t\right)\Vert }_2^2\right].\end{array}$ (3.15)

Let $\gamma$ satisfy $0<\gamma \le 1$, then (3.12) can be further written as

$\begin{array}{c}V\left(t\right)\le -\left(1+b\right){\Vert {\tilde{\omega }}_x\left(x,t\right)\Vert }_2^2+\left(1-b\right){\Vert \tilde{\omega }\left(x,t\right)\Vert }_2^2+\frac{1}{\gamma }\left[{\Vert d_M\left(x,t\right)\Vert }_2^2+{\Vert {\epsilon }_{f_M}\left(x,t\right)\Vert }_2^2\right]\\ \le \left(1-b\right){\Vert {\tilde{\omega }}_x\left(x,t\right)\Vert }_2^2+\left(1-b\right){\Vert \tilde{\omega }\left(x,t\right)\Vert }_2^2+\frac{1}{\gamma }\left[{\Vert d_M\left(x,t\right)\Vert }_2^2+{\Vert {\epsilon }_{f_M}\left(x,t\right)\Vert }_2^2\right]\\ \le 2\left(1-b\right)V\left(t\right)+\frac{1}{\gamma }\left[{\Vert d_M\left(x,t\right)\Vert }_2^2+{\Vert {\epsilon }_{f_M}\left(x,t\right)\Vert }_2^2\right].\end{array}$ (3.16)

Since $b>1$, combining Remark 3.1 with Lemma 3.4, we have that

$V\left(t\right)\le {\text{e}}^{-2\left(b-1\right)t}V\left(0\right)+\frac{1}{2\gamma \left(b-1\right)}{\left(\bar{M}+1\right)}^2{D}^2,$ (3.17)

where D is defined in (3.10).

Then, applying the Agmon’s inequality and Young’s inequality, we have

$\begin{array}{c}{\Vert \tilde{\omega }\left(x,t\right)\Vert }_{\infty }^2\le 2{\Vert \tilde{\omega }\left(x,t\right)\Vert }_2{\Vert {\tilde{\omega }}_x\left(x,t\right)\Vert }_2\\ \le {\Vert \tilde{\omega }\left(x,t\right)\Vert }_2^2+{\Vert {\tilde{\omega }}_x\left(x,t\right)\Vert }_2^2\\ \le 2{\text{e}}^{-2\left(b-1\right)t}V\left(0\right)+\frac{1}{\gamma \left(b-1\right)}{\left(\bar{M}+1\right)}^2{D}^2.\end{array}$ (3.18)

Thus, it can be concluded that

${\Vert \tilde{\omega }\left(x,t\right)\Vert }_{\infty }\le \sqrt{2{\text{e}}^{-2\left(b-1\right)t}V\left(0\right)+\frac{1}{\gamma \left(b-1\right)}{\left(\bar{M}+1\right)}^2{D}^2}$ (3.19)

where $D=\bar{d}+{\bar{\epsilon }}_f$.

For another case, i.e. $d_M\left(x,t\right)=0$ and $s_M\left(x,t\right)=0$, same conclusions can be obtained by the same method and notice that D in (3.19) is $\bar{d}$.

From (3.8) and (3.10), we can deduce that $\Vert \tilde{\omega }\left(\cdot ,t\right)\Vert \to \infty$ as $t\to \infty$ when the nonlinear function $f\left(u,x\right)$ satisfies (2.1), i.e. ${\bar{\epsilon }}_f=0$. In other words, $\tilde{\omega }$ system is exponentially stable in $L^{\infty }$ under ideal operating conditions ( $d_M\left(x,t\right)=0$ and $s_M\left(x,t\right)=0$ ).

3.2. ADF Design and Lumped Residual Evaluation

Following the discussions above, we use the lumped method to design the residual evaluation function and detection threshold. The residual evaluation function $R\left(t\right)$ and detection threshold $R_{th}^d\left(t\right)$ are defined as follows

$\{\begin{array}{l}R\left(t\right)={\displaystyle {\int }_t^{t+T}{\Vert r\left(\tau \right)\Vert }^2\text{d}\tau ,}\\ R_{th}^d\left(t\right)=\underset{s\left(x,t\right)=0}{\max }R\left(t\right),\end{array}$ (3.20)

where $T>0$ is the length of the evaluation time window.

Theorem 3.2. If the conditions in Theorem 3.1 are satisfied, by using the lumped residual evaluation function in (3.20), the time-varying detection threshold $R_{th}^d\left(t\right)$ for abnormality detection can be computed as

$R_{th}^d\left(t\right)={\displaystyle {\int }_t^{t+T}\left(1+N\left(1+\bar{L}\right)\right){\tilde{\omega }}_m^2\left(\tau \right)\text{d}\tau ,}$ (3.21)

where $\bar{L}=\underset{0\le x\le 1}{\max }{\Vert L\left(x,\tau ,t\right)\Vert }_2$.

Proof. Considering the boundary measurements $\tilde{u}\left(0,t\right)$ and N in-domain measurements $\tilde{u}\left(x_i,t\right)\left(i=1,2,\cdots ,N\right)$, we can obtain

${\Vert r\left(t\right)\Vert }^2={\displaystyle {\int }_0^1{r}^2\left(t\right)\text{d}t}={\displaystyle {\int }_0^1\left({\tilde{u}}^2\left(0,t\right)+{\tilde{u}}^2\left(x_1,t\right)+\cdots +{\tilde{u}}^2\left(x_N,t\right)\right)\text{d}x}.$ (3.22)

It can be verified that $\tilde{u}\left(0,t\right)=\tilde{\omega }\left(0,t\right)$ holds for all $t\ge 0$ by the transformation in (3.5), so (3.22) can be written as

$\begin{array}{c}{\Vert r\left(t\right)\Vert }^2={\tilde{\omega }}^2\left(0,t\right)+{\displaystyle {\int }_0^1\left({\tilde{u}}^2\left(x_1,t\right)+\cdots +{\tilde{u}}^2\left(x_N,t\right)\right)\text{d}x}\\ \le {\tilde{\omega }}^2\left(0,t\right)+N{\Vert \tilde{u}\left(\cdot ,t\right)\Vert }_{\infty }^2\\ \le {\Vert \tilde{\omega }\left(\cdot ,t\right)\Vert }_{\infty }^2+N\left(1+{\bar{L}}^2\right){\Vert \tilde{\omega }\left(\cdot ,t\right)\Vert }_{\infty }^2\\ \le \left(1+N\left(1+{\bar{L}}^2\right)\right){\tilde{\omega }}_m^2\left(t\right)\end{array}$ (3.23)

by combining (3.5) and the results in Theorem 3.1

Remark 3.2. From the conclusion of the above theorem, we design a new time-varying detection threshold for abnormality detection. The characteristic of “time-varying” is caused by exponential decreasing term ${\text{e}}^{-2\left(b-1\right)t}V\left(0\right)$ in (3.9). In addition, we consider the influence of initial errors $\tilde{\omega }\left(0\right)$ and ${\tilde{\omega }}_x\left(0\right)$ on the bounds of ${\Vert \tilde{\omega }\left(x,t\right)\Vert }_{\infty }$. Therefore, false alarms in abnormality detection can be avoided. This feature will be demonstrated in a later numerical simulation.

Hence, we can give the specific evaluation logic of abnormality detection.

Theorem 3.3. Comparing the functional relationship between $R\left(t\right)$ and $R_{th}^d\left(t\right)$, we can get the following abnormality detection evaluation logic:

$\{\begin{array}{l}R\left(t\right)>R_{th}^d\left(t\right)\Rightarrow \text{abnormalattime}t，\\ R\left(t\right)\le R_{th}^d\left(t\right)\Rightarrow \text{abnormality-freeattime}t.\end{array}$ (3.24)

4. Numerical Simulations

To evaluate the effectiveness of the proposed abnormality detection scheme, a class of nonlinear DPS whose system states can be expressed by parabolic PDE is considered.

For the purpose of numerical simulations, the distributed input $Q\left(x,t\right)$, Lipschitz continuous function $f\left(u,x\right)$ and distributed disturbance $d\left(x,t\right)$ can be defined as follows:

$Q\left(x,t\right)={\text{e}}^{-0.5\left(x-0.5\right)}\sin t,f\left(u,x\right)=x\sin t,d\left(x,t\right)=0.005{\text{e}}^{-0.5\left(x-0.5\right)}\sin t.$

Furthermore, to demonstrate the abnormality localization performance, we define $s\left(x,t\right)$ as a piecewise function as follows:

$s\left(x,t\right)=\{\begin{array}{l}150\sin 10x,0\le t<15,\\ 150\sin 10x\left[1-{\text{e}}^{-0.3\left(t-15\right)}\right]\text{,}t\ge \text{15}\text{.}\end{array}$

We use the finite element method (FDM) for numerical simulation the error system of (3.6), where $b=2$, $\gamma =\frac{1}{2}$, and the evaluation time window length T is 0.01 s.

Firstly, the performance of the error system $\tilde{\omega }\left(x,t\right)$ is analyzed. The bounds of $\tilde{\omega }\left(x,t\right)$ of the system with or without disturbance or abnormality is discussed respectively, as shown in Figure 1.

Figure 1. The performance of the error system $\tilde{\omega }\left(x,t\right)$.

It can be seen from Figure 1(a), $\tilde{\omega }\left(x,t\right)$ is bounded when the system has no disturbance and no anomaly. For the special case of Figure 1(a), i.e. ${\bar{\epsilon }}_f=0$, $\tilde{\omega }\left(x,t\right)$ decays to zreo, as shown in Figure 1(b). If the system has disturbance and no abnormality, it can be seen from Figure 1(c) that $\tilde{\omega }\left(x,t\right)$ is bounded. Furthermore, when an abnormal function $s\left(x,t\right)$ is imposed on the system, $\tilde{\omega }\left(x,t\right)$ is eventually bounded although it does not decay to zero, as shown in Figure 1(d).

Based on the proposed method, abnormality detection results are shown in Figure 2.

It can be seen from Figure 2(a) that the abnormal occurrence time $t=15\text{s}$ can be well detected. Then, we compared the detection scheme based on time-varying threshold proposed in this paper with the traditional method based on constant threshold, and the results are shown in Figure 2(b). In Figure 2(b), the blue dotted line represents the constant threshold. When $t>15\text{s}$, the residual function exceeds the constant threshold, and the system detects an abnormality. However, before the actual abnormal occurrence time, i.e. $t\le 15\text{s}$, there are still some moments when the residual function exceeds the constant threshold, so that the false alarm occurs.

Based on the results in Figure 2, the scheme in this paper adopts time-varying threshold, which is different from the previous constant threshold, and it can well avoid false alarms in the process of abnormality detection.

5. Conclusion

In this paper, the abnormality detection problem of a class of nonlinear parabolic DPS is studied by using backstepping method. The proposed scheme mainly includes two steps: firstly, the boundary observer is designed and the residual convergence is analyzed; secondly, the comprehensive residual evaluation function

Figure 2. Abnormality detection results.

is designed to realize abnormality detection and the threshold calculation formula is given. For the purpose of detection, the traditional “lumped” method is used for residual evaluation. The method based on filter is important when dealing with the implementation of the scheme in practical systems. The scheme presented in this paper realizes the abnormality detection of nonlinear distributed parameter system in time domain, and the simulation results confirm the requirements of the theory. Furthermore, we can extend the ADF in the time domain of nonlinear DPS system to the abnormality location in the space domain in the future.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Dong, J., Wang, Q., Wang, M. and Peng, K. (2018) Data-Driven Quality Monitoring Techniques for Distributed Parameter Systems with Application to Hot-Rolled Strip Laminar Cooling Process. IEEE Access, 6, 16646-16654. https://doi.org/10.1109/ACCESS.2018.2812919
[2]	Khan, F.A., Imran, M., Abbas, H. and Durad, M.H. (2017) A Detection and Prevention System against Collaborative Attacks in Mobile Ad Hoc Networks. Future Generation Computer Systems, 68, 416-427. https://doi.org/10.1016/j.future.2016.07.010
[3]	Chen, J. and Patton, R.J. (2002) Robust Model-Based Fault Diagnosis for Dynamic Systems. Automatica, 38, 1089-1094. https://doi.org/10.1016/S0005-1098(01)00290-4
[4]	Liu, J., Song, K., Feng, M., Yan, Y., Tu, Z. and Zhu, L. (2021) Semi-Supervised Anomaly Detection with Dual Prototypes Autoencoder for Industrial Surface Inspection. Optics and Lasers in Engineering, 136, Article ID: 106324. https://doi.org/10.1016/j.optlaseng.2020.106324
[5]	Dey, S., Perez, H.E. and Moura, S.J. (2017) Model-Based Battery Thermal Fault Diagnostics: Algorithms, Analysis, and Experiments. IEEE Transactions on Control Systems Technology, 27, 576-587. https://doi.org/10.1109/TCST.2017.2776218
[6]	Dey, S., Perez, H.E. and Moura, S.J. (2019) Robust Fault Detection of a Class of Uncertain Linear Parabolic PDEs. Automatica, 107, 502-510. https://doi.org/10.1016/j.automatica.2019.06.014
[7]	El-Farra, N.H. and Ghantasala, S. (2007) Actuator Fault Isolation and Reconfiguration in Transport-Reaction Processes. AIChE Journal, 53, 1518-1537. https://doi.org/10.1002/aic.11177
[8]	Ghantasala, S. and El-Farra, N.H. (2009) Robust Actuator Fault Isolation and Management in Constrained Uncertain Parabolic PDE Systems. Automatica, 45, 2368-2373. https://doi.org/10.1016/j.automatica.2009.06.024
[9]	Ferdowsi, H. and Jagannathan, S. (2014) Fault Diagnosis of a Class of Distributed Parameter Systems Modeled by Parabolic Partial Differential Equations. 2014 American Control Conference, Portland, 4-6 June 2014, 5434-5439. https://doi.org/10.1109/ACC.2014.6858836
[10]	Du, D. (2017) Fault Detection for Discrete-Time Linear Systems Based on Descriptor Observer Approach. Applied Mathematics and Computation, 293, 575-585. https://doi.org/10.1016/j.amc.2016.08.052
[11]	Li, S., Chen, Y. and Zhan, J. (2021) Simultaneous Observer-Based Fault Detection and Event-Triggered Consensus Control for Multi-Agent Systems. Journal of the Franklin Institute, 358, 3276-3301. https://doi.org/10.1016/j.jfranklin.2021.02.009
[12]	Zhao, Z., Yang, Y., Ding, S.X. and Li, L. (2018) Robust Fault Detection for Observer-Based Feedback Control Systems. Circuits, Systems, and Signal Processing, 37, 3364-3382. https://doi.org/10.1007/s00034-017-0726-z
[13]	Cai, J., Ferdowsi, H. and Sarangapani, J. (2016) Model-Based Fault Detection, Estimation, and Prediction for a Class of Linear Distributed Parameter Systems. Automatica, 66, 122-131. https://doi.org/10.1016/j.automatica.2015.12.028
[14]	Han, H., Yang, Y., Li, L. and Ding, S.X. (2018) Observer-Based Fault Detection for Uncertain Nonlinear Systems. Journal of the Franklin Institute, 355, 1278-1295. https://doi.org/10.1016/j.jfranklin.2017.12.021
[15]	Li, L., Ding, S.X., Qiu, J., Yang, Y. and Zhang, Y. (2016) Weighted Fuzzy Observer-Based Fault Detection Approach for Discrete-Time Nonlinear Systems via Piecewise-Fuzzy Lyapunov Functions. IEEE Transactions on Fuzzy Systems, 24, 1320-1333. https://doi.org/10.1109/TFUZZ.2016.2514371
[16]	Yang, Y., Ding, S.X. and Li, L. (2015) On Observer-Based Fault Detection for Nonlinear Systems. Systems and Control Letters, 82, 18-25. https://doi.org/10.1016/j.sysconle.2015.05.004
[17]	Demetriou, M.A., Ackleh, A.S. and Reich, S. (1998) Detection and Accommodation of Second Order Distributed Parameter Systems with Abrupt Changes in Input Term: Existence and Approximation. In: Theory and Practice of Control and Systems, World Scientific Publishing, Singapore, 720-725. https://doi.org/10.1142/9789814447317_0119
[18]	Armaou, A. and Demetriou, M.A. (2008) Robust Detection and Accommodation of Incipient Component and Actuator Faults in Nonlinear Distributed Processes. AIChE Journal, 54, 2651-2662. https://doi.org/10.1002/aic.11539
[19]	Lei, Y., Li, J. and Zhao, A. (2022) Spatiotemporal Fault Detection, Estimation and Control for Nonlinear Reaction-Diffusion Equations. Applied Mathematics and Computation, 418, Article ID: 126859. https://doi.org/10.1016/j.amc.2021.126859
[20]	Feng, Y., Li, H.X. and Yang, H.D. (2021) Abnormal Source Identification for Parabolic Distributed Parameter Systems. IEEE Transactions on Systems, Man and Cybernetics: Systems, 51, 5698-5707. https://doi.org/10.1109/TSMC.2019.2956985
[21]	Ferdowsi, H., Cai, J. and Jagannathan, S. (2019) Fault Detection and Estimation for a Class of Nonlinear Distributed Parameter Systems. 2019 IEEE International Conference on Prognostics and Health Management (ICPHM), San Francisco, 17-20 June 2019, 1-8. https://doi.org/10.1109/ICPHM.2019.8819432
[22]	Feng, Y., Wang, Y., Wang, J.W. and Li, H.X. (2022) Backstepping-Based Distributed Abnormality Localization for Linear Parabolic Distributed Parameter Systems. Automatica, 135, Article ID: 109930. https://doi.org/10.1016/j.automatica.2021.109930
[23]	Smyshlyaev, A. and Krstic, M. (2004) Closed-Form Boundary State Feedbacks for a Class of 1-D Partial Integro-Differential Equations. IEEE Transactions on Automatic Control, 49, 2185-2202. https://doi.org/10.1109/TAC.2004.838495
[24]	Smyshlyaev, A. and Krstic, M. (2005) Backstepping Observers for a Class of Parabolic PDEs. Systems and Control Letters, 54, 613-625. https://doi.org/10.1016/j.sysconle.2004.11.001
[25]	Meurer, T. (2013) On the Extended Luenberger-Type Observer for Semilinear Distributed-Parameter Systems. IEEE Transactions on Automatic Control, 58, 1732-1743. https://doi.org/10.1109/TAC.2013.2243312
[26]	Balakrishnan, V. (2003) All about the Dirac Delta Function. Resonance, 8, 48-58. https://doi.org/10.1007/BF02866759
[27]	Ioannou, P.A. and Sun, J. (2012) Robust Adaptive Control. Courier Corporation, New York.