A Pest Management Model with Multi-State Dependent Impulse

Ningzhe Liu

School of Mechanical Electronic & Information Engineering, China University of Mining and Technology, Beijing, China.

DOI: 10.4236/jamp.2022.104094                

Abstract

A multi-state dependent model is proposed for integrated pest management, which adopts different control methods at different thresholds. The sufficient conditions for the existence of order one periodic solution to the system are obtained by using differential equation geometry theory and successor function. Furthermore, we have discussed the existence of order-k (k ≥ 2) periodic solution by using series convergence. Besides we have proved the order one periodic solution is orbitally asymptotically stable under certain conditions with analogue of the Poincare criterion. Finally, numerical simulations are given to show the feasibility of our main results. Especially, the proved process of the existence of order one periodic solution shows that our method used in this paper is easier than the existing methods.

Keywords

Functional Design, Population Dynamics, Periodic Solution, Stability

1. Introduction and Model

Pest control is very important in agriculture. In pest management, the main ways are chemical control (pesticides-spaying) and biological control (releasing natural enemies). Usually, chemical control can lead to pest population densities reducing very rapidly, but many problems such as environmental pollution, pests’ resistance to pesticides etc. are caused if we implement chemical control as soon as pests appear. The second way, which controls pests by releasing natural enemies, can avoid problems caused by chemical control. Considering the effectiveness of the chemical control and non-pollution of the biological one, Stern introduced integrated pest management (IPM) in the late 1950s, which is a combination of biological and chemical tactics that reduce pests to tolerable levels, but it was more widely applied during the 1970s and 1980s.

In the process of practical application, people usually implement control to reduce the number of pest at a fixed time [1] [2] [3]. But this measure has some shortcomings, regardless of the growth rules of the pest and the cost of management. Another is to implement control measures only when the amount of pests reaches a certain threshold size [4] [5] [6]. The latter is more reasonable and suitable in the process of pest management. A few papers have been published based on the state feedback control strategy. A pest management epidemic model was presented with time-delay and stage-structure [7]. Tang and Chen first proposed the “Volterra” model with state-dependent and they discussed the existence and stability of order one periodic solution [8] [9]. Recently Jiang and Lu et al. also proposed pest management model with state pulse and phase structure [10] [11] [12] [13].

More and more scholars have paid close attention, and studied impulsive differential equation. Impulsive differential equation theory, especially the one in a fixed time, has been deeply developed and widely applied in various fields through years of research [14] [15] [16].

However, much research on population dynamics system with state-dependent impulsive control considers single state pulse, but in practice, we often need to use different control methods according to different states. On the basis of the above analysis, we set up the following predicator-prey system with different control methods in different thresholds, that is, when the amount of pest is small, biological control is implemented; when the amount is large, combination control is applied. The main innovations in this paper as follows: 1) The sufficient conditions for the existence of order one periodic solution to the defined system are given via differential equation geometry theory and successor function, where the method presented is intuitive and easy to understand. 2) The existence of order following predicator-prey system with different control methods in different thresholds, that is, when the amount of pest is small, biological control is implemented; when the amount is large, combination control is applied. The main innovations in this paper as follows: 1) The sufficient conditions for the existence of order one periodic solution to the defined system are given via differential equation geometry theory and successor function, where the method presented is intuitive and easy to understand. 2) The existence of order-k (k ≥ 2) periodic solution is proved by series convergence. Periodic solution is proved by series convergence.

Consider the following multi-state dependent model described as

$\{\begin{array}{l}\begin{array}{l}{x}^{\prime }\left(t\right)=x\left(t\right)\left(a-by\left(t\right)\right),\\ y^{\prime }\left(t\right)=y\left(t\right)\left(-d+cx\left(t\right)\right),\end{array}\}x\ne h_1,h_2\text{or}x=h_1,y>\frac{a}{b},\\ \begin{array}{l}\Delta x\left(t\right)=0,\\ \Delta y\left(t\right)=\delta ,\end{array}\}x=h_1,y\le \frac{a}{b},\\ \begin{array}{l}\Delta x\left(t\right)=-\alpha x\left(t\right),\\ \Delta y\left(t\right)=-\beta y\left(t\right)+\theta ,\end{array}\}x=h_2,\end{array}$ (2.1)

where $x\left(t\right)$ and $y\left(t\right)$ represent respectively the prey and the predator population densities at time t, $a,b,c,d$ and $h_1,h_2$ are all positive constants, $h_1<h_2$ and $h_2$ is the economic threshold (ET). $\delta$ is the release amount of predator when the amount of the pest reaches the threshold $h_1$ at time $t_{h_1}$. $\alpha \in \left(0,1\right),\beta \in \left(0,1\right)$ respectively represent the reducing fraction of prey and predator, $h_2$ is economic threshold, and $\theta$ is the release amount of predator. More details refer to [8].

2. Preliminaries

For late convenience, we give some useful definitions and lemmas.

Definition 2.1. A triple $\left(X,\pi ,R^{+}\right)$ is said to be a semi-dynamical system if X is a metric space, $R^{+}$ is the set of all non-negative real and $\pi \left(P,t\right):X\times R^{+}\to X$ is a continuous map such that:

i) $\pi \left(P,0\right)=P$ for all $P\in X$ ;

ii) $\pi \left(P,t\right)$ is continuous for t;

iii) $\pi \left(\pi \left(P,t\right)\right)=\pi \left(P,t+s\right)$ for all $P\in X$ and $s\in R^{+}$. Sometimes a semi-dynamical system $\left(X,\pi ,R^{+}\right)$ is denoted by $\left(X,\pi \right)$.

Definition 2.2. If

i) $\left(X,\pi \right)$ is a semi-dynamical system;

ii) M is a nonempty subset of X;

iii) Function $I:M\to X$ is continuous and for any $P\in M$ , there exists a constant $\epsilon >0$ such that for any $0<\left|t\right|<\epsilon$, $\pi \left(P,t\right)\notin M$ .

Then, $\left(X,\pi ,M,I\right)$ is called an impulsive semi-dynamical system.

Definition 2.3 (semi-continuous dynamic system) Consider state-dependent impulsive differential equations

$\{\begin{array}{l}\begin{array}{l}{x}^{\prime }\left(t\right)=P\left(x,y\right),\\ y^{\prime }\left(t\right)=Q\left(x,y\right),\end{array}\}\left(x,y\right)\notin M\left(x,y\right),\\ \begin{array}{l}\Delta x\left(t\right)=\alpha \left(x,y\right),\\ \Delta y\left(t\right)=\beta \left(x,y\right),\end{array}\}\left(x,y\right)\in M\left(x,y\right),\end{array}$ (2.2)

where the function I is continuous mapping, $I\left(M\right)=N$, I is called the impulse function. $M\left(x,y\right)$ is called impulsive set, $N\left(x,y\right)$ stands for the phase set. $M\left(x,y\right)$ and $N\left(x,y\right)$ represent the straight line or curve line on the plane.

Next we give the following lemma.

Lemma 2.1. (existence theorem of order one periodic solution [17] ) For system (1.1), if there exist $A\in N,B\in N$ satisfying successor functions $\left(A\right)f\left(B\right)<0$, then there exists a point $P\left(P\in N\right)$ between the points A and B, such that $f\left(P\right)=0$ (as shown in Figure 1), thus there is an order one periodic solution to system (1.1) (The relevant definitions refer to [17] ).

3. Existence of the Periodic Solution

Before discussing the periodic solution to system (1.1), we first consider model (1.1) without impulse effects:

$\{\begin{array}{l}{x}^{\prime }\left(t\right)=x\left(t\right)\left(a-by\left(t\right)\right),\\ y^{\prime }\left(t\right)=y\left(t\right)\left(cx\left(t\right)-d\right).\end{array}$ (3.1)

The vector graph of system (3.1) is shown in Figure 1 & Figure 2. The following results for (3.1) are easily obtained:

i) two steady states $O\left(0,0\right)$ -saddle point, and $R\left(\frac{d}{c},\frac{a}{b}\right)=R\left(x^{*},y^{*}\right)$ -stable center;

ii) a unique closed trajectory through any point in the first quadrant contained inside the point R.

By the biological background of system (1.1), we only consider $=\left\{\left(x,y\right)|x\ge 0,y\ge 0\right\}$.

Next, we investigate the existence of an order one periodic solution for system (1.1).

Figure 1. Successor function.

Figure 2. Illustration of vector graph of system (3.1).

3.1. The Existence of an Order one Periodic Solution to System (1.1)

Denote $M_1=\left\{\left(x,y\right)|x=h_1,0\le y\le \frac{a}{b}\right\}$, $M_2=\left\{\left(x,y\right)|x=h_2,y\ge 0\right\}$, $N_1=I\left(M_1\right)=\left\{\left(x,y\right)|x=h_1,\frac{a}{b}<y\le \frac{a}{b}+\delta \right\}$ and $N_2=I\left(M_2\right)=\left\{\left(x,y\right)|x=\left(1-\alpha \right)h_2,y>\theta \right\}$. Isoclinic lines are denoted respectively by lines $L_1=\left\{\left(x,y\right)|y=\frac{a}{b},x\ge 0\right\}$ and $L_2=\left\{\left(x,y\right)|x=\frac{d}{c},y\ge 0\right\}$. According to the practical significance, we assume that $h_1<\frac{d}{c}$, $\left(1-\alpha \right)h_2<\frac{d}{c}$ and $0\le x\left(0\right)<h_2$.

In the light of value of initial point, we consider the following two cases.

Case 1. $0<x_0\le h_1$ : In this case, according to the vector field of the system (1.1), a trajectory with initial point $\left(x_0,y_0\right)$ intersects $M_1$ at a point $P_1\left(h_1,y_{p_1}\right)$, and intersects $N_1$ at a point $P_0^{+}\left(h_1,y_{p_0}^{+}\right)$, we have $y_{p_1}<\frac{a}{b},y_{p_0}^{+}>\frac{a}{b}$, as shown in Figure 3(a). Thus pulse occurs at the point $P_1$, the impulsive function transfers the point $P_1$ into $P_1^{+}\left(h_1,y_{p_1}+\delta \right)$ and $P_1^{+}$ must lie on $N_1$ when $\delta \ge \frac{a}{b}$. The position of $P_1^{+}$ has the following three cases:

Case 1.1. $y_{P_1^{+}}>y_{P_0^{+}}$, as shown in Figure 3(b). In this case, the successor function of $P_0^{+}$ is $f\left(P_0^{+}\right)=y_{P_1^{+}}-y_{P_0^{+}}>0$. On the other hand, the trajectory from the point $P_1^{+}$ intersects $M_1$ at a point $P_2\left(h_1,y_{p_2}\right)$, in view of vector field and disjointness of any two trajectories, we know $y_{p_2}<y_{p_1}<\frac{a}{b}$. Suppose the point $P_2$ is subject to impulsive effects to a point $P_2^{+}\left(h_1,y_{p_2}^{+}\right)$, where

Figure 3. Case for $0<x_0\le h_1$. (a) $y_{p_1}<\frac{a}{b},y_{p_0}^{+}>\frac{a}{b}$ ; (b) $y_{P_1^{+}}>y_{P_0^{+}}$ ; (c) $y_{P_1^{+}}<y_{P_0^{+}}$.

$y_{p_2}^{+}=y_{p_2}+\delta$, and $y_{p_2}^{+}>\frac{a}{b}$ when $\delta \ge \frac{a}{b}$. Thus we have $y_{p_2}^{+}=y_{p_2}+\delta <y_{p_1}+\delta =y_{P_1^{+}}$, so the successor function of $P_1^{+}$ is $f\left(P_1^{+}\right)=y_{P_2^{+}}-y_{P_1^{+}}<0$. By Lemma 2.1, there exists an order one periodic solution for system (1.1), which passes through a point between $P_0^{+}$ and $P_1^{+}$ on the set $N_1$.

Cases 1.2. $y_{P_1^{+}}<y_{P_0^{+}}$, as shown in Figure 3(c). In this case, the successor function of $P_0^{+}$ is $f\left(P_0^{+}\right)=y_{P_1^{+}}-y_{P_0^{+}}<0$. And the same time, the trajectory from the point $P_1^{+}$ intersects $M_1$ at a point $P_2\left(h_1,y_{p_2}\right)$, in view of vector field and disjointness of any two trajectories, we know $y_{p_1}<y_{p_2}<\frac{a}{b}$. The point $P_2$ is subject to impulsive effects to point $P_2^{+}\left(h_1,y_{p_2^{+}}\right)$, where $y_{p_2^{+}}=y_{p_2}+\delta$ and $y_{p_2^{+}}>\frac{a}{b}$. So we obtain $y_{p_2^{+}}=y_{p_2}+\delta >y_{p_1}+\delta =y_{P_1^{+}}$, the successor function of $P_1^{+}$ is $f\left(P_1^{+}\right)=y_{P_2^{+}}-y_{P_1^{+}}>0$. Similar to the analysis of Case 1.1, there exists an order one periodic solution for system (1.1).

Cases 1.3. $y_{P_1^{+}}=y_{P_0^{+}}$ : In this case, $P_1^{+}$ coincides with $P_0^{+}$, the successor function of $P_0^{+}$ is $f\left(P_0^{+}\right)=0$. So there exists an order one periodic solution for system (1.1) which just passes through $P_0^{+}$.

Now we summarize the above results as the following theorem.

Theorem 3.1. If $0<x_0\le h_1$ and $\delta \ge \frac{a}{b}$, then there exists an order one periodic solution to the system (1.1).

Case 2. $h_1<x_0<h_2$. In this case, in the light of the different positions of the set $M_1$, $M_2$, $N_1$, $N_2$ and $L_2$, we consider the following four cases.

Case 2.1. $0<h_1<\left(1-\alpha \right)h_2<h_2<\frac{d}{c}$. In this case, we need consider the following two subject cases according to value of $y_0$ :

Case 2.1.1. $y_0\le \frac{a}{b}$, as shown in Figure 1 & Figure 4. Suppose a trajectory with the initial point $\left(x_0,y_0\right)$ intersects $M_2$ at a point $P_1\left(h_2,y_{p_1}\right)$, and intersects $N_2$ at a point $P_0^{+}\left(\left(1-\alpha \right)h_2,y_{p_0^{+}}\right)$. Thus pulse occurs at the point $P_1$, the impulsive function transfers the point $P_1$ into $P_1^{+}\left(\left(1-\alpha \right)h_2,\left(1-\beta \right)y_{p_1}+\theta \right)$. Without loss of generality, we assume $y_{P_1^{+}}>y_{P_0^{+}}$, the successor function of $P_0^{+}$ is $f\left(P_0^{+}\right)=y_{P_1^{+}}-y_{P_0^{+}}>0$. On the other hand, according to the vector field of system (1.1) the trajectory from $P_1^{+}$ must intersects $M_2$ at a point $P_2\left(h_2,y_{P_2}\right)$, and we have $y_{p_2}<y_{p_1}$ in view of vector field and disjointness of any two trajectories. Since $P_2$ on the set $M_2$, the point $P_2$ is subject to impulsive effects to a point $P_2^{+}\left(\left(1-\alpha \right)h_2,y_{p_2}^{+}\right)$, where $y_{p_2^{+}}=\left(1-\beta \right)y_{p_2}+\theta$. Then we obtain $y_{p_2^{+}}=\left(1-\beta \right)y_{p_2}+\theta <\left(1-\beta \right)y_{p_1}+\theta =y_{P_1^{+}}$, the successor function of $P_1^{+}$ is $f\left(P_1^{+}\right)=y_{P_2^{+}}-y_{P_1^{+}}<0$. By Lemma 2.1, there exists an order one periodic solution for system (1.1), which passes through a point between $P_0^{+}$ and $P_1^{+}$ on the set $N_2$.

Case 2.1.2. $y_0>\frac{a}{b}$. In this case, denote a trajectory of system (1.1) with the initial point $\left(x_0,y_0\right)$ as ${\Gamma }_1$, suppose ${\Gamma }_1$ intersects $L_1$ at a point A, in the light of value of $x_A$, we consider the following two cases.

Case 2.1.2.1. $x_A<h_1$. Suppose ${\Gamma }_1$ intersects $N_1$ at a point $P_0^{+}$, like Case 1, we can prove there exists an order one periodic solution for system (1.1) which passes through a point on the set $N_1$.

Case 2.1.2.2. $h_1\le x_A<h_2$, as shown in Figure 4(b). Suppose the first intersection between ${\Gamma }_1$ and $N_2$ is $P_0^{+}\left(\left(1-\alpha \right)h_2,y_{p_0}^{+}\right)$, and ${\Gamma }_1$ intersects $M_2$ at $P_1\left(h_2,y_{p_1}\right)$. Like the analysis of Case 2.1.1, there exists an order one periodic solution for system (1.1) which passes through a point on the set $N_2$.

From above discussion, we can obtain the following theorem.

Theorem 3.2. Assume that $h_1<x_0<h_2$ and $0<h_1<\left(1-\alpha \right)h_2<h_2<\frac{d}{c}$, there exists an order one periodic solution for system (1.1).

Case 2.2. $0<\left(1-\alpha \right)h_2<h_1<h_2<\frac{d}{c}$.

In this case, a trajectory of system (1.1) with initial point $\left(x_0,y_0\right)$ is denoted as ${\Gamma }_2$, suppose ${\Gamma }_2$ intersects $L_1$ at a point B, in the light of value of $x_B$, we consider the following two cases.

Case 2.2.1. $x_B<h_1$.

Like the analysis of Case 2.1.2.1, there exists an order one periodic solution for

Figure 4. $h_1\le x_A<h_2$. (a) $y_0\le \frac{a}{b}$ ; (b) $y_0>\frac{a}{b}$.

system (1.1) which passes through a point on the set $N_1$, and only biological control is implemented.

Case 2.2.2. $h_1\le x_B<h_2$, as shown in Figure 5.

Suppose ${\Gamma }_2$ intersects $M_2$ at $P_1\left(h_2,y_{p_1}\right)$, thus pulse occurs at the point $P_1$, the impulsive function transfers the point $P_1$ into $P_1^{+}\left(\left(1-\alpha \right)h_2,\left(1-\beta \right)y_{p_1}+\theta \right)$. According to the vector field of system (1.1), the trajectory from $P_1^{+}$ must intersect $M_1$ at a point $P_2\left(h_1,y_{P_2}\right)$, pulse occurs at the point $P_2$, the impulsive function transfers the point $P_2$ into $P_2^{+}\left(h_1,y_{P_2^{+}}\right)$, so in this case there does not exist an order one periodic solution for system (1.1).

From above discussion, the following theorem is obtained.

Theorem 3.3. Let $h_1<x_0<h_2$ and $0<\left(1-\alpha \right)h_2<h_1<h_2<\frac{d}{c}$, if $x_B<h_1$ , there exists an order one periodic solution to the system (1.1), if $h_1\le x_B<h_2$, there does not exist an order one periodic solution of system (1.1).

Case 2.3. $0<h_1<\left(1-\alpha \right)h_2<\frac{d}{c}<h_2$ .

Let $\Gamma$ be a closed trajectory of system (3.1) with the initial point $\left(x_0,y_0\right)$, $\Gamma$ intersects $L_1$ at two points $A_1$, $A_2$, as shown in Figure 6(a). In the light of value of $x_{A_1}$ and $x_{A_2}$, we consider the following three cases.

Case 2.3.1. $x_{A_1}<h_1$.

Like the analysis of Case 2.1.2.1, there exists an order one periodic solution for system (1.1) which passes through a point on the set $N_1$ and only biological control is implemented.

Case 2.3.2. $h_1\le x_{A_1}<x_{A_2}<h_2$.

In this case, a trajectory with initial point $\left(x_0,y_0\right)$ will stay in $\Gamma$, therefore

Figure 5. $h_1\le x_B<h_2$.

Figure 6. Case for $0<h_1<\left(1-\alpha \right)h_2<\frac{d}{c}<h_2$. (a) $\Gamma$ intersects $L_1$ at two points $A_1,A_2$ ; (b) $h_1\le x_{A_1}$ , $x_{A_2}\ge h_2$ .

there does not exist an order one periodic solution for system (1.1) and we need not control.

Case 2.3.3. $h_1\le x_{A_1}$, $x_{A_2}\ge h_2$ , as shown in Figure 6(b).

Suppose $\Gamma$ intersects $M_2$, $N_2$ at $P_1\left(h_2,y_{p_1}\right)$ and $P_0^{+}\left(\left(1-\alpha \right)h_2,y_{p_0^{+}}\right)$, respectively. Pulse occurs at the point $P_1$, the impulsive function transfers the point $P_1$ into $P_1^{+}\left(\left(1-\alpha \right)h_2,\left(1-\beta \right)y_{p_1}+\theta \right)$. Without loss of generality, we assume $y_{P_1^{+}}>y_{P_0^{+}}$, the successor function of $P_0^{+}$ is $f\left(P_0^{+}\right)=y_{P_1^{+}}-y_{P_0^{+}}>0$ . On the other hand, the trajectory from $P_1^{+}$ must intersect $M_2$ at a point $P_2\left(h_2,y_{P_2}\right)$, and we have $y_{p_2}<y_{p_1}$ in view of vector field and disjointness of any two trajectories. Since $P_2$ on the set $M_2$, the point $P_2$ is subject to impulsive effects to a point $P_2^{+}\left(\left(1-\alpha \right)h_2,y_{p_2^{+}}\right)$ , where $y_{p_2^{+}}=\left(1-\beta \right)y_{p_2}+\theta$ . Then we obtain $y_{p_2^{+}}=\left(1-\beta \right)y_{p_2}+\theta <\left(1-\beta \right)y_{p_1}+\theta =y_{P_1^{+}}$, the successor function of $P_1^{+}$ is $f\left(P_1^{+}\right)=y_{P_2^{+}}-y_{P_1^{+}}<0$. By Lemma 2.1, there exists an order one periodic solution for system (1.1), which passes through a point between $P_0^{+}$ and $P_1^{+}$ on the set $N_2$ and IPM strategy is implemented.

Summarizing the above results, we obtain the following theorem.

Theorem 3.4. Assume that $h_1<x_0<h_2$ and $0<h_1<\left(1-\alpha \right)h_2<\frac{d}{c}<h_2$.

If $x_{A_1}<h_1$ or $h_1\le x_{A_1},x_{A_2}\ge h_2$, there exists an order one periodic solution for system (1.1).

If $h_1\le x_{A_1}<x_{A_2}<h_2$, there does not exist an order one periodic solution for system (1.1).

Case 2.4. $0<\left(1-\alpha \right)h_2<h_1<\frac{d}{c}<h_2$.

Suppose a closed trajectory of system (3.1) with the initial point $\left(x_0,y_0\right)$ is $\Gamma$, which intersects $L_1$ at two points $A_1,A_2$. In the light of value of $x_{A_1}$ and $x_{A_2}$, we consider the following three cases:

Case 2.4.1. $x_{A_1}<h_1$.

Like the analysis of Case 2.1.2.1, there exists an order one periodic solution for system (1.1) which passes through a point on the set $N_1$ and only biological control is implemented.

Case 2.4.2. $h_1\le x_{A_1}<x_{A_2}<h_2$.

Like the analysis of Case 2.3.2, a trajectory with initial point $\left(x_0,y_0\right)$ will stay in $\Gamma$, there does not exist an order one periodic solution to the system (1.1) and we need not control.

Case 2.4.3. $h_1\le x_{A_1},x_{A_2}\ge h_2$.

In this case, $\Gamma$ intersects $M_2$ at $P_1\left(h_2,y_{p_1}\right)$, thus pulse occurs at the point $P_1$, the impulsive function transfers the point $P_1$ into $P_1^{+}\left(\left(1-\alpha \right)h_2,\left(1-\beta \right)y_{p_1}+\theta \right)$. According to the vector field of system (1.1), the trajectory from $P_1^{+}$ must intersect $M_1$ at a point $P_2\left(h_1,y_{P_2}\right)$, pulse occurs at the point $P_2$, the impulsive function transfers the point $P_2$ into $P_2^{+}\left(h_1,y_{P_2^{+}}\right)$, so in this case there does not exist an order one periodic solution for system(1.1).

Summarizing the above results, we obtain the following theorem.

Theorem 3.5. Assume that $h_1<x_0<h_2$ and $0<\left(1-\alpha \right)h_2<h_1<\frac{d}{c}<h_2$.

If $x_{A_1}<h_1$, there exists an order one periodic solution for system (1.1).

If $h_1\le x_{A_1}<x_{A_2}<h_2$ or $h_1\le x_{A_1},x_{A_2}\ge h_2$, there does not exist an order one periodic solution for system (1.1).

3.2. The Existence of an Order-k Periodic Solution.

In the light of value of initial point, we consider the following two cases.

Case 1. $0<x_0\le h_1$.

Suppose a trajectory with initial point $\left(x_0,y_0\right)$ intersects $M_1$ at a point $P_1\left(h_1,y_{p_1}\right)$, and intersects $N_1$ at a point $P_0^{+}\left(h_1,y_{p_0^{+}}\right)$, then due to impulsive effect, $P_1$ jumps to $P_1^{+}\left(h_1,y_{p_1^{+}}\right)$ on the set $N_1$. The trajectory starting from the point $P_1^{+}$ will intersect $M_1$ at a point $P_2\left(h_1,y_{p_2}\right)$, then $P_2$ jumps to $P_2^{+}\left(h_1,y_{p_2^{+}}\right)$ on the set $N_1$. The trajectory starting from the point $P_2^{+}$ will again intersect $M_1$ at a point $P_3\left(h_1,y_{p_3}\right)$ and so on. So we get a sequence ${\left\{P_k^{+}\right\}}_{k=1,2,\cdots }$ of the set $N_1$.

Case 1.1. If $y_{p_0^{+}}=y_{p_1^{+}}$, then system (1.1) has a positive period-1 solution.

Case 1.2. If $y_{p_0^{+}}\ne y_{p_1^{+}}$, without loss of generality, we assume $y_{P_1^{+}}<y_{P_0^{+}}$. In view of vector field and disjointness of any two trajectories, we have $y_{p_2}>y_{p_1}$, then we obtain $y_{p_2^{+}}=y_{p_2}+\delta >y_{p_1}+\delta =y_{P_1^{+}}$. Furthermore, if $y_{p_0^{+}}=y_{p_2^{+}}$, then system (1.1) has a positive period-2 solution.

Case 1.3. If $y_{p_0}^{+}\ne y_{p_1}^{+},y_{p_0}^{+}\ne y_{p_2}^{+}$, without loss of generality, we assume $y_{P_0^{+}}>y_{P_2^{+}}>y_{P_1^{+}}$, by similar method we can obtain similar results about $y_{P_1^{+}}<y_{P_0^{+}}<y_{P_2^{+}}$, as shown in Figure 7. According to conditions

$y_{P_0^{+}}>y_{P_2^{+}}>y_{P_1^{+}},y_{P_k^{+}}=y_{P_k}+\delta$, $\delta \ge \frac{a}{b}$ and disjointness of any two trajectories,

Figure 7. $0<x_0\le h_1$.

then we get a sequence ${\left\{P_k^{+}\right\}}_{k=1,2,\cdots }$ of the set $N_1$ satisfying $y_{P_1^{+}}<y_{P_3^{+}}<\cdots <y_{P_{2k-1}^{+}}<y_{P_{2k+1}^{+}}<\cdots <y_{P_{2k}^{+}}<y_{P_{2k-2}^{+}}<\cdots <y_{P_2^{+}}<y_{P_0^{+}}$, therefore there does not exist a period-k solution $\left(k\ge 3\right)$ for system (1.1).

Case 2. $h_1<x_0<h_2$, $0<h_1<\left(1-\alpha \right)h_2<h_2<\frac{d}{c}$.

In this case, in view of vector field, a trajectory with the initial point $\left(x_0,y_0\right)$ must intersect $M_2$ at a point $P_1\left(h_2,y_{p_1}\right)$, and intersect $N_2$ at a point $P_0^{+}\left(\left(1-\alpha \right)h_2,y_{p_0^{+}}\right)$. Thus pulse occurs at the point $P_1$, the impulsive function transfers the point $P_1$ into $P_1^{+}\left(\left(1-\alpha \right)h_2,\left(1-\beta \right)y_{p_1}+\theta \right)$. The trajectory starting from the point $P_1^{+}$ will intersect $M_2$ at a point $P_2\left(h_2,y_{p_2}\right)$, then $P_2$ jumps to $P_2^{+}\left(h_2,y_{p_2^{+}}\right)$ on the set $N_2$. The trajectory starting from the point $P_2^{+}$ will again intersect $M_2$ at a point $P_3\left(h_2,y_{p_3}\right)$ and so on. So we get a sequence ${\left\{P_k^{+}\right\}}_{k=1,2,\cdots }$ of the set $N_2$. Like the analysis of Case 1, we have the following cases:

Case 2.1. If $y_{p_0^{+}}=y_{p_1^{+}}$, then system (1.1) has a positive period-1 solution.

Case 2.2. If $y_{p_0^{+}}\ne y_{p_1^{+}}$, without loss of generality, we assume $y_{P_1^{+}}<y_{P_0^{+}}$. In view of vector field and disjointness of any two trajectories, we have $y_{p_2}>y_{p_1}$, then we obtain $y_{p_2^{+}}=\left(1-\beta \right)y_{p_2}+\theta >\left(1-\beta \right)y_{p_1}+\theta =y_{P_1^{+}}$. Furthermore, if $y_{p_0^{+}}=y_{p_2^{+}}$, then system (1.1) has a positive period-2 solution.

Case 2.3. If $y_{p_0^{+}}\ne y_{p_1^{+}},y_{p_0^{+}}\ne y_{p_2^{+}}$, without loss of generality, we assume $y_{P_0^{+}}>y_{P_2^{+}}>y_{P_1^{+}}$, by similar method we can obtain similar results about $y_{P_1^{+}}<y_{P_0^{+}}<y_{P_2^{+}}$, as shown in Figure 1 & Figure 8. According to conditions $y_{P_0^{+}}>y_{P_2^{+}}>y_{P_1^{+}}$, $y_{P_k^{+}}=\left(1-\beta \right)y_{P_k}+\theta$ and disjointness of any two trajectories, then we get a sequence ${\left\{P_k^{+}\right\}}_{k=1,2,\cdots }$ of the set $N_2$ satisfying

$y_{P_1^{+}}<y_{P_3^{+}}<\cdots <y_{P_{2k-1}^{+}}<y_{P_{2k+1}^{+}}<\cdots <y_{P_{2k}^{+}}<y_{P_{2k-2}^{+}}<\cdots <y_{P_2^{+}}<y_{P_0^{+}}$, therefore there does not exist a period-k $\left(k\ge 3\right)$ solution for system (1.1).

Figure 8. $h_1<x_0<h_2$.

4. Stability of the Order One Periodic Solution

Theorem 4.1. If $0<x_0\le h_1$ and $\delta \ge \frac{a}{b}$, then order one periodic solution $\left(\xi \left(t\right),\eta \left(t\right)\right)$ of system (1.1) is orbitally asymptotically stable.

Proof. Let $P\left(x,y\right)=x\left(a-by\right)$, $Q\left(x,y\right)=y\left(-d+cx\right)$, $\phi \left(x,y\right)=x-h_1$, $A\left(x,y\right)=0$, $B\left(x,y\right)=\delta$, we can calculate

$\frac{\partial P}{\partial x}=a-by,\frac{\partial Q}{\partial y}=-d+cx,\frac{\partial \phi }{\partial x}=1,\frac{\partial \phi }{\partial y}=0,\frac{\partial A}{\partial x}=0,\frac{\partial A}{\partial y}=0,\frac{\partial B}{\partial x}=\frac{\partial B}{\partial y}=0.$

Denote order one periodic solution $\left(\xi \left(t\right),\eta \left(t\right)\right)$ of system (1.1) by T, then point $\left(\xi \left(T^{+}\right),\eta \left(T^{+}\right)\right)=\left(x_1^{+},y_1^{+}\right)$ is phase of point $\left(\xi \left(T\right),\eta \left(T\right)\right)=\left(x_1,y_1\right)$, that is $x_1^{+}=x_1=h_1$, $y_1^{+}=y_1+\delta$.

We can get

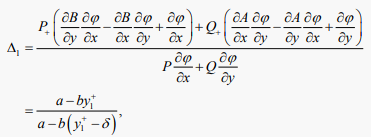
and

$\begin{array}{l}{\displaystyle {\int }_0^T\left(\frac{\partial P}{\partial x}\left(\xi \left(t\right),\eta \left(t\right)\right)+\frac{\partial Q}{\partial y}\left(\xi \left(t\right),\eta \left(t\right)\right)\right)\text{d}t}\\ ={\displaystyle {\int }_0^T\left[\left(a-b\eta \left(t\right)\right)+\left(c\xi \left(t\right)-d\right)\right]\text{d}t}\\ =\ln \frac{\xi \left(T\right)\eta \left(T\right)}{\xi \left(T^{+}\right)\eta \left(T^{+}\right)}=\ln \frac{y_1^{+}-\delta }{y_1^{+}}.\end{array}$

Therefore

$\begin{array}{c}\left|{\mu }_2\right|=\left|{\Delta }_1\exp \left[{\displaystyle {\int }_0^T\left(\frac{\partial P}{\partial x}\left(\xi \left(t\right),\eta \left(t\right)\right)+\frac{\partial Q}{\partial y}\left(\xi \left(t\right),\eta \left(t\right)\right)\right)\text{d}t}\right]\right|\\ =\left|\frac{a-b{y}_1^{+}}{a-b\left(y_1^{+}-\delta \right)}\frac{y_1^{+}-\delta }{y_1^{+}}\right|<1.\end{array}$

By Lemma 2.3 in [17], we can get that the T-periodic solution $\left(\xi \left(t\right),\eta \left(t\right)\right)$ of system (1.1) is asymptotically stable. The proof is completed.

Theorem 4.2. If $h_1<x_0<h_2$, $0<h_1<\left(1-\alpha \right)h_2<h_2<\frac{d}{c}$ and $\theta >\frac{\beta y_1^{+}\left(-d+c\left(1-\alpha \right)h_2\right)+a\beta \left(1-\alpha \right)h_2}{b\left(1-\alpha \right)h_2}$, then order one periodic solution $\left(\xi \left(t\right),\eta \left(t\right)\right)$ of system (1.1) is orbitally asymptotically stable.

Proof. Let $P\left(x,y\right)=x\left(a-by\right)$, $Q\left(x,y\right)=y\left(-d+cx\right)$, $\phi \left(x,y\right)=x-h_2$, $A\left(x,y\right)=-\alpha x$, $B\left(x,y\right)=-\beta y+\theta$.

We calculate

$\frac{\partial P}{\partial x}=a-by,\frac{\partial Q}{\partial y}=-d+cx,\frac{\partial \phi }{\partial x}=1,\frac{\partial \phi }{\partial y}=0,\frac{\partial A}{\partial x}=-\alpha ,\frac{\partial A}{\partial y}=0,\frac{\partial B}{\partial x}=0,\frac{\partial B}{\partial y}=-\beta .$

Denote order one periodic solution $\left(\xi \left(t\right),\eta \left(t\right)\right)$ of system (1.1) by T, then a point $\left(\xi \left(T^{+}\right),\eta \left(T^{+}\right)\right)=\left(x_1^{+},y_1^{+}\right)$ is phase of a point $\left(\xi \left(T\right),\eta \left(T\right)\right)=\left(x_1,y_1\right)$, that is

$x_1=h_2,x_1^{+}=\left(1-\alpha \right)h_2,y_1^{+}=\left(1-\beta \right)y_1+\theta .$

$\begin{array}{c}{\Delta }_1=\frac{P_{+}\left(\frac{\partial B}{\partial y}\frac{\partial \phi }{\partial x}-\frac{\partial B}{\partial x}\frac{\partial \phi }{\partial y}+\frac{\partial \phi }{\partial x}\right)+Q_{+}\left(\frac{\partial A}{\partial x}\frac{\partial \phi }{\partial y}-\frac{\partial A}{\partial y}\frac{\partial \phi }{\partial x}+\frac{\partial \phi }{\partial y}\right)}{P\frac{\partial \phi }{\partial x}+Q\frac{\partial \phi }{\partial y}}\\ =\frac{x_1^{+}\left(a-b{y}_1^{+}\right)+\beta y_1^{+}\left(-d+c{x}_1^{+}\right)}{x_1\left(a-b{y}_1\right)}\\ =\frac{\left(1-\alpha \right)h_2\left(a-b{y}_1^{+}\right)+\beta y_1^{+}\left(-d+c\left(1-\alpha \right)h_2\right)}{\left(1-\alpha \right)h_2\left[a\left(1-\beta \right)-b\left(y_1^{+}-\theta \right)\right]}\left(1-\alpha \right)\left(1-\beta \right)\end{array}$

and

$\begin{array}{l}{\displaystyle {\int }_0^T\left(\frac{\partial P}{\partial x}\left(\xi \left(t\right),\eta \left(t\right)\right)+\frac{\partial Q}{\partial y}\left(\xi \left(t\right),\eta \left(t\right)\right)\right)\text{d}t}\\ ={\displaystyle {\int }_0^T\left[\left(a-b\eta \left(t\right)\right)+\left(c\xi \left(t\right)-d\right)\right]\text{d}t}\\ =\ln \frac{\xi \left(T\right)\eta \left(T\right)}{\xi \left(T^{+}\right)\eta \left(T^{+}\right)}=\ln \frac{y_1^{+}-\theta }{y_1^{+}\left(1-\alpha \right)\left(1-\beta \right)}.\end{array}$

So

$\begin{array}{c}{\mu }_2={\Delta }_1\exp \left[{\displaystyle {\int }_0^T\left(\frac{\partial P}{\partial x}\left(\xi \left(t\right),\eta \left(t\right)\right)+\frac{\partial Q}{\partial y}\left(\xi \left(t\right),\eta \left(t\right)\right)\right)\text{d}t}\right]\\ =\frac{\left(1-\alpha \right)h_2\left(a-b{y}_1^{+}\right)+\beta y_1^{+}\left(-d+c\left(1-\alpha \right)h_2\right)}{\left(1-\alpha \right)h_2\left[a\left(1-\beta \right)-b\left(y_1^{+}-\theta \right)\right]}.\end{array}$

From theorem 4.2, we have $\left|{\mu }_2\right|<1$. By Lemma 2.3 in [17], we have that the T-periodic solution $\left(\xi \left(t\right),\eta \left(t\right)\right)$ of system (1.1) is asymptotically stable. The proof is completed.

5. Discussion and Numerical Simulations

In this paper, we have investigated the existence of order one periodic solution to a pest management model with multi-states dependent impulse by using differential equation geometry theory and the method of successor functions. Furthermore, we have discussed the existence of order-k (k ≥ 2) periodic solution by using series convergence. Finally, we have proved the order one periodic solution is orbitally asymptotically stable under certain conditions with analogue of the Poincare criterion. We also have shown that when the initial value of the pest is small, only biological control is taken to make pests and natural enemies in a periodic equilibrium; when the initial value of the pest is large, IPM control strategy is taken to make pests and natural enemies in a periodic equilibrium.

In order to verify the theoretical results in this paper, we next give the numerical simulations of system (1.1). Let $a=0.4$, $b=0.5$, $c=0.3$, $d=0.6$, $\delta =0.9$, $h_1=1$, $h_2=1.8$, $x_0=0.2$, $y_0=0.1$, we can obtain Figure 9. From Figure 9 it can be seen that the conditions of Theorems 3.1 4.1 hold, therefore system (1.1) has order one periodic solution and it is asymptotically stable.

Let $a=0.4$, $b=0.5$, $c=0.3$, $d=0.6$, $\delta =0.9$, $h_1=0.2$, $h_2=1.8$, $\alpha =0.6$, $\beta =0.3$, $\theta =0.8$, $x_0=0.6$, $y_0=0.3$, we can obtain Figure 10. From

Figure 9. The time series and phase diagram for system (1.1) with parameters $a=0.4$, $b=0.5$, $c=0.3$, $d=0.6$, $h_1=1$, $\delta =0.9$, $x_0=0.5$, $y_0=0.6$.

Figure 10. The time series and phase diagram for system (1.1) with parameters $a=0.4$, $b=0.5$, $c=0.3$, $d=0.6$, $h_1=0.2$, $h_2=1.8$, $\alpha =0.6$, $\beta =0.3$, $\theta =0.8$, $x_0=0.6$, $y_0=0.3$.

Figure 10, it can be seen that the conditions of Theorems 3.2 and 4.2 hold, therefore system (1.1) has order one periodic solution and order two periodic solution, order one periodic solution is asymptotically stable.

These results show that the state-dependent impulsive effects contribute significantly to the richness of the dynamic models. In the practical process of pest management, we can put a monitor on farmland, to observe the state of the pest and implement different control methods according to different states. This strategy fits with pest management, which saves manpower and protects the environment as far as possible. Furthermore, it can be seen that it is easier to prove the existence of order one periodic solution by successor functions than the existing research methods.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Onofrio, A.D. (2002) Pulse Vaccination Strategy in the SIR Epidemic Model: Global Asymptotic Stable Eradication in Presence of Vaccine Failures. Mathematical and Computer Modelling, 36, 473-489. https://doi.org/10.1016/S0895-7177(02)00177-2
[2]	Kang, B., Liu, B. and Tao, F. (2018) An Integrated Pest Management Model with Dose-Response Effect of Pesticides. Journal of Biological Systems, 26, 59-86. https://doi.org/10.1142/S0218339018500043
[3]	Li, J., Huang, Q. and Liu, B. (2019) A Pest Control Model with Birth Pulse and Residual and Delay Effects of Pesticides. Advances in Difference Equations, 2019, Article No. 117. https://doi.org/10.1186/s13662-019-1978-7
[4]	Li, Y., Li, Y., Liu, Y. and Cheng, H. (2018) Stability Analysis and Control Optimization of a Prey-Predator Model with Linear Feedback Control. Discrete Dynamics in Nature and Society, 2018, Article ID: 4945728. https://doi.org/10.1155/2018/4945728
[5]	Bainov, D. and Simeonov, P. (1993) Impulsive Differential Equations: Periodic Solutions and Applications. Longman Scientific and Technical, Vol. 66, Bookcraft (Bath) Ltd., New York.
[6]	Meng, X. and Li, Z., (2010) The Dynamics of Plant Disease Models with Continuous and Impulsive Cultural Control Strategies. Journal of Theoretical Biology, 266, 29-40. https://doi.org/10.1016/j.jtbi.2010.05.033
[7]	Ding, Y., Gao, S., Liu, Y. and Lan, Y. (2010) A Pest Management Epidemic Model with Time Delay and Stage-Structure. Applied Mathematics, 1, 215-221. https://doi.org/10.4236/am.2010.13026
[8]	Tang, S. and Cheke, R.A. (2005) State-Dependent Impulsive Models of Integrated Pest Management (IPM) Strategies and Their Dynamic Consequences. Journal of Mathematical Biology, 50, 257-292. https://doi.org/10.1007/s00285-004-0290-6
[9]	Tang, S., Xiao, Y., Chen, L. and Cheke, R.A. (2005) Integrated Pest Management Models and Their Dynamical Behaviour. Bulletin of Mathematical Biology, 67, 115-135. https://doi.org/10.1016/j.bulm.2004.06.005
[10]	Jiang, G., Lu, Q. and Peng, L. (2005) Impulsive Ecological Control of a Stage-Structured Pest Management System. Mathematical Biosciences & Engineering, 2, 329-344. https://doi.org/10.3934/mbe.2005.2.329
[11]	Yang, J. (2021) Dynamics Behaviors of a Stage-Structured Pest Management Model with Time Delay and Impulsive Effects. Mathematical Methods in the Applied Sciences, 44, 13116-13132. https://doi.org/10.1002/mma.7613
[12]	Jiao, J. and Chen, L. (2008) Global Attractivity of a Stage-Structure Variable Coefficients Predator-Prey System with Time Delay and Impulsive Perturbations on Predators. International Journal of Biomathematics, 1, 197-208. https://doi.org/10.1142/S1793524508000163
[13]	Kalra, P. and Kaur, M. (2022) Stability Analysis of an Eco-Epidemiological SIN Model with Impulsive Control Strategy for Integrated Pest Management Considering Stage-Structure in Predator. International Journal of Mathematical Modelling and Numerical Optimisation, 12, 43-68. https://doi.org/10.1504/IJMMNO.2022.119779
[14]	Cheng, H., Wang, F. and Zhang, T. (2012) Multi-State Dependent Impulsive Control for Holling I Predator-Prey Model. Discrete Dynamics in Nature and Society, 2012, Article ID: 181752. https://doi.org/10.1155/2012/181752
[15]	Zhao, W., Zhang, T., Meng, X. and Yang, Y. (2013) Dynamical Analysis of a Pest Management Model with Saturated Growth Rate and State Dependent Impulsive Effects. Abstract and Applied Analysis, 2013, Article ID: 204642. https://doi.org/10.1155/2013/204642
[16]	Cordova-Lepe, F., Robledo, G. and Cabrera-Villegas, J. (2015) Population Growth Modeling with Boom and Bust Patterns: The Impulsive Differential Equation Formalism. Journal of Biological Systems, 23, S135-S149. https://doi.org/10.1142/S0218339015400112
[17]	Cheng, H., Yin, Z. and Liu, H. (2012) Analysis of the Dynamics of Stage-Structured Pest Control Model. Mathematica Applicata, 25, 816-823. https://doi.org/10.3969.j.issn.1001-9847.2012.04.017