Coulomb Interaction between Electrons and a New Concept of Atom ()
1. Introduction
The studies of the π electron state in a flat carbon monolayer (graphene) [1] included some assumptions which were helpful for the understanding of this carbon modification. The assumptions concerned, first, the role of Coulomb interaction between neighboring electrons, which resulted in an alternating distribution of electrons on both sides of the carbon frame and the formation of two- dimensional electron crystals from them. Second, it was supposed that the formation of three resonating π bonds by one electron resulted from a pz electron rotation in the orbit in the plane parallel to the carbon frame plane. The orbit was in the limits of the 2pz state. It is important that the center of the pz electron orbits in this case was not the carbon atom nucleus, only the rotation axis passed through the nucleus. Third, to compensate for the orbital magnetic momenta of electrons, opposite directions of pz electron rotation (clockwise and counterclockwise) on opposite sides of the carbon frame were assumed. It turned out that the difference in the directions of electron rotation could replace the difference in the spin directions of the electrons forming π bonds. This result was unexpected and interesting because a physical understanding of the spin concept is still lacking. The spin is interpreted either as a purely quantum phenomenon that has no analogue in classical mechanics or as some inherent magnetic moment of the electron itself, i.e., as its property.
Since all of the above assumptions, which allowed explanation of the origin of graphene specific features concerned the behavior of electrons in the 2 pz state of carbon atoms, it was supposed that they could be useful for the consideration of the electron state in the atom as well. First of all, the influence of Coulomb interaction between electrons on their spatial distribution and also the relationship between the spin and the orbital magnetic moment of electron attracted attention.
This paper is devoted to the consideration of the atom in the approximation of a strong Coulomb interaction between electrons.
At first, a few words on the history of this research subject should be said. The development of quantum mechanics in the early 20th century sparked a serious scientific debate in the scientific community because it meant a change in the scientific approach and the transition from the consideration of real phenomena within the framework of classical mechanics to the consideration of real phenomena probabilities, i.e., moving from a deterministic approach to a non- materialized one. As a result of these disputes, the view prevailed that quantum mechanics completely solves the atomic problem. However, questions such as the reason for the periodic changes in the atomic properties with an increase in the nuclear charge; the atomic ability to form directional bonds and the mechanism of electron transition from the wave state into the particle one remain unresolved. Therefore, attempts to explain atomic properties within the framework of classical mechanics continued and continue [2] [3] [4] [5] .
2. Coulomb Interaction between Electrons and Spherically Symmetric Distribution of Electron Orbits
Let us consider the influence of Coulomb interaction between electrons on their state in the atom by using the analogy with its influence on pz electrons in graphene [1] . Let us assume, first, that electrons in the atom rotate in circular orbits centered outside the nucleus, and only the rotation axis passes through the nucleus. Second, all electron orbits in the same state are located on one equipotential surface of the nucleus electrostatic field. In the case of the atom, this surface is an equipotential sphere. In the presence of Coulomb interaction between electrons their orbits on such a sphere must lie at equal distances from each other. To keep this distance constant as electrons rotate, the electron rotation must be synchronous, with the same velocity and in the same direction relative to the sphere surface. In other words, the electron state on the equipotential surface must be strongly correlated.
It is possible to achieve a uniform distribution of electron orbits on a spherical surface by “inscribing” a regular polyhedron into the sphere. In this case the polyhedron center must be in the atomic nucleus and the number of its faces must be equal to the number of electrons in a given state. In this case each electron orbit will be on a separate face of the polyhedron and each electron state will have its own polyhedron. The discussion below will show that the number of regular polyhedra really specifies the number of electron states in the atom, and the number of faces of regular polyhedra specifies the number of electrons in each state.
Five regular polyhedra are known. However, only those the opposite faces of which are parallel to each other were found to be useful for the electron distribution in the atom. These are a hexahedron, an octahedron, a dodecahedron, and an icosahedron. It is natural to assume that a hexahedron corresponds to the s and p states, a dodecahedron corresponds to the d state and an icosahedron corresponds to the f state.
It turned out that difficulties in the description of the spatial distribution of electron orbits by using polyhedra arise primarily with electrons in the s state. There are only two of them, and the smallest number of faces in regular polyhedra with the face parallelism is six (hexahedron). Therefore, s electrons can fill their hexahedron only partially, occupying only two faces out of six (Figure 1).
The atomic structure which consists of polyhedra and also possible variants of polyhedron coalescence when the nuclear charge increases are shown schematically in Figure 2. It shows, as an example, completely filled electron shells of noble gases. The sequence of polyhedra for other atoms is the same, only the outer polyhedron remains incompletely filled.
![]()
Figure 1. Two 1s electron orbits with radius ro inscribed into two opposite faces of hexahedron with edge a (He atom).
![]()
Figure 2. Electron shells of noble gases shown by a sequence of polyhedra: incompletely filled hexahedron of s electrons (square brackets), completely filled hexahedron of p electrons (a square), octahedron (a regular triangle), dodecahedron (a regular pentagon), icosahedron (a circle). Incompletely filled icosahedra are shown by open circles. 7s + 7d dodecahedron is still incomplete. The octahedra formed by coalescence are shown by the dashed line. Replacement of the 3d state by 4d in the fourth period will be discussed in Section 4.
Figure 2 shows that the electron shell of each noble gas atom consists of a certain sequence of alternating polyhedra, each of which corresponds to a definite distribution of electron orbits in the spherically symmetric electrostatic nuclear field. Such a distribution can be regarded as a spatial quantization of electron orbits in the atomic shell.
Since each electron state in the atomic model corresponds to a definite polyhedron, a limited number of states is associated with a limited number of regular polyhedra.
3. On the Fine Structure of Electron Energy Levels
Before proceeding to a detailed discussion of the consequences of spatial quantization of electron orbits, some words should be said about regular polyhedra. It is known [6] that three spheres are associated with each regular polyhedron: a sphere circumscribed around the polyhedron and passing through all its vertices; a sphere inscribed into the polyhedron and passing through the midpoints of its faces; and a median sphere passing through the midpoints of its edges. There are certain relations between the polyhedron edge length and the radii of these three spheres, so if you know the edge length or the radius of one of the spheres, you can find all the others.
The median sphere is of greatest interest for the consideration of the electron state in the atom because it is the equipotential sphere on the surface of which electron orbits are located and which determines the electron energy. The median sphere also gives important information about the electron orbits themselves. So, the polyhedron face which cuts off a spherical segment from the median sphere determines the orbit plane, its orientation relative to the atomic nucleus, and its maximum possible radius (Figure 3). In regular polyhedra a perpendicular from the polyhedron center to the face passes through the face center. This means that the electron rotation axis must pass through the atomic nucleus because the polyhedron is centered by the nucleus.
It can be seen from Figure 3 that the electron orbit radius ro = ρsinϑ, i.e. it is determined by the radius of the median sphere ρ (which is also the electron radius-vector relative to the nucleus) and the angle ϑ between this radius and the rotation axis. The distance between the orbit center and the nucleus will be defined by the radius r of the sphere that can be inscribed into the same hexahedron.
Angle ϑ for a hexahedron is 45 degrees. For other polyhedra it is smaller and decreases when the number of faces increases. It follows that the largest radius is for the orbit inscribed into the hexahedron face, i.e. for the electrons of the s and p states.
Since each electron state corresponds to a specific polyhedron, and the median spheres of these polyhedra are different, it becomes clear that the electron energies in different states of the same period of the Mendeleev Table must also be different. This means that the electron distribution over different polyhedra leads to a quantization of electrons in energy. It is possible that the difference in energies in such a quantization is insignificant as compared with the difference in electron energies between neighboring periods of the Mendeleev Table, but the difference must exist. In other words, each energy level corresponding to any
![]()
Figure 3. An electron in orbit with radius ro lying on the surface of the median sphere with radius ρ. The orbit is inscribed into a hexahedron face.
period of the Mendeleev Table must have sublevels corresponding to different electron states. Perhaps this is the reason for the fine structure of atomic spectra observed experimentally [7] .
4. Specific Features of Polyhedron Filling, Electric Field Changes with Increasing Nuclear Charge and Quantization of Electrons in Energy Associated with Periods of the Mendeleev Table
A detailed consideration of the sequence of filling of electron states (polyhedra) presented in the general form in Figure 2 allowed us to identify a number of features in the formation of an atomic electron shell.
First, there is a certain sequence of polyhedra filling which is seen in Figure 2. However, it is important that the set of polyhedra specific for each period of the Mendeleev Table is not just a set, but a set of interconnected polyhedra, because starting from the hexahedron of s electrons each subsequent polyhedron is inscribed into the median sphere of the previous one. As a result, each set of polyhedra is a sequence of polyhedra consistently inscribed into each other. This way of formation of the set brings the median spheres, on which the electron orbits of different states are located, closer. Thus, the difference in energies between different states in each set is reduced.
Second, it seems that a weak Coulomb interaction between two s electrons makes their state unstable. Therefore, the s electrons either combine with p electrons under certain conditions to form an octahedron (e.g.: 2s and 3s electrons) or help d electrons to fill their dodecahedron (4s, 5s, 6s, 7s electrons). The only exception is the 1s state, which is closest to the nucleus, and perhaps it remains unchanged in all atoms for this reason. However, despite its instability, the s state is important for the atomic structure formation, because it is the first in each period of the Mendeleev Table and its equipotential sphere determines the energy of different electron states in the period. (A dodecahedron and then the other polyhedra are inscribed consistently into the median sphere of its hexahedron). In addition, the hexahedron of s electrons which becomes empty after the transition of s electrons into the d state is later filled with p electron orbits. Therefore, the hexahedron of p electrons is located at a larger distance from the nucleus and encloses each period of the Mendeleev Table.
Third, as long as any state, i.e., the polyhedron, is filled, the energy of the electrons filling it remains the same for all electrons despite the increase in the nuclear charge during this process. This electron energy equality is apparently maintained by compensation of a stronger electron attraction to the nucleus by an increasing Coulomb repulsion from the increasing number of electrons in the polyhedron which they fill. This is possible only under conditions of a spherically symmetric arrangement of electrons, when each electron is repelled from all other electrons in the same state.
Fourth, a periodic appearance of noble gas atoms at the end of each period of the Mendeleev Table is accompanied by a sharp change in the electric field strength at the atomic surface. The inertness of noble gases means the absence of electric field at their surfaces, i.e., a complete shielding of the nuclear charge by the electron shell (by a set of polyhedra ending with a hexahedron of p-electrons). As the nuclear charge increases further, the electric field at the atomic surface appears again, but its strength is no longer determined by the point nuclear charge. It is determined by the charge of a charged sphere with the radius equal to the radius of the noble gas atom preceding the given period of the Mendeleev Table. The nucleus remains a point charge only for the electrons of periods I and II. Therefore, for other periods the field strength at the atomic surface is determined by not only the nuclear charge, but also by the charged sphere radius: E = K ∙ Ze/(Ra + x)2, where K is a known 1/4πεo constant, Ze is the nuclear charge, Ra is the noble gas atom radius in the preceding period of the Mendeleev Table, and x is the distance to the charged sphere surface.
Finally, in addition to a certain sequence of filling, the filling of each next polyhedron begins only after a preceding polyhedron is filled. Deviations from this rule are observed only in atoms with f electrons. Perhaps that is why these atoms have a high chemical activity, which is also true for gas Rn, which occupies the position of a noble gas in the Mendeleev Table.
In Section 3 we discussed the energy quantization of electrons associated with the distribution of electron orbits over different polyhedra. A small difference in the energies of different states was assumed. The sequence of polyhedra filling considered above confirmed that the difference in energies of the states should really be low, since the polyhedra are consistently inscribed into the median sphere of the previous polyhedron. Let us call this quantization a small-scale quantization in comparison with the quantization associated with different periods, the nature of which becomes obvious from the consideration of the electron shell structure of the atom, which consists of sets of polyhedra.
Indeed, the Mendeleev Table shows that each new period begins after the nuclear charge changes by a strictly defined number of units: 8, 8, 18, 18, 32, 32. This means that the filling of each new set of polyhedra begins at the field strength quite different from the previous one. It has been shown above that the field strength depends on the nuclear charge and on the charged sphere radius. Since both the charged sphere radius and the field strength at which each new set of polyhedra begins to be filled are discrete, there must be discrete energies which the electrons can have. It is obvious that energy quantization of electrons associated with different periods of the Mendeleev Table (different sets of polyhedra) takes place already with a much larger difference in energies than quantization associated with different electron states in each period. This is a large- scale quantization.
Thus, the Coulomb interaction between electrons, which distributes electrons in a certain manner in the space around the nucleus (Figure 4), leads to two different scales of their energy quantization, i.e., quantization associated with state and period.
![]()
Figure 4. Sequence of equipotential spheres on which electron orbits are in an atomic shell (after the s electron transition into d states). Atomic shell compression when the nuclear charge is increased is ignored.
Note, that 3d electrons in Figure 4 are absent because the model does not imply electron transitions between the polyhedron sets with different energies in the cases when the electrons are not affected by an external factor (such as an external strong electric field, for instance). Therefore, the designation 3d for d electrons in period IV of the Mendeleev Table is not entirely correct. They, apparently, should be 4d electrons. This also applies to d electrons of other periods and also to f electrons.
5. Specific Features of the Electron State in a Circular Orbit Centered Outside a Nucleus
Let us consider, as an example, the forces acting on an electron in a circular orbit in the spherically symmetric field of the nucleus by using a He atom in which, as already noted, two electron orbits are on opposite sides of the hexahedron (Figure 1) Figure 5.
One can see from Figure 5 that two forces act on the electron I: the force of attraction to the nucleus Fa and the force of repulsion between electrons (I and II) Fr. The total force FΣ equal to FΣ = Fa − Fr is directed at angle ϑ to the electron rotation axis.
Let us decompose FΣ into two components, i.e., 
directed perpendicularly to the orbit plane and Fc lying in the orbit plane and directed towards its center. The momentum of force Ʈ created by force 
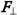and defined as the vector product Ʈ = [ro 
], where ro is the electron radius-vector relative to the orbit center, must be perpendicular to ro and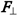 
and directed tangentially to the orbit in the direction from the reader. This direction of the force momentum Ʈ determines the direction of the electron linear velocity Ʋ in the orbit and also the direction of the electron angular velocity ω directed always along the rotation axis and away from the nucleus in this case. Normally, the presence of a force momentum Ʈ entails a change in angular velocity ω and hence impulse moment L [8] . However, if a stationary rotation axis along which the angular velocity is
![]()
Figure 5. Forces acting on an electron in a circular orbit in the nuclear field in the He atom and resolution of the total force into two components.
directed is chosen as the origin (and this case is of interest to us) the projection of force moment Ʈ on this axis is zero, since Ʈ lies in the orbit plane perpendicular to the axis. This means that the force moment Ʈ does not change the angular velocity ω in this case. Thus, ω = Const and L = Const.
As known, this is the case when the force acting on the particle perpendicular to the trajectory of its motion does not do the work [8] .
The second component Fc of the total force FΣ acting on the electron is the centripetal force, which provides a centripetal acceleration ac, depending on the angular velocity and electron radius-vector relative to the orbit center, i.e. ac = −ω2ro. This centripetal acceleration changes only the direction of electron linear velocity in the orbit (or the position of the radius-vector rо on the orbital plane).
Thus, the total force FΣ acting on the electron determines its rotation in a circular orbit in a certain direction with a constant angular velocity ω, linear velocity Ʋ equal to the vector product Ʋ = [roω], centripetal acceleration ac = −ω2ro and constant kinetic energy Ek = 1/2 mro2ω2.
Note that the Coulomb repulsion force in the He atom is determined by the interaction between two electrons alone. In the states where there are more electrons and where each electron under the condition of the spherically symmetric distribution is repelled simultaneously from all electrons in the same state, the contribution of the repulsive force to the total force is greater. Therefore, the Coulomb interaction between electrons in the atom can be considered to be strong.
Note also that it is the Coulomb repulsion force between electrons that ensures a stable position of the electron in the circular orbit centered outside a nucleus. The lack of such a force in hydrogen, apparently, explains the instability of its electron in the circular orbit and the impossibility of existence of hydrogen in the atomic state. It is known that hydrogen exists only in the form of a molecule H2 or a positively charged ion in compounds with other elements. The dissociation constant of the hydrogen molecule is only 2.56 * 10−34 at 300 K and 1.22 * 10−3 at 2000 K, dissociation energy is large 436 kJ/mole [9] .Therefore, consideration of the atom structure should begin with the He atom rather than hydrogen.
6. Electron Pairs and Physical Meaning of the Spin Concept
A spherically symmetric distribution of electron orbits on faces of regular polyhedra which are characterized by opposite face parallelism leads to the electron pair formation in any state, i.e., electron pairing. The electrons of each pair are arranged symmetrically with respect to the nucleus. This means that the electrons of the pair have a common rotation axis passing through the nucleus, but they are on opposite sides of the nucleus (Figure 5). Thus, the nucleus is the nodal point of any electron state in the atom. The electrons in such pairs have opposite directions of impulse momenta and angular velocities, and also of orbital magnetic momenta. This is not surprising, since the vectors of impulse moment and orbital magnetic moment are not true vectors. They are only pseudo-vectors which reverse their direction under mirror reflection [8] . Thus, the feature manifested itself in conditions of a spherically symmetric distribution of electrons in the atom.
Opposite directions of the electron impulse and orbital magnetic momenta in a pair mean that these electrons rotate in opposite directions relative to their common axis, while they rotate in the same direction relative to the surface of the equipotential sphere on which their orbits are located. This direction (relative to the surface) is the counterclockwise one always and is governed by the direction of the force moment acting on the electron in the orbit. In an atom, therefore, the impulse momenta of all the electrons are directed away from the nucleus, and their orbital magnetic momenta are directed towards the nucleus.
The fact that electrons in a pair have opposite directions of the orbital magnetic moment changes the concept of electron spin [10] [11] [12] . The spin turns out to be related to the orbital magnetic moment and to its direction. It essentially reflects the fact that electrons of each pair having the same axis passing through the nucleus are rotating in opposite directions relative to their axis. Since only two directions (clockwise and counterclockwise) are possible in the orbital plane, the spin has only two directions (spin up, spin down). Thus, spin is neither a property peculiar to the electron itself nor a purely quantum phenomenon. It is only one of the characteristics of electron state in the nuclear spherically symmetric field.
It follows from the above that we can still speak about the electron spin only when the electron is in one of the atomic states. Outside the atom, the concept of spin loses its meaning and only the orbital magnetic moment of the rotating electron remains.
It should be noted in this connection that the O. Stern and W. Gerlach experiment [13] which was explained by using the spin concept was successful only because the investigation was carried out with individual Ag atoms containing one unpaired electron, i.e., one electron of the pair. In this case the electrons remained in the atomic 5s state and could rotate clockwise in one atom and counterclockwise in another (relative to their rotation axis in each atom and relative to the direction of the outer magnetic field which deflected the Ag atoms).
7. Magnetic Dipole-Dipole Interaction in the Atom
Let us consider another kind of interaction between electrons in the atom connected with the electron rotation in circular orbits. In Section 6 we mentioned the electron orbital magnetic moment which depends, as known, on the current created by the electron rotation and the orbital area covered. Such a rotating electron can be regarded as a small magnetic dipole. This means that a magnetic dipole-dipole interaction must exist between neighboring electrons in the atom. Since the dipole-dipole interaction strength depends on the cosine of the angle between the dipole directions, it is maximal when the neighboring dipole directions are parallel (repulsion) or antiparallel (attraction) to each other, and is zero when their directions are perpendicular.
It follows from the geometry of polyhedra that the angle between neighboring dipole directions in the atom is 2ϑ, where ϑ is the angle between the electron radius-vector ρ relative to the nucleus and orbital axis (Figure 3). Since both the angle ϑ and radius r0 are different for electrons of different states, the dipole- dipole interaction strength will also be different. For example, if the angle between the directions of neighboring dipoles for p electrons is 90˚, there will be no magnetic dipole-dipole interaction between them. This fact distinguishes the p state from all other electron states in the atom, since the magnetic dipole- dipole interaction between neighboring electrons in the s, d and f states must exist.
The lower the angle ϑ or the shorter the distance between the dipoles, the stronger the magnetic interaction.
Since all orbital magnetic momenta (magnetic dipoles) in the atom are directed towards the nucleus, the dipole-dipole interaction between them is repulsive, i.e., it acts on the electrons just as the Coulomb repulsion does.
Despite the fact that the magnetic dipole-dipole interaction between electrons is much weaker than the Coulomb interaction, it may affect the atomic properties and, above all, its chemical activity. This is evidenced by the absence of chemical activity of noble gases where the magnetic dipole-dipole interaction between neighboring dipoles is absent.
Since each electron in the atom that creates its magnetic field is also influenced by magnetic fields of other electrons of the same state, we may conclude that the electron in the atom is in a spherically symmetric electromagnetic field which, like the electric field, varies periodically along the atomic radius. Therefore, the resulting force acting on the electron in an atom and including both electric and magnetic components should be regarded as the Lorentz force.
8. Noble Gas Atoms as Examples of Closed Systems
As it is known, atoms of noble gases differ from other atoms in that their outer electron shell is a completely filled p shell. When all states are completely filled, all p electrons are paired. In the case of a spherically symmetric distribution of electron orbits this means that the vector sums of angular momenta of all electrons, as well as their orbital magnetic momenta, are zero. The sum of all charges is also zero. In addition, there is no magnetic dipole-dipole interaction between neighboring electrons in the outer shell. At the same time there are strong interactions in the atomic system itself. However, they do not manifest themselves outside the system, remaining inside it. Such systems are typically referred to as closed systems which interact neither with other external systems nor among themselves [14] . Therefore, the atoms in question exist in the gaseous phase and as single-atomic gases.
It should be emphasized once more that the specific feature of the atomic structure is a periodic repetition (with increasing nuclear charge and number of electrons) of the atomic state as a closed system, accompanied by periodic changes in the electric and magnetic fields in the atomic shell and periodic changes in the atomic properties. All this is due to a periodic spatial electron distribution in the electron shell (Figure 4) or, speaking more generally, due to a limited number of regular polyhedra.
9. Conclusions
It has been shown that the electron shell of the atom is spatially structured and an important role in this is played by the Coulomb interaction between electrons. First, it ensures a stable rotation of electrons in the orbits centered outside the nucleus and, second, it distributes these orbits on the equipotential surfaces in a spherically symmetrical manner. This distribution is similar to “inscribing” the orbits into faces of regular polyhedra centered by the atomic nucleus. In other words, in each state the electrons are distributed so that planes of electron orbits form a regular polyhedron by crossing each other. Therefore, the number of possible electron states in an atom corresponds to the number of regular polyhedra, excluding the tetrahedron, and the number of electrons in each state is equal to the number of faces of the polyhedron corresponding to the given state, excluding the s and f states.
It has been shown that the description of the electron orbit distribution using regular polyhedra permits determination of the equipotential surfaces on which the orbits are located, the orientation of their planes and rotation axes relative to the nucleus, and also their maximum possible radius in each state.
It has been shown that a spherically symmetric distribution of electron orbits is also associated with specific features of electron states in the atom, in particular, the formation of electron pair having a common rotation axis passing through the nucleus, but with oppositely directed impulse and orbital magnetic momenta. This makes the concept of spin questionable. The spin appears to be related to the electron orbital magnetic moment or rather to the direction of the orbital rotation of the electrons in pair relative to its rotation axis passing through the nucleus. Thus, the spin seems to be one of characteristics of the electron state in the spherically symmetric field of the atom rather than a property inherent in the electron itself or a purely quantum phenomenon.
It has also been shown that the spherically symmetric distribution of electron orbits, similar to the distribution of faces in regular polyhedra, gives an insight into basic properties of the atomic system as a whole, i.e., a periodic change in the properties of atoms with increasing nuclear charge, a periodic formation of closed atomic systems and also the origin of the double quantization of electrons in energy.
To summarize, the electron shell structure of the atom and its properties are determined by the Coulomb interaction between electrons under conditions of a spherical symmetry of the nuclear field. Under these conditions, electrons behave as particles obeying the laws of classical mechanics and classical electrodynamics.