Discovery of New Terms Associated with the Navier-Stokes Momentum Balance Equation and Finding the Evidence of Its Inapplicability to Govern Fluid Flow in the Infinite Space ()
1. Introduction
Navier-Stokes equations are designed to govern the motion of fluids, including gases. Originally, they were derived based on the continuum assumption that considers fluids to be continuous. The equations are formulated by considering the mass, momentum, and energy conservations for a control volume of arbitrary size. The flow is considered continuous and differentiable so that the mass, momentum, and energy balances may be expressed as partial differential equations. However, being essential for physics and fluid dynamics, these equations are extremely difficult to solve. Moreover, for three-dimensional Navier-Stokes equations and given initial conditions, mathematicians have not yet proved that physically realistic smooth solutions always exist on all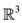
. The Clay Mathematics Institute has named this question as one of the significant obstacles confronting mathematicians and physicists in the twenty-first century.
The Navier-Stokes mass and momentum balance equations for incompressible fluid are expressed as
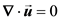(1)
and
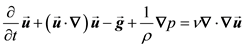, (2)
respectively, for 
and
. In the equations above, 
is the constant density of the fluid, 
is mass flow velocity evaluated at point 
and at a time t,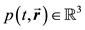 
is the pressure field, 
is the smooth on 
external force per unit mass, and 
is the kinematic viscosity. For gases, the kinematic viscosity is defined as
, (3)
where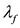 
is the mean free path, 
is the thermal velocity of a particle defined through the “average kinetic energy” as
, (4)
where 
is Boltzmann constant, T is the temperature, and m is the mass of a particle and ![]()
is a numerical coefficient the value of each varies from a typical 1/3 to ![]()
obtained via a mathematically rigorous derivation [1]. The initial condition on ![]()
at time ![]()
is given by
![]()
for![]()
, (5)
where ![]()
is a ![]()
divergence-free vector field on![]()
.
The Fundamental Problem related to the Navier-Stokes equations is: Given the initial distribution of velocity ![]()
at time ![]()
and the body force ![]()
for![]()
, one needs to determine a unique regular solution![]()
, ![]()
to (1), (2), and (5) for all times ![]()
[2].
The Clay Millennium Problem on Navier-Stokes equations for a viscous fluid (![]()
) is also presumed to be solved in the case of the breakdown of Navier-Stokes solutions on ![]()
upon the proof that “there exists no solution![]()
” of (1), (2), and (5) on ![]()
[3].
Note: in the text, the terms “fluid flow”, which mostly relates to the Navier-Stokes equations, and “gas flow”, which mainly relates to the following description of our model, have an identical meaning.
The Navier-Stokes equations assume that the fluid behaves as a continuous matter rather than discrete particles. Namely, the number of gas particles (atoms or molecules) within the smallest applicable region (infinitesimal material element used for deriving governing differential equations of fluid dynamics) is sufficient that all fluid properties are point functions. Navier-Stokes equations arise from applying Newton’s second law of motion in combination with fluid stress (due to viscosity) and a pressure term.
The pressure force is defined as the force transmitted across the closed surface ![]()
with the outer unit normal![]()
. As shown below schematically in Figure 1.
![]()
Figure 1. Schematics of defining the pressure in the confined space, the 3D Heaviside step function![]()
, and the concept the property balance in 3D gas space. The observer’s Cartesian coordinate system is labeled by index 100.
In this schematic, the observer’s coordinate system is labeled by index “100”. The net surface force due to pressure p exerted by the surroundings on the control volume (CV) is
![]()
, (6)
where ![]()
is an external force applied on the differential surface element dS of the CV [4]. Using the corollary divergence theorem (gradient theorem) to the above gives
![]()
. (7)
According to the divergence theorem, the pressure gradient ![]()
is defined only inside the CV and will have a non-zero value if the pressure is distributed non-uniformly over the surface![]()
. If the pressure p is constant on![]()
, then ![]()
inside of the CV. From this, one can expect that the term ![]()
should not appear in the Navier-Stokes momentum balance equation if it is expanded to describe the fluid flow in the infinite space ![]()
and the ambient pressure ![]()
is constant at infinity.
The Navier-Stokes equations are derived by formulating conservation of the properties of fluids (mass, momentum, or energy) in a finite arbitrary volume, called a control volume ![]()
bounded by a closed surface![]()
. Then invoking the Reynolds transport theorem, an integral relation stating that the sum of the changes of some extensive property (mass, momentum, or energy) defined over the CV must be equal to the loss or gain through the boundaries or control surface (CS) of the control volume and generation or loss by sources and sinks inside the CV. Finally, one can deduce differential equations for the mass conservation, Equation (1), and the momentum conservation, Equation (2), by using the divergence theorem [4]. The unknowns in the Navier-Stokes equation are the velocity ![]()
and the pressure![]()
. Because of three dimensions, there are three first-order non-linear differential equations having four unknown variables![]()
, ![]()
, and ![]()
and pressure p Therefore, an additional equation is needed. The continuity equation ![]()
(Equation (1)) that describes the conservation of mass of the fluid will not be too much useful as an independent equation since it has been used for deriving the Navier-Stokes Equation (2). The common mathematicians’ efforts to solve the problem are reduced mostly to prove the existence and the uniqueness of the Navier-Stokes solution.
Mathematicians recognize that “…clearly the structure of the pressure term demands dependence on u or the derivatives of u. However, in fluid flow, it should be clear that the fluid velocity u and the pressure term p are deeply connected. A fluid velocity field will produce pressure on a surface, while the pressure itself must interact with the velocity field. This dance back and forth between velocity and pressure must drive every system of fluid under study [5].” Also, “most fluid systems must function inside some form of containment. The flow of fluid in a pipe, from a tank, down a river, has physical constraints that move a fluid along a certain path. Therefore, there must be bound on the fluid velocity u, as well as the spatial derivatives ![]()
[5].”
Given the fluid flow in the form of a non-isothermal incompressible gas flow, one may conclude that the temperature gradient defined in each point of the gas space may serve as “a bound on the fluid velocity u”. Applying operator ![]()
to the equation of state of the ideal gas, the pressure gradient at a point inside the incompressible gas at the non-uniform temperature is expressed as
![]()
, (8)
where n is the particle density, which, for the incompressible gas, is constant. It implies that, in each point of the gas space![]()
, the pressure gradient is along with a temperature gradient and is directly proportional to the temperature gradient. However, at the uniform temperature, the temperature gradient and associated with it the pressure gradient is zero, so the “bound on the fluid velocity u” vanishes.
The Navier-Stokes equations originally derived solely for the bounded space appeared to describe fluid flow correctly. However, their expansion for describing the fluid flow in the infinite space without relying on the physically reasonable model is doubtful. We explain this in the following example. Assume that, based on the analysis of a certain hypothetical model, someone has derived a differential equation by analyzing a process in a small, confined interval [0, 0.5). The differential equation intending to govern some physical process has the following form
![]()
(9)
with the initial value![]()
. Is it proper to expand the application of the differential equation for governing the physical process in the interval![]()
? The general answer is no. While the solution of Equation (9) in the interval ![]()
in the form
![]()
(10)
is almost identical (with the relative error, let us say less than 0.2%) to the hypothetical experimental function, which is extrapolated as ![]()
in the interval![]()
, it unfits to be applied in the wider range of known hypothetical experimental data at![]()
. The relative error in this range is increased from 1.8% at ![]()
to 74% at![]()
, which is unacceptable.
Luckily, a new physically reasonable hypothetical model expanding its application to the interval ![]()
was proved. The derived governing equation
![]()
(11)
with the initial value ![]()
has a physically reasonable solution ![]()
for all ![]()
and a low relative error in comparison with![]()
. Applying the Taylor series expansion method to the equation above, we obtain:
![]()
(12)
According to the Taylor theorem, since ![]()
is a![]()
, then the solutions of Equations (11) and (12) are identical. The range of applicability of the equation above is ![]()
and the radius of convergence of its solution is infinity. Suppose the Taylor series is truncated after a few numbers of derivatives. In that case, the range of applicability of the truncated differential equation will be limited as well as the radius of convergence of its solution will not expand to infinity. If, for certainty, the Taylor series is truncated after the third derivative, the equation above will be reduced to Equation (9). Therefore, even without comparison with![]()
, we may conclude that the differential Equation (9) is not applicable for governing the physical process in the interval![]()
. We report a similar strategy to determine whether the Navier-Stokes momentum balance equation can govern the fluid flow in the infinite space.
Navier-Stokes equations result from applying Newton’s second law of motion to fluids. The first two left-hand terms are inertial forces, the third and fourth left-hand terms are external body force and the pressure force. The right-hand term represents viscous forces. Is this combination of the forces being exhaustive in the momentum balance equation? In other words, is there something missing in the momentum balance equation? This question may be considered unreasonable because the Navier-Stokes equations have been under intense study by many physicists and mathematicians since 1822 [6] (this year is the 200th anniversary of their discovery). Therefore, it would be difficult to imagine missing some unknown effect. However, in this paper, we report that we found the new important terms associated with the Navier-Stokes momentum balance equation. One of them relates to the component of velocity acquired by each gas particle during its free path traveling in the body force field. The other is linked to the temperature gradient in a non-isothermal fluid system.
Recently we proposed a new approach in the modeling of fluid dynamics problems. It recognizes that each gas particle moves with a probability between two points in space occupied by the gas and follows a ballistic trajectory governed by a law of motion in free space. Each gas particle is treated as a property carrier transporting one or more mass, momentum, and energy between the points of consecutive collisions. Each point in space occupied by the l gas is both a sink accumulating property delivered by converging ballistic particles from the entire gas system and a source dispersing property by diverging ballistic particles [7]. Based on this approach, we formulated the Ballistic Principle of the Property Balance in the Space (BPPBS) occupied by the gas, which may simplify and reduce computations in applications dealing with modeling of fluid dynamics problems [8] [9]. In the most recent publication [10] , we discuss a novel computationally efficient method of modeling rarefied gas flow in a microchannel based on the BPPBS. We explicitly investigated the effect of the Knudsen number on the gas flow in the microchannel. Moreover, we concluded that the assumption that the MFP varies as a function of the surface confinement (Knudsen number), widely issued in the literature, is mistaken.
This paper provides further insights into the newly discovered BPPBS and its application to formulate governing mass and momentum balance equations for incompressible gas flow in integro-differential and differential forms. Specific attention is paid to comparing the governing differential equations derived from the principles of our theory and the Navier-Stoke equations. We also paid attention to the Fundamental Problem related to the Navier-Stokes equations, which requires the answer whether there is a solution of the Navier-Stokes equation on![]()
.
In Section 2, we describe the physical principles of the Ballistic Model (BM) adapted to the three-dimensional incompressible gas flow and its application to construct the property balances.
Section 3 provides integro-differential forms of mass balance and momentum balance equations adapted to the incompressible gas flow in the infinite gas space.
Section 4 presents the technique of reducing integro-differential forms of mass and momentum balance equations to the corresponding differential forms by the Taylor expansion of the integral terms.
Section 5 signifies similarities and differences of the governing differential equations derived from the principles of our theory and the Navier-Stoke equations.
Finally, in Section 6, we present the discussion and conclusions.
2. Physical Principles of the Ballistic Model Adapted to the Three-Dimensional Incompressible Gas Flow
This section describes the physical principles of the BM adapted to the three-dimensional incompressible gas flow at the non-uniform temperature and low flow velocity (with the Mach number less than 0.3). The BM is based on the newly discovered BPPBS occupied by the gas [7] [8]. According to the BPPBS, in each nonmoving point of the gas space at a given time, the net rate of property (mass, momentum, or energy) influx per unit volume, formed by the carrying the properties converging ballistic particles (each traveling along a ballistic trajectory with certain survival probability) from an initial point within the space occupied by the gas equals to the temporal rate of property change per unit volume and the net rate of property efflux per unit volume, the efflux formed by the diverging particles dissipating their property in the surrounding space by collisions [8].
Recognizing the unconventional nature of our approach and in the interests of a better understanding of our method, we provide a short introduction to the methodology adapted to the incompressible gas flow at the non-uniform temperature in general.
2.1. Properties and Features of the Incompressible Gas
Here we assign the following properties to the gas, which are originally proposed in [7] and [8]:
1) The gas particles being in a constant state of mostly random motion and interaction by collisions participate in the transport of properties, including mass, momentum, and energy.
2) Each gas-particle moves by obeying a ballistic trajectory governed by a law of motion in free space. It overcomes a distance between any two points of the ballistic trajectory with a certain survival probability.
3) Each gas particle carries a combination of one or more properties between a point of initial collision and a point of ending collision.
4) Each point within the gas space is treated as a point of collisions for converging ballistic particles physically capable of simultaneously targeting the same ending point.
5) Each point of collisions is treated as either a point source for diverging ballistic particles or a point sink for converging ballistic particles.
6) Each ballistic particle moving from the point source to the point sink is treated as a property carrier created in the point source by obtaining one or more properties of specific values intrinsic to the gas surrounding the point source. It is ended in the point sink by transferring one or more properties of specific values in the point sink.
7) The properties carried by the ballistic particle are conserved during the ballistic traveling time.
One can note from the above that the gas properties differ from the properties typically assigned to the ideal gas (see in Introduction of [8] ).
2.2. Bases of Construction of the Property Balance in the Incompressible Gas Space
On the microscopic scale, the incompressible gas flow is characterized by the group of particles of mass m, which move randomly and interact by collisions with effective collision cross-section![]()
. In each point of gas space at a given time, the parameters quantifying gas flow are the particle density n, which is constant for the incompressible gas, the magnitude of thermal velocity ![]()
and the vector of mass flow velocity![]()
. Also, in the presence of external force, each particle is accelerated during its ballistic traveling with acceleration![]()
.
Based on the BPPBS [8] , we expect maintenance of an overall property balance in each of the collision points within the incompressible gas system. The BPPBS is formulated as follows: in each nonmoving point ![]()
at a given time t, the net rate of property influx per unit volume, ![]()
, formed the converging ballistic particles (each traveling along a ballistic trajectory with certain survival probability) from the gas space is equated to the net rate of property efflux per unit volume, ![]()
, formed the diverging ballistic particles and the temporal rate of property change per unit volume![]()
. This statement is expressed symbolically as
![]()
(13)
2.2.1. The Model Parameters
The parameters associated with defining the property balance in the 3D incompressible gas space are presented in Table 1 and Table 2.
![]()
Table 1. The list of the model parameters associated with defining the net rate of total property influx per unit volume in the 3D incompressible gas space.
![]()
Table 2. The list of the model parameters associated with defining the net rate of total property efflux per unit volume in the 3D incompressible gas space.
2.2.2. Important Assumptions and Approximations of the Model
In the following, referring to [8] , we examine the case of the collision-dominated flow regime, which implies the following assumptions and approximations:
1) For each of the gas particles, the average value of the thermal velocity![]()
, is much higher than the absolute value of the mass-flow velocity![]()
, namely:
![]()
. (14)
2) The gain/loss of the velocity because of interaction with the external field of force during the ballistic traveling time ![]()
or ![]()
is insignificant in comparison with the thermal velocity![]()
, namely:
![]()
or![]()
, (15)
where ![]()
and ![]()
are the ballistic traveling times between two consecutive collisions at ![]()
and ![]()
and ![]()
and![]()
, respectively. Moreover, nevertheless the external field of force![]()
, such as the gravitational force, may vary in space and time, its change generally is very insignificant on the length scale or time scale of several mean free paths or mean free times, respectively (see the estimations by Equations (89) and (90)). Therefore, in the following, we will treat ![]()
as a constant when differentiating or integrating.
Because of the limitations shown by Equations (14) and (15), when defining ![]()
or![]()
, we approximate trajectories of the gas particles forming fluxes as straight lines so that
![]()
, (16)
and
![]()
, (17)
where ![]()
is the time of the converging particle positioning in point![]()
, which is defined as
![]()
. (18)
3) The relative change of any property value or any parameter characterizing the gas Σ is insignificant during the period between collisions ![]()
in each point of the gas, which is expressed:
![]()
. (19)
4) The relative change of any property value or any parameter characterizing the gas is insignificant on the length scale of the average distance between the gas particles![]()
, which is expressed:
![]()
. (20)
5) For clarity and simplicity, when applying the operator![]()
, we neglect insignificant terms having![]()
, ![]()
, or![]()
. Therefore, ![]()
and ![]()
are approximated as
![]()
, (21)
respectively, where ![]()
is the unit vector of arbitrary direction from the point![]()
, which is
![]()
(22)
and ![]()
is the unit vector of arbitrary direction from the point![]()
, which is
![]()
. (23)
6) We will use analytical representations for ![]()
and ![]()
as
![]()
, (24)
and
![]()
, (25)
respectively [8]. In the equation above, ![]()
is the time of positioning in point ![]()
of the diverging from ![]()
particle, which is defined as
![]()
. (26)
7) We adapt Equation (70) of [8] to the incompressible gas flow at the non-uniform temperature, we approximate ![]()
as
![]()
, (27)
where ![]()
is expressed by Equation (24) of [8] with some minor symbolic modifications:
![]()
(28)
and ![]()
is expressed as
![]()
(29)
and ![]()
varies from zero to![]()
.
Similarly, we adapt Equation (72) of [8] , which was approximated there assuming a high frequency of collisions expressed as ![]()
and non-violent gradients of fluid parameters within the gas system, which yields
![]()
. (30)
Analogously, adapting Equation (65) of [8] to the incompressible gas flow at the non-uniform temperature, we approximate ![]()
as
![]()
, (31)
where![]()
, ![]()
is expressed by Equation (24) of [8] with some minor symbolic modifications:
![]()
(32)
and ![]()
is expressed as
![]()
(33)
and ![]()
varies from zero to![]()
. Similarly, assuming the high frequency of collisions expressed as ![]()
and non-violent gradients of fluid parameters within the gas system, this yields:
![]()
. (34)
At the uniform temperature, Equation (27) is reduced to
![]()
. (35)
8) Also, recognizing that the magnitudes of the thermal velocity of nearby particles are approximately identical, we may determine the average magnitude of the velocity with respect to each particle moving in an arbitrary direction (relative velocity) by substitution of ![]()
in Equation (28):
![]()
. (36)
Analogously, we determine the average magnitude of the velocity with respect to each particle moving in an arbitrary direction (relative velocity) by substitution of ![]()
in Equation (32):
![]()
. (37)
At the uniform temperature or in the nearby region surrounding the singular point at![]()
, Equation (27) is reduced to
![]()
(38)
and Equation (31) is reduced to
![]()
(39)
9) The mean free path ![]()
or the average distance that a gas particle pass through before experiencing a collision is found by calculating the average distance traveled![]()
:
![]()
(40)
10) The gas pressure gradient at a point inside the incompressible gas at the non-uniform temperature is
![]()
(41)
11) Using Equations (32) of [8] as the bases, we define the rates of collisions per unit volume in the point![]()
, ![]()
, and in point![]()
, ![]()
, as
![]()
(42)
and
![]()
, (43)
respectively.
12) Finally, we will use![]()
, a first vector derivative of the Green function with no boundary conditions, as
![]()
, (44)
which has the following property:
![]()
(45)
and
![]()
. (46)
13) We will also use the following relationships:
Let ![]()
is a continuously differentiable vector field defined on a neighborhood of the volume V confined by the closed surface ![]()
defined by a function![]()
, where a is a constant, ![]()
is inward normal to![]()
, and ![]()
is the Heaviside step function defined as follows:
![]()
(47)
Then
![]()
(48)
where ![]()
is the surface of the body where ![]()
![]()
(49)
where ![]()
is the region outside of ![]()
where![]()
.
14) Distribution definition: Let ![]()
is a scalar function given with continuous derivatives of all orders that vanishes outside some finite domain outside of![]()
. When
![]()
, (50)
then
![]()
(51)
15) Divergence theorem for![]()
:
![]()
. (52)
Applying the divergence theorem for the arbitrary volume containing point ![]()
we find
![]()
. (53)
16) The following relationships will also be useful for mathematical processing.
![]()
, (54)
where![]()
,
![]()
, (55)
and
![]()
(56)
where the subscript on the “nabla” symbol ![]()
indicates the variable with respect to which differentiation is performed. Namely, ![]()
does not act on the dependable variable![]()
.
Analogously, we obtain
![]()
, (57)
and
![]()
. (58)
17) The integration of these three integrals, which will be often used in the following, is performed by converting the orthogonal coordinate system into the spherical having the origin in point ![]()
followed by integration:
![]()
(59)
![]()
(60)
![]()
(61)
![]()
(62)
18) The following relationships from the vector analysis involving vectors and dyads [11] are used below
![]()
(63)
and
![]()
, (64)
where![]()
, ![]()
, and ![]()
are vector functions, and ![]()
is the unit dyad.
2.3. Analytical Representation of a Net Rate of Total Property Influx Per Unit Volume in a Nonmoving Point of Gas Space in the Collision-Dominated Flow Regime
To express analytically the net rate of total property influx per unit volume in the collision-dominated flow regime, which applies to a given non-moving point of space occupied by the gas at a given time, we will, first, define the property flux from the gas space in a given non-moving point ![]()
at time t, as schematically shown in Figure 1, by adapting Equation (34) of [8] to the incompressible gas flow at the non-uniform temperature, which is done by substituting Equations (24), (27), (42), and applying some minor symbolic modification, which yields
![]()
(65)
In the equation above, each term confined in the square brackets is the particle flux component associated, the first, with the thermal velocity![]()
, the second, with the mass velocity![]()
, and the third, with the velocity ![]()
acquired by the ballistic particle because of the external field of the force. As it was mentioned earlier, point ![]()
shall be excluded from integration because we are quantifying the total rate of the property flux in the point sink at![]()
, which is originated from the surrounding point sources of the initial collisions at![]()
. The first term in the square bracket in the equation above has a “naturally” built-up analytical structure such as the first vector derivative of the Green function, which allows vector differentiation in the singularity point and sequential zeroing the result (see Equation (46)).
However, the under integral terms in the second and the third integrals do not reflect symbolically such important physically reasonable limitation, and therefore we changed them by incorporating the Heaviside step function as a test function such as the Heaviside step function, which yields
![]()
(66)
The 3D Heaviside step function ![]()
is defined below.
Consider a space in which point ![]()
is surrounded by a region bounded by a spherical surface ![]()
of radius a, as shown in Figure 1, defined by function f:
![]()
. (67)
We expect that only the impact of particles originated from preceding collisions in the volume ![]()
outside of the volume confined by surface ![]()
may participate in forming the gas particles flow. Function f is greater than zero outside a volume enclosed by a surface ![]()
and less than zero inside the volume [12]. Then the unit normal to the surface![]()
, pointing out of the region, is given by
![]()
. (68)
Thus, using function f as an argument of the Heaviside step function, ![]()
, allows removing the impact of the flux from the region inside of the surface ![]()
[12].
Then we may find the net rate of total property influx per unit volume in a nonmoving point of gas space by applying the divergence operator ![]()
as follows
![]()
(69)
In the equation above, we introduced the minus sign because ![]()
is intended to be used in the right-hand of the balance equation. Finally, since the point ![]()
is excluded from integration in the domain of integration Ω in which![]()
, the operation of differentiation regarding a parameter ![]()
is interchangeable with the operation of integration over some other variable, which yields:
![]()
(70)
2.4. Analytical Representation of a Net Rate of Total Property Efflux Per Unit Volume From a Nonmoving Point of Gas Space in the Collision-Dominated Flow Regime
Here we use a different than in [8] scheme of defining a net rate of total property efflux per unit volume from a nonmoving point of gas space. Upon more detailed analysis, we realized that, since each point in the gas space serves as the sink of the converging gas particles and the source of the diverging gas particles, one shall consider the exhaustive combination of the transport events in each point of the gas space. Each trajectory of the ballistic particle converging in point ![]()
at time t (traveling from the past) is the trajectory of the same ballistic particle diverging from the point ![]()
at time ![]()
(traveling toward the future relative to the time![]()
). Therefore, one may conclude that the balance will not be conserved if one ignores to consider the event of delivery of the diverging ballistic particle from ![]()
at time t to ![]()
at time![]()
.
Using Equation (65) as a template, we define the property flux![]()
, which is originated from initial collisions in point ![]()
and directed toward the plurality of points ![]()
in the space occupied by the gas, as schematically shown in Figure 1, by removing ![]()
in the template Equation (because now the source at the point ![]()
is included in the integration) and by switching the source location to the point ![]()
and the think location to the plurality of points ![]()
within the gas space. This procedure will automatically lead to substituting in the template equation of![]()
, ![]()
, ![]()
, ![]()
, and ![]()
by![]()
, ![]()
, ![]()
, ![]()
, and![]()
, respectively, which are defined in the equations above. This yields the following:
![]()
(71)
Then we may find the net rate of total property efflux per unit volume from a nonmoving point of gas space by applying the divergence operator ![]()
to the quantity above as follows:
![]()
(72)
Since point ![]()
is included in integration and ![]()
exists as a continuously differentiable function of ![]()
on![]()
, then the operator ![]()
can be applied directly to the under integral function so that
![]()
(73)
2.5. A General Integro-Differential Form of Property Balance Equation in the Three-Dimensional Gas System
The general integro-differential form of property balance equation is formulated by Equation (74) given below, which is obtained by substitution of Equations (73) and (70) in Equation (13):
![]()
(74)
Remark that the integro-differential property balance equation must be formed for each unknown property/variable. Also, the number of equations in a system of balance equations is sufficient to determine each of the unknown properties characterizing the gas flow. In the following, we provide general governing integro-differential forms of mass balance and momentum balance equations [8].
3. Integro-Differential Forms of Mass and Momentum Balance Equations in the Collision-Dominated Flow Regime
We consider the fluid to be an incompressible homogeneous gas described by continuous (![]()
) functions and filling the whole space![]()
. The gas may be subjected to an external body force ![]()
defined as a time-variant vector field![]()
. The force is assumed to be independent of the velocity field![]()
.
The following analytical representations of mass and momentum balance approximations are provided.
3.1. Integro-Differential Form of the Mass Balance Equation of Incompressible Gas in the Collision-Dominated Flow Regime
Our approach in formulating mass balance equation, as we reported earlier [8] , is based on the hypothesis that there exists a unique combination of ballistic particles converging from the entire gas system in a given point at a given time and the diverging ballistic particles from the given point at the given time. Moreover, each of the converging ballistic particles originated from a preceding collision within the gas system is selected from the group of the converging ballistic particles by a ballistic trajectory governed by the law of motion, which provides an opportunity for the particle to enter point ![]()
at given time t. Such a combination of converging and diverging ballistic particles capable of targeting or escaping point ![]()
at given time t is treated as an exhaustive combination. Therefore, from a physical viewpoint, the solution ![]()
is unique [8]. To formulate a general integro-differential form of mass balance equation in a given non-moving point of space occupied by the model at a given time, we will modify Equation (74) by assigning:
![]()
. (75)
Then, upon substitution of Equations (16), (17) (42), (43), and (75) in Equation (74), we obtain the following general integro-differential form of the mass balance equation
![]()
(76)
Executing the vector differentiation in the equation above followed by applying substitution for ![]()
by Equation (30) as well as using the functional relationships presented by Equations (37), (48), (49), (51), (53), (56), and (57), gives
![]()
![]()
(77)
Here we need to admit that the second right-hand term in the equation above is insignificant compared with the first one (see the comments to Equation (19)) and will be neglected in the future analysis.
3.2. Integro-Differential Form of the Momentum Balance Equation in the Collision-Dominated Flow Regime
Here we again should note that the momentum balance equation is formed by considering a unique combination of ballistic particles converging from the entire gas system in a given point at a given time and the diverging ballistic particles from the given point at the given time [8]. Each of the gas particles carries the momentum with the vector components associated with the thermal velocity ![]()
and the mass flow velocity![]()
. Besides, each of the converging ballistic particles can target point ![]()
at given time t and originates from an initial collision within the gas system earlier than time t. Such a combination of converging and diverging ballistic particles capable of targeting or escaping point ![]()
at a given time t is an exhaustive combination. Therefore, from a physical viewpoint, the solution ![]()
is unique.
To formulate a general integro-differential form of the momentum balance equation in a given non-moving point of space occupied by the model at a given time, we may formally modify Equation (74) by assigning:
![]()
, (78)
![]()
, (79)
and
![]()
. (80)
3.2.1. Defining a Net Rate of Total Momentum Influx Per Unit Volume in the General Non-Moving Point at the Given Time
Substituting Equations (16), (42), (57), and (79) in Equation (65), we define the momentum vector flux![]()
, which is originated from impact of initial collisions within entire space occupied by the incompressible gas
![]()
(81)
In the equation above, each term in the square brackets is the particle flux component, while each the second term is the momentum carried by the ballistic particle.
As it was mentioned earlier, point ![]()
shall be excluded from integration because we are interested in calculating the total rate of the momentum flux in the point sink at![]()
, which is originated from the impact of surrounding point sources of the initial collisions at![]()
. We may note only one term in the equation above that has a “naturally” built-up analytical structure that is the first vector derivative of the Green function, which allow vector differentiation in the singularity point and sequential zeroing the result because ![]()
(see Equation (46)). The other terms do not reflect symbolically such important physically reasonable limitation and therefore need to be modified. To this aim, we changed these terms by incorporating in each of them a test function such as the Heaviside step function, ![]()
defined above, which yields:
![]()
(82)
Integration in the equation above expands over the volume ![]()
from a point at ![]()
to the infinity. The modified under integral terms will become “infinitely smooth” functions having continuous derivatives of all orders. They vanish at the infinity and within the volume confined by surface ![]()
of radius a surrounding point A positioned at![]()
. Here we need to note that ![]()
is the pressure p in ![]()
direction on the surface normal to the ![]()
direction, which is owing purely to the flux of momentum![]()
. Now we may apply the operator ![]()
to the vector distribution above, and since ![]()
exists as a differentiable function of ![]()
on![]()
, then the operator ![]()
can be applied directly to the under integral function, which yields:
![]()
(83)
In the equation above, we introduced the minus sign because ![]()
is intended to be used in the right-hand of the balance equation. Executing the vector differentiation in the equation above followed by applying substitution for ![]()
by Equation (30) as well as using the functional relationships presented by Equations (37), (48), (49), (51), (52), (53), (56), and (58) and neglecting the terms having![]()
, ![]()
, and ![]()
gives
![]()
(84)
3.2.2. Defining the Total Momentum Efflux Per Unit Volume at the Given Time from the General Non-Moving Point
Substituting Equations (17), (42), (43), and (78) in Equation (71), we define the momentum vector flux![]()
, which is originated from initial collisions in point ![]()
and directed toward the space occupied by the incompressible gas
![]()
(85)
Now we may apply the operator ![]()
to the vector distribution above, and since ![]()
exists as a differentiable function of ![]()
on![]()
, then the operator ![]()
can be applied directly to the under integral function, which yields:
![]()
(86)
Executing the vector differentiation in the equation above followed by using the functional relationships presented by Equations (37) and (53) and neglecting the terms having![]()
, ![]()
, and ![]()
gives
![]()
(87)
3.2.3. Formulating the Integro-Differential Momentum Balance Equation in the Infinite Gas Space
Now we formulate the momentum balance equation according to Equation (13), which is done by substitution of![]()
, ![]()
, and ![]()
with![]()
, ![]()
, and ![]()
of Equations (80), (84), and (87) respectively, and normalizing all the terms by mn. This yields the following:
![]()
![]()
(88)
The equation above as well as Equation (77) reveals that, at the non-uniform temperature, the momentum balance and mass balance between the converging and diverging fluxes are affected by the thermal velocity gradient ![]()
and the external field of force![]()
. Moreover, while the converging fluxes depend on the location ![]()
and time ![]()
of the initial collisions, the diverging fluxes also depend on the probability of the ballistic traveling at the advanced times following the given time (present). It may be explained that the spatial distribution of the temperature (at the advanced time) will affect the ballistic path probability through the relative velocity![]()
, which, in turn, eventually will modify the efflux from point![]()
. At the first glance, such observation may have some concerns. It implies that the future is affecting the present. However, each point in the gas space serves as the sink for the converging gas particles and the source of the diverging gas particles, each trajectory of the ballistic particle converging in point ![]()
at time t (traveling from the past) serves as the trajectory of the same ballistic particle diverging from the point ![]()
and time ![]()
(traveling toward the future relative to the time![]()
). Therefore, we may conclude that the balance will be conserved if we count the impact of the diverging particles not at the time of their leaving point ![]()
but at the time for each of them when the trajectory path is completed by a collision at the point ![]()
and time![]()
.
Here we need to admit that the second right-hand term in the equation above is insignificant compared with the first one (see the comments to Equation (19)) and will be neglected in the future analysis.
4. Reducing Integro-Differential Forms of Mass and Momentum Balance Equations to the Corresponding Differential Forms by the Taylor Series Expansion of the Integral Terms Near Point ![]()
Recognizing that, in the collision-dominated flow regime, the relative change of any property value or any parameter characterizing the gas (momentum or thermal velocity) is insignificant on the length scale of the average distance between the gas particles ![]()
and the most significant impact in the dissipation or consumption of the property occurs in the nearby region surrounding the singular point at![]()
, where the relative velocity is shown by Equation (37), we will simplify the integro-differential mass and momentum balance equations by using approximations for ![]()
and ![]()
as shown by Equations (38) and (39), respectively. But first, we verify the claim about the significance of the impact in the property dissipation in the nearby region surrounding the singular point at ![]()
by substitution of Equation (38) in the third and the sixth left-hand terms of Equation (88), executing integration over the spherical volume of the radius R having the origin in point![]()
, and comparing these results with the results of integration over the spherical volume of the radius of the infinity. Integration of the third left-hand term yields
![]()
(89)
We find that at![]()
, the ratio![]()
. Analogously, we integrate the sixth left-hand term so that
![]()
(90)
and at![]()
, the ratio![]()
. The above justifies the approximations for ![]()
and ![]()
by Equations (38) and (39), respectively, and validates using these approximations while integrating over the infinite gas space.
4.1. Approximate Integro-Differential Form of the Mass Balance Equation for Incompressible Gas
Substituting in Equation (77) ![]()
and ![]()
by Equations (35) and (39), respectively, executing integration for the infinite space in the second left-hand and the first right-hand terms (see Equation (59)), neglecting the second right-hand term because of its minor impact on the mass balance and evaluating that the third left-hand term and the fourth and the fifth right-hand terms are zeroed (since all components of the unit vector ![]()
are odd in![]()
, which is a symmetric set with respect to the coordinate plains of the coordinate system having the origin in point![]()
), we obtain the following:
![]()
. (91)
In the equation above, we returned to the traditional representation of the vector differentiation ![]()
with respect to ![]()
while keeping in mind that now ![]()
does not act on the dependable variable![]()
.
4.2. Approximate Integro-Differential Form of the Momentum Balance Equation for Incompressible Gas
Substituting in Equation (88) ![]()
and ![]()
by Equations (35) and (39), respectively, we obtain the following:
![]()
![]()
![]()
(92)
Executing integration for the infinite space in the third and sixth left-hand of the equation above (see Equations (59) and (60)) and evaluating that the fourth and the fifth left-hand terms are zeroed (since all components of the unit vectors ![]()
and ![]()
are odd in![]()
, which are symmetric sets with respect to the coordinate plains of the coordinate system having the origin in point![]()
), we obtain the following:
![]()
(93)
In the equation above, we returned to the traditional representation of the vector differentiation ![]()
with respect to ![]()
while keeping in mind that now ![]()
does not act on the dependable variable![]()
.
Let ![]()
be a solution of the system of mass and momentum balance equations shown by Equations (91) and (93) with partial derivatives of all orders on ![]()
that holds an interior point ![]()
and with initial condition
![]()
for![]()
. (94)
In the system of Equations (91) and (93), we assume that ![]()
and ![]()
are known continuous functions with partial derivatives of all orders on![]()
. The system of mass and momentum vector integro-differential Equations (91) and (93) may be reduced to a system of three first-order non-linear integro-differential equations having three independent variables![]()
, ![]()
, and![]()
. Each of the independent equations has its independent initial condition from Equation (94). Such a system of three independent equations may have only one solution. The Equations (91) and (93) system does not need a pressure gradient term because the gas system is expanded to infinity. However, if these equations are applied to a confined gas space, then the surface force due to pressure exerted by the surroundings on the confined gas space shall be considered, and the pressure term ![]()
needs to be added in the left-hand of Equation (93).
Also, we note that the BPPBS assumes that each of the converging ballistic particles originated from a preceding collision within the gas system is selected from the group of the converging ballistic particles by a ballistic trajectory governed by the law of motion, which provides an opportunity for the particle to enter point ![]()
at given time t. Such a combination of diverging and converging ballistic particles capable of targeting or escaping point ![]()
at a given time t is an exhaustive combination [8]. Moreover, in a hypothetical infinitely large system with no gravitational force, real straight-line trajectories of the particles may start from infinity so that each gas particle of the infinite gas system has a real chance to enter point ![]()
at given time t. In turn, each gas particle diverging from the point ![]()
at given time t has a real probability to reach any point within the infinite gas space. It implies that the solution of the system of integro-differential mass and momentum balance equations shown, for the non-isothermal gas system, by Equations (91) and (93), respectively, will be unique and physically reasonable on![]()
.
4.3. Approximating Integro-Differential Mass and Momentum Balance Equation Using Taylor Series Expansion of a Vector Field
Returning to the system of approximate integro-differential mass and momentum balance equations shown, for the non-isothermal gas system, by Equations (91) and (93), respectively, we may note that each of them has singularities at ![]()
with the order of the pole of one or two. To investigate the analytical behavior of the integro-differential equations in the region bounding the point of singularity, we will use the Taylor series method. Taylor series expansion method is widely used for approximating the solution of integro-differential Equations (IDE) because of its efficiency [13]. Our research particularly uses the Taylor series expansion method to transform the integro-differential mass and momentum balance equations shown by Equations (91) and (93), respectively, into the corresponding vector differential equations. More specifically, we concentrate on using zero through second order the Taylor series expansions and comparing them with the Navier-Stokes equations of mass and momentum conservation for incompressible fluid shown here by Equations (1) and (2), respectively.
Definitions: Given the region of the Taylor expansion S surrounding point![]()
, so that![]()
, the Taylor series for ![]()
about point ![]()
in the first right-hand term of Equation (93) is
![]()
, (95)
where ![]()
is the Taylor polynomial of degree m around point![]()
. We use a convenient vector form of the Taylor polynomial (5.109) of [14] in the equation above. Similarly, we transform the other original under integral functions in the right-hand terms of Equations (91) and (93):
![]()
, (96)
![]()
, (97)
![]()
, (98)
![]()
(99)
![]()
. (100)
Substituting the under integral functions of Equations (91) and (93) by the corresponding polynomials shown by Equations (95)-(100), we obtain the following transforms of Equations (91) and (93)
![]()
(101)
and
![]()
(102)
respectively. These equations become vector differential mass and momentum balance equations, respectively. Since all the polynomials of the infinite order in the vector differential mass and momentum balance Equations (101) and (102) are identical to the corresponding original functions in the vector integro-differential mass and momentum balance Equations (91) and (93), then, according to Taylor’s theorem, the solution of the system of Equations (101) and (102), ![]()
, and the radius of expansion ![]()
shall be identical to the solution of the vector integro-differential mass and momentum balance Equations (91) and (93) and the radius of expansion![]()
, namely:
![]()
and![]()
. (103)
However, it will be impossible to solve the system of Equations (101) and (102), where each has an unlimited number of terms. Therefore, the number of meaningful terms in the equations is limited for practical purposes. Fortunately, the Taylor series expansions method allows, in general, to limit the expansion to a few terms, which will result in an approximation that may be sufficiently close to the true value. Since we investigate gas flow in the collision-dominated flow regime, in which the relative change of the property value or any parameter characterizing the gas, such as momentum, is insignificant on the length scale of the average distance between the gas particles ![]()
and the most significant impact in the dissipation or consumption of the property occurs in the nearby region surrounding the singular point at ![]()
(see Equations (89) and (90) and the comments to them), in the Taylor expansions for the under integral original functions in Equations (91) and (93), we will use only terms associated with the zero, first, and second order terms in the Taylor expansion. A second order Taylor series expansion of a vector-valued function of three variables can be written as
![]()
(104)
where
![]()
. (105)
4.3.1. Applying the Taylor Series Expansion Method to Derive a Differential Form of the Mass Balance
Now, using Equation (104) as a template, we approximate in Equation (91) ![]()
by second order Taylor series expansion. Then we have:
![]()
(106)
Ignoring the error term in Equation (106) for a moment and substituting Equations (106) in Equation (91), we obtain
![]()
(107)
4.3.2. Applying the Taylor Expansion Method to Derive a Differential Form of the Momentum Balance
First, using Equation (104) as a template, we approximate vector functions![]()
, ![]()
, ![]()
, ![]()
, and ![]()
in Equation (93) by second order Taylor series expansions. Then we have:
![]()
(108)
![]()
(109)
![]()
(110)
![]()
(111)
and
![]()
(112)
Ignoring the error terms in Equations (108), (109), (110), (111), and (112) for a moment and substituting these equations in Equation (93), we obtain
![]()
![]()
![]()
![]()
(113)
We may expect that the truncation error decreases by adding terms to the Taylor series. Similarly, we may assume that, for a selected fixed truncation error, the addition of terms in the Taylor series will increase the interval of the Taylor series expansion with the acceptable tolerance.
5. Comparison of the Derived Differential Forms of Mass and Momentum Balance Equations with the Corresponding Navier-Stokes Equations
To gain insight into the formation of the mass and momentum balance in the point of singularity at ![]()
as well as to provide an estimate of the impact of the most significant terms in the mass balance Equation (107) and the momentum-balance Equation (113), we assemble zero-order and the second-order Taylor series approximations separately.
5.1. Zero-Order Polynomial Approximations of Integrals in the Mass and Momentum Balance Integro-Differential Equations
The balance by zero-order approximation only generates the most significant impact in the mass and momentum balances. For the mass balance equation, executing integration for the infinite space in the first right-hand term of Equation (107) (see Equation (59)), neglecting the second and the third right-hand terms, and rearranging the rest of the terms, we obtain the following
![]()
. (114)
We may note that the equation above, in fact, is the zero-order term of the vector differential mass balance Equation (101) that has an infinite number of the differential terms.
For the momentum balance equation, first, we select in the right-hand of Equation (113) the first, fourth, seventh, tenth, and thirteenth terms (zero-order approximation) and neglect the rest of the right-hand terms. Second, we execute integration for the infinite space in first, seventh, tenth, and thirteenth by applying Equations (59) and (60). Third, we evaluated that the fourth right-hand term is zeroed (since all components of the unit vector ![]()
are odd in ![]()
that is a symmetric set with respect to the coordinate plains of the coordinate system having the origin in point![]()
). Finally, upon rearranging the terms, we obtain:
![]()
. (115)
We may see that the equation above is the zero-order term of the differential momentum balance Equation (102) that has an infinite number of the differential terms.
Solving a system of the mass balance and the momentum balance Equations (114) and (115), and using in the resulting equation the relationships shown by Equation (41), we obtain
![]()
. (116)
The equation above is valid to describe the momentum balance only at the point![]()
. Comparing the equation with Equation (2), one may note that the first three left-hand terms in the equation above and the first three left-hand terms in Equation (2) appear identical.
Remarkably, the zero-order Taylor series expansion of the integro-differential equation formulated by applying the BPPBS revealed two new terms. One of them, the fourth term, is the temperature gradient, and the other, the fifth term, is associated with the interaction of the external force field and the mass-flow velocity. These new terms may significantly impact the momentum balance at certain conditions, but they are absent in the Navier-Stokes momentum balance equation. We will explain their appearance in the next section while analyzing the second order of the Taylor series expansion of the differential momentum balance equation.
5.2. Second-Order Polynomial Approximations of Integrals in the Mass and Momentum Balance Integro-Differential Equations
The second order of the Taylor series expansion would improve the approximation by increasing an interval with desired tolerance. The desired tolerance level will be acceptable if we reveal the Taylor series expansion terms associated with the gas viscosity. We estimate the impact of the first- and second-order approximation terms in the mass balance Equation (107) and the momentum-balance Equation (113).
5.2.1. Non-Isothermal Fluid System
For the mass balance equation, we add not yet used terms of Equation (107), namely, the second and the third right-hand terms, to the right-hand of Equation (114). One may evaluate that the second right-hand term vanishes (since all components of the unit vector ![]()
are odd in![]()
, which is a symmetric set with respect to the coordinate plains of the coordinate system having the origin in point![]()
). Applying the vector analysis rules shown in Equations (63) and (64) to the third right-hand term followed by integration for the infinite space in all right-hand (see Equation (61)), we finally obtain the following:
![]()
(117)
The equation above is a Helmholtz type equation. Its solution is a complex-valued wave function. The only real-valued solution of Equation (117) is
![]()
. (118)
For the momentum balance equation, we add not yet used terms in the right-hand of Equation (113), namely, the second, fifth, eighth, eleventh, and fourteenth, a group of the first-order terms of the Taylor expansion, and the third, sixth, ninth, twelfth, and fifteenth, a group of the second order terms of the Taylor expansion. One may evaluate that, in the group of the first order terms of the Taylor expansion, all terms except the fifth vanish (since all components of the unit vector ![]()
are odd in![]()
, which is a symmetric set with respect to the coordinate plains of the coordinate system having the origin in point![]()
). Applying the vector analysis rules shown in Equations (63) and (64) to each of the group of the second order terms of the Taylor expansion followed by integration for the infinite space in all survived terms (see Equations (59), (60), (61), and (62)), we finally obtain the following:
![]()
(119)
Solving a system of the mass balance and the momentum balance Equations (118) and (119), using in the resulting equation the relationships shown by Equations (40) and (41), and rearranging the terms, we finally obtain
![]()
(120)
In this interpretation, the fourth left-hand term can be expressed by applying Equation (8) as the gas pressure gradient associated with the temperature gradient at a point inside the incompressible gas. It may serve as “bound on the fluid velocity u, as well as the spatial derivatives ![]()
[5].”
5.2.2. Isothermal Fluid System
We also formulate the momentum balance equation at the uniform temperature by assigning ![]()
and ![]()
in Equation (120). Then we have:
![]()
(121)
5.3. Revealing an Unknown Effect Associated with the Interaction of the External Field of Force and the Mass-Flow Velocity, Which Is Missed in the Navier-Stokes Momentum Balance Equation
The fourth identical left-hand term of Equations (120) and (121), mentioned above, quantifies the interaction of the mass flow velocity ![]()
with the vector field of force![]()
. The expression ![]()
is the added velocity gained by a gas particle during its free traveling time and ![]()
is the directional derivative of ![]()
in the direction of![]()
. This new term may significantly impact the momentum balance at the high external force field and lower gas density and the temperature.
5.4. Revealing an Unknown Effect Associated with the Temperature Gradient at the Non-Uniform Temperature
Contrary to the Navier-Stokes theory, according to which only the viscosity coefficient has some temperature dependence, we admit that the derived momentum balance equation governing the gas flow in a non-isothermal gas system has additional five temperature-dependent terms in the equation. We show this by substituting Equations (3) and (4) in Equation (120), which yields:
![]()
(122)
The most significant temperature effect on the momentum balance is expected from the fourth left-hand of the equation above. In physics, the effect of the temperature gradient on the gas flow is known as the thermo-osmotic transport phenomenon [15] ; however, the underlying molecular mechanism of the transport is mostly still unexplored. We are surprised to discover this term in the momentum balance equation. However, its appearance in the momentum balance at the non-uniform temperature seems reasonable.
5.5. The Evidence of the Inapplicability of the Navier-Stokes Equations to Govern Fluid Flow in the Infinite Space
Here we shall admit the following. We may note here that the second order truncation of Equation (102) shown by Equation (120) is a significant improvement over the zero-order truncation shown by Equation (116) since it reveals the viscous term and the other two terms associated with the momentum exchange in the region surrounding point![]()
. However, the radius of convergence or the radius of the zone with given tolerance ![]()
for the differential Equation (120) is limited. In other words, while the solution of Equation (102) is ![]()
for![]()
, the solution of Equation (120), which is the second order truncation of Equation (102), is ![]()
for![]()
. Considering the fact that all the terms of the Navier-Stokes Equation (2) are built-in Equation (120), we may conclude that, for the solution of the Navier-Stokes Equation (120) ![]()
for![]()
, the radius of the zone ![]()
with the same tolerance as for the solution of Equation (120) will be equal to or less than![]()
. Symbolically, the above is reflected by the following inequality:
![]()
. (123)
Thus, we have shown that there exists no solution of the Navier-Stokes equations in![]()
.
We may conclude from the discussion above that Equations (121) and (122) may be applied only to a confined gas space. Therefore, the surface force due to pressure exerted by the surroundings on the confined gas space shall be considered (see the comments to Equation (7) in Introduction), and Equations (121)
and (122) are modified by introducing the pressure term ![]()
in the left-hand of these equations as follow:
![]()
(124)
and
![]()
(125)
Comparing Equations (124) and (125) with Equation (2), one may note that the first four left-hand terms in Equations (124) and (125) and the left-hand terms in Equation (2) are identical. Also, the first right-hand terms of Equations (124) and (125) are identical to the viscous right-hand term of Equation (2). Our derivation produces the numerical coefficient ![]()
(see Equation (3)), which is remarkably close to 0.49 obtained in [1]. However, we revealed the additional two left-hand terms and four right-hand terms in Equations (125) that are not detected in the derivation originally developed by Stokes [16] [17] and many other alterations since then. Similarly, we have one left-hand term and two right-hand terms in Equations (124) absent in the Navier-Stokes momentum balance equation.
6. Discussion and Conclusions
6.1. Approach in the Modeling Gas Flow
Our approach in the modeling gas flow is established on mimicking the movement of each particle/molecule composing the gas and then gathering that movement into macro quantities characterizing the fluid flow. It has resulted in discovering a new principle of the property (mass, momentum, and energy) balance in space, which we have named the Ballistic Principle of the Property Balance in Space. The BPPBS is based on recognizing that each particle composing the gas follows its ballistic trajectory governed by a law of motion in free space and moves with a probability between any of two points in space occupied by the gas. Each ballistic particle is treated as a property carrier transporting one or more mass, momentum, and energy between the points of consecutive collisions. Each point in space occupied by the gas is a sink accumulating property delivered by converging ballistic particles from the entire gas system and a source dispersing property by diverging ballistic particles.
In this paper, we use a different than in our original paper [8] scheme of defining a net rate of total property efflux per unit volume from a nonmoving point of gas space. We realized that each point in the gas space serves as the sink of the converging gas particles and the source of the diverging gas particles. Therefore we shall consider the exhaustive combination of the transport events in each point of the gas space. As a result, we consider the balance by taking into account the events of delivery of the diverging ballistic particle from the point source at ![]()
at time t to the point sink at ![]()
within the fluid system. Then we formulated integro-differential forms of mass balance and momentum balance equations adapted to the incompressible gas flow at the non-uniform temperature in the infinite gas space. To investigate the analytical behavior of the integro-differential equations in the region bounding the point of singularity, we used the Taylor series method. We concentrated on using zero through second order the Taylor series expansions and comparing them with the Navier-Stokes mass and momentum balance equations for incompressible fluid shown here by Equations (1) and (2).
6.2. Comparative Analysis of the Navier-Stokes Momentum Balance Equation and the Derived in Present Work Non-Isothermal and Isothermal Differential Momentum Balance Equations
Navier-Stokes equations have been known by mathematicians and engineers exactly for two hundred years. This paper's main innovation is finding that the Navier-Stokes momentum balance equation does not describe the fluid flow adequately. Particularly, it does not consider the momentum associated with the interaction of the external field of force and the mass-flow velocity and with the significant temperature dependence. These effects, which are not considered in the Navier-Stokes equations, may significantly diminish the accuracy and predictability of computer simulations in various engineering and fundamental applications under certain conditions.
Applying the BPPBS, our derivation generates all terms associated with the Navier-Stokes equations. It also has led to discovering the unknown effect associated with the part of velocity acquired by each gas particle during its free path traveling in the body force field. Furthermore, we discovered a significant effect of the temperature non-uniformity on the momentum balance. In addition, our derivation produces the numerical coefficient ![]()
in the equation for the kinematic viscosity for gases (see Equation (3)) that is remarkably close to 0.49 obtained via a mathematically rigorous derivation [1] , which may also be supplemental support of the BPPBS [8].
We also investigated the analytical behavior of the integro-differential equations in the region bounding the point of singularity by applying the Taylor series expansion method to transform the integro-differential mass and momentum balance equations into the corresponding vector differential equations. Our analysis has demonstrated that the Navier-Stokes equations are not applicable to govern fluid flow on![]()
. Therefore, we have concluded that the derived momentum-balance Equation (121) or (122), as well as the Navier-Stokes momentum balance Equation (2), can be applied only to a confined gas space.
6.3. Conclusions
From the above, we may conclude the following:
1) We derived integro-differential forms of the mass balance and momentum balance equations adapted to the incompressible non-isothermal gas flow in the infinite gas space. Since both the mass balance and momentum balance are formulated by considering an exhaustive combination of diverging and converging ballistic particles capable of targeting point or escaping point ![]()
at a given time t, we concluded that the solution of the system of integro-differential mass and momentum balance equations is unique and physically reasonable on![]()
.
2) While deriving the balance equations, we determined that the balance is conserved only if we count the impact of each of the diverging particles upon completion by each of them a trajectory path ending at ![]()
but not upon the start of the trajectory at![]()
.
3) We used the Taylor series expansion method to investigate the analytical behavior of the integro-differential equations in the region bounding the point of singularity. Particularly we applied the Taylor series expansion method to transform the integro-differential mass and momentum balance equations into the corresponding vector differential equations. We found that the transformed differential form of the incompressible mass balance equation is identical to the corresponding Navier-Stoke counterpart, which supports the validity of the BPPBS claimed in our previous publications.
4) We derived the following vector differential forms of the momentum balance equation, which apply to a confined incompressible fluid flow at the non-uniform temperature
![]()
(126)
and at the uniform temperature
![]()
(127)
We found that the derived vector differential forms of the momentum balance equation include the corresponding Navier-Stokes momentum balance equation terms in full. Namely, the first four left-hand terms and the first right-hand terms are identical to the corresponding terms of the incompressible Navier-Stokes momentum balance equation).
5) We have demonstrated that the Navier-Stokes momentum balance equation does not adequately describe the fluid flow.
a) It does not consider the momentum associated with the part of velocity acquired by each gas particle during its free path traveling in the body force field. This effect may significantly modify gas flow at low temperature and a high value of the external field of force, such as the gravitational force.
b) It ignores the influence of the temperature non-uniformity on the momentum balance. This effect may significantly modify gas flow at high-temperature gradients.
6) We have shown that:
a) The Navier-Stokes momentum balance equation is an incomplete version of the second-order approximation of the Taylor differential transformation of the integro-differential momentum balance equation based on the BPPBS.
b) The radius of expansion with a given tolerance of the second-order truncation of the Taylor differential transformation of the integro-differential equations of the mass balance and the momentum balance is limited. All the terms of the Navier-Stokes equation are built-in the second-order approximation of the Taylor differential transformation. Therefore, the solution of the Navier-Stokes equation may exist only within the limited, confined space.
c) Therefore, there exists no solution ![]()
of (1), (2), and (5) on![]()
.