A Procedure for Trisecting an Acute Angle

Lyndon O. Barton

Delaware State University, Dover, USA.

DOI: 10.4236/apm.2022.122005                

Abstract

This paper presents a graphical procedure, using an unmarked straightedge and compass only, for trisecting an arbitrary acute angle. The procedure, when applied to the 30˚ angle that has been “proven” to be not trisectable, produced a construction having the identical angular relationship with Archimedes’ Construction, in which the required trisection angle was found to be exactly one-third of the given angle (or ∠E'MA = 1/3∠E'CG = 10˚), as shown in Figure 1(D) and Figure 1(E) and Section 4 PROOF in this paper. Hence, based on this identical angular relationship between the construction presented and Archimedes’ Construction, one can only conclude that geometric requirements for arriving at an exact trisection have been met, notwithstanding the theoretical proofs of Wantzel, Dudley, and others.

Keywords

Archimedes’ Construction, College Geometry, Angle Trisection, Trisectors, Famous Problems in Mathematics, History of Mathematics

1. Introduction

The trisection of an angle problem has been one of the most intriguing geometric challenges for mathematicians for centuries [1] [2]. Simply stated and also “proven”, the trisection of an arbitrary acute angle (except 45˚)cannot be achieved using an unmarked straightedge and compass only [3] [4]. Or, as stated by Underwood Dudley, author of A Budget of Trisections [4] “There is no procedure, using only an unmarked straightedge and compasses to construct one-third of an arbitrary angle”. Yet there have been countless attempts by a number of mathematicians to either disprove this assertion or devise a construction that is as close as possible to the exact solution. Some of the more notable attempts, in both cases, that can be found in the literature, besides A Budget of Trisections [4], include The Trisectors by Underwood Dudley [5], web article on “The Trisection of an Angle” by Jim Loy [6], and many more [7] [8] [9].

The object of this paper is not to debate the established proofs alluded to, but simply to present a comprehensive graphical procedure, using an umarked straightedge and compass only, that will demonstrate one approach on how an arbitrary acute angle (of any measure) can be trisected. The procedure is based on the article entitled “Mechanism Analysis of a Trisector” published earlier [7]. In which a working model of a trisector [A1] was analyzed using principles of kinematics, instead of conventional mathematics and plane geometry, to study the trisection problem. The basis for employing this approach was the fact that while the angle trisection could not be achieved using an unmarked straightedge and compass, yet a mechanism can be built to perform this task perfectly [8]. Hence, performing a motion analysis on an actual trisector (See FigureA1) seemed a logical rationale for seeking to obtain fresh insight into understanding the trisection problem.

To be clear, Kinematics is the study of motion, and the purpose of the trisector model was simply to study and gain an understanding of its motion. Therefore, it is not a violation of the unmarked ruler and compass rule. For details on the motion analysis, see reference article [7]. It should also be noted that nowhere in the literature has this author encountered any attempt at tackling this age-old problem of the angle trisection as is demonstrated in this paper; i.e. applying the fundamental principles of kinematics (in this case motion analysis instead of conventional mathematics and plane geometry).

2. Theory

The procedure being presented is based on the well-known Archimedes’ Construction [1] represented in the diagram below, which illustrates the geometric requirements that must be met in order to arrive at an exact trisection, and the general theorem relating to arcs and angles.

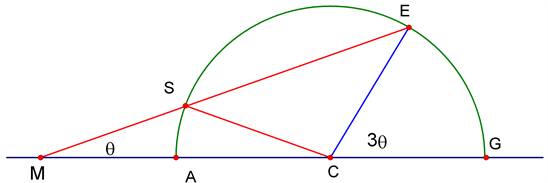
Let ÐECG (or 3Ðθ) be the required angle to be trisected. With center at C and radius CE describe a semicircle. Given that a line from point E can be drawn to cut the semicircle at S and intersect the extended side GC at some point M such that the distance SM is equal to the radius SC, then from the general theorem relating to arcs and angles,

$\angle \text{EMG}=1/2\left(\angle \text{ECG}-\angle \text{SCM}\right)$ (1)

$\text{2}\angle \text{EMG}+\angle \text{SCM}=\angle \text{ECG}$ (2)

Since ΔCSM is an isosceles Δ, $\angle \text{SCM}=\angle \text{EMG}=\angle \theta$ (3)

Therefore,

$\text{3}\angle \text{EMG}=\angle \text{ECG}$ or $\text{3}\angle \theta =\angle \text{ECG}$ or $\angle \text{EMA}=1/3\angle \text{ECG}$ . (4)

TO SUMMARIZE:,

Geometric Requirements for EXACT TRISECTION:are:

(1) Segments SM, SC, E'C, and CG are all equal, and (2) ÐSMA = ÐSCA

ONCE, these requirements are met,

THEN, the EXACT trisection of the given angle (ÐECG) is achieved or ÐEMA = 1/3ÐECG.

NOTE also that, except for the given angle (ÐECG) being an acute angle, there are no other restrictions on measure of this angle.

THEREFORE the measure of ÐECG can be ANY REAL NUMBER (or ARBITRARY).

3. Procedure

To illustrate the procedure, we consider the 30˚ angle to be trisected (i.e., divided into three exactly equal parts, using an unmarked straightedge and compass only). The construction for this angle is given in the following Figures 1(A)-(C):¹

STEP 1 See Figure 1(A)

1) Using CG as the base, erect a perpendicular CC' at C.

2) With center at C and any convenient radius, describe a semicircle from point G cutting perpendicular CC' at E, and terminating at A on GC (extended).

3) Using CE as a base, form an equilateral triangle CEV, where V is the vertex.

4) Extend segment EV to meet GC (extended) at a point F.

STEP 2 See Figure 1(B)

1) Using point E as center and CE as radius, describe an arc cutting the semicircle in STEP 1 at point E' to form the given angle ÐE'CG = 30˚

2) Construct a ray from E' through point V and locate point L on said ray such that VL = VC.

3) Construct segment E'F, cutting the semicircle at V'.

4) Join V' to C with segment V'C and extend segment V'F to V'F' such that V'F' = V'C.

5) Construct a ray from E' through point A and locate point N on said ray such that AN = AC.

STEP 3 See Figure 1(C)

1) Join L to N with segment NL.

2) Locate midpoint Y of segment NL.

3) At midpoint Y, construct a perpendicular line to segment NL meeting line E'C (extended) at point O.

4) With center at O and radius ON describe an arc 'L> from N through F' to L, cutting the baseline GF (extended) at a point M.

5) Join E' to M with E'M cutting AV at a point S to form the required trisection angle, ÐE'MG, and making ÐE'MA = 1/3ÐE'CG, in compliance with the Archimedes’ Construction [1].

6) Join S to C with a segment SC to complete the construction², which makes segment SM = SC. See Figure 1(D) and Figure 1(E) on Angular Relationship.

(A)(B)(C)(D)(E)

Figure 1. (A) Construction Step 1; (B) Construction Step 2; (C) Composite construction showing trisection of the 30˚ angle: ÐE'MA = 1/3ÐE'CG; (D) Resultant angles for 30˚ trisection: ÐE'MA = 1/3ÐE'CG; (E) Archimedes’ model for the 90˚ angle: E'MA = 1/3ÐE'CG.

4. Proof

Referring to Figure 1(D) above, and applying the general theorem relating to arcs and angles (See Section 2 on THEORY of this paper), we get

$\angle \text{<msup> <mi> E </mi> <mo> ′ </mo> </msup> MG}=1/2\left(\angle \text{<msup> <mi> E </mi> <mo> ′ </mo> </msup> CG}-\angle \text{SCM}\right)$ or $\angle \text{<msup> <mi> E </mi> <mo> ′ </mo> </msup> MA}=1/2\left(\angle \text{<msup> <mi> E </mi> <mo> ′ </mo> </msup> CG}-\angle \text{SCM}\right)$

$\text{2}\angle \text{<msup> <mi> E </mi> <mo> ′ </mo> </msup> MA}=\angle \text{<msup> <mi> E </mi> <mo> ′ </mo> </msup> CG}-\angle \text{SCM}$

$\text{2}\angle \text{<msup> <mi> E </mi> <mo> ′ </mo> </msup> MA}+\angle \text{SCM}=\angle \text{<msup> <mi> E </mi> <mo> ′ </mo> </msup> CG}$

Since $\angle \text{SCM}=\angle \text{<msup> <mi> E </mi> <mo> ′ </mo> </msup> MA}$

Then $\text{3}\angle \text{<msup> <mi> E </mi> <mo> ′ </mo> </msup> MA}=\angle \text{<msup> <mi> E </mi> <mo> ′ </mo> </msup> CG}$

Therefore $\angle \text{<msup> <mi> E </mi> <mo> ′ </mo> </msup> MA}=1/3\angle \text{<msup> <mi> E </mi> <mo> ′ </mo> </msup> CG}=1/3\times {30}^{\circ }={10}^{\circ }$ (QED}

5. Summary

A comprehensive graphical procedure, using an_unmarked straightedge and compass only, for the trisection of an acute angle has been presented. The procedure, when applied to the “non-trisectable” 30˚ angle, produced a construction having an identical angular relationship with Archimedes’ Construction [1], in which the trisection angle has been found to be exactly one–third of the given angle (or ÐE'MA) = 1/3ÐE'CG = 10˚), as shown in Figure 1(D) and Figure 1(E) as well as Section 4 PROOF in this paper. Therefore, based on the identical angular relationship between the construction presented and Archimedes’ Construction [1], one can only conclude that the geometric requirements for arriving at an exact trisection have been met, notwithstanding the theoretical proofs of Wantzel, Dudley, and others [3] [4] [8].

To be specific, the construction presented has achieved the desired objective of dividing an arbitrary acute angle (of any measure) into three exactly equal parts, using an unmarked straightedge and compass only.

Appendix

Figure A1. Angle trisector model.

Figure A2. Composite construction showing trisection of the 45˚ angle ÐE'CG. Yielding ÐE'MA = 15˚.

NOTES

¹Note: While the Geometer’s Sketch Pad [10] was employed in this procedure, the use of this software is not a violation of the unmarked straightedge and compass rule, since its sole purpose was strictly for 1) the layout of lines and arcs (for precision and not measurements, except at the end for final results), and 2) for color coding, which is appropriate for an effective graphical presentation. Otherwise, the construction can easily be hand drawn.

²See FigureA2 in Appendix for comparison when the identical construction procedure is applied to benchmark angle 45˚ that is knowm to be trisectable.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Tietze, H. (1965) Famous Problems in Mathematics. Graylock Press, New York.
[2]	Ives, H. (1990) An Introduction to the History of Mathematics. 6th Edition, Saunders College Publishing, Fort Worth.
[3]	Quine, W.V. (1990) Elementary Proof That Some Angles Cannot Be Trisected by Ruler and Compass. Mathematics Magazine, 63, 95-105. https://doi.org/10.1080/0025570X.1990.11977495
[4]	Dudley, U. (1987) A Budget of Trisections. Springer-Verlag, New York. https://doi.org/10.1007/978-1-4419-8538-5
[5]	Dudley, U. (1996) The Trisectors. The Mathematical Association of America, Washington DC.
[6]	Loy, J. (2003) Trisection of an Angle. https://web.archive.org/web/20030402133520/http://www.jimloy.com/geometry/ trisect.htm
[7]	Barton, L.O. (2008) Mechanism Analysis of a Trisector. Mechanism and Machine Theory, 43, 115-122. https://doi.org/10.1016/j.mechmachtheory.2007.10.005
[8]	Soldatos, G.T. (2020) One Method towards the Trisection of the Angle. Open Journal of Mathematical Sciences, 4, 23-26. https://doi.org/10.30538/oms2020.0090
[9]	Kempe, A.B. (2010) How to Draw a Straight Line: A Lecture on Linkages (1877). Kessinger Publishing LLC, Whitefish. https://doi.org/10.1038/scientificamerican08111877-1340supp
[10]	Bennett, D. (2002) Exploring Geometry with Geometer’s Sketch Pad. Key Curriculum Press, Emeryville, CA.