Counting and Randomly Generating k-Ary Trees

James F. Korsh

Computer and Information Science Department, Temple University, Philadelphia, USA.

DOI: 10.4236/am.2021.1212077                

Abstract

k-ary trees are one of the most basic data structures in Computer Science. A new method is presented to determine how many there are with n nodes. This method gives additional insight into their structure and provides a new algo-rithm to efficiently generate such a tree randomly.

Keywords

Combinatorial Problems, k-Ary Trees, Random Generation

1. Introduction

The number, $bn,k$, of k-ary trees with n nodes is well known and given in [1] as $C\left(kn,n\right)/\left(\left(k-1\right)n+1\right)$ where $C\left(n,k\right)$ denotes the number of ways to choose k places from n places, which is $n!/k!\left(n-k\right)!$. This paper generalizes the results from [2] on binary trees with n nodes to k-ary trees with n nodes by providing a simple direct approach to finding $bn,k$ and a new method to generate a random k-ary tree with n nodes efficiently. The direct approach here to finding $bn,k$ relies on the detailed structure of the trees developed here rather than the standard recursive description of the tree and solving the resultant recurrence relations. Another approach for the random generation is given in [3]. The numeration of k-ary trees is done in [4]. The generation of binary and k-ary trees has been and continues to be of interest [5] [6] [7] [8].

2. Representation of k-Ary Trees with n Nodes

For any n > 0, a k-ary tree with n nodes can be uniquely represented by a sequence of n k-tuples of 0’s and 1’s, one k-tuple for each node. In a node’s k-tuple, the ith entry specifies whether the node’s ith child is non-null or null: 1 for non-null and 0 for null. The k-tuples appear in the order in which the nodes are accessed in a preorder traversal of the tree. The sequence for the 3-ary tree

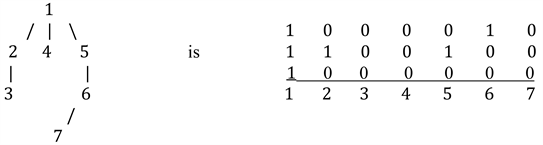
Define node i of a k-ary tree as the ith node accessed in a preorder traversal of the tree. The ith tuple corresponds to node i of the tree. The numbers are shown to indicate the node corresponding to each tuple, but only the sequence of n tuples is used to represent the tree. The tuples are written vertically rather than horizontally.

3. Construction Procedure

The unique k-ary tree that generated this sequence of tuples can easily be constructed by processing the tuples from left to right, effectively building the tree as it is being preorder traversed. This procedure builds the tree as shown below:

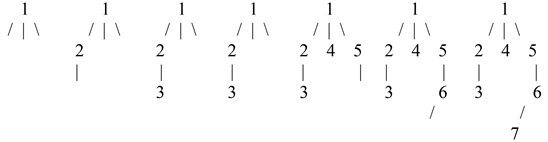
We will call these spines 1 to 7 of the tree, where spine i contains nodes 1 to i and its branches. The number of unused branches in spine i is the number of branches—(i − 1).

4. Valid Sequences

Each node of an n node k-ary tree, except for the root, has a unique branch coming into it. Since each branch corresponds to a unique 1 in the tree’s n node k-ary sequence there must be $n-1$ 1’s in the sequence. Each of the tree’s null subtrees corresponds to a unique one of the $\left(k-1\right)n+1$ 0’s in the sequence. There are $C\left(kn,n-1\right)$ of these sequences of n k-tuples, one for each way the $n-1$ 1’s can be assigned to the kn places. Not all of these allow our procedure to construct ann node k-ary tree. Those that do we call valid sequences and the others invalid.

5. A Look Ahead

The approach here is to confirm two facts. First, that our construction procedure to generate a tree from a valid sequence establishes a 1-1 correspondence between n node k-ary trees and valid sequences.

Secondly, every invalid sequence is one of the distinct n − 1 rotations generated from a unique valid sequence, and each is also distinct from the valid sequence. Thus, each invalid sequence can be associated with a unique tree. It must then be the case that

$bn,k+\left(n-1\right)bn,k=C\left(kn,n-1\right)$,

since the number of valid plus the number of invalid sequences equals the total number of sequences. Solving for $bn,k$ we obtain

$bn,k=C\left(kn,n-1\right)/n=C\left(kn,n\right)/\left(\left(k-1\right)n+1\right)$.

Rotation i of a valid sequence is obtained by shifting its first i tuples from the front to the rear of the sequence. For our example, rotation 3 is:

Applying our construction algorithm to rotation 3 produces:

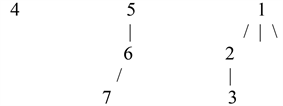
Notice that the last, and incomplete tree is spine 3 of the original tree. If the first subtree is added to the first available branch of the spine and the second to the second available branch the original tree is obtained. We will see that our construction applied to rotation i of a tree will always produce r subtrees followed by spine i and adding subtreej to the jth available branch for 1 ≤ j ≤ r produces the original tree.

6. Excess Sequences and Valid Sequences Are the Same

Let Ni be the number of 1’s in the first i k tuples of any n node k-tuple sequence. If $Ni>\left(i-1\right)$ for all i < n and $Nn=\left(n-1\right)$ we say the sequence is an excess sequence. In general, spine i + 1 is produced from spine i when node i+ 1 is processed and added to spine i. When node i + 1 is processed it becomes the child of the first available branch encountered in the preorder traversal starting from node i. This branch must be available since the first i nodes used the first i − 1 available branches encountered and Ni was greater than (i − 1). Since this is true for each $i<n-1$ the first n − 1 spines can be built. Since $Nn-1>n-2$ a branch is available for node n to be added to spine n − 1. However, since $Nn=n-1$ all the branches will then have been used and a tree has been constructed. This shows that an excess sequence is a valid sequence.

A valid sequence must have an unused branch to add node i+1 to in the construction procedure. The first i nodes usedi − 1 of the branches. So Ni must have been greater than (i − 1) for each i < n. Wheni is n, $Nn=n-1$ so after the nth node is added all the n − 1 branches have been used. Consequently, a valid sequence is an excess sequence.

7. Every Invalid Sequence Is One of the n − 1 Rotations of a Valid Sequence

If a sequence, s, is not an excess sequence it must be an invalid sequence. All n node k-ary sequences satisfy $Nn=\left(n-1\right)$ so for s to fail to be an excess sequence there must be a smallest n1 < n such that $Nn1=\left(n1-1\right)$ with $Ni>i-1$ for i < n1. Thus, the first n1 tuples of s must be an excess sequence and so represent an n1 nodek-ary tree. In fact, the sequence must look like:

justr consecutive excess sequences of lengths $n\text{1},n\text{2},\cdots ,nr$ with a last sequence of length $n-\left(n1+n2+\cdots +nr\right)$.

Each of the first r sequences then has ni − 1 1’s, i ≤ i ≤ r, and represents an ni node tree and the last sequence must have $n-1-\left(n1-1+n2-1+\cdots +nr-1\right)=n-\left(n1+n2+\cdots +nr\right)-1+r$ 1’s and has no head which is an excess sequence. Its length, N, is then $n-\left(n1+n2+\cdots +nr\right)$ and we will refer to its nodes as node 1 to N. Now $n1+n2+\cdots +nr$ cannot be n since, if it were, r must be 1 and n1 would contain all the nodes and be an excess sequence and would be the original invalid sequence. Also, r cannot be n, otherwise each ni, 1 ≤ i ≤ r, must be 1 so $n1+n2+\cdots +nr$ would be n, which we know cannot happen.

Lemma. The construction procedure applied to a last sequence L produces spine N of a tree with r unused branches.

Proof. Number the nodes of N from 1 to N and let ti be the number of 1’s in tuple i, 1 ≤ i ≤ N. After processing the first i nodes of L, the construction procedure creates spine i of a tree with $t1+t2+\cdots +ti-\left(i-1\right)$ unused branches with $Mi=t1+t2+\cdots +ti$ the number of 1’s in spine i. As long as each Mi is greater than (i − 1) node i can be added to the spine. If any Mi becomes equal to (i − 1) then nodes 1 to i are a head of L consisting of its first i tuples. Since L cannot have such a head, this cannot happen. So, spine N is produced and has $t1+t2+\cdots +tN-\left(N-1\right)=r$, unused branches.

Each of the nj sequences represent a subtree, 1 < j < r, and the first node of the jth subtree can be made the node to which the jth unused branch in spine N comes into. This effectively “hangs” the jth subtree from the jth unused branch, in preorder order. This means that the original invalid sequence was rotation r of the tree just created. Hence, every invalid sequence is one of the n − 1 rotations of a valid sequence.

8. There Is a One-to-One Correspondence between n Node k-Ary Trees and Valid Sequences

Spinei is generated by rotation i for 1 < i < n and these spines are all distinct. Consequently, the rotations that generated them must be distinct. Since each of the n − 1 spines is distinct, the n − 1 rotations that generated them must be distinct. A valid sequence generates spine n, which is the tree itself so each tree’s spine n must be distinct. This establishes a one-to-one correspondence between n node k-ary trees and valid sequences.

9. Conclusions

This confirms the two facts referred to earlier. The procedure described in the lemma allows us to construct the n node k-ary tree corresponding to any n nodek-ary sequence and to do it in O(nk) time.

To generate an n node k-ary tree at random, merely modify the algorithm in [9] so n − 1 integers are selected in step 1, let them determine where the n − 1 1’s are placed in the n k-tuples to give an n node k-ary sequence, and use our construction specified in the lemma to find the unique tree it produces. Since all the sequences are equally likely to be produced in step 2 and each tree will be produced by an equal number of sequences, this modification generates ann node k-ary tree at random. It takes O(nk) time and uses integers no larger than kn.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Knuth, D.E. (1998) The Art of Computer Programming. 3rd Edition, Addison-Wesley, Reading, Boston.
[2]	Korsh, J.F. (1993) Counting and Randomly Generating Binary Trees. Information Processing Letters, 45, 291-294. https://doi.org/10.1016/0020-0190(93)90039-C
[3]	Barcucci, E., Del Lungo, A. and Pergola, E. (1999) Random Generation of Trees and Other Combinatorial Objects. Theoretical Computer Science, 218, 219-232. https://doi.org/10.1016/S0304-3975(98)00322-3
[4]	Korsh, J.F. (2011) Fast Generation of t-Ary Trees. The Computer Journal, 54, 776-785. https://doi.org/10.1093/comjnl/bxq025
[5]	Drmota, M. (2009) Random Trees. Springer, Wien, New York. https://doi.org/10.1007/978-3-211-75357-6
[6]	Knuth, D.E. (2006) The Art of Computer Programming, Volume 4, Fascicle 4: Generating All Trees—History of Combinatorial Generation. Addison-Wesley, Reading, Boston.
[7]	Wu, R.-Y., Chang, J.-M., Chan, H.-C. and Pa, K.-J. (2014) A Loopless Algorithm for Generating Multiple Binary Tree Sequences Simultaneously. Theoretical Computer Science, 556, 25-33. https://doi.org/10.1016/j.tcs.2014.07.030
[8]	Pai, K.-J., Chang, M.C., Wu, R.-Y. and Chang, S.-C. (2019) Amortized Efficiency of Generation, Ranking and Unranking Left-Child Sequences in Lexicographic Order. Discrete Applied Mathematics, 268, 223-236. https://doi.org/10.1016/j.dam.2018.09.035
[9]	Atkinson, M.D. and Sack, J.R. (1992) Generating Binary Trees at Random. Information Processing Letters, 41, 21-23. https://doi.org/10.1016/0020-0190(92)90075-7