Introduction to Lie Algebras and Their Representations

Amor Hasić

Department of Mathematics, Faculty of Natural Sciences and Mathematics, University of Montenegro, Podgorica, Montenegro.

DOI: 10.4236/alamt.2021.113006                

Abstract

This paper is made up of a desire for me to contribute to this beautiful field of mathematics that I have encountered in recent years. In addition, I would like to mention that I am not aware that there are papers in our Balkans on Lie algebra, although this is only an introductory part for which in the near future in collaboration with several professors from abroad I will do a book in our mother tongue on Lie groups and algebras. The main content of this paper is similar to the books that have been published regarding Lie algebras, from basic definition and example, structure, killing form, classification to root system. In my opinion, this paper is important in relation to Lie algebras, because it will be helpful to all those who write papers on algebra, as well as the fact that the paper will be written in Montenegrin, which is understood by almost more than 70 percent of the population. For me, this work has the significance of being useful to all who need it.

Keywords

Algebras, Groups, Lie Groups, Lie Algebra

1. Introduction

[1] Lie theory has its roots in the work of Sophus Lie, who studied certain transformation groups that are now called Lie groups. His work led to the discovery of Lie algebras. By now, both Lie groups and Lie algebras have become essential to many parts of mathematics and theoretical physics. In the meantime, Lie algebras have become a central object of interest in their own right, not least because of their description by the Serre relations, whose generalizations have been very important.

The study of Lie Algebra requires a thorough understanding of linear algebra, group, and ring theory.

Definition 1.1. A nonempty set G equipped with an operation on it is said to form a group under that operation if the operation obeys the following laws, called the group axioms:

● Closure: For any $a,b\in G$, we have $a\cdot b\in G$.

● Associativity: For any $a,b,c\in G$, we have $a\cdot \left(b\cdot c\right)=\left(a\cdot b\right)\cdot c$.

● Identity: There exists an element $e\in G$ such that for all $a\in G$ we have $a\cdot e=e\cdot a=a$. Such an element $e\in G$ is called the identity in G.

● Inverse: For each $a\in G$ there exists an element $a^{-1}\in G$ such that $a\cdot a^{-1}=a^{-1}\cdot a=e$. Such an element $a^{-1}\in G$ is called the inverse of a in G.

Definition 1.2. Let $M_{m,n}\left(x\right)$ be the set of $m\times n$ matrices whose entries are in x. We will denote the $\left(i,j\right)$ entry of an $m\cdot n$ matrix A by $A_{ij}$ or $a_{ij}$ and also write

$A=\left[a_{ij}\right]=\left[\begin{array}{ccc}{a}_{11}& \cdots & a_{1n}\\ ⋮& \ddots & ⋮\\ a_{m1}& \cdots & a_{mn}\end{array}\right]$

We will use the special notations

$M_n\left(x\right)=M_{n,n}\left(x\right),x^n=M_{n,1}\left(x\right).$

$M_{m,n}\left(x\right)$ is a x-vector space with the operations of matrix addition and scalar multiplication. The zero vector is the $m\times n$ zero matrix $P_{m,n}$ which we will often denote P when the size is clear from the context. The matrices $E^{rs}$ with $r=1,\cdots ,m;s=1,\cdots ,n$ and

${\left(E^{rs}\right)}_{ij}={\delta }_{ir}{\delta }_{js}=\{\begin{array}{l}1\text{if}i=r\text{and}j=s\\ 0\text{otherwise}\end{array}$

form a basis of $M_{m,n}\left(x\right)$ ; hence its dimension as a x-vector space is

${\dim }_x{M}_{m,n}\left(x\right)=mn$

when n = 1 we will denote the standard basis vectors of $x^n=M_{n,1}\left(x\right)$ by

$e_r=E^{r1}\left(r=1,\cdots ,m\right).$

As well as being a x-vector space of dimension $n^2{M}_n\left(x\right)$ is also a ring with the usual addition and multiplication of square matrices, with zero $P_n=P_{n,n}$ and the $n\times n$ identity matrix I_n as its unity; $M_n\left(x\right)$ is not commutative except when $n=1$. Later we will see that $M_n\left(x\right)$ is also an important example of a finite dimensional x-algebra. The ring $M_n\left(x\right)$ acts on $x^n$ by left multiplication, giving $x^n$ the structure of a left $M_n\left(x\right)$ -module.

Definition 1.3: But $M_n\left(x\right)$ is not just a vector space. It also has a multiplication which distributes over addition (on either side).

$A\left(B+C\right)=AB+AC$

$\left(B+C\right)A=BA+CA$

Such a system is called an algebra. When we use the word algebra we will always mean one with a two-sided multiplicative identity. For $M_n\left(x\right)$,

$I=\left(\begin{array}{ccc}{1}_1& \cdots & 0\\ & \ddots & \\ 0& \cdots & 1\end{array}\right)$

is the multiplicative identity.

Definition 1.4: If G is an algebra, $x\in G$ is a unit if there exists some $y\in G$ such that $xy=1=yx$, i.e., if it has a multiplicative inverse.

Definition 1.5: The group of units in the algebra $M_n\left(R\right)$ is denoted by $GL\left(n,R\right)$, in $M_n\left(C\right)$ by $GL\left(n,r\right)$ and in $M_n\left(x\right)$ by $GL\left(n,x\right)$ These are the general linear groups.

Proposition 1.6. The determinant function $\det :M_n\left(x\right)\to x$ has the following properties.

1) For $A,B\in M_n\left(x\right)$, $\det \left(AB\right)=\det A\det B$.

2) $\det I_n=1$.

3) $A\in M_n\left(x\right)$ is invertible if and only if $\det A\ne O$.

We will use the notation

$G{L}_n\left(x\right)=\left\{A\in M_n\left(x\right):\det A\ne O\right\}$

for the set of invertible $n\times n$ matrices (also known as the set of units of the ring $M_n\left(x\right)$ ), and

$S{L}_n\left(x\right)=\left\{A\in M_n\left(x\right):\det A=1\right\}\subseteq G{L}_n\left(x\right)$ ‚

for the set of $n\cdot n$ unimodular matrices.

Definition 1.7: a matrix $A\in M_{n\times n}\left(F\right)$ is called orthogonal if $A{A}^t=I$.

Theorem 1.8: If A is a square matrix of order $n>1$, then $A\left(adjA\right)=\left(adjA\right)A=\left|A\right|I_n$. The $\left(i,j\right)$ th element of $A\left(adjA\right)$ is:

${\displaystyle \underset{k=1}{\overset{n}{\sum }}{a}_{ik}{a}_{kj}}={\displaystyle \underset{k=1}{\overset{n}{\sum }}{a}_{ij}{A}_{jk}}=\{\begin{array}{l}\left|A\right|\iff i=j\\ 0\iff i\ne j\end{array}$

Therefore $A\left(adjA\right)$ is a scalar matrix with diagonal elements all equal to $\left|A\right|$.

$\Rightarrow A\left(AdjA\right)=I_n$

$\Rightarrow \left(AdjA\right)A=\left|A\right|I_{(\; n\; )}$

where $\left|A\right|$ represents the determinant of A

Proposition 1.8. The following equation denotes the inverse of A.

$A^{-1}=\frac{AdjA}{\left|A\right|}$

2. Basic Definitions and First Examples

The study of Lie Algebra requires a thorough understanding of linear algebra, group, and ring theory. The following provides a cursory review of these subjects as they will appear within the scope of this paper.

Definition 2.1. A vector space V over a field F, is a Lie algebra if there exists a bilinear multiplication $V\times V\to V$, with an operation, denoted $\left(x,y\right)\mapsto \left[xy\right]$, such that:

1) It is skew symmetric where $\left[x,x\right]=0$ for all x in V (this is equivalent to $\left[x,y\right]=-\left[y,x\right]$ since character $F\ne 2$ ).

2) It satisfies the Jacobi identity $\left[x\left[yz\right]+y\left[z,x\right]+z\left[x,y\right]\right]=0\left(x,y,z\in V\right)$.

Example 2.2: Given an n dimensional vector space End(V), the set of all linear maps $V\mapsto V$ with associative multiplication $\left(x,y\right)\mapsto xy$ for all $x,y$, where $xy$ denotes functional composition, observe, End(V) is an associative algebra over F. Let us define a new operation on End(V) by $\left(x,y\right)\mapsto xy-yx$. If we denote $xy-yx$ by $\left[x,y\right]$, then End(V) together with the map $\left[.,.\right]$ satisfies Definition 1.1, and is thus a Lie algebra.

Proof. The first two bracket axioms are satisfied immediately. The only thing left to prove is the Jacobi identity. Given $x,y,z\in \text{End}\left(V\right)$, we have by use of the bracket operation:

$\left[x\left[yz\right]+y\left[z,x\right]+z\left[x,y\right]\right]=0$

$x\left(yz-zy\right)-\left(yz-zy\right)x+y\left(zx-xz\right)-\left(zx-xz\right)y+z\left(xy-yx\right)-\left(xy-yx\right)z=0$

$xyz-xzy-yzx+zyx+yzx-yxz-zxy+xzy+zxy-zyx-xyz+yxz=0$

$\left(xyz-xyz\right)+\left(xzy-xzy\right)+\left(yzx-yzx\right)+\left(zyx-zyx\right)+\left(yxz-yxz\right)=0$

Definition 2.3. The Lie algebra End(V) with bracket $\left[x;y\right]=xy-yx$, is denoted as gl(V), the general linear algebra.

Example 2.4. We can show that real vector space $R^3$ is a Lie algebra. Recall the following cross product properties when a, b and c represent arbitrary vectors and $\alpha ,\beta$ and $\gamma$ represent arbitrary scalars:

1) $a\times b=-\left(b\times a\right)$

2) $\alpha \times \left(\beta b+\gamma c\right)=\beta \left(a\times b\right)+\gamma \left(a\times c\right)$ and

$\left(\alpha a+\beta b\right)\times c=\alpha \left(a\times c\right)+\beta \left(b\times c\right)$

Proof. Note, $a\times a=-\left(a\times a\right)$, by property (1), letting $b=a$, therefore, $a\times a=0$. By the above properties, the cross product is both skew symmetric (property 1) and bilinear (property 2).

By vector triple product expansion: $x\times \left(y\times z\right)=y\left(x\times z\right)-z\left(x\times y\right)$. To show that the cross product satisfies the Jacobi identity, we have:

$\begin{array}{l}\left[x\left[yz\right]+y\left[z,x\right]+z\left[x,y\right]\right]=x\times \left(y\times z\right)+y\times \left(z\times x\right)+z\times \left(x\times y\right)\\ =\left[y\left(x\ast z\right)-z\left(x\ast y\right)\right]+\left[z\left(x\ast y\right)-x\left(y\ast z\right)\right]+\left[x\left(z\ast y\right)-y\left(z\ast x\right)\right]=0\end{array}$

Example 2.5. The Lie algebra $sl\left(2,C\right)$ (or $A_1$ ), $2\times 2$ matrices of trace 0. A basis is given by the three matrices

$H=\left[\begin{array}{cc}1& 0\\ 0& -1\end{array}\right],X_{+}=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right],X_{-}=\left[\begin{array}{cc}0& 0\\ 1& 0\end{array}\right]$

One computes $\left[H{X}_{+}\right]=2X_{+},\left[H{X}_{-}\right]=-2X_{-},\left[X_{+}{X}_{-}\right]=H$. This Lie algebra and these relations will play a considerable role later on.

The standard skew-symmetric (exterior) form $\det \left[X,Y\right]=x_1{y}_2-x_2{y}_1$ on $C^2$ is invariant under $sl\left(2,C\right)$ (precisely because of the vanishing of the trace), and so $sl\left(2,C\right)$ is identical with $sp\left(\text{1},C\right)$.

Example 2.6. L is itself a left L-module.

The left action of L on L is defined as $x\cdot y=\left[xy\right]$ Then, we have

$\left[\left[xy\right]z\right]=\left[x\left[yz\right]\right]-\left[y\left[xz\right]\right]$

which is a consequence of the Jacobi identity. This shows that L is a left L-module. This is called the adjoint module. We define $adx:L\to L$ by

$adx\cdot y=\left[xy\right]\text{for}x,y\in L_{-}$

Then we have

$ad\left[xy\right]=adxady-adyadx$

Now let V be a left L-module, U be a subspace of V and H a subspace of L. We define HU to be the subspace of V spanned by all elements of the form xu for $x\in H,u\in U$.

A submodule of V is a subspace U of V such that $LU\subset U$. In particular V is a submodule of V and the zero subspace $O=\left\{0\right\}$ is a submodule of V. A proper submodule of V is a submodule distinct from V and O. An L-module V is called irreducible if it has no proper submodules. V is called completely reducible if it is a direct sum of irreducible submodules. V is called indecomposable if V cannot be written as a direct sum of two proper submodules. Of course every irreducible L-module is indecomposable, but the converse need not be true.

We may also define right L-modules, but we shall mainly work with left L-modules, and L-modules will be assumed to be left L-modules unless otherwise stated.

Example 2.7. Let o(n) be the subspace of gl(n) consisting of skew-symmetric matrices, that is, $A^{\text{T}}=-A$. Then

${\left(AB-BA\right)}^{\text{T}}=B^{\text{T}}{A}^{\text{T}}-A^{\text{T}}{B}^{\text{T}}=\left(-B\right)\left(-A\right)-\left(-A\right)\left(-B\right)=-\left(AB-BA\right)$

so that o(n) is closed under $\left[ab\right]=ab-ba$, and hence is a Lie algebra.

To define a Lie bracket on a vector space with basis $e^1,\cdots ,e^n$ we need to specify the structure constants $c_{lm}^r$, that is, elements of k such that

$\left[e_l,e_m\right]={\displaystyle \underset{r=1}{\overset{n}{\sum }}{c}_{lm}^r{e}_r}$

For example,

$H=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right),X_{+}=\left(\begin{array}{cc}0& 1\\ 0& 0\end{array}\right),X_{-}=\left(\begin{array}{cc}0& 0\\ -1& 0\end{array}\right)$

is a basis of the vector space sl(2).

Definition 2.8. Ifg and $g^{-}$ are Lie algebras, a homomorphism $\varphi :g\to g^{-}$ is a linear map such that

$\phi \left(\left[x,y\right]\right)=\left[\phi \left(x\right),\phi \left(y\right)\right]$ for all $x,y\in g$

As usual, the identity map is a homomorphism, and the composition of two homomorphisms is another homomorphism.

Definition 2.9. A bijective homomorphism is an isomorphism (its inverse is clearly also an isomorphism). We write $g\cong g^{-}$ to mean that g and $g^{-}$ are isomorphic, i.e. there exists an isomorphism between them.

Proposition 2.10. [2] Any two-dimensional Lie algebra is either abelian or is isomorphic to $l_2$ .

Proof. Let g be a two-dimensional non-abelian Lie algebra with basis x, y. We need to find another basis u, v of g such that $\left[u,v\right]=v$. Suppose that $\left[x,y\right]=ax+by$. At least one of a and b is nonzero since otherwise g would be abelian. If $b\ne 0$, let $u=b^{-1}x$ and $v=ax+by$. Then

$\left[u,v\right]=b^{-1}\left[x,ax+by\right]=\left[x,y\right]=ax+by=v.$

If $b=0$, let $u=-a^{-1}y,v=x$. Then

$\left[u,v\right]=a^{-1}\left[x,y\right]=a^{-1}ax=v.$

So, in either case we are done.

The most important three-dimensional Lie algebra, namely $s{l}_2$, consisting of all 2 × 2 matrices with trace 0. The standard basis of $s{l}_2$ is e, h, f, where

$e=e_{12}=\left(\begin{array}{cc}0& 1\\ 0& 0\end{array}\right),h=e_{11}-e_{22}=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right),f=e_{21}=\left(\begin{array}{cc}0& 0\\ 1& 0\end{array}\right)$

The Lie bracket is completely specified by the brackets of these basis elements, which are given by:

Proposition 2.11. [2]

$\left[e,f\right]=h,\left[h,e\right]=2e,\left[h,f\right]=-2f.$

Proof: We get

$\left[e,f\right]=\left[e_{12},e_{21}\right]=e_{11}-e_{22}=h,$

$\left[h,e\right]=\left[e_{11},e_{12}\right]-\left[e_{22},e_{12}\right]=e_{12}+e_{12}=2e,$

$\left[h,f\right]=\left[e_{11},e_{21}\right]-\left[e_{22},e_{21}\right]=-e_{21}-e_{21}=-2f.$

Example 2.12. Suppose that g is a three-dimensional Lie algebra with basis $x_1,x_2,x_3$ such that

$\left[x_1,x_2\right]=x_1+x_2,$

$\left[x_1,x_3\right]=a{x}_1+x_3,$

$\left[x_2,x_3\right]=x_2+b{x}_3,$

for some $a,b\in C$. Determine a and b.

Example 2.13: Let V be a vector space over F, and let be a non-degenerate skew-symmetric bilinear form on V. The symplectic Lie algebra sp(V) or just sp(V) consists of the operators T on V that leave infinitesimally invariant: $\left(TX,Y\right)+\left(X,TY\right)=0$.

3. Basic Structure of a Lie Algebra

Subalgebra

Definition 3.1: A subspace K of V is called a (Lie) subalgebra if $\left[xy\right]\in K$ whenever $x,y\in K$.

Example 3.2: Important subalgebras of $g{l}_n$ are the following spans of subsets of the standard basis: the diagonal subalgebra

$D_n=\left\{\left(\begin{array}{ccccc}\ast & 0& \cdots & 0& 0\\ 0& \ast & \cdots & 0& 0\\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& \cdots & \ast & 0\\ 0& 0& \cdots & 0& \ast \end{array}\right)\right\}=C\left\{e_{ii}|1\le i\le n\right\}$

the upper-triangular subalgebra

${\alpha }_n=\left\{\left(\begin{array}{ccccc}\ast & \ast & \cdots & \ast & \ast \\ 0& \ast & \cdots & \ast & \ast \\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& \cdots & \ast & \ast \\ 0& 0& \cdots & 0& \ast \end{array}\right)\right\}=C\left\{e_{ij}|1\le i\le j\le n\right\}$

and the strictly upper-triangular subalgebra

${\beta }_n=\left\{\left(\begin{array}{ccccc}0& \ast & \cdots & \ast & \ast \\ 0& 0& \cdots & \ast & \ast \\ ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& \cdots & 0& \ast \\ 0& 0& \cdots & 0& 0\end{array}\right)\right\}=C\left\{e_{ij}|1\le i<j\le n\right\}$

The dimensions of these Lie algebras are as follows

$\dim D_n=n,\dim {\alpha }_n=\left(\begin{array}{c}n+1\\ 2\end{array}\right),\dim {\beta }_n=(\; n\; 2\; )$

Definition 3.3: A subspace I of a Lie algebra L is called an ideal of L if $x\in I;y\in L$ together imply $\left[x;y\right]\in I$. The construction of ideals in Lie algebra is analogous to the construction of normal subgroups in group theory.

By skew-symmetry, all Lie algebra ideals are automatically two sided. That is, if [x; y] 2I, then [y; x] 2 I. The kernel of a Lie algebra L and L itself are trivial ideals contained in every Lie algebra.

Proposition 3.4: [3]

1) If H, K are subalgebras of L so is $H\cap K$ .

2) If H, K are ideals of L so is $H\cap K$ .

3) If H is an ideal of L and K a subalgebra of L then H +K is a subalgebra of L.

4) If H, K are ideals of L then H + K is an ideal of L.

Proof. 1) $H\cap K$ is a subspace of L and $\left[H\cap K,H\cap K\right]\subset \left[HH\right]\cap \left[KK\right]\subset H\cap K$. Thus $H\cap K$ is a subalgebra.

2) This time we have $\left[H\cap K,L\right]\subset \left[HL\right]\cap \left[KL\right]\subset H\cap K$. Thus $H\cap K$ is an ideal of L.

3) $H+K$ is a subspace of L. Also $\left[H+K,H+K\right]\subset \left[HH\right]+\left[HK\right]+\left[KH\right]+\left[KK\right]\subset H+K$, since $\left[HH\right]\subset H$, $\left[HK\right]\subset H$, $\left[KK\right]\subset K$. Thus $H+K$ is a subalgebra.

4) This time we have $\left[H+K,L\right]\subset \left[HL\right]+\left[KL\right]\subset H+K$. Thus $H+K$ is an ideal of L.

Derivations and homomorphism

The derivative between two functionsf andg is a linear operator that satisfies the Leibniz rule:

1) ${\left(fg\right)}^{\prime }=f^{\prime }g+f{g}^{\prime }$

2) ${\left(\alpha f\right)}^{\prime }=\alpha f^{\prime }$ where $\alpha$ is a scalar.

Given an algebra A over a field F, the derivation of A is the linear map $\delta$ such that $\delta \left(f,g\right)=f\delta \left(g\right)+\delta \left(f\right)g$ for all $f,g\in A$. The set of all derivations of A is denoted by Der(A). Given $\delta \in Der\left(A\right)$, $f,g\in A$ and $\alpha \in F$.

$\left(\alpha \delta \right)\left(fg\right)=\alpha \delta \left(fg\right)=\alpha \left(f\delta \left(g\right)+\delta \left(f\right)g\right)=\alpha f\delta \left(g\right)+\alpha \delta \left(f\right)g$

where the Leibniz rule is satisfied if and only if $af=fa$ where F is a field.

Definition 3.5. Let L be a Lie algebra over an arbitrary field F. Let $L^2$ and Z(L) denote the derived algebra and the center of L, respectively. A derivation of L is an F-linear transformation $\alpha :L\to L$ such that $\alpha \left(\left[x,y\right]\right)=\left[\alpha \left(x\right),y\right]+\left[x,\alpha \left(y\right)\right]$ for all $x,y\in L$. We denote by $Der\left(L\right)$ the vector space of all derivations of L, which itself forms a Lie algebra with respect to the commutator of linear transformations, called the derivation algebra of L. For all $x\in L$, the map $a{d}_x:L\to L$ given by $y\to \left[x,y\right]$ is a derivation called the inner derivation corresponding to x. Clearly, the space $IDer\left(L\right)=\left\{a{d}_x|x\in L\right\}$ of inner derivations is an ideal of $Der\left(L\right)$.

Proposition 3.6: Let g be any Lie algebra. For any $x\in g$, define a linear transformation

$a{d}_g\left(x\right):g\to g:y\to \left[x,y\right]$

Then $a{d}_g:g\to gl\left(g\right)$ is a representation of g on g itself.

Proof: It is clear that $a{d}_g$ is a linear map. We need to show that $a{d}_g\left(\left[x,y\right]\right)=\left[a{d}_g\left(x\right),a{d}_g\left(y\right)\right]$ for all $x,y\in g$, i.e. that

$\left[\left[x,y\right],z\right]=\left[x,\left[y,z\right]\right]-\left[y,\left[x,z\right]\right]$ for all $x,y,z\in g$.

This is, however, just a form of the Jacobi identity.

Definition 3.7: [4] The map $L\to DerL$ sending x to $a{d}_x$ is called the adjoint representation of L. This is akin to taking the ad homomorphism of $g\to gl\left(g\right)$. To show ad is a homomorphism:

$a{d}_{\left(\left[x;y\right]\right)}=\left[a{d}_{\left(x\right)},a{d}_{\left(y\right)}\right]=a{d}_{\left(x\right)}a{d}_{\left(y\right)}-a{d}_{(y)}a{d}_{(\; x\; )}$

$\left[\left[x,y\right];z\right]=\left[x,\left[y,z\right]\right]-\left[y,\left[x,z\right]\right]$

$0=\left[x,\left[y,z\right]\right]+\left[y,\left[z,x\right]\right]+\left[z,\left[x,y\right]\right]$

That is, if and only if the Jacobi identity is satisfied, where $\left[\left[x,y\right],z\right]=-\left[z,\left[x,y\right]\right]$ and $-\left[y;\left[x,z\right]\right]=\left[y,\left[z,x\right]\right]$ by skew symmetry.

Example 3.8: [4] The set of all inner derivations $a{d}_x$, $x\in L$, is an ideal of $Der\left(L\right)$. Let $\delta \in Der\left(L\right)$. By definition of inner derivations, for all $y\in L$ :

$\begin{array}{c}\left[\delta ,a{d}_x\right]\left(y\right)=\left(\delta \left(a{d}_x\right)-\left(a{d}_x\right)\delta \right)\left(y\right)=\delta \left[x,y\right]-a{d}_x\left(\delta \left(y\right)\right)\\ =\left[\delta \left(x\right),y\right]+\left[x,\delta \left(y\right)\right]-\left[x,\delta \left(y\right)\right]=ad\left(\delta \left(x\right)y\right)\end{array}$

Therefore, $a{d}_x$ is an ideal of $Der\left(L\right)$.

Example 3.9: [2] In the adjoint representation of $s{l}_2$, the element e is represented by the linear transformation $ad\left(e\right)$ of $s{l}_2$, which sends any element x to $\left[e,x\right]$. On the standard basis, this linear transformation acts as follows:

$ad\left(e\right)e=\left[e,e\right]=0,ad\left(e\right)h=\left[e,h\right]=-2e,ad\left(e\right)f=\left[e,f\right]=h.$

Making similar calculations for $ad\left(h\right)$ and $ad\left(f\right)$, we deduce that the representing matrices are:

$ad\left(e\right):\left(\begin{array}{ccc}0& -2& 0\\ 0& 0& 1\\ 0& 0& 0\end{array}\right),ad\left(h\right):\left(\begin{array}{ccc}2& 0& 0\\ 0& 0& 0\\ 0& 0& -2\end{array}\right),ad\left(f\right):\left(\begin{array}{ccc}0& 0& 0\\ -1& 0& 0\\ 0& 2& 0\end{array}\right)$

Since $Z\left(s{l}_2\right)=\left\{0\right\}$ (or alternatively because these matrices are clearly linearly independent), this is a faithful representation of $s{l}_2$.

Definition 3.10: An automorphism of A is an isomorphism of A onto itself. Aut A denotes the group of all such.

The set of inner automorphisms of a ring, or associative algebra A, is given by the conjugation element, using right conjugation, such that:

${\varphi }_a:A\to A$

${\varphi }_a\left(x\right)=a^{-1}xa$

Given $x,y\in A$ :

${\varphi }_a\left(xy\right)=a^{-1}\left(xy\right)a=a^{-1}xa{a}^{-1}ya=\left(a^{-1}xa\right)\left(a^{-1}ya\right)={\varphi }_a\left(x\right){\varphi }_a(\; y\; )$

where, ${\varphi }_a$ is an (invertible) homomorphism that contains ${\varphi }_a^{-1}$.

Example 3.11: [4] Let L be a Lie algebra such that $L=sl\left(n,F\right)$ ; $g\in GL\left(n,F\right)$. The map $\varphi :L\to L$ defined by $x\to -g{x}^t{g}^{-1}$ ( $x^t$ = the transpose of x) belongs to Aut L. When n = 2, g = the identity matrix, we can prove that Aut L is inner.

$tr\left(-g{x}^t{g}^{-1}\right)=tr\left(-g{g}^{-1}{x}^t\right)=tr\left(-x^t\right)=-tr\left(x\right)$ (Since g = the identity matrix)

$tr\left(x\right)=0\iff tr\left(-g{x}^t{g}^{-1}\right)=0$

Therefore, the map is a linear automorphism of $sl\left(n,F\right)$. If we apply the transpose to the commutator, for $x,y\in L$, we have:

${\left[x,y\right]}^t={\left(xy-yx\right)}^t={\left(xy\right)}^t-{\left(yx\right)}^t=y^t{x}^t-x^t{y}^t=\left[y^t{x}^t\right]$

Therefore:

$\begin{array}{c}\varphi \left[x,y\right]=-g{\left[x,y\right]}^t{g}^{-1}=-g\left[y^t,x^t\right]g^{-1}\\ =g\left(y^t{x}^t-x^t{y}^t\right)g^{-1}=g{y}^t{x}^t{g}^{-1}-g{x}^t{y}^t{g}^{-1}\\ =\left[g{y}^t{g}^{-1},g{x}^t{g}^{-1}\right]=g{y}^t{g}^{-1}g{x}^t{g}^{-1}-g{x}^t{g}^{-1}g{y}^t{g}^{-1}\\ =\left[\varphi \left(x\right),\varphi \left(y\right)\right]\end{array}$

Therefore, $\varphi$ is a homomorphism. Thus Aut L is inner.

Cartan’s Criterion

Theorem 3.12. (Cartan’s Criterion). Let L be a subalgebra of gl(V), V finite-dimensional. Suppose that $Tr\left(xy\right)=0$ for all $x\in \left[L,L\right]$, $y\in L$, The L is solvable.

Proof: As remarked at the beginning of it will suffice to prove that $\left[L,L\right]$ is nilpotent, or just that all x in $\left[L,L\right]$ are nilpotent endomorphisms. For this we apply the above lemma to the situation: Vas given, $A=\left[L,L\right]$, $B=L$, so $M=\left\{x\in gl\left(V\right)|\left[x,L\right]\subset \left[L,L\right]\right\}$. Obviously $L\subset M$. Our hypothesis is that $Tr\left(xy\right)=0$ for $x\in \left[L,L\right]$, $y\in L$, whereas to conclude from the lemma that each $x\in \left[L,L\right]$ is nilpotent we need the stronger statement: $Tr\left(xy\right)=0$ for $x\in \left[L,L\right]$, $y\in M$.

Now if $\left[x,y\right]$ is a typical generator of $\left[L,L\right]$, and if $z\in M$, then identity (⋅) above shows that $Tr\left(\left[x,y\right]z\right)=Tr\left(x\left[y,z\right]\right)=Tr\left(\left[y,z\right]x\right)$. By definition of M, $\left[y,z\right]\in \left[L,L\right]$, so the right side is 0 by hypothesis.

The Killing form

Definition 3.13. LetL be a finite-dimensional Lie algebra over F. We define a map

$L\times L\to F$

$x,y\to \langle x,y\rangle$

given by

$\langle x,y\rangle =tr(ad\left(x\right)ad(\; y\; ))$

for $x,y\in L$. We refer to as the Killing form on L.

Proposition 3.14. Let L be a finite-dimensional Lie algebra over F. The Killing form on L is a symmetric bilinear form. Moreover, we have

$\langle \left[xy\right],z\rangle =\langle x,\left[yz\right]\rangle$

Proof:

$\langle \left[xy\right],z\rangle =tr\left(ad\left[xy\right]ad\left(z\right)\right)=tr(\left(ad\left(x\right)ad\left(y\right)-ad\left(y\right)ad\left(x\right)\right)ad(\; z\; ))$

$tr\left(ad\left(x\right)ad\left(y\right)ad\left(z\right)\right)-tr(ad\left(y\right)ad\left(x\right)ad(\; z\; ))$

$tr\left(ad\left(x\right)ad\left(y\right)ad\left(z\right)\right)-tr(ad\left(x\right)ad\left(z\right)ad(\; y\; ))$

$tr\left(ad\left(x\right)\left(ad\left(y\right)ad\left(z\right)-ad\left(z\right)ad\left(y\right)\right)\right)$

$tr\left(ad\left(x\right)ad\left[yz\right]\right)=\langle x,\left[yz\right]\rangle$

Lemma 3.15. Let L be a finite-dimensional Lie algebra over F. Let I be an ideal of L. Define

$I^{\perp }=\left\{x\in L:\langle x,I\rangle =0\right\}$

Then $I^{\perp }$ is an ideal of L.

Proof: It is evident that $I^{\perp }$ is an F-subspace of L. Let $x\in L,y\in I^{\perp }$ and $z\in I$.

Then

$\langle \left[xy\right],z\rangle =\langle x,\left[yz\right]\rangle =\langle x,0\rangle =0$

It follows that $\left[xy\right]\in I^{\perp }$.

Example 3.16: [5] $sl\left(2,C\right)$. We write the elements as $X=a{X}_{+}+bH+c{X}_{-}$.

From the brackets between the basis vectors one finds the matrix expressions

$adH=\left[\begin{array}{ccc}2& 0& 0\\ 0& 0& 0\\ 0& 0& -2\end{array}\right],ad{X}_{+}=\left[\begin{array}{ccc}0& -2& 0\\ 0& 0& 1\\ 0& 0& 0\end{array}\right],ad{X}_{-}=\left[\begin{array}{ccc}0& 0& 0\\ -1& 0& 0\\ 0& 2& 0\end{array}\right]$

and then the values $tr\left(adH\circ adH\right)$ etc. of the coefficients of the Killing form, with the result

$\kappa \langle X,X\rangle =8\left(b^2+ac\right)\left(=4tr{X}^2\right).$

The bilinear form $\kappa \langle X,Y\rangle$ is then obtained by polarization.

Lemma 3.17: [6] Let F have characteristic zero and be algebraically closed. Let n be a positive integer. For $x,y\in gl\left(n,F\right)$ define

$t\left(x,y\right)=tr(\; x\; y\; )$

The function $t:gl\left(n,F\right)\times gl\left(n,F\right)\to F$ is an associative, symmetric bilinear form. If L is a Lie subalgebra of $gl\left(n,F\right)$, L is simple, and the restriction of t to $L\times L$ is non-zero, then L is non degenerate.

Proof. It is clear that t is F-linear in each variable. Also, t is symmetric because $tr\left(xy\right)=tr\left(yx\right)$ for $x,y\in gl\left(n,F\right)$. To see that t is associative, let $x,y,z\in gl\left(n,F\right)$. Then

$\begin{array}{c}t\left(x,\left[y,z\right]\right)=tr\left(x\left(yz-zy\right)\right)\\ =tr\left(xyz\right)-tr\left(xzy\right)\\ =tr\left(xyz\right)-tr\left(yxz\right)\\ =tr\left(\left(xy-yx\right)z\right)\\ =t\left(\left[x,y\right],z\right)\end{array}$

Assume that L is a subalgebra of $gl\left(n;F\right)$, L is simple, and the restriction of t to $L\times L$ is non-zero. Let $J=\left\{y\in L:t\left(x,y\right)=0,x\in L\right\}$. We need to prove that J = 0. We claim that J is an ideal of L. Let $y\in L$ and $z\in J$ ; we need to see that $\left[y,z\right]\in J$. Let $x\in L$. Now $t\left(x,\left[y,z\right]\right)=t\left(\left[x,y\right],z\right)=0$ because $z\in J$.

It follows thatJ is an ideal. Since L is simple, J = 0 or J = L. If J = L, then the restriction of t to $L\times L$ is zero, a contradiction. Hence, J = 0.

Homomorphisms and Representations

Definition 3.18. A linear transformation $\phi :L\to L^{\prime }$ is called ahomomorphism if $\phi \left(\left[x,y\right]\right)=\left[\phi \left(x\right),\phi \left(y\right)\right]$, for all $x,y\in L$. $\phi$ is called a monomorphism if its kernal is zero, an epimorhpism if its image equals $L^{\prime }$, and an isomorphism if $\phi$ is both a monomorphism and epimorphism, that is, if $\phi$ is bijective.

[7] A representation of a Lie algebra L is a homomorphism $\phi :L\to gl\left(V\right)$ (V = vector space over F). Although we require L to be finite dimensional, it is useful to allow V to be of arbitrary dimension: gl(V) makes sense in any case. However, for the time being the only important example to keep in mind is the adjoint representation $ad:L\to gl\left(L\right)$ introduced, which sends x to ad x, where $adx\left(y\right)=\left[xy\right]$. (The image of ad is in $DerL\subset gl\left(L\right)$, but this does not concern us at the moment.) It is clear that ad is a linear transformation. To see that it preserves the bracket, we calculate:

$\begin{array}{c}\left[adx,ady\right]\left(z\right)=adxady\left(z\right)-adyadx\left(z\right)\\ =adx\left(\left[yz\right]\right)-ady\left(\left[xz\right]\right)\\ =\left[x\left[yz\right]\right]-\left[y\left[xz\right]\right]\\ =\left[x\left[yz\right]\right]+\left[\left[xz\right]y\right]\\ =\left[\left[xy\right]z\right]=ad\left[xy\right](\; z\; )\end{array}$

what is the kernel of ad? It consists of all $x\in L$ for which ad x = 0, i.e., for which [xy] = 0 (all $y\in L$ ). So Ker $ad=Z\left(L\right)$. This already has an interesting consequence: If L is simple, then $Z\left(L\right)=0$, so that $ad:L\to gl\left(L\right)$ is a monomorphism. This means that any simple Lie algebra is isomorphic to a linear Lie algebra.

Example 3.19. The special linear group $SL\left(n,F\right)$ denotes the kernel of the homomorphism

$\det :GL\left(n,F\right)\to F^x=\left\{x\in F|x\ne 0\right\}$

where F is a feld.

We will now forge a proof of Lie algebra isomorphism theorems analogous to the ring theory isomorphisms described in the introduction.

Automorphisms

Definition 3.20. The set of inner automorphisms of a ring, or associative algebra A, is given by the conjugation element, using right conjugation, such that:

${\varphi }_a:A\to A$

${\varphi }_a\left(x\right)=a^{-1}xa$

Given $x,y\in A$ :

${\varphi }_a\left(xy\right)=a^{-1}\left(xy\right)a=a^{-1}xa{a}^{-1}ya=\left(a^{-1}xa\right)\left(a^{-1}ya\right)={\varphi }_a\left(x\right){\varphi }_a(\; y\; )$

where, ${\varphi }_s$ is an (invertible) homomorphism that contains ${\varphi }_a^{-1}$. Therefore ${\varphi }_a$ constitutes an isomorphism onto itself. Since the composition of conjugation is associative, $a^{-1}xa$ is often denoted as $x^a$.

Definition 3.21. An automorphism of L is an isomorphism of L onto itself. Aut L denotes the group of all such.

An automorphism of the form exp(ad_x), with ad_x nilpotent, i.e., ${\left(a{d}_x\right)}^k=0$ for some $k>1$, is called inner.

[4] Example 3.22. Let L be a Lie algebra such that $L=sl\left(n,F\right)$, $g\in GL\left(n,F\right)$. The map $\phi :L\to L$ defined by $x\to -g{x}^t{g}^{-1}$ ( $x^t$ = the transpose of x) belongs to Aut L. When n = 2, g = the identity matrix, we can prove that Aut L is inner.

$tr\left(-g{x}^t{g}^{-1}\right)=tr\left(-g{g}^{-1}{x}^t\right)=tr\left(-x^t\right)=-tr\left(x\right)$ {Since g= the identity matrix}

$\Rightarrow tr\left(x\right)=0\iff tr\left(-g{x}^t{g}^{-1}\right)=0$

Therefore, the map is a linear automorphism of $sl\left(n,F\right)$. If we apply the transpose to the commutator, for $x,y\in L$, we have:

$\begin{array}{c}{\left[x,y\right]}^t={\left(xy-yx\right)}^t={\left(xy\right)}^t-{\left(yx\right)}^t\\ =y^t{x}^t-x^t{y}^t=\left[y^t{x}^t\right]\end{array}$

Therefore:

$\begin{array}{c}\phi \left[x,y\right]=-g{\left[x,y\right]}^t{g}^{-1}=-g\left[y^t,x^t\right]g^{-1}\left\{\text{Bypropertiesofthetranspase}\right\}\\ =g\left(y^t{x}^t-x^t{y}^t\right)g^{-1}=g{y}^t{x}^t{g}^{-1}-g{x}^t{y}^t{g}^{-1}\\ =\left[g{y}^t{g}^{-1},g{x}^t{y}^t\right]=g{y}^t{g}^{-1}g{x}^t{g}^{-1}-g{x}^t{g}^{-1}g{y}^t{g}^{-1}\\ =\left[\phi \left(x\right),\phi \left(y\right)\right]\end{array}$

Therefore, ' is a homomorphism. Thus Aut L is inner.

Definition 3.23.When ad_x is nilpotent, the inner automorphism constructed is called IntL. For $\sigma \in \text{Aut}l,x\in L$,

$\sigma \left(a{d}_x\right){\sigma }^{-1}=a{d}_{\sigma \left(x\right)}$ when $\sigma \exp \left(a{d}_x\right){\sigma }^{-1}=\exp \left(a{d}_{\sigma (\; x\; )}\right)$

[4] Example 3.24. Let $\sigma$ be the automorphism of $sl\left(2,F\right)$ give by the following: let $L\in sl\left(2,F\right)$, with standard basis (x; y; h). Define $\sigma =\exp adx\cdot \exp ad\left(-y\right)\cdot \exp adx$. We can show that $\sigma \left(x\right)=-y$, $\sigma \left(y\right)=-x$, $\sigma \left(h\right)=-h$.

We have $\left[x,y\right]=h,\left[h,y\right]=-2y,\left[h,x\right]=-2x$

$\begin{array}{c}\sigma \left(x\right)=\exp adx\cdot \exp ad\left(-y\right)\cdot \exp adx\left(x\right)\\ =\exp adx\cdot \left(1+ad\left(-y\right)+\frac{ad{\left(-y\right)}^2}{2!}\right)x\\ =\exp adx\cdot \left(x+\left(-ady\right)\left(x\right)+\frac{1}{2!}{\left(ad\left(-y\right)\right)}^2\left(x\right)\right)\\ =\exp adx\cdot \left(x-\left[y,x\right]+\frac{1}{2!}\left(ad\left(-y\right)\right)\left(h\right)\right)\\ =\exp adx\cdot \left(x+h+\left[-y,h\right]\right)\end{array}$

$\begin{array}{l}=\left(1+adx+\frac{ad\left(x^2\right)}{2!}\right)\left(x+h-y\right)\\ =\left(x+h-y\right)+\left(\left[x,x\right]+\left[x,h\right]-\left[x,y\right]\right)+\left(\frac{\left[x\left[x,x\right]\right]}{2!}+\frac{\left[x,-2x\right]}{2!}-\frac{\left[x,h\right]}{2!}\right)\\ =\left(x+h-y\right)+\left(-2x-h\right)+\left(x\right)\\ =-y\end{array}$

$\begin{array}{c}\sigma \left(y\right)=\exp adx\cdot \exp ad\left(-y\right)\cdot \exp adx\left(y\right)\\ =\exp adx\cdot \left(1+adx+\frac{ad{\left(x\right)}^2}{2!}\right)\left(y\right)\\ =\exp adx\cdot \left(y+\left[x,y\right]+\frac{\left[x,\left[x,y\right]\right]}{2}\right)\\ =\exp adx\cdot \left(1+ad\left(-y\right)+\frac{ad{\left(-y\right)}^2}{2!}\right)\left(y+h-x\right)\end{array}$

$\begin{array}{l}=\exp adx\cdot [\left(y+h-x\right)+\left(\left[-y,y\right]+\left[-y,h\right]-\left[-y,x\right]\right)\begin{array}{c}{}_{}^{}\\ \end{array}\\ +\left(\frac{\left[-y,\left[-y,y\right]\right]}{2!}+\frac{\left[-y,\left[-y,h\right]\right]}{2!}-\frac{\left[-y,\left[-y,x\right]\right]}{2!}\right)]\\ =\exp adx\cdot \left(y+h-2y-x-h+y\right)\\ =\left(1+adx+\frac{ad{\left(x\right)}^2}{2!}\right)\left(-x\right)\\ =-x\end{array}$

$\begin{array}{l}\sigma \left(h\right)=\exp adx\cdot \exp ad\left(-y\right)\cdot \exp adx\left(h\right)\\ =\exp adx\cdot \exp ad\left(-y\right)\cdot \left(1+adx+\frac{ad{\left(x\right)}^2}{2!}\right)\left(h\right)\\ =\exp adx\cdot \exp ad\left(-y\right)\cdot \left(h+\left[x,h\right]+\frac{\left[\left[x,h\right],h\right]}{2!}\right)\\ =\exp adx\cdot \left(1+ad\left(-y\right)+\frac{ad{\left(-y\right)}^2}{2!}\right)\left(h-2x\right)\\ =\exp adx\cdot \left[\left(h-2x\right)+\left(\left[-y,h\right]-2\left[-y,x\right]\right)+\left(\frac{\left[-y,\left[-y,h\right]\right]}{2!}\right)-\frac{2\left[-y,\left[-y,x\right]\right]}{2!}\right]\end{array}$

$\begin{array}{l}=\exp adx\cdot \left[\left(h-2x\right)+\left(-2y-2h\right)+\left(0+2y\right)\right]\\ =\exp adx\left(-h-2x\right)\\ =\left(1+adx+\frac{ad{\left(x\right)}^2}{2!}\right)\left(-h-2x\right)\\ =\left(-h-2x\right)+\left(-\left[x,h\right]-2\left[x,x\right]\right)+\left(-\frac{\left[x,\left[x,h\right]\right]}{2}-2\frac{\left[x,\left[x,x\right]\right]}{2}\right)\\ =\left(-h-2x\right)+\left(2x-0\right)\\ =-h\end{array}$

4. The Classical Lie Algebras

Classical algebras are finite-dimensional Lie algebras. Let F have characteristic zero and be algebraically closed. The classical Lie algebras over F are $sl\left(l+1,F\right)$, $so\left(2l+1,F\right)$, $sp\left(2l,F\right)$ and $so\left(2l,F\right)$ (for lpositive integer) has an associated algebra, represented by symmetric, skew symmetric, and orthogonal matrices.

$sl\left(l+1,F\right)$ -special linear algebra( $l\ge 1$ )

The set of all endomorphisms of V having trace zero is denoted by sl(V), the special linear algebra. $sl\left(l+1,F\right)$ is inherited from $gl\left(l+1,F\right)$, and is defined by $\left[X,Y\right]=XY-YX$ for $X,Y\in sl\left(l+1,F\right)$.

That,

$tr\left[x,y\right]=tr\left(xy\right)-tr\left(yx\right)=0$. Since the trace of a matrix preserves bilinearity g

$tr\left(\left[x,\left[y,z\right]\right]+\left[y,\left[z,x\right]\right]+\left[z,\left[x,y\right]\right]\right)=tr\left[x,0\right]+tr\left[y,0\right]+tr\left[z,0\right]=0$

so actually not only is the bracket of two endomorphisms in $sl\left(V\right)$ back in the subspace, the bracket of any two endomorphisms of $gl\left(V\right)$ lands in $sl\left(V\right)$. In other words: $\left[gl\left(V\right),gl\left(V\right)\right]=sl\left(V\right)$.

Choosing a basis, we will write the algebra as $sl\left(l+1,F\right)$. It should be clear that the dimension is ${\left(l+1\right)}^2-1$, since this is the kernel of a single linear functional on the ${\left(l+1\right)}^2$ dimensional, $gl\left(l+1,F\right)$ but let’s exhibit a basis anyway. All the basic matrices $e_{ij}$ with $i\ne j$ are traceless, so they’re all in $sl\left(n,F\right)$. Along the diagonal, $tr\left(e_{ij}\right)=1$, so we need linear combinations that cancel each other out. It’s particularly convenient to define

$h_i=e_{ii}-e_{i+1,i+1}$

So we’ve got the ${\left(l+1\right)}^2$ basic matrices, but we take away the $\left(l+1\right)$ along the diagonal. Then we add back the l new matrices $h_i$, getting ${\left(l+1\right)}^2-1$ matrices in our standard basis for $sl\left(l+1,F\right)$ verifying the dimension.

We sometimes refer to the isomorphism class of $sl\left(l+1,F\right)$ as $A_l$

$sl\left(2l+1,F\right)$ -special orthagonal algebra ( $l\ge 2$ )

The set of all endomorphisms of V with dimension $2l+1$. Let F have characteristic zero and be algebraically closed, and let l be a positive integer. Let $s\in gl\left(2l+1,F\right)$ be the matrix

$s=\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& I_l\\ 0& I_l& 0\end{array}\right]$

corresponds to the orthogonal algebra.

Here, $I_l$ is the $l\times l$ identity matrix. Recall a matrix $A\in M_{n\times n}\left(F\right)$ is called orthogonal if $A{A}^t=I$. The orthogonal algebra is a subalgebra of gl(V).

We sometimes refer to the isomorphism class of $so\left(2l+1,F\right)$ as $B_l$

$sp\left(2l,F\right)$ -simplectic algebra ( $l\ge 3$ )

The set of endomorphisms of V having $\dim V=2l$. Let F have characteristic zero and be algebraically closed, and let l be a positive integer. Let $s\in gl\left(2l,F\right)$ be the skew symmetric matrix

$s=\left[\begin{array}{cc}0& I_l\\ -I_l& 0\end{array}\right]$

Here, $I_l$ is the $l\times l$ identity matrix. Recall that a matrix $A\in M_{n\times n}\left(F\right)$ is called skew-symmetric if $A^t=-A$. We have $sp\left(2l,F\right)\subset sl\left(2l,F\right)$.

We sometimes refer to the isomorphism class of $sp\left(2l,F\right)$ as $C_l$

$so\left(2l,F\right)$ -orthogonal algebra ( $l\ge 4$ )

The set of all endomorphisms of V with dimension $\dim =2l$. Let F have characteristic zero and be algebraically closed, and let l be a positive integer. Let $s\in gl\left(2l+1,F\right)$ be the matrix

$s=\left[\begin{array}{cc}0& I_l\\ I_l& 0\end{array}\right]$

Here, $I_l$ is the $l\times l$ identity matrix. We define $so\left(2l,F\right)$ to be the Lie subalgebra of $gl\left(2l,F\right)$.We have $so\left(2l,F\right)\subset sl\left(2l,F\right)$.

We sometimes refer to the isomorphism class of $so\left(2l,F\right)$ as $D_l$

5. Root Systems

Definition 5.1: [6] Let V be a finite-dimensional vector space over R, and let $\left(.,.\right)$ be an inner product (here it is a positive definite, bilinear, symmetric form). By definition, $\left(.,.\right):V\times V\to R$ is a symmetric bilinear form such that $\left(x,x\right)>0$ for all non-zero $x\in V$. Let $v\in V$ be non-zero. We define the reflection determined by v to be the unique R linear map $s_v:V\to V$ such that $s_v\left(v\right)=-v$ and $s_v\left(w\right)=w$ for all $w\in {\left(Rv\right)}^{\perp }$. A calculation shows that $s_v$ is given by the formula

$s_v\left(x\right)=x-\frac{2\left(x,v\right)}{\left(v,v\right)}v$

for $x\in V$. Another calculation also shows that $s_v$ preserves the inner product $\left(.,.\right)$, i.e.,

$\left(s_v\left(x\right),s_v\left(y\right)\right)=\left(x,y\right)$

for $x,y\in V$ ; that is, $s_v$ is in the orthogonal group $O\left(V\right)$. Evidently,

$\det \left(s_v\right)=-1$

We will write

$\left(x,y\right)=\frac{2\left(x,y\right)}{\left(y,y\right)}$

for $x,y\in V$. We note that the function $\langle .,.\rangle :V\times V\to R$ is linear in the first variable; however, this function is not linear in the second variable. We have

$s_v\left(x\right)=x-\left(x,v\right)v$

for $x\in V$.

Definition 5.2: A root system R in V is a finite set $R⊑V$ s.t.

1) The set R is finite, does not contain 0, and spans V.

2) If $\alpha \in R$, then α and −α are the only scalar multiples of α that are contained in R.

3) If $\alpha \in R$ then $s_{\alpha }\left(R\right)=R$, so that $s_{\alpha }$ permutes the elements of R.

4) for all $\alpha ,\beta \in R$ we have $\langle \alpha ,\beta \rangle \in Z$,

Proposition 5.3: [6] Let the notation be as in the discussion preceding the proposition. The subset $\varphi$ of the inner product space V is a root system.

Proof. It is clear that (1) is satisfied. (2) is satisfied. To see that (3) is satisfied, let $\alpha ,\beta \in \varphi$. Then

$s_{\alpha }\left(\beta \right)=\beta -\frac{2\left(\beta ,\alpha \right)}{\left(\alpha ,\alpha \right)}\alpha =\beta -\beta \left(h_{\alpha }\right)\alpha$

we have $\beta -\beta \left(h_{\alpha }\right)\alpha \in \varphi$. It follows that $s_{\alpha }\left(\beta \right)\in \varphi$ so that (3) is satisfied. To prove that (4) holds, again let $\alpha ,\beta \in \varphi$. We have

$\langle \alpha ,\beta \rangle =\frac{2\left(\alpha ,\beta \right)}{\left(\beta ,\beta \right)}$

we have

$\frac{2\left(\alpha ,\beta \right)}{\left(\beta ,\beta \right)}=\alpha (\; h\; \beta \; )$

Definition 5.4: [8] Let $W:=\langle \left\{s_{\alpha }:\alpha \in R\right\}\rangle \subseteq GL\left(V\right)$. The group W is called the Weyl group of R.

Theorem 5.5: [6] (Weyl’s Theorem). Let F be algebraically closed and have characteristic zero. Let L be a finite-dimensional semi-simple Lie algebra over F. If $\left(\phi ,V\right)$ is a finite-dimensional representation of L, then V is a direct sum of irreducible representations of L.

Proof. By induction, to prove the theorem it will suffice to prove that if W is a proper, non-zero L-subspace of V, then W has a complement, i.e., there exists an L-subspace W' of V such that $V=W\oplus W^{\prime }$. Let W be a proper, non-zero L-subspace of V.

We first claim that W has a complement in the case that $\dim W=\dim V-1$. Assume that $\dim W=\dim V-1$.

We will first prove our claim when W is irreducible; assume that W is irreducible. The kernel $\ker \left(\phi \right)$ of $\phi :L\to gl\left(V\right)$ is an ideal of L. By replacing $\phi :L\to gl\left(V\right)$ by the representation $\phi :L/\ker \left(\phi \right)\to gl\left(V\right)$, we may assume that $\phi$ is faithful. Consider the quotient $V=W$. By assumption, this is a one-dimensional L-module. Since $\left[L,L\right]$ acts by zero on any one-dimensional L-module, and since $L=\left[L,L\right]$. It follows that L acts by zero on $V=W$. This implies that $\phi \left(L\right)V\subset W$. In particular, if C is the Casmir operator¹ for $\phi$ then $CV\subset W$. Hence, ker(C) is an L-submodule of V; we will prove that $V=W\oplus \ker \left(C\right)$, so that ker(C) is a complement to W. To prove that ker(C) is a complement to W it will suffice to prove that $W\cap \ker \left(C\right)=0$ and $\dim \ker \left(C\right)=1$. Consider the restriction ${C|}_W$ of C to W. This is an L-map from W to W.

Since W is irreducible, there exists a constant $a\in F$ such that $C\left(w\right)=aw$ for $w\in W$. Fix an ordered basis $w_1,\cdots ,w_t$ for W, and let $v\notin V$. Then $w_1,\cdots ,w_t$ v is an ordered basis for V, and the matrix of C in this basis has the form

$\left[\begin{array}{cccc}a& & & \ast \\ & \ddots & & \ast \\ & & a& \ast \\ & & & 0\end{array}\right]$

It follows that $tr\left(C\right)=\left(\dim W\right)a$. On the other hand,, we have $tr\left(C\right)=\dim L$. It follows that $\left(\dim W\right)a=\dim L$, and in particular, $a\ne 0$. Thus, C is injective on W and maps onto W. Therefore, $W\cap \ker \left(C\right)=0$, and $\dim \ker \left(C\right)=\dim V-\dim im\left(C\right)=\dim V-\dim W=1$. This proves our claim in the case that W is irreducible.

We will now prove our claim by induction on dim V. We cannot have $\dim V=0$ or 1 because W is non-zero and proper by assumption. Suppose that $\dim V=2$. Then $\dim W=1$, so that W is irreducible, and the claim follows from the previous paragraph. Assume now that $\dim V\ge 3$, and that for all L-modules A with $\dim A<\dim V$, if B is an L-submodule of A of codimension one, then B has a complement. If W is irreducible, then W has a complement by the previous paragraph. Assume that W is not irreducible, and let $W_1$ be a L-submodule of W such that $0<\dim W_1<\dim W$. Consider the L-submodule $W=W_1$ of $V=W_1$. This L-submodule has co-dimension one in $V=W_1$, and $\dim V=W_1<\dim V$. By the induction hypothesis, there exists an L-submodule U of $V=W_1$ such that

$V/W_1=U\oplus W/W_1$

We have $\dim U=1$. Let $p:V\to V/W_1$ be the quotient map, and set $M=p^{-1}\left(U\right)$. Then M is an L-submodule of V, $W_1\subset M$, and $M/W_1=U$. We have

$\dim M=\dim W_1+\dim U=1+\dim W_1$

Since $\dim M=1+\dim W_1<1+\dim W\le \dim V$, we can apply the induction hypothesis again: let $W_2$ be an L-submodule of M that is a complement to $W_1$ in M, i.e.,

$M=W_1\oplus W_2$

Theorem 5.6: [6] Let V be a finite-dimensional vector space over R equipt with an inner product $\left(.,.\right)$. The Cauchy-Schwartz inequality asserts that

$\left|\left(x,y\right)\right|\le \Vert x\Vert \Vert y\Vert$

for $x,y\in V$. It follows that if $x,y\in V$ are nonzero, then

$-1\le \frac{\left(x,y\right)}{\Vert x\Vert \Vert y\Vert }\le 1$

If $x,y\in V$ are nonzero, then we define the angle between x and y to be the unique number $0\le \theta \le \pi$ such that

$\left(x,y\right)=\Vert x\Vert \Vert y\Vert \cos \theta$

The inner product measures the angle between two vectors, though it is a bit more complicated in that the lengths of x and y are also involved. The term, angle does make sense geometrically. For example, suppose that $V=R^2$ and we have:

Project x onto y, to obtain ty:

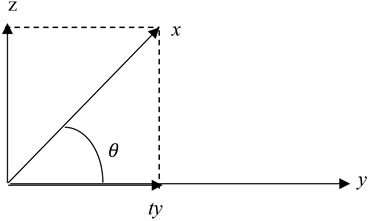
Then we have

$x=z+ty$

Taking the inner product with y, we get

$\left(x,y\right)=\left(z,y\right)+\left(ty,y\right)$

$\left(x,y\right)=0+t\left(y,y\right)$

$\left(x,y\right)=t{\Vert y\Vert }^2$

$t=\frac{\left(x,y\right)}{{\Vert y\Vert }^2}$

On the other hand,

$\cos \theta =\frac{\Vert ty\Vert }{\Vert x\Vert }$

$\cos \theta =t\frac{\Vert y\Vert }{\Vert x\Vert }$

$t=\frac{\Vert x\Vert }{\Vert y\Vert }\cos \theta$

If we equate the two formulas for t we get $\left(x,y\right)=\Vert x\Vert \Vert y\Vert \cos \theta$ We say that two vectors are orthogonal if $\left(x,y\right)=0$ ; this is equivalent to the angle between x and y being $\pi /2$. If $\left(x,y\right)>0$, then we will say that x and y form an acute angle; This is equivalent to $0<\theta <\pi /2$. If $\left(x;y\right)<0$, then we will say that x and y form an obtuse angle; this is equivalent to $\pi /2<\theta <\pi$. Non-zero vectors also define some useful geometric objects. Let $v\in V$ be non-zero. We may consider three sets that partition V:

$\left\{x\in V:\left(x,v\right)>0\right\},P=\left\{x\in V:\left(x,v\right)=0\right\},\left\{y\in V:\left(x,v\right)<0\right\}$

The first set consists of the vectors that form an acute angle with v, the middle set is the hyperplane P orthogonal to Rv, and the last set consists of the vectors that form an obtuse angle with v. We refer to the first and last sets as the half-spaces defined by P. Of course, v lies in the first half-space. The formula for the reflection s_v shows that

$\left(s_v\left(x\right),v\right)=-\left(x,v\right)$

for x in V, so that S sends one half-space into the other half-space. Also, S acts by the identity on P. Multiplication by −1 also sends one half-space into the other half-space; however, while multiplication by −1 preserves P, it is not the identity on P.

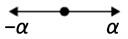
Example 5.7: A₁: The only rank 1 root system is $V=R$ with inner product $\left(x;y\right)=xy$ and roots $R=\left\{\alpha ,-\alpha \right\}=0$. Its Weyl group is given by $W=Z/2$. We call this root system A₁. This is the root system of sl₂.

Example 5.8: [8] $A_1\times A_1$ : Take $V=R^2$ with the usual inner product. Then $R=\left\{e_1,-e_1,e_2,-e_2\right\}$ with the standard basis vectors is a root system. Note that this is $A_1\times A_1$ and therefore not irreducible. Here $W=Z/2\times Z/2$ (Figure 1).

$A_2$ : Let $\alpha ={\alpha }^V,\beta ={\beta }^V\left(\alpha ,\beta \right)=-1$. Then $W=S_3$. We call this root system $A_2$, it appears as the root system of $s{l}_3$.

$B_2$ : Let $\alpha =e_1$, $\left(\alpha ,\alpha \right)=1$, $\beta =e_2-e_1$, $\left(\beta ,\beta \right)=2$, $\alpha ,\alpha +\beta$ are short

Figure 1. Root systems of rank 2.

roots, $\beta ,2\alpha +\beta$ long roots. Then W is the symmetry group of the square, i.e. $W=D_8$, the dihedral group of order 8. This is the root system of $s{p}_4$ and $s{o}_5$.

$G_2$ : Also $D_{12}$ appears as Weyl group of a root system, called $G_2$.

Example 5.9: Let V be a vector space over R with an inner product $\left(.,.\right)$. Let $x,y\in V$ and assume that x and y are both non-zero. The following are equivalent:

1) The vectors x and y are linearly dependent.

2) We have ${\left(x,y\right)}^2=\left(x,x\right)\left(y,y\right)={\Vert x\Vert }^2{\Vert y\Vert }^2$.

3) The angle between x and y is 0 or π.

Proof. Let $\theta$ be the angle between x and y. We have

${\left(x,y\right)}^2={\Vert x\Vert }^2{\Vert y\Vert }^2{\cos }^2\theta$

Assume that ${\left(x,y\right)}^2=\left(x,x\right)\left(y,y\right)={\Vert x\Vert }^2{\Vert y\Vert }^2$. Then ${\left(x,y\right)}^2={\Vert x\Vert }^2{\Vert y\Vert }^2\ne 0$, and ${\cos }^2\theta =1$, so that $\cos \theta =\pm 1$. This implies that $\theta =0$ or $\theta =\pi /2$.

Suppose that ${\left(x,y\right)}^2=\left(x,x\right)\left(y,y\right)$. We have

$\begin{array}{c}\left(y-\frac{\left(x,y\right)}{\left(x,x\right)}x,y-\frac{\left(x,y\right)}{\left(x,x\right)}x\right)=\left(y,y\right)-2\frac{\left(x,y\right)}{\left(x,x\right)}\left(x,y\right)+\frac{{\left(x,y\right)}^2}{{\left(x,x\right)}^2}\left(x,x\right)\\ =\left(y,y\right)-\frac{{\left(x,y\right)}^2}{\left(x,x\right)}\\ =\left(y,y\right)-\frac{\left(x,x\right)(y,y)}{(x,x)}\\ =\left(y,y\right)-\left(y,y\right)\\ =0\end{array}$

It follows that $y-\frac{\left(x,y\right)}{\left(x,x\right)}x=0$, so that x and y are linearly dependent.

Example 5.10: [6] Let V be a finite-dimensional vector space over R equipt with an inner product $\left(.,.\right)$, and let R be a root system in V. Let $\alpha ,\beta \in R$, and assume that $\alpha \ne \pm \beta$ and $\Vert \beta \Vert \ge \Vert \alpha \Vert$. Let $\theta$ be the angle between α and β. Exactly one of the following possibilities holds Figure 2.

Proof. By the assumption $\Vert \beta \Vert \ge \Vert \alpha \Vert$. We have $\left(\beta ,\beta \right)={\Vert \beta \Vert }^2\ge \left(\alpha ,\alpha \right)={\Vert \alpha \Vert }^2$, so that

$\left|\langle \beta ,\alpha \rangle \right|=\frac{2\left|\left(\beta ,\alpha \right)\right|}{\left(\alpha ,\alpha \right)}\ge \frac{2\left|\left(\alpha ,\beta \right)\right|}{\left(\beta ,\beta \right)}=\left|\langle \alpha ,\beta \rangle \right|$

Figure 2. Possible angles and ratio of norms between pairs of roots.

we have that $\langle \alpha ,\beta \rangle$ and $\langle \beta ,\alpha \rangle$ are integers, and we have $\langle \alpha ,\beta \rangle \langle \beta ,\alpha \rangle \in \left\{0,1,2,3\right\}$. These facts imply that the possibilities for $\langle \alpha ,\beta \rangle$ and $\langle \beta ,\alpha \rangle$ are as in the table.

Assume first that $\langle \beta ,\alpha \rangle =\langle \alpha ,\beta \rangle =0$. From above, $\langle \alpha ,\beta \rangle \langle \beta ,\alpha \rangle =4{\cos }^2\theta$.

It follows that $\cos \theta =0$, so that $\theta =\pi /2=90$.

Assume next that $\langle \beta ,\alpha \rangle \ne 0$. Now

$\frac{\langle \beta ,\alpha \rangle }{\langle \alpha ,\beta \rangle }=\frac{2\left(\beta ,\alpha \right)}{\left(\alpha ,\alpha \right)}\frac{\left(\beta ,\beta \right)}{2\left(\alpha ,\beta \right)}=\frac{\left(\beta ,\beta \right)}{\left(\alpha ,\alpha \right)}$

so that $\frac{\langle \beta ,\alpha \rangle }{\langle \alpha ,\beta \rangle }$ is positive and

$\sqrt{\frac{\langle \beta ,\alpha \rangle }{\langle \alpha ,\beta \rangle }}=\frac{\Vert \beta \Vert }{\Vert \alpha \Vert }$

This yields the $\Vert \beta \Vert /\Vert \alpha \Vert$ column. Finally,

$\langle \alpha ,\beta \rangle =\frac{2\left(\alpha ,\beta \right)}{\left(\beta ,\beta \right)}=\frac{2\Vert \alpha \Vert \Vert \beta \Vert \cos \theta }{{\Vert \beta \Vert }^2}$

$\langle \alpha ,\beta \rangle =2\frac{\Vert \alpha \Vert }{\Vert \beta \Vert }\cos \theta$

so that

$\cos \theta =\frac{1}{2}\frac{\Vert \beta \Vert }{\Vert \alpha \Vert }\langle \alpha ,\beta \rangle$

This gives the $\cos \theta$ column.

Definition 5.11: R is simply laced if all the roots are of the same length (e.g. $A_1$, $A_1\times A_1$, $A_2$, not $B_2$, $G_2$ ).

Example 5.12: [6] Let $V=R^2$ equipt with the usual inner product $\left(.,.\right)$, and let R be a root system in V. Let $\gamma$ be the length of the shortest root in R. Let S be the set of pairs $\left(\alpha ,\beta \right)$ of non-colinear roots such that $\Vert \alpha \Vert =\gamma$ and the angle θ between α and β is obtuse, and β is to the left of α. The set S is non-empty.

Fix a pair $\left(\alpha ,\beta \right)$ in S such that θ is maximal. Then

1) ( $A_2$ root system) If $\theta =120˚$ (so that $\Vert \alpha \Vert =\Vert \beta \Vert$ ) then R, α, and β are as follows Figure 3:

2) ( $B_2$ root system) If $\theta =135˚$ (so that $\Vert \beta \Vert =\sqrt{2}\Vert \alpha \Vert$ ) then R, α, and β are as follows Figure 4:

3) ( $B_2$ root system) If $\theta =150˚$ (so that $\Vert \beta \Vert =\sqrt{3}\Vert \alpha \Vert$ ) then R, α, and β are as follows Figure 5:

Proof. Let $\left(\alpha ,\beta \right)$ be a pair of non-colinear roots in R such that $\Vert \alpha \Vert =\gamma$ such a pair must exist because R contains a basis which includes α. If the angle between α and β is acute, then the angle between α and −β is obtuse. Thus, there exists a pair of roots $\left(\alpha ,\beta \right)$ in R such that $\Vert \alpha \Vert =\gamma$ and the angle between αand β is obtuse. If β is the right of α, then −β forms an acute angle with and is to the left of α; in this case, $s_{\alpha }\left(\beta \right)$ forms an obtuse angle with α and $s_{\alpha }\left(\beta \right)$ is to the left of β. It follows that S is non-empty.

Figure 3. A² root system θ = 120˚.

Figure 4. B² root system θ = 135˚.

Figure 5. B² root system θ = 150˚.

Assume that $\theta =120˚$ so that $\Vert \alpha \Vert =\Vert \beta \Vert$. It follows that $\alpha ,\beta ,\alpha +\beta ,-\alpha ,-\beta ,-\alpha -\beta \in R$. By geometry, $\Vert \alpha +\beta \Vert =\Vert \alpha \Vert +\Vert \beta \Vert$. It follows that R contains the vectors in 1. Assume that R contains a root other than $\alpha ,\beta ,\alpha +\beta ,-\alpha ,-\beta ,-\alpha -\beta$. We see that must lie halfway between two adjacent roots from $\alpha ,\beta ,\alpha +\beta ,-\alpha ,-\beta ,-\alpha -\beta$. This implies that $\theta$ is not maximal, a contradiction.

Assume that $\theta =135˚$ so that $\Vert \alpha \Vert =\sqrt{2}\Vert \beta \Vert$. We have $\alpha +\beta ,2\alpha +\beta \in R$. It follows that R contains $\alpha ,\beta ,\alpha +\beta ,2\alpha +\beta ,-\alpha ,-\beta ,-\alpha -\beta ,-2\alpha -\beta$ so that R contains the vectors in 2. Assume that R contains a root $\delta$ other than $\alpha ,\beta ,\alpha +\beta ,2\alpha +\beta ,-\alpha ,-\beta ,-\alpha -\beta ,-2\alpha -\beta$

Then $\delta$ must make an angle strictly less than 30^° with one of $\alpha ,\beta ,\alpha +\beta ,2\alpha +\beta ,-\alpha ,-\beta ,-\alpha -\beta ,-2\alpha -\beta$

Assume that $\theta =150˚$ so that $\Vert \alpha \Vert =\sqrt{3}\Vert \beta \Vert$. We have $\alpha +\beta ,3\alpha +\beta \in R$. By geometry, the angle between $\alpha$ and $3\alpha +\beta$ is 30^°. By geometry, the angle between $\beta$ and $3\alpha +\beta$ is 120^°. By $\beta +3\alpha +\beta =3\alpha +2\beta \in R$. It now follows that R contains the vectors in 3. Assume that R contains a vector $\delta$ other than $\alpha ,\beta ,\alpha +\beta ,2\alpha +\beta ,3\alpha +\beta ,3\alpha +2\beta ,-\alpha ,-\beta ,-\alpha -\beta ,-2\alpha -\beta ,-3\alpha -\beta ,-3\alpha -2\beta$. Then must make an angle strictly less than 30^° with one of $\alpha ,\beta ,\alpha +\beta ,2\alpha +\beta ,3\alpha +\beta ,3\alpha +2\beta ,-\alpha ,-\beta ,-\alpha -\beta ,-2\alpha -\beta ,-3\alpha -\beta ,-3\alpha -2\beta$.

6. The Future Perspective of This Paper

The future perspective of this paper is to support me in writing a book on Lie algebras. In addition, it is possible to do work for each of the titles in the paper. Each of the titles creates an opportunity for research, because from each title, there are many opportunities for research and to write. My future is to work on comparing many facts and applying leftist algebras in everyday life. Comparing all these disciplines with left algebras, we see closely connectivity and the need to apply and use it properly.

NOTES

¹Let L be a Lie algebra over F, let V be a finite-dimensional F-vector space, and let $\phi :L\to gl\left(V\right)$ be a representation. Define ${\beta }_V:L\times L\to F$ by ${\beta }_V\left(x,y\right)=tr\left(\phi \left(x\right)\phi \left(y\right)\right)$ for $x,y\in L$.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Erdman, K. and Wildon, M.J. (2006) Introduction to Lie Algebra. Mathematical Institute University, Oxford, UK. https://www.springer.com/gp/book/9781846280405
[2]	Henderson, A. (2012) Representations of Lie Algebras an Introduction through gl(n). School of Mathematics and Statistics, University of Sydney, 18-19, 21-27. https://www.cambridge.org/me/academic/subjects/mathematics/algebra/representations-lie-algebras-introduction-through-gln?format=PB&isbn=9781107653610
[3]	Carter, R. (2005) Lie Algebras of Finite and Affine Type. Mathematics Institute University of Warwick. http://www.cambridge.org/9780521851381
[4]	Renee Talley, A. (2017) An Introduction to Lie Algebra. California State University, San Bernardino, 38-40. https://scholarworks.lib.csusb.edu/cgi/viewcontent.cgi?article=1668&context=etd
[5]	Samelson, H. (1988) Notes on Lie Algebras. 15-16. https://pi.math.cornell.edu/~hatcher/Other/Samelson-LieAlg.pdf
[6]	Roberts, B. (2018-2019) Lie Algebras. University of Idaho, Moscow, 56-57, 85-86. https://www.freebookcentre.net/maths-books-download/Lie-Algebras-by-Brooks-Roberts.html
[7]	Humphreys, J.E. (2000) Introduction to Lie Algebras and Their Representations. Professor of Mathematics University of Massachusetts Amherst, MA 01003USA. https://www.springer.com/gp/book/9780387900537
[8]	Grojowski, L., Laugwitz, R. and Seidler, H. (2010) Introduction to Lie Algebras and Their Representations. Unofficial Lecture Notes, University of Cambridge, Cambridge, 33-36. https://book4you.org/book/2692749/b705ea?id=2692749&secret=b705ea&signAll=1&ts=2233