Fuzzy Logic in the Quantum Mechanical Worldview; Related to Zadeh, Wittgenstein, Moore, Saussure, Quine, Lewis Carroll, etc.

Shiro Ishikawa

Department of Mathematics, Faculty of Science and Technology, Keio University, Yokohama, Japan.

DOI: 10.4236/jamp.2021.97108                

Abstract

Recently we proposed the linguistic Copenhagen interpretation of quantum mechanics, which is called quantum language or measurement theory. This theory is valid for both quantum and classical systems. Thus we think that quantum language is one of the most powerful scientific theories, like statistics. In this paper we justify Zadeh’s fuzzy sets theory in quantum language, that is, fuzzy propositions are identified with binary measurements. This implies that the definition of “proposition” is, for the first time, acquired in the field of non-mathematics. Further, we assert that fuzzy logic is more natural than crisp logic in science. And furthermore, we discuss and solve Saussure’s linguistics, Moore’s paradox, Quine’s analytic-synthetic distinction and Lewis Carroll’s logical paradox. Therefore, from the philosophical point of view, our result gives a complete answer to Wittgenstein’s problem: “Why does logic work in our world?” and “What is a scientific proposition?” in his picture theory. That is, we simultaneously justify both Zadeh’s fuzzy sets and Wittgenstein’s picture theory in the quantum mechanical worldview.

Keywords

Zadeh’s Fuzzy Sets, Quantum Language, Linguistic Copenhagen Interpretation

1. Introduction

In 1965, L.A. Zadeh proposed an engineering concept called “fuzzy sets” (cf. ref. [1] ), which was enthusiastically supported by some engineers. However, R.E. Kalman did not recognize “fuzzy sets” as a scientific concept, and argued as follows (1972): “Let me say quite categorically that there is no such thing as a fuzzy concept ... We do talk about fuzzy things but they are not scientific concepts. Some people in the past have discovered certain interesting things, formulated their findings in a non-fuzzy way, and therefore we have progressed in science” (cf. ref. [2] ).

Even now, more than 50 years later, I don’t think that Kalman’s claim can be denied. In fact, the concept of “fuzzy sets” has not yet acquired the status of more than a convenient engineering method. Kalman might have thought that the basic philosophy of engineering is a mechanical worldview, and thus, “scientific concepts” = “concepts in the (classical) mechanical worldview”. Note that dynamical system theory (which is essentially the same as statistics) is considered as the mathematical representation of the (classical) mechanical worldview. That is,

(A) $\stackrel{\left(classicalmechanicalworldview\right)}{\underset{\left(statistics\right)}{\boxed{\boxed{\text{Dynamicalsystemtheory}}}}}=\underset{\left(causality\right)}{\boxed{\text{stateequation}}}+\underset{\left(probability\right)}{\boxed{\text{measurementequation}}}$

On the other hand, quantum language is characterized as follows:

(B) $\stackrel{\left(quantummechanicalworldview\right)}{\underset{\left(measurementtheory\right)}{\boxed{\boxed{\text{Quantum language}}}}}=\underset{\left(causality\right)}{\boxed{\text{A}xiom2}}+\underset{\left(measurement\right)}{\boxed{\text{A}xiom1}}+\underset{\left(howtouseAxioms1and2\right)}{\boxed{\text{l}inguistic\left(Copenhagen\right)interpretation}}$

which is a mathematical representation of quantum mechanical worldview (cf. refs. [3] [4] [5] ). And we assert that “scientific concepts” = “concepts within the quantum mechanical worldview”. If so, and if “fuzzy sets” is a scientific concept, “fuzzy sets” must be completely understood in quantum language. In this paper, we do exactly that.

I assert that the location of QL (=quantum language) in the history of world-description is as follows:

Figure 1 [The location of quantum language in the history of world-description (cf. refs. [5] [6] )] (See next page).

In this paper, I devote myself to the logical aspect of QL (i.e., ⑩ and in the above figure). That is, I simultaneously justify both Zadeh’s fuzzy sets and Wittgenstein’s picture theory in the quantum mechanical worldview.

My research on logic began with refs. [7] [8] [9]. However, my understanding of quantum language at the time was inadequate, and in hindsight, there were many aspects that I should have reconsidered. The recent improved version is ref. [10]. However, this was preoccupied with the preconceived notion that crisp logic is fundamental. This present paper is an improved version of ref. [10].

In Section 2, I explain probabilistic logic in elementary mathematics, That is, I show that probabilistic logic works as a mathematical theory. However, it is clear that mathematical justification alone would not convince Kalman. In Section 3, I prepare the basics of quantum language (B), which is a theory of quantum mechanical worldview. In Section 4, I study fuzzy logic (i.e., probabilistic logic in quantum language). That is, I propose the definition of scientific proposition, and show that fuzzy logic is more natural than crisp logic. In Section 5, I discuss and solve Saussure’s linguistics, Moore’s paradox, Quine’s analytic-synthetic

Figure 1. The history of the world-descriptions.

distinction and Lewis Carroll’s logical paradox in the relation of my proposal in Sec. 4. And I conclude that my result gives a complete answer to Wittgenstein’s question such that “Why does logic work in our world?” and, “What is a scientific proposition?” in his picture theory of Tractatus Logico Philosophicus (cf. ref. [11] ).

2. Probabilistic Logic (=Fuzzy Logic) in Elementary Mathematics

This section is written in such a way that it can be read without knowledge of quantum language. In this paper, we use the term “fuzzy logic” in quantum language (explained in Sec. 3). Since this section is not related to quantum languages, we will use the term “probabilistic logic” instead of “fuzzy logic”.

2.1. Easy Example

Let us start from the following easy example.

Example 1 For example, consider a proposition P₁ such that

$P_1=“\text{this}\text{tomato}\text{is}\text{red}”\mathrm{,}\neg P_1=“\text{this}\text{tomato}\text{is}\text{not}\text{red}”\mathrm{,}$

And suppose that there are 100 respondents, and furthermore, the following question is asked to them.

(C) Is this tomato red? (i.e., is the proposition P₁ true or not?)

Assume that the results of the responses are as follows.

(D) $\{\begin{array}{l}\text{70}\text{respondents}\text{say}“\text{Yes},\text{thistomatoisred}”\left(\text{i}\text{.e}\text{.},\text{theproposition}{P}_1\text{is}\text{ture},\text{i}\text{.e}\mathrm{.,}“T”\right)\\ \text{30}\text{respondents}\text{say}“\text{No},\text{thistomatoisnotred}”\left(\text{i}\text{.e}\text{.},\text{theproposition}{P}_1\text{is}\text{false},\text{i}\text{.e}\mathrm{.,}“F”\right)\end{array}$

This can be probabilistically interpreted as follows.

(E) When any respondent is randomly selected out of 100, the probability that this respondent will answer “yes” to question (C) is $p_1\left(=0.7\right)$. Or simply, the probability that the proposition P₁ is true is p₁. In symbolic form,

$\text{Prob}\left[P_1\mathrm{<mo>\; ;\; </mo>}\left\{T\right\}\right]=p_1\left(=0.7\right)$

Then we generally denote that

$\text{Prob}\left[P_1;\left\{T\right\}\right]=p_1,\text{Prob}\left[P_1;\left\{F\right\}\right]=1-p_1\left(\text{where}0\le p_1\le 1\right)$

Also, note that $\text{Prob}\left[\neg P_1;\left\{T\right\}\right]=\text{Prob}\left[P_1;\left\{F\right\}\right]=1-p_1$.

Remark 2. (i): In the above, it should be noted that the definition of “proposition” is not written. For example, is Descartes’ “I think, therefore I am” a scientific proposition? This is one of the most important problems in philosophy of science. The definition of scientific proposition is proposed in Sec. 4.

(ii): Zadeh often emphasized that fuzziness and probability are different concepts. However, I believe that fuzziness without a probability interpretation cannot be a scientific concept. In this sense, the above (E) is essential. Thus, the difference between fuzziness and probability are mood. As mentioned before, in this paper “probabilistic logic” in quantum language is called “fuzzy logic.

2.2. Quasi-Product Probability

In addition, assume another proposition $P_2$ such that $\text{Prob}\left[P_2;\left\{T\right\}\right]=p_2$, $\text{Prob}\left[P_2;\left\{F\right\}\right]=1-p_2$. Thus, we have two probability spaces $\left(\left\{T\mathrm{,}F\right\}{\mathrm{,2}}^{\left\{T\mathrm{,}F\right\}}\mathrm{,}{\mu }_i\right)$, $\left(i=1,2\right)$, such that

${\mu }_1\left(\left\{T\right\}\right)=p_1,{\mu }_1\left(\left\{F\right\}\right)=1-p_1,{\mu }_2\left(\left\{T\right\}\right)=p_2,{\mu }_2\left(\left\{F\right\}\right)=1-p_2$

And consider the quasi-product probability space $\left({\left\{T\mathrm{,}F\right\}}^2\mathrm{,}\mathcal{P}\left({\left\{T\mathrm{,}F\right\}}^2\right)\mathrm{,}{\mu }_1{\times }^{qp}{\mu }_2\right)$, which satisfies the following marginal conditions:

$\left({\mu }_1{\times }^{qp}{\mu }_2\right)\left(\left\{T\right\}\times \left\{T,F\right\}\right)={\mu }_1\left(\left\{T\right\}\right),\left({\mu }_1{\times }^{qp}{\mu }_2\right)\left(\left\{F\right\}\times \left\{T,F\right\}\right)={\mu }_1\left(\left\{F\right\}\right),$

and

$\left({\mu }_1{\times }^{qp}{\mu }_2\right)\left(\left\{T,F\right\}\times \left\{T\right\}\right)={\mu }_2\left(\left\{T\right\}\right),\left({\mu }_1{\times }^{qp}{\mu }_2\right)\left(\left\{T,F\right\}\times \left\{F\right\}\right)={\mu }_2\left(\left\{F\right\}\right),$

Putting the above together, we get the following table (i.e., Table 1).

Table 1. Quasi-product probability measure ${\mu }_1{\times }^{qp}{\mu }_2$.

where

$\max \left\{{\mu }_1\left(\left\{T\right\}\right)+{\mu }_2\left(\left\{T\right\}\right)-\mathrm{1,0}\right\}\le \alpha \le \min \left\{{\mu }_1\left(\left\{T\right\}\right)\mathrm{,}{\mu }_2\left(\left\{T\right\}\right)\right\}$

Thus, the quasi-product probability is not unique in general.

Remark 3. The followings (i) and (ii) are typical. Assume that $P_1=P_2$. Thus, ${\mu }_1={\mu }_2$.

(i): [Product probability space]

Assume that each respondent randomly chooses “T” [resp. “F”] with probability 0.7 [resp. 0.3] in the same way for the two questions $P_1$ and $P_2$. Then, the ${\mu }_1{\times }^{qp}{\mu }_2$ is considered as the ordinary product probability ${\mu }_1\times {\mu }_2$ such that

$\left({\mu }_1\stackrel{qp}{\times }{\mu }_2\right)\left(\left\{\left(x_1\mathrm{,}{x}_2\right)\right\}\right)={\mu }_1\left(\left\{x_1\right\}\right)\times {\mu }_1\left(\left\{x_2\right\}\right)\left(\forall \left(x_1\mathrm{,}{x}_2\right)\in {\left\{T\mathrm{,}F\right\}}^2\right)$

If we write the above in a table, we get the following table (i.e., Table 2).

(ii) [Standard situation when $P_1=P_2$ ] It is natural to think that the respondent selected in (C) will give the same answer to the same question (i.e., $P_1$ and $P_1$ ). In this case we see ${\mu }_1{\times }^{qp}{\mu }_1$ such that $\left({\mu }_1{\times }^{qp}{\mu }_1\right)\left(\left\{\left(T,T\right)\right\}\right)=p_1$ and $\left({\mu }_1{\times }^{qp}{\mu }_1\right)\left(\left\{\left(F,F\right)\right\}\right)=1-p_1$. Thus,

$\left(\underset{i=1,2}{\overset{qp}{{\displaystyle \times }}}\mu \right)\left(\left\{\left(x_1,x_2\right)\right\}\right)=(\begin{array}{ll}{p}_1\hfill & \text{if}\left(x_1,x_2\right)=\left(T,T\right)\hfill \\ 1-p_1\hfill & \text{if}\left(x_1,x_2\right)=\left(F,F\right)\hfill \\ 0\hfill & \text{if}\left(x_1,x_2\right)=\left(T,F\right),\left(F,T\right)\hfill \end{array}$

If we write the above in a table, we get the following table (i.e., Table 3).

In this paper, unless otherwise stated, this quasi-product probability measure ${\mu }_1{\times }^{qp}{\mu }_1$ will be used. However, if so, it is not necessary to ask the same question twice; we only need to ask it once. For further discussion, see Example 5 later. Also, this ${\times }_{i=1,2}^{qp}{\mu }_i\left(=\mu \right)$ is easily extended to the case that ${\times }_{i=1,2,\cdots ,n}^{qp}{\mu }_i$ (where ${\mu }_i=\mu$, $i=1,2,\cdots ,n$ ). such that

Table 2. Product probability measure ${\mu }_1{\times }^{qp}{\mu }_2\left(={\mu }_1\times {\mu }_2\right)$.

Table 3. Quasi-product probability measure ${\mu }_1{\times }^{qp}{\mu }_1$.

$\left(\underset{i=1,2,\cdots ,n}{\overset{qp}{{\displaystyle \times }}}\mu \right)\left(\left\{{\left(x_i\right)}_{i=1}^n\right\}\right)=(\begin{array}{ll}{p}_1\hfill & \text{if}{\left(x_i\right)}_{i=1}^n={\left(T\right)}_{i=1}^n\hfill \\ 1-p_1\hfill & \text{if}{\left(x_i\right)}_{i=1}^n={\left(F\right)}_{i=1}^n\hfill \\ 0\hfill & \text{others}\hfill \end{array}$

2.3. Logic Symbols and Logical Operations

For the sake of convenience, we will define as follows (also, see (G) for the formal definition):

(F) $P_1\wedge P_2=“P_1\text{and}{P}_2”$, $P_1\vee P_2=“P_1\text{or}{P}_2”$, $P_1\to P_2=“\neg P_1\text{or}{P}_2”$, $\neg P=\text{not}P$

If we write the above (i.e., $P_1\wedge P_2$, $\neg P_1\wedge P_2$, $P_1\wedge \neg P_2$, $\neg P_1\wedge \neg P_2$ ) in a table, we get the following table (i.e., Table 4).

Where $\max \left\{p_1+p_2-\mathrm{1,0}\right\}\le \alpha \le \min \left\{p_1\mathrm{,}{p}_2\right\}$. Note that Tables 1-3 are related to only quasi-product probability ${\mu }_1{\times }^{qp}{\mu }_2$, but Table 4 is related to ${\mu }_1{\times }^{qp}{\mu }_2$ and logical symbol (i.e., $\wedge \mathrm{,}\neg$ ).

Now we can explain the following example:

Example 4. [Simple probabilistic truth table] The following table (i.e., Table 5: Simple probabilistic truth table) is the same as a well-known truth table, except for the “probability column”.

Thus, it will be enough to explain hoe to use the “probability column” as follows. For example, consider the above proposition $\neg P_1$, which can be regarded as the map from ${\left\{T\mathrm{,}F\right\}}^2$ to $\left\{T\mathrm{,}F\right\}$ such that

Table 4. Quasi-product probability measure ${\mu }_1{\times }^{qp}{\mu }_2$ concerning $P_1\wedge P_2,\neg P_1\wedge P_2,P_1\wedge \neg P_2,\neg P_1\wedge \neg P_2$.

Table 5. Simple Probabilistic Truth Table (Elementary propositions P₁, P₂).

$\left[\neg P_1\right]\left(x_1,x_2\right)=(\begin{array}{ll}T\hfill & \text{if}\left(x_1,x_2\right)=\left(F,T\right),\text{or}\left(F,F\right)\hfill \\ F\hfill & \text{if}\left(x_1,x_2\right)=(T,T),\text{or}\left(T,F\right)\hfill \end{array}$

(or $\neg P_1\mathrm{<mo>\; :\; </mo>}\left\{T\mathrm{,}F\right\}\to \left\{T\mathrm{,}F\right\}$ such that $\left[\neg P_1\right]\left(T\right)=F$, $\left[\neg P_1\right]\left(F\right)=T$ ).

Thus, we see that $\text{Prob}\left[\neg P_1\mathrm{<mo>\; ;\; </mo>}\left\{T\right\}\right]$ (i.e., the probability that $\neg P_1$ is true) is equal to

$\left({\mu }_1\stackrel{qp}{\times }{\mu }_2\right)\left({\left[\neg P_1\right]}^{-1}\left(\left\{T\right\}\right)\right)=p_{\bar{1}2}+p_{\bar{1}\bar{2}}$

Next consider $\left[P_1\to P_2\right]$ $\left(=\left[\neg P_1\vee P_2\right]\right)$, which is regarded as the map from ${\left\{T\mathrm{,}F\right\}}^2$ to $\left\{T\mathrm{,}F\right\}$ such that

$\left[P_1\to P_2\right]\left(x_1,x_2\right)=(\begin{array}{ll}T\hfill & \text{if}\left(x_1,x_2\right)=\left(T,T\right)\text{or}\left(F,T\right)\text{or}\left(F,F\right)\hfill \\ F\hfill & \text{if}\left(x_1,x_2\right)=\left(T,F\right)\hfill \end{array}$

Thus, we see that $\text{Prob}\left[P_1\to P_2\mathrm{<mo>\; ;\; </mo>}\left\{T\right\}\right]$ (i.e., the probability that $\left[P_1\to P_2\right]$ is true) is equal to

$\left({\mu }_1\stackrel{qp}{\times }{\mu }_2\right)\left({\left[P_1\to P_2\right]}^{-1}\left(\left\{T\right\}\right)\right)=p_{12}+p_{\bar{1}2}+p_{\bar{1}\bar{2}}$

Similarly we see

$\text{Prob}\left[P_1\wedge P_2\mathrm{<mo>\; ;\; </mo>}\left\{T\right\}\right]=p_{12}\mathrm{,}\text{Prob}\left[P_1\vee P_2\mathrm{<mo>\; ;\; </mo>}\left\{T\right\}\right]=p_{12}+p_{\bar{1}2}+p_{1\bar{2}}$

Furthermore, we must note that

(G) $\neg P_1$, $\left[P_1\wedge P_2\right]$, $\left[P_1\vee P_2\right]$ and $\left[P_1\to P_2\right]$ can be respectively regarded as maps from ${\left\{T\mathrm{,}F\right\}}^2$ to $\left\{T\mathrm{,}F\right\}$ as shown in the above Table 5. Rather than (F), this map is the formal definition of logic symbols (i.e., $\neg$, $\wedge$, $\vee$, $\to$ ).

Example 5. [Probabilistic truth table ((i): $P_1\ne P_3$, (ii): $P_1=P_3$ )]

(i) (Simplest case: $P_1\ne P_3$ ): The following table (i.e., Table 6) is the preparation of the next (ii) (i.e., Tables 7-9). Consider the truth table of $\left[P_1\to P_2\right]\wedge P_3$ as follows.

Table 6. Probabilistic Truth Table (Elementary propositions P₁, P₂, P₃).

This says that the proposition $\left[P_1\to P_2\right]\wedge P_3$ is the map from ${\left\{T\mathrm{,}F\right\}}^3\to \left\{T\mathrm{,}F\right\}$ such that

$\begin{array}{l}\left[\left[P_1\to P_2\right]\wedge P_3\right]\left(x_1,x_2,x_3\right)\\ =(\begin{array}{ll}T\hfill & \text{if}\left(x_1,x_2,x_3\right)=\left(T,T,T\right),\left(F,T,T\right),\left(F,F,T\right)\hfill \\ F\hfill & \text{if}\left(x_1,x_2,x_3\right)=\left(T,T,F\right),\left(T,F,T\right),\left(T,F,F\right),\left(F,T,F\right),\left(F,F,F\right)\hfill \end{array}\end{array}$

Thus,

$\begin{array}{l}\text{Prob}\left[\left[\left[P_1\to P_2\right]\wedge P_3\right];\left\{T\right\}\right]\\ =\left(\underset{i=1,2,3}{\overset{qp}{{\displaystyle \times }}}{\mu }_i\right)\left({\left[\left[P_1\to P_2\right]\wedge P_3\right]}^{-1}\left(\left\{T\right\}\right)\right)=p_{123}+p_{\bar{1}\bar{2}3}+p_{1\bar{2}\bar{3}}\end{array}$

(ii) (Case; $P_1=P_3$ in the above (i)): Furthermore, assume that $P_1=P_3$ in the above. Then, recalling Remark 3 (ii), we usually assume that ${\times }_{i=1,2,3}^{qp}{\mu }_i\left(\left\{\left(x_1,x_2,x_3\right)\right\}\right)=0$ (if $x_1\ne x_3$ ). Thus, putting ${\times }_{i=1,2}^{qp}{\mu }_i\left(\left\{\left(x_1,x_2\right)\right\}\right)={\times }_{i=1,2,3}^{qp}{\mu }_i\left(\left\{\left(x_1,x_2\right)\right\}\times \left\{T,F\right\}\right)$, we see the following: (Note that Table 6, Table 7 except the probability column).

Since the case of the probability 0 (i.e., $p_{12\bar{3}}=p_{\bar{1}23}=p_{1\bar{2}\bar{3}}=p_{\bar{1}\bar{2}3}=0$ ) can be omitted, we have the following table:

Therefore, we see that $\text{Prob}\left[\left[P_1\to P_2\right]\wedge P_3\left(=P_1\right)\mathrm{<mo>\; ;\; </mo>}\left\{T\right\}\right]$ (i.e., the probability

Table 7. Probabilistic Truth Table (Overlapping elementary propositions P₁, P₂, P₃ (=P₁)).

Table 8. Probabilistic Truth Table (Overlapping elementary propositions P₁, P₂, P₃ (=P₁)).

that $\left[P_1\to F_2\right]\wedge P_1$ is true) is equal to

$\left({\mu }_1\stackrel{qp}{\times }{\mu }_2\right)\left({\left[\left[P_1\to P_2\right]\wedge P_3\left(=P_1\right)\right]}^{-1}\left(\left\{T\right\}\right)\right)=p_{12}$

Note that this is essentially the same as the following table.

Hence, we conclude that Tables 7-9 are essentially the same. And therefore, we see;

(H) the calculation will be more concise if we start with non-overlapping propositions (such as Table 9).

Example 6 [Modus ponens in probabilistic truth table] The following table (i.e., Table 10: Probabilistic truth table) is the same as a well-known truth table, except for the “probability column”.

For example, consider the proposition $\mathrm{<mo\; stretchy="false">\; [\; </mo>}{P}_1\to P_2\mathrm{<mo\; stretchy="false">\; ]\; </mo>}\wedge P_1$, which is regarded as the map from ${\left\{T\mathrm{,}F\right\}}^2$ to $\left\{T\mathrm{,}F\right\}$ such that

$\left[\left[P_1\to P_2\right]\wedge P_1\right]\left(x_1,x_2\right)=(\begin{array}{ll}T\hfill & \text{if}\left(x_1,x_2\right)=\left(T,T\right)\hfill \\ F\hfill & \text{if}\left(x_1,x_2\right)=\left(T,F\right),\left(F,T\right),\left(F,F\right)\hfill \end{array}$

Thus, we see that $\text{Prob}\left[\left[\left[P_1\to P_2\right]\wedge P_1\right]\mathrm{<mo>\; ;\; </mo>}\left\{T\right\}\right]$ (i.e., the probability that $\left[\left[P_1\to P_2\right]\wedge P_1\right]$ is true) is equal to

$\left({\mu }_1\stackrel{qp}{\times }{\mu }_2\right)\left({\left[\left[P_1\to P_2\right]\wedge P_1\right]}^{-1}\left(\left\{T\right\}\right)\right)=p_{12}$

By the same way, we can calculate as follows.

$\left({\mu }_1{\times }^{qp}{\mu }_2\right)\left({\left[\left(\left(P_1\to P_2\right)\wedge P_1\right)\to P_2\right]}^{-1}\left(\left\{T\right\}\right)\right)=p_{12}+p_{1\bar{2}}+p_{\bar{1}2}+p_{\bar{1}\bar{2}}=1$

Table 9. Probabilistic Truth Table (Non-overlapping elementary propositions P₁, P₂)

Table 10. Probabilistic Truth Table (Elementary propositions P₁, P₂).

That is,

$\text{Prob}\left[\left[\left(\left(P_1\to P_2\right)\wedge P_1\right)\to P_2\right];\left\{T\right\}\right]=p_{12}+p_{1\bar{2}}+p_{\bar{1}2}+p_{\bar{1}\bar{2}}=1$

Thus, modus ponens is always true even in probabilistic logic.

The statement (H) in Examples 5 says that it suffices to consider the case of non-overlapping propositions. Thus we have the following theorem.

Theorem 7. [Logical sample space] Let $P_1\mathrm{,}{P}_2\mathrm{,}\cdots \mathrm{,}{P}_i\mathrm{,}\cdots \mathrm{,}{P}_n$ be non-overlapping propositions (i.e., $P_i\ne P_j$ ( $\forall i\mathrm{,}j$ such that $i\ne j$, cf. (H) above), and consider the probability space $\left(\left\{T\mathrm{,}F\right\}{\mathrm{,2}}^{\left\{T\mathrm{,}F\right\}}\mathrm{,}{\mu }_i\right)$ such that ${\mu }_i\left(\left\{T\right\}\right)=\text{Prob}\left[P_i\mathrm{<mo>\; ;\; </mo>}\left\{T\right\}\right]$, ${\mu }_i\left(\left\{F\right\}\right)=\text{Prob}\left[P_i\mathrm{<mo>\; ;\; </mo>}\left\{F\right\}\right]$. Consider a quasi-product probability space $\left({\left\{T\mathrm{,}F\right\}}^n\mathrm{,}\mathcal{P}\left({\left\{T,F\right\}}^n\right),{\times }_{i=1,2,\cdots ,n}^{qp}{\mu }_i\right)$ such that

$\begin{array}{l}\left(\underset{i=1,2,\cdots ,n}{\overset{qp}{{\displaystyle \times }}}{\mu }_i\right)\left({\left\{T\mathrm{,}F\right\}}^{k-1}\times \left\{x\right\}\times {\left\{T\mathrm{,}F\right\}}^{n-k}\right)\\ =\text{Prob}\left[P_k\mathrm{<mo>\; ;\; </mo>}\left\{x\right\}\right]\left(x\in \left\{T\mathrm{,}F\right\}\mathrm{,}k=\mathrm{1,2,}\cdots \mathrm{,}n\right)\end{array}$

Then, the pair $\left[\left\{P_1\mathrm{,}{P}_2\mathrm{,}\cdots \mathrm{,}{P}_n\right\}\mathrm{<mo>\; ;\; </mo>}\left({\left\{T\mathrm{,}F\right\}}^n\mathrm{,}\mathcal{P}\left({\left\{T,F\right\}}^n\right),{\times }_{i=1,2,\cdots ,n}^{qp}{\mu }_i\right)\right]$ is called the logical sample space. Let P be a proposition which is constructed by $P_1\mathrm{,}\cdots \mathrm{,}{P}_n$. Note that P is regarded as the map from ${\left\{T\mathrm{,}F\right\}}^n\to \left\{T\mathrm{,}F\right\}$. Then, we see that

$\text{Prob}\left[P;\left\{T\right\}\right]=\left(\underset{i=1,2,\cdots ,n}{\overset{qp}{{\displaystyle \times }}}{\mu }_i\right)\left(P^{-1}\left(\left\{T\right\}\right)\right)$

Also, it is clear that the above Example 6 implies the following corollary.

Corollary 8. [Tautology in probabilistic logic] Let P be a proposition constructed from non-overlapping propositions $P_1\mathrm{,}{P}_2\mathrm{,}\cdots \mathrm{,}{P}_n$. Then, the followings are equivalent:

(i) P is a tautology in the sense of usual logic.

(ii) $\text{Prob}\left[P\mathrm{<mo>\; ;\; </mo>}\left\{T\right\}\right]=1$.

That is, tautology always holds even in probabilistic logic. For example,

· syllogism (i.e., $\left[\left[P_1\to P_2\right]\wedge \left[P_2\to P_3\right]\right]\to \left[P_1\to P_3\right]$ always holds.

3. Review: Quantum Language (=QL = Measurement Theory)

In the previous section, we discussed fuzzy symbolic logic (= probabilistic symbolic logic) in elementary mathematics. I’m sure many readers thought this was promising. However, this is not so powerful since it has no definition of “proposition”. For example, it has no power to answer the question such that “Is Descartes’ cogito proposition (i.e., ‘I think, therefore I am’) a scientific proposition?” which is generally considered to be the most important question in philosophy. Therefore, the discussion in the previous section is not sufficient as the scientific justification of Zadeh’s fuzzy logic. That is, we have to answer the next most important question.

· Why does logic work in our world? or What is the definition of a “proposition”?

which is due to Wittgenstein’s question in Tractatus Logico Philosophicus (cf. ref. [11] ).

For this, in this section, we shall review quantum language (i.e., the linguistic Copenhagen interpretation of quantum mechanics, or measurement theory), which has the following form:

(B') $\stackrel{\left(\text{quantum}\text{mechanical}\text{worldview}\right)}{\underset{\left(\text{measurement}\text{theory}\right)}{\boxed{\boxed{\text{Quantum}\text{language}}}}}=\underset{\left(\text{causality}\right)}{\boxed{\text{Axiom}\text{2}}}+\underset{\left(\text{measurement}\right)}{\boxed{\text{Axiom}\text{1}}}+\underset{\left(\text{how}\text{to}\text{use}\text{Axioms}\text{1}\text{and}\text{2}\right)}{\boxed{\text{linguistic}\left(\text{Copenhagen}\right)\text{interpretation}}}$

I think that this is the ultimate form of the usual dynamical system theory (A) (cf. refs. [3] [4] [12] ).

3.1. Mathematical Preparations

Consider an operator algebra $B\left(H\right)$ (i.e., an operator algebra composed of all bounded linear operators on a Hilbert space H with the norm ${\Vert G\Vert }_{B\left(H\right)}={\sup }_{{\Vert u\Vert }_H=1}{\Vert Gu\Vert }_H$. Let $\mathcal{A}\left(\subseteq B\left(H\right)\right)$ is a C^*-algebra, (i.e., norm-closed subalgebra of $B\left(H\right)$ ) (cf. refs. [13] [14] [15] ). Our purpose of this section is not to explain QL in general situation but to explain QL in an understandable setting. Thus, from here, we devote ourselves to the following simple cases:

(I) $\text{QL}=\{\begin{array}{l}\left({\text{I}}_1\right):\text{quantum}\text{QL}\left(\text{when}\mathcal{A}=B\left({ℂ}^n\right),\text{where}H={ℂ}^n\right)\\ \text{i}\text{.e}.,\text{the}{C}^{*}\text{-algebra}\text{composed}\text{of}\text{all}\left(n\times n\right)\text{complex}\text{matrixes}\\ \left({\text{I}}_1\right):\text{classical}\text{QL}\left(\text{when}\mathcal{A}=C\left(\Omega \right)\right),\\ \text{i}\text{.e}.,\text{the}\text{space}\text{of}\text{all}\text{continuous}\text{functions}\text{on}\text{a}\text{compact}\text{space}\Omega \end{array}$

Let $\mathcal{A}\subseteq B\left(H\right)$ be a C^*-algebra, and let ${\mathcal{A}}^{\ast }$ be the dual Banach space of $\mathcal{A}$. That is, ${\mathcal{A}}^{\ast }=\left\{\rho \mathrm{<mo>\; |\; </mo>}\rho \text{isacontinuouslinearfunctionalon}\mathcal{A}\right\}$, and the norm ${\Vert \rho \Vert }_{{\mathcal{A}}^{\ast }}$ is defined by $\sup \left\{\left|\rho \left(G\right)\left(={}_{{\mathcal{A}}^{\ast }}\langle \rho \mathrm{,}G\rangle {}_{\mathcal{A}}\right)\right|\mathrm{<mo>\; |\; </mo>}G\in \mathcal{A}\text{such}\text{that}{\Vert G\Vert }_{\mathcal{A}}\left(={\Vert G\Vert }_{B\left(H\right)}\right)\le 1\right\}$. Define the mixed state $\rho \left(\in {\mathcal{A}}^{\ast }\right)$ such that ${\Vert \rho \Vert }_{{\mathcal{A}}^{\ast }}=1$ and $\rho \left(L\right)\ge 0$ for all $L\in \mathcal{A}$ such that $L\ge 0$. And define the mixed state space ${\mathfrak{S}}^m\left({\mathcal{A}}^{\ast }\right)$ such that

${\mathfrak{S}}^m\left({\mathcal{A}}^{\ast }\right)=\left\{\rho \in {\mathcal{A}}^{\ast }\mathrm{<mo>\; |\; </mo>}\rho \text{is}\text{a}\text{mixed}\text{state}\right\}\mathrm{.}$

A mixed state $\rho \left(\in {\mathfrak{S}}^m\left({\mathcal{A}}^{\ast }\right)\right)$ is called a pure state if it satisfies that $\rho =\theta {\rho }_1+\left(1-\theta \right){\rho }_2$ for some ${\rho }_1\mathrm{,}{\rho }_2\in {\mathfrak{S}}^m\left({\mathcal{A}}^{\ast }\right)$ and $0<\theta <1$ implies $\rho ={\rho }_1={\rho }_2$. Put

${\mathfrak{S}}^p\left({\mathcal{A}}^{\ast }\right)=\left\{\rho \in {\mathfrak{S}}^m\left({\mathcal{A}}^{\ast }\right)\mathrm{<mo>\; |\; </mo>}\rho \text{is}\text{a}\text{pure}\text{state}\right\}\mathrm{,}$

which is called a state space. It is well known (cf. ref. [14] ) that

(J) $(\begin{array}{l}\left[\text{Case}\left({\text{J}}_1\right)\right]\mathrm{<mo>\; ;\; </mo>}{\mathfrak{S}}^p\left(B{\left({ℂ}^n\right)}^{\mathrm{<mo>\; *\; </mo>}}\right)=\left\{\rho =|u\rangle \langle u|\left(\text{i}\text{.e}\text{.},\text{the}\text{Dirac}\text{notation}\right)\mathrm{<mo>\; |\; </mo>}{\Vert u\Vert }_{{ℂ}^n}=1\right\}\\ \left[\text{Case}\left({\text{J}}_2\right)\right]\mathrm{<mo>\; ;\; </mo>}{\mathfrak{S}}^p\left(C{\left(\Omega \right)}^{\mathrm{<mo>\; *\; </mo>}}\right)=\left\{\rho ={\delta }_{{\omega }_0}\mathrm{<mo>\; |\; </mo>}{\delta }_{{\omega }_0}\text{is}\text{a}\text{point}\text{measure}\text{at}{\omega }_0\in \Omega \right\}\approx \Omega \mathrm{.}\\ \text{Under}\text{the}\text{identification}\mathrm{<mo>\; :\; </mo>}{\mathfrak{S}}^p\left(C{\left(\Omega \right)}^{\mathrm{<mo>\; *\; </mo>}}\right)\in {\delta }_{\omega }\leftrightarrow \omega \in \Omega \mathrm{,}\\ \omega \text{and}\Omega \text{is}\text{also}\text{called}\text{a}\text{state}\text{and}\text{state}\text{space}\text{respectively}\mathrm{.}\end{array}$

Definition 9. [Observable, Image observable] According to the noted idea (cf. refs. [16] [17] ), an observable $\text{O}=\left(X\mathrm{,}\mathcal{P}\left(X\right)\mathrm{,}G\right)$ in $\mathcal{A}$ is defined as follows:

(i) X is a finite set, $\mathcal{P}\left(X\right)$ ( $=2^X$, the power set of X).

(ii) [Additivity] G is a mapping from $\mathcal{P}\left(X\right)$ to $\mathcal{A}$ satisfying: (a): for every $\Xi \in \mathcal{P}\left(X\right)$, $G\left(\Xi \right)$ is a non-negative element in $\mathcal{A}$ such that $0\le G\left(\Xi \right)\le I$, (b): $G(\varnothing )=0$ and $G\left(X\right)=I$, where 0 and I is the 0-element and the identity in $\mathcal{A}$ respectively. (c): [additivity]

$G\left({\Xi }_1\right)+G\left({\Xi }_2\right)=G\left({\Xi }_1\cup {\Xi }_2\right)$

for all ${\Xi }_1\mathrm{,}{\Xi }_2\in \mathcal{P}\left(X\right)$ such that ${\Xi }_1\cap {\Xi }_2\mathrm{<mo>\; =\; </mo>}\varnothing$.

If $G\left(\Xi \right)=G{\left(\Xi \right)}^2$ $\left(\forall \Xi \in \mathcal{P}\left(X\right)\right)$, then $\text{O}=\left(X\mathrm{,}\mathcal{P}\left(X\right)\mathrm{,}G\right)$ in $\mathcal{A}$ is a projective observable (or, crisp observable). Also, $\text{O}=\left(X\mathrm{,}\mathcal{P}\left(X\right)\mathrm{,}G\right)$ in $\mathcal{A}$ is also called an X-valued observable. I will devote myself to binary (i.e., $\left\{T\mathrm{,}F\right\}$ -valued) observables in most of the cases in this paper. Let Y be a finite set, and let $\Theta \mathrm{<mo>\; :\; </mo>}X\to Y$ be a map. Then, $\Theta \left(\text{O}\right)=\left(Y\mathrm{,}\mathcal{P}\left(Y\right)\mathrm{,}G\left({\Theta }^{-1}(\cdot )\right)\right)$ in $\mathcal{A}$ is also an observable in $\mathcal{A}$ (which is called an image observable).

3.2. Axiom 1 [Measurement] and Axiom 2 [Causality]

With any system S, a C^*-algebra $\mathcal{A}\left(\subseteq B\left(H\right)\right)$ can be associated in which the measurement theory (2) of that system can be formulated. A state of the system S is represented by an element $\rho \left(\in {\mathfrak{S}}^p\left({\mathcal{A}}^{\ast }\right)\right)$ and an observable is represented by an observable $\text{O}=\left(X\mathrm{,}\mathcal{P}\left(X\right)\mathrm{,}G\right)$ in $\mathcal{A}$. Also, the measurement of the observable $\text{O}$ for the system S with the state $\rho$ is denoted by ${\text{M}}_{\mathcal{A}}\left(\text{O}\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ (or more precisely, ${\text{M}}_{\mathcal{A}}\left(\text{O}=\left(X\mathrm{,}\mathcal{P}\left(X\right)\mathrm{,}G\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ ). An observer can obtain a measured value $x\left(\in X\right)$ by the measurement $\text{M}\left(\text{O}\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$.

The Axiom 1 presented below is a kind of mathematical generalization of Born’s probabilistic interpretation of quantum mechanics. And thus, it is a statement without reality.

Now we can present Axiom 1 as follows.

Axiom 1. [Measurement]. The probability that a measured value $x\left(\in X\right)$ obtained by the measurement ${\text{M}}_{\mathcal{A}}\left(\text{O}=\left(X\mathrm{,}\mathcal{P}\left(X\right)\mathrm{,}G\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ is given by $\rho \left(G\left(\left\{x\right\}\right)\right)\left(\equiv {}_{{\mathcal{A}}^{\ast }}\langle \rho \mathrm{,}G\left(\left\{x\right\}\right)\rangle {}_{\mathcal{A}}\right)$.

Next, we explain Axiom 2 (which is not used in this paper). Let ${\mathcal{A}}_1\left(\subseteq B\left(H_1\right)\right)$ and ${\mathcal{A}}_2\left(\subseteq B\left(H_2\right)\right)$ be A continuous linear operator ${\Phi }_{\mathrm{1,2}}\mathrm{<mo>\; :\; </mo>}{\mathcal{A}}_2\to {\mathcal{A}}_1$ is called a Markov operator, if ${\Phi }_{\mathrm{1,2}}\left(L\right)\ge 0$ ( $\forall L\in {\mathcal{A}}_2$ such that $L\ge 0$ and ${\varphi }_{\mathrm{1,2}}\left(I_2\right)=I_1$, where $I_1$ and $I_2$ is identity maps in ${\mathcal{A}}_1$ and ${\mathcal{A}}_2$ respectively.

Now we can propose Axiom 2 (i.e., causality). (For details, see ref. [4].)

Axiom 2. [Causality]; The causality is represented by a Markov operator ${\Phi }_{\mathrm{1,2}}\mathrm{<mo>\; :\; </mo>}{\mathcal{A}}_2\to {\mathcal{A}}_1$.

3.3. The Linguistic Copenhagen Interpretation (=The Manual to Use Axioms 1 and 2)

It is well known (cf. ref. [18] ) that the Copenhagen interpretation of quantum mechanics has not been established yet. For example, about the right or wrong of the wave function collapse, opinions are divided in the Copenhagen interpretation. Also, the meaning of the errors in Heisenberg’s uncertainty relation has yet to be clarified (cf. ref. [19] ). Thus, the Copenhagen interpretation is often called so-call Copenhagen interpretation”. However, we believe that the linguistic Copenhagen interpretation of quantum language (B) (i.e., both quantum (I₁) and classical (I₂)) is uniquely determined. For example, for the quantum linguistic opinion about the wave function collapse, see ref. [20].

Now we explain the linguistic Copenhagen interpretation in what follows. In the above, Axioms 1 and 2 are kinds of spells, (i.e., incantation, magic words, metaphysical statements), and thus, it is nonsense to verify them experimentally. Therefore, what we should do is not to understand” but to use”. After learning Axioms 1 and 2 by rote, we have to improve how to use them through trial and error. We may do well even if we do not know the linguistic Copenhagen interpretation (= the manual to use Axioms 1 and 2). However, it is better to know the linguistic Copenhagen interpretation, if we would like to master quantum language early. In spite of Wittgenstein’s paradox; “no course of action could be determined by a rule”, we believe that the linguistic Copenhagen interpretation is the true Copenhagen interpretation, which does not belong to physics.

Let us start from the following figure:

In Figure 2, we remark:

(K₁) : it suffices to understand that interfere” is, for example, apply light”.

: perceive the reaction.

That is, measurement” is characterized as the interaction between observer” and measuring object (=matter)”. However,

(K₂) in measurement theory (=quantum language), interaction” must not be emphasized.

Therefore, in order to avoid confusion, it might better to omit the interaction “ and ” in Figure 2.

After all, we think that:

(K₃) it is clear that there is no measured value without observer (i.e., I”, mind”). Thus, we consider that measurement theory is composed of three key-words: measured value”, observable”, state” (cf. [4] ).

$\underset{\left(I,observer,\text{mind}\right)}{\boxed{measuredvalue}},\underset{\left(body\left(=sensoryorgan\right),thermometer,eye,ear,compass\right)}{\boxed{observable\left(=measuringinstrument\right)}},\underset{\left(matter\right)}{\boxed{state}},$

Figure 2. [Descartes Figure]: Image of “measurement (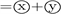)” in mind-matter dualism.

Hence, quantum language is based on dualism, i.e., a kind of mind-matter dualism.

The linguistic Copenhagen interpretation says that

(L₁) Only one measurement is permitted. Thus, the state must be constant and only one. And therefore, the state after a measurement is meaningless since it cannot be measured any longer. Thus, the collapse of the wavefunction is prohibited (cf. ref. [20]; projection postulate). We are not concerned with anything after measurement. Strictly speaking, the phrase after the measurement should not be used. Also, the causality should be assumed only in the side of system, however, a state never moves. Thus, the Heisenberg picture should be adopted, and thus, the Schrödinger picture should be prohibited.

(L₂) Observer” and system” are completely separated. Hence, the measurement ${\text{M}}_{\mathcal{A}}\left(\text{O}=\left(X{\mathrm{,2}}^X\mathrm{,}G\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ does not depend on the choice of observers. That is, any proposition in quantum language is independent of observer” (=I”), therefore, there is no observer’s space and time” in quantum language. And thus, it does not have tense (i.e., past, present, future). Simply put, it is safe not to use “I, now, here”.

(L₃) there is no probability without measurements (cf. refs. [21] [22] [23] [24], These are related to in Figure 1).

(L₄) Leibniz’s relationalism concerning space-time (e.g., time should be regarded as a parameter), (cf. ref. [25] ).

and so on.

We need the following definition for the rule (L₁) such that Only one measurement is permitted.

Definition 10 [(i): Quasi-product observable, quasi-product measurement]: Let ${\text{O}}_i=\left(X_i\mathrm{,}\mathcal{P}\left(X_i\right)\mathrm{,}{G}_i\right)$ $\left(i=1,2,\cdots ,N\right)$ be commutative observables in $\mathcal{A}$. Define a quasi-product observable ${\times }_{i=1,2,\cdots ,n}^{qp}{\text{O}}_i=\left({\times }_{i\mathrm{<mo>\; =\; </mo>1}}^n{X}_i\mathrm{,}\mathcal{P}\left({\times }_{i\mathrm{<mo>\; =\; </mo>1}}^n{X}_i\right)\mathrm{,}{\times }_{i=1,2,\cdots ,n}^{qp}{G}_i\right)$ such that

$\begin{array}{l}\left[\underset{i=1,2,\cdots ,n}{\overset{qp}{{\displaystyle \times }}}{G}_i\right]\left(X_1\times X_2\times \cdots \times X_{j-1}\times {\Xi }_j\times X_{j+1}\times \cdots \times X_n\right)\\ =G_j\left({\Xi }_j\right)\left(\forall {\Xi }_j\in \mathcal{P}\left(X_j\right),j=1,2,\cdots ,n\right)\end{array}$

Also, ${\text{M}}_{\mathcal{A}}\left({\times }_{i=1,2,\cdots ,n}^{qp}{\text{O}}_i=\left({\times }_{i\mathrm{<mo>\; =\; </mo>1}}^n{X}_i\mathrm{,}\mathcal{P}\left({\times }_{i\mathrm{<mo>\; =\; </mo>1}}^n{X}_i\right)\mathrm{,}{\times }_{i=1,2,\cdots ,n}^{qp}{G}_i\right),S_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ is called a quasi-product measurement of ${\text{M}}_{\mathcal{A}}\left({\text{O}}_i=\left(X_i\mathrm{,}\mathcal{P}\left(X_i\right)\mathrm{,}{G}_i\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ $\left(i=1,2,\cdots ,n\right)$.

[(ii): Tensor C^*-algebra, tensor quasi-product observable, tensor quasi-product measurement]: Let ${\text{O}}_i=\left(X_i\mathrm{,}\mathcal{P}\left(X_i\right)\mathrm{,}{G}_i\right)$ be observables in ${\mathcal{A}}_i$, $\left(i=1,2,\cdots ,n\right)$. Define a tensor quasi-product observable ${\otimes }_{i=1,2,\cdots ,n}^{qp}{\text{O}}_i=\left({\times }_{i\mathrm{<mo>\; =\; </mo>1}}^n{X}_i\mathrm{,}\mathcal{P}\left({\times }_{i\mathrm{<mo>\; =\; </mo>1}}^n{X}_i\right)\mathrm{,}{\otimes }_{i=1,2,\cdots ,n}^{qp}{G}_i\right)$ in the tensor C^*-algebra ${\otimes }_{i=1}^n{\mathcal{A}}_i$ such that

$\begin{array}{l}\left[\underset{i=1,2,\cdots ,n}{\overset{qp}{\otimes }}{G}_i\right]\left(X_1\times X_2\times \cdots \times X_{j-1}\times {\Xi }_j\times X_{j+1}\times \cdots \times X_n\right)\\ =\left(\underset{i=1}{\overset{j-1}{\otimes }}I\right)\otimes G_j\left({\Xi }_j\right)\otimes \left(\underset{i=j+1}{\overset{n}{\otimes }}I\right)\left(\forall {\Xi }_j\in \mathcal{P}\left(X_j\right)\mathrm{,}j=\mathrm{1,2,}\cdots \mathrm{,}n\right)\end{array}$

Also, ${\text{M}}_{{\otimes }_{i=1}^n{\mathcal{A}}_i}\left({\otimes }_{i=1,2,\cdots ,n}^{qp}{\text{O}}_i=\left({\times }_{i\mathrm{<mo>\; =\; </mo>1}}^n{X}_i\mathrm{,}\mathcal{P}\left({\times }_{i\mathrm{<mo>\; =\; </mo>1}}^n{X}_i\right)\mathrm{,}{\otimes }_{i=1,2,\cdots ,n}^{qp}{G}_i\right),S_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}{\otimes }_{i=1}^n{\rho }_i\mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ is called a tensor quasi-product measurement of ${\text{M}}_{{\mathcal{A}}_i}\left({\text{O}}_i=\left(X_i\mathrm{,}\mathcal{P}\left(X_i\right)\mathrm{,}{G}_i\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}{\rho }_i\mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ $\left(i=1,2,\cdots ,n\right)$.

We get the following result from the rule (L₂) such that Observer” and system” are completely separated.

Remark 11. [Cogito proposition is not a proposition in QL; cf. refs. [3] [26] ]: Examine the cogito proposition “I think, therefore I am”, in which it is natural to consider that

$“\text{observer}”=“\text{I}”=“\text{measurement}\text{object}\left(=\text{system}\right)”$

This is against the linguistic Copenhagen interpretation (L₂). Therefore, the cogito proposition is not a proposition in QL. The fact that the first proposition of philosophy is not a proposition is interesting.

4. Practical Fuzzy Logic in QL (Quantum and Classical Systems)

In the previous section we introduced QL, which is the theory of the quantum mechanical worldview. In this section, we introduce the practical fuzzy logic, or in short, fuzzy logic (i.e., the probabilistic logic in the quantum mechanical worldview).

4.1. Easy Example; Classical System

Although our theory is valid for quantum systems as well as classical systems, in this Sec. 4.1 we explain our idea in classical systems (i.e., the case that $\mathcal{A}=C\left(\Omega \right)$ ). Again let us start from the following example (=Example 1).

Example 12. [=Example 1]: For example, consider a proposition P₁ such that

$P_1=“\text{this}\text{tomato}\text{is}\text{red}”\mathrm{,}\neg P_1=“\text{this}\text{tomato}\text{is}\text{not}\text{red}”\mathrm{,}$

And suppose that there are 100 respondents, and furthermore, the following question is asked to them.

(C) Is this tomato red? (i.e., is the proposition P₁ true or not?)

Assume that the results of the responses are as follows.

(D) $\{\begin{array}{l}\text{70}\text{respondents}\text{say}“\text{Yes},\text{thistomatoisred}”\left(\text{i}\text{.e}\text{.},\text{theproposition}{P}_1\text{is}\text{ture},\text{i}\text{.e}\mathrm{.,}“T”\right)\\ \text{30}\text{respondents}\text{say}“\text{No},\text{thistomatoisnotred}”\left(\text{i}\text{.e}\text{.},\text{theproposition}{P}_1\text{is}\text{false},\text{i}\text{.e}\mathrm{.,}“F”\right)\end{array}$

This can be probabilistically interpreted as follows.

(E) When any respondent is randomly selected out of 100, the probability that this respondent will answer “yes” to question (C) is $p_1\left(=0.7\right)$. Or simply, the probability that the proposition P₁ is true is p₁. In symbolic form,

$\text{Prob}\left[P_1;\left\{T\right\}\right]=p_1\left(=0.7\right)$

Then we generally denote that

$\text{Prob}\left[P_1;\left\{T\right\}\right]=p_1,\text{Prob}\left[P_1;\left\{F\right\}\right]=1-p_1\left(\text{where}0\le p_1\le 1\right)$

Also, note that $\text{Prob}\left[\neg P_1;\left\{T\right\}\right]=\text{Prob}\left[P_1;\left\{F\right\}\right]=1-p_1$.

The above will be formulated in terms of QL as follows. Let $\Omega$ a state space, which is a compact space $\Omega \subseteq {ℝ}^N$ (=N-dimensional real space), where N is sufficiently large natural number. Consider many tomatoes, that is, roughly speaking, consider T as the set of all tomatoes. Assume that any tomato $t\left(\in T\right)$ is represented by a state $\omega$, which is an element of the state space $\Omega$. Thus, we have the map $\hat{\omega }\mathrm{<mo>\; :\; </mo>}T\to \Omega$. That is, the quantitative property of a tomato t is represented by $\hat{\omega }\left(t\right)$. For example, it suffices to consider $\Omega$ such that

$\begin{array}{l}\omega =({\omega }^{(1)}\left(=\text{weight}\right),{\omega }^{(2)}\left(=\text{diameter}\right),{\omega }^{(3)}\left(=\text{color}\text{value}\right),\\ {\omega }^{(4)}\left(=\text{calorie}\right),{\omega }^{(5)}\left(=\text{sugar}\text{content}\right),\cdots ,{\omega }^{(N)}\left(=\cdots \right))\in \Omega \subseteq {ℝ}^N\end{array}$

Consider a binary observable (or, $\left\{T\mathrm{,}F\right\}$ -valued observable) ${\text{O}}_1=\left(\left\{T\mathrm{,}F\right\}{\mathrm{,2}}^{\left\{T\mathrm{,}F\right\}}\mathrm{,}{G}_1\right)$ in $C\left(\Omega \right)$. The measurement ${\text{M}}_{C\mathrm{<mo\; stretchy="false">\; (\; </mo>}\Omega \mathrm{<mo\; stretchy="false">\; )\; </mo>}}\left({\text{O}}_1\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}{\delta }_{\omega }\mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ is called a (TF)-measurement, which is also called a fuzzy proposition. Axiom 1 says that

(M) the probability that measured value T is obtained by the (TF)-measurement ${\text{M}}_{C\mathrm{<mo\; stretchy="false">\; (\; </mo>}\Omega \mathrm{<mo\; stretchy="false">\; )\; </mo>}}\left({\text{O}}_1\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}{\delta }_{\omega }\mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ is given by ${\delta }_{\omega }\left(G_1\left(\left\{T\right\}\right)\right)(={}_{C{\mathrm{<mo\; stretchy="false">\; (\; </mo>}\Omega \mathrm{<mo\; stretchy="false">\; )\; </mo>}}^{\mathrm{<mo>\; *\; </mo>}}}\langle {\delta }_{\omega }\mathrm{,}{G}_1\left(\left\{T\right\}\right)\rangle {}_{C\mathrm{<mo\; stretchy="false">\; (\; </mo>}\Omega \mathrm{<mo\; stretchy="false">\; )\; </mo>}}=\left[G_1\left(\left\{T\right\}\right)\right](\; \omega \; ))$

This is the quantum linguistic representation of the above (E). That is, we identify a proposition $P_1$ with a (TF)-measurement ${\text{M}}_{C\mathrm{<mo\; stretchy="false">\; (\; </mo>}\Omega \mathrm{<mo\; stretchy="false">\; )\; </mo>}}\left({\text{O}}_1\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}{\delta }_{\omega }\mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$.

Remark 13. (i): Someone might say that the term “the set of all tomatoes” is as ambiguous as “the set of all dinosaurs”. However, for the sake of convenience, here we use the term “the set of all tomatoes”. This problem is the same as that of the Hempel’ raven paradox (i.e., “the set of all ravens” leads to contradiction). For further discussion about this, see refs. [5] [27].

(ii): If we want to consider another proposition $P_2\left(={\text{M}}_{C\mathrm{<mo\; stretchy="false">\; (\; </mo>}\Omega \mathrm{<mo\; stretchy="false">\; )\; </mo>}}\left({\text{O}}_1\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}{\delta }_{{\omega }^{\prime }}\mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\right)$ such as

$P_2=“\text{that}\text{tomato}\text{is}\text{red}”\mathrm{,}\neg P_2=“\text{that}\text{tomato}\text{is}\text{not}\text{red}”\mathrm{,}$

we must define ${\text{M}}_{C\mathrm{<mo\; stretchy="false">\; (\; </mo>}\Omega \mathrm{<mo\; stretchy="false">\; )\; </mo>}}\left({\text{O}}_1\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}{\delta }_{\omega }\mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\wedge {\text{M}}_{C\mathrm{<mo\; stretchy="false">\; (\; </mo>}\Omega \mathrm{<mo\; stretchy="false">\; )\; </mo>}}\left({\text{O}}_1\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}{\delta }_{{\omega }^{\prime }}\mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ $\left(\omega \ne {\omega }^{\prime }\right)$. This will be explained in Sec.4.3.

(iii): If we want to consider both tomato’s world ${\Omega }_1$ and apple’s world ${\Omega }_2$, it suffices to start from the tensor space $C\left({\Omega }_1\right)\otimes C\left({\Omega }_2\right)$ $\left(=C\left({\Omega }_1\times {\Omega }_2\right)\right)$. This will be also explained in Sec. 4.3.

4.2. Fuzzy Logic in QL

Let’s start with the following definition.

Definition 14. [(TF)-measurement (=Fuzzy proposition), Fuzzy set (= Membership function)] Let $\text{O}=\left(\left\{T\mathrm{,}F\right\}{\mathrm{,2}}^{\left\{T\mathrm{,}F\right\}}\mathrm{,}G\right)$ be a binary observable (or, (TF)-observable, $\left\{T\mathrm{,}F\right\}$ -valued observable) in a C^*-algebra $\mathcal{A}$. A measurement ${\text{M}}_{\mathcal{A}}\left(\text{O}\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ is called a (TF)-measurement, which is also called a fuzzy proposition. Since Axiom 1 says that the probability that a measured value T is obtained by (TF)-measurement ${\text{M}}_{\mathcal{A}}\left(\text{O}\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ is given by $\rho \left(G\left(\left\{T\right\}\right)\right)$, we say that

· a (TF)-measurement ${\text{M}}_{\mathcal{A}}\left(\text{O}\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ is true with probability $\rho \left(G\left(\left\{T\right\}\right)\right)$

Or,

· $\text{Prob}\left[{\text{M}}_{\mathcal{A}}\left(\text{O}\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\mathrm{<mo>\; ;\; </mo>}\left\{T\right\}\right]=\rho \left(G\left(\left\{T\right\}\right)\right)\left(={}_{{\mathcal{A}}^{\ast }}\langle \rho \mathrm{,}G\left(\left\{T\right\}\right)\rangle {}_{\mathcal{A}}\right)$

Also, $G\left(\left\{T\right\}\right)\left(\in \mathcal{A}\right)$ is called the membership function of $\text{O}$ (cf. Figure 3 and Definition 24 later).

In general, we must consider many propositions $\left\{P_i={\text{M}}_{{\mathcal{A}}_i}\left({\text{O}}_i\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}{\rho }_i\mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\mathrm{<mo>\; :\; </mo>}i=\mathrm{1,2,}\cdots \mathrm{,}n\right\}$. In this section, we devote ourselves to the following simple case:

(N₁) $\mathcal{A}$ is fixed, i.e., ${\mathcal{A}}_1={\mathcal{A}}_2=\cdots ={\mathcal{A}}_n$

(N₂) ${\text{O}}_1\mathrm{,}{\text{O}}_2\mathrm{,}\cdots \mathrm{,}{\text{O}}_n$ commute,

(N₃) a state $\rho$ is only one, i.e., ${\rho }_1={\rho }_2=\cdots ={\rho }_n$

For the general case, we discuss in next section (i.e., Sec. 4.3). That is, in this section, we devote ourselves to

$\left\{P_i={\text{M}}_{\mathcal{A}}\left({\text{O}}_i=\left(\left\{T\mathrm{,}F\right\}{\mathrm{,2}}^{\left\{T\mathrm{,}F\right\}}\mathrm{,}{G}_i\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\mathrm{<mo>\; :\; </mo>}i=\mathrm{1,2,}\cdots \mathrm{,}n\right\}$. However, it should be noted that the above simple case (N) is essential, that is, the general case is an easy consequence of the simple case as seen in the next section.

Definition 15. [Fuzzy logic symbols ( $\neg$, $\wedge$, $\vee$, $\to$ ))] Let ${\text{O}}_i=\left(\left\{T\mathrm{,}F\right\}{\mathrm{,2}}^{\left\{T\mathrm{,}F\right\}}\mathrm{,}{G}_i\right)$ be binary observables (or, $\left\{T\mathrm{,}F\right\}$ -valued observable) in a C^*-algebra $\mathcal{A}$. ( $i=\mathrm{1,2}$ ). Assume that ${\text{O}}_i\left(i=\mathrm{1,2}\right)$ commute. Fix the quasi-product observable ${\text{O}}_1{\times }^{qp}{\text{O}}_2=\left({\left\{T\mathrm{,}F\right\}}^2\mathrm{,}\mathcal{P}\left({\left\{T\mathrm{,}F\right\}}^2\right)\mathrm{,}{G}_1{\times }^{qp}{G}_2\right)$. Consider (TF)-measurement ${\text{M}}_{\mathcal{A}}\left({\text{O}}_i=\left(\left\{T\mathrm{,}F\right\}{\mathrm{,2}}^{\left\{T\mathrm{,}F\right\}}\mathrm{,}{G}_i\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ (which is abbreviated as $P_i$ ) in a C^*-algebra $\mathcal{A}$. Put ${\mu }_i\left(\Xi \right)=\rho \left(G_i\left(\Xi \right)\right)$ $\left(\Xi \in \left\{T,F\right\},i=0,1,2\right)$, and $\left({\times }_{i=1,2}^{qp}{\mu }_i\right)\left({\Xi }_1\times {\Xi }_2\right)=\left(\rho \left(G_1{\times }^{qp}{G}_2\right)\right)\left({\Xi }_1\times {\Xi }_2\right)$ $\left({\Xi }_1\mathrm{,}{\Xi }_2\in \left\{T\mathrm{,}F\right\}\right)$.

(i): Put $i=\mathrm{1,2}$. Define $\neg {\text{M}}_{\mathcal{A}}\left({\text{O}}_i\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ such that

$\neg {\text{M}}_{\mathcal{A}}\left({\text{O}}_i\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)={\text{M}}_{\mathcal{A}}\left({\pi }^{\neg }{\text{O}}_i\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$

where the map ${\pi }^{\neg }\left\{T\mathrm{,}F\right\}\to \left\{T\mathrm{,}F\right\}$ is defined by ${\pi }^{\neg }\left(T\right)=F\mathrm{,}{\pi }^{\neg }\left(F\right)=T$. Clearly it holds that $\text{Prob}\left[\neg {\text{M}}_{\mathcal{A}}\left({\text{O}}_i\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\mathrm{<mo>\; ;\; </mo>}\left\{T\right\}\right]=\rho \left(G_i\left(\left\{F\right\}\right)\right)={\mu }_i\left(\left\{F\right\}\right)$.

(ii): Define ${\text{M}}_{\mathcal{A}}\left({\text{O}}_1\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\wedge {\text{M}}_{\mathcal{A}}\left({\text{O}}_2\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ such that

${\text{M}}_{\mathcal{A}}\left({\text{O}}_1\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\wedge {\text{M}}_{\mathcal{A}}\left({\text{O}}_2\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)={\text{M}}_{\mathcal{A}}\left({\pi }^{\wedge }\left({\text{O}}_1{\times }^{qp}{\text{O}}_2\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$

where ${\pi }^{\wedge }\mathrm{<mo>\; :\; </mo>}{\left\{T\mathrm{,}F\right\}}^2\to \left\{T\mathrm{,}F\right\}$ is defined by ${\pi }^{\wedge }\left(T\mathrm{,}T\right)=T$, ${\pi }^{\wedge }\left(T\mathrm{,}F\right)={\pi }^{\wedge }\left(F\mathrm{,}T\right)={\pi }^{\wedge }\left(T\mathrm{,}F\right)=F$.

It holds that

$\begin{array}{l}\text{Prob}\left[{\text{M}}_{\mathcal{A}}\left({\text{O}}_1\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\wedge {\text{M}}_{\mathcal{A}}\left({\text{O}}_2\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\mathrm{<mo>\; ;\; </mo>}\left\{T\right\}\right]\\ =\rho \left(G_1{\times }^{qp}{G}_2\right)\left({\left({\pi }^{\wedge }\right)}^{-1}\left(\left\{T\right\}\right)\right)=\left({\mu }_1{\times }^{qp}{\mu }_2\right)\left(\left\{\left(T\mathrm{,}T\right)\right\}\right)\end{array}$.

(iii): Define ${\text{M}}_{\mathcal{A}}\left({\text{O}}_1\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\vee {\text{M}}_{\mathcal{A}}\left({\text{O}}_2\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ such that

Figure 3. [Membership function $m_D\mathrm{<mo>\; :\; </mo>}\Omega \to \left[\mathrm{0,1}\right]$.

${\text{M}}_{\mathcal{A}}\left({\text{O}}_1\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\vee {\text{M}}_{\mathcal{A}}\left({\text{O}}_2\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)={\text{M}}_{\mathcal{A}}\left({\pi }^{\vee }\left({\text{O}}_1{\times }^{qp}{\text{O}}_2\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$

where ${\pi }^{\vee }\mathrm{<mo>\; :\; </mo>}{\left\{T\mathrm{,}F\right\}}^2\to \left\{T\mathrm{,}F\right\}$ is defined by ${\pi }^{\vee }\left(T,T\right)={\pi }^{\vee }\left(T,F\right)={\pi }^{\vee }\left(F,T\right)=T$, ${\pi }^{\vee }\left(F,F\right)=F$.

It holds that $\begin{array}{l}\text{Prob}\left[{\text{M}}_{\mathcal{A}}\left({\text{O}}_1\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\vee {\text{M}}_{\mathcal{A}}\left({\text{O}}_2\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\mathrm{<mo>\; ;\; </mo>}\left\{T\right\}\right]\\ =\rho \left(G_1{\times }^{qp}{G}_2\right)\left({\left({\pi }^{\vee }\right)}^{-1}\left(\left\{T\right\}\right)\right)=\left({\mu }_1{\times }^{qp}{\mu }_2\right)\left(\left\{\left(T\mathrm{,}T\right)\mathrm{,}\left(T\mathrm{,}F\right)\mathrm{,}\left(F\mathrm{,}T\right)\right\}\right)\end{array}$.

(iv): Define ${\text{M}}_{\mathcal{A}}\left({\text{O}}_1\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\to {\text{M}}_{\mathcal{A}}\left({\text{O}}_2\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ such that

${\text{M}}_{\mathcal{A}}\left({\text{O}}_1\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\to {\text{M}}_{\mathcal{A}}\left({\text{O}}_2\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)={\text{M}}_{\mathcal{A}}\left({\pi }^{\to }\left({\text{O}}_1{\times }^{qp}{\text{O}}_2\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$

where ${\pi }^{\to }\mathrm{<mo>\; :\; </mo>}{\left\{T\mathrm{,}F\right\}}^2\to \left\{T\mathrm{,}F\right\}$ is defined by ${\pi }^{\to }\left(T,T\right)={\pi }^{\to }\left(F,T\right)={\pi }^{\to }\left(F,F\right)=T$, ${\pi }^{\to }\left(T,F\right)=F$.

It holds that $\begin{array}{l}\text{Prob}\left[{\text{M}}_{\mathcal{A}}\left({\text{O}}_1\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\to {\text{M}}_{\mathcal{A}}\left({\text{O}}_2\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\mathrm{<mo>\; ;\; </mo>}\left\{T\right\}\right]\\ =\rho \left(G_1{\times }^{qp}{G}_2\right)\left({\left({\pi }^{\to }\right)}^{-1}\left(\left\{T\right\}\right)\right)=\left({\mu }_1{\times }^{qp}{\mu }_2\right)\left(\left\{\left(T\mathrm{,}T\right)\mathrm{,}\left(F\mathrm{,}F\right)\mathrm{,}\left(F\mathrm{,}T\right)\right\}\right)\end{array}$.

Theorem 16. [Fundamental theorem in Fuzzy logic] Let ${\text{O}}_i=\left(\left\{T\mathrm{,}F\right\}{\mathrm{,2}}^{\left\{T\mathrm{,}F\right\}}\mathrm{,}{G}_i\right)$ be binary observables (or, $\left\{T\mathrm{,}F\right\}$ -valued observable) in a C^*-algebra $\mathcal{A}$. ( $i=\mathrm{1,2,}\cdots \mathrm{,}n$ ). Assume that ${\text{O}}_i\ne {\text{O}}_j$ ( $\forall i\mathrm{,}j$ such that $i\ne j$ ) (i.e., non-overlapping condition in Theorem 7) and ${\text{O}}_i\left(i=\mathrm{1,2,}\cdots \mathrm{,}n\right)$ commute. Fix the quasi-product ${\times }_{i=1,\cdots ,n}^{qp}{\text{O}}_i=\left({\left\{T\mathrm{,}F\right\}}^n\mathrm{,}\mathcal{P}\left({\left\{T\mathrm{,}F\right\}}^n\right)\mathrm{,}{\times }_{i=1,\cdots ,n}^{qp}{G}_i\right)$ (cf. Definition 10 before). Consider (TF)-measurement ${\text{M}}_{\mathcal{A}}\left({\text{O}}_i=\left(\left\{T\mathrm{,}F\right\}{\mathrm{,2}}^{\left\{T\mathrm{,}F\right\}}\mathrm{,}{G}_i\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ (which is abbreviated as $P_i$ ) in a C^*-algebra $\mathcal{A}$ ). And consider the quasi-product measurement $\begin{array}{l}{\times }_{i=1,\cdots ,n}^{qp}{\text{M}}_{\mathcal{A}}\left({\text{O}}_i=\left(\left\{T\mathrm{,}F\right\}{\mathrm{,2}}^{\left\{T\mathrm{,}F\right\}}\mathrm{,}{G}_i\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\\ ={\text{M}}_{\mathcal{A}}\left({\times }_{i=1,\cdots ,n}^{qp}{\text{O}}_i=\left({\left\{T\mathrm{,}F\right\}}^n\mathrm{,}\mathcal{P}\left({\left\{T\mathrm{,}F\right\}}^n\right)\mathrm{,}{\times }_{i=1,\cdots ,n}^{qp}{G}_i\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\end{array}$.

Put

· ${\mu }_i\left(\left\{x_i\right\}\right)=\rho \left(G_i\left(\left\{x_i\right\}\right)\right)\left(x_i\in \left\{T\mathrm{,}F\right\}\mathrm{,}i=\mathrm{1,2,}\cdots \mathrm{,}n\right)$

· $\begin{array}{l}\underset{i=\mathrm{1,}\cdots \mathrm{,}n}{\overset{qp}{{\displaystyle \times }}}{\mu }_i\left(\left\{\left(x_1\mathrm{,}{x}_2\mathrm{,}\cdots \mathrm{,}{x}_n\right)\right\}\right)=\rho \left(\left({\times }_{i=\mathrm{1,}\cdots \mathrm{,}n}^{qp}{G}_i\right)\left(\left\{\left(x_1\mathrm{,}{x}_2\mathrm{,}\cdots \mathrm{,}{x}_n\right)\right\}\right)\right)\\ =\left({\times }_{i=\mathrm{1,}\cdots \mathrm{,}n}^{qp}{\mu }_i\right)\left(\left\{\left(x_1\mathrm{,}{x}_2\mathrm{,}\cdots \mathrm{,}{x}_n\right)\right\}\right)\left(\forall \left(x_1\mathrm{,}{x}_2\mathrm{,}\cdots \mathrm{,}{x}_n\right)\in {\left\{T\mathrm{,}F\right\}}^n\right)\end{array}$

Here, the pair $\left[\left\{P_1\mathrm{,}{P}_2\mathrm{,}\cdots \mathrm{,}{P}_n\right\}\mathrm{<mo>\; ;\; </mo>}\left({\left\{T\mathrm{,}F\right\}}^n\mathrm{,}\mathcal{P}\left({\left\{T\mathrm{,}F\right\}}^n\right)\mathrm{,}{\times }_{i=1,2,\cdots ,n}^{qp}{\mu }_i\right)\right]$ is a logical sample space.

Then, by Theorem 7, we see the following:

· Let P be a proposition which is constructed by $P_1\mathrm{,}\cdots \mathrm{,}{P}_n$. Note that P is regarded as the map from ${\left\{T\mathrm{,}F\right\}}^n\to \left\{T\mathrm{,}F\right\}$. Then, we see that

$\text{Prob}\left[P\mathrm{<mo>\; ;\; </mo>}\left\{T\right\}\right]=\left(\underset{i=1,2,\cdots ,n}{\overset{qp}{{\displaystyle \times }}}{\mu }_i\right)\left(P^{-1}\left(\left\{T\right\}\right)\right)$

Remark 17. Since the linguistic Copenhagen interpretation says that “only one measurement is permitted”, we only take the measurement: $\begin{array}{l}{\times }_{i=1,\cdots ,n}^{qp}{\text{M}}_{\mathcal{A}}\left({\text{O}}_i=\left(\left\{T\mathrm{,}F\right\}{\mathrm{,2}}^{\left\{T\mathrm{,}F\right\}}\mathrm{,}{G}_i\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\\ ={\text{M}}_{\mathcal{A}}\left({\times }_{i=1,\cdots ,n}^{qp}{\text{O}}_i=\left({\left\{T\mathrm{,}F\right\}}^n\mathrm{,}\mathcal{P}\left({\left\{T\mathrm{,}F\right\}}^n\right)\mathrm{,}{\times }_{i=1,\cdots ,n}^{qp}{G}_i\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\end{array}$.

Therefore, the measurements (i.e., ${\text{M}}_{\mathcal{A}}\left({\pi }^{\wedge }\left({\text{O}}_1{\times }^{qp}{\text{O}}_2\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ $\left(={\text{M}}_{\mathcal{A}}\left({\text{O}}_1\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\wedge {\text{M}}_{\mathcal{A}}\left({\text{O}}_2\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\right)$ etc. in Definition 15) are not actually done. To be precise, these measurements are included in the quasi-product measurement ${\times }_{i=1,\cdots ,n}^{qp}{\text{M}}_{\mathcal{A}}\left({\text{O}}_i=\left(\left\{T\mathrm{,}F\right\}{\mathrm{,2}}^{\left\{T\mathrm{,}F\right\}}\mathrm{,}{G}_i\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$.

Example 18. [The QL version of Table 10]. Replacing $P_1$ and $P_2$ with ${\text{M}}_{\mathcal{A}}\left({\text{O}}_1\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ and ${\text{M}}_{\mathcal{A}}\left({\text{O}}_2\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$, we get Table 11, i.e., the QL version of Table 10.

Thus, we see that

$\text{Prob}\left[\left[P_1\to P_2\right]\wedge P_1\mathrm{<mo>\; ;\; </mo>}\left\{T\right\}\right]=p_{12}$

Similarly, we see the modus pones:

$\text{Prob}\left[\left[\left[P_1\to P_2\right]\wedge P_1\right]\to P_2\mathrm{<mo>\; ;\; </mo>}\left\{T\right\}\right]=1$

The following is the same as Corollary 8.

Corollary 19. [Tautology in fuzzy logic] Let $P\left(={\text{M}}_{\mathcal{A}}\left(\text{O}\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\right)$ be a proposition constructed from elementary propositions $P_1\left(={\text{M}}_{\mathcal{A}}\left({\text{O}}_1,S_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\right)\mathrm{,}{P}_2\left(={\text{M}}_{\mathcal{A}}\left({\text{O}}_2\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\right)\mathrm{,}\cdots \mathrm{,}{P}_n\left(={\text{M}}_{\mathcal{A}}\left({\text{O}}_n\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\right)$. Then, the followings are equivalent:

(i) P is a tautology in the sense of crisp logic.

(ii) $\text{Prob}\left[P\mathrm{<mo>\; ;\; </mo>}\left\{T\right\}\right]=1$.

That is, tautology always holds even in practical fuzzy logic. For example,

(O) syllogism (i.e., $\left[\left[P_1\to P_2\right]\wedge \left[P_2\to P_3\right]\right]\to \left[P_1\to P_3\right]$ always holds.

Remark 20. We have two results such that

(i) in ref. [10], I showed that syllogism does not always hold in quantum system.

(ii) in Corollary 19, I showed that syllogism always holds in classical and quantum systems.

Thus, readers may think that (i) and (ii) are contradictory. However, these are not contradictory since Corollary 19 requires that ${\text{O}}_1\mathrm{,}{\text{O}}_2\mathrm{,}{\text{O}}_3$ commute. On the other hand, in ref. [10], the commutativity of ${\text{O}}_1$ and ${\text{O}}_3$ is not required. The

Table 11. Probabilistic Truth Table (Elementary propositions ${\text{M}}_{\mathcal{A}}\left({\text{O}}_1\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\left(=P_1\right)$, ${\text{M}}_{\mathcal{A}}\left({\text{O}}_2\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\left(=P_2\right)$ ).

most important one, of course, is Corollary 19.

4.3. General Case

In previous section, we devote ourselves to $\left\{{\text{M}}_{\mathcal{A}}\left({\text{O}}_i=\left(\left\{T\mathrm{,}F\right\}{\mathrm{,2}}^{\left\{T\mathrm{,}F\right\}}\mathrm{,}{G}_i\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\mathrm{<mo>\; :\; </mo>}i=\mathrm{1,2,}\cdots \mathrm{,}n\right\}$ under the conditions (N₁)~ (N₃), which are not so wide as mentioned in Remark 13 (ii) and (iii), In this section, we consider the general case: $\left\{P_i={\text{M}}_{{\mathcal{A}}_i}\left({\text{O}}_i=\left(\left\{T\mathrm{,}F\right\}{\mathrm{,2}}^{\left\{T\mathrm{,}F\right\}}\mathrm{,}{G}_i\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}{\rho }_i\mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\mathrm{<mo>\; :\; </mo>}i=\mathrm{1,2,}\cdots \mathrm{,}n\right\}$. Put

${\hat{P}}_i={\text{M}}_{{\otimes }_{j=1}^n{\mathcal{A}}_j}\left({\hat{O}}_i=\left(\left\{T\mathrm{,}F\right\}{\mathrm{,2}}^{\left\{T\mathrm{,}F\right\}}\mathrm{,}{\hat{G}}_i\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}{\otimes }_{j=1}^n{\rho }_j\mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$

where

$\left[{\hat{G}}_i\right]\left({\Xi }_i\right)=\left({\otimes }_{j=1}^{i-1}I\right)\otimes G_i\left({\Xi }_i\right)\otimes \left({\otimes }_{j=i+1}^{n}I\right)\left(\forall {\Xi }_i\in \mathcal{P}\left(\left\{T\mathrm{,}F\right\}\right)\mathrm{,}i=\mathrm{1,2,}\cdots \mathrm{,}n\right)$

Here, note that $\left\{{\hat{P}}_i={\text{M}}_{{\otimes }_{j=1}^n{\mathcal{A}}_j}\left({\hat{O}}_i=\left(\left\{T\mathrm{,}F\right\}{\mathrm{,2}}^{\left\{T\mathrm{,}F\right\}}\mathrm{,}{\hat{G}}_i\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}{\otimes }_{j=1}^n{\rho }_j\mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\mathrm{<mo>\; :\; </mo>}i=\mathrm{1,2,}\cdots \mathrm{,}n\right\}$ satisfies that

(P₁) $\hat{\mathcal{A}}={\otimes }_{i=1}^n{\mathcal{A}}_i$ is fixed,

(P₂) ${\hat{O}}_1\mathrm{,}{\hat{O}}_2\mathrm{,}\cdots \mathrm{,}{\hat{O}}_n$ commute,

(P₃) a state ${\otimes }_{i=1}^n{\rho }_i$ is only one.

Therefore, the general case: $\left\{P_i={\text{M}}_{{\mathcal{A}}_i}\left({\text{O}}_i=\left(\left\{T\mathrm{,}F\right\}{\mathrm{,2}}^{\left\{T\mathrm{,}F\right\}}\mathrm{,}{G}_i\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}{\rho }_i\mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\mathrm{<mo>\; :\; </mo>}i=\mathrm{1,2,}\cdots \mathrm{,}n\right\}$ can be understood in the theory of Sec. 4.2.

Remark 21. (i): From the theoretical point of view, some may want to extend the above result to infinite tensor product. For this, we must prepare the W^*-algebraic formulation of QL. I think challenging this problem is a good exercise for the reader.

(ii): In this paper, we devote ourselves to binary logic (i.e., $\left\{T\mathrm{,}F\right\}$ -valued logic). If we want to consider many valued logic (i.e., X-valued logic), we can start from X-value observable. In this case, it is clear that “fuzzy many valued proposition” = “Axiom 1”.

Example 22. [Hempel’s raven problem (cf. [27] ); Any sweet tomato is red] Recall the arguments in Sec. 4.1. Consider (TF)-valued observables ${\text{O}}_{SW}=\left(\left\{T\mathrm{,}F\right\}{\mathrm{,2}}^{\left\{T\mathrm{,}F\right\}}\mathrm{,}{G}_{SW}\right)$ and ${\text{O}}_{RD}=\left(\left\{T\mathrm{,}F\right\}{\mathrm{,2}}^{\left\{T\mathrm{,}F\right\}}\mathrm{,}{G}_{RD}\right)$ in $C\left(\Omega \right)$, where ${\text{O}}_{SW}$ and ${\text{O}}_{RD}$ is respectively called the sweet observable and the red observable. It is natural to consider that “Any sweet tomato is red” is defined by

(Q) $SW\subseteq RD$

where $SW=\left\{\omega \in \Omega |G_{SW}\left(\omega \right)=1\right\}$ and $RD=\left\{\omega \in \Omega |G_{RD}\left(\omega \right)=1\right\}$. In order to examine (Q) (i.e., to answer the problem: “Is the (Q) a proposition?”), it suffices to check the following:

$\text{Prob}\left[{\text{M}}_{C\mathrm{<mo\; stretchy="false">\; (\; </mo>}\Omega \mathrm{<mo\; stretchy="false">\; )\; </mo>}}\left({\text{O}}_{RD}\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}{\delta }_{\omega }\mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\mathrm{<mo>\; ;\; </mo>}\left\{T\right\}\right]=1\left(\forall \omega \in SW\right)$

For simplicity’s sake, we assume $SW=\left\{{\omega }_1\mathrm{,}{\omega }_2\mathrm{,}\cdots \mathrm{,}{\omega }_n\right\}$. Recall the linguistic Copenhagen interpretation (L₁) such that only one measurement is permitted. Thus, consider the tensor space ${\otimes }_{i=1}^{n}C\left(\Omega \right)=C\left({\Omega }^n\right)$, and the tensor product measurement

${\text{M}}_{C\mathrm{<mo\; stretchy="false">\; (\; </mo>}{\Omega }^n\mathrm{<mo\; stretchy="false">\; )\; </mo>}}\left(\underset{i=1}{\overset{n}{\otimes }}{\text{O}}_{RD}=\left({\left\{T\mathrm{,}F\right\}}^n\mathrm{,}\mathcal{P}{\left\{T\mathrm{,}F\right\}}^n\mathrm{,}\underset{i=1}{\overset{n}{\otimes }}{G}_{RD}\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}{\delta }_{\mathrm{<mo\; stretchy="false">\; (\; </mo>}{\omega }_1\mathrm{,}{\omega }_2\mathrm{,}\cdots \mathrm{,}{\omega }_n\mathrm{<mo\; stretchy="false">\; )\; </mo>}}\mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$

where

$\left(\underset{i=1}{\overset{n}{\otimes }}{G}_{RD}\right)\left(\left\{\left(x_1\mathrm{,}{x}_2\mathrm{,}\cdots \mathrm{,}{x}_n\right)\right\}\right)=\underset{i=1}{\overset{n}{\otimes }}{G}_{RD}\left(\left\{x_i\right\}\right)\left(\forall \left(x_1\mathrm{,}{x}_2\mathrm{,}\cdots \mathrm{,}{x}_n\right)\in {\left\{T\mathrm{,}F\right\}}^n\right)$

Assume that the measured value $x=\left(x_1\mathrm{,}{x}_2\mathrm{,}\cdots \mathrm{,}{x}_n\right)$ belongs to ${\left\{T\right\}}^n$. Then, we can conclude that (Q) is true. Also, as an analogy of (ii) in Definition 15, we may consider as follows. Let ${\pi }^{\wedge }\mathrm{<mo>\; :\; </mo>}{\left\{T\mathrm{,}F\right\}}^n\to \left\{T\mathrm{,}F\right\}$ be a map such that

${\pi }^{\wedge }\left(x_1\mathrm{,}{x}_2\mathrm{,}\cdots \mathrm{,}{x}_n\right)=(\begin{array}{ll}T\hfill & \text{if}{x}_1=x_2=\cdots =x_n=T\hfill \\ F\hfill & \text{otherwise}\hfill \end{array}$

Then, (Q) is equivalent to

$\text{Prob}\left[{\text{M}}_{C\mathrm{<mo\; stretchy="false">\; (\; </mo>}{\Omega }^n\mathrm{<mo\; stretchy="false">\; )\; </mo>}}\left({\pi }^{\wedge }\left({\otimes }_{i=1}^n{\text{O}}_{RD}\right)\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}{\delta }_{\mathrm{<mo\; stretchy="false">\; (\; </mo>}{\omega }_1\mathrm{,}{\omega }_2\mathrm{,...,}{\omega }_n\mathrm{<mo\; stretchy="false">\; )\; </mo>}}\mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\mathrm{<mo>\; ;\; </mo>}\left\{T\right\}\right]=1$

Thus, (Q) is a fuzzy proposition. If SW is an infinite set, we must prepare the infinite tensor algebra (i.e., the W^*-algebraic formulation of QL (cf. refs. [4] [10] )). We omit it in this paper, since this is simply a matter of mathematics.

5. Discussion about Wittgenstein, Moore, Saussure, Quine, Lewis Carroll, etc.

Wittgenstein, Moore, Saussure, Quine, Lewis Carroll were related to the problem: “What is a scientific proposition?”. In this section, let us argue it.

5.1. Wittgenstein and Zadeh

In ref. [11] (i.e., Wittgenstein’s “Tractatus Logico Philosophicus” (abbreviated as TLP)), which is one of the most famous philosophy books of the 20th century, Wittgenstein studied “logic” in philosophy. However, in hindsight, he may have written literature on the subject of “logic” (cf. refs. [28] [29] ). It is a fact, however, that TLP was accepted by much of the general public. I think the general public felt that Boole and Frege’s “symbolic logic” was just mathematics, and that this was not sufficient as philosophy. In other words, they expected TLP to answer the question, such that “Why does logic work in our world?” or “What is the definition of non-mathematical proposition?.” Wittgenstein’s motivation of TPL would have been to answer these questions, but he was too poet and dreamer.

In 1965, L.A. Zadeh proposed an engineering concept called “fuzzy sets” (cf. ref. [1] ), which was not recognized as a scientific concept by some excellent scientists. And furthermore, Zadeh couldn’t convince them of his idea. However, ref. [1] was one of the most cited papers in the 20th century. This implies that many engineers felt that “mathematical set” is not enough, expected more from his “fuzzy set”.

I think the situation of Wittgenstein and Zadeh is very similar in the sense that they were ardently supported by a large number of the general public even though they were not supported by the best experts. I would rather trust the senses of the many general public than the senses of a few experts. And what Wittgenstein and Zadeh lacked, I believe, was a worldview.

Therefore, their claims are vague and incomprehensible, but if I understand them under the quantum mechanical worldview, I think they are claiming almost the same thing. In other words, I think Theorem 16 and related matters (i.e., “What is a non-mathematical proposition?”) were their interest.

5.2. Moore’s Paradox

George Edward Moore was, with Bertrand Russell, Ludwig Wittgenstein, and (before them) Gottlob Frege, one of the founders of analytic philosophy. Moore is also remembered for drawing attention to the peculiar inconsistency involved in uttering a sentence such as

(R₁) “It is raining, but I do not believe it is raining”,

a puzzle now commonly called “Moore’s paradox”. Recall that the claim of the linguistic Copenhagen interpretation (L₂) is

(R₂) Don’t carelessly use “I” in propositions

Therefore, this paradox is easily solved. In short, it is the same as the fact that “I think, therefore I am” is unintelligible in quantum language. For example a correct proposition should be written as follows.

(R₃) It is raining. But the audience inside the theater doesn’t know it’s raining outside.”

though it is different from (R₁).

However, the purpose here is not to examine this paradox in detail. What I have focused on is the following

(S) when Wittgenstein first heard this paradox one evening (which Moore had earlier stated in a lecture), he rushed round to Moore’s lodgings, got him out of bed and insisted that Moore repeat the entire lecture to him.

If this anecdote is true, it is because it clearly shows that the central theme of Wittgenstein’s research is “What is a scientific proposition?” And Wittgenstein must have thought: (R₁) is “what we cannot speak about”. Furthermore, he must have thought Descartes’ cogito proposition “I think, therefore I am” (which is called the first principle of philosophy) was not also a proposition (cf. Remark 11).

At that time, Russell, Moore, and McTaggart were professors in the Department of Philosophy at Cambridge University. Moore’s paradox, Russell’s “five-minute hypothesis,” and McTaggart’s “non-existence of time” (cf. ref. [25] ) were all based on the question such that “What is a scientific proposition?” (or equivalently “What is the Copenhagen interpretation?”). This was the environment in which analytic philosophy (or symbolically, “Wittgenstein”) was born.

Also, recall Russell’s paradox (i.e., if $V=\left\{U\mathrm{<mo>\; |\; </mo>}U\text{is}\text{set}\text{such}\text{that}U\notin U\right\}$ is assumed to be a set, a contradiction arises). This paradox (i.e., the discovery of something like a set but not a set) prompted the birth of axiomatic set theory (e.g., Zermelo-Fraenkel set theory), in which “mathematical proposition” can be completely defined. Similarly, the discovery of something like a proposition but not a proposition (e.g., “I think, therefore I am”, Moore’s paradox, etc.) prompted the development of the linguistic Copenhagen interpretation (which serves to distinguish between “scientific proposition” and “non-scientific proposition”).

5.3. Saussure’s Linguistics

Ferdinand de Saussure is widely considered one of the founders of 20th-century linguistics.

Now let us explain the terms “signifier” and “signified”, which were introduced by Saussure.

Definition 23. [“signifier” and “signified” in ordinary language]

For example, we explain “signifier” and “signified” concerning “dog”

(T₁) The “dog” in front of you is itself a physical being, isn’t it? The image of the dog you have in mind, the barking, or the image of the dog in your head, is “signified”.

(T₂) When this becomes a word (letter/sound) such as “dog”, it is called “signifie”.

Although Saussure’s proposal (i.e., the above definition) is very significant, his ideas are not quantitative, so they are not very useful from a scientific standpoint. As emphasized frequently throughout the paper, I consider

(U) Without a quantitative worldview, we can’t say anything solid from a scientific standpoint.

In fact, Saussure’s idea does not play an important role in science.

Thus, I will propose Definition 24, in which Saussure’s idea is realized in quantum language as follows.

Definition 24. [Membership function (= Fuzzy set, cf. ref. [1] )] Let $\Omega$ be a state space. A continuous function $m\mathrm{<mo>\; :\; </mo>}\Omega \to \left[\mathrm{0,1}\right]$ ( $=\left\{\theta \mathrm{<mo>\; |\; </mo>0}\le \theta \le 1\right\}$ ) is called a membership function. Assume that the state (i.e., quantitative property) of any animal can be expressed by a point in the state space $\Omega$. Define the membership functions $m_D\mathrm{<mo>\; :\; </mo>}\Omega \to \left[\mathrm{0,1}\right]$ of dogs as follows. Suppose that there are 100 zoologists and the following question is made them.

(V) Is this animal with the sate ${\omega }_1\left(\in \Omega \right)$ a dog or not?

The answer is as follows.

(W) $(\begin{array}{l}\text{70zoologistssaythatthisbirdisadog}\\ \text{30zoologistssaythatthisanimalisnotadog}\end{array}$

Then the value of $m_D\left({\omega }_1\right)$ is defined by 0.7. This can be probabilistically interpreted as in (C) before. For many animals with the state ${\omega }_i\left(i=2,3,\cdots ,N\right)$, repeating the experiment in the same way, the value of $m_D\left({\omega }_i\right)\left(i=2,3,\cdots ,N\right)$ is determined. And the membership function $m_D\mathrm{<mo>\; :\; </mo>}\Omega \to \left[\mathrm{0,1}\right]$ of dogs is defined by the interpolation method (which may be rather subjective).

Thus we have the dog-like observable ${\text{O}}_{\text{D}}=\left(\left\{T\mathrm{,}F\right\}{\mathrm{,2}}^{\left\{T\mathrm{,}F\right\}}\mathrm{,}{G}_{\text{D}}\right)$ in $C\left(\Omega \right)$ with the membership function $G_{\text{D}}\left(\left\{T\right\}\right)$ $\left(=m_{\text{D}}\right)$ (cf. Definition 14).

With the above preparation, Saussure proposed the following definitions.

Definition 25. [“signifier” and “signified” in quantum language]

(X₁) “signifier”-----“dog”

(X₂) “signified”-----membership function $m_D\mathrm{<mo>\; :\; </mo>}\Omega \to \left[\mathrm{0,1}\right]$

Thus, I think that Zadeh’s fuzzy theory is quantitative representation of Saussure’s linguistics.

5.4. Quine’s Analytic-Synthetic Distinction in QL; What Is a (Non-Mathematical) Proposition?

In ref. [30], Willard Van Orman Quine published the essay “Two Dogmas of Empiricism” in which he argued that the analytic-synthetic distinction is untenable. The argument at bottom is that there are no “analytic” truths, but all truths involve an empirical aspect. The question of “analytic vs. synthetic” is one of the most important philosophical questions since Kant. Many philosophers have entered the fray on this issue, but all of them argued without a “definition of proposition”. Since QL has the definition of proposition, we can easily solve it. That is, since “proposition in QL” = “(TF)-measurement (=experimental verification)”, we can naturally conclude that all propositions are synthetic in QL. Of course, different worldviews can have different ideas, and our proposal is not the only correct one. I hope that many readers will make various proposals. I think that philosophers of analytic philosophy should argue the problem after presenting a worldview. I think that logic without a worldview is just a substream of mathematical logic.

5.5. Lewis Carroll’s Logical Paradox in Fuzzy Logic

In ref. [31] “What the Tortoise said to Achilles” (1895), Lewis Carroll raised the following question.

· Is logic logical?

According to [31], let us explain it as follows.

Achilles says: “Can you understand the following modus ponens?”

Premise : $\left(P_1\to P_2\right)$

Premise : $P_1$

Conclusion: $P_2$

the Tortoise says: “I can understand and . However, why do and imply ?”

Achilles says: “I see, then, the following OK?”

Premise : $\left(P_1\to P_2\right)$

Premise : $P_1$

Premise : and are “true”, therefore is “true”

Conclusion: $P_2$

the Tortoise says: “I can understand Premises , and . However, why do , and conclude ?”

Achilles says: “I see, then, the following OK?”

Premise : $\left(P_1\to P_2\right)$

Premise : $P_1$

Premise : and are “true”, therefore is “true”

Premise d: , and are “true”, therefore is “true”

Conclusion: $P_2$

the Tortoise says: “I can understand Premises , , and . However, why do , , and conclude ?”

:(Infinite regress)

This is Lewis Carroll’s Paradox

Several philosophers have tried to resolve Carroll’s paradox. For example, Bertrand Russell discussed the paradox briefly in ref. [32]. His opinion is as follows.

(Y₁) The above , and are propositions, on the other hand, and are inference rules. And, therefore, both the Tortoise and Achilles are confusing this.

I agree to his opinion. I think that their confusion is due to the lack of a definition of proposition. Note that QL says that

(Y₂) “proposition P” = “(TF)-measurement ${\text{M}}_{\mathcal{A}}\left(\text{O}\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)$ ”. And the essence of the modus ponens is all described in Table 12 (=Table 11). Therefore, logic is a simple calculation of elementary arithmetic.

Maybe the Tortoise thought of logic as a noble discipline and tried to understand it rigorously. However, all we have to do is only what is written in the table above. Note that the above c and d are not written in this table.

Rather, in the case of mathematics, the definition of “proposition” is so clear that I think it is rare for mathematicians to take Carroll’s logical paradox seriously. Since the definition of a proposition is not clear in the case of philosophy, we tend to confuse propositions with inference rules. We know the definition of a proposition so clearly that we could avoid any confusion. Of course, the quantum mechanical worldview is not the only worldview. Thus, if you want to tackle this problem head-on, you would challenge the problem “Propose a certain

Table 12. Probabilistic Truth Table (Elementary propositions ${\text{M}}_{\mathcal{A}}\left({\text{O}}_1\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\left(=P_1\right)$, ${\text{M}}_{\mathcal{A}}\left({\text{O}}_2\mathrm{,}{S}_{\mathrm{<mo\; stretchy="false">\; [\; </mo>}\rho \mathrm{<mo\; stretchy="false">\; ]\; </mo>}}\right)\left(=P_2\right)$ ).

worldview and define propositions under it”.

I don’t know Carroll’s own intentions, but I think the reason this paradox has been of interest to people for over 100 years is that it is closely related to the question “what is a scientific proposition?”

6. Conclusions

Logic consists of “propositions” and “logical symbols”. In the case of mathematical logic, “propositions” can be regarded as mathematical propositions, so there is no confusion since we have the axiomatic set theory. On the other hand, in non-mathematical fields, we are always bothered by the definition of “proposition”. For example, we are bothered by Descartes’ cogito proposition and Moore’s paradox, etc. Also, it is clear that Quine’s analytic-synthetic distinction cannot be solved without the definition of propositions.

In this paper, we proposed a definition of proposition in quantum language and showed how to calculate its logic. That is, propositions are characterized as a kind of measurements (i.e., binary measurement). Also it should be noted that “fuzzy proposition” is more natural than “crisp proposition” in quantum languages. And further I believe that our result implies the justification of Zadeh’s fuzzy sets theory.

Recall the final chapter of Wittgenstein’s TLP, in which only “What we cannot speak about we must pass over in silence” is written. This implies that Wittgenstein’s central theme in his TLP is to draw a line between what we can speak about (=scientific propositions) and what we cannot speak about (=non-scientific propositions), which is the same as the theme of this paper (i.e., the linguistic Copenhagen interpretation). Therefore, our result can be regarded as the simultaneous justification of both Wittgenstein’ s TPL (cf. ref. [11] ) and Zadeh’s fuzzy sets (cf. ref. [1] ).

I hope the readers will examine my proposal from various perspectives.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Zadeh, L.A. (1965) Fuzzy Sets. Information and Control, 8, 338-353. https://doi.org/10.1016/S0019-9958(65)90241-X
[2]	Zadeh, L.A. (2004) Fuzzy Logic Systems: Origin, Concepts and Trends. https://wi-consortium.org/wicweb/pdf/Zadeh.pdf
[3]	Ishikawa, S. (2006) Mathematical Foundations of Measurement Theory. Keio University Press Inc., Tokyo, 335 p. http://www.keio-up.co.jp/kup/mfomt
[4]	Ishikawa, S. (2019) Linguistic Copenhagen Interpretation of Quantum Mechanics: Quantum Language [Ver. 5]. KSTS/RR-19/003, Research Report, Department of Mathematics, Keio University, Yokohama, 473 p. http://www.math.keio.ac.jp/academic/research_pdf/report/2019/19003.pdf
[5]	Ishikawa, S. (2020) History of Western Philosophy from the Quantum Theoretical Point of View [Ver. 3]. KSTS-RR-20/001, Research Report, Department of Mathematics, Keio University, Yokohama, 296 p. http://www.math.keio.ac.jp/academic/research_pdf/report/2020/20001.pdf
[6]	Ishikawa, S. (2012) Quantum Mechanics and the Philosophy of Language: Reconsideration of Traditional Philosophies. Journal of Quantum Information Science, 2, 2-9. http://www.scirp.org/journal/PaperInformation.aspx?paperID=18194 https://doi.org/10.4236/jqis.2012.21002
[7]	Ishikawa, S. (1997) Fuzzy Inferences by Algebraic Method. Fuzzy Sets and Systems, 87, 181-200. https://doi.org/10.1016/S0165-0114(96)00035-8
[8]	Ishikawa, S. (1997) A Quantum Mechanical Approach to Fuzzy Theory. Fuzzy Sets and Systems, 90, 277-306. https://doi.org/10.1016/S0165-0114(96)00114-5
[9]	Ishikawa, S. (1998) Fuzzy Logic in Measurements. Fuzzy Sets and Systems, 100, 291-300. https://www.sciencedirect.com/science/article/abs/pii/S0165011497001541 https://doi.org/10.1016/S0165-0114(97)00154-1
[10]	Ishikawa, S. (2020) Wittgenstein’s Picture Theory in the Quantum Mechanical Worldview. Journal of Quantum Information Science, 10, 104-125. https://www.scirp.org/journal/paperinformation.aspx?paperid=106233 https://doi.org/10.4236/jqis.2020.104007
[11]	Wittgenstein, L. (1921) Tractatus Logico Philosophicus. Routledge and Kegan Paul, Oxford.
[12]	Ishikawa, S. (2011) A New Interpretation of Quantum Mechanics. Journal of Quantum Information Science, 1, 35-42. https://doi.org/10.4236/jqis.2011.12005 http://www.scirp.org/journal/PaperInformation.aspx?paperID=7610
[13]	von Neumann, J. (1932) Mathematical Foundations of Quantum Mechanics. Springer Verlag, Berlin.
[14]	Sakai, S. (1971) C*-Algebras and W*-Algebras, Ergebnisse der Mathematik und ihrer Grenzgebiete (Band 60). Springer-Verlag, Berlin.
[15]	Yosida, K. (1980) Functional Analysis. Sixth Edition, Springer-Verlag, Berlin.
[16]	Davies, E.B. (1976) Quantum Theory of Open Systems. Academic Press, Cambridge.
[17]	Holevo, A.S. (1982) Probabilistic and Statistical Aspects of Quantum Theory. North-Holland Publishing Company, Amsterdam.
[18]	Howard, D. (2004) Who Invented the Copenhagen Interpretation? A Study in Mythology. Philosophy of Science, 71, 669-682. https://doi.org/10.1086/425941
[19]	Ishikawa, S. (1991) Uncertainty Relation in Simultaneous Measurements for Arbitrary Observables. Reports on Mathematical Physics, 9, 257-273. https://doi.org/10.1016/0034-4877(91)90046-P
[20]	Ishikawa, S. (2015) Linguistic Interpretation of Quantum Mechanics: Projection Postulate. Journal of Quantum Information Science, 5, 150-155. http://www.scirp.org/Journal/PaperInformation.aspx?PaperID=62464 https://doi.org/10.4236/jqis.2015.54017
[21]	Ishikawa, S. (2000) Statistics in Measurements. Fuzzy Sets and Systems, 116, 141-154. https://doi.org/10.1016/S0165-0114(98)00280-2
[22]	Ishikawa, S. (2012) A Measurement Theoretical Foundation of Statistics. Applied Mathematics, 3, 283-292. https://doi.org/10.4236/am.2012.33044 http://www.scirp.org/journal/PaperInformation.aspx?paperID=18109
[23]	Ishikawa, S. (2012) Monty Hall Problem and the Principle of Equal Probability in Measurement Theory. Applied Mathematics, 3, 788-794. http://www.scirp.org/journal/PaperInformation.aspx?PaperID=19884 https://doi.org/10.4236/am.2012.37117
[24]	Ishikawa, S. (2012) Ergodic Hypothesis and Equilibrium Statistical Mechanics in the Quantum Mechanical World View. World Journal of Mechanics, 2, 125-130. https://www.scirp.org/journal/paperinformation.aspx?paperid=18861 https://doi.org/10.4236/wjm.2012.22014
[25]	Ishikawa, S. (2018) Leibniz-Clarke Correspondence, Brain in a Vat, Five-Minute Hypothesis, McTaggart’s Paradox, etc. Are Clarified in Quantum Language. Open Journal of Philosophy, 8, 466-480. https://doi.org/10.4236/ojpp.2018.85032 https://www.scirp.org/Journal/PaperInformation.aspx?PaperID=87862
[26]	Ishikawa, S. (2017) A Final Solution to Mind-Body Problem by Quantum Language. Journal of Quantum Information Science, 7, 48-56. http://www.scirp.org/Journal/PaperInformation.aspx?PaperID=76391 https://doi.org/10.4236/jqis.2017.72005
[27]	Ishikawa, S. (2019) Philosophy of Science for Scientists: The Probabilistic Interpretation of Science. Journal of Quantum Information Science, 9, 140-154. https://www.scirp.org/Journal/paperinformation.aspx?paperid=95447 https://doi.org/10.4236/jqis.2019.93007
[28]	Conant, J. and Diamond, C. (2004) On Reading the Tractatus Resolutely: To Meredith Williams and Peter Sullivan. In: K?lbel, M. and Weiss, B., Eds., The Lasting Significance of Wittgenstein’s Philosophy, Routledge, London.
[29]	Kremer, M. (2001) The Purpose of Tractarian Nonsense, Noûs, 35, 39-73. https://doi.org/10.1111/0029-4624.00287
[30]	Quine, W.O. (1951) Two Dogmas of Empiricism. Harvard University Press, Cambridge.
[31]	Carroll, L. (1895) What the Tortoise Said to Achilles. Mind, 4, 278-280. https://doi.org/10.1093/mind/IV.14.278
[32]	Russell, B. (1937) The Principles of Mathematics. 2nd Edition, George Allen and Unwin Ltd., London.