Asymptotic Behaviors Analysis of the Spatial AK Model with Trade Costs

Hanlei Hu

Southwest Jiaotong University, Chengdu, China.

DOI: 10.4236/tel.[phone]                

Abstract

We consider a spatial economic growth model with trade costs whose spatial-temporal dynamics of the capital stock are governed by a parabolic partial differential equation and analyze the effects of the trade costs on the asymptotic behaviors of the capital in the framework of spatial AK model, where the technology is time-varying. Taking advantage of the good properties of the Green function, we formulate an explicit solution to the auxiliary partial differential equation of the original problem and derive the sufficient conditions on the consumption function that guarantee the existence and the uniqueness of the solution and obtain the convergence properties of the capital in the long run for the spatial AK model with trade costs.

Keywords

Spatial AK Model, Trade Costs, Asymptotic Behaviors

1. Introduction

Models of optimal development dealing jointly with time and space, which are regarded as a suitable vehicle for studying economic growth in a geographical context, were proposed in the seventies in (Isard & Liossatos, 1979). The dynamic spatial economic theory that incorporates space into the dynamic analysis of economic growth is developed in recent years. (Zou & Camacho, 2004) present a spatial extension of the Solow model in which the evolution of capital is governed by a parabolic partial differential equation and prove the existence and convergence of the solution to the equation. (Brito, 2004) extends the traditional neoclassical growth theory to a spatial growth theory which would provide models incapable of approximating spatial heterogeneity across regions and studies the asymptotic distribution and the local stability properties of the solution of the corresponding optimal control problem. (Camacho et al., 2008) develop a numerical algorithm to study the dynamics of capital accumulation across space. (Boucekkine et al., 2009) discuss the spatial Ramsey model with the linear utility case, which reconciles growth and geographical economics. (Boucekkine et al., 2013) formulate and analyze an optimal control problem for an AK model with spatial variations by using the dynamic programming approach, and prove that spatio-temporal dynamics lead to the convergence of time-detrended capital stocks across space in the long run. (Juchem Neto & Claeyssen, 2015) present stability analyses and numerical simulations on the spatial Solow model with capital-induced labor migration. (Fabbri, 2016) investigates the role of geography in the evolution of the spatial growth model with a general geographical structure modeled in Riemannian manifold and gives the conditions that guarantee convergence of the detrended capital across locations in the long run. (Ballestra, 2016) shows that the Pontryagin maximum principle is capable of analyzing the spatial AK model under a Michel-type transversality condition. (Aldashev et al., 2014) propose a complementary approach to analyze the asymptotic convergence of the spatial AK model, which possesses the time-varying technology parameter. More literature on spatial dynamics is referred to a survey by (Desmet & Rossi-Hansberg, 2010).

Factor mobility and transport costs are two key ingredients that set apart the new economic geography from the traditional trade theory. The implications of factor mobility for trade and the spatial structure of the economy have been analyzed in (Brito, 2004; Boucekkine et al., 2009; Boucekkine et al., 2013). However, many researchers assume that perfect mobile holds. The transport costs or other potential trade barriers, which are related to spatial heterogeneities, have always been neglected. The simplifying assumptions on trade costs in models of new economic geography causing serious consequences for the regional specialization and economic activity agglomeration are shown in (Behrens & Picard, 2011).

Inspired by the work in (Juchem Neto et al., 2018), which introduces transport costs into the spatial Solow model and discusses the effects on the dynamic behavior, we consider an extension of the spatial AK model presented in (Boucekkine et al., 2013). The mobile frictions like the transport costs or trade barriers on the mobility of the capital are added in our model, which is different from that in (Boucekkine et al., 2013). Another difference is that the technology is assumed to depend on time t. Due to the heterogeneity of the geographic distribution of capital, the time-space connection is modeled by assuming that the capital flows in the opposite direction of the gradient of the capital distribution across space, which derives that the spatio-temporal evolution of capital is expressed by a parabolic partial differential equation. The purpose of the paper is to find a non-negative classical solution of the partial differential equation that describes the dynamic of capital stock. Through formulating the explicit solution to an auxiliary parabolic partial differential equation by the approach in (Aldashev et al., 2014), we derive the sufficient conditions on the consumption function that guarantee the uniqueness and non-negativity of the solution and obtain the convergence properties of the capital in the long run for the spatial AK model with trade costs.

The rest of the paper is organized as follows. Section 2 introduces the spatial AK model with trade costs. Section 3 develops our analytical results. Section 4 concludes and gives perspectives for future research.

2. The Model

Following the works of (Boucekkine et al., 2013), we assume that the population is non-growing and spatially homogeneous distributed on unit circle $\mathbb{T}=\left[\mathrm{0,2}\pi \right]$ , where $\mathbb{T}$ is the set of spatial parameters $\theta$ under polar coordinates. Capital stock moves from locations of high concentration to locations of low concentration, which is consistent with diminishing returns to capital since the high concentration implies low marginal productivity. According to the literatures (Brito, 2004), the spatial movements of the stock of capital across locations are modeled through a trade balance approach.

At a given point $\left(\theta \mathrm{,}t\right)\in \mathbb{T}\times \left[\mathrm{0,}+\infty \right)$ , physical capital $k\left(\theta \mathrm{,}t\right)$ evolves according to

$\frac{\partial k\left(\theta \mathrm{,}t\right)}{\partial t}=y\left(\theta \mathrm{,}t\right)-c\left(\theta \mathrm{,}t\right)-\nu \left(\theta \mathrm{,}t\right)$ (1)

with initial distribution of capital stock $k\left(\theta \mathrm{,0}\right)=k_0\left(\theta \right)$ . We assume that the production function $y\left(\theta \mathrm{,}t\right)=A\left(t\right)k\left(\theta \mathrm{,}t\right)$ , where $A\left(t\right)$ represents the technology level at time t, $c\left(\theta \mathrm{,}t\right)$ and $\nu \left(\theta \mathrm{,}t\right)$ denote consumption and net trade balance at $\left(\theta \mathrm{,}t\right)$ , respectively. Capital depreciation is omitted. We assume that capital flows from regions with lower marginal productivity of capital towards the higher ones and there exist trade costs like trade barriers, transport costs or some other frictional costs.

The trade balance $\nu \left(\theta \mathrm{,}t\right)$ for region ${\Theta }_i,i=1,2,\cdots ,n$ is described as

${\displaystyle {\int }_{{\Theta }_i}}\nu \left(\theta ,t\right)\text{d}\theta =-\left[\frac{\partial k\left({\theta }_i+\Delta {\theta }_i,t\right)}{\partial \theta }-\frac{\partial k\left({\theta }_i,t\right)}{\partial \theta }\right]-bk\left(\theta ,t\right),$ (2)

where constant b is the barrier measure of capital $k\left(\theta \mathrm{,}t\right)$ . Using the fundamental theorem of calculus yields

$\frac{\partial k\left({\theta }_i+\Delta {\theta }_i,t\right)}{\partial \theta }-\frac{\partial k\left({\theta }_i,t\right)}{\partial \theta }={\displaystyle {\int }_{{\theta }_i}^{{\theta }_i+\Delta {\theta }_i}}\frac{\partial }{\partial \theta }\frac{\partial k\left(\theta ,t\right)}{\partial \theta }\text{d}\theta ={\displaystyle {\int }_{{\Theta }_i}}\frac{{\partial }^{2}k\left(\theta ,t\right)}{\partial {\theta }^2}\text{d}\theta .$ (3)

Thus, the trade balance (2) is written in the form

${\displaystyle {\int }_{{\Theta }_i}}\nu \left(\theta ,t\right)\text{d}\theta =-{\displaystyle {\int }_{{\Theta }_i}}\frac{\partial k^2\left(\theta ,t\right)}{\partial {\theta }^2}\text{d}\theta -bk\left(\theta ,t\right),$ (4)

which implies

$\nu \left(\theta ,t\right)=-\frac{\partial k^2\left(\theta ,t\right)}{\partial {\theta }^2}-b\frac{\partial k\left(\theta ,t\right)}{\partial \theta }.$ (5)

Substituting $y\left(\theta \mathrm{,}t\right)\mathrm{,}\nu \left(\theta \mathrm{,}t\right)$ into Equation (1), the budget constraint is represented by the partial differential equation

$\frac{\partial k\left(\theta \mathrm{,}t\right)}{\partial t}=A\left(t\right)k\left(\theta \mathrm{,}t\right)-c\left(\theta \mathrm{,}t\right)+\frac{\partial k^2\left(\theta \mathrm{,}t\right)}{\partial {\theta }^2}+b\frac{\partial k\left(\theta \mathrm{,}t\right)}{\partial \theta }$ (6)

with initial value condition $k\left(\theta \mathrm{,0}\right)=k_0\left(\theta \right)$ . The term $\frac{{\partial }^{2}k\left(\theta \mathrm{,}t\right)}{\partial {\theta }^2}+b\frac{\partial k\left(\theta \mathrm{,}t\right)}{\partial \theta }$ captures capital mobility across space and $b\frac{\partial k\left(\theta \mathrm{,}t\right)}{\partial \theta }$ represents trade costs,

which is different from the spatial growth model proposed in (Boucekkine et al., 2013). Note that the difference arises from the fact that our capital mobility assumption is associated with trade costs.

The problem of optimal growth in dynamic spatial economy is that the social planner maximizes a certain objective function $J\left(k_0\mathrm{,}c\left(\theta \mathrm{,}t\right)\right)$ by choosing consumption $c\left(\theta \mathrm{,}t\right)$ , subject to the instantaneous budget constraint Equation (6) with the initial value condition $k\left(\theta \mathrm{,0}\right)=k_0\left(\theta \right)$ . It is clear that the value of the capital stock $k\left(\theta \mathrm{,}t\right)$ is non-negative for any $\left(\theta \mathrm{,}t\right)$ . We study the economic growth model by the method in (Aldashev et al., 2014). The corresponding mathematical problem reads as follows.

Find a non-negative classical solution, namely a continuous function in the domain $\Omega =\mathbb{T}\times \left[0,\infty \right)$ , of the linear parabolic partial differential equation

$(\begin{array}{l}\frac{\partial k\left(\theta ,t\right)}{\partial t}=\frac{\partial k^2\left(\theta ,t\right)}{\partial {\theta }^2}+b\frac{\partial k\left(\theta ,t\right)}{\partial \theta }+A\left(t\right)k\left(\theta ,t\right)-c\left(\theta ,t\right),\\ k\left(\theta ,0\right)=k_0\left(\theta \right).\end{array}$ (7)

3. Main Results

This section aims to derive the explicit representations of the solution to the problem (7) under certain assumptions on consumption $c\left(\theta \mathrm{,}t\right)$ and study the asymptotic behavior of the stock of capital. Assuming that the consumption function $c\left(\theta \mathrm{,}t\right)$ is smooth, bounded, concave with respect to the spatial variable for any time, we have the following result.

Theorem 1. Let $\Omega =\mathbb{T}\times \left[0,\infty \right)$ . Assume that the consumption function and initial capital distribution satisfy

$\frac{b^2}{4}c\left(\theta \mathrm{,}t\right)-b{c}_{\theta }\left(\theta \mathrm{,}t\right)+c_{\theta \theta }\left(\theta \mathrm{,}t\right)\le \mathrm{0,}\forall \left(\theta \mathrm{,}t\right)\in \Omega$ (8)

and

$k_0\left(\theta \right)\ge {\displaystyle {\int }_0^t}{\text{e}}^{-{\displaystyle {\int }_0^s}\left(A\left(\tau \right)-\frac{b^2}{4}\right)\text{d}\tau }c\left(\theta \mathrm{,}s\right)\text{d}s\mathrm{,}$ (9)

respectively. The problem (7) admits a unique non-negative classical solution in $\Omega$ .

3.1. Proof of Theorem 1

Before solving the problem (7), we consider an auxiliary problem in the following Lemma.

Lemma 2. Let $h\left(\theta \mathrm{,}t\right)$ be a positive function defined in $\Omega$ , and $h\left(\theta \mathrm{,}t\right)=u^{-1}\left(\theta \right)k\left(\theta \mathrm{,}t\right)$ . Then the equation

$\frac{\partial h\left(\theta ,t\right)}{\partial t}=\frac{{\partial }^{2}h\left(\theta ,t\right)}{\partial {\theta }^2}+\left(A\left(t\right)-\frac{b^2}{4}\right)h\left(\theta ,t\right)-\hat{c}\left(\theta ,t\right)$ (10)

with initial condition $h\left(\theta ,0\right)=h_0\left(\theta \right)=u^{-1}\left(\theta \right)k_0\left(\theta \right)$ , where $u\left(\theta \right)=\exp \left\{-\frac{b\theta }{2}\right\}$ , $\hat{c}\left(\theta \mathrm{,}t\right)=u^{-1}\left(\theta \right)c\left(\theta \mathrm{,}t\right)$ , is equivalent to system (7).

Proof. For all $\left(\theta \mathrm{,}t\right)\in \Omega$ , since $k\left(\theta \mathrm{,}t\right)=h\left(\theta \mathrm{,}t\right)u\left(\theta \right)$ and $u\left(\theta \right)=\exp \left\{-\frac{b}{2}\theta \right\}$ , we obtain

$\frac{\partial k\left(\theta \mathrm{,}t\right)}{\partial t}=\frac{\partial h\left(\theta \mathrm{,}t\right)}{\partial t}u\left(\theta \right),\frac{\partial k\left(\theta \mathrm{,}t\right)}{\partial \theta }=\frac{\partial h\left(\theta \mathrm{,}t\right)}{\partial \theta }u\left(\theta \right)-\frac{b}{2}h\left(\theta \mathrm{,}t\right)u\left(\theta \right)$ (11)

and

$\begin{array}{l}\frac{\partial k^2\left(\theta \mathrm{,}t\right)}{\partial {\theta }^2}+b\frac{\partial k\left(\theta \mathrm{,}t\right)}{\partial \theta }+A\left(t\right)k\left(\theta \mathrm{,}t\right)\\ =u\left(\theta \right)\left[\frac{\partial h^2\left(\theta \mathrm{,}t\right)}{\partial {\theta }^2}+\left(A\left(t\right)-\frac{b^2}{4}\right)h\left(\theta \mathrm{,}t\right)\right]\mathrm{.}\end{array}$ (12)

Substituting Equations (11) and (12) into Equation (7) and dividing by $u\left(\theta \right)$ yield

$\frac{\partial h\left(\theta ,t\right)}{\partial t}=\frac{{\partial }^{2}h\left(\theta ,t\right)}{\partial {\theta }^2}+\left(A\left(t\right)-\frac{b^2}{4}\right)h\left(\theta ,t\right)-\hat{c}\left(\theta ,t\right),$ (13)

where $\hat{c}\left(t\mathrm{,}\theta \right)=u^{-1}\left(\theta \right)c\left(\theta \mathrm{,}t\right)$ .

Recalling that $k\left(\theta \mathrm{,0}\right)=k_0\left(\theta \right)$ , it is easy to verify that $h\left(\theta \mathrm{,0}\right)=u^{-1}\left(\theta \right)k_0\left(\theta \right)$ . Thus, system (10) is equivalent to system (7).

Noting that if we choose $b=0$ , there will be no trade costs in the economy. In this case, the auxiliary problem is exactly the system considered in (Aldashev et al., 2014). We intend to remove the term $A\left(t\right)h\left(\theta \mathrm{,}t\right)$ in Equation (10) by using the following Lemma.

Lemma 3. Let $g\left(\theta \mathrm{,}t\right)$ be a positive function defined in $\Omega$ , which is related to $h\left(\theta \mathrm{,}t\right)$ by

$g\left(\theta \mathrm{,}t\right)=\exp \left\{-{\displaystyle {\int }_0^t}\left(A\left(s\right)-\frac{b^2}{4}\right)\text{d}s\right\}h\left(\theta \mathrm{,}t\right)\mathrm{.}$ (14)

Then $h\left(\theta \mathrm{,}t\right)$ is a solution of Equation (10) if and only if $g\left(\theta \mathrm{,}t\right)$ is a solution of

$\frac{\partial g\left(\theta ,t\right)}{\partial t}=\frac{{\partial }^{2}g\left(\theta ,t\right)}{\partial {\theta }^2}-\zeta \left(\theta ,t\right),\forall \left(\theta ,t\right)\in \Omega ,$ (15)

with initial condition $g\left(\theta \mathrm{,0}\right)=h_0\left(\theta \right)$ , where

$\zeta \left(\theta \mathrm{,}t\right)=\exp \left\{-{\displaystyle {\int }_0^t}\left(A\left(s\right)-\frac{b^2}{4}\right)\text{d}s+\frac{b\theta }{2}\right\}c\left(\theta \mathrm{,}t\right)\mathrm{.}$ (16)

Proof. By direct computation, we have

$\frac{{\partial }^{2}g\left(\theta \mathrm{,}t\right)}{\partial {\theta }^2}=\exp \left\{-{\displaystyle {\int }_0^t}\left(A\left(s\right)-\frac{b^2}{4}\right)\text{d}s\right\}\frac{{\partial }^{2}h\left(\theta \mathrm{,}t\right)}{\partial {\theta }^2}\mathrm{.}$ (17)

Combining with Equation (10) yields

$\begin{array}{c}\frac{\partial g\left(\theta \mathrm{,}t\right)}{\partial t}={\text{e}}^{-{\displaystyle {\int }_0^t}\left(A\left(s\right)-\frac{b^2}{4}\right)\text{d}s}\frac{\partial h\left(\theta ,t\right)}{\partial t}-\left(A\left(t\right)-\frac{b^2}{4}\right){\text{e}}^{-{\displaystyle {\int }_0^t}\left(A\left(s\right)-\frac{b^2}{4}\right)\text{d}s}h\left(\theta \mathrm{,}t\right)\\ =\exp \left\{-{\displaystyle {\int }_0^t}\left(A\left(s\right)-\frac{b^2}{4}\right)\text{d}s\right\}[\frac{{\partial }^{2}h\left(\theta ,t\right)}{\partial {\theta }^2}+\left(A\left(t\right)-\frac{b^2}{4}\right)h\left(\theta \mathrm{,}t\right)\\ -u^{-1}\left(\theta \right)c\left(\theta \mathrm{,}t\right)-\left(A\left(t\right)-\frac{b^2}{4}\right)h\left(\theta \mathrm{,}t\right)]\\ =\frac{{\partial }^{2}g\left(\theta \mathrm{,}t\right)}{\partial {\theta }^2}-\exp \left\{-{\displaystyle {\int }_0^t}\left(A\left(s\right)-\frac{b^2}{4}\right)\text{d}s+\frac{b\theta }{2}\right\}c\left(\theta \mathrm{,}t\right)\\ =\frac{{\partial }^{2}g\left(\theta \mathrm{,}t\right)}{\partial {\theta }^2}-\zeta \left(\theta ,t\right),\end{array}$ (18)

which implies that Equation (15) holds.

Proposition 4. For any positive integer n, define the Green function

$G\left(\theta ,\xi ,t\right)={\displaystyle \underset{n\ge 0}{\sum }}{\text{e}}^{-{\lambda }_{n}t}\cos \left[n\left(\theta -\xi \right)\right],\forall \left(\theta ,\xi ,t\right)\in \mathbb{T}\times \mathbb{T}\times \left[0,+\infty \right),$ (19)

where ${\lambda }_n=n^2$ , then $g\left(\theta \mathrm{,}t\right)$ is given by

$g\left(\theta ,t\right)=\frac{1}{\pi }{\displaystyle {\int }_0^{2\pi }}G\left(\theta ,\xi ,t\right)g_0\left(\xi \right)\text{d}\xi -\frac{1}{\pi }{\displaystyle {\int }_0^t}\text{d}\tau {\displaystyle {\int }_0^{2\pi }}G\left(\theta ,\xi ,t-\tau \right)\zeta \left(\xi ,\tau \right)\text{d}\xi ,$ (20)

which is a formal solution of Equation (15).

Proof. Observing that the Green function $G\left(\theta \mathrm{,}\xi \mathrm{,}t\right)$ satisfies the following homogeneous partial differential equation

$\frac{\partial G\left(\theta \mathrm{,}\xi \mathrm{,}t\right)}{\partial t}-\frac{{\partial }^{2}G\left(\theta \mathrm{,}\xi \mathrm{,}t\right)}{\partial {\theta }^2}=\mathrm{0,}\left(\theta \mathrm{,}\xi \mathrm{,}t\right)\in \mathbb{T}\times \Omega \mathrm{,}$ (21)

and

$\underset{t\to 0}{lim}G\left(\theta \mathrm{,}\xi \mathrm{,}t\right)=\delta \left(\theta -\xi \right)\mathrm{,}$ (22)

where $\delta \left(x\right)$ is the Dirac delta function, which is a generalized function, satisfying ${\displaystyle \int \delta \left(x\right)\text{d}x}=1$ .

Substituting $g\left(\theta \mathrm{,}t\right)$ given by Equation (20) into Equation (15) and exchanging the derivatives with the integrals yield

$\begin{array}{c}\frac{\partial g\left(\theta \mathrm{,}t\right)}{\partial t}-\frac{{\partial }^{2}g\left(\theta \mathrm{,}t\right)}{\partial {\theta }^2}=\frac{1}{\pi }{\displaystyle {\int }_0^{2\pi }}\left[\frac{\partial G\left(\theta ,\xi ,t\right)}{\partial t}-\frac{{\partial }^{2}G\left(\theta ,\xi ,t\right)}{\partial {\theta }^2}\right]g_0\left(\xi \right)\text{d}\xi \\ -\frac{1}{\pi }{\displaystyle {\int }_0^t}\text{d}\tau {\displaystyle {\int }_0^{2\pi }}\left[\frac{\partial G\left(\theta ,\xi ,t-\tau \right)}{\partial t}-\frac{{\partial }^{2}G\left(\theta ,\xi ,t-\tau \right)}{\partial {\theta }^2}\right]\zeta \left(\xi ,\tau \right)\text{d}\xi \\ -\frac{1}{\pi }{\displaystyle {\int }_0^{2\pi }}\underset{t\to \tau }{lim}G\left(\theta ,\xi ,t-\tau \right)\zeta \left(\xi ,\tau \right)\text{d}\xi .\end{array}$ (23)

Recalling Equation (21), the first two terms on the right-hand side of Equation (23) vanish and the remaining term reduces to $-\zeta \left(\theta \mathrm{,}t\right)$ . Thus, $g\left(\theta \mathrm{,}t\right)$ that solves Equation (15) is verified.

Proposition 5. The function $g\left(\theta \mathrm{,}t\right)$ formulated in Equation (20) is a unique, classical solution of Equation (15) with the initial condition $g\left(\theta \mathrm{,0}\right)=h_0\left(\theta \right)$ .

Proof. The Green function defined by Equation (19) could be rewritten in the form

$G\left(\theta ,\xi ,t\right)=1+{\displaystyle \underset{n\ge 1}{\sum }}{\text{e}}^{-{\lambda }_{n}t}\cos \left[n\left(\theta -\xi \right)\right].$ (24)

Observing that

$\left|{\text{e}}^{-{\lambda }_{n}t}\cos \left[n\left(\theta -\xi \right)\right]\right|\le {\text{e}}^{-{\lambda }_{n}t}={\text{e}}^{-n^{2}t}\mathrm{,}\forall \left(\theta \mathrm{,}\xi \mathrm{,}t\right)\in \mathbb{T}\times \Omega \mathrm{,}$ (25)

we derive

${\displaystyle \underset{n\ge 1}{\sum }}{\text{e}}^{-{\lambda }_{n}t}\cos \left[n\left(\theta -\xi \right)\right]\le {\text{e}}^{-t}{\displaystyle \underset{m\ge 0}{\sum }}{\text{e}}^{-2mt}=\frac{{\text{e}}^{-t}}{1-{\text{e}}^{-2t}},$ (26)

which implies the norm convergence and the smoothness of the Green function $G\left(\theta \mathrm{,}\xi \mathrm{,}t\right)$ , as well as $g\left(\theta \mathrm{,}t\right)$ .

Suppose that $g_1\left(\theta \mathrm{,}t\right)$ and $g_2\left(\theta \mathrm{,}t\right)$ are two different classical solutions of the Equation (15). Set $f\left(\theta ,t\right)=g_1\left(\theta ,t\right)-g_2\left(\theta ,t\right)$ , which solves the homogeneous partial differential equation

$\frac{\partial f\left(\theta ,t\right)}{\partial t}-\frac{{\partial }^{2}f\left(\theta ,t\right)}{\partial {\theta }^2}=0,\forall \left(\theta ,t\right)\in \Omega$ (27)

with initial condition $f\left(\theta \mathrm{,0}\right)=0$ . Substituting the Green function $G\left(\theta \mathrm{,}\xi \mathrm{,}t\right)$ into $g_1\left(\theta \mathrm{,}t\right)$ and $g_2\left(\theta \mathrm{,}t\right)$ , we derive that $f\left(\theta \mathrm{,}t\right)=0$ on $\Omega$ , which implies $g_1\left(\theta ,t\right)=g_2\left(\theta ,t\right)$ . 口

Considering the above-mentioned results and using Lemmas 2 and 3, we conclude that

$\begin{array}{c}k\left(\theta ,t\right)=\exp \left\{{\displaystyle {\int }_0^t}\left(A\left(s\right)-\frac{b^2}{4}\right)\text{d}s\right\}u\left(\theta \right)g\left(\theta ,t\right)\\ =\exp \left\{{\displaystyle {\int }_0^t}\left(A\left(s\right)-\frac{b^2}{4}\right)\text{d}s-\frac{b\theta }{2}\right\}[\frac{1}{\pi }{\displaystyle {\int }_0^{2\pi }}G\left(\theta ,\xi ,t\right)u^{-1}\left(\xi \right)k_0\left(\xi \right)\text{d}\xi \\ -\frac{1}{\pi }{\displaystyle {\int }_0^t}\text{d}\tau {\displaystyle {\int }_0^{2\pi }}G\left(\theta ,\xi ,t-\tau \right)\zeta \left(\xi ,\tau \right)\text{d}\xi ]\end{array}$ (28)

is the unique classical solution of Equation (7).

Proposition 6. Let $g\left(\theta \mathrm{,}t\right)$ be the classical solution of Equation (15) with initial condition $g\left(\theta \mathrm{,0}\right)=h_0\left(\theta \right)\ge 0$ , $\forall \theta \in \mathbb{T}$ . Assume that $\zeta \left(\theta \mathrm{,}t\right)\ge 0$ , $\forall \left(\theta \mathrm{,}t\right)\in \Omega$ . If

$\frac{{\partial }^2\zeta \left(\theta \mathrm{,}s\right)}{\partial {\theta }^2}\le 0$ (29)

and

$k_0\left(\theta \right)\ge {\displaystyle {\int }_0^t}{\text{e}}^{-{\displaystyle {\int }_0^s}\left(A\left(\tau \right)-\frac{b^2}{4}\right)\text{d}\tau }c\left(\theta \mathrm{,}s\right)\text{d}s\mathrm{,}$ (30)

it holds that

$g\left(\theta \mathrm{,}t\right)\ge 0.$ (31)

Proof. For any $\epsilon >0$ , define an auxiliary function

$v\left(\theta \mathrm{,}t\right)=g\left(\theta \mathrm{,}t\right)+\epsilon t+{\displaystyle {\int }_0^t}\zeta \left(\theta \mathrm{,}s\right)\text{d}s\mathrm{,}$ (32)

for all $\left(\theta \mathrm{,}t\right)\in \mathbb{T}\times \left[\mathrm{0,}T\right]$ , where $T>0$ is finite.

Combining with Equations (15) and (29), we get

$\begin{array}{l}\frac{\partial v\left(\theta \mathrm{,}t\right)}{\partial t}-\frac{{\partial }^{2}v\left(\theta \mathrm{,}t\right)}{\partial {\theta }^2}\\ =\frac{\partial g\left(\theta \mathrm{,}t\right)}{\partial t}+\epsilon +\zeta \left(\theta \mathrm{,}t\right)-\frac{{\partial }^{2}g\left(\theta \mathrm{,}t\right)}{\partial {\theta }^2}-{\displaystyle {\int }_0^t}\frac{{\partial }^2\zeta \left(\theta ,s\right)}{\partial {\theta }^2}\text{d}s\\ =\epsilon -{\displaystyle {\int }_0^t}\frac{{\partial }^2\zeta \left(\theta ,s\right)}{\partial {\theta }^2}\text{d}s\ge \epsilon >0.\end{array}$ (33)

Assume that $v\left(\theta \mathrm{,}t\right)$ attains its minimum at $\left(\bar{\theta }\mathrm{,}s\right)\in \mathbb{T}\times \left(\mathrm{0,}T\right]$ , by elementary calculus, we have

$\frac{\partial v\left(\bar{\theta }\mathrm{,}s\right)}{\partial t}\le 0\text{and}\frac{{\partial }^{2}v\left(\bar{\theta }\mathrm{,}s\right)}{\partial {\theta }^2}\ge \mathrm{0,}$ (34)

from which we derive

$\frac{\partial v\left(\bar{\theta }\mathrm{,}s\right)}{\partial t}-\frac{{\partial }^{2}v\left(\bar{\theta }\mathrm{,}s\right)}{\partial {\theta }^2}\le \mathrm{0,}$ (35)

which contradicts with inequality (33). Thus, $\left(\bar{\theta }\mathrm{,}s\right)\in \mathbb{T}\times \left\{0\right\}$ , which implies $v\left(\theta \mathrm{,}t\right)\ge v\left(\theta \mathrm{,0}\right)$ . Hence

$g\left(\theta \mathrm{,}t\right)+\epsilon t+{\displaystyle {\int }_0^t}\zeta \left(\theta \mathrm{,}s\right)\text{d}s\ge g_0\left(\theta \right)\mathrm{,}\forall \left(\theta \mathrm{,}t\right)\in \mathbb{T}\times \left[\mathrm{0,}T\right]\mathrm{.}$ (36)

From inequality (30), we derive $g_0\left(\theta \right)\ge {\displaystyle {\int }_0^t}\zeta \left(\theta \mathrm{,}s\right)\text{d}s$ and

$g\left(\theta \mathrm{,}t\right)+\epsilon t\ge g_0\left(\theta \right)-{\displaystyle {\int }_0^t}\zeta \left(\theta \mathrm{,}s\right)\text{d}s\ge 0.$ (37)

Letting $\epsilon \to 0$ , we conclude that

$g\left(\theta \mathrm{,}t\right)\ge 0.$ (38)

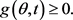
Since the solution $k\left(\theta \mathrm{,}t\right)$ has the same sign with the function $g\left(\theta \mathrm{,}t\right)$ , we know that $k\left(\theta \mathrm{,}t\right)$ is also non-negative in $\Omega$ which concludes the proof of Theorem 1. Our results above show that both consumption function and trade costs affect the spatial growth process. The conditions on the consumption function and the initial distribution of the capital are different from the assumptions in (Aldashev et al., 2014), which are due to the introducing of the trade costs.

3.2. Asymptotic Behaviors of Capital Stock

In this subsection, the asymptotic behaviors of the capital stock $k\left(\theta \mathrm{,}t\right)$ in the long time are discussed relying on the properties of the Green function $G\left(\theta \mathrm{,}\xi \mathrm{,}t\right)$ .

Theorem 7. If (9) holds, $k\left(\theta \mathrm{,}t\right)$ is the classical non-negative solution of problem (7). Consider the case $A\left(t\right)=A$ and assume that $\forall \epsilon \in \left(\mathrm{0,}A\right)$ , there exists a positive constant $B_{\epsilon }$ such that

$\tilde{c}\left(t\right)\le B_{\epsilon }{\text{e}}^{\left(A-\frac{b^2}{4}-\epsilon \right)t},\forall t>0.$ (39)

Then the capital

$\underset{t\to \infty }{lim}k\left(\theta ,t\right){\text{e}}^{-\left(A-\frac{b^2}{4}\right)t}={\text{e}}^{-\frac{b\theta }{2}}\left[{\tilde{k}}_0-{\displaystyle {\int }_0^{\infty }}{\text{e}}^{-\left(A-\frac{b^2}{4}\right)s}\tilde{c}\left(s\right)\text{d}s\right]$ (40)

is heterogeneous on $\Omega$ in the long run, where

${\tilde{k}}_0=\frac{1}{\pi }{\displaystyle {\int }_0^{2\pi }}{\text{e}}^{\frac{b\theta }{2}}{k}_0\left(\theta \right)\text{d}\theta ,\tilde{c}\left(t\right)=\frac{1}{\pi }{\displaystyle {\int }_0^{2\pi }}{\text{e}}^{\frac{b\theta }{2}}c\left(\theta ,t\right)\text{d}\theta .$ (41)

Proof. In the case $A\left(t\right)=A$ , the solution $k\left(\theta \mathrm{,}t\right)$ of problem (7) is expressed in the form

$\begin{array}{c}k\left(\theta ,t\right)=\exp \left\{\left(A-\frac{b^2}{4}\right)t-\frac{b\theta }{2}\right\}[\frac{1}{\pi }{\displaystyle {\int }_0^{2\pi }}G\left(\theta ,\xi ,t\right)u^{-1}\left(\xi \right)k_0\left(\xi \right)\text{d}\xi \begin{array}{c}\\ \\ \end{array}\\ -\frac{1}{\pi }{\displaystyle {\int }_0^t}\text{d}s{\displaystyle {\int }_0^{2\pi }}G\left(\theta ,\xi ,t-s\right){\text{e}}^{-\left(A-\frac{b^2}{4}\right)s}{u}^{-1}\left(\xi \right)c\left(\xi ,s\right)\text{d}\xi ],\end{array}$ (42)

from which we have

$\begin{array}{l}k\left(\theta ,t\right){\text{e}}^{-\left(A-\frac{b^2}{4}\right)t}\\ ={\text{e}}^{-\frac{b\theta }{2}}\{\frac{1}{\pi }{\displaystyle {\int }_0^{2\pi }}\left[G\left(\theta ,\xi ,t\right)-1\right]u^{-1}\left(\xi \right)k_0\left(\xi \right)\text{d}\xi +{\tilde{k}}_0\begin{array}{c}\\ \\ \end{array}\\ -\frac{1}{\pi }{\displaystyle {\int }_0^t}\text{d}s{\displaystyle {\int }_0^{2\pi }}\left[G\left(\theta ,\xi ,t-s\right)-1\right]{\text{e}}^{-\left(A-\frac{b^2}{4}\right)s}{u}^{-1}\left(\xi \right)c\left(\xi ,s\right)\text{d}\xi \\ -{\displaystyle {\int }_0^t}{\text{e}}^{-\left(A-\frac{b^2}{4}\right)s}\tilde{c}\left(s\right)\text{d}s\},\end{array}$ (43)

where ${\tilde{k}}_0$ and $\tilde{c}\left(s\right)$ are defined in Equations (41).

Recalling inequality (26), we have

$\underset{t\to \infty }{lim}\left|G\left(\theta \mathrm{,}\xi \mathrm{,}t\right)-1\right|\le \underset{t\to \infty }{lim}\frac{{\text{e}}^{-t}}{1-{\text{e}}^{-2t}}=\mathrm{0,}\forall \left(\theta \mathrm{,}\xi \right)\in {\mathbb{T}}^2\mathrm{,}$ (44)

which implies

$\underset{t\to \infty }{lim}\frac{1}{\pi }{\displaystyle {\int }_{-\pi }^{\pi }}\left[G\left(\theta \mathrm{,}\xi \mathrm{,}t-s\right)-1\right]u^{-1}\left(\xi \right)k_0\left(\xi \right)\text{d}\xi =0.$ (45)

Combining with inequality (25), we derive that

$\begin{array}{l}\frac{1}{\pi }{\displaystyle {\int }_0^t}\text{d}s{\displaystyle {\int }_0^{2\pi }}\left[G\left(\theta ,\xi ,t-s\right)-1\right]{\text{e}}^{-\left(A-\frac{b^2}{4}\right)s}{u}^{-1}\left(\xi \right)c\left(\xi ,s\right)\text{d}\xi \\ \le \frac{1}{\pi }{\displaystyle {\int }_0^t}\text{d}s{\displaystyle {\int }_0^{2\pi }}{\displaystyle \underset{n\ge 1}{\sum }}{\text{e}}^{-n^2\left(t-s\right)}{\text{e}}^{-\left(A-\frac{b^2}{4}\right)s}{u}^{-1}\left(\xi \right)c\left(\xi ,s\right)\text{d}\xi \\ ={\displaystyle {\int }_0^t}\tilde{c}\left(s\right){\displaystyle \underset{n\ge 1}{\sum }}{\text{e}}^{-n^2\left(t-s\right)-\left(A-\frac{b^2}{4}\right)s}\text{d}s\\ \le {\displaystyle {\int }_0^t}{B}_{\epsilon }{\text{e}}^{\left(A-\frac{b^2}{4}-\epsilon \right)s}{\displaystyle \underset{n\ge 1}{\sum }}{\text{e}}^{-n^2\left(t-s\right)-\left(A-\frac{b^2}{4}\right)s}\text{d}s\\ ={\displaystyle {\int }_0^t}{B}_{\epsilon }{\displaystyle \underset{n\ge 1}{\sum }}{\text{e}}^{-n^{2}t+\left(n^2-\epsilon \right)s}\text{d}s=B_{\epsilon }{\displaystyle \underset{n\ge 1}{\sum }}{\text{e}}^{-n^{2}t}\frac{{\text{e}}^{\left(n^2-\epsilon \right)t}-1}{n^2-\epsilon }\\ =B_{\epsilon }{\displaystyle \underset{n\ge 1}{\sum }}\frac{{\text{e}}^{-\epsilon t}}{n^2-\epsilon }-B_{\epsilon }{\displaystyle \underset{n\ge 1}{\sum }}\frac{{\text{e}}^{-n^{2}t}}{n^2-\epsilon }\to 0\left(\text{as}t\to \infty \right),\end{array}$ (46)

which means

$\underset{t\to \infty }{lim}\left[\frac{1}{\pi }{\displaystyle {\int }_0^t}\text{d}s{\displaystyle {\int }_0^{2\pi }}\left[G\left(\theta \mathrm{,}\xi \mathrm{,}t-s\right)-1\right]{\text{e}}^{-\left(A-\frac{b^2}{4}\right)s}{u}^{-1}\left(\xi \right)c\left(\xi \mathrm{,}s\right)\text{d}\xi \right]=0.$ (47)

Substituting Equation (45) and Equation (47) into Equation (43) yields Equation (40).

Corollary 1. If (9) holds, $k\left(\theta \mathrm{,}t\right)$ is the classical non-negative solution of problem (7). Assume that there exists $\bar{A}>0$ such that $A\left(t\right)>\bar{A}$ for all $t>0$ , and a positive constant $D_{\epsilon }\mathrm{,}\forall \epsilon \in \left(\mathrm{0,}\bar{A}\right)$ such that

$\tilde{c}\left(t\right)\le D_{\epsilon }{\text{e}}^{\left(\bar{A}-\frac{b^2}{4}-\epsilon \right)t},\forall t>0.$ (48)

Then the capital

$\underset{t\to \infty }{\lim }k\left(\theta ,t\right){\text{e}}^{-{\displaystyle {\int }_0^t}\left(A\left(s\right)-\frac{b^2}{4}\right)\text{d}s}={\text{e}}^{-\frac{b\theta }{2}}\left[{\tilde{k}}_0-{\displaystyle {\int }_0^{\infty }}{\text{e}}^{-{\displaystyle {\int }_0^s}\left(A\left(\tau \right)-\frac{b^2}{4}\right)\text{d}\tau }\tilde{c}\left(s\right)\text{d}s\right]$ (49)

is heterogeneous on $\Omega$ in the long time, where ${\tilde{k}}_0$ and $\tilde{c}\left(t\right)$ are defined in Equation (41).

Proof. We know that

${\text{e}}^{-{\displaystyle {\int }_0^t}\left(A\left(s\right)-\frac{b^2}{4}\right)\text{d}s}\le {\text{e}}^{-\left(\bar{A}-\frac{b^2}{4}\right)t},\forall t>0.$ (50)

Equation (49) could be verified by the similar proof of Theorem 7.

Compared to the work of Aldashev et al. (2014), the forms of capital stock in the long run is different because of the introduction of the trade cost. From Theorem 7, if $b\in \left(0,B\right),B<+\infty$ , the trade cost measure b has a negative effect on the capital stock $k\left(\theta \mathrm{,}t\right)$ . The larger b is, the more barriers of the capital mobilities, which is consistent with the view of Thisse and Fujita (2002) who believe that agglomeration is a result of the trade-off between transport costs and increasing returns.

If $b\to +\infty$ , the discounted capital is exhausted in the long run and resources can not move in because of the high trade costs. If the trade costs coefficient $b=0$ , the initial spatial inequality of the capital disappears and the growth dynamics which satisfies the condition (9) lead to spatial convergence in capital over time. If $b<0$ , the trade cost is negative, we can take the situation as there exist preferential policies, that the local governments provide subsidies to attract investments and promote the economic development.

4. Conclusion

In the present work, we introduce the trade costs into the spatial AK model whose spatial-temporal dynamics of the capital stock are governed by a parabolic partial differential equation. Taking advantage of the good properties of the Green function, we formulate an explicit solution to the auxiliary partial differential equation of the original problem and derive the sufficient conditions on the consumption function that guarantee the existence and the uniqueness of the solution. We also analyze the effects of the trade costs on the asymptotic behaviors of the capital in the framework of spatial AK growth model, where the technology is time-varying. In addition, the technology might depend not only on time but also on space. The spatial heterogeneities of technology A could be taken into account for future research, which may reflect spatial externality associated with location.

Acknowledgements

The author would like to thank anonymous referees and editor for their helpful comments.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Aldashev, G., Aldashev, S., & Carletti, T. (2014). On Convergence in the Spatial AK Growth Models (pp. 1-18). https://arxiv.org/abs/1401.4887
[2]	Ballestra, L. V. (2016). The Spatial AK Model and the Pontryagin Maximum Principle. Journal of Mathematical Economics, 67, 87-94. https://doi.org/10.1016/j.jmateco.2016.09.012
[3]	Behrens, K., & Picard, P. M. (2011). Transportation, Freight Rates, and Economic Geography. Journal of International Economics, 85, 280-291. https://doi.org/10.1016/j.jinteco.2011.06.003
[4]	Boucekkine, R., Camacho, C., & Fabbri, G. (2013). Spatial Dynamics and Convergence: The Spatial AK Model. Journal of Economic Theory, 148, 2719-2736. https://doi.org/10.1016/j.jet.2013.09.013
[5]	Boucekkine, R., Camacho, C., & Zou, B. (2009). Bridging the Gap between Growth Theory and the New Economic Geography: The spatial Ramsey Model. Macroeconomic Dynamics, 13, 20-45. https://doi.org/10.1017/S1365100508070442
[6]	Brito, P. (2004). The Dynamics of Growth and Distribution in a Spatially Heterogeneous World (pp. 1-45). https://core.ac.uk/download/pdf/7027939.pdf
[7]	Camacho, C., Zou, B., & Briani, M. (2008). On the Dynamics of Capital Accumulation Across Space. European Journal of Operational Research, 186, 451-465. https://doi.org/10.1016/j.ejor.2007.02.031
[8]	Desmet, K., & Rossi-Hansberg, E. (2010). On Spatial Dynamics. Journal of Regional Science, 50, 43-63. https://doi.org/10.1111/j.1467-9787.2009.00648.x
[9]	Fabbri, G. (2016). Geographical Structure and Convergence: A Note on Geometry in Spatial Growth Models. Journal of Economic Theory, 162, 114-136. https://doi.org/10.1016/j.jet.2015.12.004
[10]	Isard, W., & Liossatos, P. (1979). Spatial Dynamics and Optimal Space-Time Development. Amsterdam: North-Holland.
[11]	Juchem Neto, J., Claeyssen, J., & Prto Jnior, S. (2018). Economic Agglomerations and Spatio-Temporal Cycles in a Spatial Growth Model with Capital Transport Cost. Physica A: Statistical Mechanics and its Applications, 494, 76-86. https://doi.org/10.1016/j.physa.2017.12.036
[12]	Juchem Neto, J. P., & Claeyssen, J. C. R. (2015). Capital-Induced Labor Migration in a Spatial Solow Model. Journal of Economics, 115, 25-47. https://doi.org/10.1007/s00712-014-0404-6
[13]	Thisse, J., & Fujita, M. (2002). Economics of Agglomeration. Cambridge: Cambridge University Press. https://doi.org/10.1017/CBO9780511805660
[14]	Zou, B., & Camacho, C. (2004). The Spatial Solow Model. Economics Bulletin, 18, 1-11.