On Two Classes of Extended 3-Lie Algebras

Yu Cheng¹, Yansha Gao²

¹School of Data Science and Software Engineering, Baoding University, Baoding, China.
²College of Mathematics and Information Science, Hebei University, Baoding, China.

DOI: 10.4236/jamp.2021.94056                

Abstract

In this paper, based on the existing research results, we obtain the unary extension 3-Lie algebras by one-dimensional extension of the known Lie algebra L. For two known 3-Lie algebras H, M, the (μ, ρ, β)-extension of H through M is given, and the necessary and sufficient conditions for the (μ, ρ, β)-extension algebra of H through M being 3-Lie algebra are obtained, and the structural characteristics and properties of these two kinds of extended 3-Lie algebras are given.

Keywords

The Unary Extension 3-Lie Algebras, Lie Algebra, (μ, ρ, β)-Extension

1. Introduction

In recent years, the study of 3-Lie algebra has been paid much attention because of its wide application in mathematics and physics. 3-Lie algebra is a special form of n-Lie algebra, which is an algebraic system with ternary linearly oblique symmetric multiplication table satisfying the generalized Jacobi equation [1]. 3-Lie algebra has extremely profound and rich algebraic and analytical structure. In this paper, the extension problem of 3-Lie algebra is studied on the basis of the existing research. Firstly, we define the unary extended 3-Lie algebra for a known Lie algebra L by one-dimensional extension, and study its properties. Secondly, for two known 3-Lie algebras H, M, the $\left(\mu ,\rho ,\beta \right)$ -extension of H through M is defined, and the $\left(\mu ,\rho ,\beta \right)$ -extension of H through M is given as a necessary and sufficient condition for the 3-Lie algebra. Finally, the structure and properties of this extended 3-Lie algebra are discussed. Thus, it lays a foundation for the further study of the properties of the derivatives of two kinds of 3-Lie algebras.

2. Fundamental Notions

Firstly, the basic knowledge [1] - [9] to be used in this paper is given.

Definition 2.1 Let A be a vector space over a domain F and have a 3-element linear operation $\left[,,\right]:A\wedge A\wedge A\to A$, satisfied for arbitrary, $x_1,x_2,x_3,y_2,y_3\in A$

$\left[\left[x_1,x_2,x_3\right],y_2,y_3\right]={\displaystyle \underset{i=1}{\overset{3}{\sum }}\left[x_1,\left[x_i,y_2,y_3\right],x_3\right]}$, (1)

$\left(A,\left[,,\right]\right)$ is called 3-Lie algebra. Without confusion, A is called 3-Lie algebra for short.

Definition 2.2 Let A be a 3-Lie algebra, and D be a linear transformation ofA, if this equation is satisfied

$\left[D\left(x\right),y,z\right]+\left[x,D\left(y\right),z\right]+\left[x,y,D\left(z\right)\right]=D\left(\left[x,y,z\right]\right)$, $x,y,z\in A$ (2)

Then D is the derivative of A, and the set of derivatives is denoted by $Der\left(A\right)$. It is easy to prove that $Der\left(A\right)$ is a subalgebra of the general linear Lie algebra $gl\left(A\right)$.

The map

$ad\left(x_1,x_2\right):A\to A$, $ad\left(x_1,x_2\right)\left(x\right)=\left[x_1,x_2,x\right]$

for $x\in A$ is called the left multiplication defined by elements $x_1,x_2\in A$. Obviously the left multiplication is the derivative. The linear combination of the left multiplication is called the inner derivative, denoted by $ad\left(A\right)$.

Let B be a subspace ofA, and if $\left[B,B,B\right]\subseteq B\left(\left[B,A,A\right]\subseteq B\right)$, then B be a subalgebra (ideal) of A. And if $\left[B,B,B\right]=0\left(\left[B,B,A\right]=0\right)$, then B is called a Abel subalgebra

(Abel ideal). In particular, the subalgebra spanned by $\left[x_1,x_2,x_3\right]\left(\forall x_1,x_2,x_3\in A\right)$ is called the derivative algebra of A, denoted by $A^1$. If $A^1=0$, then A is called Abel algebra. If an ideal I of A is a Abel subalgebra but not an Abel ideal, that is $\left[I,I,I\right]=0$, but $\left[I,I,A\right]\ne 0$, then I is called an hypo-abelian ideal.

The ideal I of a 3-Lie algebra A is called s-solvable, $2\le s\le 3$, if $I^{\left(k,s\right)}=0$ for some $k\ge 0$, where $I^{\left(0,s\right)}=I$, $I^{\left(k+1,s\right)}$ is defined as

$I^{\left(k+1,s\right)}\text{=}\left[\underset{s}{\underset{︸}{I^{\left(k,s\right)},\cdots ,I^{\left(k,s\right)}}},\underset{3-s}{\underset{︸}{A,\cdots ,A}}\right]$. Where 2-solvable is also called solvable, and $I^{\left(k,s\right)}$ is abbreviated as $I^{\left(k\right)}$.

An ideal I of a 3-Lie algebra A is called nilpotent if $I^s=0$ for some $s\ge 0$, where $I^0=I$ and $I^s=\left[I^{s-1},I,A\right]$.

The center of A is denoted by $Z\left(A\right)=\left\{x\in A|\left[x,A,A\right]=0\right\}$. Obviously $Z\left(A\right)$ is the Abel ideal of A.

Let A is a 3-Lie algebra over the field F, V is a vector space, $\rho :A\wedge A\to End\left(V\right)$ is a linear mapping, if $\rho$ satisfies for any $x_1,x_2,x_3,x_4\in A$

$\left[\rho \left(x_1,x_2\right),\rho \left(x_3,x_4\right)\right]=\rho \left(\left[x_1,x_2,x_3\right]x_4\right)-\rho \left(\left[x_1,x_2,x_4\right]x_3\right),$ (3)

$\begin{array}{c}\rho \left(\left[x_1,x_2,x_3\right],x_4\right)=\rho \left(x_1,x_2\right)\rho \left(x_3,x_4\right)+\rho \left(x_2,x_3\right)\rho \left(x_1,x_4\right)\\ +\rho \left(x_3,x_1\right)\rho \left(x_2,x_4\right)\end{array}$ (4)

Then $\left(V,\rho \right)$ is called the representation of A (or $\left(V,\rho \right)$ is A-module).

Lemma 2.1 Let A is a 3-Lie algebra over the field F, V is a vector space, $\rho :A\wedge A\to End\left(V\right)$ is a linear mapping. If $\left(V,\rho \right)$ is an A-module, then for any $x,y,z,u\in A$, the following equation is true:

$\rho \left(\left[x,y,z\right],u\right)-\rho \left(\left[x,y,u\right],z\right)+\rho \left(\left[x,z,u\right],y\right)-\rho \left(\left[y,z,u\right],x\right)=0$, (5)

$\begin{array}{l}\rho \left(x,u\right)\rho \left(y,z\right)+\rho \left(y,z\right)\rho \left(x,u\right)+\rho \left(x,y\right)\rho \left(z,u\right)+\rho \left(z,u\right)\rho \left(x,y\right)\\ -\rho \left(x,z\right)\rho \left(y,u\right)-\rho \left(y,u\right)\rho \left(x,z\right)=0.\end{array}$ (6)

3. The Unary Extension 3-Lie Algebra of Lie Algebras

Definition 3.1 Let $\left(L,\left[,\right]\right)$ be a Lie algebra over a field F, let $A=L\oplus F{x}_0$ $x_0\in F$, and $x_0\notin L$. Linear operation $\left[,,\right]:A\wedge A\wedge A\to A$ for all $x,y,z\in L$ that satisfy the following multiplication table:

$\left[x,y,x_0\right]=\left[x,y\right],\left[x,y,z\right]=0$. (7)

Then A is called the unary extension of Lie algebra L. If $\left(A,\left[,,\right]\right)$ is a 3-Lie algebra, then $\left(A,\left[,,\right]\right)$ is a unary extension 3-Lie algebra of the Lie algebra L.

Lemma 3.1 let L be a Lie algebra over a field F. If let $A=L\oplus F{x}_0$ $x_0\in F$, $x_0\notin L$ and the multiplication of is defined by (7), then A is a 3-Lie algebra, and for positive integers m, the following equation holds

$A^{\left(m\right)}=L^{\left(m\right)},A^{\left(m,2\right)}=L^{\left(m,2\right)}=L^{\left(m\right)},A^{\left(2,3\right)}=0.$

Proof: By multiplication (7), direct calculation A is 3-Lie algebra. Due to the

$A^1=\left[A,A,A\right]=\left[L,L,L\right]+\left[L,L,F{x}_0\right]=L^1$,

$A^2=\left[A^1,A,A\right]=\left[L^1,L,F{x}_0\right]=L^2$,

Assume $A^{m-1}=L^{m-1}$, then

$A^m=\left[A^{m-1},A,A\right]=\left[L^{m-1},L+F{x}_0,L+F{x}_0\right]=\left[L^{m-1},L\right]=L^m$.

similarly, $A^{\left(m,2\right)}=L^{\left(m,2\right)}=L^{\left(m\right)}$ and $A^{\left(2,3\right)}=0$. The conclusion is proved.

Theorem 3.1 Let L be a Lie algebra on the field F and $A=L\oplus F{x}_0$ be a unary extension 3-Lie algebra, where $x_0\in F$ and $x_0\notin L$, then

1) A is 2-solvable if and only if L is a solvable Lie algebra.

2) A is nilpotent if and only if L is a nilpotent Lie algebra.

3) A is 3-solvable.

4) $Z\left(A\right)=Z\left(L\right)$.

Proof: According to lemma 3.1, (1), (2) and (3) can be obtained directly. It is proved below that (4) is true. If $L^1=0$, then $A^1=L^1=0$ and $Z\left(A\right)=Z\left(L\right)$. If $L^1\ne 0$, then exists $y,z\in L$ such that $\left[y,z\right]\ne 0$. For any $x\in L$, $\lambda \in F$, $x+\lambda x_0\in Z\left(A\right)$, because of $\left[x+\lambda x_0,y,z\right]=\lambda \left[y,z\right]=0$, therefore $\lambda =0$.And because $\left[x+\lambda x_0,A,x_0\right]=\left[x,L\right]=0$, so $x\in Z\left(L\right)$. Therefore $Z\left(A\right)\subseteq Z\left(L\right)$. Obviously, the conclusion of $Z\left(L\right)\subseteq Z\left(A\right)$ is true.

Theorem 3.2 Let L be a Lie algebra on the field F and I be a subspace ofL:

1) I is an ideal of A if and only if I is an ideal of L.

2) Let $J=I\oplus F{x}_0$, then J is ideal of A if and only if $L^1\subseteq I$.

3) If $L^1\subseteq I$, then for positive integers m, $J^{\left(m,2\right)}\subseteq I^{\left(m-1\right)}$. If I is a solvable ideal of L, then J is a 2-solvable ideal of A.

4) If L is a simple Lie algebra, then L is hypo-abelian ideal of A.

Proof: From $\left[I,A,A\right]=\left[I,L,x_0\right]=\left[I,L\right]$, we can get (1). From Equation (7),

$\left[J,A,A\right]=\left[I,L,x_0\right]+\left[x_0,L,L\right]=\left[I,L\right]+\left[L,L\right]$,

So $\left[J,A,A\right]\subseteq J$ if and only if $\left[L,L\right]\subseteq I$. That means (2) is true.

If I is the ideal of L and $L^1\subseteq I$, then

$J^{\left(1,2\right)}=\left[J,J,A\right]=\left[I,I\right]+\left[I,L\right]=I^{\left(1\right)}+\left[I,L\right]\subseteq I^{\left(1\right)}+I\subseteq I=I^{\left(0\right)}$,

$J^{\left(2,2\right)}=\left[J^{\left(1,2\right)},J^{\left(1,2\right)},A\right]=\left[I,I,L+F{x}_0\right]\subseteq I^{\left(1\right)}$,

Assuming $J^{\left(m-1,2\right)}\subseteq I^{\left(m-2\right)}$ is true, then

$J^{\left(m,2\right)}=\left[J^{\left(m-1,2\right)},J^{\left(m-1,2\right)},A\right]\subseteq \left[I^{\left(m-2\right)},I^{\left(m-2\right)},L+F{x}_0\right]\subseteq I^{\left(m-1\right)}$.

Therefore (3) holds. If L is a simple Lie algebra, then L is ideal of A, and $\left[L,L,L\right]=0$, $\left[L,L,A\right]=\left[L,L,x_0\right]=L^1\ne 0$. Therefore, L is hypo-abelian ideal of A. That’s the end of the argument.

4. $\left(\mu ,\rho ,\beta \right)$ -Extension of 3-Lie Algebras

Definition 4.1 Let $\left(H,{\left[,,\right]}_H\right)$ and $\left(M,{\left[,,\right]}_M\right)$ be two 3-Lie algebras over the field F, $A=M\oplus H$, and

$\rho :M\wedge M\to Der\left(H\right)$, $\beta :M\wedge H\to Der\left(H\right)$, $\mu :M\wedge M\wedge M\to H$

is linear mappings. Define a linear operation ${\left[,,\right]}_{\mu \rho \beta }:A\wedge A\wedge A\to A$, for any $x,y,z\in M$, $h,h_1,h_2\in H$ that satisfies the multiplication table:

${\left[x,y,z\right]}_{\mu \rho \beta }={\left[x,y,z\right]}_M+\mu \left(x,y,z\right)$, ${\left[x,y,h\right]}_{\mu \rho \beta }=\rho \left(x,y\right)h$ (8)

${\left[h_1,h_2,h_3\right]}_{\mu \rho \beta }={\left[h_1,h_2,h_3\right]}_H$, ${\left[x,h_1,{\begin{array}{c}h\end{array}}_2\right]}_{\mu \rho \beta }=\beta \left(x,h_1\right)h_2$.

Then $\left(A,{\left[,,\right]}_{\mu \rho \beta }\right)$ is called the $\left(\mu ,\rho ,\beta \right)$ -extension of H through M. If $\left(A,{\left[,,\right]}_{\mu \rho \beta }\right)$ is a 3-Lie algebra, then $\left(A,{\left[,,\right]}_{\mu \rho \beta }\right)$ is $\left(\mu ,\rho ,\beta \right)$ -extension algebra of 3-Lie algebra. If $\beta =0$, then A is called $\left(\mu ,\rho \right)$ -extension of H through M, and ${\left[,,\right]}_{\mu \rho \beta }$ denoted as ${\left[,,\right]}_{\mu \rho }$. For convenience, we will abbreviate ${\left[,,\right]}_M$ and ${\left[,,\right]}_H$ as $\left[,,\right]$ and ${\left[,,\right]}_{\mu \rho \beta }$ as ${\left[,,\right]}_A$.

Lemma 4.1 Let $\left(H,{\left[,,\right]}_H\right)$ and $\left(M,{\left[,,\right]}_M\right)$ be two 3-Lie algebras over the field F, and A be the $\left(\mu ,\rho ,\beta \right)$ -extension of H through M, and for all $x_1,x_2,x_3,x_4\in M$ satisfy

$\begin{array}{c}\rho \left(x_4,\left[x_1,x_2,x_3\right]\right)=\rho \left(x_3,x_1\right)\rho \left(x_4,x_2\right)-\rho \left(x_2,x_1\right)\rho \left(x_4,x_3\right)\\ +\rho \left(x_2,x_3\right)\rho \left(x_4,x_1\right)-\beta \left(x_4,\mu \left(x_1,x_2,x_3\right)\right).\end{array}$ (9)

Then Equation (6) is true if and only if the following equation

$\begin{array}{l}\rho \left(x_4,\left[x_1,x_2,x_3\right]\right)\\ =\rho \left(x_3,\left[x_1,x_2,x_4\right]\right)-\beta \left(x_4,\mu \left(x_1,x_2,x_3\right)\right)+\beta \left(x_3,\mu \left(x_1,x_2,x_4\right)\right)\\ -\rho \left(x_1,x_2\right)\rho \left(x_3,x_4\right)+\rho \left(x_3,x_4\right)\rho \left(x_1,x_2\right).\end{array}$ (10)

Proof: From Equation (9), we can get

$\begin{array}{c}\rho \left(x_3,\left[x_1,x_2,x_4\right]\right)=\rho \left(x_2,x_4\right)\rho \left(x_3,x_1\right)-\rho \left(x_1,x_4\right)\rho \left(x_3,x_2\right)\\ +\rho \left(x_1,x_2\right)\rho \left(x_3,x_4\right)-\beta \left(x_3,\mu \left(x_1,x_2,x_4\right)\right),\end{array}$

$\begin{array}{l}\rho \left(x_4,\left[x_1,x_2,x_3\right]\right)-\rho \left(x_3,\left[x_1,x_2,x_4\right]\right)\\ =\rho \left(x_1,x_3\right)\rho \left(x_2,x_4\right)-\rho \left(x_1,x_2\right)\rho \left(x_3,x_4\right)-\rho \left(x_2,x_3\right)\rho \left(x_1,x_4\right)\\ -\beta \left(x_4,\mu \left(x_1,x_2,x_3\right)\right)+\rho \left(x_2,x_4\right)\rho \left(x_1,x_3\right)-\rho \left(x_1,x_4\right)\rho \left(x_2,x_3\right)\\ -\rho \left(x_1,x_2\right)\rho \left(x_3,x_4\right)+\beta \left(x_3,\mu \left(x_1,x_2,x_4\right)\right)\end{array}$

$\begin{array}{l}=\rho \left(x_1,x_3\right)\rho \left(x_2,x_4\right)+\rho \left(x_2,x_4\right)\rho \left(x_1,x_3\right)-\rho \left(x_2,x_3\right)\rho \left(x_1,x_4\right)\\ -\rho \left(x_1,x_4\right)\rho \left(x_2,x_3\right)-2\rho \left(x_1,x_2\right)\rho \left(x_3,x_4\right)-\beta \left(x_4,\mu \left(x_1,x_2,x_3\right)\right)\\ +\beta \left(x_3,\mu \left(x_1,x_2,x_4\right)\right).\end{array}$

So Equation (10) holds. On the other hand, if

$\begin{array}{c}\rho \left(x_4,\left[x_1,x_2,x_3\right]\right)=\rho \left(x_2,x_4\right)\rho \left(x_3,x_1\right)-\rho \left(x_1,x_4\right)\rho \left(x_3,x_2\right)\\ +\rho \left(x_1,x_2\right)\rho \left(x_3,x_4\right)-\beta \left(x_3,\mu \left(x_1,x_2,x_4\right)\right)\\ -\beta \left(x_4,\mu \left(x_1,x_2,x_3\right)\right)+\beta \left(x_3,\mu \left(x_1,x_2,x_4\right)\right)\\ -\rho \left(x_1,x_2\right)\rho \left(x_3,x_4\right)+\rho \left(x_3,x_4\right)\rho \left(x_1,x_2\right).\end{array}$

Through Equation (9), it can be concluded that Equation (6) holds.

Lemma 4.2. Let A be the $\left(\mu ,\rho ,\beta \right)$ -extension of H through M, for all $x_1,x_2\in M$, $h_1,h_2,h\in H$ satisfies

$\begin{array}{l}\beta \left(y,h_2\right)\beta \left(x,h_1\right)h-\beta \left(y,h\right)\beta \left(x,h_1\right)h_2-\beta \left(x,h_1\right)\beta \left(y,h_2\right)h\\ =\left[\rho \left(x,y\right)h_1,h_2,h\right]\end{array}$ (11)

There are

$\begin{array}{l}\rho \left(x,y\right)\left[h_1,h_2,h\right]+\beta \left(y,h_1\right)\beta \left(x,h_2\right)h-\beta \left(x,h_1\right)\beta \left(y,h_2\right)h\\ =\left[\rho \left(x,y\right)h_1,h_2,h\right]\end{array}$ (12)

Proof: From Equation (11) and the $\rho \left(x,y\right)$ is derivative of H, we can get

$\begin{array}{l}\left[h_1,\rho \left(x,y\right)h_2,h\right]\\ =\beta \left(y,h_1\right)\beta \left(x,h\right)h_2+\beta \left(y,h\right)\beta \left(x,h_2\right)h_1+\beta \left(x,h_2\right)\beta \left(y,h_1\right)h\end{array}$

$\begin{array}{l}\left[h_1,h_2,\rho \left(x,y\right)h\right]\\ =\beta \left(y,h_2\right)\beta \left(x,h_1\right)h+\beta \left(y,h_1\right)\beta \left(x,h\right)h_2+\beta \left(x,h\right)\beta \left(y,h_2\right)h_1\end{array}$

$\begin{array}{l}\rho \left(x,y\right)\left[h_1,h_2,h\right]\\ =2\left(\beta \left(y,h_1\right)\beta \left(x,h\right)h_2+\beta \left(y,h_2\right)\beta \left(x,h_1\right)h+\beta \left(y,h\right)\beta \left(x,h_2\right)h_1\right)\\ +\beta \left(x,h_1\right)\beta \left(y,h\right)h_2+\beta \left(x,h_2\right)\beta \left(y,h_1\right)h+\beta \left(x,h\right)\beta \left(y,h_2\right)h_1,\end{array}$

so

$\begin{array}{l}\beta \left(y,h_1\right)\beta \left(y,h\right)h_2+\beta \left(y,h_2\right)\beta \left(x,h_1\right)h+\beta \left(y,h\right)\beta \left(x,h_2\right)h_1\\ +\beta \left(x,h_1\right)\beta \left(y,h\right)h_2+\beta \left(x,h_2\right)\beta \left(y,h_1\right)h+\beta \left(y,h\right)\beta \left(y,h_2\right)h_1=0,\end{array}$

$\begin{array}{l}\rho \left(x,y\right)\left[h_1,h_2,h\right]\\ =\beta \left(y,h_1\right)\beta \left(x,h\right)h_2+\beta \left(y,h_2\right)\beta \left(x,h_1\right)h+\beta \left(y,h\right)\beta \left(x,h_2\right)h_1\end{array}$

Namely

$\begin{array}{l}\beta \left(y,h_2\right)\beta \left(x,h_1\right)h-\beta \left(y,h\right)\beta \left(x,h_1\right)h_2\\ =\rho \left(x,y\right)\left[h_1,h_2,h\right]+\beta \left(y,h_1\right)\beta \left(x,h_2\right)h.\end{array}$

Using Equation (11) again, Equation (12) can be obtained.

Lemma 4.3. Let A be the $\left(\mu ,\rho ,\beta \right)$ -extension of H through M. If for all $x\in M$, satisfies

(13)

Then

(14)

Proof: According to Equation (13),

Because of, therefore

Hence, Equation (14) holds.

Theorem 4.1. Let A be the -extension of H through M, then A is a 3-Lie algebra if and only if for any, , Equations (6), (9), (11), (13) and the following are true,

(15)

(16)

(17)

Proof: If A is a 3-Lie algebra, the Equations (11), (15), (16) and (17) are obtained from the Equations (1). The following proves that Equations (6), (9) and (13) are true.

For, , according to (8),

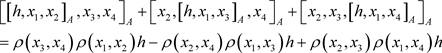
As a result,

In the above formula, is replaced by, and Equation (9) can be obtained.

Because,

So Equation (10) holds. Equation (6) is obtained from lemma 4.1.

For arbitrary, , it can be known from (8) that,

As a result,

Because of, therefore

Equation (13) holds.

Conversely, to prove that A is a 3-Lie algebra, it is only necessary to prove that (8) satisfies Equation (1).

Case 1. For all, known by (8)

From Equation (17), we can get

Case 2. For all, , know from (8)

In Equation (9), by substitution for, we can get

As a result,

Due to the,

Through lemma 4.1 and Equation (9), we can get

According to Equations (6) and (10),

Case 3. For all, , it is obtained from Equations (15), (16)

Because,

Through the direct calculation of Equations (15) and (16),

As a result,

Case 4. For all, , due to the, it can be concluded from Equation (11) that,

Because of,

Then

According to lemma 4.2,

Using Equation (11) again, we can get

namely

.

Case 5. For all, , because, through Equation (13),

To sum up, (8) satisfies Equation (1). The conclusion is proved.

Theorem 4.2 Let be the -extension of 3-Lie algebra H through M. So is M-module if and only if.

Proof: If, obviously is an M-module.

On the other hand, to any, by theorem 4.1 and Equation (9), (10),

As a result,

According to Equation (9),. And the theorem is proved.

Theorem 4.3 Let be the -extension of 3-Lie algebra H through M and be an M-module. So A is a 3-Lie algebra if and only if, and Equation (17) is true.

Proof: If A is a 3-Lie algebra, Equation (17) holds by theorem 4.1. Since is M-module, then. And, can be obtained by Equations (9) and (13). Conversely, from theorems 4.1 and 4.2, A is a 3-Lie algebra.

The above conclusions about 3-Lie algebras will be helpful for further study of their derivation algebras.

Funding

Science and Technology Research Project of Higher Education Department of Hebei Province (Z2015009).

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Filippov, V.T. (1985) n-Lie Algebras. Siberian Mathematical Journal, 26, 126-140. https://doi.org/10.1007/BF00969110
[2]	Lu, F.Y. (2007) Lie Triple Derivations on Nest Algebras. Mathematische Nachrichten, 280, 882-887. https://doi.org/10.1002/mana.200410520
[3]	Papageorgakis, C. and Samann, C. (2011) The 3-Lie Algebra (2, 0) Tensor Multiplet and Equations of Motion on Loop Space. Journal of High Energy Physics, 2011, Article No. 99. https://doi.org/10.1007/JHEP05(2011)099
[4]	Bremner, M. and Elgendy, H. (1987) Universal Associative Envelopes of (n + 1)-Dimensional n-Lie Algebras.
[5]	Bai, R.P., Bai, C.M. and Wang, J.X. (2010) Realizations of 3-Lie Algebras. Journal of Mathematical Physics, 51, Article ID: 063505. https://doi.org/10.1063/1.3436555
[6]	Bai, R. and Wu, Y. (2015) Constructions of 3-Lie Algebras. Linear and Multilinear Algebra, 63, 2171-2186. https://doi.org/10.1080/03081087.2014.986121
[7]	Bai, R., Wu, W. and Li, Z. (2012) Some Results on Metric n-Lie Algebras. Acta Mathematics Sinica, English Series, 28, 1209-1220. https://doi.org/10.1007/s10114-011-0231-4
[8]	Bai, R., Chen, S. and Cheng, R. (2016) Symplectic Structures on 3-Lie Algebras.
[9]	Bai, R., Wu, W. and Li, Y. (2012) Module Extensions of 3-Lie Algebras. Linear and Multilinear Algebra, 60, 433-447. https://doi.org/10.1080/03081087.2011.603728