Sixth Order Finite Difference Method for Three Coupled Nonlinear Schrödinger Equations

Khadijah Alamoudi, Mohmmad Said Hammoudeh

Department of Math, King Abdulaziz University, Jeddah, Saudi Arabia.

DOI: 10.4236/apm.2021.114017                

Abstract

In this work, we will derive a numerical method of sixth order in space and second order in time for solving 3-coupled nonlinear Schrödinger equations. The numerical method is unconditionally stable. We use the exact single soliton solution and the conserved quantities to check the accuracy and the efficiency of the proposed schemes. Also, we study the interaction dynamics of two solitons. It is found that both elastic and inelastic collisions can take place under suitable parametric conditions.

Keywords

Three Coupled Nonlinear Schrodinger Equations, Sixth Order Method, Interaction of Two Solitons

1. Introduction

In recent years the concept of soliton has been receiving considerable attention in optical communications. Since soliton is capable of propagating over long distances without change of shape and velocity, it has been found that the soliton propagating through optical fiber arrays is governed by a set of equations related to the coupled nonlinear Schrödinger equation [1] [2] [3].

$i{q}_{jt}+q_{jxx}+2\left[{\displaystyle {\sum }_{p=1}^N{\left|q_p\right|}^2}\right]q_j=0,j=1,2,\cdots ,N$ (1)

where $i^2=-1$, $q_j$ is the envelope or the amplitude of the jth wave packets. Equation (1) reduces to the standard nonlinear Schrödinger equation for $N=1$, to Manakov integrable system for $N=2$, and recently for this case the exact two soliton solution obtained and novel shape changing in elastic collision property has been brought out. The system for $N=3$ is of physical interest, in optical communication, and in biophysics, this system can be used to study the lunching and propagation of solitons along the three spines of an alpha-helix shape changing in protein [1] [2] [4] [5]. In this work, we are going to derive a numerical solution for the three coupled nonlinear Schrödinger equations

$i{q}_{1t}+q_{1xx}+2\left({\left|q_1\right|}^2+{\left|q_2\right|}^2+{\left|q_3\right|}^2\right)q_1=0,$ (2)

$i{q}_{2t}+q_{2xx}+2\left({\left|q_1\right|}^2+{\left|q_2\right|}^2+{\left|q_3\right|}^2\right)q_2=0,$ (3)

$i{q}_{3t}+q_{3xx}+2\left({\left|q_1\right|}^2+{\left|q_2\right|}^2+{\left|q_3\right|}^2\right)q_3=0,$ (4)

with initial conditions

$q_j\left(x,0\right)=g_j\left(x\right),x_L\le x\le x_R,j=1,2,3.$ (5)

and the homogenous boundary conditions

$q_j\left(x_L,t\right)=q_j\left(x_R,t\right)=0,j=1,2,3.$ (6)

The exact soliton solution of the 3-coupled nonlinear Schrödinger equation [2] [3], is given by

$q_j\left(x,t\right)=A_j{k}_{1R}{\text{e}}^{i{\lambda }_I}\text{sech}\left({\lambda }_R+\frac{R}{2}\right),j=1,2,3.$ (7)

${\text{Δ}}^2={\left|{\alpha }_1^{\left(1\right)}\right|}^2+{\left|{\alpha }_1^{\left(2\right)}\right|}^2+{\left|{\alpha }_1^{\left(3\right)}\right|}^2,$

$A_1=\frac{{\alpha }_1^{\left(1\right)}}{\text{Δ}},A_2=\frac{{\alpha }_1^{\left(2\right)}}{\text{Δ}},A_2=\frac{{\alpha }_1^{\left(3\right)}}{\text{Δ}}$

${\text{e}}^R=\frac{{\Delta }^2}{{\left(k_1+k_1^{\text{*}}\right)}^2},\lambda =k_1\left(x+i{k}_{1}t\right),j=1,2,3.$

where ${\alpha }_1^{\left(j\right)},k_1,j=1,2,3$ are four arbitrary complex parameters. Further $2k_{1I}$ gives the amplitude of the jth mode and $2k_{1I}$ the soliton velocity.

The proposed system is of physical interest, in optical communication, and in biophysics. This system can be used to study the lunching and propagation of solitons along the three spines of an alpha-helix shape changing in protein [1] [2] [4] [5]. In this work we are going to derive a numerical method of sixth order in space and second order in time for the three coupled nonlinear Schrödinger Equations (2)-(4).

Many numerical methods for solving the coupled nonlinear Schrödinger equation are derived in the last two decades. Finite difference and finite element methods are used to solve this system by Ismail [3] [6] [7] [8] [9] [10] [11]. A conservative compact finite difference schemes are given in [12] [13]. Xing Lü studied the bright soliton collisions with shape change by intensity for the coupled Sasa-Satsuma system in the optical fiber communications in [4] and [5]. To avoid complex computations, we assume

$\begin{array}{l}{q}_1=u_1+i{u}_2\\ q_2=u_3+i{u}_4\\ q_3=u_5+i{u}_6\end{array}$ (8)

where $u_i\left(x,t\right),i=1,2,\cdots ,6$ are real functions, by separating the real and imaginary parts, and we write,

$u_1\left(x,0\right)=g_{1R}\left(x\right),u_2\left(x,0\right)=g_{1\text{I}}(\; x\; )$

$u_3\left(x,0\right)=g_{2R}\left(x\right),u_4\left(x,0\right)=g_{2\text{I}}(\; x\; )$

$u_5\left(x,0\right)=g_{3R}\left(x\right),u_6\left(x,0\right)=g_{3\text{I}}(\; x\; )$

and we have assumed

$g_1\left(x\right)=g_{1R}+i{g}_{1I},g_2\left(x\right)=g_{2R}+i{g}_{2I}\text{and}{g}_3\left(x\right)=g_{3R}+i{g}_{3I}$

where $g_{jR}\text{and}{g}_{jI},j=1,2,3$ are real functions.

by substituting (8) into(2)-(4), the following system is obtained:

$\frac{{\partial }^2{u}_1}{\partial x^2}=\frac{\partial u_2}{\partial t}-2\omega u_1$ (9)

$\frac{{\partial }^2{u}_2}{\partial x^2}=-\frac{\partial u_1}{\partial t}-2\omega u_2$ (10)

$\frac{{\partial }^2{u}_3}{\partial x^2}=\frac{\partial u_4}{\partial t}-2\omega u_3$ (11)

$\frac{{\partial }^2{u}_4}{\partial x^2}=-\frac{\partial u_3}{\partial t}-2\omega u_4$ (12)

$\frac{{\partial }^2{u}_5}{\partial x^2}=\frac{\partial u_6}{\partial t}-2\omega u_5$ (13)

$\frac{{\partial }^2{u}_6}{\partial x^2}=-\frac{\partial u_5}{\partial t}-2\omega u_6$ (14)

where

$\omega =\left(u_1^2+u_2^2\right)+\left(u_3^2+u_4^2\right)+\left(u_5^2+u_6^2\right)$ (15)

the system (2)-(4) can be written in a matrix-vector form as

$\frac{\partial u}{\partial t}+A\frac{{\partial }^{2}u}{\partial x^2}+2F\left(u\right)u=0$ (16)

where

$u=\left[\begin{array}{c}{u}_1\\ u_2\\ u_3\\ u_4\\ u_6\\ u_6\end{array}\right],A=\left[\begin{array}{cccccc}0& 1& 0& 0& 0& 0\\ -1& 0& 0& 0& 0& 0\\ 0& 0& 0& 1& 0& 0\\ 0& 0& -1& 0& 0& 0\\ 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& -1& 0\end{array}\right],F\left(u\right)=\left[\begin{array}{cccccc}0& \omega & 0& 0& 0& 0\\ -\omega & 0& 0& 0& 0& 0\\ 0& 0& 0& \omega & 0& 0\\ 0& 0& -\omega & 0& 0& 0\\ 0& 0& 0& 0& 0& \omega \\ 0& 0& 0& 0& -\omega & 0\end{array}\right]\text{.}$

Proposition 1: The three coupled nonlinear Schrödinger equations have the conserved quantities

$I_1={\displaystyle {\int }_{x_L}^{x_R}{\left|q_1\left(x,t\right)\right|}^2\text{d}x}=\cdots ={\displaystyle {\int }_{x_L}^{x_R}{\left|q_1\left(x,0\right)\right|}^2\text{d}x}$ (17)

$I_2={\displaystyle {\int }_{x_L}^{x_R}{\left|q_2\left(x,t\right)\right|}^2\text{d}x}=\cdots ={\displaystyle {\int }_{x_L}^{x_R}{\left|q_2\left(x,0\right)\right|}^2\text{d}x}$ (18)

$I_3={\displaystyle {\int }_{x_L}^{x_R}{\left|q_3\left(x,t\right)\right|}^2\text{d}x}=\cdots ={\displaystyle {\int }_{x_L}^{x_R}{\left|q_3\left(x,0\right)\right|}^2\text{d}x}$ (19)

$\begin{array}{l}{I}_4=\frac{1}{2}{\displaystyle {\int }_{x_L}^{x_R}\{-{\left|\frac{\partial q_1}{\partial x}\right|}^2-{\left|\frac{\partial q_2}{\partial x}\right|}^2-{\left|\frac{\partial q_3}{\partial x}\right|}^2+2\left({\left|q_1\right|}^2{\left|q_2\right|}^2+{\left|q_1\right|}^2{\left|q_3\right|}^2+{\left|q_2\right|}^2{\left|q_3\right|}^2\right)}\\ \begin{array}{c}\\ \end{array}+\left({\left|q_1\right|}^4+{\left|q_2\right|}^4+{\left|q_3\right|}^4\right)\}\text{d}x\end{array}$ (20)

To prove the first conserved quantity (17), we have

$\frac{\partial u_1\left(x,t\right)}{\partial t}+\frac{{\partial }^2{u}_2\left(x,t\right)}{\partial x^2}+\omega u_2\left(x,t\right)=0$ (21)

$\frac{\partial u_2\left(x,t\right)}{\partial t}-\frac{{\partial }^2{u}_1\left(x,t\right)}{\partial x^2}-\omega u_1\left(x,t\right)=0$ (22)

by multiplying (21) by $u_1\left(x,t\right)$ and (22) by $u_2\left(x,t\right)$, and by adding the resulting equations to obtain

$\frac{\partial }{\partial t}\left[u_1^2\left(x,t\right)+u_2^2\left(x,t\right)\right]+\frac{\partial }{\partial x}\left[u_1\left(x,t\right)\frac{\partial u_2\left(x,t\right)}{\partial x}-u_2\left(x,t\right)\frac{\partial u_1\left(x,t\right)}{\partial x}\right]=0$ (23)

Integrating Equation (23) with respect to x from x_L to x_R and using the vanishing boundary conditions to obtain

$\frac{\partial }{\partial t}{\displaystyle {\int }_{x_L}^{x_R}\left[u_1^2\left(x,t\right)+u_2^2\left(x,t\right)\right]\text{d}x}=0$

and this is the proof of the first conserved quantity (17) The other two conserved quantities (18) and (19) can be proved in the same way.

The exact values of the conserved quantities using the exact soliton solution (7) are given by the following formula

$I_j=\frac{2k_{1R}{\left|{\alpha }_1^{\left(j\right)}\right|}^2}{\left[{\left|{\alpha }_1^{\left(1\right)}\right|}^2+{\left|{\alpha }_1^{\left(2\right)}\right|}^2+{\left|{\alpha }_1^{\left(3\right)}\right|}^2\right]},j=1,2,3$ (24)

The paper is organized as follows. In Section 2, we derived the high order compact finite difference scheme. The Fixed-Point scheme is derived in Section 3 to solve the block nonlinear penta-diagonal systems obtained in Section 2. In Section 4, we study the stability of our scheme. The numerical results of the derived method are reported in Section 6. Finally, we draw some conclusions in Section 7.

The scheme in (33)-(38) is of sixth order accuracy in space and second order in time, and it is unconditionally stable using von-Neumann stability analysis. A nonlinear block tridiagonal system must be solved at each time step. Fixed point method is used to do this job, and this will be discussed later.

2. High Order Compact Finite Difference Scheme

The compact finite difference is a numerical method to compute finite difference approximations. Such approximations tend to be more accurate for their stencil size (i.e. their compactness) and, for hyperbolic problems, have favorable dispersive error and dissipative error properties when compared to explicit schemes [14]. In order to develop a numerical method for solving the system given in (2)-(4), the region $R=\left[x_L<x<x_R\right]\times \left[t>0\right]$ will be covered with a rectangular mesh of points with coordinates,

$x_m=x_L+mh,m=0,1,2,\cdots ,M$

$t=t_n=nk,n=0,1,2,\cdots$

where h and k are the space and time increments respectively. We denote the exact and numerical solution at the grid point $\left(x_m,t_n\right)$ by $u_{i,m}^n$ and $U_{i,m}^{n+1}$, respectively. To evaluate the second derivatives at interior nodes, we assume that they can be obtained by solving the following penta-diagonal system [14]

$\alpha {\left(\frac{{\partial }^2{u}_i}{\partial x^2}\right)}_{m-1}+{\left(\frac{{\partial }^2{u}_i}{\partial x^2}\right)}_m+\alpha {\left(\frac{{\partial }^2{u}_i}{\partial x^2}\right)}_{m+1}=\frac{b}{4h^2}{\delta }_{\hat{x}}^2{U}_{i,m}+\frac{a}{h^2}{\delta }_x^2{U}_{i,m}$ (25)

where

${\delta }_x^2{U}_{i,m}=U_{i,m+1}-2U_{i,m}+U_{i,m-1}$

${\delta }_{\hat{x}}^2{U}_{i,m}=U_{i,m+2}-2U_{i,m}+U_{i,m-2},$

and $i=1,2,\cdots ,6$.

Now, by Taylor Expansion, we can have the truncation error as the following

$\begin{array}{l}R\equiv \left(2\alpha +1-b-a\right){\left(\frac{{\partial }^2{u}_i}{\partial x^2}\right)}_m+\left(\alpha -\frac{1}{3}b-\frac{1}{12}a\right)h^2{\left(\frac{{\partial }^4{u}_i}{\partial x^4}\right)}_m\\ +\left(\frac{1}{12}\alpha -\frac{2}{45}b-\frac{1}{360}a\right)h^4{\left(\frac{{\partial }^6{u}_i}{\partial x^6}\right)}_m\end{array}$

if we solve $\left(2\alpha +1-b-a\right)=0$ and $\left(\alpha -\frac{1}{3}b-\frac{1}{12}a\right)=0$, we get

$a=\frac{4}{3}\left(1-\alpha \right)\text{and}b=\frac{1}{3}\left(10\alpha -1\right)$

so, the truncation error becomes

$R\equiv -\frac{4}{6!}\left(11\alpha -2\right)h^4{\left(\frac{{\partial }^6{u}_i}{\partial x^6}\right)}_m+O(\; h\; 6\; )$

if $\alpha =0$ then $a=\frac{4}{3}$ and $b=-\frac{1}{3}$ which gives the explicit fourth-order scheme for the second derivative. Furthermore, when $\alpha =\frac{2}{11}$, the scheme becomes sixth order accurate, in this case $a=\frac{12}{11}$ and $b=\frac{3}{11}$. By substituting these on formula (25) and after simplification, the space derivative of sixth order can be given implicitly as

$\frac{1}{11}\left[2{u^{″}}_{m-1}+11u_m+2{u^{″}}_{m+1}\right]=\frac{3}{44h^2}\left[u_{m-2}+16u_{m-1}-34u_m+16u_{m+1}+u_{m+2}\right]$ (26)

Imposing the approximation given on the spatial direction, by using (9)-(14) into Equation (26), we get

$\begin{array}{l}\left(2u_{1t,m-1}+11u_{1t,m}+2u_{1t,m+1}\right)\\ =-\frac{3}{4h^2}\left[u_{2,m-2}+16u_{2,m-1}-34u_{2,m}+16u_{2,m+1}+u_{2,m+2}\right]\\ -\left(2\omega u_{2,m-1}+11\omega u_{2,m}+2\omega u_{2,m+1}\right)\end{array}$ (27)

$\begin{array}{l}\left(2u_{2t,m-1}+11u_{2t,m}+2u_{2t,m+1}\right)\\ =\frac{3}{4h^2}\left[u_{1,m-2}+16u_{1,m-1}-34u_{1,m}+16u_{1,m+1}+u_{1,m+2}\right]\\ +\left(2\omega u_{1,m-1}+11\omega u_{1,m}+2\omega u_{1,m+1}\right)\end{array}$ (28)

$\begin{array}{l}\left(2u_{3t,m-1}+11u_{3t,m}+2u_{3t,m+1}\right)\\ =-\frac{3}{4h^2}\left[u_{4,m-2}+16u_{4,m-1}-34u_{4,m}+16u_{4,m+1}+u_{4,m+2}\right]\\ -\left(2\omega u_{4,m-1}+11\omega u_{4,m}+2\omega u_{4,m+1}\right)\end{array}$ (29)

$\begin{array}{l}\left(2u_{4t,m-1}+11u_{4t,m}+2u_{4t,m+1}\right)\\ =\frac{3}{4h^2}\left[u_{3,m-2}+16u_{3,m-1}-34u_{3,m}+16u_{3,m+1}+u_{3,m+2}\right]\\ +\left(2\omega u_{3,m-1}+11\omega u_{3,m}+2\omega u_{3,m+1}\right)\end{array}$ (30)

$\begin{array}{l}\left(2u_{5t,m-1}+11u_{5t,m}+2u_{5t,m+1}\right)\\ =-\frac{3}{4h^2}\left[u_{6,m-2}+16u_{6,m-1}-34u_{6,m}+16u_{6,m+1}+u_{6,m+2}\right]\\ -\left(2\omega u_{6,m-1}+11\omega u_{6,m}+2\omega u_{6,m+1}\right)\end{array}$ (31)

$\begin{array}{l}\left(2u_{6t,m-1}+11u_{6t,m}+2u_{6t,m+1}\right)\\ =\frac{3}{4h^2}\left[u_{5,m-2}+16u_{5,m-1}-34u_{5,m}+16u_{5,m+1}+u_{5,m+2}\right]\\ +\left(2\omega u_{5,m-1}+11\omega u_{5,m}+2\omega u_{5,m+1}\right)\end{array}$ (32)

The Crank-Nicolson discretization on the temporal direction of the 3-CNLS equation to obtain the numerical scheme

$\begin{array}{l}\left(2U_{1,m-1}^{n+1}+11U_{1,m}^{n+1}+2U_{1,m+1}^{n+1}\right)+p\left(U_{2,m-2}^{n+1}+16U_{2,m-1}^{n+1}-34U_{2,m}^{n+1}+16U_{2,m+1}^{n+1}+U_{2,m+2}^{n+1}\right)\\ =\left(2U_{1,m-1}^n+11U_{1,m}^n+2U_{1,m+1}^n\right)-p\left(U_{2,m-2}^n+16U_{2,m-1}^n-34U_{2,m}^n+16U_{2,m+1}^n+U_{2,m+2}^n\right)\\ -\left(2F_{2,m-1}^{n+1}+11F_{2,m}^{n+1}+2F_{2,m+1}^{n+1}\right)\end{array}$ (33)

$\begin{array}{l}\left(2U_{2,m-1}^{n+1}+11U_{2,m}^{n+1}+2U_{2,m+1}^{n+1}\right)-p\left(U_{1,m-2}^{n+1}+16U_{1,m-1}^{n+1}-34U_{1,m}^{n+1}+16U_{1,m+1}^{n+1}+U_{1,m+2}^{n+1}\right)\\ =\left(2U_{2,m-1}^n+11U_{2,m}^n+2U_{2,m+1}^n\right)+p\left(U_{1,m-2}^n+16U_{1,m-1}^n-34U_{1,m}^n+16U_{1,m+1}^n+U_{1,m+2}^n\right)\\ +\left(2F_{1,m-1}^{n+1}+11F_{1,m}^{n+1}+2F_{1,m+1}^{n+1}\right)\end{array}$ (34)

$\begin{array}{l}\left(2U_{3,m-1}^{n+1}+11U_{3,m}^{n+1}+2U_{3,m+1}^{n+1}\right)+p\left(U_{4,m-2}^{n+1}+16U_{4,m-1}^{n+1}-34U_{4,m}^{n+1}+16U_{4,m+1}^{n+1}+U_{4,m+2}^{n+1}\right)\\ =\left(2U_{3,m-1}^n+11U_{3,m}^n+2U_{3,m+1}^n\right)-p\left(U_{4,m-2}^n+16U_{4,m-1}^n-34U_{4,m}^n+16U_{4,m+1}^n+U_{4,m+2}^n\right)\\ -\left(2F_{4,m-1}^{n+1}+11F_{4,m}^{n+1}+2F_{4,m+1}^{n+1}\right)\end{array}$ (35)

$\begin{array}{l}\left(2U_{4,m-1}^{n+1}+11U_{4,m}^{n+1}+2U_{4,m+1}^{n+1}\right)-p\left(U_{3,m-2}^{n+1}+16U_{3,m-1}^{n+1}-34U_{3,m}^{n+1}+16U_{3,m+1}^{n+1}+U_{3,m+2}^{n+1}\right)\\ =\left(2U_{4,m-1}^n+11U_{4,m}^n+2U_{4,m+1}^n\right)+p\left(U_{3,m-2}^n+16U_{3,m-1}^n-34U_{3,m}^n+16U_{3,m+1}^n+U_{3,m+2}^n\right)\\ +\left(2F_{3,m-1}^{n+1}+11F_{3,m}^{n+1}+2F_{3,m+1}^{n+1}\right)\end{array}$ (36)

$\begin{array}{l}\left(2U_{5,m-1}^{n+1}+11U_{5,m}^{n+1}+2U_{5,m+1}^{n+1}\right)+p\left(U_{6,m-2}^{n+1}+16U_{6,m-1}^{n+1}-34U_{6,m}^{n+1}+16U_{6,m+1}^{n+1}+U_{6,m+2}^{n+1}\right)\\ =\left(2U_{5,m-1}^n+11U_{5,m}^n+2U_{5,m+1}^n\right)-p\left(U_{6,m-2}^n+16U_{6,m-1}^n-34U_{6,m}^n+16U_{6,m+1}^n+U_{6,m+2}^n\right)\\ -\left(2F_{6,m-1}^{n+1}+11F_{6,m}^{n+1}+2F_{6,m+1}^{n+1}\right)\end{array}$ (37)

$\begin{array}{l}\left(2U_{6,m-1}^{n+1}+11U_{6,m}^{n+1}+2U_{6,m+1}^{n+1}\right)-p\left(U_{5,m-2}^{n+1}+16U_{5,m-1}^{n+1}-34U_{5,m}^{n+1}+16U_{5,m+1}^{n+1}+U_{5,m+2}^{n+1}\right)\\ =\left(2U_{6,m-1}^n+11U_{6,m}^n+2U_{6,m+1}^n\right)+p\left(U_{5,m-2}^n+16U_{5,m-1}^n-34U_{5,m}^n+16U_{5,m+1}^n+U_{5,m+2}^n\right)\\ +\left(2F_{5,m-1}^{n+1}+11F_{5,m}^{n+1}+2F_{5,m+1}^{n+1}\right)\end{array}$ (38)

where

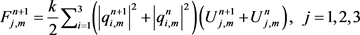(39)

and $p=\frac{3k}{8h^2}$.

Equations (33)-(38) form a block pentadiagonal system as the following

$\left[\begin{array}{cccccccc}C& D& E& 0& \cdots & \cdots & \cdots & 0\\ B& C& D& E& 0& & & ⋮\\ A& B& C& D& E& 0& & ⋮\\ 0& \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & ⋮\\ ⋮& \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & 0\\ ⋮& & 0& A& B& C& D& E\\ ⋮& & & 0& A& B& C& D\\ 0& \cdots & \cdots & \cdots & 0& A& B& C\end{array}\right]\left[\begin{array}{c}{\underset{\_}{U}}_{i,1}\\ {\underset{\_}{U}}_{i,2}\\ {\underset{\_}{U}}_{i,3}\\ ⋮\\ ⋮\\ {\underset{\_}{U}}_{i,M-3}\\ {\underset{\_}{U}}_{i,M-2}\\ {\underset{\_}{U}}_{i,M-1}\end{array}\right]=\left[\begin{array}{c}{G}_{i,1}\\ G_{i,2}\\ G_{i,3}\\ ⋮\\ ⋮\\ G_{i,M-3}\\ G_{i,M-2}\\ G_{i,M-1}\end{array}\right]$ (40)

where $i=1,2,3$.

$\begin{array}{l}{\underset{\_}{U}}_{1,m}=\left[\begin{array}{c}{U}_{1,m}^{n+1}\\ U_{2,m}^{n+1}\end{array}\right],{\underset{\_}{U}}_{2,m}=\left[\begin{array}{c}{U}_{3,m}^{n+1}\\ U_{4,m}^{n+1}\end{array}\right],{\underset{\_}{U}}_{3,m}=\left[\begin{array}{c}{U}_{5,m}^{n+1}\\ U_{6,m}^{n+1}\end{array}\right]\\ A=\left[\begin{array}{cc}0& -p\\ p& 0\end{array}\right]=E\\ B=\left[\begin{array}{cc}2& -16p\\ 16p& 2\end{array}\right]=D\\ C=\left[\begin{array}{cc}11& 34p\\ -34p& 11\end{array}\right]\\ G_{1,m}=\left[\begin{array}{c}{f}_{1,m}\\ f_{2,m}\end{array}\right],G_{2,m}=\left[\begin{array}{c}{f}_{3,m}\\ f_{4,m}\end{array}\right],G_{3,m}=\left[\begin{array}{c}{f}_{5,m}\\ f_{6,m}\end{array}\right]\end{array}$

$\begin{array}{c}{f}_{1,m}=\left(2U_{1,m-1}^n+11U_{1,m}^n+2U_{1,m+1}^n\right)\\ -p\left(U_{2,m-2}^n+16U_{2,m-1}^n-34U_{2,m}^n+16U_{2,m+1}^n+U_{2,m+2}^n\right)\\ -\left(2F_{2,m-1}^{n+1}+11F_{2,m}^{n+1}+2F_{2,m+1}^{n+1}\right)\end{array}$

$\begin{array}{c}{f}_{2,m}=\left(2U_{2,m-1}^n+11U_{2,m}^n+2U_{2,m+1}^n\right)\\ +p\left(U_{1,m-2}^n+16U_{1,m-1}^n-34U_{1,m}^n+16U_{1,m+1}^n+U_{1,m+2}^n\right)\\ +\left(2F_{1,m-1}^{n+1}+11F_{1,m}^{n+1}+2F_{1,m+1}^{n+1}\right)\end{array}$

$\begin{array}{c}{f}_{3,m}=\left(2U_{3,m-1}^n+11U_{3,m}^n+2U_{3,m+1}^n\right)\\ -p\left(U_{4,m-2}^n+16U_{4,m-1}^n-34U_{4,m}^n+16U_{4,m+1}^n+U_{4,m+2}^n\right)\\ -\left(2F_{4,m-1}^{n+1}+11F_{4,m}^{n+1}+2F_{4,m+1}^{n+1}\right)\end{array}$

$\begin{array}{c}{f}_{4,m}=\left(2U_{4,m-1}^n+11U_{4,m}^n+2U_{4,m+1}^n\right)\\ +p\left(U_{3,m-2}^n+16U_{3,m-1}^n-34U_{3,m}^n+16U_{3,m+1}^n+U_{3,m+2}^n\right)\\ +\left(2F_{3,m-1}^{n+1}+11F_{3,m}^{n+1}+2F_{3,m+1}^{n+1}\right)\end{array}$

$\begin{array}{c}{f}_{5,m}=\left(2U_{5,m-1}^n+11U_{5,m}^n+2U_{5,m+1}^n\right)\\ -p\left(U_{6,m-2}^n+16U_{6,m-1}^n-34U_{6,m}^n+16U_{6,m+1}^n+U_{6,m+2}^n\right)\\ -\left(2F_{6,m-1}^{n+1}+11F_{6,m}^{n+1}+2F_{6,m+1}^{n+1}\right)\end{array}$

$\begin{array}{c}{f}_{6,m}=\left(2U_{6,m-1}^n+11U_{6,m}^n+2U_{6,m+1}^n\right)\\ +p\left(U_{5,m-2}^n+16U_{5,m-1}^n-34U_{5,m}^n+16U_{5,m+1}^n+U_{5,m+2}^n\right)\\ +\left(2F_{5,m-1}^{n+1}+11F_{5,m}^{n+1}+2F_{5,m+1}^{n+1}\right)\end{array}$

The present method is of second order accuracy in time and sixth order in space, it is unconditionally stable, see Ismail [11]. The resulting system is a block nonlinear penta-diagonal system which can be solved by fixed point method and this will be discussed next.

3. Fixed Point Method

Since the compact finite difference scheme (40) is nonlinear and implicit, an iterative method is needed to solve it. The fixed point for solving the resulting system can be given in a matrix vector form as follows [6] [14].

$\left[\begin{array}{cccccccc}C& D& E& 0& \cdots & \cdots & \cdots & 0\\ B& C& D& E& 0& & & ⋮\\ A& B& C& D& E& 0& & ⋮\\ 0& \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & ⋮\\ ⋮& \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & 0\\ ⋮& & 0& A& B& C& D& E\\ ⋮& & & 0& A& B& C& D\\ 0& \cdots & \cdots & \cdots & 0& A& B& C\end{array}\right]\left[\begin{array}{c}{\underset{\_}{U}}_{i,1}^{\left(s+1\right)}\\ {\underset{\_}{U}}_{i,2}^{\left(s+1\right)}\\ {\underset{\_}{U}}_{i,3}^{\left(s+1\right)}\\ ⋮\\ ⋮\\ {\underset{\_}{U}}_{i,M-3}^{\left(s+1\right)}\\ {\underset{\_}{U}}_{i,M-2}^{\left(s+1\right)}\\ {\underset{\_}{U}}_{i,M-1}^{\left(s+1\right)}\end{array}\right]=\left[\begin{array}{c}{G}_{i,1}^{\left(s\right)}\\ G_{i,2}^{\left(s\right)}\\ G_{i,3}^{\left(s\right)}\\ ⋮\\ ⋮\\ G_{i,M-3}^{\left(s\right)}\\ G_{i,M-2}^{\left(s\right)}\\ G_{i,M-1}^{\left(s\right)}\end{array}\right]$ (41)

where $i=1,2,3$ then

$\begin{array}{l}{\underset{\_}{U}}_{1,m}^{\left(s+1\right)}=\left[\begin{array}{c}{U}_{1,m}^{n+1,\left(s+1\right)}\\ U_{2,m}^{n+1,\left(s+1\right)}\end{array}\right],{\underset{\_}{U}}_{2,m}^{\left(s+1\right)}=\left[\begin{array}{c}{U}_{3,m}^{n+1,\left(s+1\right)}\\ U_{4,m}^{n+1,\left(s+1\right)}\end{array}\right],{\underset{\_}{U}}_{3,m}^{\left(s+1\right)}=\left[\begin{array}{c}{U}_{5,m}^{n+1,\left(s+1\right)}\\ U_{6,m}^{n+1,\left(s+1\right)}\end{array}\right]\\ G_{1,m}^{\left(s\right)}=\left[\begin{array}{c}{f}_{1,m}^{\left(s\right)}\\ f_{2,m}^{\left(s\right)}\end{array}\right],G_{2,m}=\left[\begin{array}{c}{f}_{3,m}^{\left(s\right)}\\ f_{4,m}^{\left(s\right)}\end{array}\right],G_{3,m}=\left[\begin{array}{c}{f}_{5,m}^{\left(s\right)}\\ f_{6,m}^{\left(s\right)}\end{array}\right]\end{array}$

$\begin{array}{c}{f}_{1,m}=\left(2U_{1,m-1}^n+11U_{1,m}^n+2U_{1,m+1}^n\right)\\ -p\left(U_{2,m-2}^n+16U_{2,m-1}^n-34U_{2,m}^n+16U_{2,m+1}^n+U_{2,m+2}^n\right)\\ -\left(2F_{2,m-1}^{n+1,\left(s\right)}+11F_{2,m}^{n+1,\left(s\right)}+2F_{2,m+1}^{n+1,(\; s\; )}\right)\end{array}$

$\begin{array}{c}{f}_{2,m}=\left(2U_{2,m-1}^n+11U_{2,m}^n+2U_{2,m+1}^n\right)\\ +p\left(U_{1,m-2}^n+16U_{1,m-1}^n-34U_{1,m}^n+16U_{1,m+1}^n+U_{1,m+2}^n\right)\\ +\left(2F_{1,m-1}^{n+1,\left(s\right)}+11F_{1,m}^{n+1,\left(s\right)}+2F_{1,m+1}^{n+1,(\; s\; )}\right)\end{array}$

$\begin{array}{c}{f}_{3,m}=\left(2U_{3,m-1}^n+11U_{3,m}^n+2U_{3,m+1}^n\right)\\ -p\left(U_{4,m-2}^n+16U_{4,m-1}^n-34U_{4,m}^n+16U_{4,m+1}^n+U_{4,m+2}^n\right)\\ -\left(2F_{4,m-1}^{n+1,\left(s\right)}+11F_{4,m}^{n+1,\left(s\right)}+2F_{4,m+1}^{n+1,(\; s\; )}\right)\end{array}$

$\begin{array}{c}{f}_{4,m}=\left(2U_{4,m-1}^n+11U_{4,m}^n+2U_{4,m+1}^n\right)\\ +p\left(U_{3,m-2}^n+16U_{3,m-1}^n-34U_{3,m}^n+16U_{3,m+1}^n+U_{3,m+2}^n\right)\\ +\left(2F_{3,m-1}^{n+1,\left(s\right)}+11F_{3,m}^{n+1,\left(s\right)}+2F_{3,m+1}^{n+1,(\; s\; )}\right)\end{array}$

$\begin{array}{c}{f}_{5,m}=\left(2U_{5,m-1}^n+11U_{5,m}^n+2U_{5,m+1}^n\right)\\ -p\left(U_{6,m-2}^n+16U_{6,m-1}^n-34U_{6,m}^n+16U_{6,m+1}^n+U_{6,m+2}^n\right)\\ -\left(2F_{6,m-1}^{n+1,\left(s\right)}+11F_{6,m}^{n+1,\left(s\right)}+2F_{6,m+1}^{n+1,(\; s\; )}\right)\end{array}$

$\begin{array}{c}{f}_{6,m}=\left(2U_{6,m-1}^n+11U_{6,m}^n+2U_{6,m+1}^n\right)\\ +p\left(U_{5,m-2}^n+16U_{5,m-1}^n-34U_{5,m}^n+16U_{5,m+1}^n+U_{5,m+2}^n\right)\\ +\left(2F_{5,m-1}^{n+1,\left(s\right)}+11F_{5,m}^{n+1,\left(s\right)}+2F_{5,m+1}^{n+1,(\; s\; )}\right)\end{array}$

$F_{j,m}^{n+1,\left(s\right)}=\frac{k}{2}\underset{L=1}{\overset{3}{{\displaystyle \sum }}}\left({\left|q_i^{n+1,\left(s\right)}\right|}^2+{\left|q_{i,m}^n\right|}^2\right)\left(U_{j,m}^{n+1,\left(s\right)}+U_{j,m}^n\right),j=1,2,3$

where the superscript s denotes the sth iterate for solving the nonlinear system of equations for each iteration. The system in (41) can be solved by Crout’s method, where we need only one LU factorization for the block-pentadiagonal matrix at the beginning of the calculation, and the solutions of lower and upper pentadiagonal block systems at each iteration are required only. The initial iterate $U_m^{n+1,\left(0\right)}$ can be chosen as $U_m^{n+1,\left(0\right)}=U_m^n$. We apply the iterative schemes till the following condition

${\Vert U_m^{n+1,\left(s+1\right)}-U_m^{n+1,\left(s\right)}\Vert }_{\infty }\le {10}^{-6}$

is satisfied.

4. Stability

To study the stability of the scheme (2)-(4) we use the Von Neumann method, we do the following.

As we know Von Neumann method can be applied only for linear schemes, so we must study the linear version of (2)-(4) by freezing the nonlinear terms by assuming

$\omega =\frac{k}{2}m\underset{j=1}{\overset{3}{{\displaystyle \sum }}}{\left|q_j\right|}^2=\text{constant}$

where $j=1,2,3$.

The linear version of imposing the approximation given on the spatial direction (26) and the Crank-Nicolson discretization on the temporal direction of the Equations (2)-(4) can be displayed as follows:

$\begin{array}{l}i\left(2q_{j,m-1}^{n+1}+11q_{j,m}^{n+1}+2q_{j,m+1}^{n+1}\right)+\omega p_2\left(2q_{j,m-1}^{n+1}+11q_{j,m}^{n+1}+2q_{j,m+1}^{n+1}\right)\\ +p_1\left(q_{j,m-2}^{n+1}+16q_{j,m-1}^{n+1}-34q_{j,m}^{n+1}+16q_{j,m+1}^{n+1}+q_{j,m+2}^{n+1}\right)\\ =i\left(2q_{j,m-1}^n+11q_{j,m}^n+2q_{j,m+1}^n\right)-\omega p_2\left(2q_{j,m-1}^n+11q_{j,m}^n+2q_{j,m+1}^n\right)\\ -p_1\left(q_{j,m-2}^n+16q_{j,m-1}^n-34q_{j,m}^n+16q_{j,m+1}^n+q_{j,m+2}^n\right)\end{array}$ (42)

where $p_1=p=\frac{3k}{8h^2}$ and $p_2=\frac{k}{2}$.

We assume

$q_{j,m}^n={\text{e}}^{\alpha nk}{\text{e}}^{i\beta mh},j=1,2,3.$ (43)

By using (43) we can deduce the following relations

$q_{j,m-1}^n-2q_{j,m}^n+q_{j,m+1}^n=-4{\sin }^2\left(\frac{\beta h}{2}\right)q_j^n{\text{e}}^{i\beta mh}$ (44)

By substituting (43) and (44) into (42), we can get

$\begin{array}{l}i\left[11+4\cos \left(\beta h\right)\right]{\text{e}}^{\alpha \left(n+1\right)k}+\omega p_2\left[11+4\cos \left(\beta h\right)\right]{\text{e}}^{\alpha \left(n+1\right)k}\\ +2p_1\left[\cos \left(\beta h\right)+16\cos \left(\beta h\right)-17\right]{\text{e}}^{\alpha \left(n+1\right)k}\\ =i\left[11+4\cos \left(\beta h\right)\right]{\text{e}}^{\alpha nk}-\omega p_2\left[11+4\cos \left(\beta h\right)\right]e^{\alpha nk}\\ -2p_1\left[\cos \left(\beta h\right)+16\cos \left(\beta h\right)-17\right]{\text{e}}^{\alpha nk}\end{array}$ (45)

We can write equations (45) as

$\left[\left(\omega p_2{\gamma }_1+2p_1{\gamma }_2\right)+i{\gamma }_1\right]{\text{e}}^{\alpha k}=-\left(\omega p_2{\gamma }_1+2p_1{\gamma }_2\right)+i{\gamma }_1$

where

${\gamma }_1=11+4\cos \left(\beta h\right)$ and ${\gamma }_2=2p_1\left[\cos \left(\beta h\right)+16\cos \left(\beta h\right)-17\right]$

then

${\text{e}}^{\alpha k}=\frac{-\left(\omega p_2{\gamma }_1+2p_1{\gamma }_2\right)+i{\gamma }_1}{\left(\omega p_2{\gamma }_1+2p_1{\gamma }_2\right)+i{\gamma }_1}$

${\left|{\text{e}}^{\alpha k}\right|}^2=\frac{{\left(\omega p_2{\gamma }_1+2p_1{\gamma }_2\right)}^2+{\gamma }_1^2}{{\left(\omega p_2{\gamma }_1+2p_1{\gamma }_2\right)}^2+{\gamma }_1^2}=1$

So, the necessary condition for stability using Von Neumann is the absolute maximum of ${\text{e}}^{\alpha k}$ is less than or equal 1 and it is clearly satisfied then the scheme is unconditionally stable according to Von Neumann stability analysis.

5. Numerical Results

In this section we conduct some typical numerical examples to verify the accuracy, conservation laws, computational efficiency and some physical interaction phenomena described by 3-coupled nonlinear Schrödinger equations.

5.1. Single Soliton

In this test, we choose the initial condition as

$q_j\left(x,0\right)=A_j{k}_{1R}\exp \left(i{k}_{1I}x\right)\text{sech}\left(k_{1R}x+\frac{R}{2}\right)$ (46)

$A_j=\frac{{\alpha }_1^{\left(j\right)}}{\Delta },{\text{e}}^R=\frac{{\Delta }^2}{{\left(k_1+k_1^{*}\right)}^2},{\Delta }^2=\underset{j=1}{\overset{3}{{\displaystyle \sum }}}{\left|{\alpha }_1^{\left(j\right)}\right|}^2,j=1,2,3$

The following set of parameters are used

$\begin{array}{l}h=0.1,k=0.001,x_l=-30,t=0,2,\cdots ,10\\ {\alpha }_1^{\left(1\right)}=1+i,{\alpha }_1^{\left(2\right)}=0.8+0.8i,{\alpha }_1^{\left(3\right)}=0.5+0.5i,k_1=1+0.5i\end{array}$

The conserved quantities and the error for our scheme are displayed in Table 1. We have noticed that the method is conserved the conserved quantities exactly and highly accurate results are obtained. The profile of $\left|q_1\right|,\left|q_2\right|$ and $\left|q_3\right|$ at different times are displayed in Figure 1, Figure 2 and Figure 3 respectively.

To test the convergent rate in space and time of the proposed schemes. We define the $L_{\infty }$ error norm by

where $u_{1.m}^n$ and $U_{1,m}^n$ are respectively the exact and the numerical solution at the grid point $\left(x_m,t_n\right)$. In this experiment, we take $T=10$.

The convergent rate “order” is calculated by the formula.

Table 1. Errors & conserved quantities of single solitons.

Figure 1. Simulation of single soliton ${\left|q_1\right|}^2$.

Figure 2. Simulation of single soliton ${\left|q_2\right|}^2$.

Figure 3. Simulation of single soliton ${\left|q_3\right|}^2$.

order (rate of convergent in space) $=\frac{\ln \left(\frac{L_{\infty }\left(h_1\right)}{L_{\infty }\left(h_2\right)}\right)}{\ln \left(\frac{h_1}{h_2}\right)}$

order (rate of convergent in time) $=\frac{\ln \left(\frac{L_{\infty }\left(k_1\right)}{L_{\infty }\left(k_2\right)}\right)}{\ln \left(\frac{k_1}{k_2}\right)}$

To calculate the convergent rate in space, we take the time step k sufficiently small and the error from temporal truncation is relatively small $k=0.0001$. From Table 2, we can easily see that the rate of convergent is 6 as we claim in this work.

To check the temporal convergent rate, we fix the spatial step h small enough so that the truncation from space is negligible such as $h=0.01$. The results are given in Table 3 which indicate that the order is 2 as we claim in the text.

To improve the temporal accuracy of the proposed method, we use Richardson Extrapolation on the computed solution to eliminate the lower-order term in the truncation error.

Since our method applied to the scheme is in the form $O\left(k^2\right)+O\left(h^6\right)$, we use

$u_m^n\approx \frac{4U_m^n\left(k/2\right)-U_m^n\left(k\right)}{3}$ (47)

to eliminate the term $O\left(k^2\right)$, which makes the final solution fourth-order accurate in time dimension. Although the extrapolation requires two times as

Table 2. Rate of convergence of single solitons ( $k=0.0001$ ).

Table 3. Rate of convergence of single solitons ( $h=0.01$ ).

much computation as the original scheme plus the application of the formula (47). By using the parameters

$\begin{array}{l}h=0.1,k=0.002,0.001,k_1=1+0.5i,\\ {\alpha }_1^{\left(1\right)}=1+i,{\alpha }_1^{\left(2\right)}=0.8+0.8i,{\alpha }_1^{\left(3\right)}=0.5+0.5i\end{array}$

with the extrapolation formula (47), we obtain results which are displayed in Table 4.

5.2. Interaction of Two Solitons

To study the interaction of two solitons with different parameters, we choose the initial condition as a sum of two single solitons of the form

$q_j\left(x,t=0\right)=q_j^{\left(1\right)}\left(x,0\right)+q_j^{\left(2\right)}\left(x,0\right),j=1,2,3.$ (48)

where

$q_j^{\left(1\right)}\left(x,0\right)=A_j^{\left(1\right)}{k}_{1R}\exp \left(i{k}_{1I}\left(x+x_0\right)\right)\text{sech}\left(k_{1R}\left(x+x_0\right)+\frac{R}{2}\right)$

$q_j^{\left(2\right)}\left(x,0\right)=A_j^{\left(2\right)}{k}_{1R}\exp \left(i{k}_{1I}\left(x-x_0\right)\right)\text{sech}\left(k_{1R}\left(x-x_0\right)+\frac{R}{2}\right)$

For all examples in the case of interaction, we choose the set of parameters

$h=0.1,k=0.01,x_L=-50,x_R=50,x_0=25$

$k_1=1+0.8i,k_2=1-0.4i$

together with different values of $\left\{{\alpha }_1^{\left(j\right)},{\alpha }_2^{\left(j\right)},j=1,2,3\right\}$ for each test. We will study the dynamics of the following cases.

5.2.1. Case 1

In this test we choose the set of parameters

${\alpha }_1^{\left(1\right)}=5,{\alpha }_1^{\left(2\right)}=3.5,{\alpha }_1^{\left(3\right)}=1,{\alpha }_2^{\left(1\right)}=10,{\alpha }_2^{\left(2\right)}=7,{\alpha }_2^{\left(3\right)}=2.$

For this test, we have noticed that

$\frac{{\alpha }_1^{\left(1\right)}}{{\alpha }_2^{\left(1\right)}}=\frac{{\alpha }_1^{\left(2\right)}}{{\alpha }_2^{\left(2\right)}}=\frac{{\alpha }_1^{\left(3\right)}}{{\alpha }_2^{(\; 3\; )}}$

which gives us elastic interaction. The interaction scenario is displayed in Figure 4.

Table 4. Richardson extrapolation using $L_{\infty }$ norm.

5.2.2. Case 2

In this test we choose the set of parameters

${\alpha }_1^{\left(1\right)}=5,{\alpha }_1^{\left(2\right)}=3.5,{\alpha }_1^{\left(3\right)}=1,{\alpha }_2^{\left(1\right)}=2,{\alpha }_2^{\left(2\right)}=2.5,{\alpha }_2^{\left(3\right)}=0.4$

For this test, we have noticed that the formula

$\frac{{\alpha }_1^{\left(1\right)}}{{\alpha }_2^{\left(1\right)}}\ne \frac{{\alpha }_1^{\left(2\right)}}{{\alpha }_2^{\left(2\right)}}\ne \frac{{\alpha }_1^{\left(3\right)}}{{\alpha }_2^{(\; 3\; )}}$

is unsatisfied which gives us inelastic interaction and it is clear in Figure 5.

For all cases, the conserved quantities given in Table 5, we have noticed that our method is conserved the conserved quantities exactly.

Figure 4. Elastic interaction of two solitons.

Figure 5. Inelastic interaction of two solitons.

Table 5. Conserved quantities of interaction of two solitons.

6. Conclusion

In this work, we have derived a highly accurate finite difference scheme for solving the 3-coupled nonlinear Schrödinger equation. The scheme is of sixth order in space and second order in time, it is unconditionally stable. A fixed point is used to solve the nonlinear block penta-diagonal system obtained. Single soliton solution and the conserved quantities are used to highlight the robustness of the method. The interaction of two solitons is discussed in detail for different parameters to produce elastic and inelastic interactions. This behavior is agreeing with [1] [2] [3] with the highest accuracy. The derived method can be used to solve similar nonlinear problems.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Kanna, T. and Lakshmanan, M. (2003) Exact Soliton Solutions of Coupled Nonlinear Schrödinger Equation: Shape-Changing Collisions, Logic Gates and Partially Co-Herent Soliton. Physical Review, 67, 046617-046625. https://doi.org/10.1103/PhysRevE.67.046617
[2]	Kanna, T. and Lakshmanan, M. (2001) Exact Soliton Solutions, Shape Changing Collisions and Partially Coherent Solitons in Coupled Nonlinear Schrödinger Equations. Physical Review Letter, 86, 5043-5046. https://doi.org/10.1103/PhysRevLett.86.5043
[3]	Ismail, M.S. and Alaseri, S.H. (2016) Computational Methods for Three Coupled Nonlinear Schrödinger Equations. Applied Mathematics, 7, 2110-2131. https://doi.org/10.4236/am.2016.717168
[4]	Lü X. and Lin, F.H. (2016) Soliton Excitation and Shape-Changing Collisions in Alpha Helical Portions with Interspine Coupling at Higher Order. Communications in Nonlinear Science and Numerical Simulation, 32, 241-261. https://doi.org/10.1016/j.cnsns.2015.08.008
[5]	Lü, X. (2014) Bright-Soliton Collisions with Shape Change by Intensity Redistribution for the Coupled Sasa-Satsuma System in the Optical Fiber Communications. Communications in Nonlinear Science and Numerical Simulation, 19, 3969-3987. https://doi.org/10.1016/j.cnsns.2014.03.013
[6]	Ismail, M.S. (2008) Numerical Solution of Coupled Nonlinear Schrödinger Equation by Galerkin Method. Mathematics and Computers in Simulation, 78, 532-547. https://doi.org/10.1016/j.matcom.2007.07.003
[7]	Ismail, M.S., Al-Basyouni, K.S. and Aydin, A. (2015) Conservative Finite Difference Schemes for the Chiral Nonlinear Schrödinger Equation. Boundary Value Problem, 2015, Article No. 89. https://doi.org/10.1186/s13661-015-0350-4
[8]	Ismail, M.S. (2008) A Fourth-Order Explicit Schemes for the Coupled Nonlinear Schrödinger Equation. Applied Mathematics and Computation, 196, 273-284. https://doi.org/10.1016/j.amc.2007.05.059
[9]	Ismaila, M.S. and Tahab, T.R. (2001) Numerical Simulation of Coupled Nonlinear Schrödinger Equation. Mathematics and Computers in Simulation, 56, 547-562. https://doi.org/10.1016/S0378-4754(01)00324-X
[10]	Ismail, M.S. and Alamri, S.Z. (2004) Highly Accurate Finite Difference Method for Coupled Nonlinear Schrödinger Equation. International Journal of Computer Mathematics, 81, 333-351. https://doi.org/10.1080/00207160410001661339
[11]	Ismail, M.S. and Tahab, T.R. (2007) A Linearly Implicit Conservative Scheme for the Coupled Nonlinear Schrödinger Equation. Mathematics and Computers in Simulation, 74, 302-311. https://doi.org/10.1016/j.matcom.2006.10.020
[12]	Hu, X.L. and Zhang, L.M. (2014) Conservative Compact Difference Schemes for the Coupled Nonlinear Schrödinger System. Numerical Methods Partial Differential Equations, 30, 749-772. https://doi.org/10.1002/num.21826
[13]	Kong, L.H., Hong, J.L., Ji, L.H. and Zhu, P.F. (2015) Compact and Efficient Conservative Schemes for Coupled Nonlinear Schrödinger Equations. Numerical Methods Partial Differential Equations, 31, 1814-1843. https://doi.org/10.1002/num.21969
[14]	Li, J.C. and Chen, Y.-T. (2008) Computational Partial Differential Equations Using MATLAB. Chapman and Hall, New York. https://doi.org/10.1201/9781420089059