Effect of the Number of Donor Atoms in Calix[4]arene Derivatives for Selective Complexation and Extraction of Mercury(II) Cations, Thermodynamics and Extraction Studies ()
1. Introduction
Mercury (Hg) is a highly toxic metal that contaminates our water and air supplies. Approximately two-thirds of the Hg in natural environments are of anthropogenic origin [1]. Burning of fossil fuels, such as petroleum, natural gas and coal, is the most important contributor to the total environmental Hg budget, since they contain approximately 0.2 ppm of Hg2. Mercury can be found in significant amounts in wastes from chlor-alkali manufacturing plants, electrical and electronics manufacturing, and sulphide ore roasting operations. Exposure to Hg can have toxic effects on reproduction, the central nervous system, liver, and kidneys, and cause sensory and psychological impairments. Mercury in industrial effluents and flue gas is usually recovered using chelating agents, which are not reusable after Hg is removed by distillation [2]. Alternative treatment methods are greatly needed to keep Hg out of the environment.
In order to minimize the adverse effects of Hg in the environment, it is desirable to find ways to capture it before it becomes a problem. Several techniques are available for this including precipitation, ion exchange and adsorption.
The ability of a material to capture metals is controlled in part by the number of available functional groups used for binding metals. Functional groups with a known affinity for specific metals can be attached to other substances in order to create an effective adsorbent [3]. The thiol (-SH) group is known to form stable complexes with soft heavy metals of high polarizability such as Hg, Ag, Au, and to a lesser extent, Cd and Zn, while failing to coordinate well with the more abundant smaller, lighter metals such as Ca, Na, and Mg [4].
Recent studies speculated that the reaction between mercury and sulphur groups present in the adsorbent materials accounted for high adsorption capacity, in this direction, Meng et al. [5] reported the ability of used tyre rubber containing sulphur groups to scavenging the Hg(II) from solutions [6]. Sreedhar et al. [7] performed batch experiments with polysulphide treated coconut husk for Hg(II) binding. Since mercury species show a high affinity towards sulphur, a method of improving adsorption potential of activated carbon could be based on immobilising sulphur on the material. Serrano et al. [8] utilised commercial activated carbon loaded with sulphur groups for the removal of Hg(II), Pb(II) and Cd(II) ions from aqueous solutions.
Calixarenes [9], cyclic oligomers of phenol-formaldehyde condensates, have received much attention over the past decade as a fascinating class of cyclophanes possessing ionic and molecular-binding properties. Derivatives containing a wide range of functional groups have been synthesized and shown to exhibit different degrees of receptor ionophoric activity [10]. A number of calixarene derivatives containing pendant ether, amide, ketonic, and ester groups have been reported thermodynamic of complexation with unit and bivalent cations [11] [12].
In this work, the effect of the number of donor atoms over the binding Hg2+ metal cation is reported. Thermodynamic data (conductivity, calorimetry and potentiometry) and extraction result in an immiscible solvent system.
2. Experimental Part
2.1. Chemicals
p-tert-Butylcalix[4]arene, bromoacetonitrile, diethyl chlorothiophosphate potassium carbonate and potassium hydrogen carbonate were purchased from Aldrich, Lithium aluminium tetra hydride, 18-crown-6 (18C6), Tetra-n-butylammonium perchlorate (TBAP) and tetra-n-butylammonium bromide were purchased from Fluka were used without further purification. Metal cation salts as perchlorate mecury(II) and potassium(I), were dried over P4O10 under vacuum for several days before use.
Acetonitrile (HPLC grade, Hayman Limited, high purity reagent), THF (tetrahidrofuran), methanol (Fisher reagent, 99%) ethanol (HPLC grade Fisher) dichloromethane (Fisher) was used without further purification, picric acid analytical grade was purchased from Aldrich.
2.2. Synthesis
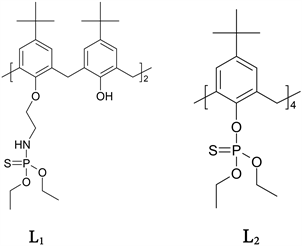
The ligands 5,11, 17, 23-tetra-tert-butyl[25, 27-bis(diethylthiophosphate amino)ethoxy-26, 28-bis(hydroxy)]-calix[4]arene, (L1) and 5, 11, 17, 23-tetra-tertbutylcalix[4]arene, tetra diethyl thiophosphate; (L2) was have synthesize, following of technique were descript by our group [13] [14] and in the search the selective macrocycle ligand for the attach mercury metal cations was found the functionalized arms groups that have donor atoms phosphorus, sulphur, nitrogen and oxygen. The oxygen as a hard Lewis base atom that interacts preferentially with cation type hard Lewis acid, while nitrogen is borderline base, sulphur and phosphorus are typical soft atoms interacts preferentially with soft cations, such as silver and mercury [2].
Synthesis of 5,11, 17, 23-tetra-tert-butyl[25, 27-bis(diethylthiophosphate amino)ethoxy-26, 28-bis(hydroxy)]-calix[4]arene, (L1)
L1 was synthesized by the method previously described by Danil de Namor and co-workers [13], the ligand was characterized by Thermo Scientific Flash Smart Series Elemental Analyzers equipment. Elemental analysis was carried out at the University of Surrey, calculated % C, 64.71, H, 8.15, N 2.70; found % C 64.62, H 8.12, N 2.67. and 1H and 13 C NMR.
1H NMR (300 MHz, in CDCl3); δ (ppm), J (Hz); 8.59 (s, 2H, Ar-OH), 7.03 (s, 8H, Ar-H), 5.60 (t, 2H, J = 11.10, -CH2-NH-), 4.34 (d, 4H, J = 13.20, Ar-CH2ax-Ar), 4.13 (m, 12H, -O-CH2-CH2, O-CH2-CH3), 3.62 (m, 4H, -CH2-CH2-NH), 3.38 (d, 4H, J = 12.91, Ar-CH2eq-Ar), 1.32 (t, 12H, O-CH2-CH3), 1.24 (s, 18H, -C-(CH3)3), 1.15 (s, 18H, -C-(CH3)3).
13C NMR (300 MHz) (CDCl3) δC ppm; 149.88, 148.84, 147.97, 142.41, 133.48, 127.67, 126.09, 125.62 (Ar), 77.26 (OCH2CH2NH), 63.08, 62.99 (OCH2CH3), 42.44 (OCH2CH2NH), 34.25, 33.88 (C(CH3)3, 32.41 (ArCH2Ar), 31.63, 31.51 (C(CH3)3, and 16.15, 16.04 (OCH2CH3).
Synthesis of 5, 11, 17, 23-tetra-tert-butylcalix[4]arene, tetra diethyl thiophosphate (L2)
L2 was synthesized as previously reported by our group [14] [15], the ligand was characterized by Elemental analysis was carried out at the University of Surrey, calculated % C, 57.31, H, 7.37; found % C 57.13, H 7.59 and 1H and 13C NMR.
1H NMR (300 MHz, in CDCl3); δ (ppm), J (Hz); 8.90 (s, 8H, Ar-H), 4.85 (d, 4H, J = 14.10, Ar-CH2ax-Ar), 4.29 (m, 16H, -O-CH2-CH3), 3.24 (d, 4H, J = 13.80, Ar-CH2eq-Ar), 1.34 (t, 24H, O-CH2-CH3), 1.07 (s, 36H, -C-(CH3)3).
13C NMR (300 MHz) (CDCl3) δC ppm; 146.78, 143.24, 134.32, 125.92 (Ar), 65.52 (OCH2CH3), 34.36 (C(CH3)3, 32.41 (ArCH2Ar), 31.80 (C(CH3)3, and 16.44 (OCH2CH3).
2.3. Conductimetric
The Wayne-Kerr B642 is an autobalance ratio arm bridge for the measurement of impedance. During the conductance measurements, the magnitude of the capacitance and the conductance are monitored on the two meters. Each of these meters has for decades, which are operated in succession. Small signal are placed between the decade control knobs to indicate the decimal points. The control knobs are selected automatically by operation of the range switch. The sensitivity of the meter can be switched to one of these normal positions to adjust the apparatus manually, the accuracy of the bridge is determinated by its internal sources and it was found to be 0.1% for all decades in use.
For the determination of the cell constant of the conductivity cell, an aqueous solution of KCl (0.10 mol∙dm−3) was added by steps to the deionized water containing cell. The cell was kept in the thermostatic bath at 298.15 K. The conductance of the water was measured in advance and subtracted from each conductance change recorded. The corresponding molar conductance (S∙cm2∙mol−1) was calculated from the equation of Lind, Zwolenik, and Fuoss [16] the molar conductance of KCl was used to calculate corresponding values of the specific conductance and then the cell constant.
2.4. Conductance Measurements at 298.15 K
Fresh solution of both the metal-ion salt and the ligands under investigation were made up for each experimental run. The conductance cell was cleaned, dried, and the accurately weighed the solution of metal-ion salt in acetonitrile and dichloromethane-water solvent system (~25 ml charged, ~3.0 × 10−4), after thermal equilibrium, the ligand is added to the cell from a hypodermic syringe (~10 ml, ~1.0 × 10−3). All measurements were taken at 298.15 K.
2.5. Potentiometric
The stability constant of L (L1 and L2) and mercury (II) cation were measured by potentiometry titration was using Metrohm, 716 DMS Titrinio) equipped with calomel (Hg2Cl2/Hg) reference double junction electrode (Russell). Its inner electrolyte was a LiCl solution saturated in ethanol, whilst the outer (salt bridge) electrolyte, separate the electrode from the titration cell, was a solution of tetra-n-butylammonium perchlorate (TBAP, 0.05 mol∙dm−3) in acetonitrile. The concentration of the free mercury ion was measured using mercury indicator electrode, both electrodes were connected to a compact automatic titrator-processor Titrinio, all titrations were carried out under a flow of nitrogen. For the calibration experiments the vessel filled with (20 ml solution TBAP 0.05 mol∙dm−3), the burette filled with solution Hg(ClO4)2 (~3 × 10−3 mol∙dm−3) after equilibrium starting automatic addition, collecting all data by Hyperaccess data system, the Nernstian behavior of the electrode was evaluated from the slope of a plot of potential against –log[Hg2+].
For the determination of the stability constant, the ligand solution (~1.0 × 10−3 mol∙dm−3) were prepared in TBAP solution (0.05 mol∙dm−3) in the typical experiment filled this solution in the burette and added into the vessel solution containing a known concentration of Hg2+ allowing the formation of the 1:1 mercury calixarenate complex. Data collecting by Hyperaccess system used for the calculation stability constant by the use of a computer program SUPERQUAD [17].
2.6. Calorimetric
Macrocalorimetric titrations, the Tronac 450 calorimeter were used as an isoperibol titration calorimeter [18]. It is equipped with a 2 cm3 burette connected by a silicone tube to the reaction vessel. The reproducibility of the apparatus was checked by (i) calibrating the burette [19] and (ii) chemical calibration using the standard reaction of protonation of an aqueous solution of tris(hydroxymethyl)-aminomethane (THAM) in hydrochloric acid (HCl, 0.1N) at 298.15 K. Therefore, an aqueous solution of THAM was placed in the burette and incrementally titrated into the reaction vessel containing the solution of HCl (50 ml). The value determined −47.63 ± 0.19 kJ∙mol−1 is in agreement with the one reported by Öjelund and Wadsö (−47.49 kJ∙mol−1) using an LKB reaction calorimeter [20].
A direct calorimetric titration was carried out when log Ks < 6, in which a solution of the metal ion salt (concentration range 2.0 × 10−2 to 5.0 × 10−2 mol dm−3) was prepared in acetonitrile, placed in the burette, and titrated into the vessel containing a solution of the ligand of interest, (50 cm3, concentration range 6.0 × 10−4 to 1.5 × 10−3 mol dm−3) prepared in the same solvent.
2.7. Partition Experiments
Potassium picrate solution was prepare as described elsewhere [21], was used to prepare mercury (II) picrate in situ by dissolving and excess of mercury (II) perchlorate, left overnight white precipitate of potassium perchlorate appears, after filter check concentration of mercury in liquid phase by technique EDTA replacement titrations [22].
Partition experiments were carried out in the absence of ligand, equal volumes (10 cm3) of the aqueous phase containing different concentrations of metal-ion picrate in aqueous phase (5.1 × 10−5 - 1.7 × 10−4 mol∙dm−3), were mixed with dichloromethane, the mixtures were shaken for a period of 30 minutes, and then were left overnight in an isothermal bath at 298.15 K. Aliquots from the aqueous phase were taken and analyzed by spectrophotometric measurements.
Extraction experiments were carried out in the presence of ligand, accurate volumes of aqueous solution (10 cm3) containing metal-ion solution (1.7 × 10−4 mol∙dm−3) and the (10 cm3) organic solution containing the ligand in different concentration (4.27 × 10−5 - 2.17 × 10−4 mol∙dm−3) were placed in stoppered flask. The mixture was vigorously shaken were left overnight in a thermostatic bath at 298.15 K. Aliquots from the aqueous phase were taken and analyzed by spectrophotometric measurements
3. Results and Discussion
3.1. Structural Conformation of L1 and L2 in Solution
It is well established [23] that the difference in chemical shifts between the axial and the equatorial protons (∆δax−eq = δax − δeq) provides information regarding the conformation of the ligand in a given solvent and the indication of the flattening degree of the “cone”. Thus ∆δax−eq value of 0.9 ± 0.2 ppm is expected for the ligand in a perfect cone conformation while ∆δax−eq value of 0.5 ± 01 ppm corresponds to the flattened ligand in a “cone” conformation.
The pair of doublets found in the 1H NMR spectra for L1 and L2 which corresponding to the axial (4.34 ppm for L1 and 4.85 ppm for L2) and the equatorial (3.38 ppm for L1 and 3.24 ppm for L2) protons of the bridging provide information to measure of the flattening of the cone. As far as the value for L1 is ∆δax−eq = 0.96 ppm this corresponding when L1 adopt a perfect cone conformation, while the value found for L2 (∆δax−eq = 1.61 ppm) corresponding when the ligand adopts a distorted cone conformation.
However these conformations for L1 and L2 are easily to explain, (i) L1 is a partially substituted differently in which play a predominant role the hydrogen bond between the ethereal oxygen and phenolic proton to give to this derivative a more symmetry structure as reporting in previous works Danil de Namor et.al. [14], (ii) In fully substituted calix[4]derivatives most of these derivatives adopts the distorted cone conformation in solution and in solid state, in which the hydrophobic cavity decrease what that of the hydrophilic cavity increase, that may attributed to higher electrostatic repulsion between the pendant arms in L2.
3.2. Conductance Measurements
The main aim of conductance measurements was to establish the composition of the metal-ion complexes in acetonitrile at 298.15 K. Information that is required to proceed with the thermodynamic characterization of the complexation process involving these ligands and Hg2+ metal cation in acetonitrile.
Plots of molar conductance (Ʌm) against the ligand/metal-ion mol ratio showed for both ligands well-defined changes of curvature to 1:1 stoichiometry are observed, that represent strong complexes in both cases. The interesting feature is observed when moving from L1, in which the dangling arms have two sulphur atoms as binding site, while L2, increases the number of binding sites (sulphur atoms) to four, the changes in molar conductance are more pronounced in L2, as shown in Figure 1. The decrease in molar conductance is observed with the addition of the ligand to the metal cation in acetonitrile, this can be attributed to the size of the cation as it changes from free (small) cations to cationic (large) complexes, as a result of this size change the mobility decreases until the end point or stoichiometry of the complexation is reached.
3.3. Thermodynamic of Complexations
Stability constants (log Ks) and derived Gibbs energy of complexation, ∆cGo, enthalpies, ∆cHo and entropies, ∆cSo of these ligands with mercury(II) metal cations in acetonitrile at 298.15 K are listed Table 1, these data were obtained from titration macrocalorimetry and potentiometry measurements.
The complex composition found in previous discussions is required to formulate a representative equation of the complexation process. Taking into account speciation of the multicharged electrolyte in solution by conductance measurements, Figure 2 in which a linear relationship is obtained when the
![]()
Figure 1. Conductometric curve for the titration of mercury(II), (as perchlorate) and L in acetonirile at 298.15 K.
![]()
Figure 2. Molar conductance, Ʌm, against the square root of the ionic strength, I1/2, for Hg2+ (as perchlorate) in acetonitrile at 298.15 K
![]()
Table 1. Thermodynamic parameters for the complexation of Hg2+ (as perchlorate) and L (L1 and L2) in acetonitrile at 298.15 K by the titration classical calorimetry and titration potentiometric.
apotentiometric data, bmacrocalorimetry data.
molar conductance, (Ʌm) of Hg(ClO4)2 in acetonitrile is plotted against the square root of the ionic strength (I1/2) of the electrolyte in solution. The results in this Figureclearly demonstrated that ionic are the predominant species in solution. These finding were also corroborated by performing thermodynamic measurements at different concentration of the electrolyte in solution, not variation in stability constant values are observed.
On basis to these findings the thermodynamic process for the complexation this ligands with mercury(II) metal cations is described as:
(1)
The standard deviation of the data also included in Table 1.
Stability constant for mercury was derived from data obtained by direct potentiometry using the calomel reference electrode and mercury indicator electrode. Typical potentiometric titration curve for the titration of mercury (II) as perchlorate with this ligand shown in Figure 3 and Figure 4 where potential reading in mV is plotted against legal/metal ratio was observed, indicating that one metal cation with one ligand unit as demonstrated from conductance measurements.
The enthalpy has been determined by titration calorimetry and the entropies values were calculated through the relationship
(2)
The complexation curves,E/ mV versus [L]/[Hg2+] ratio (i) or the first derivative (ii) for the titration mercury(II), are shown in Figure 3 (representative
![]()
Figure 3. Potentiometric curve for the titration (i) and the first derivative to indicate the end point (ii) of the potentiometric titration of mercury(II) (as perchlorate) with L1 in acetonitrile at 298.15 K.
example) in acetonitrile at 298.15 K. The experimental data in both cases indicate that the inflection point in (i) or the minimum point in (ii) corresponds to the 1:1 (L:Hg2+) complex stoichiometry. This is in accord with the results observed from conductimetric studies. Potentiometric data were analyzed by the use of the SUPERQUAD [17] computer program.
The highest stability was found for L2 and Hg2+ in acetonitrile. This stability decreases in L1. These changes of complex stability with the ligand can be quantitatively assessed by taking the stability constant ratio for Hg2+ and L2 in acetonitrile relative to L1 (S = [Ks(L2)]/[Ks(L1)]).
Thus, the complexation of Hg2+ and L2 is more stable in acetonitrile than L1 complex by a factor of ~1.95. The difference in stability of complex formation for the same system in going from the L1 to L2 reveals the role of the number of the binding sites on the complexation process.
Analysis of data in Table 1, shows that the complexation process of L with mercury(II) is enthalpically controlled, possible due to the strong electrostatic (ion-dipole) interactions between these soft metal cation and the donor atoms of the ligands.
3.4. Phase Transfer Involving Bivalent Cations
The extraction of univalent cations from the aqueous to the organic phase in the absence and in the presence of a neutral macrocycle has been previously discussed by us [24] [25]. In this paper we formulate a treatment for the derivation of the partition, Kp and the ion-par formation, Ka, constants for the process represented in Equations (3) and (5) involving a 2:1 metal-ion salt.
(3)
where Kp expressed in terms of concentrations may be defined as.
(4)
and Kais referred to the process given in Equation (5)
(5)
Therefore,
(6)
Combination of (3) and (5) leads to Equation (7)
(7)
Thus, the distribution constant, Kd may be expressed as
(8)
Kpand Kd are referred to the mutually saturated solvents and Ka to the water saturated organic phase.
From distribution experiments on the assumption that M2+ and MX2 are the predominant species in the organic phase (saturated with water), the distribution ratio, DM can be defined.
(9)
Based on mass balance and electroneutrality and combining Equations ((4), (6) and (9)), it follows that.
(10)
Then a plot of DM against
should give a straight line of slope equal
and an intercept =
.
Distribution ratios for HgPi2, were carried out at 298.15 K in the water-dichloromethane (mutually saturated) solvent system. Thus, plots of DM values against
are shown in Figure 4 The lineal relationships observed in both cases led to the calculation of Kp, Ka and Kd and these data are shown in Table 2.
The data show that for the system involving Hg2+, Kp although small makes a favorable contribution to Kd values. However, the high Kd values observed for these systems are mostly due to the high degree of ion-pair formation of the metal-ion salts in the water-dichloromethane solvent system.
![]()
Figure 4. Distribution curve for mercury(II) (as picrate) in the water-dichloromethane solvent system at 298.15 K.
![]()
Table 2. Equilibrium data for the individual processes involved in the distribution of mercury(II) picrate in the water-dichloromethane solvent system at 298.15 K.
3.5. Distribution Data in the Presence of L in the Organic Phase
A general equation for the process taking place when a bivalent cation is extracted from water by the presence of a neutral macrocycle in the organic phase may be written as follows,
(11)
The extraction constant, Kex can be defined as
(12)
Taking into account Equations ((8), (9) and (12)) it follows that
(13)
To investigate the effect of L (L1 and L2) on the distribution of Hg2+ (as picrate) in the water-dichloromethane solvent system, distribution experiments were carried out in presence of the ligands. To demonstrate the stoichiometry of the extraction process, plots of the percentage of extraction, %E, against the ligand:metal cation total concentration ratio, [L]/[Mn+] are shown in Figure 5.
The percentage of the extraction of the metal cation was calculated from
(14)
In Equation (14); [Mn+]o and [Mn+]F are the initial and equilibrium concentrations of the metal cation in the aqueous phase.
Plots in Figure 5 show changes in the gradient at a ligand/metal cation ratio equal to unity. Thus, the stoichiometry of the process is defined by the intercept of these two lines. These findings are in accord with conductance studies for the complexation of these ligands and this metal cation.
Therefore, a plot of DM/[M2+]2(H2O) against [L](s) should give a straight line of slope = 4Kex and intercept equal to 4Kd. Distribution data (carried out in the presence of the ligand in the organic phase) against [L](s) for Hg2+ as picrate, in the water-dichloromethane solvent system are shown in Figure 6. Kex and Kd values are reported in Table 3. Excellent agreement is found between the Kd values obtained from distribution data in the absence of these ligands (Table 3).
![]()
Figure 5. Percentage of extraction (% E) against [L]/[Hg2+] concentration ratio obtained from the distribution data for mercury(II) picrate in the presence of L in the organic phase at 298.15 K.
![]()
Table 3. Distribution and extraction data for mercury(II) and by L (L1 and L2) in the water-dichloromethane solvent system at 298.15 K.
*Values obtained in the absence of L, Kd= Kp × Ka.
![]()
Figure 6. Plot of DM/[Hg2+(H2O)]2 against the equilibrium concentration of ligand, [L(s)] in the organic phase in the water-dichloromethane solvent system at 298.15 K.
The interesting aspect of the data is that Hg2+ is better extracted by L2 by a factor of ~148 times more relative to L1.
4. Conclusions
On the basis of these discussions, can be drawn:
1) The number of the binding sites in calixarene derivatives increases the strength of the complexations process by factor ~2. From partially substituted calixarenes in which the binding sites are two, to fully substitute (four binding sites), the strength of the ion-dipole interaction increases. As a result, the mrcury(II) complex is more stable in L2 relative to L1 in came solvent.
2) Extraction of Hg2+ from water to the organic phase, also increased by a factor of 148 times for the latter relative to the former ligand.
Acknowledgements
I would like to thank the European Union for the financial support given under contract ICA3-2000-30006. Many thanks to my supervisor Prof. Angela F. Danil de Namor. I feel very privileged for having worked under her supervision and finally, I would like to thank the University of Surrey for hosting me in their classrooms during my doctoral studies and postdoctoral work.
List of Abbreviations
L1: 5,11, 17, 23-tetra-tert-butyl[25, 27-bis(diethylthiophosphate amino)ethoxy-26, 28-bis(hydroxy)]-calix[4]arene
L2: 5, 11, 17, 23-tetra-tert-butylcalix[4]arene, tetra diethyl thiophosphate
Hg, Ag, Cd, Zn, Ca, Na, Mg: mercury, silver, cadmium, lead, zinc, magnesium, respectively
-SH: Thiol group
TBAP: Tetra-n-butylammonium perchlorate.
18C6: 18-crown-6
THAM: tris(hydroxymethyl)aminomethane
1H and 13 C NMR: proton and carbon, nuclear magnetic resonance