Describing a Baryon as a Meson Pair

Teruo Kurai

IEEE, Tokyo, Japan.

DOI: 10.4236/jmp.2020.1111114                

Abstract

We propose a new description of a baryon as a pair of mesons. This description is an extension of the previously proposed description of a nucleon as a pair of pions. The purpose of this article is to show the following two possibilities. The first one is that it shows the qualitative explanation to support our description of a nucleon as a pair of pions and the second one is that it gives the systematic way of estimation of baryon mass not only for light baryons but also for heavy baryons (charm baryons and bottom baryons). Each isospin group is constructed of both baryons and antibaryons. This way of construction is consistent with that of mesons. The results obtained are listed in tables (Tables 1-9). This shows that the generalized Gell-Mann-Nishijima relation equation holds under the condition that the baryon number is 0 and that the obtained masses are fairly good, even for heavy baryons. Our description also yields several examples of baryon decay modes.

Keywords

Baryon Description, Baryon Isospin, Baryon Mass, Baryon Decay Mode

1. Introduction

The widely accepted theory of baryon composition is the SU(6) quark model [1] [2] based on the eightfold way proposed by Gell-Mann [3] and Ne’eman [4]. According to this theory, baryons are composed of three quarks and antibaryons are composed of three antiquarks. The isospin group is constructed of only baryons, and that of antibaryons is constructed of only antiquarks. This theory is well supported by evidence and seems to be a complete formalism under the condition that the intrinsic spin of composing quarks determines baryon spin. However, in 1987, the European Muon Collaboration discovered that proton spin is not determined by the intrinsic quark spin [5]. Presently, it is clear that the contribution of the intrinsic spin of quarks to proton spin is at most 30% [6]. This result means that proton spin cannot tell us the number of composing quarks. In other word, it is not evident that a proton is composed of three quarks. From this fact, a different possibility for the composition of a proton can be considered. In this report, we propose a description of a nucleon as a pair of pions and obtain a plausible result for nucleon electromagnetic form factors (e.m. FFs) [7]. Because all baryons decay to a proton as a final state, it is a fair consideration that any baryon spin is not determined by the intrinsic spin of composing quarks. Thus, it is not obvious that any baryons are composed of three quarks. From this view point, we extend our consideration of proton composition to all baryons by describing a baryon as a pair of mesons. In this case, we have to reconsider the way that isospin groups are constructed. In the case of mesons, all isospin groups are constructed from both a particle and an antiparticle. Thus, it is consistent that any isospin group of baryons is also constructed from both a particle and an antiparticle. Our proposition is based on this consideration. Mass splitting of baryons is explained well by the Gell-Mann-Okubo equation [3] [8] for light baryons, but this equation no longer holds when heavy baryons (charm baryons and bottom baryons) are included. For example, their generalized equation gives us equal mass for ${\Xi }_{\text{c}}$ and ${{\Xi }^{\prime }}_{\text{c}}$ (each charged and neutral cases) because all isospin, strangeness, and C value are same for both baryons, but their masses are different about 100 MeV (100 MeV is almost 70% of the mass difference between ${\Xi }^{*}$ and ${\Omega }^{-}$ ; thus, we cannot neglect it). There is no useful formula to estimate baryon mass. Therefore, we need another way of estimating baryon mass. In this paper, we estimate baryon mass even though one generalized including C and B values. The previous description of a nucleon as a pair of pions shows good results for e.m. FF, especially, G_E/G_D for proton), but it is not obvious the reason why a nucleon can be described as a pair of pions. In this paper, we show the qualitative aspect of baryon description as a pair of mesons. This gives a support to our proposition of a nucleon description as a pair of pions.

2. Description of Properties

The basic meson operator is defined by the Bethe-Salpeter-like amplitude of the hadronic operator as

$\chi \left(1,2\right)=\langle 0|q\left(1,2\right)|P\rangle$ (1)

where $|0\rangle$ and $|P\rangle$ denote a vacuum and physical state, respectively.

The gauge-invariant bi-local operator $q\left(1,2\right)$ is defined in the non-Abelian gauge field as

$q\left(1,2\right)=T_r^c{q}_{\beta }^{+}\left(2\right)P\exp \left(ig{\displaystyle {\int }_1^2\text{d}\stackrel{\to }{x}}\stackrel{\to }{A^a}\left(x\right)\frac{{\lambda }_a}{2}\right)q_{\alpha }\left(1\right)$ (2)

Here $\alpha$ and $\beta$ denote the Dirac indices, P denotes the path ordering, and the $\frac{{\lambda }_a}{2}$ component generates the adjoint representation of the SU(N) color gauge group. The trace is calculated for color spin a. Suura first proposed this definition [9] [10], and later we applied it to the case of the t’Hoot model, the light meson mass spectra and the pion e.m. FF [11] [12]. We then proposed that a nucleon can be described as a pair of pions and obtained the e.m. FFs and distribution functions of nucleon [7]. The results of Ref. [7] encouraged us to extend this kind description to the consideration that a baryon can be described as a pair of mesons. In Ref. [7], a nucleon operator is defined as

$\chi \left(1;2,3\right)=\langle 0|q\left(1;,2,3\right)|P\rangle$ (3)

where $q\left(1;2,3\right)=q\left(1,2\right)+q\left(1,3\right)$ (4)

Extending this consideration to all baryons, any baryon operator is defined as having the same form as Equation (3) and Equation (4), but quark field considerations indicate u, d, s, c, and b quarks instead of only u, d quarks for the nucleon case. For the case that antiquarks are bounded, it is easy to describe by using $\chi \left(1,2;3\right)$ instead of $\chi \left(1;2,3\right)$.

We show baryons described as a pair of mesons composed of u,d, and s quarks in Table 4 (spin 1/2) and Table 5 (spin 3/2). Baryons described as a pair of mesons composed of c and b quarks are shown in Tables 6-9 (Table 6 and Table 7 for spin 1/2, Table 8 and Table 9 for spin 3/2). The terms listed in columns are paired mesons, isospin, the third component of isospin, strangeness, c value, b value, binding quarks, binding energy, excited energy, estimated mass and mass measured by experiment.

It is obvious to see that each baryon satisfies the generalized Gell-Mann-Nishijima relation equation [13] [14]. The generalized Gell-Mann-Nishijima relation equation is given as

$Q=I_3+\frac{1}{2}\left(S+B_a+C+B\right)$ (5)

where Q: charge value;

$I_3$ : the third component of isospin;

$B_a$ : baryon number;

S: strangeness;

C: c-value $c=+1,\bar{c}=-1$ ;

B: b-value $b=-1,\bar{b}=+1$.

Because a baryon is composed of a pair of mesons, we need these values to determine the isospin, the third component of isospin, and the strangeness and to estimate the mass of each baryon. Table 1 shows the properties of mesons composed of u, d, and s quarks only for the spin 0 case.

Table 2 shows the properties of mesons with spin 0 composed by c and b quarks baryons.

Table 3 shows the properties of mesons with spin 1 composed by c and b quarks baryons.

Using the values of Tables 1-3, we construct the isospin of a baryon and describe a baryon as a pair of mesons. To construct the isospin, we regroup the

Table 1. Properties of mesons (u,d,s quarks only).

Notes: The listed mass of f⁰ is from ref [12]. All other mass are from Oliver et al. [15]. We use ${\kappa }_s^0,{\kappa }_L^0$ (short and long decay time of κ⁰) instead of ${\kappa }^0,\overline{{\kappa }^0}$ because ${\kappa }^0,\overline{{\kappa }^0}$ are strong eigenstates that are considered not to decay. Normally, ${\kappa }_s^0,{\kappa }_L^0$ are both noted not to be eigenstates of strangeness, however, we denote strangeness 0 for these because the quark representation of these two are $\frac{d\bar{s}+\bar{d}s}{\sqrt{2}}$ and $\frac{d\bar{s}-\bar{d}s}{\sqrt{2}}$, respectively, and from these expression we can consider their strangeness to be 0. By setting this strangeness value, isospin of ${\kappa }_s^0,{\kappa }_L^0$ must be 0, due to the Gell-Mann-Nishijima relation equation. All isospin and strangeness values (except ${\kappa }_s^0$ and ${\kappa }_L^0$ ) are from Ref. [15].

Table 2. Properties of mesons (c,b quarks; spin 0).

Notes: The listed values are taken from Ref. [15] including mass values. All baryon numbers are 0. The listed isospin values are determined by the fact that the isospin of u( $\bar{u}$ ) and d( $\bar{d}$ ) quarks is $\frac{1}{2}$, and that of other quarks is 0.

Table 3. Properties of mesons (c,b quarks; spin 1).

Notes: The listed values are taken from Ref. [15] including mass values. All baryon numbers are 0.

baryons including antiparticles. For example, in the nucleon case, we consider p⁻ (an antiparticle of proton p⁺) and constitute p⁺, p⁰ (n⁰: neutron), p⁻ as one group so that the isospin is 1 instead of the normally considered value of $\frac{1}{2}$. This isospin determination is following. The isospin of pions is 1, thus the the possible isospin of a pair of pions is 2, 1 and 0 because of 1 + 1 = 2. Then, we take 1 for the isospin of proton group. We use this way of determination of isospin for other baryons. The composing meson pairs are selected by their charge and composing quarks and mass. We show the results of light baryons with the spin $\frac{1}{2}$ case in Table 4. We use a baryon number of 0 for all baryons as proposed in Ref. [7].

The binding energies for uu, dd, ud are determined by the mass difference between a proton and the sum of the masses of π⁺ and π⁰. We call this binding energy the strong binding energy, and calculate it to be 664.02 MeV. A similar consideration gives the binding energy for us and ds, using the mass difference between Λ⁰ and the sum of the masses of π⁺ and κ⁻ or π⁻ and κ⁺. We call this the weak binding energy and calculate it to be 482.43 MeV. The estimated mass of each baryon is obtained by the following equation.

$\begin{array}{c}\text{Mass of baryon}=\text{Sum of mass of composing mesons}\\ +\text{Binding energy}+\text{Excited energy}\end{array}$ (6)

In Table 4, there is no excitation energy term, although this term appears in later tables.

Table 4. Properties of light baryons (spin 1/2).

Notes: All values of the baryon number B_a are 0. All C and B values are 0.

The measured mass in Table 4 and in later tables is taken from Beringer et al. [16].

Table 5 shows the properties of light baryons with spin $\frac{3}{2}$.

The excited energy for Δ baryons is determined using the fact that Δ⁺ and Δ⁰ are normally considered as the excitation states of p⁺, and p⁰ (n⁰) (proton and neutron), respectively. Thus, by setting the mass of Δ⁺ of 1232 MeV, we obtain this excited energy value of 293.43 MeV.

Table 6 shows the properties of heavy baryons with spin $\frac{1}{2}$ composed by c quarks.

Note that we denote the isospin of ${\text{Σ}}_c^0$ to be 0. Because the total isospin of a pair of mesons is 3 (we consider that ${\text{Σ}}_c^0$ is a mixture of $D^{+}+{\pi }^{-}$ and $D^{-}+{\pi }^{+}$, thus $\frac{3}{2}+\frac{3}{2}=3$ ), the possible isospin is 3, 2, 1, and 0. Thus we can take 0 for the isospin of ${\text{Σ}}_c^0$. The same consideration determines that the strangeness and C value become 0. Another possible meson pair of ${\text{Σ}}_c^0$ is the mixture of $D^0+{\pi }^0$ and $\overline{D^0}+{\pi }^0$. Although we do not adopt this pair in our consideration, we address it in the Discussion. We use the same consideration for the ${\Xi }_c^0$ and ${{\Xi }^{\prime }}_c^0$ cases, and adopt it in later tables.

To extend our consideration to heavy baryons, the binding energy for cu and cd is determined by the mass difference between the mass of ${\Lambda }_c^{+}$ and the sum of the masses of D⁺ and π⁰. To determine the binding energy for cs, we use the the difference between strong and weak binding energies (664.02 − 482.43 = 181.59 MeV).

The binding energy for cs is determined by the subtraction of above energy difference from the binding energy for cu and cd (281.87 − 181.59 = 100.28 MeV).

Table 5. Properties of light baryons (spin 3/2).

Note: All values of the baryon number B_a are all 0.

Table 6. Properties of heavy baryons (c quark; spin 1/2).

Note: All values of the baryon number B_a are 0 and all B value are 0.

At this point in our argument, we notice that the binding energy between quarks becomes smaller as the mass of each bound quark becomes heavier. Thus, we set the binding energy for cc to be nearly 0. A meson pair of baryons is determined using the following argument. 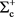is originally considered as a pair of D⁺ and η⁰ because Σ⁺ is composed by π⁺ and η⁰. 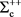However, the existence of the double charged charm sigma baryon indicates that is composed of D⁺ and π⁺. Because 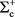should have a mass that is equal to the sum of the masses of D⁺ and η⁰ (1869.61 + 547.86 = 2417.47 MeV), the composing pions must be excited.

The excited energy of a pion is determined by the difference between the sum of the masses of D⁺ and η⁰ and the sum of the masses of D⁺ and π⁰ (2417.47 – 2286.46 = 131.01 MeV). To extend this consideration to the bottom sigma baryons case, we use the same excited energy (131.01 MeV) even though there are no double-charged bottom sigma baryons. Interestingly, there is no entry for 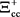(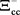) values in Table 6. It is possible that the composition of a meson with isospin is 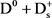(), but the third component of isospin I₃ becomes 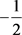() to hold to the Gell-Mann-Nishijima relation equation. This cannot be allowed if the consistency of isospin argument is to be maintained. Thus, () is forbidden in our consideration.

Table 7 shows the properties of heavy baryons with spin composed by b quarks.

The determination of binding energy is based on the same considerations used in the charm baryon case.

The reason that the strangeness of () is 0 is that the strangeness of () is +1 (−1) and that of κ⁻ (κ⁺) is −1 (+1) so that the total of strangeness becomes 0.

Table 8 shows the properties of heavy baryons with spin composed by c quarks.

Table 9 shows the properties of heavy baryons with spin composed by b quarks.

3. Baryon Decay Mode

We show here several examples of baryon decay modes. The basic consideration

Table 7. Properties of heavy baryons (b quark; spin 1/2).

Note: All values of the baryon number B_a are all 0 and all C value are 0.

Table 8. Properties of heavy baryons (c quark; spin 3/2).

Note: All values of the baryon number B_a are 0 and all B values are 0.

Table 9. Properties of heavy baryons (b quark; spin 3/2).

Note: All values of the Baryon number B_a are 0 and all C values are 0.

is exactly the same as in the quark model case. Thus, we use the following weak decay and strong decay examples.

Example of weak decay

Example of strong decay

Following are examples of decay modes for cases.

Note that π⁻ directly decays to.

In the case that Λ⁰ is described as, the decay mode is made obvious by noticing the fact that κ⁻ decays to or.

The mass difference between the original baryon (in this case Σ⁺) and the generated baryon (in this case n⁰) is not large enough for two pions.

Thus, means that η⁰ directly decays to.

From the representation that and the fact that the mass of Ω⁻ can afford to allow only one Λ⁰, the graph above indicates

Note that the above graph uses instead of the more common form,. We use this because the mass difference between and is large enough to generate two pions, unlike other baryon decay modes.

The reason this Ω⁻ decay mode has two π⁰ instead of only one π⁰ is the same as for the previous Ω⁻ decay mode.

We do not know the decay mode of, but if we assume it exists, then we could explain the above decay mode, which has been seen experimentally. These decay modes are given in Ref. [16].

4. Conclusions

In Section 2 and Section 3, we show the qualitative aspects of baryons described as a meson pair. From Tables 4-9, we can demonstrate that all baryons satisfy the generalized Gell-Mann-Nishijima relation Equation (5) with baryon number 0. This result supports our proposition [7] that all baryons have a baryon number of 0 instead of 1.

The difference between the estimated mass and the measured mass of any baryon is less than 100 MeV except for the case which is a difference about 200 MeV. Thus, the obtained results are reasonable even though the estimation method is simple. Also, baryon decay mode can be explained by a pair of mesons as shown in Section 3. These results indicate that the description of baryons as a meson pair shows the most important aspects of baryons.

5. Discussion

During the presentation of Table 6, we mention that the reason we omit and is for the consistency of the isospin argument. To be precise, the other isospin case shows that a positive charge particle has an I₃ of and the negative charge particle has an I₃ of, as is the case for and in the same table.

However, for and, I₃ must be and, respectively, to satisfy the generalized Gell-Mann-Nishijima relation equation. Thus, we consider that and to be forbidden. To this point, the claimed discovery of has been controversial because of questionable experimental data [17]. If they are observed, our way of constructing isospin group may have to be reconsidered. In this respect, whether or not and exist is an important point in our consideration.

The reason that the pair of mesons for (and other neutral particle) is a mixture of and (positive charge meson + negative charge meson) instead of a mixture of and is that a neutron is composed of π⁺ and π⁻. We derived the charge distribution function of a neutron in a previous paper [7]. Because we consider that any neutral baryons should have a charge distribution, we adopt this mixture instead of that of a pair of neutral mesons.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Greenberg, O.W. (1964) Physical Review Letters, 13, 398. https://doi.org/10.1103/PhysRevLett.13.598
[2]	Zweig, G. (1964) CERN Rep. No. 8182/TH, 401.
[3]	Gell-Mann, M. (1961) OSTI GOV TID-12608, CTSL 20.
[4]	Ne’eman, Y. (1961) Nuclear Physics, 26, 222. https://doi.org/10.1016/0029-5582(61)90134-1
[5]	Ashman, J., et al. (1988) Physics Letters B, 206, 364.
[6]	Thomas, A.W. (2008) arXiv: 0803. 2775v1 [hep-ph] JLAB-THY-08-780
[7]	Kurai, T. (2020) Journal of Modern Physics, 11, 741. https://doi.org/10.4236/jmp.2020.115048
[8]	Okubo, S. (1962) Progress of Theoretical Physics, 27, 949. https://doi.org/10.1143/PTP.27.949
[9]	Suura, H. (1978) Physical Review D, 17, 460. https://doi.org/10.1103/PhysRevD.17.469
[10]	Suura, H. (1979) Physical Review D, 20, 1429. https://doi.org/10.1103/PhysRevD.20.1412
[11]	Kurai, T. (2014) Progress of Theoretical and Experimental Physics, 2014, 053B01.
[12]	Kurai, T. (2018) Results in Physics, 10, 865-881. https://doi.org/10.1016/j.rinp.2018.07.034
[13]	Noshijima, K. and Nakano, T. (1953) Progress of Theoretical Physics, 10, 581. https://doi.org/10.1143/PTP.10.581
[14]	Gellman, M. (1956) Nuovo Ciment, 4, 848. https://doi.org/10.1007/BF02748000
[15]	Olive, K.A., et al. (2014) Chinese Physics C, 38, Article ID: 090001. https://doi.org/10.1088/1674-1137/38/9/090001
[16]	Beringer, J., et al. (2012) Physical Review D, 86, Article ID: 010001.
[17]	CERN (2017) The LHCb Experiment Is Charmed to Announce Observation of a New Particle with Two Heavy Quarks.