Gravitational Space-Time Quantization for Charged Wormholes and the Diophantine Uncertainty Relation

Yu. A. Khlestkov, A. Yu. Khlestkov, P. Yu. Lukashin, M. Yu. Lukashin, N. Yu. Lukashina

National Research Nuclear University (MEPhI), Moscow, Russia.

DOI: 10.4236/jmp.2020.1111109                

Abstract

This research work proceeds from the assumption, which was still considered by Einstein, that the quantization of gravity does not require additional external procedures: quantum phenomena can be a consequence of the properties of the universal gravitational interaction, which maps any physical field upon the space-time geometry. Therefore, an attempt is made in this research work to reduce the quantization of physical fields in GRT to the space-time quantization. Three reasons for quantum phenomena are considered: Partition of space-time into a set of unconnected Novikov’s R- and T-domains impenetrable for light paths; the set is generated by the invariance of Einstein’s equations with respect to dual mappings; The existence of electric charge quanta of wormholes, which geometrically describe elementary particles in GRT. This gives rise to a discrete spectrum of their physical and geometric parameters governed by Diophantine equations. It is shown that the fundamental constants (electric charge, rest masses of an electron and a proton) are interconnected arithmetically; The existence of the so-called Diophantine catastrophe, when fluctuations in the values of physical constants tending to zero lead to fluctuations in the number of electric charges and the number of nucleons at the wormhole throats, which tend to infinity, so that the product of the increments of these numbers by the increment of physical constants forms a relation equivalent to the uncertainty relation in quantum mechanics. This suggests that space-time cannot but fluctuate, and, moreover, its fluctuations are bounded from below, so that all processes become chaotic, and the observables become averaged over this chaos.

Keywords

Quantization of Gravitation, Novikov’s R- and T-Domains, Diophantine Uncertainty Relations, Discretization of Space-Time

1. Statement of the Problem

A natural approach to the problem of quantizing gravity, to which Einstein (the creator of the general theory of relativity) inclined, is considered: quantum phenomena should be a consequence of the gravitational field properties. The logic is as follows: GRT (general theory of relativity) is a geometrizing model. Any physical field must be mapped onto the geometry of a curved space-time, the curvature of which, for its part, is equivalent to a universal gravitational field [1] ¹. It is enough to solve the Einstein equations linking physics with geometry, together with Maxwell’s equations for an electromagnetic field, to express all physical quantities characterizing, say, electromagnetic interaction, through the metric of pseudo-Riemannian space.

Moreover, the arbitrary functions of the radial coordinate arising in this case in the Cauchy problem for the initial conditions (the first integrals) describe the geometric images of the sources of the electromagnetic field, i.e. electric charges [2], which were not present in the formulation of the problem and which, therefore, are formed by the gravitational field itself. That is, the sources of the field are formed by space-time itself. As it turned out, they have a non-trivial topology of pulsating wormholes with non-closing static throats [2]. We got the opportunity to investigate the internal structure of elementary particles by eliminating in this way the main singularity in the flat space of the special theory of relativity, i.e. the Coulomb divergence of a point charge field.

That is, GRT can really reduce the quantization of a physical field to the quantization of the multidimensional pseudo-Riemannian space-time. Quantization of space-time means the existence of two phenomena: discretization of 4-dimensional pseudo-Riemannian space, i.e. dividing it into a set of unrelated domains, and the impossibility of accurately determining its geometric characteristics, which acquire a fluctuating character and, by analogy with quantum mechanics, are linked by the gravitational uncertainty relation. This is what we should get.

The results of the work are presented in three sections and in Appendix 1, which provides a proof for the complete geometrization of an electromagnetic spherically symmetric field consisting of a free radial electric field and dust-like neutral matter in a synchronous accompanying frame of reference. According to the exact particular solution of the Einstein and Maxwell equations [2], it is a periodic in space and time chain of pulsating wormholes with static throats (holes, necks) of extreme dimensions geometrically, which are geometric images of electric charges formed by the electromagnetic (and hence gravitational) field in curved space-time (Figure 1).

The second section describes a fundamental property of centrally symmetric Einstein’s equations, i.e. their invariance in relation to dual mappings the mutual

Figure 1. One period of a wormhole with two electric charges ±Q—necks (throats) of radius R_h that exit into two parallel static Reissner-Nordstrom vacuum worlds, in the state of maximum expansion (R_max) and in the state of maximum compression (R_min). The arrows show the direction of the radial electric field.

replacement of the time coordinate with the spatial radial coordinate. This leads to the existence of one more exact particular solution of the Einstein-Maxwell equations, dual conjugated to the given one, and to the emergence of a discrete set of so-called Novikov’s R- and T-domains [3], which are closed and unconnected with each other, and which boundaries “B” are impenetrable for light paths (being isotropic geodesic lines) [4]. This is the first effect of natural “self-quantization” of the gravitational field.

As it will be illustrated in this section, this leads to the fact that the flux of photons continuously emitted by the source will come to an observer located at another point in space in discrete portions, i.e. quanta. This is the second effect of “self-quantization” of the curved space-time.

It was shown in [2] that the gravitational-electromagnetic interaction is sufficient to construct the simplest classical model uniting an electron, proton and neutron, with eliminating the main contradictory prohibitions, and to calculate their radii of curvature at unclosed throats of wormholes that go out into two parallel vacuum spaces. The radii of the proton and neutron are in good agreement with their experimental values (for a proton, with an accuracy of 0.04%). An electron, which in the flat space regarding to the special theory of relativity (SRT) would have to be single-point, i.e. structureless, also turns out to be a structural object in this model, having a finite radius of curvature of the throat much larger than that of a proton. Note that the very fact that the proton turned out to be not a single-point structured object is direct experimental evidence that the space-time in the microworld is also curved. That is, the gravitational interaction is universal.

In the third section of this research work, it will be shown that, according to this exact solution of the Einstein’s and Maxwell’s equations, the relationship between the physical and geometric parameters of particles at the throat is described by a Diophantine equation (an integer variable equation with rational coefficients). This requirement of the rationality of the coefficients inevitably leads to the fact that an arithmetic relationship arises between the rest mass, electric charge and the radius of the Gaussian curvature of the throat, which has the discrete spectra nature. That is, the physical characteristics (masses and charges) are quantized.

The phenomenon of a “Diophantine catastrophe” is considered in the fourth section of this work. This phenomenon takes place when large fluctuations of the number of electric charges and the number of nucleons at the throats of wormholes arise under the action of small random fluctuations of physical constants (these always take place, as it can be assumed). Those fluctuations are related to each other with the Diophantine uncertainty relation: the product of an increment of the rational Diophantine equation coefficient, which depends on the increment of physical constants (rest masses of electrons, protons, and an electric charge), by the increment in the number of electric charges and the number of nucleons at the throat is not less than a certain value, that is, it is limited from below. This means that fluctuations of such quantities cannot but exist; they will be maintained by the gravitating system itself, since as the increments of physical constants tend to zero, the increment in the number of charges and the number of nucleons at the throat would tend to infinity, which is impossible.

2. Dual Spaces. Discretization of Novikov’s R- and T-Domains

Einstein’s equations in GRT:

$G_{\mu \nu }=\kappa T_{\mu \nu },\kappa =\frac{8\pi k}{c^4},\mu ,\nu =\left\{0,1,2,3\right\}$ (1)

in 4-dimensional pseudo-Riemannian space in the coordinate system

$x^{\mu }=\left\{x^0,x^i=x^1,x^2,x^3\right\}$ (2)

in a set of arbitrary metrics that transform into each other,

$x^{\tilde{\mu }}=x^{\tilde{\mu }}\left(x^{\alpha }\right)$, (3)

with a non-degenerate Jacobian

$\tilde{J}=\left|x_{,\alpha }^{\mu }\right|$, (4)

in a class of metrics

$\text{d}{s}^2=g_{\mu \nu }\text{d}{x}^{\mu }\text{d}{x}^{\nu }$, (5)

with a Lorentzian signature

signature $g_{\mu \nu }=+---$, (6)

implemented by physical bodies [1]:

$\begin{array}{l}{g}_{00}>0,\\ \left|\begin{array}{cc}{g}_{00}& g_{01}\\ g_{10}& g_{11}\end{array}\right|<0,\\ \det \left[\begin{array}{ccc}{g}_{00}& \cdots & g_{02}\\ ⋮& \ddots & ⋮\\ g_{20}& \cdots & g_{22}\end{array}\right]>0,g=\det \left(g_{\mu \nu }\right)<0,\end{array}$ (7)

within the framework of centrally symmetric spaces with orthogonalized metric

$\text{d}{s}^2=e^{\nu \left(\tau ,r\right)}\text{d}{\tau }^2-e^{\lambda \left(\tau ,r\right)}\text{d}{r}^2-R^2\left(\tau ,r\right)\left(\text{d}{\theta }^2+{\sin }^2\theta \text{d}{\phi }^2\right)$, (8)

which transform into themselves at the following dual mapping:

$\begin{array}{l}{x}^0\leftrightarrow x^1,\left(\tau \leftrightarrow r\right),\\ g_{00}\leftrightarrow g_{11},\left(e^{\nu }\leftrightarrow -e^{\lambda }\right),\\ G_0^0\leftrightarrow G_1^1\left({\nu }^{.}\leftrightarrow {\lambda }^{\prime },{\lambda }^{\cdot }\leftrightarrow {\nu }^{\prime }\right),\\ \left(\cdot =\frac{\partial }{\partial \tau },\text{'}=\frac{\partial }{\partial r}\right).\end{array}$ (9)

with this mapping, the signature is preserved; the time coordinate $\tau \left(x^0=\tau ,g_{00}=g_{\tau \tau }>0\right)$, and the radial coordinate $r\left(x^1=r,g_{11}=g_{rr}<0\right)$ change places and the whole 4-dimensional space-time is divided into Novikov’s R- domains:

$x^0=\tau ,x^1=r,g_{00}=g_{\tau \tau }>0,g_{11}=g_{rr}<0$ (10)

and Novikov’s T-domains [4]:

$x^0=r,x^1=\tau ,g_{00}=g_{rr}<0,g_{11}=g_{\tau \tau }>0$ (11)

which are new solutions of GRT equations being dually conjugated to a given one supplementing any exact particular solution of Equation (1) to a complete one that already describes the entire space-time. The latter means that the entire space-time, with the exception of a finite number of singular points and hypersurfaces “B” (boundary), on which the Jacobian (4) and the second-order determinant (7) degenerate:

$“\text{B}”:x_{,0}^{\tilde{0}}{x}_{,1}^{\tilde{1}}-x_{,1}^{\tilde{0}}{x}_{,0}^{\tilde{1}}=0\text{or}\infty ,g_{\widetilde{00}}{g}_{\widetilde{11}}-g_{\widetilde{01}}^2=0\text{or}\infty ,$ (12)

can be completely covered by a family of geodesic lines [5].

Thus, using the invariance of the GRT equations with respect to dual maps, we have a way to generate new exact partial solutions of the Einstein equations that describe space-time more fully.

Let’s give a simple illustrative example. Let’s take the well-known Schwarzschild solution for a gravitational field of a point mass m [1]:

$\text{d}{s}^2=\left(1-\frac{r_g}{r}\right)\text{d}{\tau }^2-\frac{\text{d}{r}^2}{\left(1-\frac{r_g}{r}\right)}-r^2\left(\text{d}{\theta }^2+{\sin }^2\theta \text{d}{\phi }^2\right),$ (13)

where $r_g$ is a gravitational radius. It has a singularity $r=0$ and an event horizon $r=r_g$ [1]. This is Novikov’s R-domain. It describes the space of a black hole in the $r>r_g$ region (Figure 2, right side).

We now construct the dual-conjugate (13) Novikov’s T-domain by the mapping $\tau \leftrightarrow r$, $e^{\nu }\leftrightarrow -e^{\lambda }$ :

$\text{d}{s}^2=\frac{\text{d}{\tau }^2}{\left(\frac{r_g}{\tau }-1\right)}-\left(\frac{r_g}{\tau }-1\right)\text{d}{r}^2-{\tau }^2\left(\text{d}{\theta }^2+{\sin }^2\theta \text{d}{\phi }^2\right)$. (14)

One can make sure quite simply by substituting solution (14) into Einstein’s Equation (1) [1] that we have obtained a new solution missing for the domain $r<r_g$, in which the radial coordinate r has turned into a time coordinate $\tau$, and time $\tau$ has become a radial coordinate r (Figure 2, left side).

Part of a boundary hypersurface “B” is a surface $r=r_g$ in R-domain, it is also $\tau =r_g$ in T-domain (Figure 2, left side).

Since the time and the radial coordinate that create the “B” boundary are different characteristics, then R- and T-domains are not related in any way. Therefore, no signal can cross the “B” boundary from the R domain to the T domain and back.

We construct a family of light paths for this example,

$\text{d}{s}^2=0.$ (15)

Substituting (15) in (13) and (14), we obtain the expressions for the coordinate velocity of light ${\beta }_l^{“\text{R}”}$ and ${\beta }_l^{“\text{T}”}$ which is tangential for isotropic geodesic lines:

Figure 2. Parts of “R” and “T” Novikov regions in the Schwarzschild point mass field and light trajectories. In parentheses are the coordinate axes in the “T” area. “B” is the boundary between these regions—the event horizon, impenetrable for light trajectories. In the “T” region, the time coordinate τ and the radial coordinate r are reversed.

$\begin{array}{l}{\beta }_l^{“\text{R}”}=\pm \left|1-\frac{r_g}{r}\right|,\\ {\beta }_l^{“\text{T}”}=\pm \frac{1}{\left|1-\frac{r_g}{\tau }\right|}.\end{array}$ (16)

It is easy to construct qualitatively the envelopes of the families themselves (Figure 2) along these tangents to the light paths. Two paths are constructed for each domain in Figure 2, one of which begins (ends) at the boundary “B” in asymptotics, the other ends (begins) at the boundary “B” in asymptotics.

What qualitative conclusions follow from this picture?

- Space-time is divided in a gravitational field into a discrete set of unconnected R-T-domains.

- R-domains are limited in space from below, and T-domains are limited in time from above.

- Time and radial coordinate are swapped at the boundary “B” between R- and T-domains; light paths do not cross the boundary “B”.

- Since T-domain is limited in time from above, then in the case of time-periodic solutions it will periodically disappear for observers in the R-domains. Consequently, the propagation of signals in the case of closed or semi-closed solutions (such as Friedman or Tolman solutions) will be discontinuous, that is, will occur in a quantum manner.

Attempts to accurately construct a family of geodesic paths for the solution in [2] describing the internal structure of elementary charged particles (electron, proton, neutron) in the microworld, as well as megamaximons in astrophysics in the megaworld [4] [6] [7] [8] [9] have not yet been successful, both analytically and numerically due to mathematical difficulties. Therefore, we have depicted in Figure 3 only a qualitative picture of this family for semi-closed solutions, which clearly illustrates this phenomenon of curved space-time discretization.

If some observer resting in the “R”-domain continuously emits light rays, then observers in the “T”-domains will not see these signals at all, and observers at other points of the “R”-domains will see intermittent flux of light quanta. That is, the quantization of light turns out to be a property of curved space-time.

We also note that the integral gravitational action $S_g$ for each of these discrete domains of space-time is finite [1]:

$S_g=-\frac{c^3}{16\pi k}{\displaystyle \int \mathcal{R}\sqrt{-g}\text{d}\Omega }=\frac{e^2}{c}\psi$, (17)

where $\mathcal{R}$ is a trace of the Ricci tensor, $\frac{e^2}{c}$ is the gravitational “quantum of action”, $\text{d}\Omega$ is an element of 4-dimensional volume, $\psi$ is a form factor depending on the geometry of R and T-domains. Note that if $\psi =1/\alpha$, where $\alpha$ is the fine structure constant, then

$S_g=\hslash$, (18)

Figure 3. Quantization of a continuous stream of photons by “R” and “T” Novikov regions. “B” is the border between them, impenetrable for light trajectories.

where $\hslash$ is Planck’s constant. Thus, the fundamental constant of quantum mechanics can also have a gravitational origin.

The results obtained in GRT allow us to take a fresh look at the event cone known in SRT (Figure 4(a)). This event cone consisting of two timelike domains of the past and future with a positive square of the interval $\text{d}{s}^2>0$, and of two spatially similar domains with a negative square of the interval $\text{d}{s}^2<0$ being unattainably “absolutely remote”, with superluminal paths, can be interpreted differently. It represents the degeneration of “R”- and “T”-domains of curved space-time in the limiting case of disappearance of matter, therefore identical equality to zero of the Riemann-Christoffel curvature tensor according to the above-mentioned general relativistic principle of equivalence. This means flattening of this space. In this case, the entire space-time is divided into four time-like domains (Figure 4(b)): two “R”- and two “T”-ones, all with a positive square of the interval $\text{d}{s}^2>0$, which turns to zero at the boundaries of these

Figure 4. Degeneration of the light cone—“R” and “T”—Novikov regions in an empty flat space SRT. In parentheses are the coordinate axes in the “T” regions: (а) the usual interpretation of SRT, (b) possible representation of GRT.

domains, where the time and space coordinates are swapped in the neighbouring domains, and the metric remains Lorentzian, and the boundary “B” remained impassable. The presence of such a passage to the limit confirms that the chosen interpretation of the appearance of quantum properties in a curved space-time by means of its discretization by “R”- and “T”-dually conjugated domains is correct.

3. Discrete Diophantine Spectra of Wormhole Parameters and Relationship of Fundamental Constants

Consider the simplest centrally symmetric system consisting of a dusty substance (without pressure and temperature) and a free radial electric field (without sources) in an accompanying frame of reference. When integrating the Einstein and Maxwell equations in the Cauchy problem, three first integrals arise, being three arbitrary functions of the radial coordinate r, the setting of which is equivalent to setting the initial conditions for the dust energy density ${\epsilon }_s$, the radius of the 2-dimensional Gaussian curvature R and the rate of its change $R^{\cdot }$ : the electric charge Q, the total energy of the gravitational field ${\epsilon }_g$ and the function f characterizing the curvature of space inside the wormhole and at its throats, through which it can be extended into two parallel external Reissner-Nordström vacuum spaces [5].

The GRT equations can be integrated to the end in three cases when one of the first integrals becomes a constant [2] [10]. We will consider the simplest solution, in which the electric charge becomes a constant:

$Q=const=e{N}_Q$, (19)

where e is a fundamental charge, it is an irrational number for our world and N_Q is an integer number of such charges.

If we take into account that we initially considered a free electric field without sources, then the appearance of a new physical constant ±Q during integration means that space-time itself has formed a source of the electromagnetic field, i.e. an electric charge ±Q (for elementary particles ±e) geometrically representing a pulsating wormhole [2]:

$\begin{array}{l}{e}^{\nu }=1,\\ e^{\lambda }=\frac{{R^{\prime }}^2}{f^2},\\ R=\frac{R_g}{2\left(1-f^2\right)}\left(1-\delta \sin \eta \right),\\ \tau =\frac{R_g}{2{\left(1-f^2\right)}^{3/2}}\left(\eta -\delta \sin \eta -\pi \right),\\ \delta =\sqrt{1-\frac{4R_c^2}{R_g^2}\left(1-f^2\right)},\end{array}$ (20)

with two static throats, the radius of the 2-dimensional Gaussian curvature $R_h$ of which is always equal to twice the classical (electromagnetic) radius:

$R_f=\frac{Q^2}{2{\epsilon }_g\left(r\right)}$ (21)

At the throats under $r=0,r=r_h$ [2]:

$R_h=2R_{fh}=\frac{R_{gh}}{2}{\xi }^2=\xi R_c.$ (22)

Here $R_g=\frac{\kappa {\epsilon }_g}{4\pi }$ is a gravitational radius proportional to the total gravitational energy ${\epsilon }_g\left(r\right)$,

$R_c=\frac{Q\sqrt{k}}{c^2}$ (23)

is the critical radius proportional to the electric charge Q of the particle, which is always paired with its antiparticle, the throat of which can be extended into a parallel vacuum space;

$\xi =\frac{Q}{M_{gh}\sqrt{k}}\ge 1$ (24)

is the charge to the mass ratio of the inner world, $M_g={\epsilon }_g/c^2$, taken at the throat.

Recall that there are two fundamental constants in the GRT: k is an Einstein’s constant, which relates physics with geometry (that is, makes them indistinguishable), and c is the speed of light, which locally limits the speed of propagation of any signals. The fundamental electric charge Q appears only when integrating the equations of GRT. Its quantum e can be found purely geometrically by measuring the space-time curvature values at any of its points, both inside an elementary particle, and in the Reissner-Nordström vacuum space glued to it through the throats:

$e=\frac{c^2}{\sqrt{k}}{\mathcal{K}}_{0r}^{{\left(2\right)}^{-1}}{\left({\mathcal{K}}_0^{\left(1\right)}-{\mathcal{K}}^{\left(4\right)}\right)}^{1/2},$ (25)

where ${\mathcal{K}}_{0r}^{\left(2\right)}=\frac{1}{R^2\left(\tau ,r\right)}$ is the intrinsic Gaussian curvature of 2-spheres $r=const$.

${\mathcal{K}}_0^{\left(4\right)}=G_0^0$ is the curvature of 4-dimenional areas orthogonal to the time coordinate $\tau$ and equal to the zero mixed component of the geometric Einstein tensor $G_{\mu }^{\nu }$.

${\mathcal{K}}^{\left(4\right)}=G$ is the scalar (Gaussian) space-time curvature equal to the trace of the Einstein tensor.

Thus, we can say that e is a geometric quantum of electric charge, i.e. a topological characteristic of a given particle. Along with it, we can introduce a quantum of mass, the critical mass $m_c$ that differs from the charge only by a constant:

$m_c=\frac{e}{\sqrt{k}}$ (26)

and the quantum of length, which is a critical radius $r_c$ :

$r_c=\frac{e\sqrt{k}}{c^2}$, (27)

where the classical (electromagnetic) and gravitational radius are compared in magnitude.

Taking into account (24), Equation (22) could be as follows with introducing the mass at the throat

$M_h=m_p{N}_p+m_e{N}_e$, (28)

where $N_e$ is the number of electrons at the throat of the wormhole, taking into account that

$N_e=N_p-N_Q$, (29)

can be rewritten in the form of a Diophantine equation:

$N_p=\lambda N_Q$, (30)

where $N_p$ and $N_Q$ are integer variables; $\lambda$ is a rational coefficient equal to:

$\lambda =\frac{m_e+m_c/\xi }{m_e+m_p}$. (31)

Despite the seeming simplicity of relations (30), (31), they contain a new meaning for us. The logic behind this decision is simple. Equation (30) has nontrivial solutions only if $\lambda \in \mathbb{Z}$, belongs to the set of rational numbers. Let us assume that the masses of an electron, a proton and the mass of the $m_c$ quantum are irrational. Let particle in (31) is a friedmon for simplicity, i.e. $\xi =1$. Then, for there to be a solution to Equation (30), the sums of irrational numbers in the numerator and in the denominator must be rational. This is possible, but not for all $m_e,m_c,m_p$. The admissible values of these physical quantities will form a discrete spectrum:

$\begin{array}{l}{m}_e+m_c\in \mathbb{Z},\\ m_e+m_p\in \mathbb{Z}\text{.}\end{array}$ (32)

We will not solve arithmetic relations (31) and (32) here. We will make only a qualitative conclusion: first, the masses of the electron $m_e$, quanton $m_c$, and proton $m_p$ are related arithmetically, i.e. depend on each other. Second, they have discrete spectra of values, outside of which the conditions for the existence of a stationary throat are not satisfied. Therefore, the considered gravitational system (wormhole) will be nonequilibrium, which means that it will fluctuate. This statement obtained within the framework of this gravitational model obviously can be verified experimentally. That is, the nature of quantum fluctuations is non-fulfilment of arithmetic equilibrium conditions.

We present below the procedure for solution of the Diophantine equation (30). We represent the rational coefficient $\lambda$ as the sum of an integer $\Lambda$ and a proper fraction $\frac{a}{b}$, $\left|a\right|<b$, where $a,b\in \mathbb{Z}$, then, dividing the fraction by the greatest common divisor (GCD) $\left(a,b\right)$ (or the fraction $b={10}^n,n=1,2,\cdots$ ) in the decimal representation, we transform the fraction $\frac{a}{b}$ into an irreducible fraction $\frac{a_1}{b_1}$.

$\lambda =\Lambda +\frac{a}{b}=\Lambda +\frac{a}{{10}^n}=\Lambda +\frac{a_1}{b_1}=\Lambda +\frac{a/\left(a,b\right)}{{10}^n/\left(a,{10}^n\right)}$. (33)

Diophantine Equation (30) has the following discrete spectrum of solutions:

$\begin{array}{l}{N}_Q=b_{1}i,i=1,2,\cdots \\ N_p=\left(\text{Λ}{b}_1+a_1\right)i.\end{array}$ (34)

Or, in more detail:

$N_Q=\frac{{10}^n}{\left(a,{10}^n\right)}i,N_p=\left(\Lambda \frac{{10}^n}{\left(a,{10}^n\right)}+\frac{a}{\left(a,{10}^n\right)}\right)i.$ (35)

Here is the simplest illustrative example of this arithmetic:

$N_2=32.25N_1=\left(32+\frac{25}{{10}^2}\right)N_1=\left(32+\frac{1}{4}\right)N_1$,

$a=25,b={10}^2,\left(a,b\right)=25,a_1=1,b_1=4,n=2,\Lambda =32,$

$N_1=b_{1}i=4i=4,8,12,\cdots$

$N_2=\left(\text{Λ}{b}_1+a_1\right)i=\left(32\times 4+1\right)i=129,258,387,\cdots$

Using this example, let’s see what happens to the equilibrium spectrum of integer solutions $N_1$, $N_2$ of this solution if we introduce a perturbation for a rational coefficient of the given equation $\lambda =32.25$, say, with 1/1000. Let

$\tilde{\lambda }=32.251:\text{Λ}=32,a=251,b={10}^3,\left(a,b\right)=1,a_1=251,b_1={10}^3,$

$\tilde{\lambda }=\lambda +\delta \lambda ,\lambda =32,25,\delta \lambda ={10}^{-3},$

$\widetilde{N_1}=N_1+\text{Δ}{N}_1={10}^{3}i=1000;2000;3000;\cdots$

$\widetilde{N_2}=N_2+\text{Δ}{N}_2=\left(32\times {10}^3+251\right)i=32251;64502;96753;\cdots ,$

$\Delta N_1=996;1992;3988;\cdots ,$

$\Delta N_2=32122;64254;96366;\cdots .$

The result is obvious: With small perturbations of the physical constants included in the rational coefficient of the Diophantine equation, the spectra of the required number of charges $N_Q$ increase sharply in their magnitude, so that as the fluctuations of the constants tend to zero, the fluctuations of the required number of electric charges $N_Q$ and the number of nucleons $N_p$ tend to infinity: $\delta \lambda \to 0$, $\Delta N_{Q,p}\to \infty$. This is a Diophantine catastrophe. We will discuss it below.

The same qualitative disturbances will be expected for the spectrum of the necessary throat radii:

$R_h=r_p\frac{N_Q}{\lambda \left(1+m_e/m_p\right)}$. (36)

As a result, if there would be no such values of $m_e,m_p$, fluctuations of the values of $N_Q,N_p$ will not decay in principle.

4. Fluctuations of Fundamental Constants, Wormhole Parameters and Diophantine Uncertainty Relation

What is the cause of a Diophantine catastrophe? The fluctuations of physical constants (electric charge, rest masses of elementary particles) tending to zero cause an infinitely large required increment in the number of charges and the number of nucleons to ensure a stationary state of wormhole throats. Since such numbers are not found, the gravitational system begins to fluctuate.

The perturbed system is described by a perturbed Diophantine equation:

$\widetilde{N_p}=\tilde{\lambda }\widetilde{N_Q},$ (37)

in which the perturbed rational coefficient can be represented as:

$\tilde{\lambda }=\lambda +\delta \lambda ,$ (38)

and we write the fluctuation $\delta \lambda \ll \lambda$ itself in the form:

$\delta \lambda =\frac{\alpha }{{10}^{m+n}},m=1,2,\alpha =1,2,3,\cdots$ (39)

The unperturbed rational coefficient has the same form:

$\lambda =\Lambda +\frac{a}{{10}^n}$ (40)

Therefore, the perturbed coefficient is as follows:

$\tilde{\lambda }=\Lambda +\frac{a}{{10}^n}+\frac{\alpha }{{10}^{n+m}}.$ (41)

Hence, the solution for an integer $\widetilde{N_Q}$ with perturbation $\tilde{\lambda }$ looks like this:

$\widetilde{N_Q}=c{10}^{n+m},c=1,2,3,\cdots$ (42)

and for the integer value $\widetilde{N_p}$ :

$\widetilde{N_p}=\left(\text{Λ}+\frac{a}{{10}^n}+\frac{\alpha }{{10}^{n+m}}\right)c{10}^{n+m}$, (43)

or

$\widetilde{N_p}=c\left(\Lambda {10}^{n+m}+a{10}^m+\alpha \right)$. (44)

Now let’s find the increment $\Delta N_p$ :

$\Delta N_p=\widetilde{N_p}-N_p=c\left(\Lambda {10}^{n+m}+a{10}^m+\alpha \right)-i\left(\Lambda b_1+a_1\right)$. (45)

Find the product of fluctuations $\delta \lambda$ and $\Delta N_p$ :

$\delta \lambda \Delta N_p=\alpha \left(c\left(\Lambda +a{10}^{-n}+\alpha {10}^{-\left(n+m\right)}\right)-\left(\Lambda b_1+a_1\right)i{10}^{-\left(n+m\right)}\right)$. (46)

Let $\delta \lambda \to 0$, so $n,m\gg 1$, therefore,

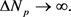(47)

From (45), leaving the largest term and taking into account the arbitrariness of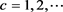, we obtain the required Diophantine uncertainty relation:

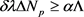. (48)

Proceeding in the same way with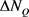, we obtain a similar relation for it:

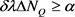. (49)

Consequently, when the number of fundamental charges is bounded from above, the fluctuations of the physical constants are bounded from below. This means that the gravitational system of elementary particles cannot but fluctuate.

5. Conclusions

The invariance of Einstein’s equations in GRT with respect to dual mappings is considered. First, this symmetry makes it possible to obtain new exact partial solutions of the Einstein equations that complement the obtained ones to a more complete description of space-time. Secondly, this symmetry leads to discretization of space-time, or its division into a set of unconnected Novikov’s R- and T-domains impenetrable for light paths. This is the first effect of “self-quantization” of the gravitational field. This, in turn, leads to discretization of the flux of photons continuously emitted by an emitter in separate portions, or quanta. This is the second self-quantization effect of a curved space-time.

It is shown that the relationship between physical and geometric parameters at the wormhole throats, which are exact particular solutions of the Einstein-Maxwell equations, and which describe the internal structure of elementary charged particles, is described by a Diophantine equation in integer variables with a rational coefficient. This leads to the appearance of discrete spectra of physical and geometric parameters of wormholes. This is the third effect of “self-quantization” of the gravitational field.

Finally, the presence of arbitrarily small fluctuations of fundamental constants (charges, masses and radii of elementary particles) leads to the phenomenon of “Diophantine catastrophe”, when the increments of the number of charges and the number of nucleons at the throats tend to infinity as the increments of the fundamental constants tend to zero. A Diophantine uncertainty relation arises, which is similar to the uncertainty relation in quantum mechanics: the product of the increment at the throat in the number of charges or the number of nucleons (elementary particle, atomic nucleus) required to maintain equilibrium by the increment in physical constants (rational coefficient of the Diophantine equation) must be no less than a certain value.

The authors thank Jane Gao for her cooperation.

Appendix 1. Geometrization of an Electromagnetic Field and Dusty Matter

Consider a pseudo-Riemannian centrally symmetric geometry with a metric

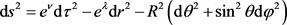(A1)

And the geometric conservative Einstein tensor 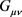expressed through it; it is generated by an electromagnetic field of strength 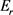with an energy density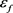, with an electric charge Q, a dusty substance with an energy density 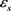and with a total gravitational energy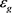. According to the exact particular solution of the Einstein and Maxwell equations in GRT, these physical characteristics are expressed through the geometry [2]:

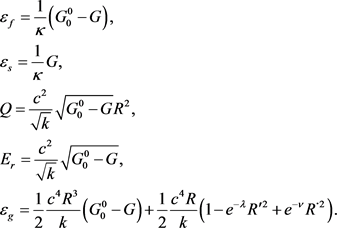(A2)

Here,.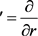

The problem is in expressing the scalar potential in terms of geometry. The partial derivative of with respect to the radial coordinate is expressed in the synchronous accompanying frame of reference through the radial component of the electric field strength:

. (A3)

Substituting from (A2) into (A3), we obtain:

(A4)

Using the Lorentz gage,

, (A5)

and equality to zero of the spatial components of the vector potential in the given frame of reference, we obtain from (A5) an expression for the partial time derivative with regard to time:

. (A6)

Knowledge of the two partial derivatives and makes it possible to find the connection between and the geometry through the integral equation:

(A7)

However, using the permutation of the second partial derivatives

, (A8)

and, substituting the partial derivatives and from (A5) and (A6) in (A8),

, (A9)

it is possible to obtain from (A9) the explicit required expression for the scalar potential in terms of the geometry:

. (A10)

NOTES

¹Recall that this relativistic principle of equivalence is well known in Newtonian nonrelativistic physics and is very accurately carried out experimentally in the form of equality of the inertial mass of a body (an analogue of matter) and its gravitational mass (an analogue of a gravitational field) in Newton’s second law, as a result of which all bodies in a vacuum being in a gravitation field falls with the same acceleration.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Landau, L.D. and Lifshitz, E.M. (1975) The Course of Theoretical Physics. Vol. 2, The Classical Theory of Fields. Butterworth-Heinemann, London.
[2]	Khlestkov, A.Yu. and Khlestkov, Yu.A. (2019) Russian Physics Journal, 62, 264-283. https://doi.org/10.1007/s11182-019-01709-9
[3]	Novikov, I.D. (1964) Soobshenie GAISh. No. 132.
[4]	Khlestkov, Yu.A., Sukhanova, L.A. and Trushkin, N.S. (2016) Chinese Journal of Physics, 54, 614-627. https://doi.org/10.1016/j.cjph.2016.07.008
[5]	Hawking, S.V. and Ellis, G.F.R. (1973) The Large Scale Structure of Space-Time. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511524646
[6]	Khlestkov, Yu.A., Lukashina, N.Yu., Lukashin, M.Yu. and Lukashin, P.Yu. (2019) Journal of Modern Physics, 10, 1299-1309. https://doi.org/10.4236/jmp.2019.1011086
[7]	Khlestkov, Yu.A. (2003) Nauchnaya Sessiya MEPhI-2003. Vol. 5, Moscow, 177.
[8]	Khlestkov, A.Yu., Sukhanova, L.A. and Khlestkov, Yu.A. (2005) Nauchnaya Sessiya MEPhI-2005. Vol. 11, Sbornik Nauchnich Trudov, Moscow, 128-138.
[9]	Gavrilin, D.Yu., Matyuk, N.N., Podoplelov, A.M., Lukashina, N.Yu. and Khlestkov, A.Yu. (2005) Nauchnaya Sessiya MEPhI-2005. Vol. 11, Sbornik Nauchnich Trudov, Moscow, 123-128.
[10]	Khlestkov, Yu.A. (2005) Zh. Eksp. Theor. Fiz., 128, 300-311.
[11]	Landau, L.D. and Lifshitz, E.M. (1975) The Course of Theoretical Physics. Vol. 2, The Classical Theory of Fields. Butterworth-Heinemann, London.
[12]	Khlestkov, A.Yu. and Khlestkov, Yu.A. (2019) Russian Physics Journal, 62, 264-283. https://doi.org/10.1007/s11182-019-01709-9
[13]	Novikov, I.D. (1964) Soobshenie GAISh. No. 132.
[14]	Khlestkov, Yu.A., Sukhanova, L.A. and Trushkin, N.S. (2016) Chinese Journal of Physics, 54, 614-627. https://doi.org/10.1016/j.cjph.2016.07.008
[15]	Hawking, S.V. and Ellis, G.F.R. (1973) The Large Scale Structure of Space-Time. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511524646
[16]	Khlestkov, Yu.A., Lukashina, N.Yu., Lukashin, M.Yu. and Lukashin, P.Yu. (2019) Journal of Modern Physics, 10, 1299-1309. https://doi.org/10.4236/jmp.2019.1011086
[17]	Khlestkov, Yu.A. (2003) Nauchnaya Sessiya MEPhI-2003. Vol. 5, Moscow, 177.
[18]	Khlestkov, A.Yu., Sukhanova, L.A. and Khlestkov, Yu.A. (2005) Nauchnaya Sessiya MEPhI-2005. Vol. 11, Sbornik Nauchnich Trudov, Moscow, 128-138.
[19]	Gavrilin, D.Yu., Matyuk, N.N., Podoplelov, A.M., Lukashina, N.Yu. and Khlestkov, A.Yu. (2005) Nauchnaya Sessiya MEPhI-2005. Vol. 11, Sbornik Nauchnich Trudov, Moscow, 123-128.
[20]	Khlestkov, Yu.A. (2005) Zh. Eksp. Theor. Fiz., 128, 300-311.