A Mathematical Comparison of the Schwarzschild and Kerr Metrics ()
1. Introduction
In order to explain the type of problems we want to solve, let us start adding a constant parameter to the example provided by Macaulay in 1916 that we have presented in a previous paper for other reasons [1]. However, before doing so, we first recall the following key definition and formal theorem before sketching the main results obtained in this paper:
DEFINITION 1.1: A system of order q on E is an open vector subbundle 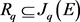 with prolongations
with prolongations 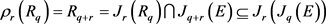 and symbols
and symbols 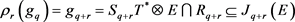 only depending on
only depending on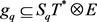 . For
. For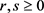 , we denote by
, we denote by 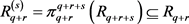 the projection of
the projection of 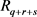 on
on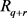 , which is thus defined by more equations in general. The system
, which is thus defined by more equations in general. The system 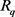 is said to be formally integrable (FI) if we have
is said to be formally integrable (FI) if we have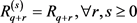 , that is if all the equations of order
, that is if all the equations of order 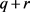 can be obtained by means of only r prolongations. The system
can be obtained by means of only r prolongations. The system 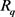 is said to be involutive if it is FI with an involutive symbol
is said to be involutive if it is FI with an involutive symbol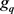 . We shall simply denote by
. We shall simply denote by 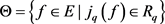 the “set” of (formal) solutions. It is finally easy to prove that the Spencer operator
the “set” of (formal) solutions. It is finally easy to prove that the Spencer operator 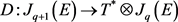 restricts to
restricts to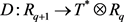 .
.
The most difficult but also the most important theorem has been discovered by M. Janet in 1920 [2] and presented by H. Goldschmidt in a modern setting in 1968 [3]. However, the first proof with examples is not intrinsic while the second, using the Spencer operator, is very technical and we have given a quite simpler different proof in 1978 ( [2], also [4] [5] ) that we shall use later on for studying the Killing equations for the Schwarzschild and Kerr metrics:
THEOREM 1.2: If 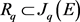 is a system of order q on E such that its first prolongation
is a system of order q on E such that its first prolongation  is a vector bundle while its symbol
is a vector bundle while its symbol ![]() is also a vector bundle, then, if
is also a vector bundle, then, if ![]() is 2-acyclic, we have
is 2-acyclic, we have![]() .
.
COROLLARY 1.3: (PP procedure) If a system ![]() is defined over a differential field K, then one can find integers
is defined over a differential field K, then one can find integers ![]() such that
such that ![]() is formally integrable or even involutive.
is formally integrable or even involutive.
The paper will be organized as follows:
· First of all, starting with an arbitrary system![]() , the purpose of the next motivating examples is to prove that the generating CC of the operator:
, the purpose of the next motivating examples is to prove that the generating CC of the operator:
![]()
though they are of course fully determined by the first order CC of the final involutive system ![]() produced by the prolongation/projection (PP) procedure, are in general of order
produced by the prolongation/projection (PP) procedure, are in general of order ![]() like the Riemann or Weyl operators, but may be of strictly lower order.
like the Riemann or Weyl operators, but may be of strictly lower order.
· The same procedure will be applied to the two first order systems of infinitesimal Lie equations allowing to define the Killing operator for the S-metric and the K-metric while comparing the respective results obtained. We may say that the case of the S-metric has already been treated in the publication quoted in the abstract but that it took us two years just for daring to engage in dealing similarly with the K-metric as anybody can understand by looking at the components of the Riemann tensor in the literature. It has been a surprising “miracle” to discover in the proof of Theorem 4.2 that there was a unique but tricky way to bring this problem to a purely mathematical and relatively simple computation on Lie equations and their prolongations.
· In the case of the S-metric, starting with the system![]() , we shall obtain
, we shall obtain ![]() but
but ![]() with a strict inclusion both with
with a strict inclusion both with ![]() again with a strict inclusion but in such a way that
again with a strict inclusion but in such a way that ![]() is FI though not involutive because only its first prolongation is involutive. From this result we shall exhibit 15 (generating) second order CC and 4 (generating) unexpected third order CC without having to refer to any specific technical relativistic tool.
is FI though not involutive because only its first prolongation is involutive. From this result we shall exhibit 15 (generating) second order CC and 4 (generating) unexpected third order CC without having to refer to any specific technical relativistic tool.
· Then, the case of the K-metric seems to be similar as it is also leading to the strict inclusions ![]() of systems but the new systems are quite different and in particular
of systems but the new systems are quite different and in particular ![]() is now involutive, a result providing 14 (generating) second order CC and 4 (generating) third order CC. As in the motivating examples, it does not seem that the total numbers
is now involutive, a result providing 14 (generating) second order CC and 4 (generating) third order CC. As in the motivating examples, it does not seem that the total numbers ![]() or
or ![]() have any intrinsic mathematical meaning. In both cases, using the Spencer operator, we explain why the important object is the group of invariance of the metric but not the metric itself.
have any intrinsic mathematical meaning. In both cases, using the Spencer operator, we explain why the important object is the group of invariance of the metric but not the metric itself.
· Finally, we are able to relate these results to the computation of certain extension modules in differential homological algebra, showing why the mathematical foundations of conformal geometry in arbitrary dimension and general relativity must be entirely revisited in the light of these results.
MOTIVATING EXAMPLE 1.4: With![]() , let us consider the second order linear system
, let us consider the second order linear system ![]() with
with ![]() and parametric jets
and parametric jets![]() , defined by the two inhomogeneous PD equations where a is a constant parameter:
, defined by the two inhomogeneous PD equations where a is a constant parameter:
![]()
First of all we have to look for the symbol ![]() defined by the two linear equations
defined by the two linear equations![]() . The coordinate system is not
. The coordinate system is not ![]() -regular and exchanging
-regular and exchanging ![]() with
with![]() , we get the Janet board:
, we get the Janet board:
![]()
![]() is involutive, thus 2-acyclic and we obtain from the main theorem
is involutive, thus 2-acyclic and we obtain from the main theorem![]() . However,
. However, ![]() with a strict inclusion because
with a strict inclusion because ![]() is now defined by adding the equations
is now defined by adding the equations![]() . We may start afresh with
. We may start afresh with ![]() and study its symbol
and study its symbol ![]() with Janet tabular:
with Janet tabular:
![]()
Since that moment, we have to consider the two possibilities:
· ![]() : The initial system becomes
: The initial system becomes![]() ,
, ![]() and has an involutive symbol. It is thus involutive because it is trivially FI as the left members are homogeneous with only one generating first order CC, namely
and has an involutive symbol. It is thus involutive because it is trivially FI as the left members are homogeneous with only one generating first order CC, namely![]() . We have
. We have ![]() and the following commutative and exact diagrams:
and the following commutative and exact diagrams:
![]()
![]()
We have thus the Janet sequence:
![]()
or, equivalently, the exact sequence of differential modules over ![]() :
:
![]()
where p is the canonical projection onto the residual differential module.
· ![]() : When the coefficients are in a differential field of constants, for example if
: When the coefficients are in a differential field of constants, for example if ![]() is invertible, we may choose
is invertible, we may choose ![]() like Macaulay [1]. It follows that
like Macaulay [1]. It follows that ![]() is still involutive but we have the strict inclusion
is still involutive but we have the strict inclusion ![]() and thus the strict inclusion
and thus the strict inclusion ![]() because
because![]() . We may thus continue the PP procedure and obtain the new strict inclusion
. We may thus continue the PP procedure and obtain the new strict inclusion ![]() because
because ![]() as
as ![]() is defined by the 4 equations with Janet tabular:
is defined by the 4 equations with Janet tabular:
![]()
As ![]() is easily seen to be involutive, we achieve the PP procedure, obtaining the strict intrinsic inclusions and corresponding fiber dimensions:
is easily seen to be involutive, we achieve the PP procedure, obtaining the strict intrinsic inclusions and corresponding fiber dimensions:
![]()
Finally, we have![]() .
.
It remains to find out the CC for ![]() in the initial inhomogeneous system. As we have used two prolongations in order to exhibit
in the initial inhomogeneous system. As we have used two prolongations in order to exhibit![]() , we have second order formal derivatives of u and v in the right members. Now, as we have an involutive system, we have first order CC for the new right members and could hope therefore for third order generating CC. However, we have the 4 CC:
, we have second order formal derivatives of u and v in the right members. Now, as we have an involutive system, we have first order CC for the new right members and could hope therefore for third order generating CC. However, we have the 4 CC:
![]()
It follows that we have only one second order and one third order CC:
![]()
but, surprisingly, we are left with the only generating second order CC ![]() which is coming from the fact that the operator P commutes with the operator Q.
which is coming from the fact that the operator P commutes with the operator Q.
We let the reader prove as an exercise (see [1] [6] for details) that ![]() ,
, ![]() and thus
and thus![]() ,
, ![]() in the following commutative and exact diagrams where E is the trivial vector bundle with
in the following commutative and exact diagrams where E is the trivial vector bundle with ![]() and
and![]() :
:
![]()
We have thus the formally exact sequence:
![]()
or, equivalently, the exact sequence of differential modules over D as before:
![]()
which is nevertheless not a Janet sequence because R2 is not involutive.
MOTIVATING EXAMPLE 1.5: We now prove that the case of variable coefficients can lead to strikingly different results, even if we choose them in the differential field ![]() of rational functions in the coordinates that we shall meet in the study of the S and K metrics. We denote by
of rational functions in the coordinates that we shall meet in the study of the S and K metrics. We denote by ![]() the ring of differential operators with coefficients in K. For this, let us consider the simplest situation met with the second order system
the ring of differential operators with coefficients in K. For this, let us consider the simplest situation met with the second order system![]() :
:
![]()
We may consider successively the following systems of decreasing dimensions![]() :
:
![]()
![]()
![]()
The last system is involutive with the following Janet tabular:
![]()
The generic solution is of the form ![]() and it is rather striking that such a system has constant coefficients (This will be exactly the case of the S and K metrics but similar examples can be found in [5] ). We could hope for 9 generating CC up to order 4 but tedious computations, left to the reader as a tricky exercise, prove that we have in fact, as before, only 2 generating third order CC described by the following involutive system, namely:
and it is rather striking that such a system has constant coefficients (This will be exactly the case of the S and K metrics but similar examples can be found in [5] ). We could hope for 9 generating CC up to order 4 but tedious computations, left to the reader as a tricky exercise, prove that we have in fact, as before, only 2 generating third order CC described by the following involutive system, namely:
![]()
![]()
satisfying the only first order CC:![]() .
.
We obtain the sequence of D-modules:
![]()
where the order of an operator is written under its arrow. This example proves that even a slight modification of the parameter can change the corresponding differential resolution.
MOTIVATING EXAMPLE 1.6: We comment a tricky example first provided by M. Janet in 1920, that we have studied with details in [4] [7]. With![]() ,
, ![]() ,
, ![]() ,
, ![]() and using jet notations, let us consider the inhomogeneous second order system:
and using jet notations, let us consider the inhomogeneous second order system:
![]()
We let the reader prove that the space of solutions has dimension 12 over ![]() and that we have
and that we have ![]() in such a way that
in such a way that ![]() is involutive and even finite type with a zero symbol. Accordingly, we have
is involutive and even finite type with a zero symbol. Accordingly, we have![]() . Passing to the differential module point of view, it follows that
. Passing to the differential module point of view, it follows that ![]() and
and![]() . According to the general results presented, we have thus to use 5 prolongations and could therefore wait for CC up to order … 6!!!. In fact, and we repeat that there is no hint at all for predicting this result in any intrinsic way, we have only two generating CC, one of order 3 and … one of order 6 indeed, namely:
. According to the general results presented, we have thus to use 5 prolongations and could therefore wait for CC up to order … 6!!!. In fact, and we repeat that there is no hint at all for predicting this result in any intrinsic way, we have only two generating CC, one of order 3 and … one of order 6 indeed, namely:
![]()
![]()
satisfying the only fourth order CC
![]()
It follows that we have the unexpected differential resolution:
![]()
with, from left to right, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and Euler-Poincaré characteristic
and Euler-Poincaré characteristic ![]() as expected. In addition, if we introduce a constant parameter a by replacing the coefficient
as expected. In addition, if we introduce a constant parameter a by replacing the coefficient ![]() by
by![]() , we obtain
, we obtain ![]() and obtain the same conclusions as before. We point out the fact that, when
and obtain the same conclusions as before. We point out the fact that, when![]() , the system
, the system![]() , which is trivially FI because it is homogeneous, has a symbol
, which is trivially FI because it is homogeneous, has a symbol ![]() which is neither involutive (otherwise it should admit a first order CC), nor even 2-acyclic because we have the parametric jets:
which is neither involutive (otherwise it should admit a first order CC), nor even 2-acyclic because we have the parametric jets:
![]()
and the long δ-sequence:
![]()
![]()
in which![]() ,
,![]()
![]() .
.
However, ![]() is involutive with the following Janet tabular for the vertical jets
is involutive with the following Janet tabular for the vertical jets![]() :
:
![]()
Accordingly, R3 is thus involutive and the only CC ![]() is of order 2 because we need one prolongation only to reach involution and thus 2-acyclicity.
is of order 2 because we need one prolongation only to reach involution and thus 2-acyclicity.
MOTIVATING EXAMPLE 1.7: With![]() , let us consider the inhomogeneous second order system:
, let us consider the inhomogeneous second order system:
![]()
We obtain at once through crossed derivatives ![]() and, by substituting, two fourth order CC for
and, by substituting, two fourth order CC for![]() , namely:
, namely:
![]()
satisfying![]() . However, we may also obtain a single CC for
. However, we may also obtain a single CC for![]() , namely
, namely ![]() and we check at once
and we check at once![]() ,
, ![]() while
while![]() . We let the reader prove that
. We let the reader prove that![]() ,
,![]() . Hence, if
. Hence, if ![]() is a section of
is a section of ![]() while C is a section of
while C is a section of![]() , the jet prolongation sequence:
, the jet prolongation sequence:
![]()
![]()
is not formally exact because![]() , while the corresponding long sequence:
, while the corresponding long sequence:
![]()
![]()
is indeed formally exact because
![]()
but not strictly exact because ![]() is quite far from being FI as we have even
is quite far from being FI as we have even![]() .
.
It follows from these examples and the many others presented in [6] that we cannot agree with [8] [9] [10] [11]. Indeed, it is clear that one can use successive prolongations in order to look for CC of order ![]() and so on, selecting each time the new generating ones and knowing that Noetherian arguments will stop such a procedure … after a while!
and so on, selecting each time the new generating ones and knowing that Noetherian arguments will stop such a procedure … after a while!
However, as long as the numbers r and s are not known, it is not effectively possible to decide in advance about the maximum order that must be reached. Therefore, it becomes clear that exactly the same procedure MUST be applied when looking for the CC of the Killing operators we want to study, the problem becoming only a “mathematical” one but surely not a “physical” one.
IMPORTANT REMARK 1.8: The intrinsic properties of a system with constant coefficients may drastically depend on these coefficients, even if the systems do not appear to be quite different at first sight. Using jet notations, let us consider the second order system ![]() depending on a constant parameter a and defining a differential module M by residue. When
depending on a constant parameter a and defining a differential module M by residue. When ![]() we have the differential sequence:
we have the differential sequence:
![]()
and the adjoint sequence:
![]()
though the CC sequence that must be used with ![]() is:
is:
![]()
On the contrary, if ![]() say
say![]() , we have the differential sequence:
, we have the differential sequence:
![]()
and the CC sequence does coincide with the adjoint sequence:
![]()
It is thus essential to notice that ![]() generates the CC of
generates the CC of ![]() when
when![]() , a result leading to
, a result leading to ![]() but this is not true when
but this is not true when![]() , a result leading to
, a result leading to ![]() [5] [12] [13] [14].
[5] [12] [13] [14].
Comparing the sequences obtained in the previous examples, we may state:
DEFINITION 1.9: A differential sequence is said to be formally exact if it is exact on the jet level composition of the prolongations involved. A formally exact sequence is said to be strictly exact if all the operators/systems involved are FI (see [1] for more details). A strictly exact sequence is called canonical if all the operators/systems are involutive. The only known canonical sequences are the Janet and Spencer sequences that can be defined independently from each other.
With canonical projection![]() , the various prolongations are described by the following commutative and exact introductory diagram:
, the various prolongations are described by the following commutative and exact introductory diagram:
![]()
Applying the standard “snake” lemma, we obtain the useful long exact connecting sequence:
![]()
which is thus connecting in a tricky way FI (lower left) with CC (upper right).
We finally recall the Fundamental Diagram I that we have presented in many books and papers, relating the (upper) canonical Spencer sequence to the (lower) canonical Janet sequence, that only depends on the left commutative square ![]() with
with ![]() when one has an involutive system
when one has an involutive system ![]() over E with
over E with ![]() and
and ![]() is the derivative operator up to order q:
is the derivative operator up to order q:
![]()
We shall use this result, first found exactly 40 years ago [2] but never acknowledged, in order to provide a critical study of the comparison between the S and K metrics.
EXAMPLE 1.10: The Janet tabular in Example 1.4 with ![]() provides the fiber dimensions:
provides the fiber dimensions:
![]()
We notice that 6 − 16 + 14 − 4 = 0, 1 − 10 + 20 − 15 + 4 = 0 and 1 − 4 + 4 − 1 = 0. In this diagram, the Janet sequence seems simpler than the Spencer sequence but, sometimes as we shall see, it is the contrary and there is no rule. We invite the reader to treat similarly the cases ![]() and
and![]() .
.
2. Schwarzschild versus Kerr
2.1. Schwarzschild Metric
In the Boyer-Lindquist (BL) coordinates![]() , the Schwarzschild metric is
, the Schwarzschild metric is ![]() and
and![]() , let us introduce
, let us introduce ![]() with the 4 formal derivatives
with the 4 formal derivatives![]() ,
,
![]() . With speed of light
. With speed of light ![]() and
and ![]() where m is a constant, the metric can be written in the diagonal form:
where m is a constant, the metric can be written in the diagonal form:
![]()
with a surprisingly simple determinant![]() .
.
Using the notations of differential modules or jet theory, we may consider the infinitesimal Killing equations:
![]()
where we have introduced the Christoffel symbols ![]() through the standard Levi-Civita isomorphism
through the standard Levi-Civita isomorphism ![]() while setting
while setting ![]() in the differential field K of coefficients [15]. As in the Macaulay example just considered and in order to avoid any further confusion between sections and derivatives, we shall use the sectional point of view and rewrite the previous 10 equations in the symbolic form
in the differential field K of coefficients [15]. As in the Macaulay example just considered and in order to avoid any further confusion between sections and derivatives, we shall use the sectional point of view and rewrite the previous 10 equations in the symbolic form ![]() where L is the formal Lie derivative:
where L is the formal Lie derivative:
![]()
Though this system ![]() has 4 equations of class 3, 3 equations of class 2, 2 equations of class 1 and 1 equation of class 0, it is far from being involutive because it is finite type with second symbol
has 4 equations of class 3, 3 equations of class 2, 2 equations of class 1 and 1 equation of class 0, it is far from being involutive because it is finite type with second symbol ![]() defined by the 40 equations
defined by the 40 equations ![]() in the initial coordinates. From the symmetry, it is clear that such a system has at least 4 solutions, namely the time translation
in the initial coordinates. From the symmetry, it is clear that such a system has at least 4 solutions, namely the time translation ![]() and, using cartesian coordinates
and, using cartesian coordinates![]() , the 3 space rotations
, the 3 space rotations![]() .
.
We obtain in particular, modulo![]() :
:
![]()
We may also write the Schwarzschild metric in cartesian coordinates as:
![]()
and notice that the ![]() matrix of components of the three rotations has rank equal to 2, a result leading surely, before doing any computation, to the existence of one and only one zero order Killing equation
matrix of components of the three rotations has rank equal to 2, a result leading surely, before doing any computation, to the existence of one and only one zero order Killing equation ![]() . Such a result also amounts to say that the spatial projection of any Killing vector on the radial spatial unit vector
. Such a result also amounts to say that the spatial projection of any Killing vector on the radial spatial unit vector ![]() vanishes beause r must stay invariant.
vanishes beause r must stay invariant.
However, as we are dealing with sections, ![]() implies
implies![]() ,
, ![]() ,
, ![]() … but NOT (care)
… but NOT (care)![]() , these later condition being only brought by one additional prolongation and we have the strict inclusions
, these later condition being only brought by one additional prolongation and we have the strict inclusions ![]() that we rename as
that we rename as![]() . Hence, it remains to determine the dimensions of these subsystems and their symbols, exactly like in the Macaulay example. We shall prove in the next section that two prolongations bring the five new equations:
. Hence, it remains to determine the dimensions of these subsystems and their symbols, exactly like in the Macaulay example. We shall prove in the next section that two prolongations bring the five new equations:
![]()
and a new prolongation only brings the single equation![]() .
.
Knowing that![]() ,
, ![]() ,
, ![]() , we have thus obtained the 15 equations defining
, we have thus obtained the 15 equations defining ![]() with
with ![]() and let the reader draw the corresponding Janet tabular for the 4 equations of class 3, the 4 equations of class 1, the 3 equations of class 0 and the 3 equations of class 2. The symbol
and let the reader draw the corresponding Janet tabular for the 4 equations of class 3, the 4 equations of class 1, the 3 equations of class 0 and the 3 equations of class 2. The symbol ![]() has the two parametric jets
has the two parametric jets ![]() and is not 2-acyclic. Adding
and is not 2-acyclic. Adding![]() , we finally achieve the PP procedure with the 16 equations defining the system
, we finally achieve the PP procedure with the 16 equations defining the system ![]() with
with![]() , namely:
, namely:
![]()
and we have replaced by “×” the only “dot” (non-multiplicative variable) that cannot provide vanishing crossed derivatives and thus involution of the symbol ![]() with the only parametric jets
with the only parametric jets![]() . It is easy to check that
. It is easy to check that![]() , having minimum dimension equal to 4, is formally integrable, though not involutive as it is finite type with
, having minimum dimension equal to 4, is formally integrable, though not involutive as it is finite type with ![]() with parametric jet
with parametric jet ![]() and to exhibit 4 solutions linearly independent over the constants. We let the reader prove as an exercise that the dimension of the Spencer
and to exhibit 4 solutions linearly independent over the constants. We let the reader prove as an exercise that the dimension of the Spencer ![]() -cohomology at
-cohomology at ![]() is
is ![]() but we have proved in [15] that its restriction to
but we have proved in [15] that its restriction to ![]() is of dimension 1 only. We obtain:
is of dimension 1 only. We obtain:
THIS SYSTEM IS NOT INVOLUTIVE BUT DOES NOT DEPEND ON m ANY LONGER
Denoting by ![]() with
with ![]() the prolongation of
the prolongation of![]() , it is the involutive system provided by the prolongation/projection (PP) procedure. We are in position to construct the corresponding canonical/involutive (lower) Janet and (upper) Spencer sequences along the following fundamental diagram I that we recalled in the Introduction. In the present situation, the Spencer sequence is isomorphic to the tensor product of the Poincaré sequence by the underlying 4-dimensional Lie algebra G, namely:
, it is the involutive system provided by the prolongation/projection (PP) procedure. We are in position to construct the corresponding canonical/involutive (lower) Janet and (upper) Spencer sequences along the following fundamental diagram I that we recalled in the Introduction. In the present situation, the Spencer sequence is isomorphic to the tensor product of the Poincaré sequence by the underlying 4-dimensional Lie algebra G, namely:
![]()
In this diagram, not depending any longer on m, we have now ![]() and
and ![]() is of order 2 like
is of order 2 like ![]() while all the other operators are of order 1:
while all the other operators are of order 1:
![]()
We notice the vanishing of the Euler-Poincaré characteristics:
![]()
We point out that, whatever is the sequence used or the way to describe![]() , then
, then ![]() is parametrizing the Cauchy operator
is parametrizing the Cauchy operator ![]() for the S metric. However, such an approach does not tell us explicitly what are the second and third order CC involved in the initial situation.
for the S metric. However, such an approach does not tell us explicitly what are the second and third order CC involved in the initial situation.
In actual practice, all the preceding computations have been finally used to reduce the Poincaré group to its subgroup made with only one time translation and three space rotations! On the contrary, we have proved during almost fourty years that one must increase the Poincaré group (10 parameters), first to the Weyl group (11 parameters by adding 1 dilatation) and finally to the conformal group of space-time (15 parameters by adding 4 elations) while only dealing with he Spencer sequence in order to increase the dimensions of the Spencer bundles, thus the number ![]() of potentials and the number
of potentials and the number ![]() of fields (compare to [16] ).
of fields (compare to [16] ).
2.2. Kerr Metric
We now write the Kerr metric in Boyer-Lindquist coordinates:
![]()
where we have set ![]() as usual and we check that:
as usual and we check that:
![]()
as a well known way to recover the Schwarschild metric. We notice that t or ![]() do not appear in the coefficients of the metric. As the maximum subgroup of invariance of the Kerr metric must be contained in the maximum subgroup of invariance of the Schwarzschild metric because of the above limit when
do not appear in the coefficients of the metric. As the maximum subgroup of invariance of the Kerr metric must be contained in the maximum subgroup of invariance of the Schwarzschild metric because of the above limit when![]() , we shall obtain the only two possible infinitesimal generators
, we shall obtain the only two possible infinitesimal generators![]() . We shall prove that the new first order system
. We shall prove that the new first order system ![]() is involutive, contrary to the case of the S metric. Accordingly, we have the fundamental diagram I with fiber dimensions:
is involutive, contrary to the case of the S metric. Accordingly, we have the fundamental diagram I with fiber dimensions:
![]()
with Euler-Poincaré characteristic![]() . Comparing the surprisingly high dimensions of the Janet bundles with the surprisingly low dimensions of the Spencer bundles needs no comment on the physical usefulness of the Janet sequence, despite its purely mathematical importance. In addition, using the same notations as in the preceding section, we shall prove that we have now the additional zero order equations
. Comparing the surprisingly high dimensions of the Janet bundles with the surprisingly low dimensions of the Spencer bundles needs no comment on the physical usefulness of the Janet sequence, despite its purely mathematical importance. In addition, using the same notations as in the preceding section, we shall prove that we have now the additional zero order equations![]() ,
, ![]() produced by the non-zero components of the Weyl tensor and thus, at best,
produced by the non-zero components of the Weyl tensor and thus, at best, ![]() as these zero order equations will be obtained after only two prolongations. They depend on
as these zero order equations will be obtained after only two prolongations. They depend on ![]() and we should obtain therefore eventually
and we should obtain therefore eventually ![]() CC of order 2 without any way to know about the desired third order CC.
CC of order 2 without any way to know about the desired third order CC.
Using now cartesian space coordinates ![]() with
with![]() ,
, ![]() , we have only to study the following first order involutive system for
, we have only to study the following first order involutive system for ![]() with coefficients no longer depending on
with coefficients no longer depending on![]() , providing the only generator
, providing the only generator![]() :
:
![]()
and the fundamental diagram
![]()
The involutive system produced by the PP procedure does not depend on ![]() any longer. Accordingly, this final result definitively proves that, as far as differential sequences are concerned:
any longer. Accordingly, this final result definitively proves that, as far as differential sequences are concerned:
THE ONLY IMPORTANT OBJECT IS THE GROUP, NOT THE METRIC
2.3. Schwarzschild Metric Revisited
Let us now introduce the Riemann tensor ![]() and use the metric in order to raise or lower the indices in order to obtain the purely covariant tensor
and use the metric in order to raise or lower the indices in order to obtain the purely covariant tensor![]() . Then, using r as an implicit summation index, we may consider the formal Lie derivative on sections:
. Then, using r as an implicit summation index, we may consider the formal Lie derivative on sections:
![]()
that can be considered as an infinitesimal variation. As for the Ricci tensor![]() , we notice that
, we notice that ![]() though we have only:
though we have only:
![]()
The 6 non-zero components of the Riemann tensor are known to be:
![]()
First of all, we notice that:
![]()
![]()
We obtain therefore:
![]()
![]()
Similarly, we also get:
![]()
We also obtain for example, among the second order CC:
![]()
and thus, among the first prolongations, the third order CC that cannot be obtained by prolongation of the various second order CC while taking into account the Bianchi identities [15]. Using the Spencer operator and the fact that![]() , we first obtain the 3 third order CC:
, we first obtain the 3 third order CC:
![]()
However, introducing ![]() in the right member as in the motivating examples, we have 3 PD equations for
in the right member as in the motivating examples, we have 3 PD equations for![]() , namely:
, namely:
![]()
Using two prolongations and eliminating the third order jets, we obtain successively:
![]()
![]()
![]()
![]()
![]()
![]()
Summing, we see that all terms in ![]() and
and ![]() disappear and that we are only left with terms in
disappear and that we are only left with terms in![]() , including in particular the second order jets
, including in particular the second order jets![]() , namely:
, namely:
![]()
Setting![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() with
with ![]() , we obtain the additional strikingly unusual third order CC for
, we obtain the additional strikingly unusual third order CC for![]() :
:
![]()
Nevertheless, in our opinion at least, we do not believe that such a purely “technical” relation could have any “physical” usefulness and let the reader compare it with the CC already found in ( [15], Lemma 3.B.3). Finally, we have:
![]()
![]()
a result showing that certain third order CC may be differential consequences of the Bianchi identities (see [15] for details). Finally, we notice that:
![]()
and, comparing to the previous computation for![]() , nothing can be said about the generating CC as long as the PP procedure has not been totally achieved with a FI or involutive system.
, nothing can be said about the generating CC as long as the PP procedure has not been totally achieved with a FI or involutive system.
2.4. Kerr Metric Revisited
Though we shall provide explicitly all the details of the computations involved, we shall change the coordinate system in order to confirm these results by only using computer algebra as less as possible. The idea is to use the so-called “rational polynomial” coefficients while setting anew:
![]()
in order to obtain over the differential field ![]() :
:
![]()
with now ![]() and
and ![]() . For a later use, it is also possible to set
. For a later use, it is also possible to set
![]() .
.
As this result will be crucially used later on, we have:
LEMMA 4.1:![]() .
.
Proof: As an elementary result on matrices, we have:
![]()
with ![]() because
because ![]() and
and ![]() is thus equal to:
is thus equal to:
![]()
that is, after division by ![]() and
and![]() :
:
![]()
Finally, after eliminating the last term, we get:
![]()
that is (Compare to [ ] and [ ]):
![]()
in a coherent way with the result ![]() obtained
obtained
for the S metric when![]() . For a later use, we have obtained
. For a later use, we have obtained ![]() .
.
Q.E.D.
Contrary to the S-metric, the main “trick” for studying the K-metric is to take into account that the partition between the zero and nonzero terms will not change if we use convenient coordinates, even if the nonzero terms may change. Meanwhile, we notice that the most important property of the K-metric is the
existence of the off-diagonal term![]() , that is
, that is ![]() the
the
coefficient of ![]() in the metric
in the metric ![]() which is indeed
which is indeed![]() . We may obtain therefore successively the Killing equations for the Kerr type metric, using sections of jet bundles and writing simply
. We may obtain therefore successively the Killing equations for the Kerr type metric, using sections of jet bundles and writing simply ![]() while framing the principal derivative
while framing the principal derivative ![]() of
of![]() :
:
![]()
With![]() , multiplying
, multiplying ![]() by
by![]() ,
, ![]() by
by ![]() and adding, we notice that:
and adding, we notice that:
![]()
Similarly, multiplying ![]() by
by ![]() (care to the factor 2), we get:
(care to the factor 2), we get:
![]()
Substracting, we obtain therefore the tricky formula (see the previous Lemma):
![]()
Substituting, we obtain:
![]()
a situation leading to modify![]() ,
, ![]() and
and![]() , similar to the one found in the Minkowski case with
, similar to the one found in the Minkowski case with![]() ,
, ![]() ,
, ![]() when
when![]() . We also obtain with
. We also obtain with ![]() and
and![]() :
:
![]()
and with ![]() and
and![]() :
:
![]()
Finally, multiplying ![]() by
by![]() ,
, ![]() by
by ![]() and adding, we finally obtain (see the Lemma again)
and adding, we finally obtain (see the Lemma again)
![]()
Using the rational coefficients belonging to the differential field ![]() , the nonzero components of the corresponding Riemann tensor can be found in textbooks.
, the nonzero components of the corresponding Riemann tensor can be found in textbooks.
One has the classical orthonormal decomposition:
![]()
and defining:
![]()
in which the coefficient of ![]() is
is ![]() while the coefficient of
while the coefficient of ![]() is
is ![]() indeed. We have
indeed. We have
![]() and make thus the Minkowski metric appearing in a purely algebraic way. We now use the new coordinates
and make thus the Minkowski metric appearing in a purely algebraic way. We now use the new coordinates![]() ,
, ![]() and it follows that the conditions
and it follows that the conditions![]() ,
, ![]() are invariant under such a change of basis because dX1 and dX2 are respectively proportional to
are invariant under such a change of basis because dX1 and dX2 are respectively proportional to ![]() and
and![]() . Indeed, as
. Indeed, as ![]() and thus
and thus![]() , the new symbol
, the new symbol ![]() of
of ![]() while
while ![]() as mixed tensors.
as mixed tensors.
We may obtain simpler formulas in the corresponding basis, in particular the 6 components with only two different indices are proportional to ![]() while the 3 components with all four different indices are proportional to
while the 3 components with all four different indices are proportional to![]() .
.
In the original rational coordinate system, the main nonzero components of the Riemann tensor can only be obtained by means of computer algebra. For helping the reader to handle the literature, for example the book “Computations in Riemann Geometry” written by Kenneth R. Koehler that can be found on the net with a free access, we refer to the seventh chapter on “Black Holes”. We notice that ω→−ω, that is to say changing the sign of the metric, does not change the Christoffel symbols (![]() ) and the Riemann tensor (
) and the Riemann tensor (![]() ) but changes the sign of (
) but changes the sign of (![]() ). For this reason, we have adopted the sign convention of this reference for the explicit computation of these later components as the products and quotients used in the sequel will not be changed.
). For this reason, we have adopted the sign convention of this reference for the explicit computation of these later components as the products and quotients used in the sequel will not be changed.
We have successively:
![]()
It must be noticed that we have been able to factorize the six components with only two different indices by ![]() and the three components with four different indices by
and the three components with four different indices by![]() , a result not evident at first sight but coherent with the orthogonal decomposition.
, a result not evident at first sight but coherent with the orthogonal decomposition.
After tedious computations, we obtain:
![]()
which is indeed vanishing when ![]() for the S metric, both with:
for the S metric, both with:
![]()
![]()
Introducing the formal Lie derivative ![]() and using the fact that
and using the fact that ![]() is a tensor, the system
is a tensor, the system ![]() contains the new equations:
contains the new equations:
![]()
Taking into account the original first order Killing equations, we obtain successively:
![]()
and we must add:
![]()
These linear equations are not linearly independent because:
![]()
Also, linearizing while using the Kronecker symbol![]() , we get:
, we get:
![]()
Thus, introducing the Ricci tensor and linearizing, we get:
![]()
It follows that ![]() and we have in particular
and we have in particular![]() :
:
![]()
The first row proves that ![]() is a linear combination of
is a linear combination of ![]() and
and![]() . Then, if we want to solve the three other equations with respect to
. Then, if we want to solve the three other equations with respect to![]() ,
, ![]() and
and![]() , the corresponding determinant is, up to sign:
, the corresponding determinant is, up to sign:
![]()
Accordingly, we only need to take into account![]() .
.
Similarly, we also obtain![]() :
:
![]()
where we have to set![]() .
.
Hence, taking into account![]() , we just need to use
, we just need to use ![]() and
and![]() .
.
However, using the previous lemma, we obtain the formal Lie derivative:
![]()
and thus ![]() with
with![]() .
.
In addition, we have ![]() and thus
and thus ![]() .
.
We have also:
![]()
The following invariants are obtained successively in a coherent way:
![]()
![]()
However, as![]() , then
, then ![]() and
and ![]() can be both divided by a and we get the new invariant:
can be both divided by a and we get the new invariant:
![]()
These results are leading to![]() ,
, ![]() , thus to
, thus to![]() ,
, ![]() and
and ![]() after substitution. In the case of the S-metric, only the first invariant can be used in order to find
after substitution. In the case of the S-metric, only the first invariant can be used in order to find![]() .
.
Taking into account the previous result, we obtain the two equations:
![]()
Using the fact that we have now:
![]()
we may multiply the first equation by![]() , the second by
, the second by ![]() and sum in order to obtain:
and sum in order to obtain:
![]()
Using the previous identity for![]() , we obtain therefore:
, we obtain therefore:
![]()
Taking into account the fact that ![]() and substituting, we finally obtain:
and substituting, we finally obtain:
![]()
A similar procedure could have been followed by using ![]() and
and![]() .
.
Now, we must distinguish among the 20 components of the Riemann tensor along with the following tabular where we have to take into account the identity![]() :
:
![]()
In this tabular, the vanishing components obtained by computer algebra are put in a box, the nonzero components of the left column do not vanish when ![]() and the other components vanish when
and the other components vanish when![]() . Also, the 11 (care) lower components can be known from the 10 upper ones.
. Also, the 11 (care) lower components can be known from the 10 upper ones.
Keeping in mind the study of the S-metric and the fact that![]() ,
, ![]() ,
, ![]() ,
, ![]() while framing the leading terms not vanishing when
while framing the leading terms not vanishing when![]() , we get:
, we get:
![]()
Then, taking into account the fact that![]() , we obtain similarly:
, we obtain similarly:
![]()
The leading determinant does not vanish when ![]() because, in this case, all terms are vanishing and we are left with the two linearly independent framed terms, a result amounting to
because, in this case, all terms are vanishing and we are left with the two linearly independent framed terms, a result amounting to ![]() and
and ![]() in the case of the S-metric in [15].
in the case of the S-metric in [15].
In the case of the K-metric, we may use the relations already framed in order to keep only the four parametric jets ![]() on the right side. We may also rewrite them as follows:
on the right side. We may also rewrite them as follows:
![]()
if we use the fact that ![]() in the inverse metric.
in the inverse metric.
As a byproduct, we are now left with the two (complicated) equations ![]() and
and ![]() where the dots mean linear combinations of
where the dots mean linear combinations of ![]() with coefficients in K and the study of the Killing operator is quite more difficult in the case of the K-metric. Of course, it becomes clear that the use of the formal theory is absolutely necessary as an intrinsic approach could not be achieved if one uses solutions instead of sections. Indeed the strict inclusion
with coefficients in K and the study of the Killing operator is quite more difficult in the case of the K-metric. Of course, it becomes clear that the use of the formal theory is absolutely necessary as an intrinsic approach could not be achieved if one uses solutions instead of sections. Indeed the strict inclusion ![]() cannot be even imagined if one does believe that
cannot be even imagined if one does believe that![]() ,
, ![]() brings
brings ![]() and
and![]() . The computation could have been done with
. The computation could have been done with ![]() and
and ![]() because
because ![]() and
and![]() .
.
The next hard step will be to prove that the other linearized components of the Riemann tensor do not produce any new different first order equation. The main idea will be to revisit the new linearized tabular with:
![]()
Putting the leading terms into a box, we have the identity ![]() that must be combined with the following formulas
that must be combined with the following formulas![]() :
:
![]()
![]()
![]()
and so on, allowing to compute the 11 (care) lower terms from the 2 + 4 + 4 = 10 upper ones.
We have thus the following successive eleven logical inter-relations:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Keeping in mind the four additional equations and their consequences that have been already framed, both with the vanishing components of the Riemann tensor, namely:
![]()
we get successively:
![]()
As we have already exhibited an isomorphism![]() , we may use only the later right set of parametric jet components. Using the previous logical relations while framing the leading terms not vanishing a priori when
, we may use only the later right set of parametric jet components. Using the previous logical relations while framing the leading terms not vanishing a priori when![]() , there is only one possibility to choose four components of the linearized Riemann tensor, namely:
, there is only one possibility to choose four components of the linearized Riemann tensor, namely:
![]()
In order to understand the difficulty of the computations involved, we propose to the reader, as an exercise, to prove “directly” that the two following relations:
![]()
![]()
are only linear combinations of the previous ones![]() .
.
We are facing two technical problems “spoilting”, in our opinion, the use of the K metric:
· With ![]() in place of
in place of![]() , we have
, we have ![]() and the leading term of
and the leading term of ![]() becomes proportional to
becomes proportional to ![]() with a wrong sign that cannot allow using
with a wrong sign that cannot allow using![]() . A similar comment is valid for the four successive leading terms.
. A similar comment is valid for the four successive leading terms.
· We also discover the summation ![]() in
in ![]() with a wrong sign that cannot allow introducing
with a wrong sign that cannot allow introducing ![]() as one could hope. A similar comment is valid for the four successive summations.
as one could hope. A similar comment is valid for the four successive summations.
Nevertheless, we obtain the following unexpected formal linearized result that will be used in a crucial intrinsic way for finding out the generating second order and third order CC:
THEOREM 4.2: The rank of the previous system with respect to the four jet coordinates ![]() is equal to 2, for both the S and K-metrics. We obtain in particular the two striking identities:
is equal to 2, for both the S and K-metrics. We obtain in particular the two striking identities:
Proof: In the case of the S-metric with![]() , only the framed terms may not vanish and, denoting by “~” a linear proportionality, we have already obtained
, only the framed terms may not vanish and, denoting by “~” a linear proportionality, we have already obtained![]() :
:
![]()
Hence, the rank of the system with respect to the 4 parametric jets ![]() just drops to 2 and this fact confirms the existence of the 5 additional first order equations obtained, as we saw, after two prolongations.
just drops to 2 and this fact confirms the existence of the 5 additional first order equations obtained, as we saw, after two prolongations.
In the case of the K-metric with![]() , the study is much more delicate.
, the study is much more delicate.
With![]() , the coefficients of the
, the coefficients of the ![]() metric of the previous system on the basis of the above parametric jets are proportional to the symmetric matrix:
metric of the previous system on the basis of the above parametric jets are proportional to the symmetric matrix:
![]()
Indeed, we have successively for the common factor![]() :
:
![]()
![]()
![]()
![]()
and similarly for the common factor![]() :
:
![]()
![]()
![]()
![]()
We do not believe that such a purely computational mathematical result, though striking it may look like, could have any useful physical application and this comment will be strengthened by the next theorem provided at the end of this section.
Q.E.D.
COROLLARY 4.3: The Killing operator for the K metric has 14 generating second order CC.
Proof: According to the previous theorem, we have ![]() as we can choose the 4 parametric jets
as we can choose the 4 parametric jets ![]() and
and![]() . Using the introductory diagram with
. Using the introductory diagram with ![]() and thus
and thus ![]() , we obtain at once
, we obtain at once ![]() in a purely intrinsic way. We may thus start afresh with the new first order system
in a purely intrinsic way. We may thus start afresh with the new first order system ![]() obtained from
obtained from ![]() after 2 prolongations. This result is thus obtained totally independently of any specific GR technical object like the Teukolski scalars, the Killing-Yano tensors or even the Penrose spinors introduced in [8] [9] [10] [11] [16].
after 2 prolongations. This result is thus obtained totally independently of any specific GR technical object like the Teukolski scalars, the Killing-Yano tensors or even the Penrose spinors introduced in [8] [9] [10] [11] [16].
Q.E.D.
Finally, we know from [2] [4] [12] [15] [17] [18] [19] that if ![]() is a system of infinitesimal Lie equations, then we have the algebroid bracket
is a system of infinitesimal Lie equations, then we have the algebroid bracket ![]() defined on sections by the following formula not depending on the lift
defined on sections by the following formula not depending on the lift ![]() of
of![]() :
:
![]()
with the algebraic bracket bilinearly defined by ![]() and such that:
and such that:
![]()
It follows that ![]() is such that
is such that ![]() with
with ![]() because we have obtained a total of 6 new different first order equations. We have on sections (care again) the 16 (linear) equations of
because we have obtained a total of 6 new different first order equations. We have on sections (care again) the 16 (linear) equations of ![]() as follows:
as follows:
![]()
and we may choose only the 2 parametric jets ![]() among
among ![]() to which we must add
to which we must add ![]() in any case as they are not appearing in the Killing equations and their prolongations.
in any case as they are not appearing in the Killing equations and their prolongations.
The system is not involutive because it is finite type with ![]() and
and ![]() cannot be thus involutive.
cannot be thus involutive.
It remains to make one more prolongation in order to study ![]() with strict inclusions in order to study the third order CC for
with strict inclusions in order to study the third order CC for ![]() already described for the Schwarzschild metric in [15].
already described for the Schwarzschild metric in [15].
![]()
Surprisingly and contrary to the situation found for the S metric, we have now a trivially involutive first order system with only solutions![]() ,
, ![]() ,
, ![]() ,
,![]() . However, the difficulty is to know what second members must be used along the procedure met for all the motivating examples. In particular, we have again identities to zero like
. However, the difficulty is to know what second members must be used along the procedure met for all the motivating examples. In particular, we have again identities to zero like![]() ,
, ![]() or, equivalently,
or, equivalently, ![]() ,
, ![]() and thus 4 third order CC coming from the 4 following components of the Spencer operator:
and thus 4 third order CC coming from the 4 following components of the Spencer operator:
![]()
a result that cannot be even imagined from [8] [9] [10] [11] [16]. Of course, proceeding like in the motivating examples, we must substitute in the right
members the values obtained from ![]() and set for example
and set for example ![]()
while replacing ![]() and
and ![]() by the corresponding linear combinations of the Riemann tensor already obtained for the right members of the two zero order equations.
by the corresponding linear combinations of the Riemann tensor already obtained for the right members of the two zero order equations.
Using one more prolongation, all the sections (care again) vanish but ![]() and
and![]() , a result leading to
, a result leading to ![]() in a coherent way with the only nonzero Killing vectors
in a coherent way with the only nonzero Killing vectors![]() . We have indeed:
. We have indeed:
![]()
Like in the case of the S metric, ![]() is not involutive but
is not involutive but ![]() is involutive. However, contrary to the S metric with
is involutive. However, contrary to the S metric with![]() , now
, now ![]() for the K metric and
for the K metric and ![]() is trivially involutive with a full Janet tabular having 16 rows of first order jets and 2 rows of zero order jets.
is trivially involutive with a full Janet tabular having 16 rows of first order jets and 2 rows of zero order jets.
REMARK 4.4: We have in general ( [2] [5] p 339, 345):
![]()
that is, in our case![]() . However, we have indeed the equality
. However, we have indeed the equality ![]() even if the conditions of Theorem 1.1 are not satisfied because
even if the conditions of Theorem 1.1 are not satisfied because ![]() is not 2-acyclic. Indeed, the Spencer map
is not 2-acyclic. Indeed, the Spencer map ![]() is not injective and we let the reader check as an exercise that its kernel is generated by
is not injective and we let the reader check as an exercise that its kernel is generated by ![]() and the Spencer δ-cohomology is such that
and the Spencer δ-cohomology is such that ![]() because the cocycles are defined by the equations
because the cocycles are defined by the equations![]() . Hence, contrary to what could be imagined, the major difference between the S and K-metrics is not at all the existence of off-diagonal terms but rather the fact that
. Hence, contrary to what could be imagined, the major difference between the S and K-metrics is not at all the existence of off-diagonal terms but rather the fact that ![]() is not involutive with
is not involutive with ![]() for the S-metric while
for the S-metric while ![]() is involutive with
is involutive with ![]() for the K-metric. This is the reason for which one among the four third order CC must be added with two prolongations for the S-metric while the four third order CC are obtained in the same way from the Spencer operator for the K-metric. Of course no classical approach can explain this fact which is lacking in [8] [9] [10] [11].
for the K-metric. This is the reason for which one among the four third order CC must be added with two prolongations for the S-metric while the four third order CC are obtained in the same way from the Spencer operator for the K-metric. Of course no classical approach can explain this fact which is lacking in [8] [9] [10] [11].
The following result even questions the usefulness of the whole previous approach:
THEOREM 4.5: The operator ![]() admits a minimum parametrization by the operator
admits a minimum parametrization by the operator ![]() with 1 potential when
with 1 potential when![]() , found in 1863. It admits a canonical self-adjoint parametrization by the operator
, found in 1863. It admits a canonical self-adjoint parametrization by the operator ![]() with 6 potentials when
with 6 potentials when![]() , found in 1892 and modified to a mimimum parametrization by the operator Maxwell with 3 potentials, found in 1870 or Morera found in 1892. More generally, it admits a canonical parametrization by the operator
, found in 1892 and modified to a mimimum parametrization by the operator Maxwell with 3 potentials, found in 1870 or Morera found in 1892. More generally, it admits a canonical parametrization by the operator ![]() with
with ![]() potentials that can be modified to a relative parametrization by
potentials that can be modified to a relative parametrization by ![]() with
with ![]() potentials which is nevertheless not minimum when
potentials which is nevertheless not minimum when![]() , found in 2007. In all these cases, the corresponding potentials have nothing to do with the perturbation of the metric. Such a result is also valid for any Lie group of transformations, in particular for the conformal group in arbitrary dimension.
, found in 2007. In all these cases, the corresponding potentials have nothing to do with the perturbation of the metric. Such a result is also valid for any Lie group of transformations, in particular for the conformal group in arbitrary dimension.
Proof: We provide successively the explicit corresponding parametrizations:
· ![]() : Multiplying the linearized Riemann operator by a test function
: Multiplying the linearized Riemann operator by a test function ![]() and integrating by parts, we obtain (care to the factor 2 involved):
and integrating by parts, we obtain (care to the factor 2 involved):
![]()
![]()
Cauchy operator ![]()
Airy operator ![]()
![]()
It is clear that the test function f has nothing to do with the metric ω ( [5], Introduction).
· ![]() We now present the original Beltrami parametrization:
We now present the original Beltrami parametrization:
![]()
which does not seem to be self-adjoint but is such that![]() . Accordingly, the Beltrami parametrization of the Cauchy operator for the stress is nothing else than the formal adjoint of the Riemann operator. However, modifying slightly the rows, we get the new operator matrix:
. Accordingly, the Beltrami parametrization of the Cauchy operator for the stress is nothing else than the formal adjoint of the Riemann operator. However, modifying slightly the rows, we get the new operator matrix:
![]()
which is indeed self-adjoint. Keeping ![]() with
with![]() , we obtain the Maxwell parametrization:
, we obtain the Maxwell parametrization:
![]()
which is minimum because![]() . However, the corresponding operator is FI because it is homogeneous but it is not evident at all to prove that it is also involutive as we must look for δ-regular coordinates (see [20] for the technical details).
. However, the corresponding operator is FI because it is homogeneous but it is not evident at all to prove that it is also involutive as we must look for δ-regular coordinates (see [20] for the technical details).
· ![]() This is far more complicated and we do believe that it is not possible to avoid using differential homological algebra, in particular extension modules. As we found it already in many books [4] [12] [17] [21] or papers [12] [13] [14] [15] [22], the linear Spencer sequence is (locally) isomorphic to the tensor product of the Poincaré sequence for the exterior derivative by a Lie algebra
This is far more complicated and we do believe that it is not possible to avoid using differential homological algebra, in particular extension modules. As we found it already in many books [4] [12] [17] [21] or papers [12] [13] [14] [15] [22], the linear Spencer sequence is (locally) isomorphic to the tensor product of the Poincaré sequence for the exterior derivative by a Lie algebra ![]() with
with ![]() equal to the dimension of the largest group of invariance of the metric involved. When
equal to the dimension of the largest group of invariance of the metric involved. When![]() , this dimension is 10 for the M-metric, 4 for the S-metric and 2 for the K-metric. As a byproduct, the adjoint sequence roughly just exchanges the exterior derivatives up to sign and one has for example, when
, this dimension is 10 for the M-metric, 4 for the S-metric and 2 for the K-metric. As a byproduct, the adjoint sequence roughly just exchanges the exterior derivatives up to sign and one has for example, when![]() , the relations
, the relations![]() ,
,![]() . It follows that, if D2 generates the CC of D1, then
. It follows that, if D2 generates the CC of D1, then ![]() is parametrizing
is parametrizing![]() , a fact not evident at all, even when
, a fact not evident at all, even when ![]() for the Cosserat couple-stress equations exactly described by
for the Cosserat couple-stress equations exactly described by ![]() [18]. Passing to the differential modules point of view with the ring (even an integral domain)
[18]. Passing to the differential modules point of view with the ring (even an integral domain) ![]() of differential operators with coefficients in a differential field K, this result amounts to say that
of differential operators with coefficients in a differential field K, this result amounts to say that![]() . As it is known that such a result does not depend on the differential resolution used or, equivalently, on the differential sequence used, if
. As it is known that such a result does not depend on the differential resolution used or, equivalently, on the differential sequence used, if ![]() generates the CC of
generates the CC of ![]() in the Janet sequence, then
in the Janet sequence, then ![]() is parametrizing
is parametrizing ![]() and this result is still true even if
and this result is still true even if ![]() is not involutive. In such a situation, which is the one considered in this paper, the Killing operators for the M-metric, the S-metric and the K-metric are such that, whatever are the generating CC
is not involutive. In such a situation, which is the one considered in this paper, the Killing operators for the M-metric, the S-metric and the K-metric are such that, whatever are the generating CC ![]() (second order for the M-metric, a mixture of second and third order for the S-metric and K-metric), then
(second order for the M-metric, a mixture of second and third order for the S-metric and K-metric), then ![]() is, in any case, parametrizing the Cauchy operator
is, in any case, parametrizing the Cauchy operator ![]() for any
for any![]() . Once more, the central object is the group, not the metric. The same results are also valid for any Lie group of transformations, in particular for the conformal group in arbitrary dimension, even if the operator
. Once more, the central object is the group, not the metric. The same results are also valid for any Lie group of transformations, in particular for the conformal group in arbitrary dimension, even if the operator ![]() is of order 3 when
is of order 3 when ![]() as we shall see below [6] [13] [14] [23].
as we shall see below [6] [13] [14] [23].
Q.E.D.
REMARK 4.6: Accordingly, the situation met today in GR cannot evolve as long as people will not acknowledge the fact that the components of the Weyl tensor are the torsion elements (the so-called Lichnerowicz waves in [22] ) for the equations ![]() because the Einstein equations cannot be parametrized and the extension modules are torsion modules [5] [7] [13] [19]. Such a result is only depending on the group structure of the conformal group of space-time that brings the canonical splitting
because the Einstein equations cannot be parametrized and the extension modules are torsion modules [5] [7] [13] [19]. Such a result is only depending on the group structure of the conformal group of space-time that brings the canonical splitting ![]() without any reference to a background metric as it is usually done [4] [15] [19] [22] [23]. It is an open problem to know why one may sometimes find a self-adjoint operator. It is such a confusion that led to introducing the so-called Einstein parametrizing operator [19] [22]. A minimum parametrization of the Cauchy operator when
without any reference to a background metric as it is usually done [4] [15] [19] [22] [23]. It is an open problem to know why one may sometimes find a self-adjoint operator. It is such a confusion that led to introducing the so-called Einstein parametrizing operator [19] [22]. A minimum parametrization of the Cauchy operator when ![]() with 6 potentials can be found by keeping only the Lagrange multipliers
with 6 potentials can be found by keeping only the Lagrange multipliers ![]() with
with ![]() used in [13] while setting
used in [13] while setting ![]() like Morera when
like Morera when![]() .
.
EXAMPLE 4.7: (Weyl tensor for ![]() and euclidean metric) We proved in ( [21], p 156-158) and more recently in [14] [22] [23] that, for
and euclidean metric) We proved in ( [21], p 156-158) and more recently in [14] [22] [23] that, for![]() , the natural “geometric object” corresponding to the Weyl tensor is no longer providing a second order differential operator but by a third order Weyl operator
, the natural “geometric object” corresponding to the Weyl tensor is no longer providing a second order differential operator but by a third order Weyl operator ![]() with first order CC
with first order CC ![]() in the differential sequence:
in the differential sequence:
![]()
corresponding to the differential sequence of D-modules where p is the canonical residual projection:
![]()
The true reason is that the symbol ![]() of
of ![]() is finite type with second prolongation
is finite type with second prolongation ![]() while its first prolongation
while its first prolongation ![]() is not 2-acyclic. It is important to notice that the operators are acting on the left on column vectors in the upper sequence but on the right on row vectors in the lower sequence though we have in any case the identities
is not 2-acyclic. It is important to notice that the operators are acting on the left on column vectors in the upper sequence but on the right on row vectors in the lower sequence though we have in any case the identities ![]() and
and![]() .
.
Of course, these operators can be obtained by using computer algebra like in ([21], Appendix 2) but one may check at once that ![]() and
and ![]() are completely different operators while the operator
are completely different operators while the operator ![]() is far from being self-adjoint even though it is described by a
is far from being self-adjoint even though it is described by a ![]() operator matrix. Our purpose is to prove that it can be nevertheless transformed in a very tricky way to a self-adjoint operator, exactly like the
operator matrix. Our purpose is to prove that it can be nevertheless transformed in a very tricky way to a self-adjoint operator, exactly like the ![]() curl operator in 3-dimensional classical geometry because
curl operator in 3-dimensional classical geometry because![]() . It does not seem that these results are known today.
. It does not seem that these results are known today.
The starting point is the ![]() first order operator matrix defining the conformal Killing operator
first order operator matrix defining the conformal Killing operator![]() , namely:
, namely:
![]()
Substracting the fourth row from the first row and multiplying the fourth row by![]() , we obtain the operator matrix:
, we obtain the operator matrix:
![]()
Adding the fourth row to the first, we obtain the operator matrix:
![]()
Adding the first row to the fourth row and dividing by 2, we obtain the operator matrix:
![]()
Multiplying the second, fourth and fifth row by −1, then multiplying the central column of the matrix thus obtained by −1, we finally obtain the operator matrix![]() :
:
![]()
We now care about transforming ![]() given in ( [21], p 158) by the
given in ( [21], p 158) by the ![]() operator matrix:
operator matrix:
![]()
Dividing the first column by 2 and the fourth column by −2, then using the central row as a new top row while using the former top row as new bottom row, we obtain the operator matrix![]() :
:
![]()
and check that ![]() like in the Poincaré sequence for
like in the Poincaré sequence for ![]() where
where![]() . As the new corresponding operator
. As the new corresponding operator ![]() is homogeneous and of order 3 (care), we obtain locally
is homogeneous and of order 3 (care), we obtain locally![]() , a result not evident at first sight (compare to [21], p 157).
, a result not evident at first sight (compare to [21], p 157).
The combination of this example with the results announced in [14] [23] brings the need to revisit almost entirely the whole conformal geometry in arbitrary dimension and we notice the essential role performed by the Spencer δ-cohomology in this new framework.
3. Conclusion
First of all, comparing the M-metric, the S-metric and the K-metric by using the corresponding systems of first order infinitesimal Lie equations, we may summarize the results previously obtained by repeating that, when E = T, the smaller is the background Lie group, the smaller are the dimensions of the Spencer bundles and the higher are the dimensions of the Janet bundles. As a byproduct, we claim that the only solution for escaping is to increase the dimension of the Lie group involved, adding successively 1 dilatation and 4 elations in order to deal with the conformal group of space-time while using the Spencer sequence instead of the Janet sequence. In particular, the Ricci tensor only depends on the elations of the conformal group of space-time in the Spencer sequence where the perturbation of the metric tensor does not appear any longer contrary to the Janet sequence. It finally follows that Einstein equations are not mathematically coherent with group theory and formal integrability. In other papers and books, we have also proved that they were also not coherent with differential homological algebra which is providing intrinsic properties as the extension modules, which are torsion modules, do not depend on the sequence used for their definition, a quite beautiful but difficult theorem indeed. The main problem left is thus to find the best sequence and/or the best group that must be considered. Presently, we hope to have convinced the reader that only the Spencer sequence is clearly related to the group background and must be used, on the condition to change the group. As a byproduct, we may thus finally say that the situation will not evolve in GR as long as people will not acknowledge the existence of these new purely mathematical tools like Lie algebroids or differential extension modules and their purely mathematical consequences. Summarizing this paper in a few words, we do really believe that “God used group theory rather than computer algebra when He created the World”!