Some New Nonlinear Wave Solutions for a Higher-Dimensional Shallow Water Wave Equation

Longmin Dong, Zhu Guo, Yinghui He

Department of Mathematics, Honghe University, Mengzi, China.

DOI: 10.4236/jamp.2020.89139                

Abstract

In this manuscript, we first perform a complete Lie symmetry classification for a higher-dimensional shallow water wave equation and then construct the corresponding reduced equations with the obtained Lie symmetries. Moreover, with the extended F-expansion method, we obtain several new nonlinear wave solutions involving differentiable arbitrary functions, expressed by Jacobi elliptic function, Weierstrass elliptic function, hyperbolic function and trigonometric function.

Keywords

Shallow Water Wave Equations, Nonlinear Wave Solution, Lie Symmetry Analysis, Extended F-Expansion Method

1. Introduction

It is well-known that a lot of phenomena in many fields of science can be described by nonlinear evolution equations (NLEEs). Therefore, the investigation of the exact solutions to NLEEs becomes more and more important in mathematical physics. In order to better understand the working to the physical problem, many powerful and direct methods for finding travelling wave solutions of NLEEs have been proposed. However, the study on nonlinear wave solution is few and there is no unified approach. We know that Lie symmetry group [1] [2] is efficient to study NLEEs. In decades, Lie symmetry group method has been applied in different fields and several physical models were studied. In this manuscript, a nonlinear wave solution of a higher-dimensional shallow water wave equation is discussed by Lie symmetry analysis combined with extending F-expansion method [3] [4].

The following higher-dimensional shallow water wave equation is introduced by Wazwaz [5]

$u_{xzt}+u_{xxxyz}-2\left(u_{xx}{u}_{yz}+u_y{u}_{xxz}\right)-4\left(u_x{u}_{xyz}+u_{xy}{u}_{xz}\right)=0.$ (1)

We find that Equation (1) can be reduced to the potential KdV equation when $z=y=x$. The generalized shallow water wave equations studied by Ablowitz [6] arise as reduction of this equation.

In [5], Wazwaz investigated multiple soliton solutions and multiple singular soliton solutions of Equation (1) and pointed out that this equation is a completely integrable equation. In [7], Yiren Chen and Rui Liu obtained general multiple soliton solutions and some nonlinear wave solutions of Equation (1) by simplified Hirotas method [8] [9] and Dynamical system approach [10]. However, study on nonlinear wave solution is few and Lie symmetry analysis on this equation is not given in related literatures.

Three goals are set for this work. Firstly, we aim to obtain geometric vector fields of Equation (1). Secondly, we tend to present the symmetry reductions. Finally, we want to get new nonlinear wave solutions of Equation (1) by investigate the reduced equations using extended F-expansion method.

2. Lie Symmetries for Equation (1)

First of all, let us consider a one-parameter Lie group of infinitesimal transformation:

$\begin{array}{l}x\to x+ϵ\xi \left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\mathrm{,}u\right)\mathrm{,}\\ y\to y+ϵ\eta \left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\mathrm{,}u\right)\mathrm{,}\\ z\to z+ϵ\tau \left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\mathrm{,}u\right)\mathrm{,}\\ t\to t+ϵ\xi \left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\mathrm{,}u\right)\mathrm{,}\\ u\to u+ϵ\xi \left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\mathrm{,}u\right)\mathrm{,}\end{array}$ (2)

with a small parameter $ϵ\ll 1$. The vector field associated with the above group of transformations can be written as

$\begin{array}{l}V=\xi \left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\mathrm{,}u\right)\frac{\partial }{\partial x}+\eta \left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\mathrm{,}u\right)\frac{\partial }{\partial y}+\mu \left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\mathrm{,}u\right)\frac{\partial }{\partial z}\\ +\tau \left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\mathrm{,}u\right)\frac{\partial }{\partial t}+\varphi \left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\mathrm{,}u\right)\frac{\partial }{\partial u}\mathrm{.}\end{array}$ (3)

The symmetry group of Equation (1) will be generated by the vector field of the form (3). Applying the fourth prolongation $p{r}^{\left(5\right)}V$ to Equation (1), we find that the coefficient functions $\xi \mathrm{,}\eta \mathrm{,}\mu \mathrm{,}\tau$ and $\varphi$ must satisfy the symmetry condition

$\begin{array}{l}{\varphi }^{xzt}+{\varphi }^{xxxyz}+2\left(u_{yz}{\varphi }^{xx}+u_{xx}{\varphi }^{yz}+u_{xxz}{\varphi }^y+u_y{\varphi }^{xxz}\right)\\ +4\left(u_{xyz}{\varphi }^x+u_x{\varphi }^{xyz}+u_{xz}{\varphi }^{xy}+u_{xy}{\varphi }^{xz}\right)=0\end{array}$ (4)

where ${\varphi }^x\mathrm{,}{\varphi }^y\mathrm{,}{\varphi }^{xx}\mathrm{,}{\varphi }^{xy}\mathrm{,}{\varphi }^{xz}\mathrm{,}{\varphi }^{yz}\mathrm{,}{\varphi }^{xyz}\mathrm{,}{\varphi }^{xxz}\mathrm{,}{\varphi }^{xzt}\mathrm{,}{\varphi }^{xxxyz}$ are the coefficients of $p{r}^{\left(5\right)}V$. Furthermore, we have

$\begin{array}{l}{\varphi }^x=D_x\left(\varphi -\xi u_x-\eta u_y-\mu u_z-\tau u_t\right)+\xi u_{xx}+\eta u_{xy}+\mu u_{xz}+\tau u_{xt},\\ {\varphi }^y=D_y\left(\varphi -\xi u_x-\eta u_y-\mu u_z-\tau u_t\right)+\xi u_{xy}+\eta u_{yy}+\mu u_{yz}+\tau u_{yt},\\ {\varphi }^{xx}=D_x{D}_x\left(\varphi -\xi u_x-\eta u_y-\mu u_z-\tau u_t\right)+\xi u_{xxx}+\eta u_{xxy}+\mu u_{xxz}+\tau u_{xxt},\\ {\varphi }^{xy}=D_y{D}_x\left(\varphi -\xi u_x-\eta u_y-\mu u_z-\tau u_t\right)+\xi u_{xxy}+\eta u_{xyy}+\mu u_{xyz}+\tau u_{xyt},\\ {\varphi }^{xz}=D_z{D}_x\left(\varphi -\xi u_x-\eta u_y-\mu u_z-\tau u_t\right)+\xi u_{xxz}+\eta u_{xyz}+\mu u_{xzz}+\tau u_{xzt},\end{array}$

$\begin{array}{l}{\varphi }^{yz}=D_z{D}_y\left(\varphi -\xi u_x-\eta u_y-\mu u_z-\tau u_t\right)+\xi u_{xyz}+\eta u_{yyz}+\mu u_{yzz}+\tau u_{yzt},\\ {\varphi }^{xyz}=D_z{D}_y{D}_x\left(\varphi -\xi u_x-\eta u_y-\mu u_z-\tau u_t\right)+\xi u_{xxyz}+\eta u_{xyyz}+\mu u_{xyzz}+\tau u_{xyzt},\\ {\varphi }^{xxz}=D_{z}D{D}_x^2\left(\varphi -\xi u_x-\eta u_y-\mu u_z-\tau u_t\right)+\xi u_{xxxz}+\eta u_{xxyz}+\mu u_{xxzz}+\tau u_{xxzt},\\ {\varphi }^{xzt}=D_t{D}_z{D}_x\left(\varphi -\xi u_x-\eta u_y-\mu u_z-\tau u_t\right)+\xi u_{xxzt}+\eta u_{xyzt}+\mu u_{xzzt}+\tau u_{xztt},\\ {\varphi }^{xxxyz}=D_z{D}_y{D}_x^3\left(\varphi -\xi u_x-\eta u_y-\mu u_z-\tau u_t\right)+\xi u_{xxxxyz}+\eta u_{xxxyyz}+\mu u_{xxxyzz}\\ +\tau u_{xxxyzt},\end{array}$ (5)

where $D_x^3=D_x{D}_x{D}_x,D_x^2=D_x{D}_x$, $D_x\mathrm{,}{D}_y\mathrm{,}{D}_z$ and $D_t$ are the total derivatives with respect to $x\mathrm{,}y\mathrm{,}z$ and t respectively.

Substituting (5) into (4), combined with Equation (1), we can find the determining equations for the symmetry group of Equation (1), then standard symmetry group calculations lead to the following forms of the coefficient functions:

$\begin{array}{l}\xi =\frac{1}{4}\left({F^{\prime }}_1\left(t\right)-2c_1\right)x+F_5\left(t\right),\eta =\left(\frac{1}{2}{F^{\prime }}_1\left(t\right)+c_1\right)y+F_3\left(t\right),\\ \mu =F_4\left(z\right),\tau =F_1\left(t\right),\\ \varphi =\left(-\frac{1}{4}{F^{\prime }}_1\left(t\right)+\frac{c_1}{2}\right)u-\frac{1}{8}\left({F^{″}}_1\left(t\right)y+2{F^{\prime }}_3\left(t\right)\right)x-\frac{y}{2}{F^{\prime }}_5\left(t\right)+F_2\left(z,t\right).\end{array}$ (6)

where $F_1\left(t\right)\mathrm{,}{F}_2\left(t\right)\mathrm{,}{F}_3\left(z\mathrm{,}t\right)\mathrm{,}{F}_4\left(z\right)$ and $F_5\left(t\right)$ are arbitrary functions on their variables, $c_1$ is an arbitrary constants.

Thus, according to the Lie symmetry analysis method, the geometric vector fields of Equation (1) can be obtained as follows

$\begin{array}{l}{V}_1\left(F_1\right)=\frac{x}{4}{F^{\prime }}_1\left(t\right)\frac{\partial }{\partial x}+\frac{y}{2}{F^{\prime }}_1\left(t\right)\frac{\partial }{\partial y}+F_1\left(t\right)\frac{\partial }{\partial t}-\left(\frac{u}{4}{F^{\prime }}_1\left(t\right)+\frac{xy}{8}{F^{″}}_1\left(t\right)\right)\frac{\partial }{\partial u},\\ V_2\left(F_2\right)=F_2\left(z,t\right)\frac{\partial }{\partial u},V_3\left(F_3\right)=F_3\left(t\right)\frac{\partial }{\partial y}-\frac{x}{4}{F^{\prime }}_3\left(t\right)\frac{\partial }{\partial u},V_4\left(F_4\right)=F_4\left(z\right)\frac{\partial }{\partial z},\\ V_5\left(F_5\right)=F_5\left(t\right)\frac{\partial }{\partial x}-\frac{y}{2}{F^{\prime }}_5\left(t\right)\frac{\partial }{\partial u},V_6=-\frac{x}{2}\frac{\partial }{\partial x}+y\frac{\partial }{\partial y}+u\frac{\partial }{\partial u},\end{array}$ (7)

the symmetry of Equation (3) can be written as

$V=V_1\left(F_1\right)+V_2\left(F_2\right)+V_3\left(F_3\right)+V_4\left(F_4\right)+V_5\left(F_5\right)+V_6\mathrm{.}$ (8)

3. Symmetry Reductions

In terms of the infinitesimals (5), the similarity variables can be obtained by solving the corresponding characteristic equations

$\frac{\text{d}x}{\xi }=\frac{\text{d}y}{\eta }=\frac{\text{d}z}{\mu }=\frac{\text{d}t}{\tau }=\frac{\text{d}u}{\varphi },$ (9)

or the invariant surface conditions

$\begin{array}{c}\Phi =\xi \frac{\partial }{\partial x}u\left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\right)+\eta \frac{\partial }{\partial y}u\left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\right)+\mu \frac{\partial }{\partial z}u\left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\right)\\ +\tau \frac{\partial }{\partial t}u\left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\right)-\varphi \mathrm{.}\end{array}$ (10)

While solving the above invariant surface conditions, one has to distinguish between cases in which some of the functions $F_1\left(t\right)\mathrm{,}{F}_2\left(z\mathrm{,}t\right)\mathrm{,}{F}_3\left(t\right)\mathrm{,}{F}_4\left(z\right)\mathrm{,}{F}_5\left(t\right)$ and $c_1$ are identical to zero and cases where they are not. This leads to different relations between the similarity variables $\left(X\mathrm{,}Y\mathrm{,}Z\mathrm{,}U\right)$ and the original variables $\left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\mathrm{,}u\right)$. As a result, we obtain the following cases:

Case 1. Let $c_1=1,F_1\left(t\right)=F_2\left(z,t\right)=F_3\left(t\right)=F_4\left(z\right)=F_5\left(t\right)=0$, then

$\Phi =-\frac{x}{2}{u}_x+y{u}_y-\frac{u}{2}.$ (11)

Solving the differential equation $\Phi =0$ one can get

$u=\frac{U\left(Y,z,t\right)}{x},Y=x^{2}y.$ (12)

Substituting (12) into Equation (1), we can reduce it to

$\begin{array}{l}{U}_{tz}+\left(8U{U}_{YYz}-8U_Y{U}_{Yz}+9U_{YY}{U}_z+2U_{YYz}\right)Y\\ +\left(-24U_{YYz}{U}_Y-24U_{YY}{U}_{Yz}+24U_{YYYz}\right)Y^2+8U_{YYYz}{Y}^3=0.\end{array}$ (13)

Case 2. Let $c_1=F_1\left(t\right)=1,F_4\left(z\right)=F_5\left(t\right)=0$, then

$\Phi =u_t-F_2\left(z,t\right)+F_3\left(t\right)u_y+\frac{x}{4}{F^{\prime }}_3\left(t\right).$ (14)

Solving the differential equation $\Phi =0$ one can get

$u=U\left(x,Y,z\right)+{\displaystyle \int F_2\left(z,t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right),Y=y-{\displaystyle \int F_3}\left(t\right)\text{d}t.$ (15)

Substituting (15) into Equation (1), we can reduce it to

$\begin{array}{l}{U}_{xxxYz}-2\left(U_{xx}{U}_{Yz}+U_Y{U}_{xxz}\right)-4\left(U_{Yx}{U}_{xz}+U_x{U}_{xYz}\right)=0.\hfill \end{array}$ (16)

Case 3. Let $c_1=0,F_1\left(t\right)=F_2\left(z,t\right)=F_3\left(t\right)=1,F_5\left(t\right)=0$, then

$\Phi =u_t+u_y+F_4\left(z\right)u_z-1.$ (17)

Solving the differential equation $\Phi =0$ one can get

$u=U\left(x,Y,Z\right)+{\displaystyle \int }\frac{1}{F_4\left(z\right)}\text{d}z,Y=y-{\displaystyle \int }\frac{1}{F_4\left(z\right)}\text{d}z,Z=t-{\displaystyle \int }\frac{1}{F_4\left(z\right)}\text{d}z.$ (18)

Substituting (18) into Equation (1), we can reduce it to

$\begin{array}{l}{U}_{xYZ}-U_{xxxZZ}-U_{xxxYZ}+2U_{xx}\left(U_{ZZ}+U_{YZ}\right)+2U_{xxZ}\left(U_z+U_y\right)\\ +4U_x\left(U_{xZZ}+U_{xYZ}\right)+4U_{xz}\left(U_{xZ}+U_{xY}\right)=0.\end{array}$ (19)

Case 4. Let $c_1=F_1\left(t\right)=F_2\left(z,t\right)=F_4\left(z,t\right)=0,F_5\left(t\right)=1$, then

$\Phi =u_x+F_3\left(t\right)u_y+\frac{x}{4}{F^{\prime }}_3\left(t\right).$ (20)

Solving the differential equation $\Phi =0$ one can get

$u=U\left(z,t,Y\right)-\frac{x^2}{8}{F^{\prime }}_3\left(t\right),Y=y-x{F}_3\left(t\right).$ (21)

Substituting (21) into Equation (1), we can reduce it to

$\begin{array}{l}-F_3{\left(t\right)}^3{U}_{YYYYz}-6F_3{\left(t\right)}^2\left(U_Y{U}_{YYz}+U_{YZ}{U}_{YY}\right)-F_3\left(t\right)U_{tYz}-\frac{1}{2}{F^{\prime }}_3\left(t\right)U_{Yz}=0.\hfill \end{array}$ (22)

Case 5. Let $c_1=F_1\left(t\right)=F_3\left(t\right)=0,F_5\left(t\right)=1$, then

$\Phi =F_4\left(z\right)u_z-F_2\left(z,t\right).$ (23)

Solving the differential equation $\Phi =0$ one can get

$u=U\left(x\mathrm{,}y\mathrm{,}t\right)+{\displaystyle \int }\frac{F_2\left(z\mathrm{,}t\right)}{F_4\left(z\right)}\text{d}z\mathrm{.}$ (24)

Substituting (24) into Equation (1), we find that $U\left(x\mathrm{,}y\mathrm{,}t\right)$ is an arbitrary function. That is, the solution of Equation (1) can be expressed as (24).

Case 6. Let $c_1=F_1\left(t\right)=0,F_2\left(z,t\right)=F_3\left(t\right)=1,F_4\left(z\right)=F_5\left(t\right)=0$, then

$\Phi =u_y-1.$ (25)

Solving the differential equation $\Phi =0$ one can get

$u=U\left(x\mathrm{,}z\mathrm{,}t\right)+y\mathrm{.}$ (26)

Substituting (26) into Equation (1), we can reduce it to

$U_{xtz}-2U_{xxz}=0,$ (27)

whose solution is

$U\left(x,z,t\right)=r_1\left(t,z\right)+r_3\left(t,x\right)+r_4\left(z,2t+x\right),$ (28)

where $r_1\left(t\mathrm{,}z\right)\mathrm{,}{r}_3\left(t\mathrm{,}x\right)$ and $r_4\left(z\mathrm{,2}t+x\right)$ are arbitrary functions. So, Equation (1) owns the following solution

$u\left(x,y,z,t\right)=y+r_1\left(t,z\right)+r_3\left(t,x\right)+r_4\left(z,2t+x\right),$ (29)

4. The New Nonlinear Wave Solutions

Obviously, it is easier for us to seek the explicit solutions to the reduction equations than to solve Equation (1). For example, we will consider the exact solutions of Equation (16) and Equation (19) by using the extended F-expansion method in this section.

4.1. Solutions of Equation (16)

Using a traveling wave variable of Equation (16) as

$U\left(x,Y,t\right)=f\left(\xi \right),\xi =kx+bY+cz.$ (30)

where $Y=y-{\displaystyle \int F_3\left(t\right)\text{d}t}$, $k\mathrm{,}b$ and c are constants, Equation (16) can be reduced to the following ODE

$k{f}^{\left(5\right)}-6{\left(f^{″}\right)}^2-6f^{\prime }{f}^{‴}=\mathrm{0,}$ (31)

where $f^{\prime }=\frac{\text{d}f}{\text{d}\xi },f^{″}=\frac{{\text{d}}^{2}f}{\text{d}{\xi }^2},\cdots$. If let $f^{\prime }\left(\xi \right)=\varphi \left(\xi \right)$, then (31) becomes

$k{\varphi }^{\left(4\right)}-6{\left({\varphi }^{\prime }\right)}^2-6\varphi {\varphi }^{″}=\mathrm{0,}$ (32)

Balancing ${\varphi }^{\left(4\right)}$ and ${{\varphi }^{\prime }}^2$ in (32), we obtain $n+4=2\left(n+1\right)$ which gives $n=2$. Suppose that Equation (32) owns the solutions in the form

$\varphi \left(\xi \right)=A_0+A_{1}F\left(\xi \right)+A_2{F}^2\left(\xi \right)+\frac{B_1}{F\left(\xi \right)}+\frac{B_2}{F{\left(\xi \right)}^2},$ (33)

where $F\left(\xi \right)$ satisfies the following equation

${\left(F^{\prime }\left(\xi \right)\right)}^2=h_0+h_2{F}^2\left(\xi \right)+h_4{F}^4\left(\xi \right)\mathrm{,}$ (34)

where $h_0\mathrm{,}{h}_2$ and $h_4$ are constant.

Substituting (33) and (34) into Equation (32) and then setting all the coefficients of $F^k\left(k=-6,\cdots ,6\right)$ of the resulting system to zero, we can obtain the following results.

$A_0=\frac{2}{3}k{h}_2,A_1=0,A_2=0,B_1=0,B_2=2k{h}_0,$ (35)

$A_0=\frac{2}{3}k{h}_2,A_1=0,A_2=2k{h}_4,B_1=0,B_2=0,$ (36)

$A_0=\frac{2}{3}k{h}_2,A_1=0,A_2=2k{h}_4,B_1=0,B_2=2k{h}_0,$ (37)

where $h_0\mathrm{,}{h}_2$ and $h_4$ are arbitrary constants, k is a nonzero constant.

Substituting (35)-(37) into (33), we obtain respectively the following solutions of Equation (32)

$\varphi \left(\xi \right)=\frac{2}{3}k{h}_2+\frac{2k{h}_0}{F{\left(\xi \right)}^2},$ (38)

$\varphi \left(\xi \right)=\frac{2}{3}k{h}_2+2k{h}_{4}F{\left(\xi \right)}^2,$ (39)

$\varphi \left(\xi \right)\mathrm{<mo>\; =\; </mo>}\frac{2}{3}k{h}_2+\frac{2k{h}_0}{F^2\left(\xi \right)}+2k{h}_{4}F{\left(\xi \right)}^2\mathrm{,}$ (40)

where $\xi =kx+bY+cz=kx+b\left(y-{\displaystyle \int F_3\left(t\right)\text{d}t}\right)+ct$.

The solutions of Equation (34) are given in Table 1. Combining (38)-(40) with Table 1, many exact solutions of Equation (1) can be obtained. For simplicity, we just give out the first case in Table 1; the other cases can be discussed similarly.

When $h_0=1,h_2=-\left(m^2+1\right),h_4=m^2$, the solution of Equation (33) is $F\left(\xi \right)=\text{sn}\left(\xi \mathrm{,}m\right)$ or $F\left(\xi \right)=\text{cd}\left(\xi \mathrm{,}m\right)$. Substituting them into Equation (38)-(40), we can obtain the following Jacobi Elliptic function solutions of Equation (32).

From (38), one has

Table 1. Solutions of $F\left(\xi \right)$ in ${F^{\prime }}^2=h_0+h_2{F}^2+h_4{F}^4$.

$f^{\prime }\left(\xi \right)=\varphi \left(\xi \right)=-\frac{2}{3}k\left(m^2+1\right)+2k{\text{ns}}^2\left(\xi ,m\right),$ (41)

$f^{\prime }\left(\xi \right)=\varphi \left(\xi \right)=-\frac{2}{3}k\left(m^2+1\right)+2k{\text{dc}}^2\left(\xi ,m\right).$ (42)

Therefore, solutions of Equation (1) can be expressed as

$\begin{array}{c}u\left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\right)=f\left(\xi \right)+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\\ =-\frac{2}{3}k\left(m^2+1\right)\xi -2k\text{EllipticE}\left(\text{sn}\left(\xi \mathrm{,}m\right)\mathrm{,}m\right)\\ -2k\frac{\text{ds}\left(\xi \mathrm{,}m\right)\text{cs}\left(\xi \mathrm{,}m\right)}{\text{ns}\left(\xi \mathrm{,}m\right)}+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\mathrm{.}\end{array}$ (43)

$\begin{array}{c}u\left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\right)=f\left(\xi \right)+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\\ =-\frac{2}{3}k\left(m^2+1\right)\xi -2k\text{EllipticE}\left(\text{sn}\left(\xi \mathrm{,}m\right)\mathrm{,}m\right)\\ +2k\frac{\text{dc}\left(\xi \mathrm{,}m\right)\text{sc}\left(\xi \mathrm{,}m\right)}{\text{nc}\left(\xi \mathrm{,}m\right)}+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\mathrm{.}\end{array}$ (44)

when $m\to 1$, $\text{ns}\left(\xi \mathrm{,}m\right)\to coth\left(\xi \right)$, solution (41) becomes

$f^{\prime }\left(\xi \right)=\varphi \left(\xi \right)=-\frac{4k}{3}+2k{\coth }^2\left(\xi \right).$ (45)

Thus, one has

$\begin{array}{c}u\left(x,y,z,t\right)=f\left(\xi \right)+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\\ =-\frac{4k}{3}\xi -k\left(2\coth \left(\xi \right)-\ln \frac{1+\coth \left(\xi \right)}{1-\coth \left(\xi \right)}\right)\\ +{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right).\end{array}$ (46)

when $m\to 0$, $\text{ns}\left(\xi \mathrm{,}m\right)\to csc\left(\xi \right)$, solution (41) becomes

$f^{\prime }\left(\xi \right)=\varphi \left(\xi \right)=-\frac{4k}{3}+2k{\csc }^2\left(\xi \right).$ (47)

Thus, one has

$\begin{array}{c}u\left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\right)=f\left(\xi \right)+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\\ =-\frac{4k}{3}\xi -2k\cot \left(\xi \right)+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\mathrm{.}\end{array}$ (48)

when $m\to 0$, $\text{dc}\left(\xi \mathrm{,}m\right)\to sec\left(\xi \right)$, solution (42) becomes

$f^{\prime }\left(\xi \right)=\varphi \left(\xi \right)=-\frac{4k}{3}+2k{\sec }^2\left(\xi \right).$ (49)

Thus, one has

$\begin{array}{c}u\left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\right)=f\left(\xi \right)+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\\ =-\frac{4k}{3}\xi -2k\tan \left(\xi \right)+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\mathrm{.}\end{array}$ (50)

when $m\to 1$, $\text{dc}\left(\xi \mathrm{,}m\right)\to 1$, solution (42) becomes

$f^{\prime }\left(\xi \right)=\varphi \left(\xi \right)=-\frac{4k}{3}.$ (51)

Thus, one has

$u\left(x,y,z,t\right)=f\left(\xi \right)+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)=-\frac{4k}{3}\xi +{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right).$ (52)

From (39), we have

$f^{\prime }\left(\xi \right)=\varphi \left(\xi \right)\mathrm{<mo>\; =\; </mo>}-\frac{2}{3}k\left(m^2+1\right)+2k{m}^2{\text{sn}}^2\left(\xi \mathrm{,}m\right)\mathrm{,}$ (53)

$f^{\prime }\left(\xi \right)=\varphi \left(\xi \right)=-\frac{2}{3}k\left(m^2+1\right)+2k{m}^2{\text{cd}}^2\left(\xi \mathrm{,}m\right)\mathrm{.}$ (54)

Therefore, solutions of Equation (1) can be expressed as

$\begin{array}{c}u\left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\right)=f\left(\xi \right)+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\\ =-\frac{2}{3}k\left(m^2-2\right)\xi -2k\text{EllipticE}\left(\text{sn}\left(\xi \mathrm{,}m\right)\mathrm{,}m\right)\\ +{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\mathrm{.}\end{array}$ (55)

$\begin{array}{c}u\left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\right)=f\left(\xi \right)+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\\ =-\frac{2}{3}k\left(m^2-2\right)\xi -2k\text{EllipticE}\left(\text{sn}\left(\xi \mathrm{,}m\right)\mathrm{,}m\right)\\ +2k{m}^2\frac{\text{sd}\left(\xi \mathrm{,}m\right)\text{cd}\left(\xi \mathrm{,}m\right)}{\text{nd}\left(\xi \mathrm{,}m\right)}+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\mathrm{.}\end{array}$ (56)

when $m\to 1$, $\text{sn}\left(\xi \mathrm{,}m\right)\to tanh\left(\xi \right)$, solution (53) becomes

$f^{\prime }\left(\xi \right)=\varphi \left(\xi \right)=-\frac{4k}{3}+2k{\tanh }^2\left(\xi \right),$ (57)

Thus, one has

$\begin{array}{c}u\left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\right)=f\left(\xi \right)+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\\ =-\frac{4k}{3}\xi -k\left(2\tanh \left(\xi \right)-\ln \frac{1+\tanh \left(\xi \right)}{1-\tanh \left(\xi \right)}\right)\\ +{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\mathrm{.}\end{array}$ (58)

From (40), we have

$f^{\prime }\left(\xi \right)=\varphi \left(\xi \right)=-\frac{2}{3}k\left(m^2+1\right)+2k{m}^2{\text{sn}}^2\left(\xi \mathrm{,}m\right)+2k{\text{ns}}^2\left(\xi \mathrm{,}m\right)\mathrm{,}$ (59)

$f^{\prime }\left(\xi \right)=\varphi \left(\xi \right)=-\frac{2}{3}k\left(m^2+1\right)+2k{m}^2{\text{cd}}^2\left(\xi \mathrm{,}m\right)+2k{\text{dc}}^2\left(\xi \mathrm{,}m\right)\mathrm{.}$ (60)

Therefore, solutions of Equation (1) can be expressed as

$\begin{array}{c}u\left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\right)=f\left(\xi \right)+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\\ =-\frac{2}{3}k\left(m^2-5\right)\xi -4k\text{EllipticE}\left(\text{sn}\left(\eta \mathrm{,}m\right)\mathrm{,}m\right)\\ -2k\frac{\text{ds}\left(\xi \mathrm{,}m\right)\text{cs}\left(\xi \mathrm{,}m\right)}{\text{ns}\left(\xi \mathrm{,}m\right)}+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\mathrm{.}\end{array}$ (61)

$\begin{array}{c}u\left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\right)=f\left(\xi \right)+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\\ =-\frac{2}{3}k\left(m^2-5\right)\xi -4k\text{EllipticE}\left(\text{sn}\left(\eta \mathrm{,}m\right)\mathrm{,}m\right)\\ +2k\frac{\text{dc}\left(\xi \mathrm{,}m\right)\text{sc}\left(\xi \mathrm{,}m\right)}{\text{nd}\left(\xi \mathrm{,}m\right)}+2k{m}^2\frac{\text{sd}\left(\xi \mathrm{,}m\right)\text{cd}\left(\xi \mathrm{,}m\right)}{\text{nd}\left(\xi \mathrm{,}m\right)}\\ +{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\mathrm{.}\end{array}$ (62)

when $m\to 1$, $\text{sn}\left(\xi \mathrm{,}m\right)\to tanh\left(\xi \right)$, solution (59) becomes

$f^{\prime }\left(\xi \right)=\varphi \left(\xi \right)=-\frac{4k}{3}+2k{\tanh }^2\left(\xi \right)+2k{\coth }^2\left(\xi \right),$ (63)

Thus, one has

$\begin{array}{c}u\left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\right)=f\left(\xi \right)+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\\ =-\frac{4k}{3}\xi -2k\left(\tanh \left(\xi \right)+\coth \left(\xi \right)\right)\\ +k\ln \frac{\left(1+\tanh \left(\xi \right)\right)\left(1+\coth \left(\xi \right)\right)}{\left(1-\tanh \left(\xi \right)\right)\left(1-\cot \left(\xi \right)\right)}+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right).\end{array}$ (64)

Remark 1. Let $F\left(\xi \right)$ in (33) satisfies the following equation

${\left(F^{\prime }\left(\xi \right)\right)}^2=h_0+h_{1}F\left(\xi \right)+h_3{F}^3\left(\xi \right)\mathrm{,}$ (65)

where $h_0\mathrm{,}{h}_1$ and $h_3$ are constant. In this situation, we have the following result.

$A_0=0,A_1=\frac{1}{2}k{h}_3,A_2=0,B_1=0,B_2=0.$ (66)

Substituting Equation (66) into (33), we obtain the following solution of Equation (32):

$\varphi \left(\xi \right)=\frac{1}{2}k{h}_{3}F\left(\xi \right)\mathrm{.}$ (67)

where $\xi =kx+bY+cz=kx+b\left(y-{\displaystyle \int F_3\left(t\right)\text{d}t}\right)+ct$.

The solution of Equation (65) is the Weierstrass elliptic doubly periodic type solution:

$F\left(\xi \right)=\text{WeierstrassP}\left(\frac{\sqrt{h_3}}{2}\xi ,g_2,g_3\right),h_3>0.$ (68)

where $g_2=-\frac{4h_1}{h_3}$, $g_3=-\frac{4h_0}{h_3}$ and $h_3>0$. Substituting Equation (68) into (67), the solution of Equation (32) is

$f^{\prime }\left(\xi \right)=\varphi \left(\xi \right)=\frac{1}{2}k{h}_3\text{WeierstrassP}\left(\frac{\sqrt{h_3}}{2}\xi \mathrm{,}{g}_2\mathrm{,}{g}_3\right)\mathrm{.}$ (69)

Therefore, exact solutions of Equation (1) can be expressed

$\begin{array}{c}u\left(x\mathrm{,}y\mathrm{,}z\mathrm{,}t\right)=f\left(\xi \right)+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\\ =-k\sqrt{h_3}\text{WeierstrassZeta}\left(\frac{\sqrt{h_3}}{2}\xi \mathrm{,}{g}_2\mathrm{,}{g}_3\right)+{\displaystyle \int F_2\left(z\mathrm{,}t\right)\text{d}t}-\frac{x}{4}{F}_3\left(t\right)\mathrm{.}\end{array}$ (70)

4.2. Solutions of Equation (19)

Using a traveling wave variable of Equation (19) as

$U\left(x,Y,Z\right)=f\left(\xi \right),\xi =kx+bY+cZ.$ (71)

where $Y=y-{\displaystyle \int }\frac{1}{F_4\left(z\right)}\text{d}z,Z=t-{\displaystyle \int }\frac{1}{F_4\left(z\right)}\text{d}z$ and $k\mathrm{,}b$ and c are constants, Equation (19) can be reduced to the following ODE

$b{k}^2{f}^{\left(5\right)}+c{f}^{‴}-6bk{f}^{\prime }{f}^{‴}-6bk{f^{″}}^2=0,$ (72)

where $f^{\prime }=\frac{\text{d}f}{\text{d}\xi },f^{″}=\frac{{\text{d}}^{2}f}{\text{d}{\xi }^2},\cdots$. If let $f^{\prime }\left(\xi \right)=\varphi \left(\xi \right)$, then (72) becomes

$b{k}^2{\varphi }^{\left(4\right)}+c{\varphi }^{″}-6bk\varphi {\varphi }^{″}-6bk{{\varphi }^{\prime }}^2=\mathrm{0,}$ (73)

Balancing ${\varphi }^{\left(4\right)}$ and ${{\varphi }^{\prime }}^2$ in (73), we obtain $n+4=2\left(n+1\right)$ which gives $n=2$. Suppose that Equation (73) owns the solutions in the form

$\varphi \left(\xi \right)=A_0+A_{1}F\left(\xi \right)+A_2{F}^2\left(\xi \right)+\frac{B_1}{F\left(\xi \right)}+\frac{B_2}{F{\left(\xi \right)}^2}\mathrm{,}$ (74)

where $F\left(\xi \right)$ satisfies the following equation

${\left(F^{\prime }\left(\xi \right)\right)}^2=h_0+h_2{F}^2\left(\xi \right)+h_4{F}^4\left(\xi \right)\mathrm{,}$ (75)

where $h_0\mathrm{,}{h}_2$ and $h_4$ are constant.

Substituting (74) and (75) into Equation (73) and then setting all the coefficients of $F^k\left(k=-6,\cdots ,6\right)$ of the resulting system to zero, we can obtain the following results.

$A_0=\frac{4b{k}^2{h}_2+c}{6bk},A_1=0,A_2=0,B_1=0,B_2=2k{h}_0,$ (76)

$A_0=\frac{4b{k}^2{h}_2+c}{6bk},A_1=0,A_2=2k{h}_4,B_1=0,B_2=0,$ (77)

$A_0=\frac{4b{k}^2{h}_2+c}{6bk},A_1=0,A_2=2k{h}_4,B_1=0,B_2=2k{h}_0,$ (78)

where $h_0\mathrm{,}{h}_2$ and $h_4$ are arbitrary constants, $k\mathrm{,}b$ and c are nonzero constants.

Substituting (76)-(78) into (74), we obtain respectively the following solutions of Equation (73)

$\varphi \left(\xi \right)=\frac{4b{k}^2{h}_2+c}{6bk}+\frac{2k{h}_0}{F{\left(\xi \right)}^2},$ (79)

$\varphi \left(\xi \right)=\frac{4b{k}^2{h}_2+c}{6bk}+2k{h}_{4}F{\left(\xi \right)}^2\mathrm{,}$ (80)

$\varphi \left(\xi \right)=\frac{4b{k}^2{h}_2+c}{6bk}+\frac{2k{h}_0}{F^2\left(\xi \right)}+2k{h}_{4}F{\left(\xi \right)}^2,$ (81)

where $\xi =kx+by-\left(b+c\right){\displaystyle \int }\frac{1}{F_4\left(z\right)}\text{d}z+ct$.

Substituting $F\left(\xi \right)$ in Table 1, we can got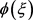. Then by solving 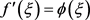and using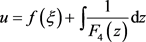, we can obtain solutions of Equation (1). The procedure is similar. We omit it for simplicity.

5. Figures of Some Exact Solutions

The obtained solutions include some arbitrary functions. Taking some special functions we can get different solutions and graphics. In order to better understand the solutions, some typical figures of the solutions are given as follows:

In Figure 1, 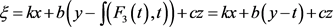, which is a travelling wave transformation and the figure is a classic periodic wave.

In Figure 2, 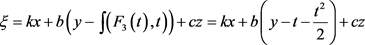, which is not a travelling wave transformation and the figure is a unknown one.

In Figure 3, 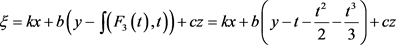, which is not a travelling wave transformation and the figure is unknown.

Figure 1. Figure of solution (50) with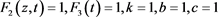. (a) 3D figure; (b) 2D figure.

Figure 2. Figure of solution (50) with. (a) 3D figure; (b) 2D figure.

In Figure 4, 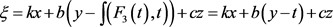, which is a travelling wave transformation and the figure is a plane.

In Figure 5, 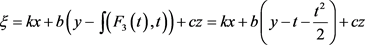, which is not a travelling wave transformation and the figure is a solitary wave.

In Figure 6, 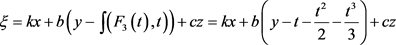, which

Figure 3. Figure of solution (50) with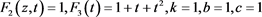. (a) 3D figure; (b) 2D figure.

Figure 4. Figure of solution (51) with.(a) 3D figure; (b) 2D figure.

Figure 5. Figure of solution (51) with. (a) 3D figure; (b) 2D figure.

Figure 6. Figure of solution (50) with. (a) 3D figure; (b) 2D figure.

is not a travelling wave transformation and the figure is a kink wave.

6. Conclusions

In this manuscript, a higher-dimensional shallow water wave Equation (1) is studied by Lie symmetry analysis method and extended F-expansion method and some new exact solutions are obtained. It is interesting that these solutions contain some arbitrary functions and. Taking these functions as special ones, we can get nonlinear wave solutions and wave solutions of Equation (1). The method is effective to high-dimensional differential equations, and can also be applied to other nonlinear evolution ones. Our main work list as follows:

· All of the geometric vector fields of the equation are obtained.

· The symmetry reductions are presented.

· Some new linear and nonlinear wave solutions are obtained.

· Some typical figures are given.

Acknowledgements

This research is supported by innovation and entrepreneurship training Program of university Students of Yunnan (DCXM193009) and innovation and entrepreneurship training Program of university Students of Honghe University (DCXL181045).

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Liu, H.Z. and Li, J.B. (2014) Symmetry Reductions, Dynamical Behavior and Exact Explicit Solutions to the Gordon Types of Equations. Journal of Computational and Applied Mathematics, 257, 144-56. https://doi.org/10.1016/j.cam.2013.08.022
[2]	Liu, H.Z. and Geng, Y.X. (2013) Symmetry Reductions and Exact Solutions to the Systems of Carbon Nanotubes Conveying Fluid. Journal of Differential Equations, 254, 2289-2303. https://doi.org/10.1016/j.jde.2012.12.004
[3]	Fan, E. (2003) Uniformly Constructing a Series of Explicit Exact Solutions to Nonlinear Equations in Mathematical Physics. Chaos, Solitons and Fractals, 16, 819-839. https://doi.org/10.1016/S0960-0779(02)00472-1
[4]	Yomba, E. (2005) The Extended Fan’s Sub-Equation Method and Its Application to KdV-MKdV, BKK and Variant Boussinesq Equations. Physics Letters A, 336, 463-476. https://doi.org/10.1016/j.physleta.2005.01.027
[5]	Wazwaz, A.M. (2009) Multiple-Soliton Solutions and Multiple-Singular Soliton Solutions for Two Higher-Dimensional Shallow Water Wave Equations. Applied Mathematics and Computation, 211, 495-501. https://doi.org/10.1016/j.amc.2009.01.071
[6]	Clarkson, P.A., Mansfield, E.L. and Mansfield, E.L. (1994) On a shallow Water Wave Equation. Nonlinearity, 7, 975-1000. https://doi.org/10.1088/0951-7715/7/3/012
[7]	Chen, Y.R. and Liu, R. (2015) Some New Nonlinear Wave Solutions for Two (3+1)-Dimensional Equations. Applied Mathematics and Computation, 260, 397-411. https://doi.org/10.1016/j.amc.2015.03.098
[8]	Hirota, R. (2004) The Direct Method in Soliton Theory. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511543043
[9]	Hirota, R. (1971) Exact Solutions of the Korteweg-Devries Equation for Multiple Collisions of Solutions. Physical Review Letters, 27, 1192-1194. https://doi.org/10.1103/PhysRevLett.27.1192
[10]	Li, J.B. and Liu, Z.R. (2000) Smooth and Non-Smooth Traveling Waves in a Nonlinearly Dispersive Equation. Applied Mathematical Modelling, 25, 41-56. https://doi.org/10.1016/S0307-904X(00)00031-7