Generalized Method of Moments and Generalized Estimating Functions Using Characteristic Function ()
1. Introduction and an Overview of GMM Procedures Based on Empirical Characteristic Function
1.1. Introduction
In many applied fields, data analysts often have to use distributions with density functions having complicated forms. They are often expressed using mean of series representations but model characteristic functions are simpler and have closed form expressions. For actuarial sciences, the compound Poisson distributions are classical examples and for finance, the stable distributions fall into the same category. These are infinitely divisible and many infinitely divisible distributions share the same property of having much simpler characteristic functions than density functions. We shall examine in more details using the Generalized Normal Laplace (GNL) distribution which is obtained by adding a normal component to the GAL random variable hence can be viewed as created by a convolution operation. The GNL distribution was introduced by Reed [1] and we shall use it to motivate inferences procedures based on characteristic functions instead of densities. Both the GNL and GAL distributions provide better fit to log returns data in finance. The density of the GNL distribution is more complicated than the density of the GAL distribution. The book by Kotz et al. [2] gives a very comprehensive account of the GAL distribution. Obviously, if these distributions with properties just mentioned are used for modelling, we still want to be able to estimate the parameters and perform tests for validating the models used. Often maximum likelihood (ML) procedures are difficult to implement due to the lack of closed form for the density functions for the models being used and even the ML estimators are available, when they are used with the Pearson chi-square statistics in general do not lead to distribution free statistics further complicate ML procedures. Therefore, it is natural that we aim at a unified approach to estimation and testing. Inferences developed in this paper will be unified using GMM approach but with the use of estimating function theory to select sample moments using moment conditions extracted from model characteristic function or more precisely the square of its modulus for constructing the GMM objective function. Subsequently, estimation and testing can be carried out. Before giving more details of the developed GMM procedures of this paper and how they differ from GMM procedures in the literature and the advantages of the new procedures, we shall give more details about the GNL distribution where the use of characteristic function appears to be more natural than the use of the model density. The GMM methods developed are also less simulation intensive than simulated methods which appear in the paper by Luong and Bilodeau [3] and faster in computing time for implementing.
The GNL generalizes the GAL distribution, the density of the GAL can be obtained in closed form but depend on Bessel functions, see Kotz et al. [2] (page 189), Luong [4] and since the GAL distribution can also be obtained from the distribution of the difference of two gamma random variables, we shall consider first the characteristic function of the gamma distribution in example 1 and subsequently in example 2 and example 3, we shall consider respectively the characteristic function of the GAL and GNL distributions.
First, recall that the characteristic function
of a random variable X is a complex function defined as
and it can be expressed as
with the real and imaginary parts of
given respectively by
and
. We can also use polar forms instead of algebraical forms to express complex numbers or functions.
The modulus of
is defined as
and the argument
of
is defined as
. This
allows to express
and depending on situations, the polar form of
can be simpler to handle than its algebraical form as illustrated in example 1 which gives the characteristic function of the gamma random variable using both representations for the gamma distribution.
Example 1 (characteristic function of the gamma distribution)
It is well known than the characteristic function of the Gamma distribution in algebraical form is given by
with
being the scale parameter and
being the shape parameter,
and
. Now before giving the polar form of
, we give the polar form of
first and using properties of the modulus as well as properties of the argument of a complex number we then give the polar form for
. The modulus of
is denoted by
and the argument of
and since the function
is odd,
. This allows the representation in polar form for
.
Using properties of the modulus, since
, so
. With
and since
, it is easy to see that the characteristic function of the gamma distribution is given by
,
using polar form.
Using the characteristic function of the gamma distribution in polar form, we can find the characteristic function of the GAL distribution which can be considered as the difference of two independent gamma random variables.
Example 2 (characteristic function of the GAL distribution)
Among many representations in distribution of the GAL distribution, the one which makes use of two independent random gamma random variables allows the following representation for the GAL random variable X, see proposition
4.1.3 given by Kotz et al. [2] (p 183),
with
being
an equality in distribution,
and
are independent and identically distributed as G which follows a gamma distribution with scale parameter equals to one and shape parameter being
, the parameter
is a location parameter with
. The parameter
controls the skewness of the GAL distribution,
and if
, the distribution is symmetric. The parameter
is a scale parameter with
. Using the representation with gamma random variables it is easy to see that by letting
and
,
if
.
The characteristic function
for the GAL distribution in polar form is given by
,
, using the characteristic function of
the gamma distribution in polar form as given by example 1. Instead of using, replace it by
then
Using this parametrization, it is easier to connect with the GNL distribution with the representation of the GNL random variable as the convolution of a normal random variable with a GAL random variable. The GAL is symmetric if
and its characteristic function can be further simplified and reduced to
or
.
Observe that often it is relatively simple to find characteristic function of a distribution of a convolution of two independent random variables using characteristic functions of the component independent random variables and also the characteristic function of the GAL distribution does not depend on the Bessel functions and is much simpler than its density despite the density of the GAL density has closed form expression. The GNL random variable X can be created by adding an independent normal random variable to a GAL random variable and allows the following representation as introduced by Reed [1] (p 475),
or equivalently,
.
Z is a standard normal random variable and independent of
and
with
and
are as defined as in example 2. Since the characteristic function for
the standard normal random variable is
and the characteristic function of
the GAL distribution is already obtained, the polar form of the GNL distribution can be also obtained and it is given in the following example.
Example 3 (characteristic function of the GNL distribution)
From the representation of the GNL random variable it is easy to see that the characteristic function of the GNL distribution in algebraical form is
which is given by Reed [1] (p 474) and in polar form
with
and
are as defined in example 2.
Using the modulus of
,
,
we also have
As for the GAL distribution, if
, the GNL distribution is symmetric and its characteristic function is further simplified and is given by
with
Reed [1] using the characteristic function also established expressions for the k-th cumulants
with
,
The GNL distribution provides a better fit to log returns data than the GAL distribution and both these distributions provide much better fit to log returns data than the normal distribution. In addition, all integer moments exist for these distributions and they are also infinitely divisible like the normal distribution which makes them being good alternatives to the normal distribution. From the characteristic function of the GNL distribution, it is easy to see that the real and imaginary part of the characteristic function are given respectively as
and
.
1.2. Empirical Characteristic Function and GMM Procedures in the Literature
For inferences, we assume that we have a random sample of size n which consists of
of independent and identically distributed continuous random variables and they are distributed as X, with common characteristic function
,
is a p by 1 vector of parameters of interests with
,
is the vector of the true parameters with
, the parameter space is assumed to be compact. The number of parameters in the model is p. In fact, most inferences procedures based on characteristic function proposed in the literature are still valid if X has a discontinuity point with mass attributed at the origin such as in the cases of the compound distributions. If X is discrete, it is often preferred to work with probability generating function rather characteristic function and for related procedures using probability generating function, see Luong [5].
Commonly proposed GMM procedures in the literature are based on the empirical characteristic function which is the counterpart of the theoretical one and it is defined as
with the real and imaginary parts given respectively by
and
.
For example, the K-L procedures proposed by Feuerverger and McDunnough [6] p 20-23) can be viewed as equivalent to GMM procedures based on 2k sample moments of the following forms with the first k sample moments which make use respectively the chosen points
from the real part of empirical characteristic function and the real part of the model characteristic function
and the rest of moments are similarly formed but based on the imaginary part of the empirical characteristic function and the imaginary part of the model characteristic function,
.
By letting
and define S to be the limit covariance matrix of the vector
under the true parameter
when
and let
be a preliminary consistent estimate of
and from which we can obtain a preliminary consistent estimate
for the inverse of S then the related GMM objective function
can be formed, i.e.,
and minimizing
will give the vector of K-L estimators.
The following expectation properties are quite obvious and the elements of the covariance matrix for
can be found explicitly using the following identities which are established using properties of trigonometric functions, we have:
,
,
,
,
(1)
The above identities are results of Proposition 3.1 given by Groparu-Cojocaru and Doray [7] (p 1992) or results from Koutrouvelis [8] (p 919).
Observe that for the K-L procedures or GMM procedures based on the above 2k sample moments, we need to fix the points
where we can make use of the real and imaginary part of the model characteristic function
and there is still a lack of general criteria on how to choose these points, see discussions by Tran [9] but it is recommended that these points are equally spaced, i.e., consider
and the optimum choice for
has the property that
when
.
Koutrouvelis [8] (p 920) has shown that in general, since the variances of
and
have the following properties
and
as
.
and argued that we should select points in the range of
as points near 0 that we need to focus when extracting information from the model characteristic functions. Despite that the K-L procedures have good potentials for generating good efficiencies for estimators but it is often numerical difficult to implement, as the studies of Groparu-Cojocaru and Doray [7] (p 1996) have shown that in practice we need at least
which means that at least 20 sample moments are needed for the procedures to have good efficiency and in these situations, the matrices
and
are often nearly singular and inverting such large matrix often create difficulties and we shall see that GMM procedures proposed in this paper with the use of theory of estimation function to select sample moments will only need a number of sample moments which is less than 10 in general instead of at least 20. In addition, the number of points from the model characteristic function used to construct sample moments also goes to infinity as the sample size
.
The proposed GMM procedures with the selection of the sample moments based on estimating function theory will be developed in the next section. With the original sample, we also transform it to a sample of n observations which are still independent and we work with the original sample and the transformed sample to construct moment conditions.
Carrasco and Florens [10] have introduced GMM methods with a continuum of moment conditions and Carrasco and Kotchoni [11] have used the empirical characteristic function and developed GMM procedures based on objective functions which match the empirical characteristic function with the model counterpart using points which belong to a continuum interval. Using a continuum of moment conditions is a solution for the arbitrariness choice of selecting points of the characteristic functions to extract information but the procedures might be difficult to implement for practitioners meanwhile our procedures remain simple and closer to the classical GMM procedures with a finite number of moments but we shall use estimation theory to select sample moments and the number of points will be selected equally spaced in the interval
and the number of points will go to infinity as
.
In fact, the points
of our procedures are selected with
and observe that the spacing used is
, as
and also observe that
the spacing mimics the behavior of the optimum spacing and numerically it bypasses the difficulties of having to find explicitly the value of the optimum spacing by minimizing the determinant of the asymptotic covariance of the K-L estimators if the K-L procedures are used.
For the proposed methods, we need the additional assumption that the first four integer moments of the model distribution exist but in practical situations, this assumption is often met.
The proposed procedures make use of sample moments which focus on extracting information from the square of the modulus of the characteristic function
using the points
and clearly there will be as many points as the sample size.
For model, with a location parameter
, the modulus
and consequently
will not depend on the location parameter
and we need another two sample moments beside the sample moments which make use of
to take care of this situation. The example given below will help to clarify the problem that we might encounter when the modulus
or the square of the modulus
is used for inferences.
For the normal distribution with the vector of parameters
, the characteristic function is
and its modulus is
and the square of the modulus is
,
The location parameter
is missing in
and consequently, in
. This is to illustrate that there might be one parameter being left out if inferences procedures are solely based on
or
. This also means that for GMM procedures which make use of sample moments formed using
or
, there should also be other sample moments to take into account the parameters being left out and if there are parameters being left out, it only affects the location parameter of the model in general, so if we use two additional sample moments which take care of the parameters being left out beside the sample moments which make use of
, the GMM procedures will be viable. As mentioned often at most there is one parameter in the model which is not included in
so the proposed will make use of additional moments which are based on the mean and variance of the model distribution beside the moments based on
using
We hope to achieve good efficiency yet preserve simplicity by not using more than ten sample moments, this achieved by using the theory of estimating function for building sample moments which make use of
using
Therefore, it is relatively simple to implement and all can be done within the classical context of GMM procedures without having to rely on a continuum of moment conditions which the practitioners might find difficult to implement. The use of theory of estimating function appears to be new and not included in proposed GMM procedures in the literature which focused on the use of the empirical characteristic function. The new procedures also make use of transformed observations besides the original observations.
The paper is organized as follows. Section 1 introduces the commonly used GMM procedures which are based on empirical characteristic function, the approach taken here does not use the empirical characteristic function and relies on estimating function theory to select sample moments based on the square of the modulus of the model characteristic function. The new GMM procedures are introduced in Section 2.1 with the choice of selected sample moments aiming to provide efficiency for GMM estimation. In Section 2.2 the chi-square test for moment restrictions which can be interpreted as goodness-of-fit is presented. In Section 3, illustrations for implementing the methods using the GNL distribution and normal distribution, the methods appear to be relatively simple to implement yet being very efficient based on the limited studies and appear to be better alternatives the method of moments (MOM) in general.
2. The Proposed GMM Procedures Based on Theory of Estimating Functions
2.1. Estimation
The theory of GMM procedures are well established in the literature, see Martin et al. [12], Hayashi [13], Hamilton [14] but based on the assumption that sample moments are already selected. In this paper, we focus on how to select moments for model with characteristic function being simple and has closed form but the model density is complicated and we do not make use of the classical empirical characteristic function as other GMM procedures being proposed in the literature. Here, we focus on the square of the modulus of the model characteristic function to build sample moments and since the modulus might not include all the parameters of the model such as the case when there is a location parameter, we shall also include two moments which focus on the model distribution mean and variance to complete the set of sample moments and for practical applications, we do not need more than ten sample moments for the use of the proposed GMM procedures.
We shall define the sample moments focusing on
. Let us consider the basic estimating functions
Clearly, the basic estimating functions are unbiased, i.e.,
Using
, we can also express
(2)
Now we can construct the optimum estimating functions for estimating
or more precisely for parameters which appear in
using results of Godambe and Thompson [15] (p 139) or Morton [16] (p 229). The optimum estimating functions which are linear combinations of elements of the set
and with
can be expressed as
(3)
and
denote the variance of
and can be obtained explicitly, see expression (1).
We would like to make a few remarks here. First note that it is easy to show that
using
and
and clearly if there is one parameter of the model says
which does not appear in
then
and there is no optimum estimating function for this parameter and if we want to estimate all the parameters, we need an extra estimating function. We use the following notation for the vector of optimum estimating function discarding the ones with
. The vector of optimum estimating functions for parameters included in
adopting the convention discarding those with
is given by
where we partition the vector
into two components,
with the property that all the parameters appear in
form the vector
and all the
remaining parameters are included in the vector
. In general, if
in then
is reduced to a scalar. Therefore, the vector of optimum estimating function in general is either a vector of p elements or
elements and consequently when these estimating functions are converted to sample moments, we shall have either p or
sample moments.
We shall let
be vector the sample moments which make use of points of
as
,
can be obtained using the real and imaginary parts of the model characteristic function and from the definition of
, it then follows that
(4)
Using the identities as given by expression (1), the variance of
is
(5)
and the variance of
and the covariance
are given respectively by
, (6)
. (7)
These variances and covariance terms can also be obtained using results given by Groparu-Cojocaru and Doray [7] (p 1993). Asymptotic properties of estimators obtained by solving estimating equations have been given by Yuan and Jennrich [17] but we emphasize GMM estimation in this paper.
Now define two additional sample moments
and
,
The location parameter if it belongs to the model but is not included in
, it will appear in
which is the mean of the model distribution and it can be obtained by differentiating the model characteristic function and for GMM procedures we prefer to have the number of sample moments exceeding the number of parameters in the model, so we also consider the following sample moment which makes use of the variance of the model distribution
and it can also be obtained by differentiating twice the model characteristic function, i.e.,
.
The vector sample moments for the developed GMM procedures is given by
and notice
makes use of the transformed observations
but
and
make use of the original sample observations
.
The vector of the proposed GMM estimators
is obtained by minimizing the criterion function,
with
being a positive definite matrix with probability one and it will be defined subsequently after the definition of
and its inverse
,
is a consistent estimate of
.
For finding elements of the matrix, we can first express the components of the vector of sample moments as
with
,
,
, 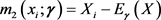 ,
,
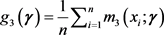 ,
, 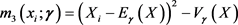 ,
,
and let
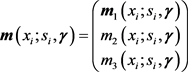 .
.
The matrix 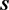 is defined as
is defined as
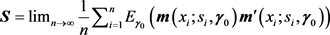 .
.
Now if we have a preliminary consistent estimate 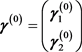 for the vector
for the vector 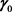 then an estimate for
then an estimate for 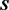 which is
which is 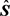 can be defined with
can be defined with
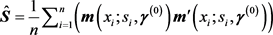
and its inverse which is 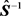 is a consistent estimate of
is a consistent estimate of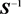 , often a numerical algorithm is used to minimize
, often a numerical algorithm is used to minimize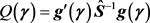 , the vector of the GMM estimators is obtained after the convergence of a numerical iterative process, at each iteration we might want to readjust
, the vector of the GMM estimators is obtained after the convergence of a numerical iterative process, at each iteration we might want to readjust 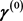 in a similar way as when performing an iteratively feasible nonlinear weighted least-squares procedures where the weights are re-estimated at each step of the iterations.
in a similar way as when performing an iteratively feasible nonlinear weighted least-squares procedures where the weights are re-estimated at each step of the iterations.
The vector of the GMM estimators 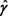 is consistent in general, this follows from general theory of GMM procedures, i.e., we have
is consistent in general, this follows from general theory of GMM procedures, i.e., we have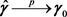 , with
, with 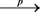 denotes convergence in probability. In addition, under suitable differentiability imposed on the vector (
denotes convergence in probability. In addition, under suitable differentiability imposed on the vector (![]() ), the vector of GMM estimators
), the vector of GMM estimators ![]() has an asymptotic multivariate normal distribution, i.e.,
has an asymptotic multivariate normal distribution, i.e.,
![]() ,
, ![]()
![]() denotes convergence in law with
denotes convergence in law with
![]()
which is a r by p matrix, r is the number of sample moments used or equivalently the number of elements of the vector![]() .
. ![]() can be estimated by
can be estimated by
![]()
and ![]() can be estimated by
can be estimated by
![]()
and consequently, the asymptotic variance of ![]() can be estimated.
can be estimated.
2.2. Testing Moment Restrictions
One of the advantages of GMM procedures is that it can lead to distribution free chi-square test. The asymptotic null distribution of the statistic no longer depends on the parameters using statistic based on the same objective function to obtain the vector of GMM estimators![]() . Howewer, the test for moment restrictions when used as goodness-of-fit test, it might not be consistent as it might fail to detect departures from the specified model even as the sample size
. Howewer, the test for moment restrictions when used as goodness-of-fit test, it might not be consistent as it might fail to detect departures from the specified model even as the sample size![]() . The inclusion of some more relevant sample moments so that the number of sample moments used r is still manageable and as results of this will make the test more powerful yet without creating too many numerical difficulties on inverting the matrix
. The inclusion of some more relevant sample moments so that the number of sample moments used r is still manageable and as results of this will make the test more powerful yet without creating too many numerical difficulties on inverting the matrix ![]() in the same vein as for chi-square test for count models using probability generating function as given by Luong [17] is a topic for further studies.
in the same vein as for chi-square test for count models using probability generating function as given by Luong [17] is a topic for further studies.
For testing the moment restrictions
![]()
Assuming we have already minimized ![]() to obtain
to obtain![]() , it follows from standard results of GMM theory that the following statistic can be used and the statistic has an asymptotic chi-square distribution with
, it follows from standard results of GMM theory that the following statistic can be used and the statistic has an asymptotic chi-square distribution with ![]() degrees of freedom, assuming
degrees of freedom, assuming![]() , i.e.,
, i.e.,
![]() . (8)
. (8)
3. Numerical Illustrations and Simulations
For illustrations of the newly developed methods, we shall examine the symmetric GNL distribution and compare the efficiencies of GMM estimators vs the efficiencies of method of moment estimators (MOM) as given by Reed [1] (p 47). The characteristic function of the symmetric GNL distribution only has 4 parameters as![]() , it is easy to see that its characteristic function is reduced to
, it is easy to see that its characteristic function is reduced to
![]() ,
,![]() .
.
The location parameter instead of being ![]() we can use
we can use ![]() and Reed’s MOM estimator for
and Reed’s MOM estimator for ![]() can be obtained independently of
can be obtained independently of![]() .
.
It is not difficult to see that
![]() (9)
(9)
![]() (10)
(10)
The vector of parameters of the symmetric GNL distribution is![]() . Since the model has a location parameter it is expected that the modulus of the characteristic function only has three parameters, it is easy to see that indeed this is the case with
. Since the model has a location parameter it is expected that the modulus of the characteristic function only has three parameters, it is easy to see that indeed this is the case with
![]()
![]()
which gives the following derivatives
![]() ,
,
![]()
![]()
and the variance of the basic estimating equation ![]() can be obtained using expression (1), the number of sample moments will be
can be obtained using expression (1), the number of sample moments will be![]() , i.e. there will be 5 elements for the vector
, i.e. there will be 5 elements for the vector![]() .
.
The first two cumulants which give the mean and the variance of the distribution
are![]() ,
, ![]() and the method of moment estimators (MOM) estimators can be obtained in closed form. Let
and the method of moment estimators (MOM) estimators can be obtained in closed form. Let ![]() be the i-th sample cumulant, the MOM estimators have been given by Reed [1] (p 477) with
be the i-th sample cumulant, the MOM estimators have been given by Reed [1] (p 477) with![]() ,
, ![]() ,
, ![]() and
and![]() .
.
Reed [1] (p 477) also noted that the MOM estimators often give a negative sign value for positive parameters like ![]() or
or![]() . It might be due to the lack of efficiency for MOM estimators for these parameters and therefore it is natural to consider alternatives like the GMM estimators. For financial applications with log returns data recorded as percentages being small in magnitudes, the parameters
. It might be due to the lack of efficiency for MOM estimators for these parameters and therefore it is natural to consider alternatives like the GMM estimators. For financial applications with log returns data recorded as percentages being small in magnitudes, the parameters ![]() tend to have small values in magnitude only
tend to have small values in magnitude only ![]() is around 18. GMM procedures with a number of sample moments larger than 20 might lead to the inverse of the matrix
is around 18. GMM procedures with a number of sample moments larger than 20 might lead to the inverse of the matrix ![]() difficult to obtain numerically.
difficult to obtain numerically.
By fixing ![]() we consider the ranges
we consider the ranges ![]() and
and![]() . We simulate
. We simulate ![]() samples of size
samples of size ![]() each and compute the MOM estimators and the GMM estimators. The GMM estimator for the location parameter
each and compute the MOM estimators and the GMM estimators. The GMM estimator for the location parameter ![]() is identical to the MOM estimator and only with this parameter that MOM estimator performs well. For other parameters, GMM estimators perform much better than MOM estimators.
is identical to the MOM estimator and only with this parameter that MOM estimator performs well. For other parameters, GMM estimators perform much better than MOM estimators.
Using simulated samples, we can estimate the individual mean square error for each parameter for each estimator. The vector of GMM estimators is denoted by![]() . For GMM estimators, the following mean square errors are estimated using simulated samples,
. For GMM estimators, the following mean square errors are estimated using simulated samples, ![]() ,
, ![]() ,
, ![]() ,
,![]() . Similarly, we also estimate
. Similarly, we also estimate
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
with these quantities estimated, we can estimate the asymptotic overall relative of efficiency of these two methods as
![]() .
.
Since GMM procedures perform better than MOM procedures for estimating ![]() and consequently overall GMM procedures perform much better based on the limited simulation study. More numerical studies should be conducted but it appears that the GMM procedures have the potentials to outperform MOM procedures for many models especially with models with more than 3 parameters as sample moments of order greater than 3 often are not stable in general. The results are displayed in table A in the Appendix.
and consequently overall GMM procedures perform much better based on the limited simulation study. More numerical studies should be conducted but it appears that the GMM procedures have the potentials to outperform MOM procedures for many models especially with models with more than 3 parameters as sample moments of order greater than 3 often are not stable in general. The results are displayed in table A in the Appendix.
In the second limited study, we consider the normal distribution which is also used for modelling log-returns data. The normal distribution is![]() , the ML estimators for
, the ML estimators for ![]() and
and ![]() are
are ![]() and
and![]() . They are given respectively by the sample mean and the sample variance. The characteristic function for the normal distribution is
. They are given respectively by the sample mean and the sample variance. The characteristic function for the normal distribution is
![]() ,
, ![]() ,
,
![]() ,
, ![]() , (11)
, (11)
![]() and
and ![]() and
and ![]() (12)
(12)
We only have 3 sample moments for GMM estimation for the normal model and we also use ![]() simulated samples each with size
simulated samples each with size ![]() to obtains GMM estimators and ML estimators for
to obtains GMM estimators and ML estimators for ![]() and
and ![]() for the range of parameters with
for the range of parameters with ![]() and
and![]() . The ranges of the parameters are often encountered for financial data and we estimate the individual mean square errors for the GMM estimators
. The ranges of the parameters are often encountered for financial data and we estimate the individual mean square errors for the GMM estimators ![]() and ML estimators
and ML estimators![]() . We found GMM estimator for
. We found GMM estimator for ![]() is slightly less efficient than ML estimator but overall, GMM estimators are nearly as efficient as ML estimators based on the simulation results obtained and we estimate the overall relative efficiency
is slightly less efficient than ML estimator but overall, GMM estimators are nearly as efficient as ML estimators based on the simulation results obtained and we estimate the overall relative efficiency
![]() ,
,
the estimate ARE is close to 1 for the parameters being considered in TableA1 & TableA2.
4. Conclusion
Based on theoretical results and numerical results, it appears that:
1) The new GMM procedures are relatively simple to implement. The number of sample moments can be kept below the number ten yet the methods appear to have good efficiencies and offer good alternatives to MOM procedures which in general are not efficient for models with more than three parameters.
2) The proposed procedures are simpler to implement than GMM procedures based on a continuum of moment conditions and consequently might be of interests for practitioner who want to use these methods to analyze date where the model characteristic function is simple and have closed form but the density function is complicated, these situations often occur in practice.
3) The methods are less simulation oriented and consequently faster in computing time for implementations.
4) The estimators obtained have good efficiencies for some models being considered but more numerical and simulation works are needed to confirm the efficiencies using different parametric models and larger scale of simulations. In addition, further studies are needed for the topic on adding sample moments to make the chi-square goodness-of-fit test consistent without creating extensive numerical difficulties when it comes to obtaining the efficient matrix which is used for the quadratic form of the GMM objective function.
Acknowledgements
The helpful and constructive comments of a referee which lead to an improvement of the presentation of the paper and support from the editorial staff of Open Journal of Statistics to process the paper are all gratefully acknowledged.
Appendix
![]()
Table A1. Overall estimate asymptotic relative efficiencies of the GMM estimators vs MOM estimators.
Simulation studies for symmetric GNL distributions with![]() .
.
![]()
Table A2. Overall estimate asymptotic relative efficiencies of the GMM estimators vs ML estimators.
Simulation studies for normal distributions![]() .
.