There Also Can Be Fuzziness in Quantum States Itself—Breaking through the Framework and the Principle of Quantum Mechanics ()
1. Introduction
The research on combining fuzzy mathematics and quantum mechanics has been done in the prior work [1] - [8]. These theories, which are using fuzzy mathematics to understand quantum mechanics, can be regarded as the equivalent theory of quantum mechanics. They do not break through quantum mechanics.
In order to be able to break through quantum mechanics and find a deeper principle of the universe, in this article a mathematical theory named “fuzzy quantum probability” is proposed. Different from the prior theories, the theory in this paper is not using fuzzy mathematics to understand quantum mechanics, but using fuzzy mathematics to fuzzify the state function of quantum mechanics so that a fuzzy (unsharp) probability can be obtained. This work is not the equivalent theory of quantum mechanics but a breaking through quantum mechanics.
In a sense, quantum mechanics is a theory of probability (so-called “quantum probability”). This kind of probability is different from the classical probability in the traditional mathematical probability and statistics theory. It is a kind of probability associated with volatility and calculated by wave function.
After the birth of fuzzy mathematics, people use the method of fuzzy mathematics to fuzzify classical probability to obtain fuzzy probability (the probability of uncertain and imprecise values, also called “language probability”). Then, can we use the method of fuzzy mathematics to also blur quantum probability to obtain fuzzy quantum probability (see Figure 1)?
In fuzzy mathematics there are two directions for developing classical probability into fuzzy probability: one is to introduce fuzziness into the event, whereas the probability is clear or determined, so as to obtain the probability of fuzzy event. The other is to introduce fuzziness into the probability, while the event is clear, so as to obtain the fuzzy probability of the event. Similarly, we also can try to develop quantum probability into fuzzy quantum probability along these two directions. This article is dedicated to the work in the second direction, i.e. doing the work of “the fuzzification of quantum probability” with the method of fuzzy mathematics (the work of the first direction will be done in another paper).
The calculation of the quantum probability of the event is realized by means of a wave function, and the value of the quantum probability is obtained by squaring the modulus of the (normalized) wave function. Therefore, it can be assumed that the fuzzification of the quantum probability should first be the fuzzification of the wave function (state function), and the value of the fuzzy quantum probability can be obtained by the square of the modulus of the fuzzy wave function. The concept of fuzzy wave function was first put forward by Markus Müller [9], but he did not conduct in-depth research. In this paper I will discuss the mathematical description of fuzzy wave function in detail and how to calculate out a fuzzy quantum probability of the event from fuzzy wave function. In addition, the evolution equation of fuzzy wave function also is established.
As the Russian mathematician Lobachevsky said, any branch of mathematics, no matter how abstract it is, will one day find applications in the real world. As the application of fuzzy mathematical methods to quantum mechanical probabilities, the theory of fuzzy quantum probabilities will eventually be applied in
![]()
Figure 1. This figure shows the logical clues to the development of probability theory.
reality one day even though now we cannot find its specific application. Fuzzy quantum probability is mainly used to describe and compute the probability that is difficult to accurately estimate. Then, where could there be such a kind of probability? Maybe in the field of particle decay, maybe in the field of economics and finance, maybe in small closed regions of space as proposed by Markus Müller in his paper, .... One day, we will find a place where fuzzy quantum probability comes into play.
In this paper, fuzzy wave function and fuzzy quantum probability (density) are discussed in Section 2. The equation of the membership function of the fuzzy wave function is established in Section 3. In Section 4, the concept of membership degree amplitude is introduced and discussed. Fuzzy probability amplitude is also discussed in this Section. Lastly, in Appendix 1 the list of the used variables in the paper is provided, whereas in Appendix 2 some important concepts pertaining to the fuzzy mathematics are illustrated.
2. Fuzzy Wave Function
Usually, in quantum mechanics it is thought that the value of the probability for the event
is clear and certain, correspondingly, the probability wave
also is clear and certain. However, if the probability value is unsharp or imprecise, this kind of probability should be described by fuzzy number. Correspondingly, the probability wave also should be depicted by fuzzy plural. Such a fuzzy wave function is denoted by
(fuzzification plural function). According to fuzzy mathematics,
is depicted by a membership function
, where
is one of all possible values of
. Here it should be pointed out that
is an independent variable, the variety of which no longer depends on the event
because the value of fuzzy wave function is uncertain. This is similar to the case in quantum mechanics, where the coordinate
is an independent variable, the variety of which no longer relies on the time
because the value of the coordinate is uncertain. From classical mechanics to quantum mechanics, and then to fuzzy quantum probability, the relationship between variables and the changes in the status of variables can be seen in Figure 2.
The membership function
tells us about the distribution of the membership degrees of all possible values of the fuzzy probability wave about the event
. The meaning of the fuzzy wave function depicted by the membership function is showed in Figure 3.
can be represented as
.
Here
is the plural set. The symbol “
” does not represent integration but a sign, whereas “/” does not represent division but a kind of corresponding symbol.
The normalization problem of
will be discussed in Section 4.
Now it should be considered how to calculate fuzzy probability from
. This is by means of the membership function. The specific approach is considered as follows:
![]()
Figure 2. This figure shows that quantum mechanics breaks through the principle of classical mechanics by replacing certainty with probability, while fuzzy quantum probability breaks through the principle of quantum mechanics by replacing clarity with ambiguity (using the uncertainty of probability (wave) to replace the certainty of probability (wave)).
![]()
Figure 3. This figure shows that the normalized fuzzy probability wave of a specific event
takes much possible plural values, and each value has a (generally different) degree of membership (credibility or truth). For instance, if
is depicted by such a membership function with the form as follow:
the credibility of
taking one value
is 0.79984, while that of
taking another value
is 0.30348.
Calculating the fuzzy quantum probability of the event
is by computing
;
Calculating
is by computing
;
Order
, i.e.
represents the (fuzzy) modulus of the fuzzy wave function of the event
. Then calculating
is by determining the membership function
of
. Here
, the membership degree of which is
, represents a possible value of
.
can be computed from
, and the specific method is as follows:
Order
(or
), then
can be equivalently rewritten as
(or
). Thus,
is determined from
. Then how to determine the value of
? About
, it is usually such a case that for the specified event
, one value of
corresponds to much different values of membership degree because of the variation of
.
should take the maximal value of membership degree according to the assignment rule of the membership degree of the possible value of fuzzy number in fuzzy mathematics. For instance, suppose when
,
takes maximum value
. Then,
can be assigned the value
, i.e.
(see Figure 4)
Thus, the membership function of
has been got.
By using
, the membership function of the fuzzy wave strength
can be obtained
where I, the membership degree of which is
, represents a possible value of the fuzzy wave strength
of the event
.
By using
, the fuzzy quantum probability (density) of the event
can be obtained. The specific method is as follows:
![]()
Figure 4. This figure shows how the membership function of
of a specific event
is determined from that of
(this fuzzy wave function is mentioned in Figure 3). This is by finding the maximum value of
in the case of a fixed value of
. The bright white line in the figure is the function curve of
.
This is a possible function form (the membership degree of this form is
) of the fuzzy wave strength
.
From
, one possible quantum probability (density) (the membership degree of this quantum probability (density) is
) of the event
can be derived
where
is the normalization constant.
Thus, the fuzzy quantum probability (density) of the event
has been obtained
,
In addition, the membership function of
can be easily solved as follows:
Order
, then one can have
. This is the membership function for
. Thus,
can be rewritten as
.
3. The Membership Function Equation
Next, an equation will be established for the membership function
. The membership function can be normalized, i.e. it should satisfy
(1)
where
. The normalized membership function reads as
Schrödinger equation is
. Order
,
. Then Schrödinger equation turns into real form
As we know, the deterministic mechanical quantity in classical mechanics can be considered as a statistical average of the corresponding indeterministic mechanical quantity in quantum mechanics. Similarly, here one can regard the clear or deterministic wave function in quantum mechanics as the result of the non-fuzzification [10] [11] of fuzzy wave function
Putting (4), (5) into (2) and shifting items, one can obtain
Therefore, the integrand in the bracket is a function whose integral is zero about R, I.
Order
(6)
Then
satisfies
Similarly, by bringing (4) and (5) into (3), one can derive
(7)
where
satisfies
Order
Then (6), (7) can be written as
Again order
Then the above equations about
can be simply written in a matrix form
(8)
This is the membership function equation, which determines the evolution of the fuzzy wave function
, accompanied by constraints:
(9)
Equation (8) is a nonhomogeneous equation. The nonhomogeneous item
can be interpreted as fuzzy source which leads to the blurring and uncertainty of probability and probability wave. If there is no fuzzy source, there is no fuzziness of probability and probability wave, and Equation (8) loses meaning. This point can be proved as follows:
In fact, by ordering
in Equation (8), one can obtain
It can been seen that
has only one value
. This is a meaningless result. Thereby, Equation (8) without fuzzy source is meaningless. So, the equation of the membership function of the fuzzy wave function only can be a nonhomogeneous one.
4. The Membership Degree Amplitude and Fuzzy Probability Amplitude
In order to discuss the normalization of fuzzy wave function and the calculation of fuzzy probability amplitude, a new concept is now introduced, named “membership degree amplitude”
(
is the plural set), the square of the modulus of which denotes the membership degree, i.e.
From
, it can be derived that
This is one possible form (the membership degree of this form is
) of
. And
can be denoted as
.
If for
, the wave function
is normalized (multiplying by the normalization constant
)
then the fuzzy wave function
is normalized
.
The membership degree amplitude of
can be derived
The membership degree of
is
. From
, the fuzzy quantum probability (density)
can be derived with the train of thought in Section 2 of this paper.
Now one can discuss the calculation problem of fuzzy probability amplitude
which is defined by
(10)
or
,
i.e.
where
is the normalized eigenfunction of the mechanical quantity operator
, satisfying
.
It should be pointed out that the sum rule in Equation (10) about the fuzzy plurals is different from the general that of fuzzy plurals, the operation rule in (10) need ensure the normalization of
.
The fuzzy probability from
can be solved as follows:
The membership degree of
is
. From
, the fuzzy quantum probability
can be derived with the train of thought in Section 2 of this paper.
Next, an equation will be established for the normalized membership degree amplitude function
which satisfies
where
is the normalized membership function which satisfies Equation (1).
For simplicity, the real number form is adopted. Order
, then
can be equivalently rewritten as
here
and
are the real and imaginary parts of
respectively.
And then
(11)
Putting (11) into (8), one can derive out
By
,
, one can respectively obtain
By sorting out the above two formulas, an equation set is established for
(14)
Here
can be regarded as the fuzzy source.
Now let me prove the rationality of the above designing fuzzy probability amplitude. This only need prove that the result of the non-fuzzification of fuzzy probability amplitude satisfies the equation of probability amplitude in quantum mechanics. A derivation as follows can be done:
1) The equation of probability amplitude in quantum mechanics is
(15)
Order
,
. Then (15) turns into real form
(16)
Here
2) By solving (14), it can be obtain that
(17)
By solving (17), one can obtain
Thus,
.
So,
(18)
Order
Bringing them into (18), one can derive
(19)
By using (19), the real part of the non-fuzzification of
can be obtained
(20)
Similarly, the imaginary part of the non-fuzzification of
is
3) By differentiating the variable
at both sides of (20), and by using (2) and (3), it can be derived out that
(21)
In quantum mechanics
(22)
Substituting (22) into (21), one can get
Similarly, it can be derived that
These two results are completely consistent with (16), so the above design of fuzzy probability amplitude is rational.
5. Conclusions
The subject of this paper is to do the work of “the fuzzification of quantum probability” with the method of fuzzy mathematics. The mathematical framework of fuzzy quantum probability has been established. It includes fuzzy wave function depicted by a membership function, the equation of the membership function of deciding the evolution of fuzzy wave function, fuzzy probability amplitude computed by a membership degree amplitude, the equation of the membership degree amplitude, the method of obtaining fuzzy probability from fuzzy wave function and fuzzy probability amplitude.
Unlike the work on using fuzzy mathematics to understand quantum mechanics is equivalent to quantum probability in a certain sense, my work on bluring quantum probability with the method of fuzzy mathematics in this paper is not equivalent to quantum probability. Quantum probability theory only advocates the uncertainty of events, while probability and probability waves are determined. Fuzzy quantum probability theory advocates not only the uncertainty of events, but also the uncertainty (fuzziness, unclearness) of probability and probability wave. The core concepts of quantum probability theory are probability wave and wave equation, while the core concepts of fuzzy quantum probability theory are membership degree (membership degree amplitude) and membership degree equation (membership degree amplitude equation).
Acknowledgements
I sincerely express my heartfelt thanks to Wang Suyun from the Department of Physics, College of Science, Shihezi University for his technical support for the work of this paper!
Appendix 1: The Main Used Variables in the Paper
Appendix 2: The Important Concepts in Fuzzy Mathematics
Since famous American automatic control expert Zadeh, L.A. pioneered the theory of fuzzy sets. Fuzziness has caused widespread concern and research. Its application has become increasingly widespread and in-depth. Here several pairs of important concepts are introduced.
1) Fuzziness and clarity
This pair of concepts is used to describe the property and state of things. “Clarity” refers to an unequivocal and certain property-state, whereas “Fuzziness” to an equivocal and uncertain one. For instance, “far larger than 5”, “pretty girl”, “tall man” etc. are all fuzzy conceptions and there is no categorical or unambiguous boundary about them. “Larger than 5”, “Chinese people”, “round table” etc. are all clear concepts with distinct or certain boundaries about them.
2) Fuzziness and chance
These two concepts both refer to uncertainty. However, the former means uncertain property-state of things, whereas the latter means uncertain the results of the event. The most critical quantity to depict fuzziness is “membership degree” (look below), whereas the most critical quantity describing chance is “probability”.
3) General set and fuzzy set
There is a categorical boundary about classical set: an object either belongs to a classic set or does not belong to this classic set, whereas there is not a clear boundary about fuzzy set: the membership relation about an object belongs to a fuzzy set is uncertain, and we only can say how large is the degree of membership of an object for a fuzzy set? Order U represents a collection of some objects, called “discussion domain”. For a classical set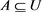 , we may use a characteristic function
, we may use a characteristic function 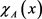 to indicates the membership degree for
to indicates the membership degree for . When
. When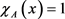 , x belongs to A. When
, x belongs to A. When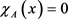 , x does not belong to A. From this we may define a fuzzy set
, x does not belong to A. From this we may define a fuzzy set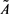 . On the discussion domain U,
. On the discussion domain U, 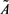 is depicted using a real-valued function
is depicted using a real-valued function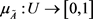 .
.
For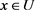 ,
, 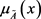 is called the membership degree for
is called the membership degree for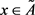 , whereas the function
, whereas the function 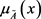 is named “membership function” of
is named “membership function” of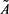 . Because of
. Because of![]() , it means that x does not Completely absolutely belong to
, it means that x does not Completely absolutely belong to![]() , i.e. x belongs to
, i.e. x belongs to ![]() only in a certain of degree. This membership relation is inexplicit. A fuzzy set is entirely depicted by its membership function.
only in a certain of degree. This membership relation is inexplicit. A fuzzy set is entirely depicted by its membership function.
If U is the finite set, ![]() is marked in the form
is marked in the form
![]()
when U is the infinite set, ![]() can be expressed as
can be expressed as![]() . Here
. Here ![]() respectively is not summation, integration and division.
respectively is not summation, integration and division.
4) Fuzzy number and fuzzy plural
Normal fuzzy set: For a fuzzy set![]() , if there is at least one element
, if there is at least one element![]() , satisfying
, satisfying![]() . Then
. Then ![]() is called “normal fuzzy set”.
is called “normal fuzzy set”.
Convex fuzzy set: For a fuzzy set![]() , if
, if![]() , always satisfying
, always satisfying![]() . Then
. Then ![]() is called “convex fuzzy set”.
is called “convex fuzzy set”.
Fuzzy number: A normal convex fuzzy set ![]() on real domain is called “fuzzy number”.
on real domain is called “fuzzy number”.
Fuzzy plu-set: A fuzzy set ![]() on plural domain is called “fuzzy plu-set”.
on plural domain is called “fuzzy plu-set”.
Normal fuzzy plu-set: For a fuzzy plu-set![]() , if there is at least one element
, if there is at least one element![]() , satisfying
, satisfying![]() . Then
. Then ![]() is called “normal fuzzy plu-set”.
is called “normal fuzzy plu-set”.
Convex plu-set: For a classical set Z on plural domain (plural plane), if the connection of any two points in the set Z is entirely inside this set. Then Z is called “convex plu-set”.
Convex fuzzy plu-set: For a fuzzy plu-set![]() , if its any cut set is Convex plu-set. Then
, if its any cut set is Convex plu-set. Then ![]() is called “convex fuzzy plu-set”.
is called “convex fuzzy plu-set”.
Fuzzy plural: A normal convex fuzzy plu-set ![]() is called “fuzzy plural”.
is called “fuzzy plural”.
5) Modulus of fuzzy plural![]() : Modulus of fuzzy plural
: Modulus of fuzzy plural ![]() is written as
is written as![]() . Its membership function is
. Its membership function is![]() , i.e. the supremum of
, i.e. the supremum of![]() .
.
6) Fuzzification and non-fuzzification
Fuzzification: Fuzzification is a process which blurs the clear, certain amount. We can have such a concise understanding: many quantities, which are thought to be clear and certain ones, factually are not uncertain at all. They have great uncertainty. If the uncertainty results from inaccuracy, ambiguity, the variable may be fuzzy and should be depicted using fuzzy number.
Non-fuzzification: Non-fuzzification is a process of converting the fuzzy amount into a certain one. The most popular non-fuzzification method is “centroid method” with the equation [10] [11]
![]()
7) Fuzzy probability
After the fuzzification of classical probability, one can obtain fuzzy probability, whereas classical probability can be regarded as the result of the non-fuzzification of fuzzy probability.
8) Fuzzification function and fuzzification plural function
Fuzzification function from X to Y is the ordinary function from X to![]() ,
,![]() . Where X, Y are the two real number fields, whereas
. Where X, Y are the two real number fields, whereas ![]() is the set of all fuzzy numbers on Y.
is the set of all fuzzy numbers on Y.
Fuzzification plural function from X to C is the ordinary function from X to![]() ,
,![]() . Where C is the plural field, whereas
. Where C is the plural field, whereas ![]() is the set of all fuzzy plurals on C.
is the set of all fuzzy plurals on C.