Partial Variable Stability for a Class of Nonlinear Systems with Time Delay ()
1. Introduction
In 1892, Lyapunov, a Russian mathematician, mechanician and physicist, proposed the notion of the stability of motion. He gave the general research methods in his doctoral dissertation “The general problem of the stability of motion” [1], in which he established the foundation of the stability theory. When studying nonlinear systems, especially studying dynamic systems or control systems, we cannot study the stability of all variables because of the technology difficulties, the limitation of practical conditions, or it is not necessary to study all variables considering the actual need. As a result, studying the partial stability of differential equations becomes more important. In addition, the partial stability is widely used in science and technology. For instance the absolute stability of famous Lurie adjusting systems can be changed into a problem of partial stability. In a word, it is of practical significance to study the partial stability of differential equations.
Since Bellman created a class of integral inequalities in 1958, integral inequalities have been greatly developed. The main results are:
In 1960, Li Yuesheng gave the following inequality in [2]:
In 2005, Sligeng discussed the following inequality in [3]:
In 2009, the author discussed a new class of inequalities in [4].
Vorotnikov, V.I. [5] [6] considered the following system
and studied the double stability as
and
.
In 2002, Wang Feng used the differential inequality of delay in article [7] to study the following delay system:
In 2006, Siligeng used the integral inequality extended in [3] in [8] to discuss the double stability of the following system to some variables:
In this paper the author consider a new class of the nonlinearly perturbed differential systems with time-delay
It is obvious that the above system is a generalization of the systems in [5] [6] [7] [8].
The aim of this paper is to investigate the double stability of neutural differential equations, including Uniform stability and Uniform Lipschitz stability. The author uses the method of differential inequalities with time-delay and integral inequalities to establish double stability criteria.
2. Preliminaries
Consider the following system:
(1)
where
,
,
,
,
,
is a nonnegative constant. Let
be a continuous function, for
.
Definition 1 [9] [10] [11] The trivial solution of system (1) has uniform stability and exponential asymptotic stability with respect to y if, for
,
,
, and
, when
(for
), such that
Definition 2 [9] [10] [11] The trivial solution of system (1) has Lipschitz stability with respect to y if, there exists constants
and
, when
(for
), such that
Definition 3 [9] [10] [11] The trivial solution of system (1) has equi-exponential Lipschitz asymptotic stability with respect to y if, there exists
,
and
, when
(for
), such that
Definition 4 [9] [10] [11] The trivial solution of system (1) has uniform exponential Lipschitz asymptotic stability with respect to y if, K and
in definition 3 are ndependent of
.
Lemma 1 [4] The following conditions are established on
:
i)
are non-negative constants;
ii) 1)
2)
where:
,
,
,
,
are non-negative continuous function on
, and:
,
,
are all constants greater than 1, and
,
,
set:
,
iii) let:
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
iv) Let:
And
,
,
,
v) Assume:
then:
,
.
3. Main Results
Consider the following system
(2)
where
is a constant, initial condition is:
is an
matrix,
is an
matrix,
is an
matrix, they are all continuous for
and satisfy the condition of existence and uniqueness theorem.
Set
and
satisfied:
,
Theorem If (2) satisfies the following conditions:
i)
,
;
ii)
iv)
where:
,
,
,
,
are non-negative continuous monotonic non-increasing functions on
, and:
,
,
are all constants greater than 1,
,
,
let:
,
iv) Set:
and
,
,
,
v) Set:
then:
1) when
, the trivial solution of (2) is
,
with respect to y;
2) when
, the trivial solution of (2) is,
with respect to.
Proof Apply constant variation method to system (2), it can be deduced that:
(3)
(4)
By the condition of the theory, available from (3):
 (5)
(5)
however, set
,
,
,
,
,
Set:
Obviously,
,
are monotonous, and defined by,
,
, we have
,
So substituting (5) into (2) gives:
Similarly available:
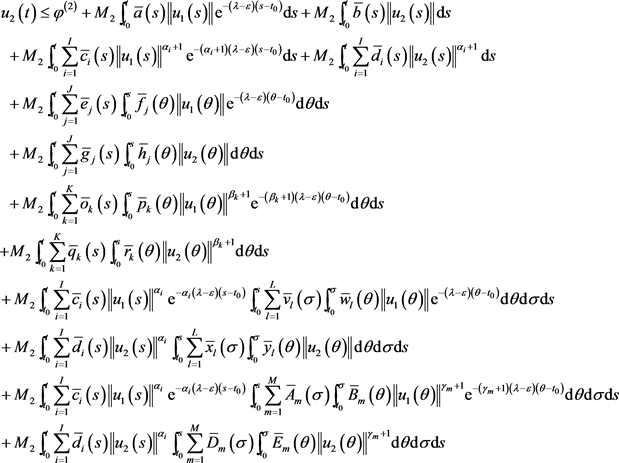
where
.
So it can be obtained from Lemma:
,
here
,
,
As the lemma states, then:
,
(6)
here:
;
;
.
Notice the theorem conditions, we have
is a constant that has nothing to do with
,
and
are constants that has nothing to do with
.
Therefore, when
, (6) means the trivial solution of (2) is
,
with respect to y; when
, (6) means the trivial solution of (2) is
,
with respect to y.
Note: The differential system discussed in this paper is the time-differential form of the ordinary differential system in [5] [6]. The time-differential system in [7] is generalized to a neutral system, and the Lipschitz stability in [8] is further extended to equi-exponential Lipschitz asymptotic stability and uniform exponential Lipschitz asymptotic stability and added global results
4. Conclusion
In this paper, we use the method of integral inequalities to establish double stability criteria. As a result, studying the partial stability of differential equations becomes more important. In addition, the partial stability of differential equations is widely used in science and technology.