Some mathematical aspects of the Lie groups
SU (2) and

in realization by two pairs of boson annihilation and creation operators and in the parametrization by the vector parameter
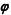
instead of the Euler angles
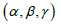
and the vector parameter
c of Fyodorov are developed. The one-dimensional root scheme of
SU (2) is embedded in two-dimensional root schemes of some higher Lie groups, in particular, in inhomogeneous Lie groups and is represented in text and figures. The two-dimensional fundamental representation
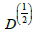
of
SU (2) is calculated and from it the composition law for the product of two transformations and the most important decompositions of general transformations in special ones are derived. Then the transition from representation
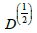
of
SU (2) to
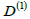
of

is made where in addition to the parametrization by vector
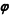
the convenient parametrization by vector
c is considered and the connections are established. The measures for invariant integration are derived for

and for
SU (2) . The relations between 3D-rotations of a unit sphere to fractional linear transformations of a plane by stereographic projection are discussed. All derivations and representations are tried to make in coordinate-invariant way.