Time Complexity of the Oracle Phase in Grover’s Algorithm ()
ABSTRACT
Since
Grover’s algorithm was first introduced, it has become a category of quantum
algorithms that can be applied to many problems through the exploitation of
quantum parallelism. The original application was the unstructured search
problems with the time complexity of O( ). In Grover’s algorithm, the key is Oracle and
Amplitude Amplification. In this paper, our purpose is to show through examples
that, in general, the time complexity of the Oracle Phase is O(N), not
O(1). As a result, the time complexity of Grover’s algorithm is O(N),
not O(
). In Grover’s algorithm, the key is Oracle and
Amplitude Amplification. In this paper, our purpose is to show through examples
that, in general, the time complexity of the Oracle Phase is O(N), not
O(1). As a result, the time complexity of Grover’s algorithm is O(N),
not O(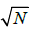 ). As a secondary purpose, we also attempt to restore
the time complexity of Grover’s algorithm to its original form, O(
). As a secondary purpose, we also attempt to restore
the time complexity of Grover’s algorithm to its original form, O(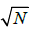 ), by introducing an O(1) parallel algorithm for
unstructured search without repeated items, which will work for most cases. In
the worst-case scenarios where the number of repeated items is O(N), the
time complexity of the Oracle Phase is still O(N) even after additional
preprocessing.
), by introducing an O(1) parallel algorithm for
unstructured search without repeated items, which will work for most cases. In
the worst-case scenarios where the number of repeated items is O(N), the
time complexity of the Oracle Phase is still O(N) even after additional
preprocessing.
Share and Cite:
Liu, Y. (2024) Time Complexity of the Oracle Phase in Grover’s Algorithm.
American Journal of Computational Mathematics,
14, 1-10. doi:
10.4236/ajcm.2024.141001.
Cited by
No relevant information.