Computational Prooving of Riemann’s Hypothesis ()
ABSTRACT
Formulated in 1859 by the mathematician Bernhard
Riemann, the Riemann hypothesis is a
conjecture. She says that the Riemann’s Zeta function non-trivial zeros
of all have real part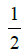 
. This demonstration would improve the prime numbers
distribution knowledge. This conjecture constitutes one of the most important
mathematics unsolved problems of the 21st century: it is one of the famous
Hilbert problems proposed in 1900. In this article, a method for solving this
conjecture is given. This work has been started by finding an analytical function which gives a
best accurate 10-8 of particular zeros sample that this number has increased gradually and finally prooving that this function is always
irrational. This demonstration is important as allows Riemann’s zeta function
to be a model function in the Dirichlet series theory and be at the crossroads
of many other theories. Also, it is
going to serve as a motivation and guideline for new studies.
Share and Cite:
Tougma, J. (2023) Computational Prooving of Riemann’s Hypothesis.
American Journal of Computational Mathematics,
13, 632-643. doi:
10.4236/ajcm.2023.134035.
Cited by
No relevant information.