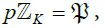The goal of this paper is to show that there are infinitely many number fields K/Q, for which there is no inert prime p ∈ N*, i.e. ∀p ∈ N* a prime number, prime ideal of K such that where: Z_k is the Dedekind domain of the integer elements of K. To prove such a result, consider for any prime p, the decomposition into a product of prime ideals of Z_k, of the ideal 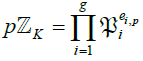. From this point, we use on the one hand: 1) The well- known property that says: If , then the ideal pZ_k decomposes into a product of prime ideals of Z_k as following: 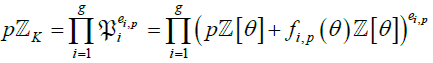. (where: 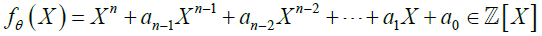; is the irreducible polynomial of θ, and, 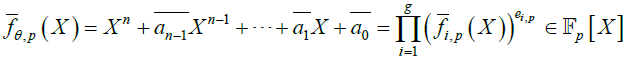is its reduction modulo p, which leads to a product of irreducible polynomials in Fp[X]). It is clear that because if 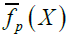is reducible in Fp[X], then consequently p is not inert. Now, we prove the existence of such p, by proving explicit such p as follows. So we use on the other hand: 2) this property that we prove, and which is: If 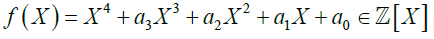, is an irreducible normalized integer polynomial, whose splitting field is , then for any prime number p ∈ N: is always a reducible polynomial. 3) Consequently, and this closes our proof: let’s consider the set (whose cardinality is infinite) of monogenic biquadratic number fields: 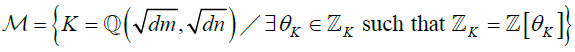. Then each f_θ(X) checks the above properties, this means that for family M, all its fields, do not admit any inert prime numbers p ∈ N.

2020-Mathematics Subject Classification (MSC2020)

11A41 - 11A51 - 11D25 - 11R04 - 11R09 - 11R11 - 11R16 - 11R32 - 11T06 - 12E05 - 12F05 -12F10 -13A05-13A15 - 13B02 - 13B05 - 13B10 - 13B25 -13F05