Author(s)

Adenike Olusola Adeniji^*, Janet Ifiok Obafemi

Department of Mathematics, Faculty of Science, University of Abuja, Abuja, Nigeria.

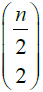
Set of integers, Z_n is split into even-odd parts. The even part is arranged in ways, while the odd part fixes one point at a time to compliment the even part thereby forming the semigroup, AZ_n. Thus, -spaces are filled choosing maximum of two even points at a time. Green’s relations have formed important structures that enhance the algebraic study of transformation semigroups. The semigroup of Alternating Nonnegative Integers for n-even (AZ_n-even) is shown to have only two D-classes, and there are -classes for n≥4. The cardinality of L-classes is constant. Certain cardinalities and some other properties were derived. The coefficients of the zigzag triples obtained are 1, and . 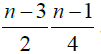The second and third coefficients can be obtained by zigzag addition.

Green’s Relations, Partial Order Relation, Idempotents, Band, Generator

Adeniji, A. and Obafemi, J. (2022) Transformation Semigroup of Alternating Nonnegative Integers. Advances in Pure Mathematics, 12, 614-623. doi: 10.4236/apm.2022.1211047.