From Kantian-Reinen Vernunft to the Real Dark Energy Density of the Cosmos via the Measure Concentration of Convex Geometry in Quasi Banach Spacetime ()
1. Introduction
The present work is devoted mainly to clarifying problems connected to Einstein’s relativity (Rindler, 2004; Okun, 2009; Helal et al., 2013; He & Marek-Crnjac, 2013; Helal, Marek-Crnjac, & He, 2013.; Auffray, 2014; El Naschie, 2011, 2013a-k, 2014a-m) and the missing dark energy of the cosmos (Auffray, 2014; El Naschie, 2011, 2012a-2, 20131-k, 2014a-m; He, 2013a; He & Marek-Crnjac, 2013b; Marek-Crnjac, 2013a; Marek-Crnjac & El Naschie, 2013b; Marek-Crnjac & He, 2013c; Marek-Crnjac, El Naschie, & He, 2013d; Tang et al., 2014) as well as quantum gravity and high energy physics (El Naschie, 2011-2014; Ball, 1991; Pisier, 1989; Kasin, 1977; Guedon, 2013; He & El Naschie, 2012; He 2013a; He & Marek-Crnjac, 2013b; He, 2014; Connes, 1994; Krantz & Parks, 2008) using pure mathematics (Kant, 1974; Baumgartner, 1988; Sartre, 2004, 2012; Reichenbach, 1951; Ayer, 1954; El Naschie, 1994) . Taking a bird’s eye view of things it is reasonably safe, even for a theoretical physicist and engineering scientist like the present author, to state that almost the entire modern philosophical framework of our present society is shaped by and stands on Kant’s critique of pure reason as well as his critique of practical reason (Kant, 1974; Baumgartner, 1988) . From there German idealism invaded the intellectual foundations of not only European civilization but the entire world which culminated in the work of F. Hegel giving rise to Marxism and existentialism. In fact the hero of the present author in his youth and early life was J. P. Sartre (Sartre, 2004, 2012) . In particular Sartre’s critique of the dialectic reason and in no minor measure his main monumental work, being and nothingness influenced the writer to discover the zero set as the quantum particle and the empty set as the quantum wave and introduced Mandelbrot’s notion of the degrees of emptiness of an empty set to the transfinite set theory used by him and the E-infinity school of high energy physics (El Naschie 1994, 2014a-m; He & El Naschie, 2012) . Looking back without any Osbornian anger, it is clear to the author that he believed rather strongly that philosophy has a real, indispensible role in exact science, a belief many disputed in physics but is held highly by many pure mathematicians, notably G. Cantor and in modern times, also by leading mathematicians working also in physics such as Field Medalist (A. Connes, 1994) . This was all fine and good and things remained as they are until the present ideas constituting the main body of the present work dawned on the author. A seemingly harmless theorem in the mathematics of convex geometry in very high dimensions related to Banach spaces states that for manifolds of this mould, 96 percent of the measure volume will be concentrated near to the surface of the manifold (Ball, 1991; Pisier, 1989; Kasin, 1977; Guedon, 2013) . Suddenly a mental analogue of atomic chain reaction was triggered in the mind of the author and it became evident for him that this theorem is the counter part of Kant’s pure reason applied to the “experimentally” discovered mystery of the “missing” dark energy of the universe (El Naschie, 2012a-c, 20131-k, 2014a-m; He 2013a; He & Marek-Crnjac, 2013b; Marek-Crnjac, 2013a; Marek-Crnjac & El Naschie, 2013b; Marek-Crnjac & He, 2013c; Marek-Crnjac et al., 2013d) . This would, and the present author believe it is a clear cut generic and fundamental example for the power of scientific philosophical thinking in reaching in a direct way a resolution for fundamental problems in quantum physics and cosmology. To try to persuade the reader that this is the case requires some knowledge of math and physics but none of it is so hard or extremely specialized that the non-specialist cannot follow as we hope to show next.
2. General Background Information
Einstein’s most famous formula states the equivalence of matter and energy and relates them via the constant speed of light in the jewel of special relativity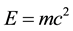 
where 
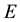is the energy, 
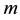is the mass and 
is the speed of light (Rindler, 2004; Okun, 2009; Helal et al., 2013) . Intensive effort motivated by the unexpected discovery of the accelerated expansion of the cosmos and the related problem of the dark matter and dark energy 95% density deficit revealed that Einstein’s energy “density” equation is the sum of two parts (Auffray, 2014) . The first is a measurable ordinary energy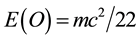 
and the second which cannot be measured in any conventional way is the dark energy density 
so that at the end
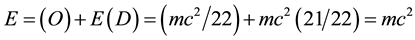. To arrive at this result two main groups of methods were employed (Helal et al., 2013; Auffray, 2014; El Naschie, 2011, 2012a-c, 2013a-k, 2014a-m; He, 2013a; He & Marek-Crnjac, 2013b; Marek-Crnjac, 2013a; Marek-Crnjac & El Naschie, 2013b; Marek-Crnjac & He, 2013c; Marek-Crnjac et al., 2013d; Tang et al., 2014) . The first may be loosely described as mainly physical based on the structure of the standard model of elementary high energy particles while the second may be equally loosely described as largely mathematical starting from Cantor transfinite set theory.
In the present paper by contrast we tackle the problem afresh using a purely topological-geometrical methodology based on some remarkable mathematical results from the modern theory of high dimensional convex geometry and the associated phenomenon of concentration of measure studied initially in Banach spaces and then lead to Dvoretzky’s theorem and the subsequent relevant research (Ball, 1991; Pisier, 1989; Kasin, 1977; Guedon, 2013) .
We stress again that the final result is a complete confirmation of the dissection of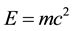 
into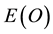 
of the quantum particle and 
of the quantum wave in addition to being a deep insight into the relation between physics, geometry and algebra as well as the unity of classical and quantum mechanics (Ball, 1991; Pisier, 1989; Kasin, 1977; Guedon, 2013; Connes, 1994; Krantz & Parks, 2008) . Our main message in this paper is that real fundamental, physical and cosmological facts could be found using pure reason (Kant, 1974; Baumgartner, 1988; Sartre, 2004, 2012; Reichenbach, 1951; Ayer, 1954; El Naschie, 1994) .
3. Further Background Information and Preliminary Considerations
Cantorian spacetime is a monadic space (He, 2012) in a sense akin to that of K-theory, E-infinity rings and n- category theory. The building blocks of this space are zero sets of a Hausdorff dimension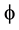 
embedded into empty sets of a Hausdorff 
which are distributed in a uniform randomness to form via an infinite number of unions and intersections a hierarchical-infinite dimensional Cantor set. This Suslin-like operation (Krantz & Parks, 2008) entails few fundamental equations which determine all what is required to deduce various vital invariant properties of this space which we use to mimic our own physical macro and micro quantum spacetime. Based on the above we were able to show in the last four years beyond reasonable doubt that the jewel of special relativity, i.e.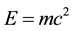 
is in fact the sum of two partial equations. As mentioned earlier on in the introduction, the first part 
gives us the real measurable energy density which is due to the particle side of quantum mechanics as modelled by the zero set in Kaluza-Klein five dimensional spacetime. The second part on the other hand is the dark energy which cannot be measured in the ordinary way 
and which is due to the wave nature of the quantum particle-wave duality as modelled by the empty set in the same K-K spacetime. A trivial computation shows then that 1/22 = 4.5% and 21/22 = 95.5% of Einstein’s total energy density in complete agreement with all modern cosmological measurements. Again in the last four years numerous derivations of the preceding dissection of Einstein’s basic energy-mass relation was given by the author and his collaborators using a variety of physical and algebraic derivation and all leading to the same fundamental conclusion.
The present work is not intended to review or discuss in details past derivations but is mainly concerned with giving a new purely geometrical derivation showing that the so called missing 95.5% dark energy is a well established geometrical phenomena completely understood since many years in the mathematical literature without drawing or suspecting any physical conclusion or relation to high energy quantum physics or cosmology (Ball, 1991; Pisier, 1989; Kasin, 1977; Guedon, 2013) . We are talking here about the phenomenon of measure concentration of convex geometry with high dimensionality which is an off spring of research works on Banach spaces (El Naschie, 2012a-c) . The next section is mainly concerned with outlining and explaining this fascinating new connection between pure geometry, quantum physics and cosmology as well as how classical mechanics arise from the deeper mechanics of the quantum and the even deeper mathematics of transfinite set theory and infinite dimensional Banach spaces.
4. Cantorian Spacetime as a Convex Geometry in Very High Dimensions
4.1. Short Review of the Relevant Results in Convex Geometry
The aim of this minimalistic section is to show the failure of our low dimensionality intuition when dealing with geometrical objects of higher dimensionality which start in earnest with 
(El Naschie, 1997, 1999) . Similar ideas were discussed by the present author many years ago while attempting to connect string theory and the geometry of spacetime with sphere backing and chess board tiling. The present fundamental example goes in the same main direction and even beyond to the degree that it becomes of fundamental importance in the cosmology of dark energy. To start let us calculate the ![]()
dimensional slice of a unit ball. The relatively elementary consideration involving the use of the stirling formula leads to an accurate approximation of the volume of the smaller slice (Ball, 1991; Pisier, 1989; Kasin, 1977; Guedon, 2013)
![]()
, (1)
where ![]()
fixes the width of parallel slices. That way we can conclude that the volume “mass”
volume “mass” distribution is Gaussian and for a fixed slab width almost 95.5% of the mass lies in this slice (Ball, 1991) . Now as hinted at earlier, our intuition could lead us to wrongly think that this 95.5% measure concentration is located in dimension ![]()
at the centre of the ![]()
-dimensional space. The mathematical-geome- trical truth however is exactly the opposite and careful consideration reveals that for large ![]()
the measure concentration is asymptotically near to the surface (Ball, 1991) . For ![]()
the 95.5% is for all practical reasons the surface itself. The mathematical literature is in the meantime abounds with various extensions of this remarkable result which is based on A. Dvoretzky’s theorem and the work of V. Milman and its mathematical-geometrical ramifications (Ball, 1991; Pisier, 1989; Kasin, 1977; Guedon, 2013) . In the present work however our evident interest is clearly in the obvious relevance of the above conclusion to dark energy cosmology. We start by showing the almost one to one correspondence of the above with the Cantorian-fractal holographic boundary of E-infinity spacetime and its dark energy content.
4.2. The Measure Concentration of E-Infinity Spacetime as an Explanation for Dark Energy
As mentioned earlier on in the introduction, the building blocks of E-infinity Cantorian spacetime are zero sets embedded into an empty set as their surface or cobordism. Since the zero set ![]()
has a Hausdorff dimension ![]()
and the empty set ![]()
has a Hausdorff dimension ![]()
then in ![]()
Kaluza-Klein spacetime the unit volumetric measure would be the average of intersectional ![]()
zero set volume ![]()
nd the additive ![]()
empty set volume ![]()
here we interpreted ![]()
and ![]()
s a Hausdorff volume or topological probability as an extension of the classical notion of geometrical probability (Helal et al., 2013; Marek-Crnjac, 2013a; Marek-Crnjac & El Naschie, 2013b; Marek-Crnjac & He, 2013c; Marek-Crnjac et al., 2013d; Auffray, 2014; El Naschie, 2004, 2009) . Consequently the average volume is simply (Connes, 1994)
![]()
. (2)
The corresponding average energy is therefore nothing else but Einstein’s celebrated formula [28]
![]()
(3)
From [28]
![]()
(4)
and
![]()
(5)
where ![]()
is the topological mass of ‘tHooft’s renormalon which could be thought of as made of two entangleon ![]()
particles because![]()
, our main result follows, namely that
![]()
(6)
So far we have looked at a single monadic building block of our space (He, 2012). However due to self similarity we expect the above relation to hold true on all scales. To show that this expectation is correct and leads to our fundamental conclusion about the measure concentration, we reason as follows:
Our E-infinity spae is infinite dimensional![]()
, however it has a finite expectation value of ![]()
and ![]()
for its topological and Hausdorff dimension apart of the Menger-Urysohn topological dimension of exactly 4 (El Naschie, 2004, 2009) . Thus although infinite dimensional, because of its hierarchal geometry reflected in its Suslin expansion (Krantz & Parks, 2008)
![]()
(7)
it is still compact with a boundary at infinity. This shows up clearly in the hyperbolic projection of E-infinity space which manifests itself as a modular fractal space of the Klein-Penrose type as explained in great detail in previous older and more recent publications. Now our result follows because in the Poincare-Beltrami projection we have at the center about 336 degrees of freedom corresponding to the internal dimension of the original Klein modular space
![]()
(8)
This represents the holographic boundary without the “compactified” edge. At this edge however, which is located at infinity, we have infinitely more degrees of freedom. Thus although the edge seems to us from the middle to be infinitely think it is really where the bulk of absolute measure is located, namely the 95.5%. For us low dimensional creatures, the situation may strike us as paradoxical especially when we are making measurements of the total energy density of the cosmos. In this sense the COBE, WMAP and Planck measurement makes absolute sense when we realize that this 95.5% is related to the quantum wave of the universe which collapses on measurement and cannot be detected but can be indirectly inferred from cosmological observations extended to the edge of the universe.
5. Discussion
The quantum wave and wave collapse may be a familiar face of the quantum world but this does not change its deep status as the greatest puzzle in physics. How could something which has no energy, no matter and no momentum have such a crucial effect on the motion of quantum objects. Suddenly however cosmology started becoming equally puzzling, if not more puzzling, with the discovery of a type of energy which may be the possible cause behind the accelerated cosmic expansion of the universe although it is de facto not there because it cannot be measured and if we try very hard, we find only 4.5% ordinary energy and ordinary matter leaving the 95.5% shrouded in mystery. These things which are there but are really not there remind anyone working in deterministic chaos, nonlinear dynamics and fractals with the paradoxical nature of a Cantor set (El Naschie, 2004, 2009) . These transfinite sets possess no measure, being of measure zero which means no length at all and consequently “physically” not there. However they do have a substantial Hausdorff dimension, namely ![]()
for the original Cantor set and ![]()
for a uniformally random Mauldin-Williams Cantor set. Now we ask ourselves how did we succeed in applying an Occam razon magnum to these three paradoxical factors? The short answer is by reducing dark energy to the non-ordinary energy of the quantum wave and the quantum wave to an empty set dimension ![]()
which happens to be the surface of the zero set quantum particle with a Hausdorff dimension ![]()
That way we seem to have eliminated the problem by illuminating it via the light of fractal Cantorian geometry and transfinite set theory as well as the associated E-infinity algebra of the highly structured golden mean ring which can deal with the most complex computation with unheard of simplicity. Thus the present work shows a clear and profound example of how pure reason and pure mathematics guided by scientific philosophy and accurate measurements and observations can lead in a simple way to profound information about the real world.
6. Conclusion
The present work demonstrates that at the most fundamental quantum level the universe is best studied by pure reason and pure mathematics. We cannot experimentally probe either zero and nothingness or the uncountably infinite. However the present work clearly shows that the disection of Einstein’s energy density into two parts is a completely natural consequence of a very high dimensional geometry and its associated measure concentration which results in almost 96% of the volume being located near to the surface of the concerned manifold (Ball, 1991; Guedon, 2013) as well as modelling the quantum particle with a five dimensional zero set and modelling the quantum wave with a five dimensional empty set (El Naschie, 2013a-k) . Applied to our cosmos as modelled by E-infinity Cantorian spacetime manifold, the missing dark energy becomes a natural consequence of the geometry and topology of E-infinity. Together with our anticlastic, anti-curvature and antigravity explanation of real material-like spacetime (El Naschie, 2014a-m) , dark energy and accelerated cosmic expansion find in the above a rational mathematical-geometrical and consequently physical explanation.