1. Introduction
Let P be a poset. For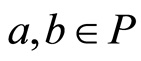
, we say a covers b, denoted by
; if 
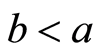and there doesn’t exist 
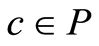such that
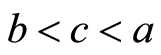. If P has the minimum (resp. maximum) element, then we denote it by 0 (resp. 1) and say that P is a poset with 0 (resp. 1). Let P be a finite poset with 0. By a rank function on P, we mean a function r from P to the set of all the integers such that 
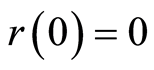and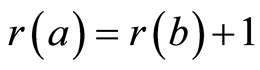 
whenever
. Observe the rank function is unique if it exists. P is said to be ranked whenever P has a rank function.
Let P be a finite ranked poset with 0 and 1. The polynomial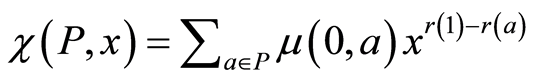 
is called the characteristic polynomial of P, where 
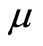is the 
function on P and r is the rank function of P. A poset P is said to be a lattice if both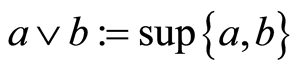 
and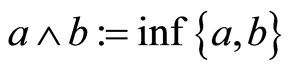 
exist for any two elements
. 
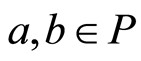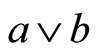and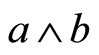 
are called the join and meet of a and b, respectively. Let P be a finite lattice with 0. By an atom in P, we mean an element in P covering 0. We say P is atomic if any element in 
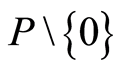is the join of atoms. A finite atomic lattice P is said to be a geometric lattice if P admits a rank function 
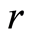satisfying
,
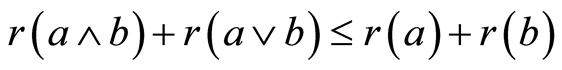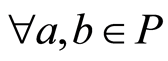. Notations and terminologies about posets and lattices will be adopted from books [1] [2] .
The special lattices of rough algebras were discussed in [3] . The lattices generated by orbits of subspaces under finite (singular) classical groups were discussed in [4] [5] . Wang et al. [6] -[8] constructed some sublattices of the lattices in [4] . The subspaces of a d-bounded distance-regular have similar properties to those of a vector space. Gao et al. [9] -[11] constructed some lattices and posets by subspaces in a d-bounded distance-regular graph. In this paper, we continue this research, and construct some new sublattices of the lattices in [4] , discussing their geometricity and computing their characteristic polynomials.
Let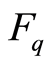 
be a finite field with q elements, where q is a prime power. For a positive integer
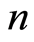, let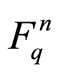 
be the n-dimensional row vector space over
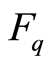. Let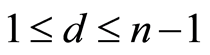
. For a fixed
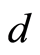-dimensional subspace 
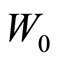of
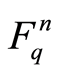, let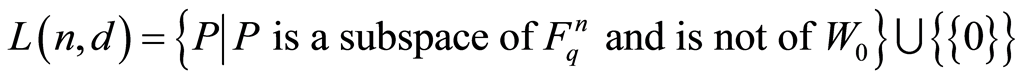
.
If we define the partial order on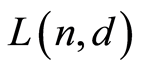 
by ordinary inclusion (resp. reverse inclusion), then 
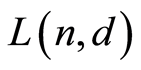is a poset, denoted by 
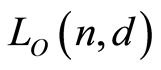(resp.
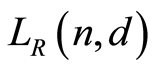). In the present paper we show that both 
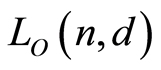and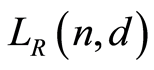 
are finite atomic lattices, discuss their geometricity and compute their characteristic polynomials.
2. The Lattice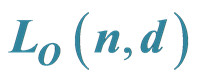 
In this section we prove that the lattice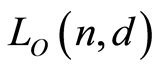 
is a finite geometric lattice, and compute its characteristic polynomial. We begin with a useful proposition.
Proposition 2.1. ([12] , Lemma 9.3.2 and [13] , Corollaries 1.8 and 1.9). For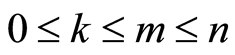
, the following hold:
1) The number of k-dimensional subspaces contained in a given m-dimensional subspace of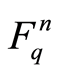 
is
.
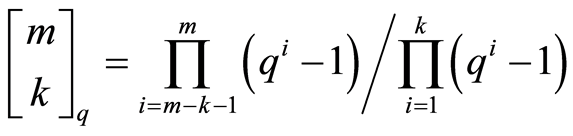2) The number of m-dimensional subspaces containing a given k-dimensional subspace of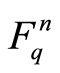 
is
.
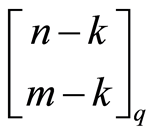3) Let P be a fixed m-dimensional subspaces of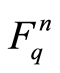
. Then the number of k-dimensional subspaces Q of 
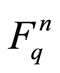satisfying 
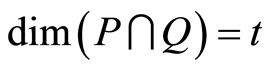is
.
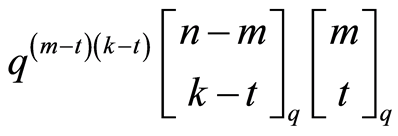Theorem 2.2.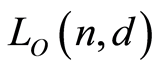 
is a geometric lattice.
Proof. For any two elements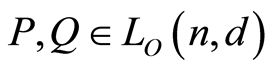
,
Therefore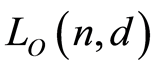 
is a finite lattice. Note that 
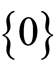is the unique minimum element. Let 
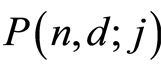be the set of all the 
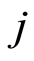-dimensional subspaces of
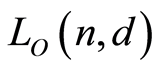, where
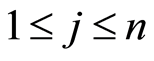. Then 
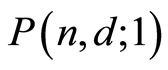is the set of all the atoms in
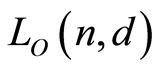. In order to prove 
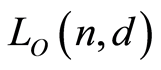is atomic, it suffices to show that every element of 
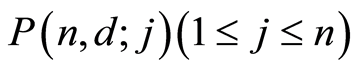is a join of some atoms. The result is trivial for
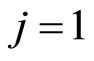. Suppose that the result is true for
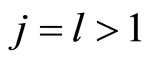. Let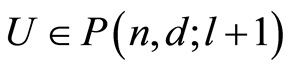
. By Proposition 2.1 and
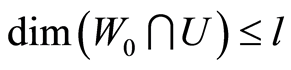, the number of 
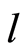-dimensional subspaces of 
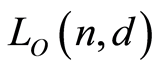contained in 
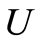at least is
.
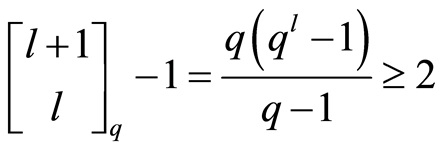Therefore there exist two different l-dimensional subspaces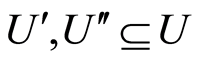 
of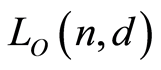 
such that
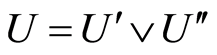. By induction
is a join of some atoms. Hence 
is a finite atomic lattice. For any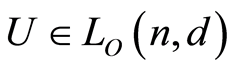 
, define
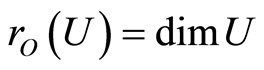. It is routine to check that 
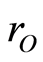is the rank function on
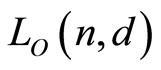. For any
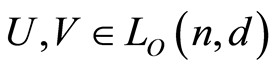, we have
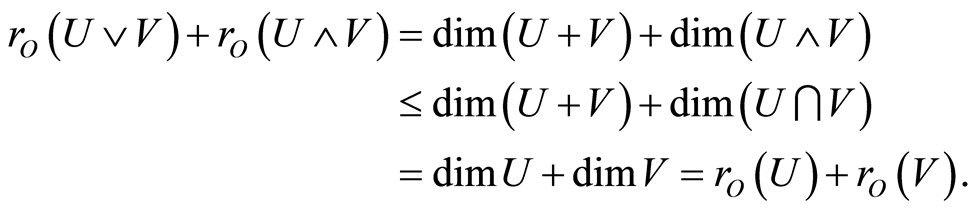
Hence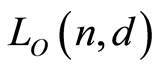 
is a geometric lattice. 
Lemma 2.3. For any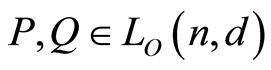
, suppose that
, 
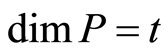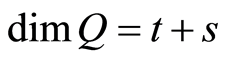and
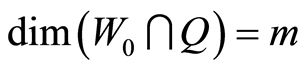. Then the 
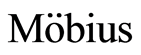function of 
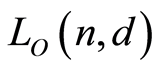is
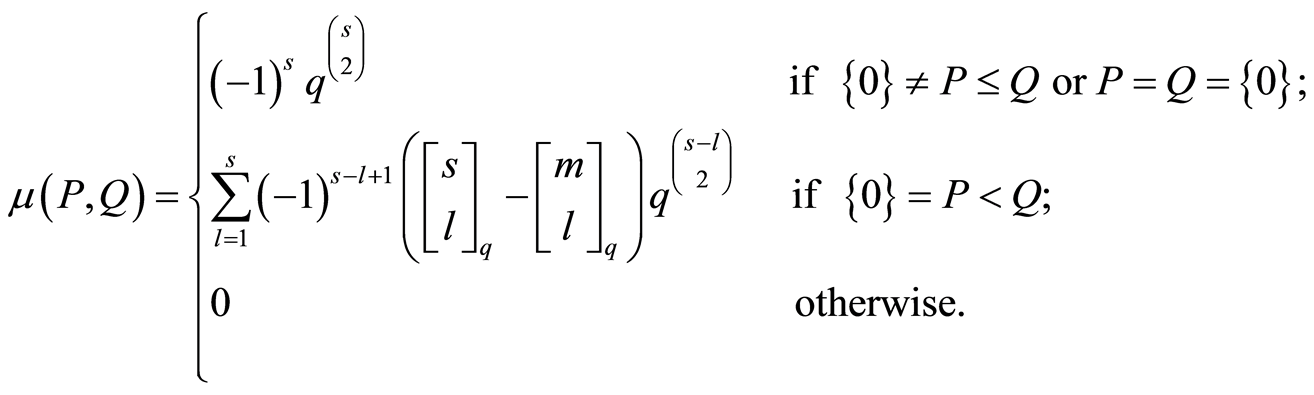
Proof. The 
function of 
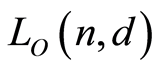is
By Proposition 2.1, we have
.
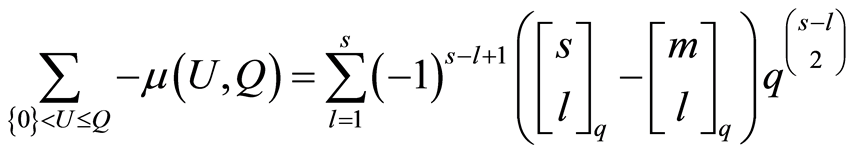Thus, the assertion follows. 
Theorem 2.4. The characteristic polynomial of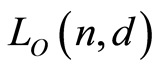 
is
Proof. By Proposition 2.1 and Lemma 2.3, we have
3. The Lattice 
In this section we prove that the lattice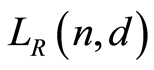 
is a finite atomic lattice, classify its geometricity and compute its characteristic polynomial.
Theorem 3.1. The following hold:
1) 
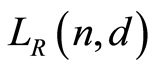is a finite atomic lattice.
2) 
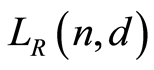is geometric if and only if
.
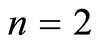Proof. 1) For any two elements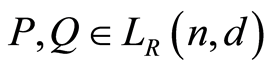
, 
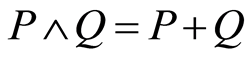and
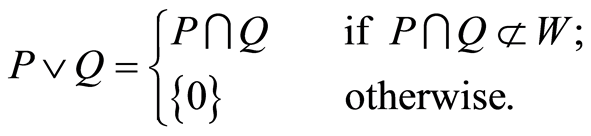
Therefore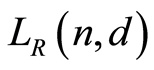 
is a finite lattice. Note that 
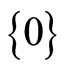is the unique minimum element. Let 
be the set of all the j-dimensional subspaces of
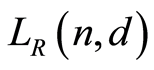, where
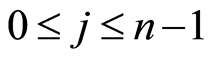. Then 
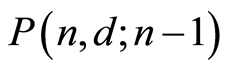is the set of all the atoms in
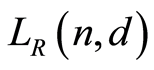. In order to prove 
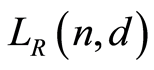is atomic, it suffices to show that every element of 
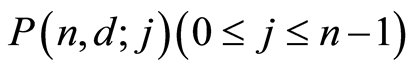is a join of some atoms. The result is trivial for
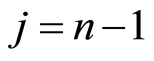. Suppose that the result is true for
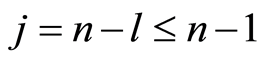. Let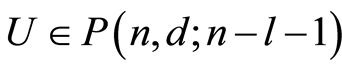
. By Proposition 2.1, the number of 
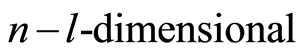subspaces of 
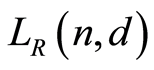containing 
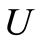is equal to
.
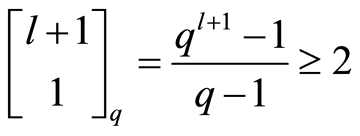Then there exist two different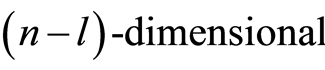 
subspaces 
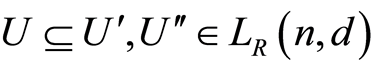such that
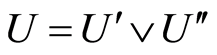. By induction 
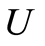is a join of some atoms. Therefore 
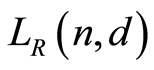is a finite atomic lattice.
2) For any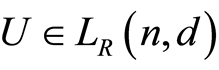
, we define
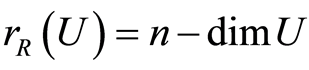. It is routine to check that 
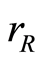is the rank function on
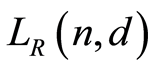. It is obvious that 
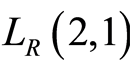is a geometric lattice. Now assume that
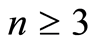. Let P be a 
-dimensional subspace of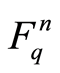 
and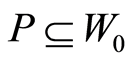
. By Proposition 2.1, the number of 2-dimensional subspaces of 
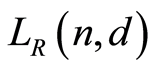containing P is equal to
Therefore, there exist two different 2-dimensional subspaces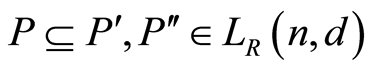 
such that
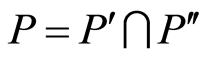. So
,
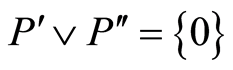. Hence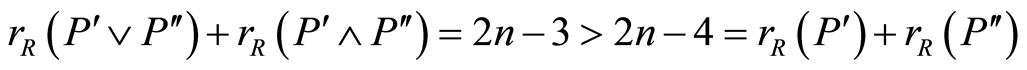
, which implies that 
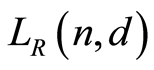is not a geometric lattice when
. 
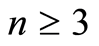Lemma 3.2. For any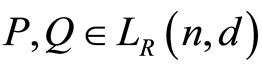
, suppose that
, 
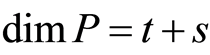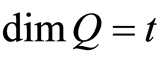and
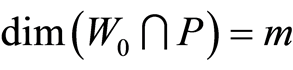. Then the 
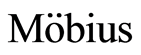function of 
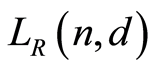is
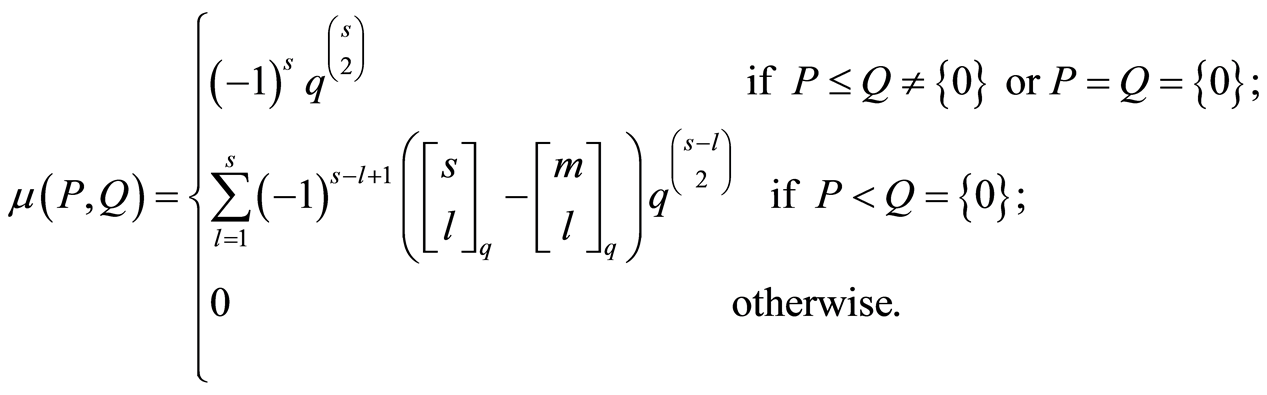
Proof. The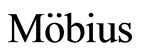 
function of 
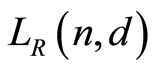is
Proposition 2.1 implies that
.
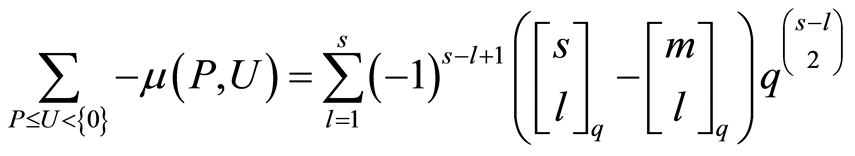Theorem 3.3. The characteristic polynomial of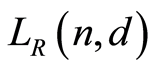 
is
.
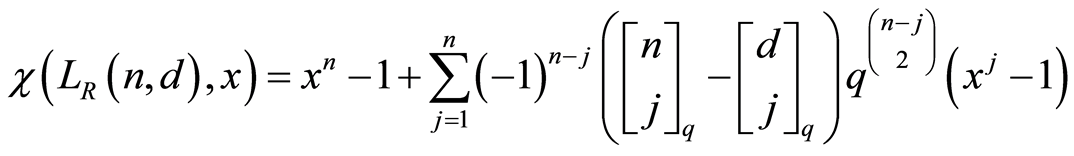Proof. By Proposition 2.1, we have
