Daniel C. Mayer
Naglergasse 53, Graz, Austria.
DOI: 10.4236/apm.2019.94017   PDF    HTML   XML   587 Downloads   1,262 Views   Citations

Abstract

By making use of our generalization of Barrucand and Cohn’s theory of principal factorizations in pure cubic fields and their Galois closures with 3 possible types to pure quintic fields and their pure metacyclic normal fields with 13 possible types, we compile an extensive database with arithmetical invariants of the 900 pairwise non-isomorphic fields N having normalized radicands in the range 2≤D<10³. Our classification is based on the Galois cohomology of the unit group U_N, viewed as a module over the automorphism group Gal(N/K) of N over the cyclotomic field K=Q(ξ₅), by employing theorems of Hasse and Iwasawa on the Herbrand quotient of the unit norm index (U_k:N_N/K(U_N)) by the number #(P_N/K/P_K) of primitive ambiguous principal ideals, which can be interpreted as principal factors of the different D_N/K. The precise structure of the F₅-vector space of differential principal factors is expressed in terms of norm kernels and central orthogonal idempotents. A connection with integral representation theory is established via class number relations by Parry and Walter involving the index of subfield units (U_N:U₀)_. The statistical distribution of the 13 principal factorization types and their refined splitting into similarity classes with representative prototypes is discussed thoroughly.

Keywords

Pure Quintic Fields, Pure Metacyclic Fields, Units, Galois Cohomology, Differential Principal Factorization Types, Similarity Classes, Prototypes, Class Group Structure

Share and Cite:

1. Introduction

At the end of his 1975 article on class numbers of pure quintic fields, Parry suggested verbatim: In conclusion, the author would like to say that he believes a numerical study of pure quintic fields would be most interesting ( [1] p. 484). Of course, it would have been rather difficult to realize Parry’s desire in 1975. But now, 40 years later, we are in the position to use the powerful computer algebra systems PARI/GP [2] and MAGMA [3] [4] [5] for starting an attack against this hard problem. Prepared by [6] [7] [8] [9] , this will actually be done in the present paper.

Even in 1991, when we generalized Barrucand and Cohn’s theory [10] [11] of principal factorization types from pure cubic fields to pure quintic fields 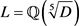and their pure metacyclic normal closures 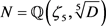[12] , it was still impossible to verify our hypothesis about the distinction between absolute, intermediate and relative differential principal factors (DPF) ( [6] (6.3)) and about the values of the unit norm index 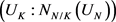( [6] (1.3)) by actual computations.

All these conjectures have been proven by our most recent numerical investigations. Our classification is based on the Hasse-Iwasawa theorem about the Herbrand quotient of the unit group 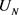of the Galois closure N of L as a module over the relative group 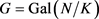with respect to the cyclotomic subfield. It only involves the unit norm index and our 13 types of differential principal factorizations ( [6] Thm. 1.3), but not the index of subfield units ( [6] §5) in Parry’s class number formula ( [6] (5.1)).

We begin with a collection of explicit multiplicity formulas in §2 which are required for understanding the subsequent extensive presentation of our computational results in twenty tables of crucial invariants in §3. This information admits the classification of all 900 pure quintic fields with normalized radicands into 13 DPF types and the refined classification into similarity classes with representative prototypes in §4.

We draw the attention to remaining open questions in §3.3, and we collect theoretical consequences of our experimental results in §4.3. The exposition is concluded with a retrospective final §5.

2. Collection of Multiplicity Formulas

For the convenience of the reader, we provide a summary of formulas for calculating invariants of pure quintic fields with normalized fifth power free radicands and their associated pure metacyclic normal fields with a primitive fifth root of unity.

Let f be the class field theoretic conductor of the relatively quintic Kummer extension N/K over the cyclotomic field. It is also called the conductor of the pure quintic field L. The multiplicity of the conductor f indicates the number of non-isomorphic pure metacyclic fields N sharing the common conductor f, or also, according to ( [6] Prop. 2.1), the number of normalized fifth power free radicands whose fifth roots generate non-isomorphic pure quintic fields L sharing the common conductor f. The cardinality of a set S is denoted #S.

We adapt the general multiplicity formulas in ( [13] Thm. 2, p. 104) to the quintic case. If L is a field of species 1a ( [6] (2.6) and Exm. 2.2), i.e., then where. The explicit values of m in dependence on t are given in Table 1.

If L is a field of species 1b ( [6] (2.6) and Exm. 2.2), i.e., then where, and $X_j:=\frac{1}{5}\left(4^j-{\left(-1\right)}^j\right)$ , that is. The explicit values of m in dependence on u and v are given in Table 2.

If L is a field of species 2 ( [6] (2.6) and Exm. 2.2), i.e., then where, and

$X_j:=\frac{1}{5}\left(4^j-{\left(-1\right)}^j\right)$ , that is. The explicit values of m in dependence on u and v are given in Table 3.

3. Classification by DPF Types in 20 Numerical Tables

3.1. DPF Types

The following twenty Tables 6-25 establish a complete classification of all 900 pure metacyclic fields with normalized radicands in the range. With the aid of PARI/GP [2] and MAGMA [5] we have determined the differential principal factorization type, T, of each field N by means of other invariants ( [6] Thm. 6.1). After several weeks of CPU time, the date of completion was September 17, 2018.

The possible DPF types are listed in dependence on in Table 4, where the symbol × in the column, resp., indicates the existence of a unit, resp., such that, resp.. The 5-valuation of the unit norm index is abbreviated by U ( [6] (1.3), (6.3)]. Here, $\eta =\frac{1}{2}\left(1+\sqrt{5}\right)$ denotes the fundamental unit of $K^{+}=Q\left(\sqrt{5}\right)$ .

3.2. Justification of the Computational Techniques

The steps of the following classification algorithm are ordered by increasing requirements of CPU time. To avoid unnecessary time consumption, the algorithm stops at early stages already, as soon as the DPF type is determined unambiguously. The illustrating subfield lattice of N is drawn in Figure 1.

Algorithm 3.1 (Classification into 13 DPF types.)

Input: a normalized fifth power free radicand.

Step 1: By purely rational methods, without any number field constructions, the prime factorization of the radicand D (including the counters, §4.2) is determined. If, , , then N is a Polya field of type; stop. If, or, then N is a Polya field of type; stop.

Step 2: The field L of degree 5 is constructed. The primes dividing the conductor f of N/K are determined, and their overlying prime ideals in L are computed. By means of at most principal ideal tests of

the elements of, the number , that is the cardinality of, is determined. If, then N is a Polya field. If, then N is of type; stop. If, , , then N is of type; stop. If, , then N is of type; stop.

Step 3: If or, then the field M of degree 10 is constructed. For the 2-split primes among the primes dividing the conductor f of N/K, the overlying prime ideals in M are computed. By means of at most principal ideal tests of the elements of , where for , the number, that is the cardinality of, is determined. If, then N is of type; stop. If, , then N is of type; stop.

Step 4: If, then the field N of degree 20 is constructed. For all 4-split primes among the primes dividing the conductor f of N/K, the overlying prime ideals in N are computed. By means of at most principal ideal tests of the elements of , where and for, the number, that is the cardinality of, is determined. If, then N is of type; stop. If, , then N is of type; stop. If, , then N is of type; stop.

Step 5: If the type of the field N is not yet determined uniquely, then and there remain the following possibilities. If, then N is of type, if, of type, if, and of type, if. If, then a fundamental system of units is constructed for the unit group of the field N of degree 20, and all relative norms of these units with respect to the cyclotomic subfield K are computed. If for some, , then N is of type, if, of type, if, and of type, if. Otherwise the conclusions are the same as for.

Output: the DPF type of the field and the decision about its Polya property.

Proof. The claims of Step 1 concerning the types are proved in items (1) and (2) of ( [6] Thm. 10.1).

For Step 2, the formulas (4.1) and (4.2) in ( [6] Thm. 4.1) give an -basis of the space of absolute differential factors, and the formulas (4.3) and (4.4) in ( [6] Cor. 4.1) determine bounds for the -dimension A of the space of absolute DPF in the field L of degree 5. The Polya property was characterized in ( [6] Thm. 10.5)], the claim concerning type follows from ( [6] Thm. 6.1), and the claims about the types from ( [6] Thm. 8.1 and Thm. 6.1).

For Step 3, the formulas (4.5) and (4.6) in ( [6] Thm. 4.3) give an -basis of the space of intermediate differential factors, and the formulas (4.7) and (4.8) in ( [6] Cor. 4.2) determine bounds for the -dimension I of the space of intermediate DPF in the field M of degree 10. The claims concerning the types are consequences of ( [6] Thm. 6.1),

For Step 4, the formulas (4.9) and (4.10) in ( [6] Thm. 4.4) give an -basis of the space of relative differential factors, and the formulas (4.11) and (4.12) in ( [6] Cor. 4.3) determine bounds for the -dimension R of the space of relative DPF in the field N of degree 20. The claims concerning the types are consequences of ( [6] Thm. 6.1).

Concerning Step 5, the signature of N is, whence the torsion free Dirichlet unit rank of N is given by. The claims about all types are consequences of ( [6] Thm. 6.1), including information on the constitution of the norm group.

Remark 3.1 Whereas the execution of Step 1 and 2 in Algorithm 3.1, implemented as a Magma program [5] , is a matter of a few seconds on a machine with two Intel XEON 8-core processors and clock frequency 2 GHz, the CPU time for Step 3 lies in the range of several minutes. The time requirement for Step 4 and 5 can reach hours or even days in spite of code optimizations for the calculation of units, in particular the use of the Magma procedures IndependentUnits() and SetOrderUnitsAreFundamental() prior to the call of UnitGroup().

3.3. Open Problems

We conjecture that considerable amounts of CPU time can be saved in our Algorithm 3.1 by computing the logarithmic 5-class numbers of the fields, which admit the determination of the logarithmic indices E, resp., of subfield units in the Parry [1] , resp. Kobayashi [14] [15] , class number relation, according to the formulas

(3.1)

However, first there would be required rigorous proofs of the heuristic connections between and the DPF types in Table 5, where implies type, implies type, implies type, but admits types, admits types, admits types, admits types, and admits types. seems to be impossible.

3.4. Conventions and Notation in the Tables

The normalized radicand of a pure metacyclic field N of degree 20 is minimal among the powers, , with corresponding exponents reduced modulo 5. The normalization of the radicands D provides a warranty that all fields are pairwise non-isomorphic ( [6] Prop. 2.1).

Prime factors are given for composite radicands D only. Dedekind’s species, S, of radicands is refined by distinguishing (species 1a) and (species 1b) among radicands (species 1). By the species and factorization of D, the shape of the conductor f is determined. We give the fourth power to avoid fractional exponents. Additionally, the multiplicity m indicates the number of non-isomorphic fields sharing a common conductor f (§2). The symbol briefly denotes the 5-valuation of the order of the class group of a number field F. By E we denote the exponent of the power in the index of subfield units.

An asterisk denotes the smallest radicand with given Dedekind kind, DPF type and 5-class groups,. The latter are usually elementary abelian, except for the cases indicated by an additional asterisk (see §4.4).

Principal factors, P, are listed when their constitution is not a consequence of the other information. According to ( [6] Thm. 7.2., item (1)) it suffices to give the rational integer norm of absolute principal factors. For intermediate principal factors, we use the symbols with or with a prime element (which implies and thus also). Here, when a prime divides the radicand D. For relative principal factors, we use the symbols and with. Here, when a prime number divides the radicand D. (Kernel ideals in [6] §7)

The quartet indicates conditions which either enforce a reduction of possible DPF types or enable certain DPF types. The lack of a prime divisor together with the existence of a prime divisor and of D is indicated by a symbol × for the component 1. In these cases, only the two DPF types and can occur ( [6] Thm. 8.1).

A symbol × for the component 2 emphasizes a prime divisor of D and the possibility of intermediate principal factors in M, like and. A symbol × for the component 4 emphasizes a prime divisor of D and the possibility of relative principal factors in N, like and. The × symbol is replaced by if the facility is used completely, and by (×) if the facility is only used partially.

If D has only prime divisors or, a symbol × is placed in component 5. In these cases, can occur as a norm of some unit in. If it actually does, the × is replaced by ( [6] §8).

4. Statistical Evaluation and Refinements

4.1. Statistics of DPF Types

The complete statistical evaluation of the following twenty Tables 6-25 is given in Table 26. The first ten columns show the absolute frequencies of pure metacyclic fields with various DPF types for the ranges with. The eleventh column lists the relative percentages of the five most frequent DPF types for the complete range of normalized radicands.

Among our 13 differential principal factorization types, type with 3-dimensional absolute principal factorization, , is clearly dominating with more than one third (36%) of all occurrences in the complete range, followed by type with 2-dimensional absolute principal factorization, , which covers nearly one quarter (23%) of all cases. The third place (nearly 18%) is occupied by type with mixed absolute and intermediate principal factorization, ,.

It is striking that type with 2-dimensional relative principal factorization, , and type with 2-dimensional intermediate principal factorization, , are populated rather sparsely, in favour of a remarkable contribution by type with mixed intermediate and relative principal factorization, (place four with 8%).

The appearance of the four types with norm representation, , of the primitive fifth root of unity is marginal ( [6] Thm. 8.2), in spite of the parametrized contribution by all prime conductors to type, as we shall prove in Theorem 4.1 (1) in §4.3.

4.2. Similarity Classes and Prototypes

In [7] , we came to the conviction that for deeper insight into the arithmetical structure of the fields under investigation, the prime factorization of the class field theoretic conductor f of the abelian extension N/K over the cyclotomic field and the primary invariants of all involved 5-class groups must be taken in consideration. These ideas were inspired by [16] [17] and have lead to the concept of similarity classes and representative prototypes, which refines the differential principal factorization (DPF) types

Let t be the number of primes distinct from 5 which divide the conductor f. Among these prime numbers, we separately count free primes, restrictive primes, 2-split primes, and 4-split primes. The multiplicity is given in terms of, according to §2, and the dimensions of various spaces of primitive ambiguous ideals over the finite field are given in terms of

, according to [6] §4. By we denote the fundamental unit

of. The dimensions of the spaces of absolute, intermediate and relative DPF over are denoted by A, I and R, identical with the additive (logarithmic) version in ( [6] Thm. 6.1). Further, let be the maximal real intermediate field of N/L, and denote by the subgroup of the unit group of generated by the units of all conjugate fields of and of, where is a primitive fifth root of unity. For a number field F, let be the 5-valuation of the class number of F.

Definition 4.1 A set of normalized fifth power free radicands is called a similarity class if the associated pure quintic fields share the following common multiplets of invariants:

• the refined Dedekind species, where

(4.1)

• the differential principal factorization type, where

(4.2)

• the structure of the 5-class groups, where

(4.3)

Warning 4.1 To reduce the number of invariants, we abstain from defining additional counters and for free splitting prime divisors of the conductor f. However, we point out that occasionally a similarity class in the sense of Definition 4.1 will be split in two separate classes, having the same invariants, but distinct contributions to the counters u and, resp.. For instance, the similarity classes [77] and [202] with and share identical multiplets of invariants (species 1b), (type), and. But and are due to 7, and are due to 11, in the former case, whereas and are due to 2, and are due to 101, in the latter case. Therefore, the contributions by primes congruent to will be indicated by writing and, resp..

We also emphasize that in the rare cases of non-elementary 5-class groups, the actual structures (abelian type invariants) of the 5-class groups will be taken into account, and not only the 5-valuations.

Definition 4.2 The minimal element of a similarity class (with respect to the natural order of positive integers) is called the representative prototype of the class, which is denoted by writing its prototype in square brackets.

The remaining elements of a similarity class, which are bigger than the prototype, only reproduce the arithmetical invariants of the prototype and do not provide any additional information, exept possibly about other primary components of the class groups, that is the structure of ℓ-class groups of the fields for.

Whereas there are only 13 DPF types of pure quintic fields, the number of similarity classes is obviously infinite, since firstly the number t of primes dividing the conductor is unbounded and secondly the number of states, defined by the triplet of 5-valuations of class numbers, is also unlimited.

Given a fixed refined Dedekind species, the set of all associated normalized fifth power free radicands D usually splits into several similarity classes defined by distinct DPF types (type splitting). Occasionally it even splits further into different structures of 5-class groups, called states, with increasing complexity of abelian type invariants (state splitting).

The 134 prototypes of pure quintic fields are listed in the Tables 27-30. By we denote the number of elements of the similarity class defined by the prototype, truncated at the upper bound of our systematic investigations.

4.3. General Theorems on DPF Types and Polya Fields

There is only a single finite similarity class [5] = {5}, characterized by the

exceptional number of primes dividing the conductor f (here). The invariants of this unique metacyclic Polya field N are given by

[5], species 1a, ,

type, , and. (4.4)

We conjecture that all the other similarity classes are infinite. Precisely four of them can actually be given by parametrized infinite sequences in a deterministic way aside from the intrinsic probabilistic nature of the occurrence of primes in

residue classes and of composite integers with assigned shape of prime decomposition. This was proved in ( [6] Thm. 10.1)and ( [7] Thm. 2.1).

Theorem 4.1 Each of the following infinite sequences of conductors unambiguously determines the DPF type of the pure metacyclic fields N in the associated multiplet with members.

1) with, gives rise to a singulet, , with DPF type,

2) with, , gives rise to a singulet, , with DPF type,

3) with, , gives rise to a quartet, , with homogeneous DPF type,

4) with, , gives rise to a singulet, , with DPF type.

In fact, the shape of the conductors in Theorem 4.1 does not only determine the refined Dedekind species and the DPF type, but also the structure of the 5-class groups of the fields L, M and N.

Corollary 4.1 The invariants of the similarity classes defined by the four infinite sequences of conductors in Theorem 4.1 are given as follows, in the same order:

[7], species 2, ,

type, $\left(U,\eta ,\zeta ;A,I,R\right)=\left(0,\times ,\times ;1,0,0\right)$ , and; (4.5)

[2], species 1b, ,

type, , and; (4.6)

[10], species 1a, ,

type, , and; (4.7)

[18], species 2, ,

type, , and. (4.8)

The pure metacyclic fields N associated with these four similarity classes are Polya fields.

Remark 4.1 The statements concerning 5-class groups in Corollary 4.1 were proved by Parry in ( [1] Thm. IV, p. 481), where Formula (10) gives the shape of radicands associated with the conductors in our Theorem 4.1.

Proof. (of Theorem 4.1 and Corollary 4.1) It only remains to show the claims for the composite radicands associated with conductors and. See ( [6] Thm. 10.6).

For similarity classes distinct from the four infinite classes in Theorem 4.1 we cannot provide deterministic criteria for the DPF type and for the homogeneity of multiplets with. In general, the members of a multiplet belong to distinct similarity classes, thus giving rise to heterogeneous DPF types. We explain these phenomena with the simplest cases where only two or three DPF types are involved (type splitting).

Theorem 4.2 Each of the following infinite sequences of conductors admits precisely three DPF types of the pure metacyclic fields N in the associated quartet with members.

1) with, gives rise to a quartet with possibly heterogeneous DPF type, , conjecturally always,

2) with, gives rise to a quartet with possibly heterogeneous DPF type, , conjecturally always.

Example 4.1 It is quite easy to find complete quartets, whose members are spread rather widely. The smallest quartet belonging to the first infinite sequence contains the member outside of the range of our systematic computations. We have determined its DPF type separately and thus discovered a homogeneous quartet of type. However, we cannot generally exclude the occurrence of heterogeneous quartets.

Corollary 4.2 The invariants of the similarity classes defined by the two infinite sequences of conductors in Theorem 4.2 are given as follows, in the same order. The statements concerning 5-class groups are only conjectural. Each sequence splits in two similarity classes.

The classes for are:

[35], species 1a, ,

type, , and; (4.9)

[785], species 1a, ,

type, , and. (4.10)

The classes for are:

[301], species 2, ,

type, , and; (4.11)

[749], species 2, ,

type, , and. (4.12)

All pure metacyclic fields N associated with these four similarity classes are Polya fields.

Proof. (of Theorem 4.2 and Corollary 4.2) We use, and ( [6] Thm. 6.1).

Remark 4.2. The statements on 5-class groups in Corollary 4.2 have been verified for all examples with by our computations. In particular, the occurrence of the radicands and, both with, proves the impossibility of the general claim for the two situations mentioned in ( [18] Lem. 3.3 (ii) and (iv), p. 204) and ( [15] Thm. 5 (ii) and (iv), p. 5), partially also indicated in ( [1] Thm. IV (11), p. 481).

Theorem 4.3 Each of the following infinite sequences of conductors admits precisely two DPF types of the pure metacyclic fields N in the associated hexadecuplet with members.

1) with, , both gives rise to a hexadecuplet with possibly heterogeneous DPF type, ,

2) with, , only one gives rise to a hexadecuplet with possibly heterogeneous DPF type,.

Example 4.2 It is not difficult to find complete hexadecuplets, whose members are spread rather widely. The smallest hexadecuplet

belonging to the first infinite sequence contains the members outside of the range of our systematic computations. We have determined their DPF type separately and thus discovered a heterogeneous hexadecuplet (in the same order) of type

Corollary 4.3 The invariants of the similarity classes defined by the two infinite sequences of conductors in Theorem 4.3 are given as follows, in the same order. The statements concerning 5-class groups are only conjectural. Each sequence splits into two similarity classes.

The classes for, both are:

[30], species 1a, ,

type, , and; (4.13)

[180], species 1a, ,

type, , and. (4.14)

The classes for, only one are:

[70], species 1a, ,

type, , and; (4.15)

[140], species 1a, ,

type, , and. (4.16)

Only the pure metacyclic fields N of type associated with (14) and (16) are Polya fields.

Proof. (of Theorem 4.3 and Corollary 4.3) See ( [6] Thm. 10.7).

Theorem 4.4 A pure metacyclic field with prime radicand has a prime conductor, and possesses the Polya property, regardless of its DPF type and the complexity of its 5-class group structure.

Proof. This is an immediate consequence of ( [6] Thm. 10.5 and Thm. 6.1), taking into account that we have the value for the number of primes dividing the conductor in the present situation, and thus the estimate in ( [6] Cor. 4.1) yields. For the Polya property we must have, according to ( [6] Thm. 10.5), which admits the DPF types or ( [6] Thm. 1.3 and Tbl. 1). However, DPF type is excluded by ( [6] Cor. 4.2), since the requirement cannot be fulfilled in our situation where either and for or and for.

Theorem 4.5 A pure metacyclic field with prime radicand but has a composite conductor, and the following conditions are equivalent:

1) N possesses the Polya property.

2).

3) The prime ideal with is principal.

4) N is of DPF type either or or.

Proof. This is a consequence of ( [6] Thm. 10.5 and Thm. 6.1), taking into account that the prime 5 is not included in the current definition of the counter t (with value in the present situation), and thus the estimate in ( [6] Cor. 4.1) must be replaced by. For the Polya property we must have ( [6] Thm. 10.5), which determines the DPF types or ( [6] Thm. 1.3 and Tbl. 1). However, DPF type is excluded by the prime dividing the conductor (( [6] Thm. 8.1)).

Inspired by the last two theorems, it is worth ones while to summarize, for each kind of prime radicands, what is known about the possibilities for differential principal factorizations.

Theorem 4.6 Let be a pure metacyclic field with prime radicand.

1) If with or, then N is of type.

2) If with, then N is of one of the types.

3) If with, then N is of one of the types.

4) If with but, then N is of type.

5) If with but, then N is of one of the types.

6) If with but, then N is of one of the types.

A pure metacyclic field with prime radicand can never be of any of the types.

Proof. By making use of the bounds [6] §4 for -dimensions of spaces of differential principal factors (DPF),

(4.17)

we can determine the possible DPF types of pure metacyclic fields with prime radicands. We start with a few general observations.

Firstly, if, resp., is prime, then N is of Dedekind species 2, resp. 1a, with prime power conductor, resp., and, whence and the types with are forbidden. However, if and is prime, then the congruence requirement eliminates the types, the field N is of Dedekind species 1b with composite conductor, and, whence and type with is discouraged. So, the types and are generally forbidden for prime radicands.

Secondly, for a prime radicand which splits in M, the space of radicals is a 1-dimensional subspace of absolute DPF contained in the 2-dimensional space of differential factors generated by the two prime ideals of M over D. Consequently, in this special situation there arises an additional constraint for the dimension of the space of intermediate DPF, which must be contained in the 1-dimensional complement. This generally excludes type with for prime radicands.

1) If with, then, , and thus,. These conditions eliminate the types with either or or, and only type remains admissible.

2) If with, then, , and thus, , , whence the types with either or or are excluded, and only the types remain admissible.

3) If with, then, , and thus, , , whence the types with either or are excluded, and only the types remain admissible.

4) If with but, then, , and thus,. These conditions eliminate the types with either or or, and only the types remain admissible. However, the congruence requirement modulo 25 discourages the types, and only type is possible.

5) If with but, then, , , and thus, , , whence the types with either or or are forbidden. The types are excluded by congruence conditions, and only the types remain admissible.

6) If with but then, , , and thus, , , whence the types with either or are forbidden. The types are excluded by congruence conditions, and only the types remain admissible.

Example 4.3 Concerning numerical realizations of Theorem 4.6, we refer to Corollary 4.1 for the parametrized infinite sequences [7] and [2] which realize item (1) and (4). (See also Tables 23 and 19 for the types and.) In all the other cases, there occurs type splitting:

The similarity class [149] partially realizes item (2). (See Table 38 for the type.) Outside the range of our systematic investigations, we found that the similarity class [1049] realizes type. Realizations of the type are unknown up to now.

The similarity classes [401], [151] and [101] partially realize item (3). (See Table 31, Table 32 and Table 40 for the types, and.) Outside the range of our systematic investigations, we found that the similarity class [1151], resp. [3251], realizes type, resp.. Realizations of the types and are unknown up to now.

The similarity classes [139], [19] and [379] completely realize item (5). (See Table 35, Table 38 and Table 39 for the types, and.)

The similarity classes [31], [11], [191] and [211] partially realize item (6). (See Table 31, Table 32, Table 34 and Table 37 for the types, , and.) Realizations of the types, and are unknown up to now.

4.4. Non-Elementary 5-Class Groups

Although most of the 5-class groups of pure metacyclic fields N, maximal real subfields M and pure quintic subfields L are elementary abelian, there occur sparse examples with non-elementary structure. For instance, we have only 8 occurrences within the range of our computations:

1), for (type),

2), , for prime (type),

3), for (type),

4), for (type),

5), , , for (type),

6), for (type),

7), , for (type),

8), , , for (type).

However, outside the range of systematic computations, we additionally found:

a), , , for prime (type),

b), , for prime (type),

c), , , for prime (type),

d), , , for prime (type).

We point out that in all of the last four examples, the normal field N is a Polya field, since the radicands D are primes, the conductors are primes, and thus all primitive ambiguous ideals are principal, generated by the radical and its powers. Consequently, there seems to be no upper bound for the complexity of 5-class groups of pure metacyclic Polya fields N in Theorem 4.4.

4.5. Refinement of DPF Types by Similarity Classes

Based on the definition of similarity classes and prototypes in §4.2, on the explicit listing of all prototypes in the range between 2 and 10³ in Tables 27-30, and on theoretical foundations in §4.3, we are now in the position to establish the intended refinement of our 13 differential principal factorization types into similarity classes in Tables 31-43, as far as the range of our computations for normalized radicands is concerned. The cardinalities refine the statistical evaluation in Table 26.

DPF types are characterized by the multiplet, refined Dedekind species, S, by the multiplet, and 5-class groups by the multiplet.

DPF type splits into 3 similarity classes in the ground state and 2 similarity classes in the first excited state. Summing up the partial frequencies 6+3 of these states in Table 31 yields the modest absolute frequency 9 of type in the range, as given in Table 26. The logarithmic subfield unit index of type is restricted to the single value. Type is the unique type with 2-dimensional relative principal factorization,.

The logarithmic subfield unit index of DPF type can take two values, either or. Type with splits into 5 similarity classes in the ground state and 6 similarity classes in the first excited state. Type with splits into 7 similarity classes in the ground state and 4 similarity classes in the first excited state. Summing up the partial frequencies 40 + 7, resp. 24 + 4, of these states in Table 32 yields the considerable absolute frequency 75 of type in the range, as given in Table 26. Type is the unique type with mixed intermediate and relative principal factorization,.

DPF type splits into 4 similarity classes in the ground state and 1 similarity class in the first excited state. Summing up the partial frequencies 7 + 1 of these states in Table 33 yields the modest absolute frequency 8 of type in the range, as given in Table 26. The logarithmic subfield unit index of type is restricted to the unique value. Type is the unique type with 2-dimensional intermediate principal factorization,.

The logarithmic subfield unit index of DPF type can take two values, either or. Type with consists of 3 similarity classes in the ground state. Type with splits into 5 similarity classes in the ground state and 2 similarity classes in the first excited state. Summing up the partial frequencies 9, resp. 12 + 2, of these states in Table 34 yields the modest absolute frequency 23 of type in the range, as given in Table 26. Type is the unique type with mixed absolute and relative principal factorization, and.

DPF type splits into 16 similarity classes in the ground state and 9 similarity classes in the first excited state. Summing up the partial frequencies 146 + 15 of these states in Table 35 yields the high absolute frequency 161 of type in the range, as given in Table 26. The logarithmic subfield unit index of type is restricted to the unique value. Type is the unique type with mixed absolute and intermediate principal factorization, and.

DPF type splits into 6 similarity classes in the ground state , 16 similarity classes in the first excited state , and 5 similarity classes in the second excited state . Summing up the partial frequencies 188+128+8 of these states in Table 36 yields the maximal absolute frequency 324 of type among all 13 types in the range , as given in Table 26. The logarithmic subfield subfield unit index of type is restricted to the unique value . Type is the unique type with 3-dimensional absolute principal factorization,. However, the 1-dimensional subspace is formed by radicals, and only the complementary 2-dimensional subspace is non-trivial.

The logarithmic subfield unit index of DPF type can take two values, either or. Type with splits into 2 similarity classes in the ground state. Type with consists of 1 similarity class in the ground state. Summing up the partial frequencies 6+1 of these states in Table 37 yields the modest absolute frequency 7 of type in the range, as given in Table 26. Type is a type with 1-dimensional relative principal factorization,.

DPF type splits into 4 similarity classes in the ground state and 1 similarity class in the first excited state. Summing up the partial frequencies 52+1 of these states in Table 38 yields the considerable absolute frequency 53 of type in the range, as given in Table 26. The logarithmic subfield unit index of type is restricted to the unique value. Type is a type with 1-dimensional intermediate principal factorization,.

DPF type splits into 3 similarity classes in the ground state, 16 similarity classes in the first excited state, and 3 similarity classes in the second excited state. Summing up the partial frequencies 139+61+8 of these states in Table 39 yields the high absolute frequency 208 of type in the range, as given in Table 26. The logarithmic subfield unit index of type is restricted to the unique value. Type is a type with 2-dimensional absolute principal factorization,.

The logarithmic subfield unit index of DPF type is restricted to the unique value. Type consists of 1 similarity class in the ground state. The frequency 1 of this state in Table 40 coincides with the negligible absolute frequency 1 of type in the range, as given in Table 26. Type is a type with 1-dimensional relative principal factorization,.

DPF type consists of 3 similarity classes. The modest absolute frequency 5 of type in the range, given in Table 26, is the sum 2+1+2 of partial frequencies in Table 41. Type only occurs with logarithmic subfield

unit index. It is a type with 1-dimensional intermediate principal factorization,.

DPF type splits in 2 similarity classes, [35] and [301]. The modest absolute frequency 7 of type in the range, given in Table 26, is the sum 6+1 of partial frequencies in Table 42. Type only occurs with logarithmic subfield unit index. It is a type with 2-dimensional absolute principal factorization,. However, it should be pointed out that outside of the range of our systematic investigations we found an excited state for the similarity class [1505], where has three prime divisors, additionally to the ground state .

DPF type splits into the unique finite similarity class [5] with only a single element and the infinite parametrized sequence [7] consisting of all prime radicands congruent to . The small absolute frequency 19 of type in the range , given in Table 26, is the sum in Table 43. Since no theoretical argument disables the occurrence of type for composite radicands D with prime factors 5 and, we conjecture that such cases will appear in bigger ranges with. Type only occurs with logarithmic subfield unit index, and is the unique type where every unit of K occurs as norm of a unit of N, that is.

4.6. Increasing Dominance of DPF Type for

In this final section, we want to show that the careful book keeping of similarity classes with representative prototypes in Tables 31-43 is useful for the quantitative illumination of many other phenomena. For an explanation, we select the phenomenon of absolute principal factorizations.

The statistical distribution of DPF types in Table 26 has proved that type with 324 occurrences, that is 36%, among all 900 fields with normalized radicands in the range is doubtlessly the high champion of all DPF types. This means that there is a clear trend towards the maximal possible extent of 3-dimensional spaces of absolute principal factorizations, , in spite of the disadvantage that the estimate in the formulas (4.3) and (4.4) of ( [6] Cor. 4.1) prohibits type for conductors f with prime divisors.

For the following investigation, we have to recall that the number T of all prime factors of is given by for fields of Dedekind’s species 1, where, and by for fields of Dedekind’s species 2, where.

Conductors f with prime factors occur in six tables,

1 case of type in a single similarity class of Table 32,

1 case of type in a single similarity class of Table 33,

7 cases of type in a single similarity class of Table 34,

10 cases of type in 5 similarity classes of Table 35,

126 cases of type in 16 similarity classes of Table 36,

8 cases of type in 3 similarity classes of Table 39,

that is, a total of 153 cases, with respect to the complete range of our computations. Consequently, we have an increase of type from 36.0%,

with respect to the entire database, to, with respect to.

The feature is even aggravated for conductors f with prime factors, which exclusively occur in Table 36. There are 4 similarity classes with, namely [462], [546], [798], [858], with a total of 6 elements, all (100%) with associated fields of type.

5. Conclusions

In this paper, it was our intention to realize Parry’s suggestion ( [1] p. 484) concerning a numerical investigation of pure quintic number fields. For this purpose, we first developed theoretical foundations in a series of preparatory papers [6] [7] [8] [9] which expand the original germs in [12] . Since the non-Galois fields L do not contain the full wealth of arithmetical structures, we had to consider their pure metacyclic normal closures of degree 20.

On the one hand, this enabled us to use the Galois cohomology of the unit group U_N with respect to the relative automorphism group over the cyclotomic field for defining 13 exhaustive and mutually exclusive differential principal factorization (DPF) types (Table 4 in §3.1), based on the unit norm index, where, which is connected with the order of the group of primitive ambiguous principal ideals via the Takagi/Hasse/Iwasawa-Theorem on the Herbrand quotient of U_N, and on a natural decomposition into the dimensions of the -vector spaces of absolute, intermediate and relative differential principal factors ( [6] , eqn. (6.3)).

On the other hand, our theory of the relatively cyclic quintic Kummer extension N/K as a 5-ring class field modulo the conductor over K admitted the calculation of the multiplicity of the conductor f (§2), which is the number of non-isomorphic pure metacyclic fields N sharing the common conductor f and forming a multiplet [8] .

Equipped with this theoretical background, we were able to develop our Classification Algorithm 3.1 in §3.2, and to prove that it determines the DPF type of L and N in finitely many steps. It also decides whether the normal field N is a Polya field or not. (It is known that L is a (trivial!) Polya field if and only if it possesses class number [6] .)

The algorithm was implemented as a Magma program script [3] [4] [5] and applied to the 900 fields N with normalized fifth power free radicands in the range, after some preliminary experiments with Pari/GP [2] . The result is documented in the twenty Tables 6-25 of §3.4. It is in perfect accordance with our theoretical predictions in 1991 [12] . Actually, each type occurs indeed, the most hardboiled type not earlier than for the radicand, and it is interesting to study the statistical distribution of the types in §4.1, Table 6. Concerning the reliability of our extensive database, and for understanding the degree of precision contained in our paper, we point out that all tables have been thoroughly double checked with respect to misprints and copy-paste errors for at least three times.

Nevertheless, after the completion of the statistics in §4, we came to the conviction that for deeper insight into the arithmetical structure of pure metacyclic fields N, the prime factorization of the class field theoretic conductor f of the abelian extension N/K (invariants) and the primary invariants of all involved 5-class groups, partially given by the 5-valuations, should be taken in consideration. In the last section, we present a corresponding refinement of the DPF types in similarity classes (§4.2), which is very useful for various applications. It reduces the number 900 of investigated radicands to 134 representative prototypes (§4.5). The remaining 766 radicands, which are bigger than the prototype of their similarity class, only reproduce the arithmetical invariants of the prototype and do not provide any additional relevant information. The rare phenomenon of non-elementary 5-class groups is documented in §4.4. Theorems on DPF-types of members of multiplets are proved in §4.3, and the striking dominance of type with 3-dimensional (maximal) absolute principal factorization for radicands with three and more prime divisors is presented and discussed in §4.6.

Acknowledgements

We gratefully acknowledge that our research was supported by the Austrian Science Fund (FWF): project P 26008-N25. This work is dedicated to the memory of Charles J. Parry († 25 December 2010) who suggested a numerical investigation of pure quintic number fields. We are indebted to the anonymous referees for valuable suggestions concerning an improvement of the paper’s layout.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Parry, C.J. (1975) Class Number Relations in Pure Quintic Fields. Symposia Mathematica, 15, 475-485.
[2]	PARI Developer Group (2018) PARI/GP, Version 64 bit 2.11.1, Bordeaux. http://pari.math.u-bordeaux.fr
[3]	Bosma, W., Cannon, J. and Playoust, C. (1997) The Magma Algebra System. I. The User Language. Journal of Symbolic Computation, 24, 235-265. https://doi.org/10.1006/jsco.1996.0125
[4]	Bosma, W., Cannon, J.J., Fieker, C. and Steels, A., Eds. (2018) Handbook of Magma functions. Edition 2.24, Sydney.
[5]	MAGMA Developer Group (2018) MAGMA Computational Algebra System. Version 2.24-3, Sydney. http://magma.maths.usyd.edu.au
[6]	Mayer, D.C. (2018) Differential Principal Factors and Polya Property of Pure Metacyclic Fields. Accepted by Int. J. Number Theory. arXiv:1812.02436v1 [math.NT]
[7]	Mayer, D.C. (2018) Similarity Classes and Prototypes of Pure Metacyclic Fields. Preprint.
[8]	Mayer, D.C. (2018) Homogeneous Multiplets of Pure Metacyclic Fields. Preprint.
[9]	Mayer, D.C. (2018) Coarse Cohomology Types of Pure Metacyclic Fields. arXiv:1812.09854v1 [math.NT]
[10]	Barrucand, P. and Cohn, H. (1970) A Rational Genus, Class Number Divisibility, and Unit Theory for Pure Cubic Fields. Journal of Number Theory, 2, 7-21. https://doi.org/10.1016/0022-314X(70)90003-X
[11]	Barrucand, P. and Cohn, H. (1971) Remarks on Principal Factors in a Relative Cubic Field. Journal of Number Theory, 3, 226-239. https://doi.org/10.1016/0022-314X(71)90040-0
[12]	Mayer, D.C. (1991) Classification of Dihedral Fields. Preprint, Department of Computer Science, University of Manitoba, Manitoba.
[13]	Mayer, D.C. (1993) Discriminants of Metacyclic Fields. Canadian Mathematical Bulletin, 36, 103-107. https://doi.org/10.4153/CMB-1993-015-x
[14]	Kobayashi, H. (2016) Class Numbers of Pure Quintic Fields. Journal of Number Theory, 160, 463-477. https://doi.org/10.1016/j.jnt.2015.09.017
[15]	Kobayashi, H. (2016) Class Numbers of Pure Quintic Fields. Ph.D. Thesis, Osaka University Knowledge Archive (OUKA).
[16]	Aouissi, S., Mayer, D.C., Ismaili, M.C., Talbi, M. and Azizi, A. (2018) 3-Rank of Ambiguous Class Groups in Cubic Kummer Extensions. arXiv:1804.00767v4 [math.NT]
[17]	Aouissi, S., Mayer, D.C. and Ismaili, M.C. (2018) Structure of Relative Genus Fields of Cubic Kummer Extensions. arXiv:1808.04678v1 [math.NT]
[18]	Iimura, K. (1977) A Criterion for the Class Number of a Pure Quintic Field to Be Divisible by 5. Journal für die Reine und Angewandte Mathematik, 292, 201-210.