Vladimir Leontiev¹, Garib Movsisyan², Arthur Osipyan¹, Zhirayr Margaryan^3
1Moscow State University, Moscow, Russia.
²BIT Group, Moscow, Russia.
³Yerevan State University, Yerevan, Armenia.
DOI: 10.4236/jis.2014.54017   PDF    HTML     2,826 Downloads   3,950 Views   Citations

Abstract

The notion of a communication channel is one of the key notions in information theory but like the notion “information” it has not any general mathematical definition. The existing examples of the communication channels: the Gaussian ones; the binary symmetric ones; the ones with symbol drop-out and drop-in; the ones with error packets etc., characterize the distortions which take place in information conducted through the corresponding channel.

Keywords

Additive Communication Channel, Error, Matrix Channel, Neighborhood, Correcting Code, Alphabet

Share and Cite:

1. Introduction

We confine our discussion to the following situation.

Let 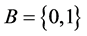be a binary alphabet and be the set of all words with finite length in the alphabet,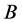. We take the dictionary function as the following partial mapping:

.

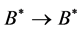Saying a communication channel, we mean an arbitrary multi-valued mapping, having the following form:

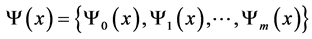, (1)

where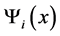, 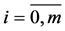is some dictionary function.

As to the content, equality (1) means that when the word 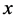is transferred we have one of the words 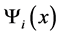at the exit.

Below we take 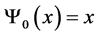without any loss of generality.

We denote the set of all binary words with the length 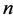by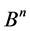; below the terms, “a word”and “a Boolean vector”are synonyms.

Example.

1) Mapping (1) is called a standard communication channel if it has a limited number of distortions of the form: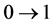, , where

.

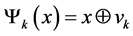Besides, we say that there are no more than errors in the channel if does not exceed. (Here is Hamming weight of the word). On the other hand, the following holds:

,

where is the cardinality of the sphere with the radius in.

The notion of the code that corrects the errors of the channel is completely analogous to the classic definition of the code, correcting the distortions of the form:,.

Definition 1. The code corrects the errors of the channel:

, if the following is valid:

(2)

for,;,.

Condition (2) means that consequences of errors are different; hence we can restore one to one the initial information at the exit. The decision process at the exit usually is formalized in the form of the “decoding table” [1] :

Error “correction” through the table takes place as follows. According to definition, every “transferred” word is transformed by the channel into, which is at least in one of the columns of the table.

Then the code vector in the first row of any row is the “prototype” of the transferred word.

It is clear that if the word belongs to the only one of the columns in the table, then the “decoding” process leads to a right result.

Condition (2) can be formulated in a little different way using the notion of “neighborhood” which gives certain advantage when making estimates of the cardinality of the correcting code.

The neighborhood of the th order of the word built up with respect to the set:

,

Is formed by the following induction:

(3)

Condition (3) shows that the neighborhood of the th order of the word is the union of the neighborhood of the 1st order of all words belonging to the neighborhood of the th order of the word.

In the term of the neighborhood condition (2) of error correction takes the following form:

(4)

We denote by the code correcting the errors of the channel.

In the terms of the above introduced notions for the given channel the problem is to build the code of the maximum cardinality.

It is obvious that this cardinality depends on the “structure” of.

Among the codes the so called perfect codes are of special interest.

Definition 2. The code is called perfect if:

Definition 3 [2] . The channel is called algebraic if:

, for all.

Assume that for all, that if then

We consider the graph, adjacency of the vertices are defined as follows. The vertices are adjacent iff there exists a satisfying the condition or. The distance on the graph between any vertices is the minimum number of the arcs in the chain connecting the vertices and the infinity if there does not exist such a chain.

It is not difficult to prove the following condition. In the graph the distance between any two vertices from no less than three it is necessary and sufficient that be an error correcting code of the algebraic channel.

Further we discuss a special but having certain interest type of communication channel which is carried out by linear mappings,.

2. Matrix Channels [3]

Let be a finite field of two elements and be the set of matrices of the order with the elements belonging to the field with the usual operations of addition and multiplication for. If

then the set, defines a matrix channel in the sense of (1):

.

Examples.

2) Let such “errors” take place in a “real” channel, which are connected with wrong reading of adjacent letters of the transferred vector,; and this means the following transformation:

.

This situation can be modelized by the matrix channel where is the unit matrix:

Indeed, when transferring through the channel we have a vector of the following form at the exit:

,

where.

3) if a “drop-out” of symbols takes place in the channel, i.e. the length of the word is changed, then it can be presented in the matrix form as follows. Let is the initial word in which just one symbol can be lost. We discuss the following set of matrices belonging to:

Then:

.

The notion of the code that corrects the errors of the matrix channel M is completely analogous to the classic definition of the code, correcting the distortions of the form:,.

Definition 4. The code corrects the errors of the channel

if the following condition is valid:

for all,; and,.

The neighborhood of the th order of the word built with respect to the set, is defined as in (3):

.

In the terms of neighborhood the error correction condition becomes as follows:

.

3. The Group Matrix Channels

Let be the group of the non-degenerated matrices of the order on the field and be the subgroup of. We discuss the matrix channel generated by the subgroup:

,

where is a divisor of the number:

We can consider that the group, operates in the set, as follows:

, where,.

Moreover, the transitive set:

,

coincides with the neighborhood of the first order of the point, i.e..

These neighborhoods do not intersect and thus, form the partition. Consequently, if we take an arbitrary representative from each transitive set, we will have a code, correcting the errors of the group channel,.

Lemma 1. For the group matrix channel, any code containing one representative of all transitive sets, is a code with the maximum cardinality, correcting the errors of the channel.

Proof. As it was mentioned, the code, built as it was said above, corrects the errors of the matrix channel,. On the other hand, if some code correcting the errors of the group channel contains more points that the number of the transitive sets then at least one of these transitive sets contains two points of which contradicts condition (4). Q. E. D.

The above Lemma completely describes all the codes of the maximum cardinality, correcting the errors of the group channel.

The cardinality of the neighborhood of an arbitrary point can be calculated by thestabilizer of the same point or of the subgroup:

.

In other words, the following formula is valid:

.

The cardinality of the code can be expressed by Burnside’s Lemma [4] [5] .

Let be the set of the motionless points of the transformation or in another way (which is the same) let it be the set of the eigen vectors of the matrix corresponding the eigen value, that is, let it be the set of the solutions of the following equation:

.

Lemma (Burnside’s) 2. The following formula holds true:

(5)

Examples.

4) Let be the transformation of the cyclic shift in:

,

and be the matrix, corresponding to this transformation:

.

We discuss the group matrix channel. According to the definition, this channel operates as follows. If the word is put in then we get one of the cyclic shifts of this word at the exit. We call the positive integer the period of the word if is the smallest integer for which. Then the neighborhood of the first order of the word has the following form:

.

It is clear that the first order neighborhoods carry out a partitioning of into classes of equivalence. If is the number of the equivalence classes the elements of which have the period d then the following obviously holds:

(6)

Let us note that the maximum cardinality code is any set of the representatives of the transitive sets and its cardinality is given by Formula (5) which has the following form for this case:

(7)

Through the standard calculation technique, we get from (6) and (7) the well-known expression:

where is Euler’s function which gives the amount of the numbers less than and which are coprime with respect to it.

In particular, if is a prime number, then:

.

5) Let there be a communication channel through which the transmitted word:

,

is transformed into the binary word:

,

where either, and, or, for.

Let us describe the physical meaning of this channel. Saying “transmittance of the word x through the communication channel” we understand successive transmittance of symbols or, as they say, transmittance of the pulses (signals), taking into account that the symbols with the odd indices are transmitted without any distortion, and the rest of them:, can have distortions defined by the directly preceding symbols.

Thus, having the symbol at the exit, we can get either or.

Now we give this description of the channel by the matrix “language”. Let we have the set of the matrices where is the unit matrix:

We discuss the group matrix channel the constituent of which is the set. As any matrix of coin-

cides with its inverse matrix in the group, i.e., then, , and is consisted of all possible products of the matrices of; therefore, the

order of the group is. It follows from the description of the channel that the code, correcting its errors, also corrects the errors of the channel with overlay. The converse proposition also is true.

Let us partition the group into the non-intersecting sets, where and be the set of the matrices generated the products of any i different elements, belonging to M\{M₀}, i.e. the matrix if, where,.

Talking figuratively if we enumerate the matrix rows of the group from the top to the bottom, then the set, is consisted of all matrices having the dimension and which have two units in their -th rows with odd numbers on their diagonal positions and immediately on the right, but in the rows numbered by the unit is only in a diagonal position. The other elements of the matrices are zero.

It immediately follows from the definition of the set that, and for any matrix the number of the motionless points of the transformation is:

As we have:

,

then it follows from Lemma 2 that for the maximum cardinality code the following holds true:

Let us discuss Example 5 for, i.e. that there is a word which can be transformed into one of the words:

,

when transmitted through the channel. For the given case the set of the matrices is the following:

.

The group channel having the set as its constituent is consisted of the following matrices:

Let us find the set of the motionless points of the transformation for each element of the group. As it was said above the set of the solutions of the equation:

(8)

corresponds to the set,. For the matrix Equation (8) is as follows:

,

and the set of solutions of it is the set. Consequently,.

Then, from (8) for the cases:, , , we find for the respective sets of the solutions:

And, applying Lemma 2 we get the cardinality of the code:

6) Let us discuss a little modified channel of Example 2. Namely, we take that when transmitting the vector some “transposition” errors of the following form take place:

,

taking into account that such inversions can take place in a few places.

In the terms of matrix channels the model is as follows. We have the set of the matrices, where is the unit matrix:

.

Considerations analogous in the preceding example let us establish the following facts. The matrix channel consisting of all possible products of the elements of the set is a group one. Besides the order of the group is and the code, correcting the errors of the channel also corrects the errors of the channel with the transpositions. Then, following the same logic and, using Formula (5) for the maximum cardinality code we get:

.

4. The Metrics and Codes in the Additive Channel

Definition 5 (See [6] ). The arbitrary subset that carries out the function , where is called additive channel. Here.

Definition 6 (See [7] ). The code corrects the errors of the additive channel if where, , , ,.

As in the preceding section we define the neighborhood of -th order of the word as follows:

.

NB 1. For the additive channel the following equality holts true:

,

For any,

Definition 7. (See [8] [9] ) The code correcting the errors of the additive channel is called perfect if:

Note that the perfect code has maximum cardinality though the convers statement is not always valid.

NB 2. Any word from belongs to the neighborhood of the first order of only one word of the perfect code

The standard and most used metric in code theory is Hamming’s metric [9] , i.e. the following function:

.

It can be taken that this metric is connected with the “natural” basis in the following way:

.

It is clear that if another basis is chosen, for instance, if is taken, then another metric will be generated:

.

A more general procedure of metric generation shown above is as follows. For the given subset and the vector we consider all “expansions” of into, i.e. the expression of the following form:

(9)

and we put the following number:

,

into correspondence to (9).

Now choosing the least number of these we define the following norm ( [1] ; the MLM norm) connected with:

(10)

Lemma 3. The function is a metric (below, “MLM metric”) for any subset.

In terms of graph theory the described situation is as follows. Let us give the following binary relation on the set of vertices:

for some.

This relation defines adjacency of vertices and we get a graph, i.e. the set of arcs, which is given by the equality:.

The distance among the vertices of this graph is given in the standard way: the minimum number of the arcs in the chain connecting these vertices; and the infinity if there is not such a chain.

Example.

7) If then the MLM norm has the following form:

.

In particular, for the MLM norms of the vectors in are as follow:

If is an arbitrary additive channel then the set generates an MLM norm in given by Formula (10). The statement presented below shows that the ability of the code to correct the errors of the additive channel can be formulated in terms of the MLM norm generated by the set.

Lemma 4. The code corrects the errors of the additive channel iff the following conditions hold:

, for.

Proof: If, then according to definition:

,

or in another way:

(11)

But it follows from (11) that the code does not correct the errors of the additive channel.

And if, then:

,

where. But the equality:

,

is impossible; hence, the code corrects the errors of the additive channel.

Let us discuss an arbitrary basis of the space and the linear reversible transformation defined in the following way:

The image of any set is denoted by

, and,

and the spectra and, have no any simple connec-

tion. The situation will be changed to an extent if we consider different MLM norms and introduce limitations on the subject transformations.

Definition 8. The MLM metric is called a basis one if is a basis.

Lemma 5. For the basis MLM metrics and the following relations hold true:

(12)

where,.

For the given MLM metric all the standard definitions of the correcting code theory can be modified replacing Hamming’s metric by any basis MLM metric. In particular, the perfect code with the distance is a partition of the set in the union of the spheres of the radius in the MLM metric. According to (12) the perfect codes in one metric are transformed into perfect codes in another metric. Besides Formulas (12) allow various interpretations of geometrical character. We present two facts which we use further.

Lemma 6.

a) The subset, with the metric and the subset with the basis metric simultaneously are spheres with the radius.

b) The code with the basis metric and the code with the basis metric simultaneously are perfect with the distance.

Example.

9) We discuss in the perfect code in Hamming’s metric, with the distance. When choosing the basis the image of this perfect code in the transformation is the following code where is the matrix with the following vectors of the set as its rows:

.

Then the spheres with the unit radius having their centres at the points of the code have the following forms:

,

.

(See example 7). Thus is a perfect code with the distance 3 in the MLM metric:

.

Though the metrics with different bases can strongly differ the spectrum of distances of the space is always the same.

Lemma 7. Let be the number of the points from with. Then, for an arbitrary basis.

Proof. According to the definition, is the number of the vectors of the basis included into the expansion of the vector x:

.

Therefore, the number of the vectors with is equal to the number of the solutions of the following equation:

,

where, i.e. it is equal to.

NB 3. If the basis is chosen as in Example 7 then the preceding statement is equivalent to the following formula:

.

The preceding statements make possible to build the perfect codes in for arbitrary basis metrics if one such code is already built for one basis metric at least. In particular, if is the basis for the subspace then the following statement holds true:

Theorem 1. The perfect codes in, correcting the errors of the additive channel for, exist only for the following values of m and:

a),

b).

Proof. We discuss the basis of the space where, and the linear reversible transformation, is defined above.

Necessity. Let be a perfect code in with the basis metric.

It follows from Lemma 6 that the code also is perfect in with the basis metric, correcting the errors of the channel Then as and for holds the following:, and we have:

Taking this and NB 1 and 2 into account we see that the code:

,

is perfect in and it corrects the errors of the channel:

,

with the basis metric. It is possible only for or, [9] .

Sufficiency. We discuss the perfect code where for, (Hamming’s code) or, (Gallаy’s code) [10] .

Now, as for any the following inequality holds true:

,

then it follows from Lemma 4 that the code corrects the errors of the channel:

On the other hand, we have:

,

i.e. is perfect in with the basis metric and consequently (according to Lemma 6 the code is perfect in with the basis metric. Q. E. D.

5. The Upper and Lower Limits of the Cardinality of the Matrix Channel

The case of an arbitrary cannel does not make possible to obtain simple solutions for the code cardinality and even to obtain some universal Hamming and Varshamov-Gilbert type boundaries and requires some special restrictions on the structure for the matrix channel.

Let the channel is algebraic, i.e. all the matrices in are reversible and belong to with their reverse ones. We introduce two parameters connected with. Let:

,

.

Lemma 8. The following inequalities hold true:

(13)

here is a matrix algebraic channel.

We consider the matrix channel from Example 2. This channel exchanges the places of two neighboring letters in the word.

Let where, , for. We denote the number of the sequences of the word, by. Then and.

If then. Consequently:

.

As is the neighborhood of the first order of the word then all the words obtained from by transposition of the neighboring letter are included into. Every one of these words has no more than sequences and the number of such words exactly equals to. It follows from this that:

,

and, according to Lemma 8 universal limitations (13) have the form:

.

Roughness of these limits is connected with the great generality of the above considerations.

Below we present more accurate limits, taking the specification of the matrix channel into account.

6. The Upper Limit for

We partition into the two subsets and such that the first one includes the words with their sequence number not exceeding and the second one includes those exceeding. Then we have:

and

(14)

The first inequality follows from the fact that the number of the words in having exactly sequences

equals to see [2] ), and the second one results in the fact that the cardinality of the neighborhood of

the first order of the word equals to the number of the sequences of. We choose the parameter such that to minimize the upper limit. Then we have from (14) for

.

Choosing and applying Sterling’s formula for [2] :

we get:

.

7. The Lower Limit for

We discuss the following additive channel This channel corresponds to that

essential situation when the errors rise in pairs and in neighboring places. The connection of this channel with the matrix channel is explained by the following statement.

Lemma 9. Every code that corrects the errors of the additive channel also corrects the errors of the matrix channel.

Proof: We assume that the code corrects the errors of the channel:

,

and that there exist the matrices:

such that for some, takes place the equality:

.

Hence we have:

,

where,. Then taking into account that we get:

or

Consequently, the following variants are possible:

a) and.

Then the following equality takes place:

,

which is a contradiction.

If:

b) and,

c) and,

then the following equalities take place, respectively:

which also contradict the conditions of the Lemma. Q. E. D..

It follows from Lemma 9 that the maximum cardinality of the code, correcting the errors of the channel is

the lower estimation for the cardinality, i.e.. Taking into account Theorem 1 we get the lower estimation of for:

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Leontiev, V.K., Movsisyan, G.L. and Margaryan, J.G. (2012) Geometry of the Additive Channel. Reports at NAS, 112, 7-18.
[2]	Leontiev, V.K. and Movsisyan, G.L. (2007) Algebraic Communication Channels. The First International Algebra and Geometry Conference, Yerevan, 16-20 May 2007, 16-20.
[3]	Leontiev, V.K., Movsisyan, G.L. and Osipyan, A.A. (2012) Matrix Communication Channels. Materials of the XI International Seminar Discrete Mathematics and Its Application, Moscow State University, 415-416.
[4]	Sachkow, W.N. (1977) Combinatoric Methods of Descret Mathematics. Nauka, Moscow.
[5]	Lang, S. (1968) Algebra. Mir, Moscow.
[6]	Deza, M.E. (1964) On Correction of Arbitrary Noise and on Worst Noise. Theory of Information Communication, Moscow, 26-31.
[7]	Leontiev, V.K., Movsisyan, G.L. and Margaryan, J.G. (2004) On the Additive Communication Channel. Reports at NAS, 104, 23-27.
[8]	Leontiev, V.K., Movsisyan, G.L. and Margaryan, J.G. (2008) On Perfect Codes in Additive Channels. Information Transfer Problems, 44, 12-19.
[9]	Leontiev, V.K., Movsisyan, G.L. and Margaryan, J.G. (2006) Perfect Codes in Additive Channels. Reports at RAS, 411, 306-309.
[10]	Mac Williams, F.J. and Sloane, N.J.A. (1979) The Theory of Error-Correcting Codes. Svjaz, Moscow.