Computational Methods in the Theory of Synthesis of Radio and Acoustic Radiating Systems ()
1. Introduction
In many practical applications at the optimal design of various types of radio and acoustic radiating systems the requirements are only to the energy characteristics of the directivity of the radiated field (amplitude directivity pattern (DP) or DP by the power). Therefore there is a need to approximate real finite functions by modules of onedimensional or two-dimensional and discrete Fourier transform dependent on the real physical parameters. At the same time the absence of requirements to phase characteristics of field is used to improve the quality of approximation of synthesized DP to given.
Later on the variational formulations of different types of inverse problems in mean-square approach, which in further are reduced to investigation and numerical solution of one-dimensional or two-dimensional nonlinear integral equations of the Hammerstein type with separate module and argument of desired complex-valued function, are considered. Nonuniqueness and branching (or bifurcation) of solutions dependent on the change of the physical parameters characterizing the radiating system are characteristic features of such equations. Problems on finding the set of branching points (bifurcation) are not investigated nonlinear one-parameter or two-parameter spectral problems.
The existence of connected components of the spectrum, which in the case of real parameters are of spectral lines, is essential difference between the two-dimensional and one-dimensional spectral problems. The problem on finding the spectral lines is reduced to numerical solution of the Cauchy problem for an ordinary differential equation of the first order.
The degenerate of kernels in linear operators of the Hammerstein type equations is feature of the synthesis problems of antenna arrays. It allows to reduce nonlinear two-parameter spectral problems on finding the set of branching points of solutions to the corresponding systems of linear algebraic equations with nonlinear occurrence of the spectral parameters in the coefficients of system.
In the basis of construction of numerical algorithms for finding the optimal solutions are taken such princeples: localization of existing solutions dependent on the value of the physical parameters of the problem by means the use of numerical methods of solving the non-linear one-parameter and two-parametric spectral problems, and methods of the branching theory of solutions—construction and justification of the convergence of iterative processes for numerical finding the various types of existing solutions of basic equations (equations of Hammerstein type)—analysis of the effectiveness of found solutions.
2. Formulation of Problems. Basic Equations of Synthesis
In general case, the analysis problems (direct problems) of radio (or acoustic) radiating systems are reduced to solution the corresponding boundary problems of electrodynamics (acoustic) at a given excitation sources of fields [1-4] on the basis of Maxwell’s equations (wave equation). The directivity pattern  is one of the basic characteristics of the emitted field on large distances from the radiating system. It describes the properties of the field in space dependent on the angular coordinates of a spherical coordinate system. In general case, the DP
is one of the basic characteristics of the emitted field on large distances from the radiating system. It describes the properties of the field in space dependent on the angular coordinates of a spherical coordinate system. In general case, the DP  is a vector of complex-valued function which has the form [5,6]
is a vector of complex-valued function which has the form [5,6]
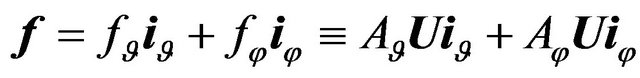 . (1)
. (1)
Here 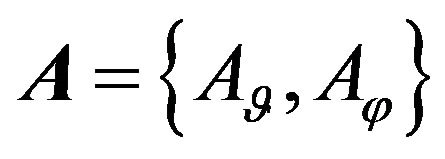 is linear operator acting from some functional Hilbert space
is linear operator acting from some functional Hilbert space  (the space of square integrable functions in the domain
(the space of square integrable functions in the domain , describing the distribution of extraneous fields (currents)
, describing the distribution of extraneous fields (currents)  in volume
in volume ) into the space of complex-valued continuous functions
) into the space of complex-valued continuous functions 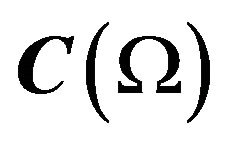 defined in some domain
defined in some domain 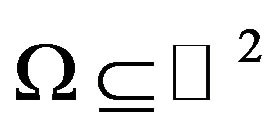 (or
(or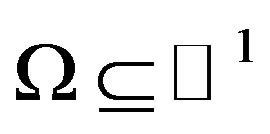 ) [7]. The form and properties of operators
) [7]. The form and properties of operators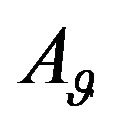 ,
, 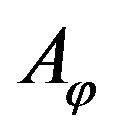 are defined by type and geometry of the radiating system. The set (domain) of values of the operator
are defined by type and geometry of the radiating system. The set (domain) of values of the operator 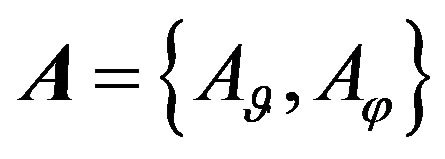 is called [8,9] set or class of realized directivity patterns. This means that for any DP
is called [8,9] set or class of realized directivity patterns. This means that for any DP  from this class there exists such function of distribution of the currents (fields)
from this class there exists such function of distribution of the currents (fields) 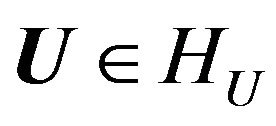 that realizes this DP, i.e.
that realizes this DP, i.e. 
In the simplest form the inverse problem (the synthesis problem) according to the prescribed amplitude DP can be formulated as the problem on finding the solutions of nonlinear operator equation of the first kind
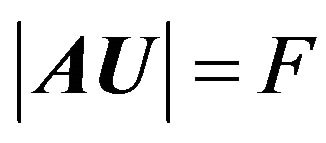 , (2)
, (2)
where 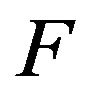 is a given amplitude DP. In staged thus the synthesis problem all three correct conditions of problems by Hadamard [10-12]: existence of the solution, uniqueness of the solution, continuous dependence of the solution of the input data, can be violated simultaneously. Violation of condition (1) in the first place is connected with the fact that the given DP
is a given amplitude DP. In staged thus the synthesis problem all three correct conditions of problems by Hadamard [10-12]: existence of the solution, uniqueness of the solution, continuous dependence of the solution of the input data, can be violated simultaneously. Violation of condition (1) in the first place is connected with the fact that the given DP 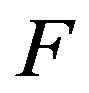 can not belong to the class realized, that is to the domain of values of the operator
can not belong to the class realized, that is to the domain of values of the operator . In other words, such DP can not be obtained at any distribution of field in the aperture of the radiating system belonging to the space
. In other words, such DP can not be obtained at any distribution of field in the aperture of the radiating system belonging to the space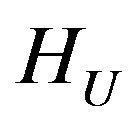 . Trying to recreate the DP
. Trying to recreate the DP 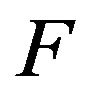 just leads to effect of superdirectivity [5]. The system becomes resonance and critical to change of parameters.
just leads to effect of superdirectivity [5]. The system becomes resonance and critical to change of parameters.
Condition (2) is violated due to the nonlinearity of the problem.
Therefore, the variational formulations of problems, which in addition to the requirements of the basic characteristics of DP also contain requirements to the distribution function of the currents (fields) in the aperture of the radiating system, are considered. At that is required not complete coincidence obtained DP 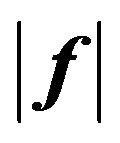 with given
with given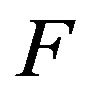 , but only the best (in the sense of the selected criterion) approximation to it.
, but only the best (in the sense of the selected criterion) approximation to it.
An important feature of the variational formulation of synthesis problems is the fact that in the optimization criterion can introduce functionals describing certain other requirements to amplitude-phase distribution (APD) of outside excitation sources. Their mean-square deviation, as a rule, will be used as the criterion of proximity of amplitudes of the given and synthesized DP.
2.1. The Case of Linear Polarization of Extraneous Field
First we consider the scalar case of problems when extraneous fields (currents) in the radiating system is linearly polarized [7,13], and created by their DP (1) has only one component. Let the operator A acts from some Hilbert functional space 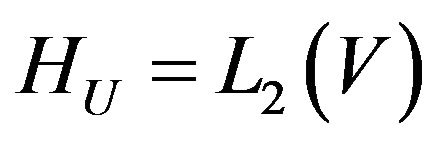 into the complex space of continuous and square integrable functions in domain
into the complex space of continuous and square integrable functions in domain  (or
(or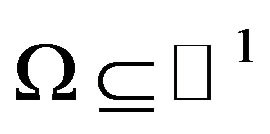 )
)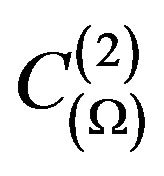 .
.
In space 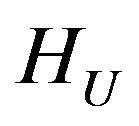 we introduce the scalar product and norm
we introduce the scalar product and norm
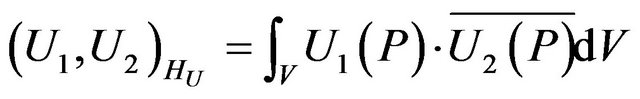 ,
,
 , (3)
, (3)
where 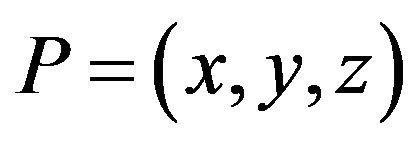 is a point of integration.
is a point of integration.
Along with the Chebyshev norm
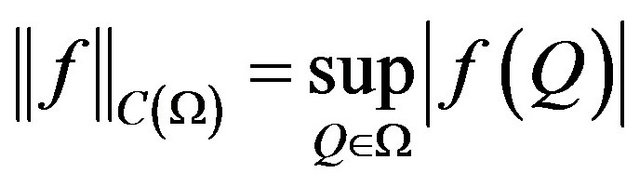 , (4)
, (4)
in the space we introduce scalar product and the generated by it norm and metric 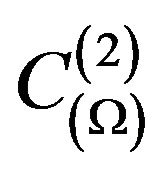 as follows:
as follows:
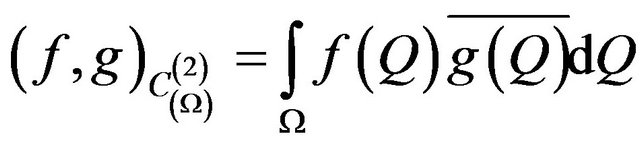 ,
, 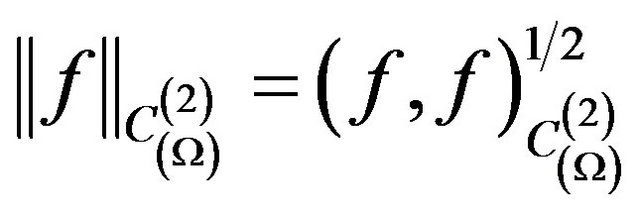 ,
,
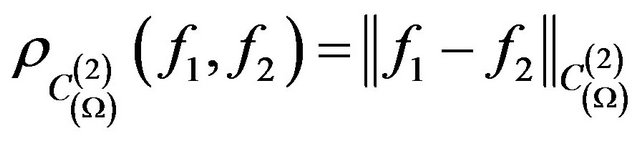 . (5)
. (5)
Note, space 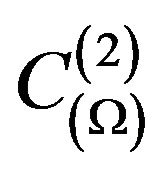 is a Banach space relatively uniform norm (4) and it is incomplete space concerning norm defined according to (5) [14].
is a Banach space relatively uniform norm (4) and it is incomplete space concerning norm defined according to (5) [14].
We consider also that the operator  has the izometric property or it is completely continuous. Let the given amplitude DP
has the izometric property or it is completely continuous. Let the given amplitude DP 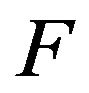 is real positive (nonnegative) continuous function which different from nonzero in some limited closed domain
is real positive (nonnegative) continuous function which different from nonzero in some limited closed domain 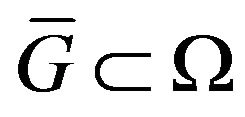 and identically equal zero on complement
and identically equal zero on complement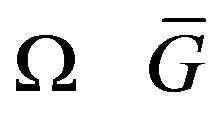 . Let
. Let  is isometric operator, that is for any
is isometric operator, that is for any 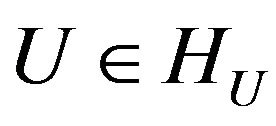 and
and 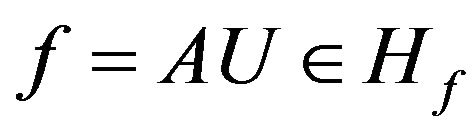 equality is satisfied
equality is satisfied
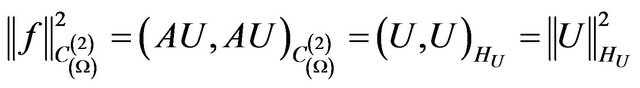 . (6)
. (6)
In [15-17] the synthesis problem of given amplitude DP 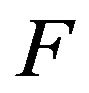 is formulated (is investigated) as a minimization problem in the Hilbert space
is formulated (is investigated) as a minimization problem in the Hilbert space  of the functional
of the functional
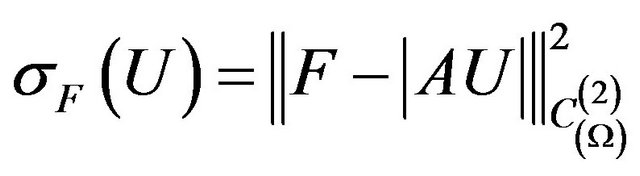 (7)
(7)
characterizing the value of mean-square deviation of modules of given and synthesized DP in domain . For the formulated problem occurs [18,19]
. For the formulated problem occurs [18,19]
Theorem 2.1. Let the linear operator
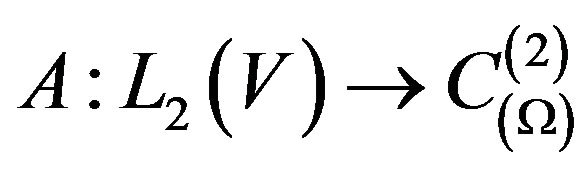 is isometric relatively mean-square metric and it is continuous operator from
is isometric relatively mean-square metric and it is continuous operator from 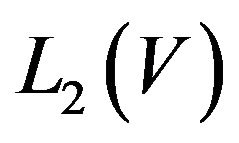 into
into
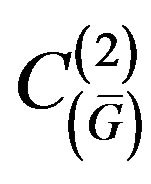 concerning uniform metric of the space
concerning uniform metric of the space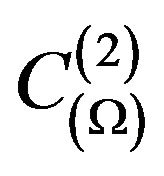 , and the given amplitude DP
, and the given amplitude DP 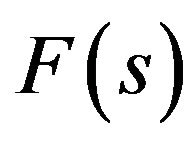 is a real positive (nonnegative) continuous function in the domain
is a real positive (nonnegative) continuous function in the domain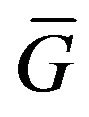 .
.
Then at least one point of absolute minimum of the functional (7) exists in the space 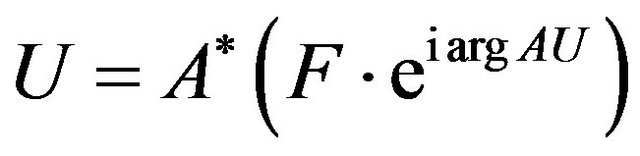 and a subsequence which converges weakly to one of points of absolute minimum can be selected from any minimizing sequence.
and a subsequence which converges weakly to one of points of absolute minimum can be selected from any minimizing sequence.
On the base of the necessary condition for an extremum of the functional (zero equality of its Hato differential [20])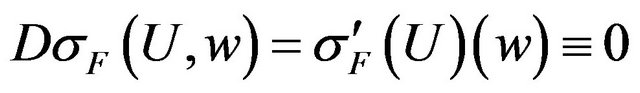 , we obtain the equation with respect to the optimal distribution of excitation sources
, we obtain the equation with respect to the optimal distribution of excitation sources
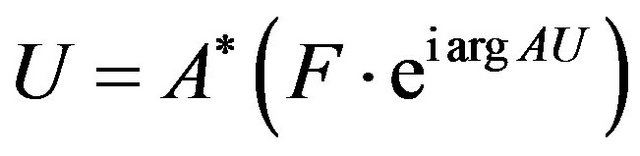 , (8)
, (8)
where 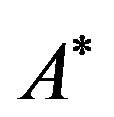 is the conjugate with
is the conjugate with  operator.
operator.
Let the set of zeros  of the operator A consists of only one zero element
of the operator A consists of only one zero element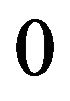 . Then acting on both parts of (8) by operator
. Then acting on both parts of (8) by operator , we obtain the equivalent to (8) equation in space
, we obtain the equivalent to (8) equation in space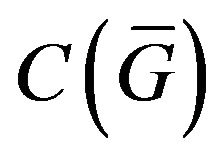 :
:
 . (9)
. (9)
By solutions 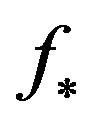 of this equation the optimal distribution of excitation sources in radiating system are defined by the formula
of this equation the optimal distribution of excitation sources in radiating system are defined by the formula
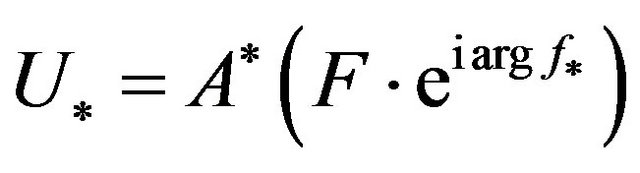 . (10)
. (10)
From Theorem 2.1 and the properties of functional 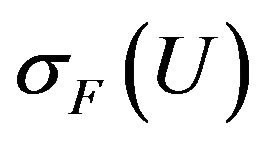 follows Corollary 2.1. Since functional
follows Corollary 2.1. Since functional  is differentiable in
is differentiable in 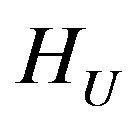 by Hato, it is growing [21] and according to Theorem 2.1 has at least one point of absolute minimum, then (8) in the space
by Hato, it is growing [21] and according to Theorem 2.1 has at least one point of absolute minimum, then (8) in the space 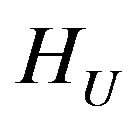 and (9) in the space
and (9) in the space 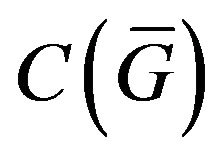 have at least one solution.
have at least one solution.
Lemma 2.1. Between solutions of (8) and (9) there exists bijection, that is if 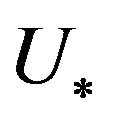 is the solution of (8), then
is the solution of (8), then 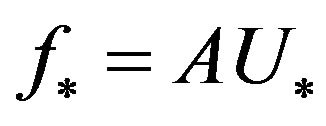 is the solution of (9). On the contrary, if
is the solution of (9). On the contrary, if 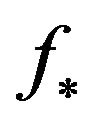 is the solution of (9), then the corresponding solution of (8) is defined by (10).
is the solution of (9), then the corresponding solution of (8) is defined by (10).
The possibility of investigation of solutions of synthesis problems, using (8) or (9) follows from Lemma. Note, Equation (9) is simpler as (8), since the latter contains the operator exponent.
Note, solutions of synthesis problems according to the prescribed amplitude DP are determined with precision to value 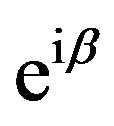 (
( is arbitrary constant), since
is arbitrary constant), since
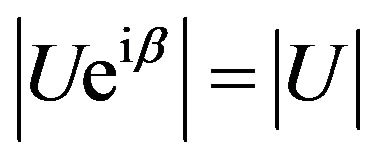 . So if there exists the solution of Equations (8) (or (9)), then there is also generated by its family of solutions in which one solution different from another by phase constant. For the uniqueness of desired solutions additional conditions impose on the functions
. So if there exists the solution of Equations (8) (or (9)), then there is also generated by its family of solutions in which one solution different from another by phase constant. For the uniqueness of desired solutions additional conditions impose on the functions 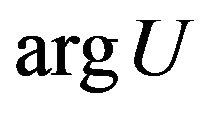 or
or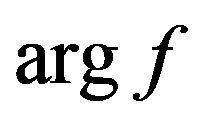 .
.
In the case completely continuous operator describing DP of radiating system the smoothing Tikhonov type functional [11]
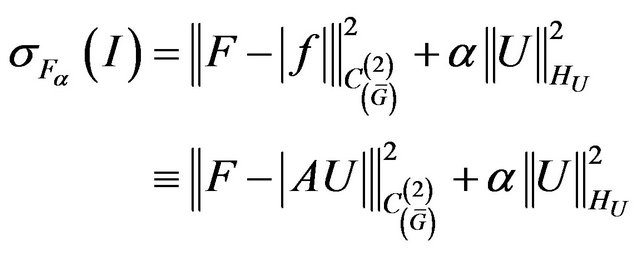 (11)
(11)
which includes requirements as to the mean-square deviation of DP, so to norm of current, is used [18,22] for the synthesis of various types of antennas. The parameter α can be viewed as regularization parameter [11,23] or as a weighing coefficient, by means of which can control ratio between the first and second summand of functional.
Theorem 2.2. Let the linear operator  acts from the complex Hilbert space
acts from the complex Hilbert space 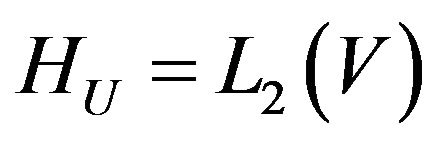 into the complex space of continuous functions
into the complex space of continuous functions  and it is completely continuous, and given DP is real positive (nonnegative) and continuous function in
and it is completely continuous, and given DP is real positive (nonnegative) and continuous function in 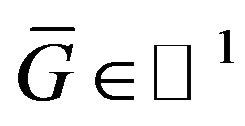 (or in
(or in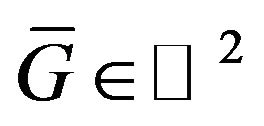 ).
).
Then at least one point of absolute minimum of functional 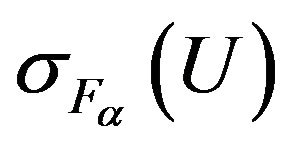 exists in
exists in 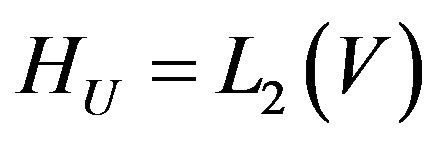 and a subsequence which converges weakly to one of the points of absolute minimum can be selected from any minimizing sequence.
and a subsequence which converges weakly to one of the points of absolute minimum can be selected from any minimizing sequence.
Differentiating functional 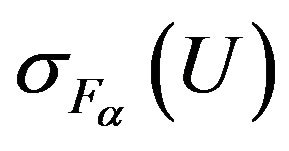 by Hato and performing appropriate transformations, we obtain the equation [22,24]
by Hato and performing appropriate transformations, we obtain the equation [22,24]
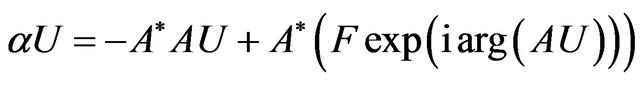 (12)
(12)
in the space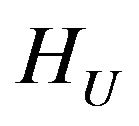 .
.
Equation with respect to synthesized DP based on equality 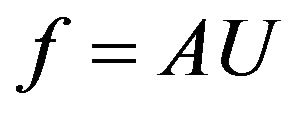 and (12) has the form
and (12) has the form
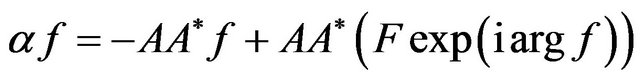 . (13)
. (13)
Lemma similar to Lemma 2.1 is valid for (12) and (13).
From Theorem 2.2 and properties of functional 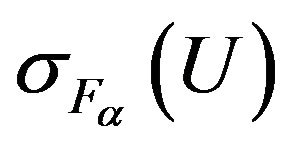 follows [7,18]
follows [7,18]
Corollary 2.2. Since differentiable in 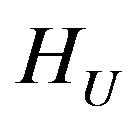 by Hato functional
by Hato functional 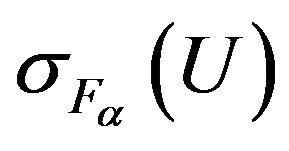 is growing and according to Theorem 2.2 has at least one point of absolute minimum, then (12) in space
is growing and according to Theorem 2.2 has at least one point of absolute minimum, then (12) in space 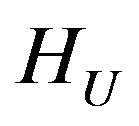 and (13) in the space
and (13) in the space 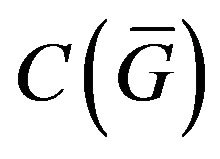 have at least one by one solution.
have at least one by one solution.
2.2. The Case of Arbitrary Polarization of Excitation Fields
Consider the more general case when the excitation fields (or currents) in the radiating system and generated by it DP have vector character [5,6]. In this case, we set that the operator  is completely continuous and it acts from
is completely continuous and it acts from 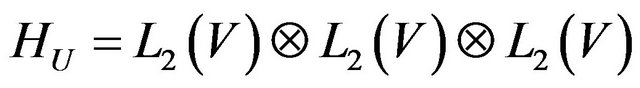 complex space of square integrable in the domain
complex space of square integrable in the domain 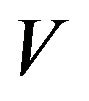 vector-valued functions, into the complex space of continuous functions on the compact
vector-valued functions, into the complex space of continuous functions on the compact  vector-valued functions
vector-valued functions
 equipped by scalar product. We introduce the scalar product and generated by it norm in
equipped by scalar product. We introduce the scalar product and generated by it norm in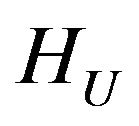 :
:

(14)
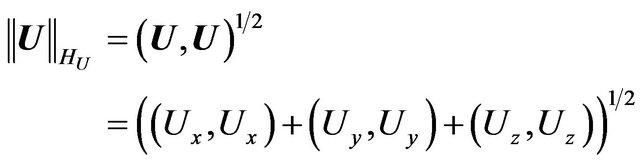 . (15)
. (15)
We define module of vector  as following:
as following:
 .
.
In the space 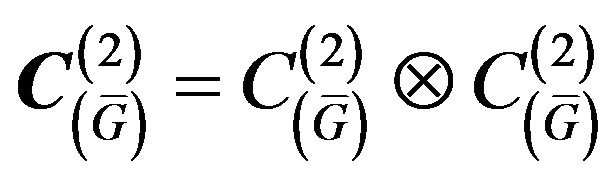 along with the Chebyshev norm
along with the Chebyshev norm
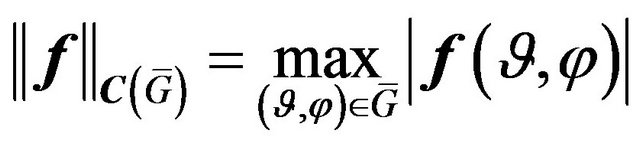 , (16)
, (16)
where
 we introduce the scalar product and generated by it the mean-square norm and metric
we introduce the scalar product and generated by it the mean-square norm and metric

(17)
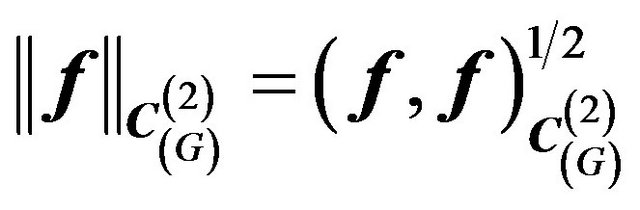 . (18)
. (18)
If DP of radiating system has two components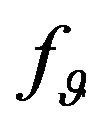 ,
, 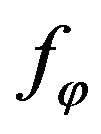 , i.e. it is described by (1), then as the optimization criterions are used the following functionals [7]:
, i.e. it is described by (1), then as the optimization criterions are used the following functionals [7]:
 (19)
(19)
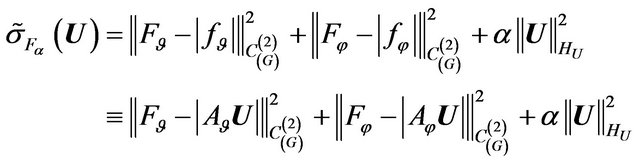 .
.
(20)
In the functional (20), 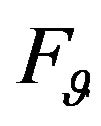 ,
, 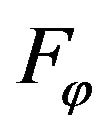 are the given amplitude of components of required DP. At that
are the given amplitude of components of required DP. At that
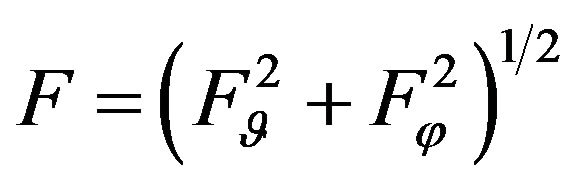 ,
,  and functions
and functions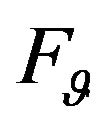 ,
, 
can be given with account of existing requirements to polarization characteristics of emitted field.
If in the synthesis problem functional (19) is used as the optimization criterion, the problem on finding the minimum points is reduced to finding the solutions of the equation
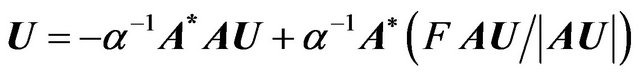 (21)
(21)
in the space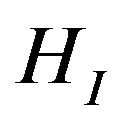 . Equivalent to (21) equation with respect to vector DP
. Equivalent to (21) equation with respect to vector DP  in space
in space 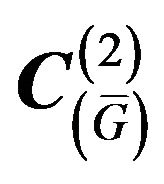 has the form
has the form
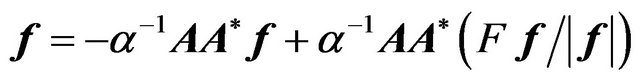 . (22)
. (22)
In this case the following theorem is valid [7].
Theorem 2.3. Let linear completely continuous operator  acts from the complex Hilbert space
acts from the complex Hilbert space
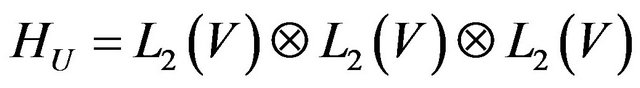 into the complex space of continuous functions
into the complex space of continuous functions 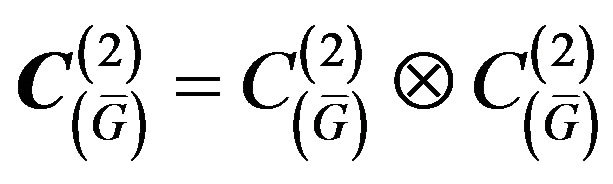 equipped by the scalar product, and given DP is a real positive continuous function on the compact
equipped by the scalar product, and given DP is a real positive continuous function on the compact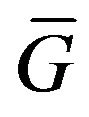 .
.
Then in 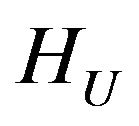 there exists at least one point of absolute minimum of functional
there exists at least one point of absolute minimum of functional 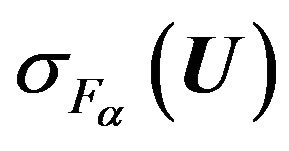 and a subsequence which converges weakly to one of the points of absolute minimum can select from any minimizing sequence.
and a subsequence which converges weakly to one of the points of absolute minimum can select from any minimizing sequence.
For the functional (20) is true Theorem 2.4. At conditions of Theorem 2.3 functional 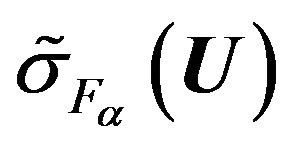 in the space
in the space 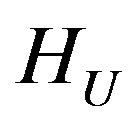 has at least one point of absolute minimum and subsequence which converges weakly to one of points of absolute minimum can be selected from any minimizing sequence.
has at least one point of absolute minimum and subsequence which converges weakly to one of points of absolute minimum can be selected from any minimizing sequence.
For minimizing of the functional 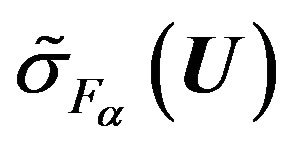 in the space
in the space 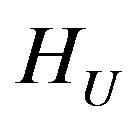 we obtain equation [7]
we obtain equation [7]
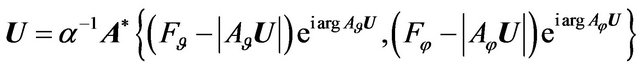 .
.
(23)
Equivalent to (23) equation with respect to synthesized DP  in the space
in the space 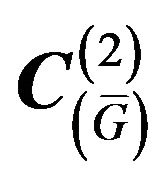 has the form
has the form
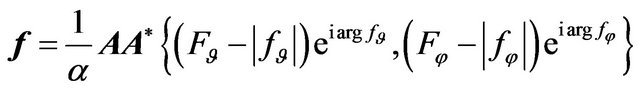 . (24)
. (24)
The existence of solutions of (23) in space 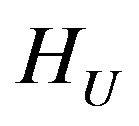 and (24) in the space
and (24) in the space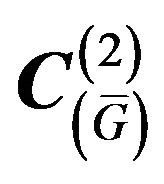 , respectively, follows from necessary condition of functional minimum
, respectively, follows from necessary condition of functional minimum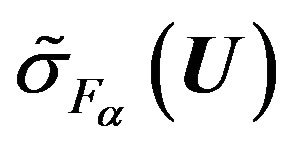 .
.
If necessary the weight function [15,17] can introduce in the functionals 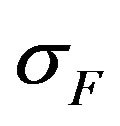 and
and 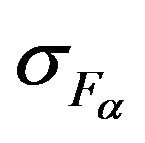 by means entering appropriate scalar products and affect on quality of the approximation of synthesized and given DP in a certain range of angles.
by means entering appropriate scalar products and affect on quality of the approximation of synthesized and given DP in a certain range of angles.
2.3. Simultaneous Optimization of the Geometry of Aperture and Excitation Fields
The synthesis problems with optimization of geometry of radiating system are more complicated class of problems. These problems need to find a configuration of the radiating system and amplitude-phase distribution of excitation fields (currents) in it [25,26]. Moreover, the operator  depends on two functions: function
depends on two functions: function  describing the geometry of the system, and amplitude-phase distribution function of excitation sources
describing the geometry of the system, and amplitude-phase distribution function of excitation sources  i.e.
i.e.
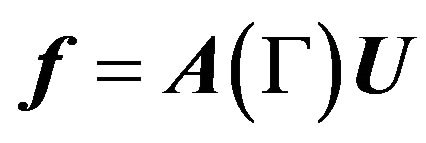 . (25)
. (25)
In addition, the function  has, as rule, vector character, and the operator
has, as rule, vector character, and the operator  is a nonlinear concerning the function
is a nonlinear concerning the function . Later on we shall consider the synthesis problem of a flat aperture, in which in addition to amplitude-phase distribution (APD) desired is too the function that describes the boundary of aperture. The basis of the formulation of such problems can be put the functionals (7), (11) and (20), expanding their by corresponding requirements to geometry of radiating system.
. Later on we shall consider the synthesis problem of a flat aperture, in which in addition to amplitude-phase distribution (APD) desired is too the function that describes the boundary of aperture. The basis of the formulation of such problems can be put the functionals (7), (11) and (20), expanding their by corresponding requirements to geometry of radiating system.
2.4. Synthesis Problem of Discrete Radiating Systems―Antenna Arrays
In many radio engineering systems antenna arrays (AR) have gained widespread use. Antenna array is [4,6,27] antenna, which consists of 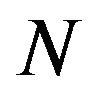 identical (or differenttype) radiators placing corresponding way in space and they collate by common system of power and control. In [28-37] investigations of nonlinear synthesis problems and planar antenna arrays according to the prescribed amplitude DP are presented.
identical (or differenttype) radiators placing corresponding way in space and they collate by common system of power and control. In [28-37] investigations of nonlinear synthesis problems and planar antenna arrays according to the prescribed amplitude DP are presented.
To describe the electromagnetic characteristics of antenna arrays are used different by precision mathematical models [38-42]. In the base of construction of mathematical models is imposed [40,42] that the excitation of each radiator is characterized by a unique complex number  -complex amplitude of excitation. It’s the physical meaning depends on the type of radiating system. On the base on the linearity of the Maxwell’s equations the complex excitation amplitudes enter linearly in the expression for DP of array, that is
-complex amplitude of excitation. It’s the physical meaning depends on the type of radiating system. On the base on the linearity of the Maxwell’s equations the complex excitation amplitudes enter linearly in the expression for DP of array, that is
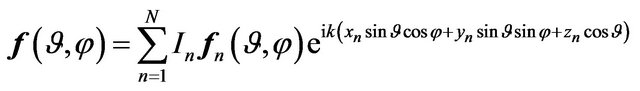 , (26)
, (26)
where 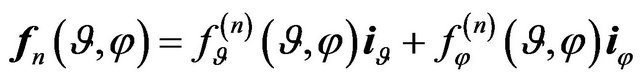 is vector DP
is vector DP 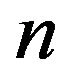 -th radiator. Vector
-th radiator. Vector  is called vector excitation of array or vector of amplitude-phase distribution of currents in the array.
is called vector excitation of array or vector of amplitude-phase distribution of currents in the array.
In general, the construction of high-accuracy mathematical models of array is reduced to solving the corresponding exterior boundary problem of high-frequency electrodynamics for system of the Maxwell’s equations in multiply-connected domain [1,39-41]. In the particular case, where the elements of the array are ideally leading talamy accounting of the mutual influence is based on the method of induced electromotive forces (IEF) and it is reduced to solution the corresponding system of linear integral equations [42]
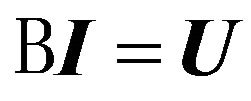 , (27)
, (27)
where 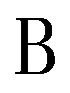 is matrix-integral linear operator; I is complexvalued vector distribution function of surface currents on radiators;
is matrix-integral linear operator; I is complexvalued vector distribution function of surface currents on radiators; 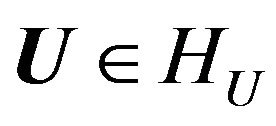 is vector-valued function describing the outside fields (voltage) which is necessary to create in the system of power of array. Allocating in the space
is vector-valued function describing the outside fields (voltage) which is necessary to create in the system of power of array. Allocating in the space 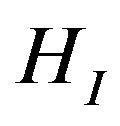 compact class of solutions (where (27) is correct), solution of (27) is written as
compact class of solutions (where (27) is correct), solution of (27) is written as
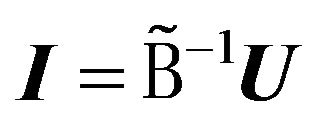 . (28)
. (28)
Here it is assumed that the corresponding regularized system1 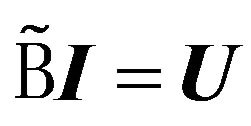 exists for the system of (27). Then on the basis of (28) formula for DP of array takes the form
exists for the system of (27). Then on the basis of (28) formula for DP of array takes the form
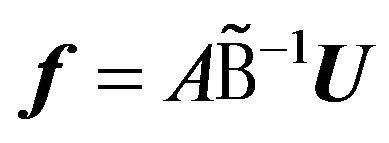 . (29)
. (29)
This relation allows to formulate the synthesis problem of antenna array according to the prescribed amplitude DP with account of the mutual influence of elements as the problem on finding the vector  minimizing the functional
minimizing the functional
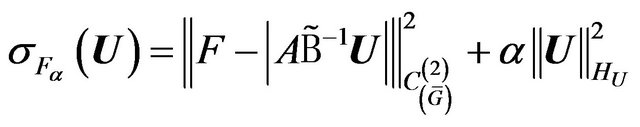 (30)
(30)
in space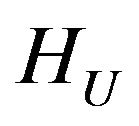 .
.
At need to take into account the component-wise approximation of modules of given and synthesized DP’s, the functional [43-45]
 (31)
(31)
analogously to (20) can be used as optimizing criterion.
By the desired solutions of this problem the optimal vector of extraneous voltages on inputs of radiators is determined on the basis of (27).
Thus, the basic requirements for synthesis problems of different types of radiating systems according to the prescribed amplitude DP are formulated. Note that recorded functionals is not convex [21], and therefore may have nonunique extreme point. In further the above statements of problems allow to obtain relatively simple nonlinear integral or matrix equations for the study and solution of which can be applied numerical methods of nonlinear analysis methods.
Integral equations method [40,42] is used widely in such classes of problems. The method of synthesis of antenna arrays from cylindrical dipoles with account of mutual influence is proposed in [43-45]. Analysis of problem of nonuniqueness solutions is studied there by means computational experiments.
2.5. Nonlinear Synthesis Problem of Radiating Systems with Use of Energy Criterion
In spite of the fact that from the amplitude DP 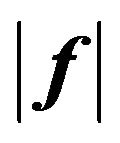 is easy to obtain the DP by power
is easy to obtain the DP by power  and vice versa, in the mathematical aspect the synthesis problems of given amplitude DP
and vice versa, in the mathematical aspect the synthesis problems of given amplitude DP 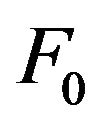 and given energy DP
and given energy DP 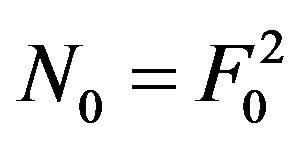 are different tasks. For example, if
are different tasks. For example, if  is the optimal solution of some variational synthesis problem of amplitude DP, then
is the optimal solution of some variational synthesis problem of amplitude DP, then  will not be the optimal solution of a similar problem for the given DP
will not be the optimal solution of a similar problem for the given DP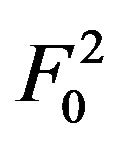 . On this basis, in [46-49] on the operator level are considered statements of synthesis problems with use of two types of stabilizing functionals, in which the vector character of the electromagnetic fields takes into account.
. On this basis, in [46-49] on the operator level are considered statements of synthesis problems with use of two types of stabilizing functionals, in which the vector character of the electromagnetic fields takes into account.
Consider the synthesis problem of given energy DP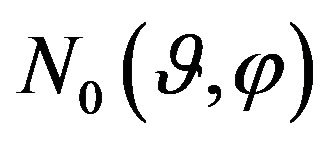 . Taking into account the expression for DP
. Taking into account the expression for DP
 in the simplest form this problem can be formulated as a problem on finding the solutions of nonlinear operator equation of the first kind
in the simplest form this problem can be formulated as a problem on finding the solutions of nonlinear operator equation of the first kind
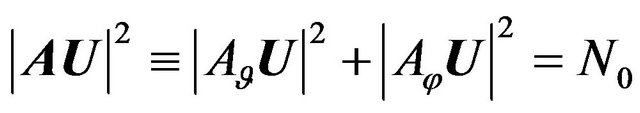 , (32)
, (32)
where 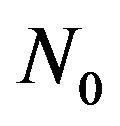 is a real positive continuous function in
is a real positive continuous function in
 (at that
(at that ) which can not belong to the domain of values of the operator
) which can not belong to the domain of values of the operator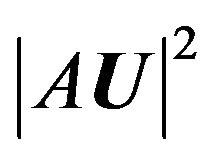 . It is known [11] that (32) is severely ill-posed problem. In this connection, we consider the problem on best meansquare approximation of the real positive continuous (in the domain
. It is known [11] that (32) is severely ill-posed problem. In this connection, we consider the problem on best meansquare approximation of the real positive continuous (in the domain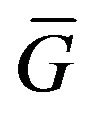 ) function
) function 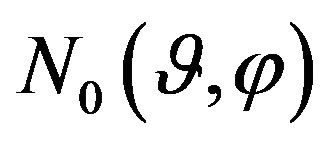 by function
by function 
( ,
,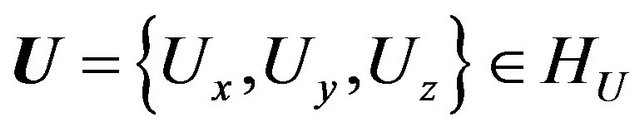 ).
).
Formulate it as minimizing problem of functional [49]
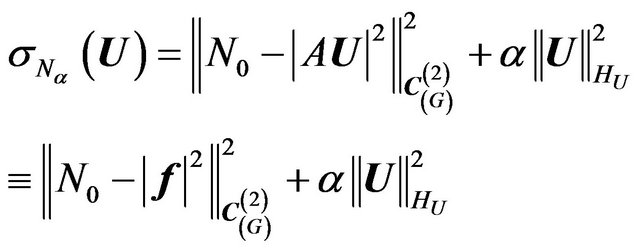 (33)
(33)
in the space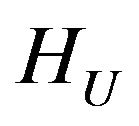 . In this functional the first summand characterizes mean-square deviation of given and synthesized DP by power. Second summand imposes restrictions on norm of currents in the radiating system. Real parameter
. In this functional the first summand characterizes mean-square deviation of given and synthesized DP by power. Second summand imposes restrictions on norm of currents in the radiating system. Real parameter 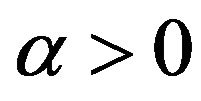 we shall consider as a weighing multiplier. The existence of at least one point of minimum functional
we shall consider as a weighing multiplier. The existence of at least one point of minimum functional 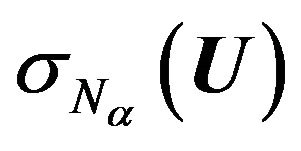 in the space
in the space  states [7,49]
states [7,49]
Theorem 2.5. Let the linear operator  acts from the space
acts from the space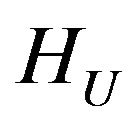 into
into 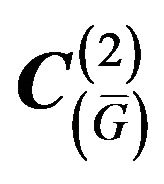 and it is completely continuous,
and it is completely continuous, 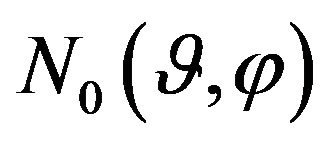 is given nonnegative continuous the function in
is given nonnegative continuous the function in , at that
, at that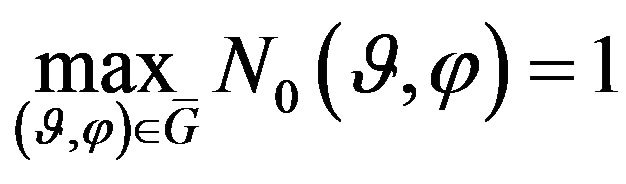 .
.
Then in the space HU there exists at least one point of absolute minimum of the functional 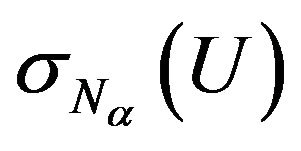 and subsequence that converges weakly to one of the points of absolute minimum can be selected from any minimizing sequence.
and subsequence that converges weakly to one of the points of absolute minimum can be selected from any minimizing sequence.
On the base of necessary condition of minimum functional is obtained the equation [7]
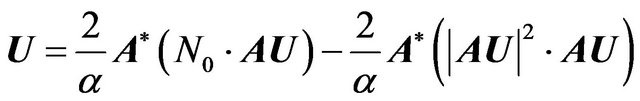 (34)
(34)
with respect to optimal currents in the space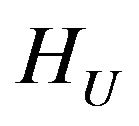 . This equation is a nonlinear operator equation having in the right part linear operator along with the Hammerstein type operator. If the set of zeros
. This equation is a nonlinear operator equation having in the right part linear operator along with the Hammerstein type operator. If the set of zeros 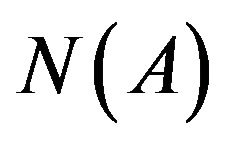 consists of only the zero element
consists of only the zero element , then acting on both parts of (34) by operator
, then acting on both parts of (34) by operator , we obtain equation an equivalent to (34) with respect to synthesized DP in the space
, we obtain equation an equivalent to (34) with respect to synthesized DP in the space 
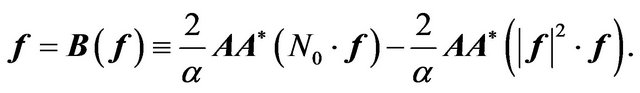 (35)
(35)
In [49] is shown that the functional 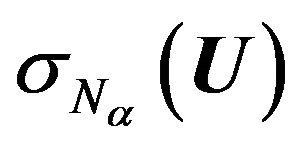 has
has  -property [50], that is the minimum point of the functional is interior point of some convex weakly closed set of the space
-property [50], that is the minimum point of the functional is interior point of some convex weakly closed set of the space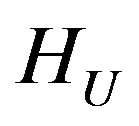 . On this basis from Theorem 2.5 follows [7]
. On this basis from Theorem 2.5 follows [7]
Corollary 2.3. Since the functional 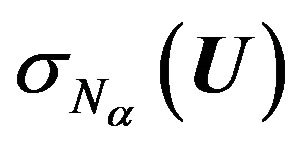 is differentiable in
is differentiable in 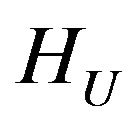 by Hato, has at least one minimum point and
by Hato, has at least one minimum point and  property, then (34) in the space
property, then (34) in the space 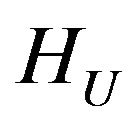 and
and
(35) in the space 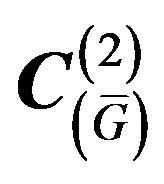 have at least by one solution.
have at least by one solution.
Lemma 2.2. At conditions of Theorem 2.5 and limited values of parameter 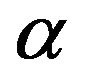 operator
operator
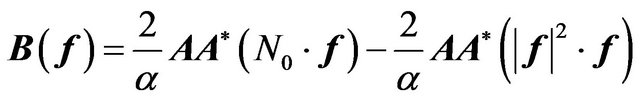 (36)
(36)
is compact in the space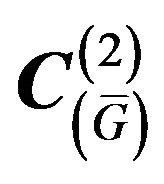 .
.
Since for elements relatively compact set of normalized space the strong and weak convergence coincide [51] then with Theorem 2.5 and Lemma 2.2 follows Corollary 2.4. If 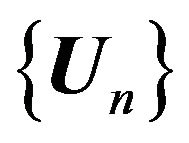 is minimizing sequence of the functional
is minimizing sequence of the functional 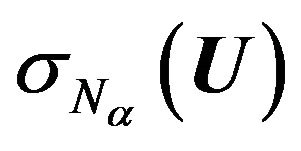 converging weakly to the minimum point
converging weakly to the minimum point , then the sequence
, then the sequence 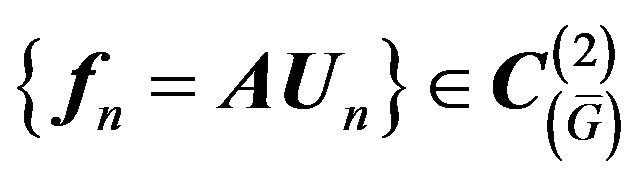 converges uniformly in
converges uniformly in 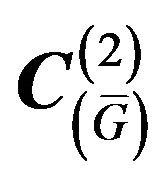 to
to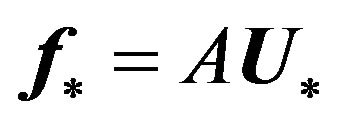 .
.
3. About Branching of Solutions of the Basic Equations of Synthesis. Partial Cases
Here on the example of scalar synthesis problems of linear radiator and radiating system with a flat aperture are presented the results of investigation of nonuniqueness problem of solutions corresponding to these tasks nonlinear integral equations of Hammerstein type depending on the change of the physical parameters.
3.1. The Case of a Linear Radiator
We put that the linear antenna is linear electric conductor of length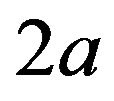 , sizes of cross-section of which are much less than the wavelength. Due to these limitations the excitation currents in the antenna shall have only directaxis current [5]. Introduce the Cartesian and connected with spherical coordinate systems such that the origin of coordinates coincides with the middle of the antenna. We direct the axis
, sizes of cross-section of which are much less than the wavelength. Due to these limitations the excitation currents in the antenna shall have only directaxis current [5]. Introduce the Cartesian and connected with spherical coordinate systems such that the origin of coordinates coincides with the middle of the antenna. We direct the axis 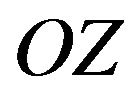 along the antenna. Then the current vector in a Cartesian coordinate system will have only z-component
along the antenna. Then the current vector in a Cartesian coordinate system will have only z-component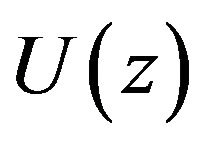 . We shall introduce the dimensionless coordinates
. We shall introduce the dimensionless coordinates ,
, 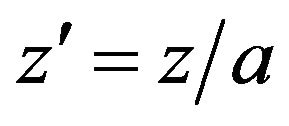 , and parameter
, and parameter
 , (37)
, (37)
connecting the electric size of antenna with angle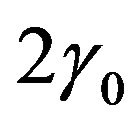 , outside of which given amplitude DP
, outside of which given amplitude DP 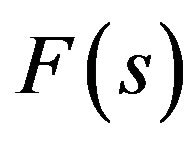 identically zero. Then the formula for DP of linear antenna takes the form [7]
identically zero. Then the formula for DP of linear antenna takes the form [7]
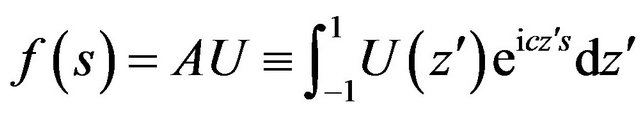 . (38)
. (38)
For DP of antenna the Parseval equality [8]
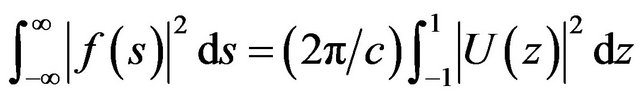 (39)
(39)
is valid, that is the operator  is isometric.
is isometric.
Taking into account that  is finite function with compact carrier
is finite function with compact carrier  and expressions for the operators
and expressions for the operators  and
and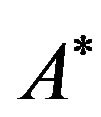 , we obtain the expanded form of (8):
, we obtain the expanded form of (8):
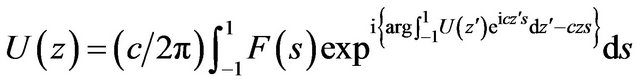 . (40)
. (40)
On the basis of (9), (38) we obtain the Hammerstein type equation concerning optimal DP
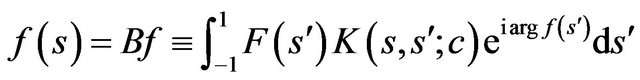 (41)
(41)
in the space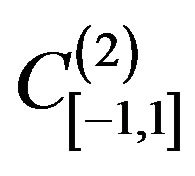 , where
, where
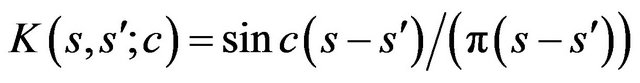 . (42)
. (42)
The existence of at least one solution of (40) in the space 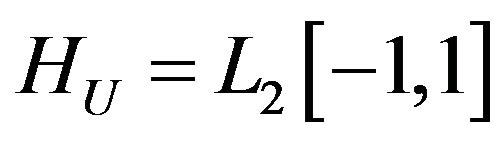 and (41) in the space
and (41) in the space 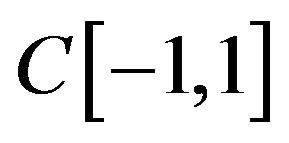 follows from Corollary 2.1.
follows from Corollary 2.1.
We shall present three important properties of (41).
1) If 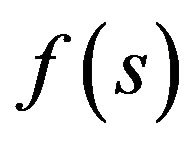 is the solution of (41), then complexconjugate function
is the solution of (41), then complexconjugate function 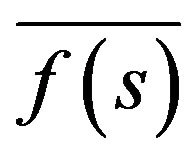 is the solution of (41) too.
is the solution of (41) too.
2) If 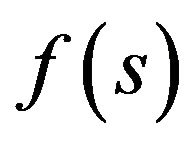 is the solution of (41), then
is the solution of (41), then 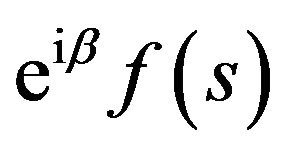 is the solution of (41) too, where β is an arbitrary real constant.
is the solution of (41) too, where β is an arbitrary real constant.
3) For even functions 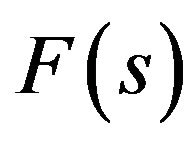 nonlinear operator
nonlinear operator , which is in the right part of (41), transfers even phase DP
, which is in the right part of (41), transfers even phase DP 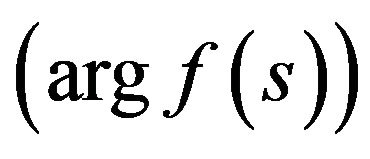 in even, and odd—in an odd. That is the operator
in even, and odd—in an odd. That is the operator 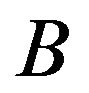 is invariant with respect to the type of parity of function
is invariant with respect to the type of parity of function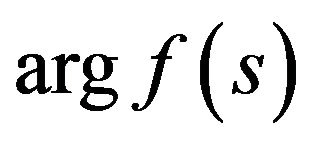 . Due to this property the existence of fixed points of the operator
. Due to this property the existence of fixed points of the operator 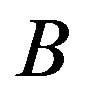 -solutions of (41) is possible in the classes of even and odd phase DP’s.
-solutions of (41) is possible in the classes of even and odd phase DP’s.
In [16,52] is shown that (41) has two solutions in the class of real functions:
 , (43)
, (43)
which is called the primary solution of the first type and
 (44)
(44)
is the primary solution of the second type. Point 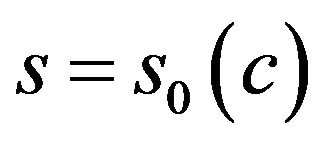 is determined from the condition
is determined from the condition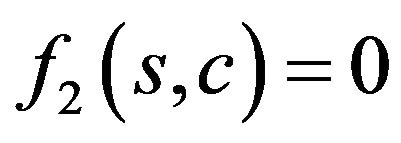 . For the even
. For the even 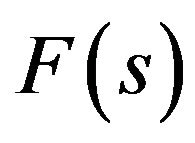
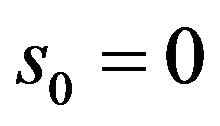 , that is the solution (44) is a real odd function (the corresponding to it amplitude DP is even function).
, that is the solution (44) is a real odd function (the corresponding to it amplitude DP is even function).
These solutions are effective only at small values of parameter . With the growth of this parameter there exist branching points
. With the growth of this parameter there exist branching points 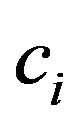 at which more effective (in the sense value of functional
at which more effective (in the sense value of functional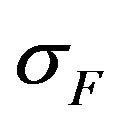 ) complex solutions branch-off from real solutions.
) complex solutions branch-off from real solutions.
Consider according to [7,16] results of investigation of branchings of primary solution of the first type of solutions of (41). Using the procedure of decomplexification of the space 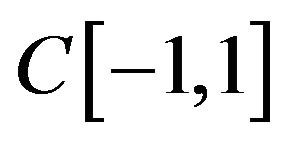 [14] from (41) we move to the equivalent system
[14] from (41) we move to the equivalent system

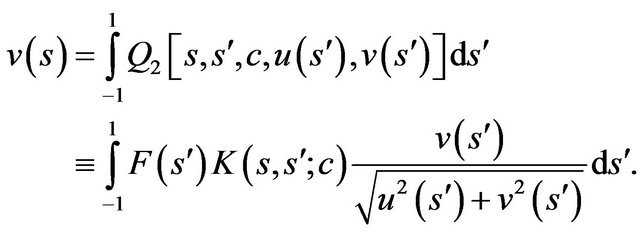 (45)
(45)
On the base of the branching theory of solutions [53] the problem on finding such values of parameter  (branching points) and all different from
(branching points) and all different from 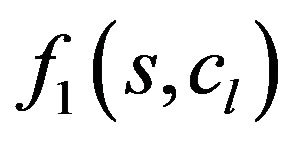 solutions of system of (45) satisfying the conditions
solutions of system of (45) satisfying the conditions
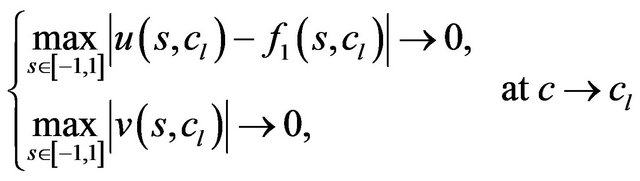 , (46)
, (46)
are considered. Condition (46) means that it is necessary to find small continuous solutions

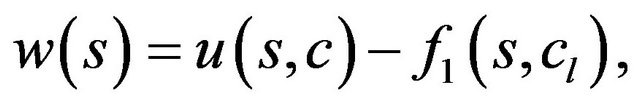 converging uniformly to zero at
converging uniformly to zero at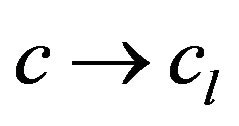 . Putting in (45)
. Putting in (45)
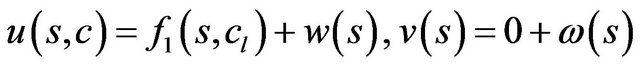 (47)
(47)
and expanding the integrand ,
,  in the vicinity of the point
in the vicinity of the point 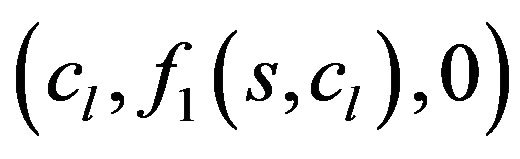 in the power series by
in the power series by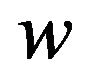 ,
,  and
and , and taking into account that the function
, and taking into account that the function  is its solution, we obtain system of integral equations of Lyapunov-Schmidt type [53] with respect to small solutions
is its solution, we obtain system of integral equations of Lyapunov-Schmidt type [53] with respect to small solutions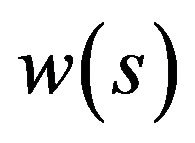 ,
,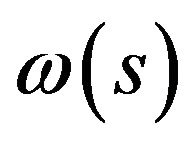 :
:
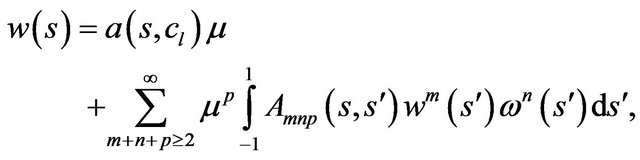 (48)
(48)
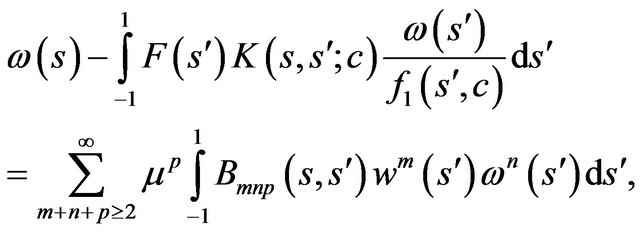 (49)
(49)
where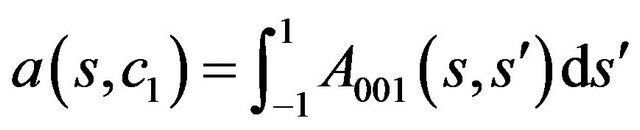 . On the base of the left part of (49) we obtain linear homogeneous integral equation
. On the base of the left part of (49) we obtain linear homogeneous integral equation
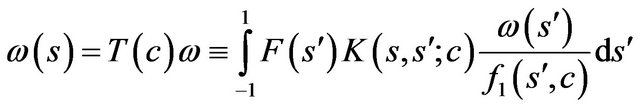 (50)
(50)
for finding the points of possible branching of solutions.
Equation (50) is a nonlinear one-parameter spectral problem concerning parameter . It is shown in [7,16] that for a given even amplitude DP
. It is shown in [7,16] that for a given even amplitude DP  there exist branching points of two types: eigenvalues of multiplicity two correspond to the first type, eigenvalues the multiplicity of three—to the second type. It is found in [54] analytical expressions for eigenfunctions of (50) and are obtained systems of transcendental equations for finding the possible branching points.
there exist branching points of two types: eigenvalues of multiplicity two correspond to the first type, eigenvalues the multiplicity of three—to the second type. It is found in [54] analytical expressions for eigenfunctions of (50) and are obtained systems of transcendental equations for finding the possible branching points.
Using for finding the solutions of branching equation the Newton diagram method, it is shown [53] that two complex-conjugate between themselves solutions, which in the first approximation, have the form
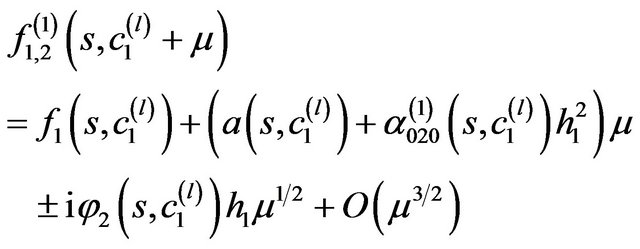 , (51)
, (51)
branch-off from the real solution 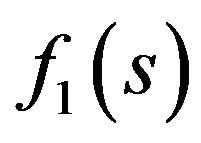 in the branching points of the first type
in the branching points of the first type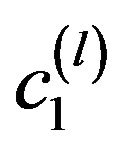 . Here
. Here ,
,
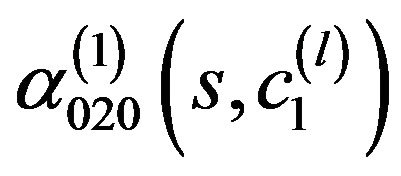 are even by s functions which are obtained by means corresponding transformations,
are even by s functions which are obtained by means corresponding transformations,
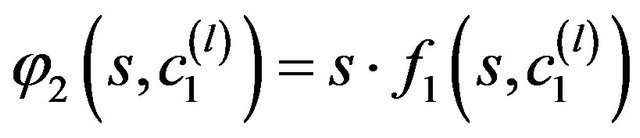 is the second eigenfunction of
is the second eigenfunction of
(50) at the points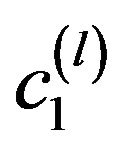 .
.
In [7] it is shown also that the branching-off solutions branch-off too. Analogous investigations are performed in branching points of the second type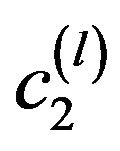 .
.
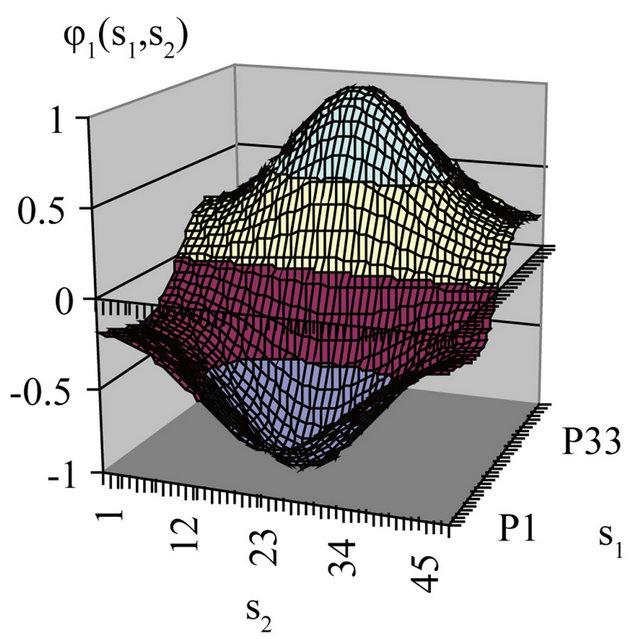
To estimate the effectiveness of different types of solutions we consider value of the functional 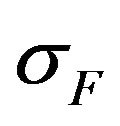 depending on the parameter
depending on the parameter , which it takes on these solutions. For example, in Figure 1 are shown the values of the functional for
, which it takes on these solutions. For example, in Figure 1 are shown the values of the functional for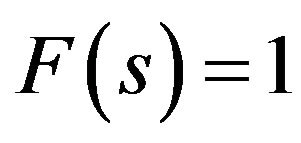 . The most effective solution images envelope which: on the segments I corresponds to the primary solution
. The most effective solution images envelope which: on the segments I corresponds to the primary solution , on II-branching-off solutions
, on II-branching-off solutions 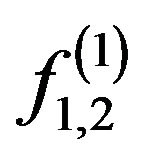 at the point
at the point 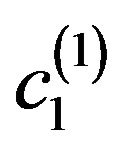 with odd phase DP, on III-solutions
with odd phase DP, on III-solutions 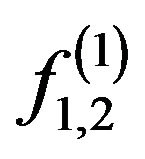 and branching-off solutions
and branching-off solutions 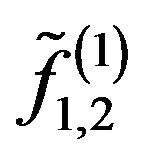 from theseon IV-solutions
from theseon IV-solutions  and branching-off solutions
and branching-off solutions  at the point
at the point 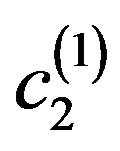 with even phase, на V-branching-off at the point
with even phase, на V-branching-off at the point 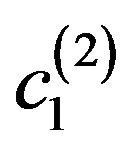 solutions of the type
solutions of the type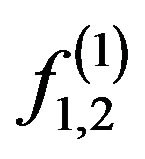 , on VI-solutions
, on VI-solutions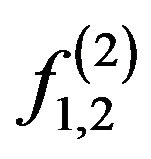 .
.
Thus, the analytical investigations [7,16,52,54] and the results of numerical experiments enable to describe the general structure of the solutions of the problem dependeing on change of the value of the parameter .
.
Because the values of the functional on some types of solutions in a given interval of change of the parameter  may be equal, the curves shown in Figure 1, does not map the full structure of the existing solutions. For greater clarity this structure can be represented schematically as a “tree” of solutions. In Figure 2 it is shown for the case of even DP. The primary solution
may be equal, the curves shown in Figure 1, does not map the full structure of the existing solutions. For greater clarity this structure can be represented schematically as a “tree” of solutions. In Figure 2 it is shown for the case of even DP. The primary solution 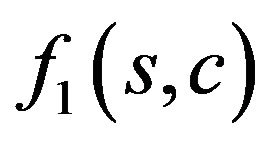 is central. The solution
is central. The solution 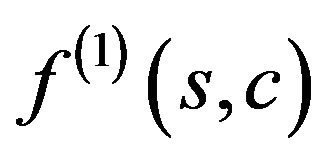 with odd phase DP
with odd phase DP
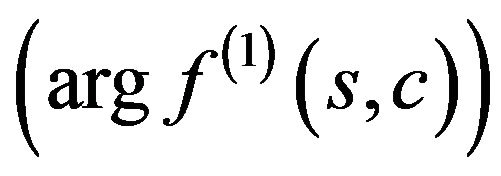 branches first. At the point
branches first. At the point 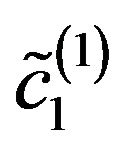 solution
solution

Figure 1. The value of the functional σF on the first primary and branching-off solutions for F(s) = 1.
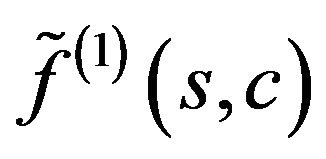 branches from branching solution
branches from branching solution , and solution
, and solution 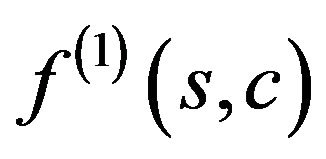 enter in a real solution in a neighborhood of the point
enter in a real solution in a neighborhood of the point 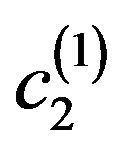 at
at , tending to
, tending to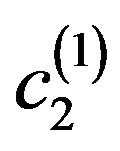 . At the same point
. At the same point 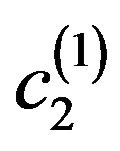 solution with even phase DP
solution with even phase DP
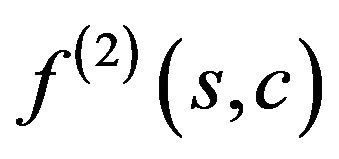 branches from primary solution. The solution of the type
branches from primary solution. The solution of the type 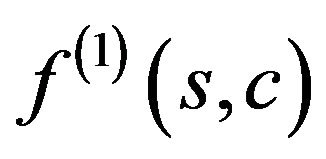 with an odd phase DP branches at the point
with an odd phase DP branches at the point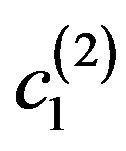 , which is located directly behind
, which is located directly behind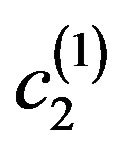 . The solutions of the type
. The solutions of the type 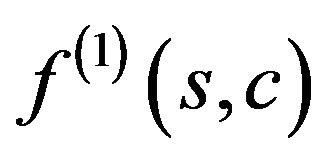 and the type
and the type 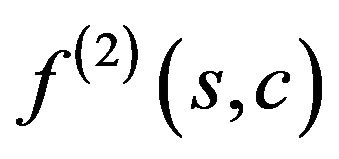 form basic branches of “tree”. The possible branching points of branching-off solutions are shown on these branches.
form basic branches of “tree”. The possible branching points of branching-off solutions are shown on these branches.
3.2. Radiating System with a Flat Aperture
3.2.1. Basic Equations and Relations
Consider according with [55-58] the synthesis problems of a flat aperture assuming that form of aperture 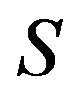 is known and a field has elliptical polarization. Let the plane in which aperture is located, coincides with the plane
is known and a field has elliptical polarization. Let the plane in which aperture is located, coincides with the plane 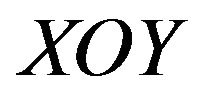 of the Cartesian coordinate system. Then the radiated field in the far zone can be represented by the formula [6]:
of the Cartesian coordinate system. Then the radiated field in the far zone can be represented by the formula [6]:
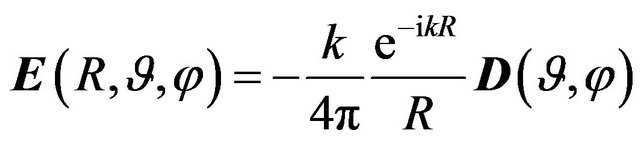 where
where
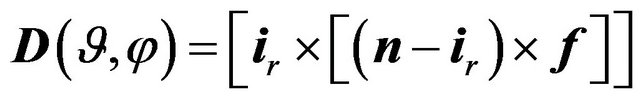 ,
,
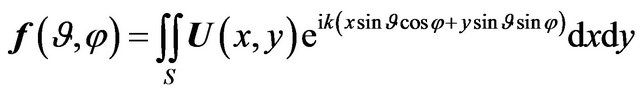 , (52)
, (52)
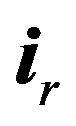 is radial ort of spherical coordinate system,
is radial ort of spherical coordinate system,  ,
, 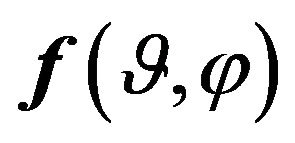 is a vector DP of flat aperture
is a vector DP of flat aperture . Since
. Since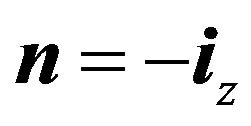 , function
, function 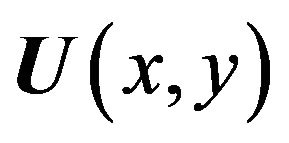 describes the tangential component of the electric vector
describes the tangential component of the electric vector  or vector of current flowing through the aperture
or vector of current flowing through the aperture :
:
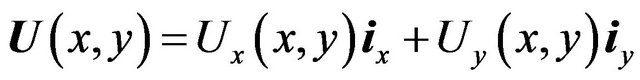 . (53)
. (53)
Introducing in a far zone special coordinate system [6] ,
,  ,
,  connected with orts of spherical coordinate system by formulas
connected with orts of spherical coordinate system by formulas
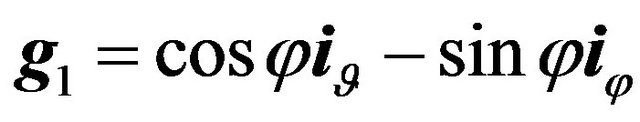 ,
, 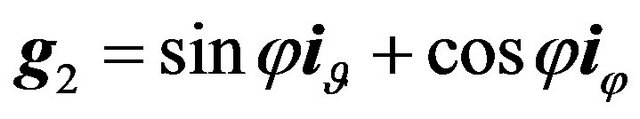 ,
,
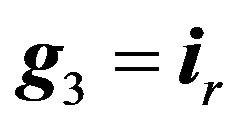 (54)
(54)
enables the vector synthesis problem to reduce to two independent scalar synthesis problems.
Obviously, the system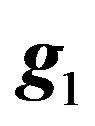 ,
, 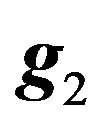 ,
,  is orthonormal, and transformation (54) is rotation of spherical coordinate system on an angle
is orthonormal, and transformation (54) is rotation of spherical coordinate system on an angle 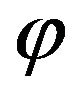 around the vector
around the vector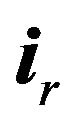 . At that vector
. At that vector  in the coordinate system (54) has the form [6]
in the coordinate system (54) has the form [6]
 , (55)
, (55)
where
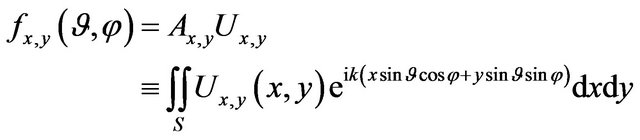 . (56)
. (56)
For mappings (56) the Parseval equality [59]:
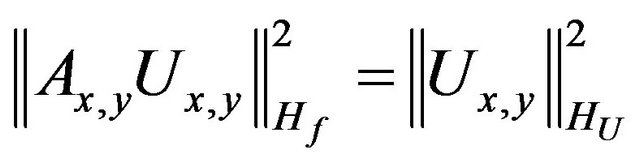 (57)
(57)
are valid, that is operators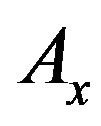 ,
,  are isometric.
are isometric.
Consider the synthesis problem of a flat aperture, in which component-wise deviation of modules given and synthesized diagrams is taken into account. As optimization criterion we choose the functional type
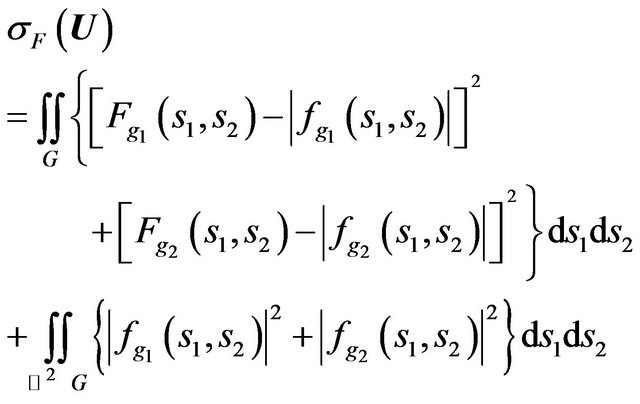 (58)
(58)
where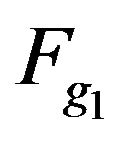 ,
, 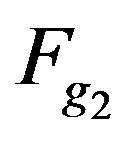 are modulus of components of the given amplitude DP
are modulus of components of the given amplitude DP 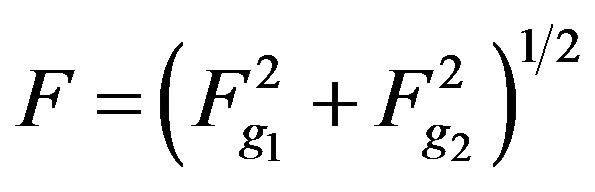 in closed domain
in closed domain
 . This criterion provides not only proximity of modules of given
. This criterion provides not only proximity of modules of given  and synthesized
and synthesized 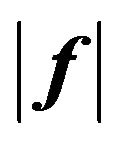 DP’s, but it allows certain to influence on the polarization characteristics of the radiated field [5]. On the base of the necessary minimum condition of the functional (58) and the corresponding transformation we obtain system equations (these equations is not connected between themselves) concerning components of synthesized DP:
DP’s, but it allows certain to influence on the polarization characteristics of the radiated field [5]. On the base of the necessary minimum condition of the functional (58) and the corresponding transformation we obtain system equations (these equations is not connected between themselves) concerning components of synthesized DP:
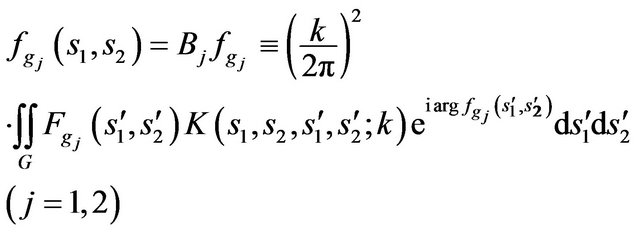 (59)
(59)
where

(60)
is a kernel. In the case of rectangular aperture the kernel  takes the form
takes the form
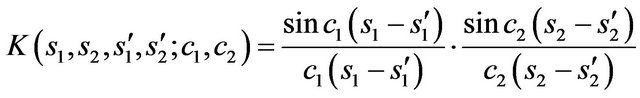 (61)
(61)
where
 (62)
(62)
are real numeric parameters characterizing the sizes of aperture ,
, 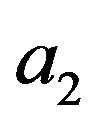 in wavelengths,
in wavelengths, 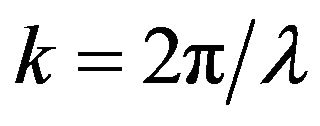 is wave number,
is wave number, 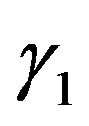 ,
, 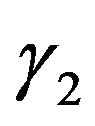 are angles that characterize the domain
are angles that characterize the domain  (solid angle), in which different from the identity components of amplitude DP
(solid angle), in which different from the identity components of amplitude DP 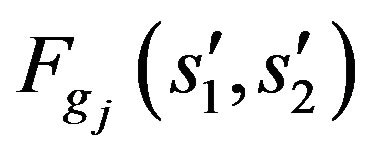 are given.
are given.
Later on we omit index in (59) and shall investigate the solutions of one equation
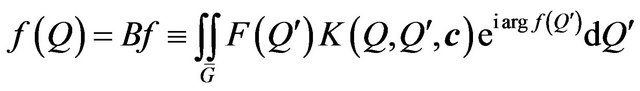 , (63)
, (63)
where for reduction of records we introduce the following notations
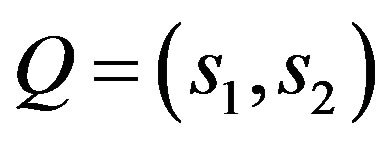 ,
, 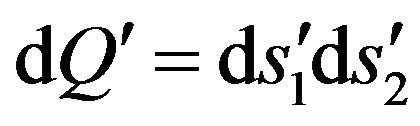 ,
,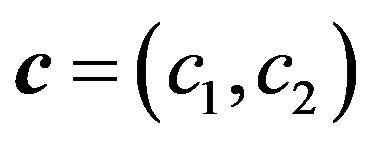 .
.
Thus, the synthesis problem of flat radiating system with arbitrary polarization of irradiation according to the prescribed amplitude DP is reduced to two independent and simpler synthesis problems with linearly polarized fields in the aperture.
Equation (63) is a nonlinear two-dimensional integral equation of the Hammerstein type and it has nonunique solutions. Their quality and properties depend on the form of aperture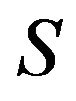 , the values of parameters
, the values of parameters 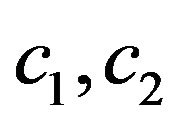 and properties of given amplitude DP
and properties of given amplitude DP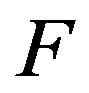 .
.
On the base of decomplexification [14] we shall consider the complex space 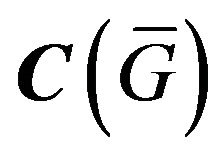 as a direct sum of two real spaces of continuous functions
as a direct sum of two real spaces of continuous functions
 in the domain
in the domain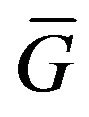 . The elements of this space are written as:
. The elements of this space are written as: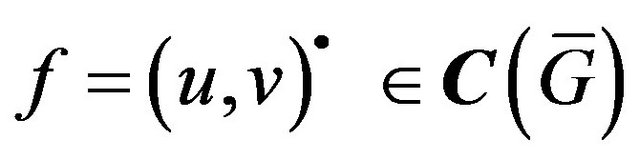 ,
,
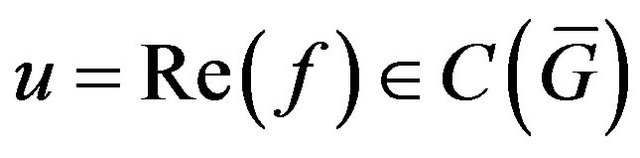 ,
,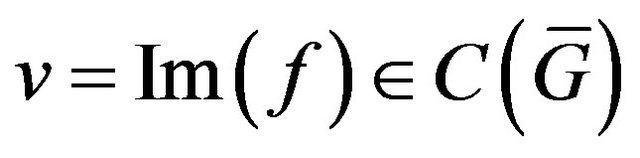 . Norms in these spaces have the form:
. Norms in these spaces have the form:
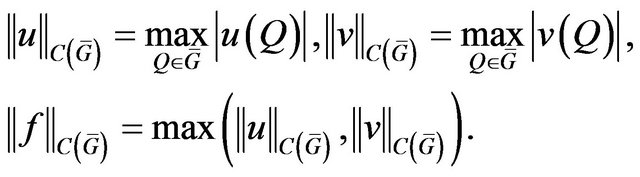 (64)
(64)
Equation (63) in the decomplexified space  is reduced to equivalent to it system of equations
is reduced to equivalent to it system of equations
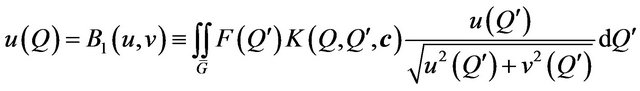 ,
,
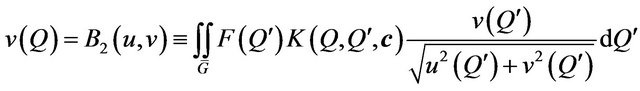 .
.
(65)
Denote the closed convex set of continuous functions as 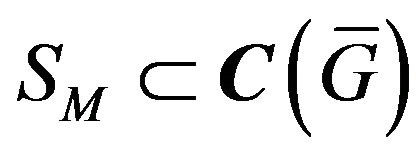 setting that
setting that
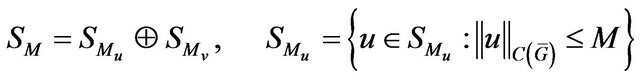 ,
,
 ,
,
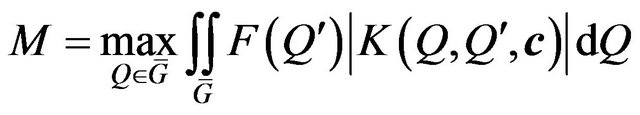 .
.
Consider one of the properties of the function 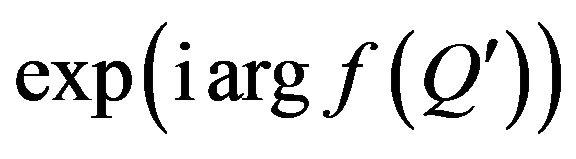 that included in (62) at
that included in (62) at . Obviously,
. Obviously,
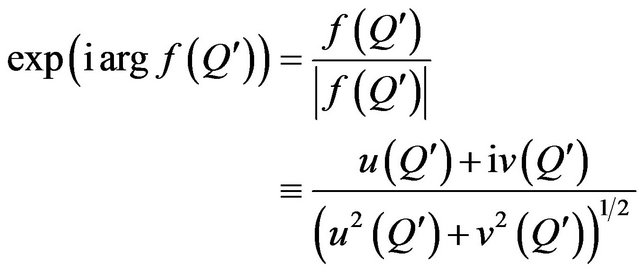 (66)
(66)
is a continuous function if 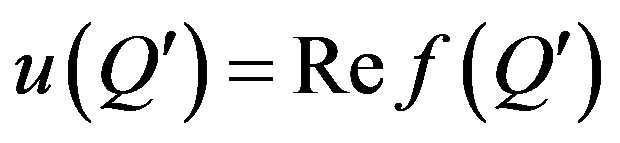 and
and
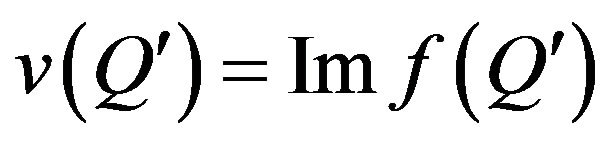 are continuous functions, at that
are continuous functions, at that
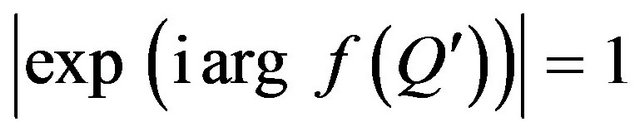 for any
for any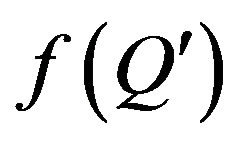 . If
. If 
and 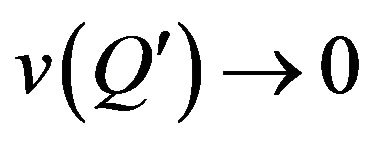 simultaneously, then
simultaneously, then 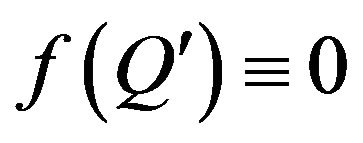 is a complex zero with undefined argument by definition [60, p. 20]. On this basis at
is a complex zero with undefined argument by definition [60, p. 20]. On this basis at 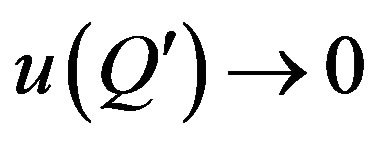 and
and 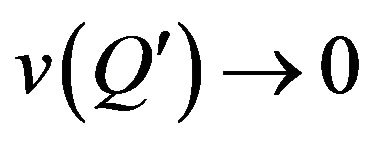 we redefine
we redefine 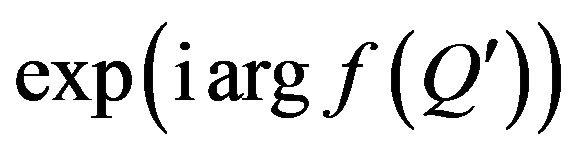 as function, module of which is equal to one and argument is undefined.
as function, module of which is equal to one and argument is undefined.
Theorem 3.1. The operator 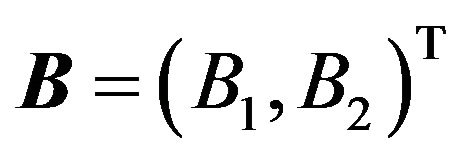 determined by the formulas (65) maps a closed convex set
determined by the formulas (65) maps a closed convex set  of the Banach space
of the Banach space  in itself and it is completely continuous.
in itself and it is completely continuous.
As the corollary from the Theorem 3.1 follows satisfaction of conditions of the Schauder principle [14, p.
411] according to which the operator  has a fixed point
has a fixed point  belonging to the set
belonging to the set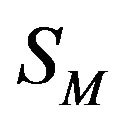 . This point is a solution of a system of (65) and (63), respectively.
. This point is a solution of a system of (65) and (63), respectively.
Easily to be convinced that function
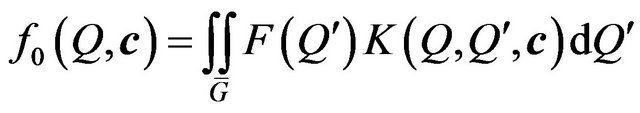 (67)
(67)
is one of solutions of (63) in the case of symmetric domain .
.
In [56,58] it is shown that the operator

is positive on the cone of nonnegative functions  of the space
of the space 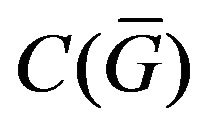 [61]. According to this the operator
[61]. According to this the operator  leaves invariant cone
leaves invariant cone , that is
, that is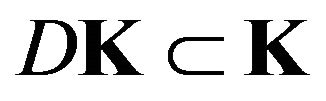 . Since
. Since , the primary solution
, the primary solution 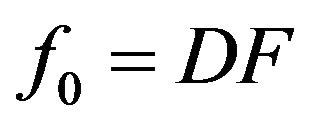 is also nonnegative function in the domain
is also nonnegative function in the domain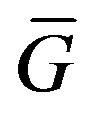 .
.
To find the branching lines and complex solutions of (63) that branch-off from the real (primary) solution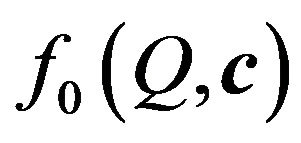 , we shall consider the problem on finding such a set of parameter values
, we shall consider the problem on finding such a set of parameter values 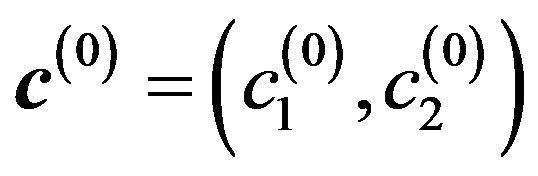 and all different from
and all different from  solutions of (65) that at
solutions of (65) that at
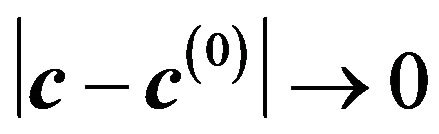 satisfy the conditions
satisfy the conditions
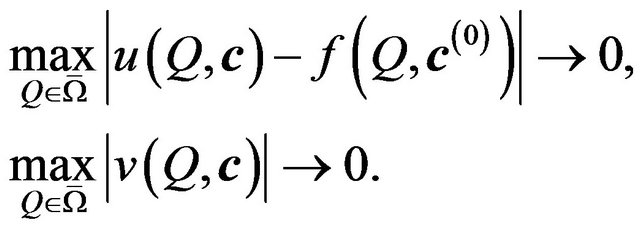 (68)
(68)
These conditions indicate the need to find such small continuous in  solutions,
solutions,
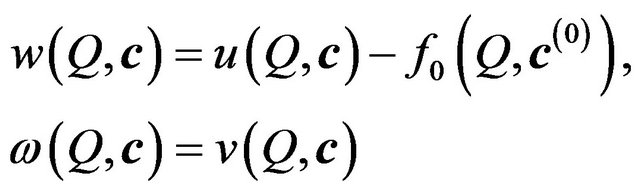 (69)
(69)
which converge uniformly to zero as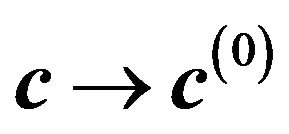 . At that it should take into account also the direction of movement of vector
. At that it should take into account also the direction of movement of vector  to vector
to vector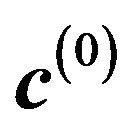 .
.
Set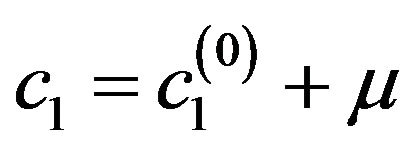 ,
, 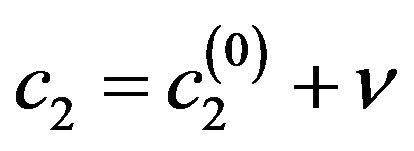 , and desired solutions we find in the form
, and desired solutions we find in the form
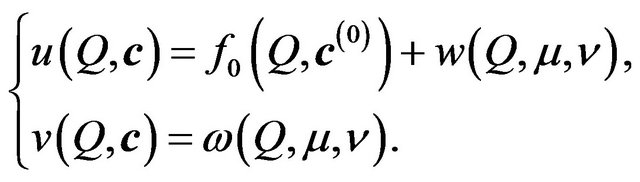 (70)
(70)
We write the system of nonlinear integral equations of Lyapunov-Schmidt with respect to small solutions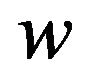 ,
,  as
as

(71)

(72)
Here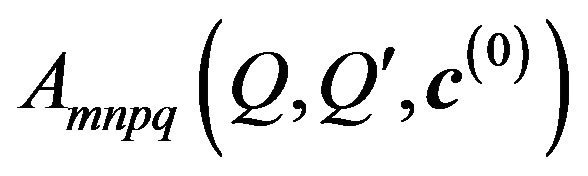 ,
, 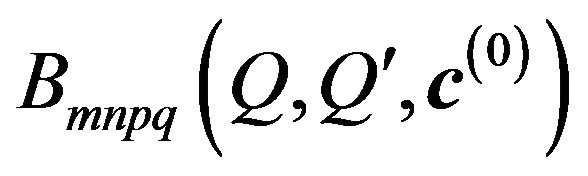 are coefficients of expansion of integrand functions of (65) in uniform convergent power series.
are coefficients of expansion of integrand functions of (65) in uniform convergent power series.
The problem on finding the set of possible branching points of solutions of (71) and (72) is reduced [56,58] to find the eigenvalues of two-dimensional linear homogeneous integral equation
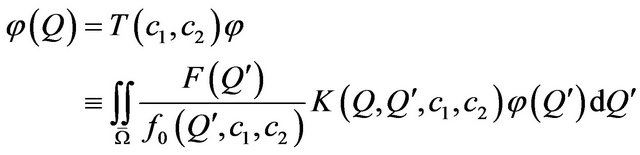 (73)
(73)
at condition . Eigenfunctions of (73) are used [58] at the construction of branching-off solutions of (71) and (72).
. Eigenfunctions of (73) are used [58] at the construction of branching-off solutions of (71) and (72).
3.2.2. Nonlinear Two-Parameter Spectral Problem
Note that (73) in the general case is a nonlinear two-parameter spectral problem. For the numerical finding the approximate solutions it is necessary to construct its digitization and consider the corresponding problem in finite-dimensional spaces. It should be noted that in the literature, in particular in [62,63], more attention is given to the construction of numerical methods for solving the nonlinear one-parameter problems.
In [64-67] a general method for finding the approximate solutions of (73), which may be applicable to a wide range of nonlinear two-parameter spectral problems is proposed.
Denote the spectral parameters as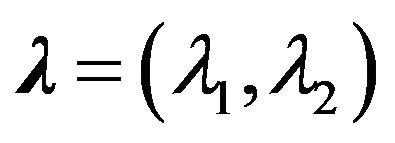 . Let E and V are complex Banach spaces, and the vector parameter
. Let E and V are complex Banach spaces, and the vector parameter  belongs to domain (open connected set)
belongs to domain (open connected set) 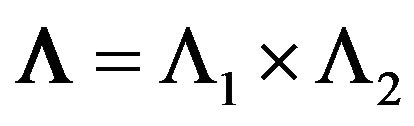 of the complex space
of the complex space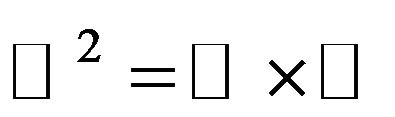 , where
, where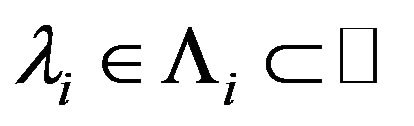 ,
, 
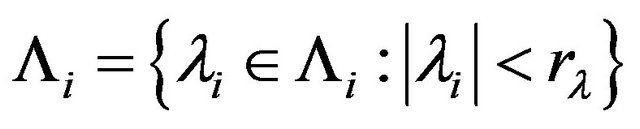 ,
, 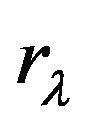 is some real constant. Consider the operator-function
is some real constant. Consider the operator-function , where to every
, where to every 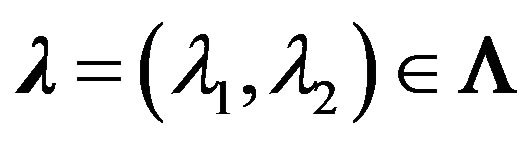 is put in correspondence operator
is put in correspondence operator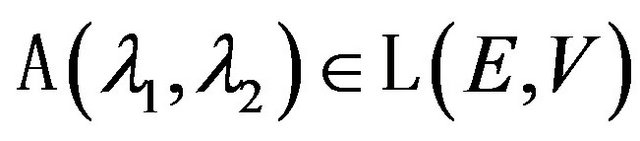 .
.
Here the space of linear bounded operators [14] is marked as .
.
We shall consider the nonlinear two-parameter spectral problem of the form
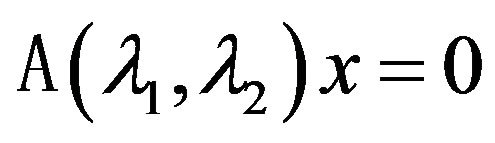 , (74)
, (74)
where necessary to find the eigenvalues
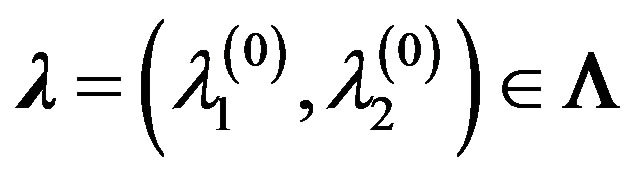 and corresponding eigenvectors
and corresponding eigenvectors

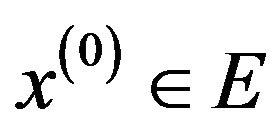 such that
such that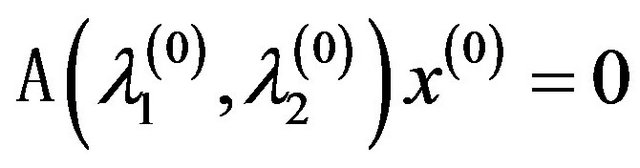 .
.
Let the Banach spaces 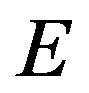 and
and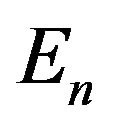 ,
, 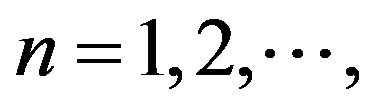 be given and also a system
be given and also a system 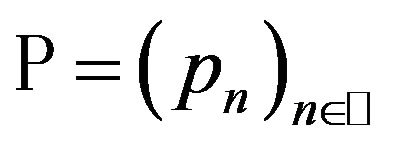 of linear bounded operators
of linear bounded operators 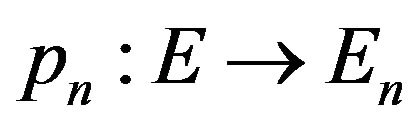 such that
such that
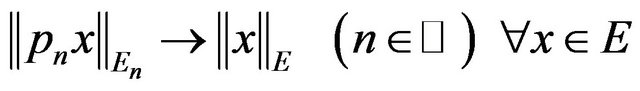 . (75)
. (75)
Operators  are called connecting [14,68]. Note, by the principle of uniform boundedness [14] with (73) follows inequality
are called connecting [14,68]. Note, by the principle of uniform boundedness [14] with (73) follows inequality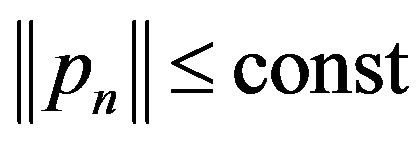 . Let in every space
. Let in every space 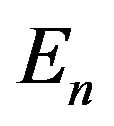 the element
the element 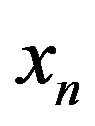 be selected. Writing these elements in order to increase the numbers we shall form a sequence
be selected. Writing these elements in order to increase the numbers we shall form a sequence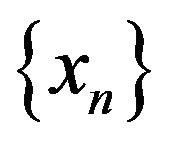 .
.
Let element 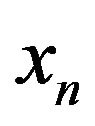 is selected in each space
is selected in each space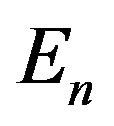 . Writing these elements in ascending numerical order, we form sequence
. Writing these elements in ascending numerical order, we form sequence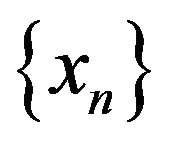 .
.
Definition 3.1 [68]. The sequence 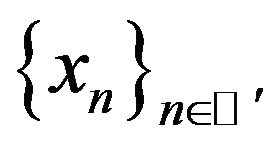 from
from 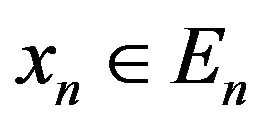
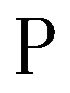 –converges (discrete converges) to
–converges (discrete converges) to 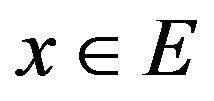 if
if
 ; we denote
; we denote 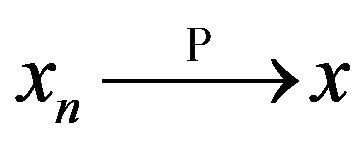
 .
.
Definition of different types of convergence of operators 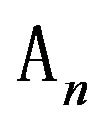 to
to  is given in [68]. Later on only required in further definition of stable convergence2
is given in [68]. Later on only required in further definition of stable convergence2 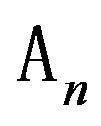 to
to  is presented.
is presented.
Discretization of initial problem (74), the choice of the space 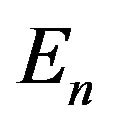 and definition of operators
and definition of operators 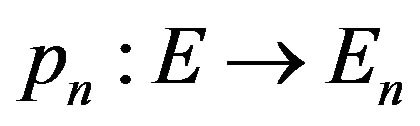 can be differentially. In particular, one of the approaches to the digitization of (74) if the operator-function
can be differentially. In particular, one of the approaches to the digitization of (74) if the operator-function 
is described by formula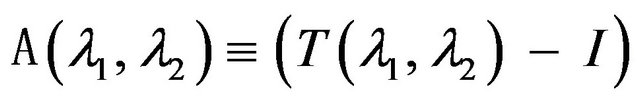 where
where 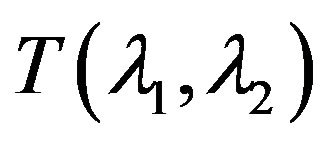 is a linear continous operator and
is a linear continous operator and 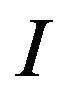 is unique operator in the separable (infinite-dimensional) Hilbert space
is unique operator in the separable (infinite-dimensional) Hilbert space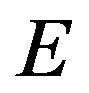 , consists in following. Take an arbitrary complete orthonormal system of functions
, consists in following. Take an arbitrary complete orthonormal system of functions 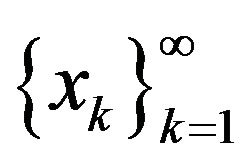 in
in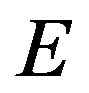 . Each element
. Each element 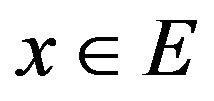 is represented as a series
is represented as a series
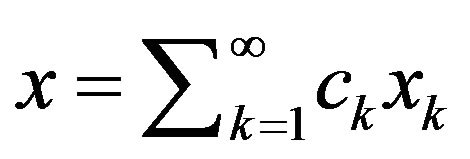 , where
, where 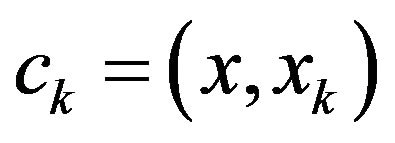 is Fourier coefficient of element
is Fourier coefficient of element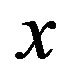 . Since
. Since 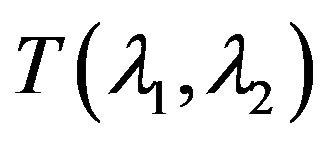 is linear continuous operator acting in separable Hilbert space, it admits the matrix representation [69]:
is linear continuous operator acting in separable Hilbert space, it admits the matrix representation [69]:
 , (76)
, (76)
where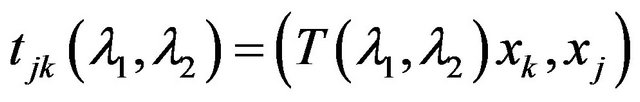 . At that sequence of the Fourier coefficients of element
. At that sequence of the Fourier coefficients of element 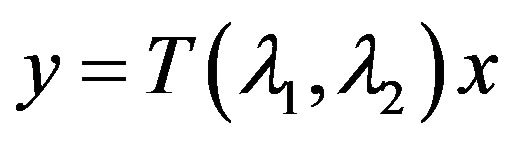 is obtained from the sequence of Fourier coefficients of element x by means transformation matrix
is obtained from the sequence of Fourier coefficients of element x by means transformation matrix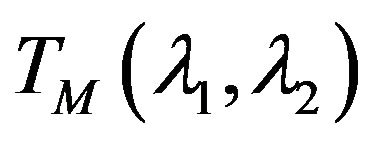 .
.
Using the matrix representation of the operator 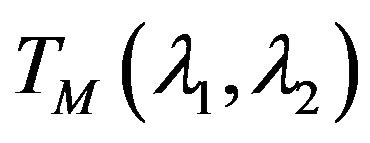 in particular case (concerning Equation (73)) the spectral problem (74) is formulated as
in particular case (concerning Equation (73)) the spectral problem (74) is formulated as
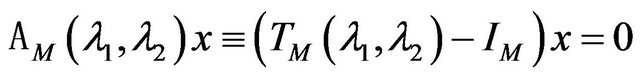 , (77)
, (77)
where 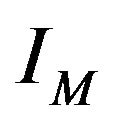 is identity matrix in the space of sequences
is identity matrix in the space of sequences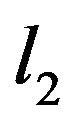 . Thus, the operators
. Thus, the operators 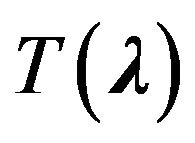 and
and 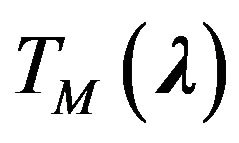 are equivalent in the sense that they put in correspondence one and the same element
are equivalent in the sense that they put in correspondence one and the same element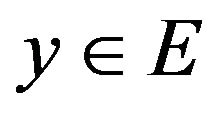 , but we obtain the Fourier coefficients of element
, but we obtain the Fourier coefficients of element  as a result of operation of operator
as a result of operation of operator 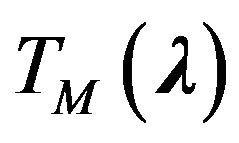 on element
on element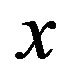 . Obviously, that the spectrums of these operators coincide, that is the spectral problem (77) and the problem
. Obviously, that the spectrums of these operators coincide, that is the spectral problem (77) and the problem

are equivalent.
According to [14,68] applying to the problem (74) other discretization methods, including the following: quadrature (cubature) processes in the case of homogeneous integral equations and changing the derivatives by difference analogues in differential equations, we obtain the approximation problems for approximate finding the eigenvalues and eigenfunctions in finite-dimensional spaces
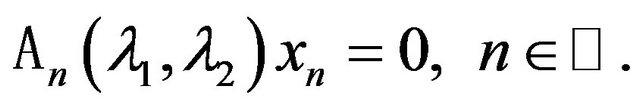 (78)
(78)
At that the problem on finding the eigenvalues is reduced to finding the roots of the 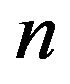 -th order determinant, i.e. the roots of the equation
-th order determinant, i.e. the roots of the equation
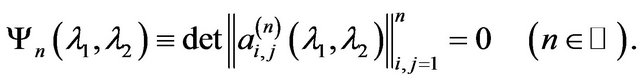 (79)
(79)
Consider the necessary in further auxiliary one-parameter spectral problem as a particular case of (74). Set that variable 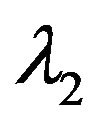 in the operator-function
in the operator-function 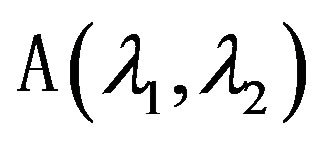 is expressed by some unique differentiable function
is expressed by some unique differentiable function
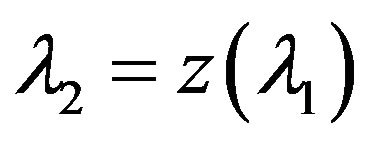 mapping domain
mapping domain 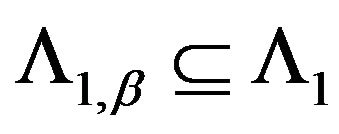 in some subdomain
in some subdomain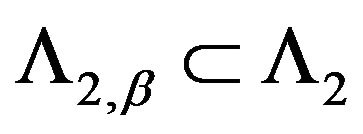 . In the simplest case we put
. In the simplest case we put 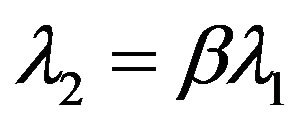 , where
, where  is a real parameter. Introduce into consideration at
is a real parameter. Introduce into consideration at 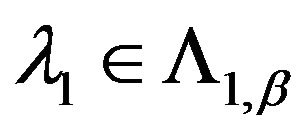 operator function
operator function
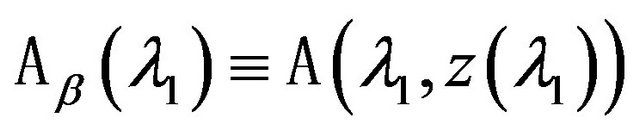 (narrowing of operator-function
(narrowing of operator-function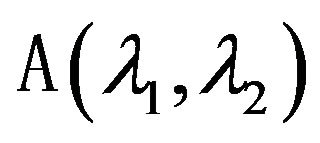 ). One-parameter nonlinear spectral problem
). One-parameter nonlinear spectral problem
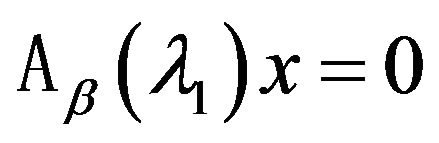 (80)
(80)
is connected with it. Here to each value
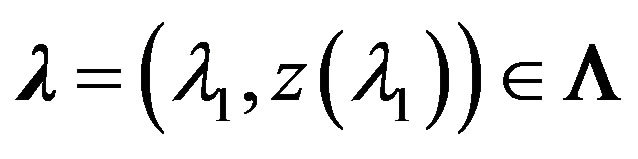 operator
operator 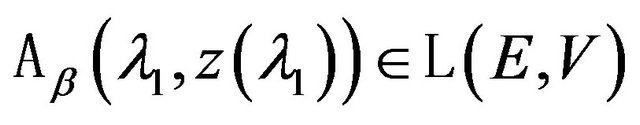 is put in correspondence.
is put in correspondence.
Analogously to (78) we consider approximating sequence of discretizing problems (80) at 
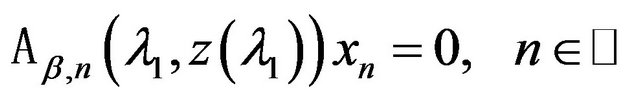 . (81)
. (81)
The spectrum of operator-function 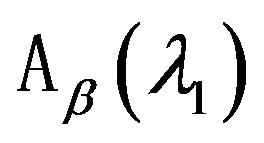 is denoted as
is denoted as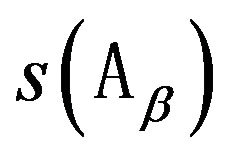 . Suppose that
. Suppose that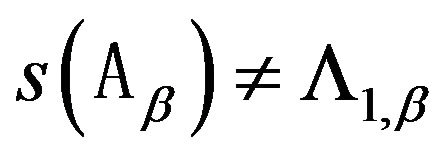 . For spectral
. For spectral 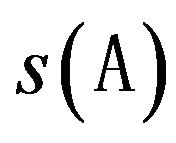 of (74) holds [56,67].
of (74) holds [56,67].
Theorem 3.2. Let the following conditions be satisfied:
1) operator-function  is holomorphic, and
is holomorphic, and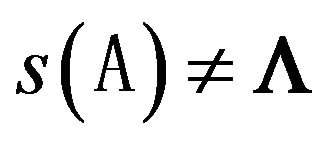 ;
;
2) operator-functions  are holomorphic and for any closed bounded set
are holomorphic and for any closed bounded set 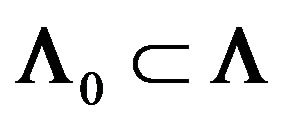 the following inequality
the following inequality

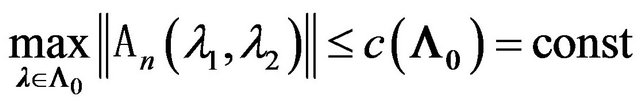 is valid;
is valid;
3) operators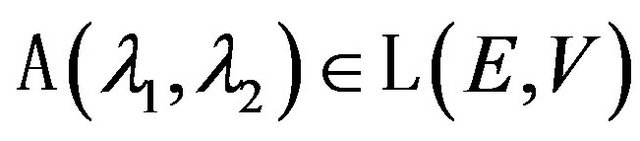 ,
,

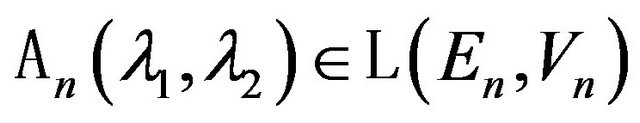 are the Fredholm operators with zero index for any
are the Fredholm operators with zero index for any ;
;
4) spectrum 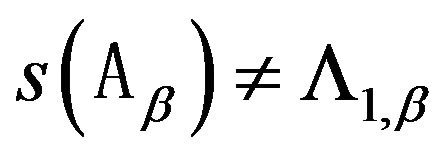 and a sequence of functions
and a sequence of functions 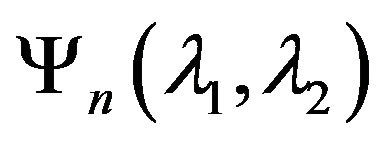 are differentiable in the domain
are differentiable in the domain ;
;
5)  is stable for any
is stable for any
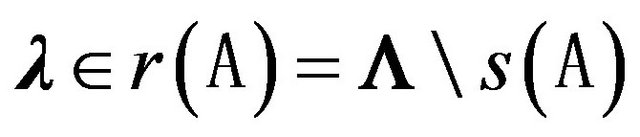 .
.
Then the following statements are true:
1) every point of spectrum 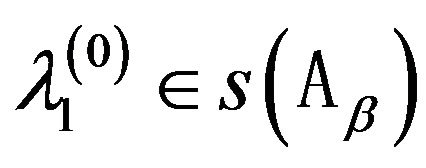 is isolated, it is eigenvalue of the operator
is isolated, it is eigenvalue of the operator , the finite-dimensional eigensubspace
, the finite-dimensional eigensubspace  and the finite-dimensional root subspace correspond to it;
and the finite-dimensional root subspace correspond to it;
2) for each 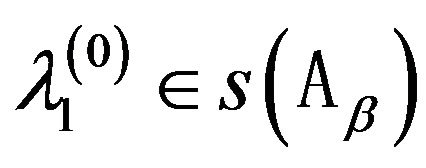 there exists a sequence
there exists a sequence
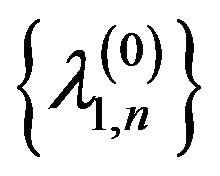 from
from 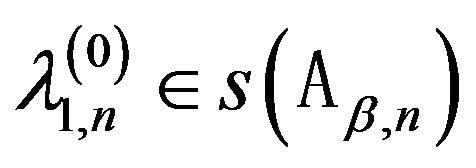
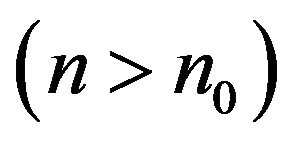 , such that
, such that
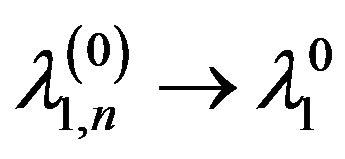 ;
;
3) each point 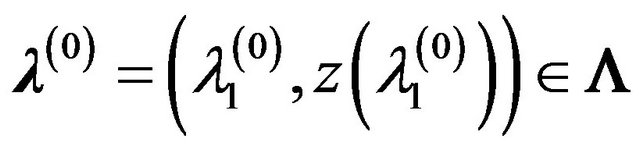 is a spectrum point of the operator-function
is a spectrum point of the operator-function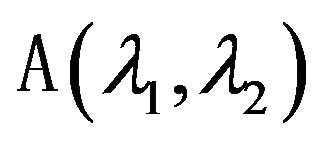 ;
;
4) if in some small  -neighborhood of the point
-neighborhood of the point
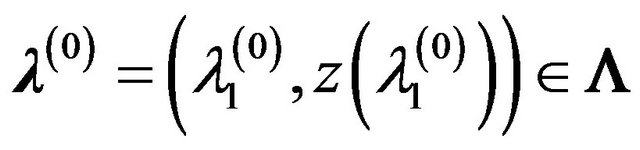 at all n larger any number
at all n larger any number 
(corresponding , according to definition of limit of sequence p. 2)) the sequence of partial derivates
, according to definition of limit of sequence p. 2)) the sequence of partial derivates
 is nonzero, then in an arbitrarily small
is nonzero, then in an arbitrarily small  -neighborhood of point
-neighborhood of point 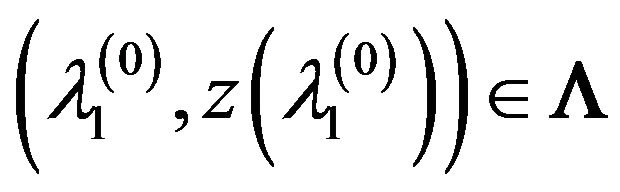 there exists a continuous differentiable function
there exists a continuous differentiable function
 , which is solution of (89), at that
, which is solution of (89), at that
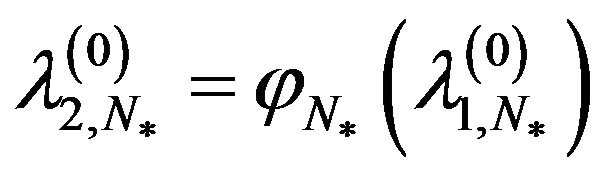 and at the point
and at the point
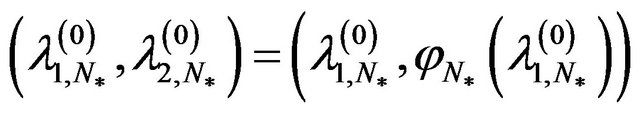 however little differs from point of a spectrum of auxiliary one-parameter problem (91)
however little differs from point of a spectrum of auxiliary one-parameter problem (91) ; that is in some bicylindrical domain
; that is in some bicylindrical domain
 there exists a connected component of spectrum of the operator-function
there exists a connected component of spectrum of the operator-function 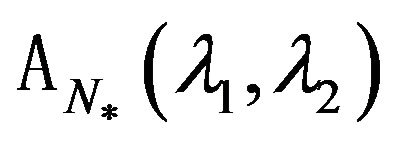 (
( ,
,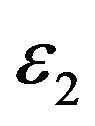 are small real constants).
are small real constants).
Proof. The proof of the theorem is given in [56] and is based on Theorems 1 and 2 with [68, pp. 68-69] and the Theorem about existence of implicit function (see, for example, [70]).
If the points 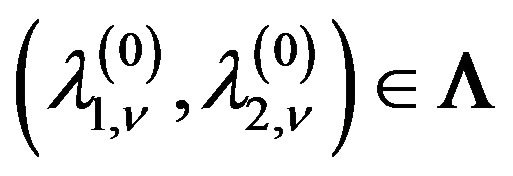 are the eigenvalues of
are the eigenvalues of
(78) and derivatives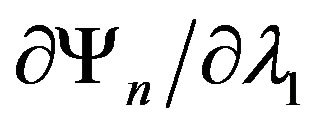 ,
, 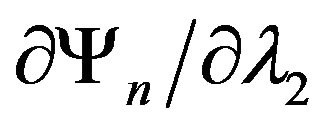 in these points are nonzero, to find connected components of the spectrum of this problem on the base of (79) Cauchy problem [56,57,65] we solve the in a neighborhood of each point
in these points are nonzero, to find connected components of the spectrum of this problem on the base of (79) Cauchy problem [56,57,65] we solve the in a neighborhood of each point 
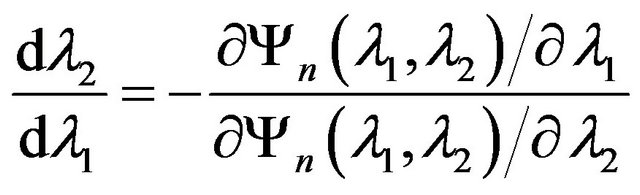 , (82)
, (82)
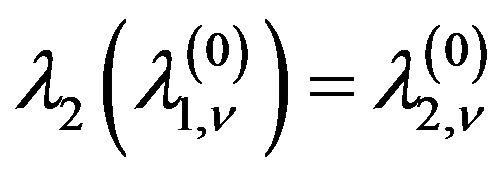 . (83)
. (83)
3.2.3. Numerical Algorithms for Finding the Possible Branching Lines of Solutions
Return to finding the solutions of (73), in which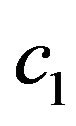 ,
, 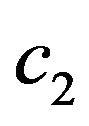 are spectral parameters. Let
are spectral parameters. Let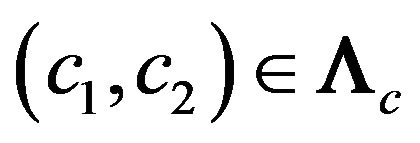 ,
,
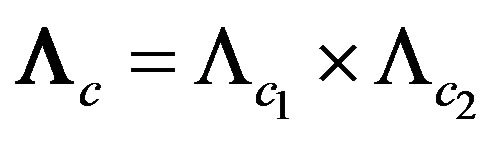 , where
, where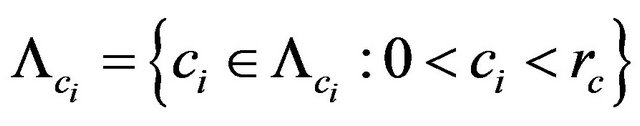 . By direct check we set that for arbitrary values of the parameters
. By direct check we set that for arbitrary values of the parameters 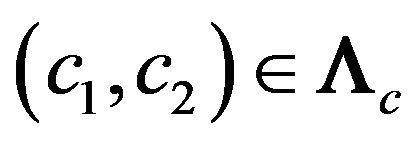 the function
the function
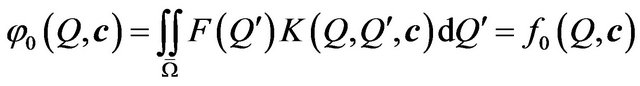 (84)
(84)
is one of the eigenfunctions, that is there exists a connected set of the spectrum, coinciding with the domain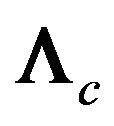 . As a result of this, the condition
. As a result of this, the condition 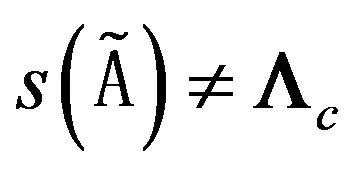 is not satisfied. To find another connected components of spectrum we exclude eigenfunction (73) from the kernel of integral equation, namely, consider the equation
is not satisfied. To find another connected components of spectrum we exclude eigenfunction (73) from the kernel of integral equation, namely, consider the equation
 , (85)
, (85)
where
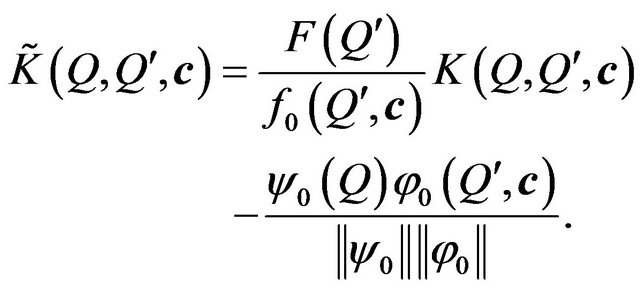 (86)
(86)
Here 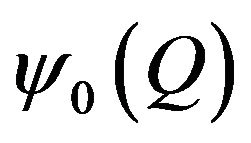 is adjoint with (73) eigenfunction of equation of From Lemma Schmidt [53, p. 132] follows that from spectrum of operator
is adjoint with (73) eigenfunction of equation of From Lemma Schmidt [53, p. 132] follows that from spectrum of operator  is excluded coherent component coinciding with the domain
is excluded coherent component coinciding with the domain  and the corresponding to the function
and the corresponding to the function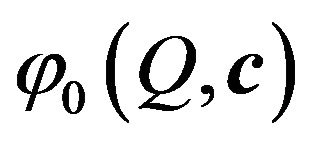 .
.
Using to (73) certain convergent cubature process with coefficients 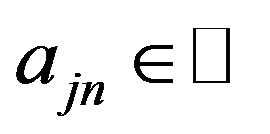 and nodes
and nodes 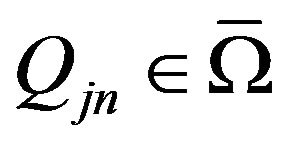
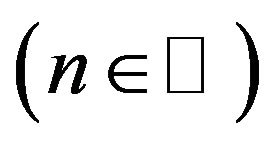 and rejecting in it remainder, we obtain homogeneous system of linear algebraic equations (SLAE)
and rejecting in it remainder, we obtain homogeneous system of linear algebraic equations (SLAE)
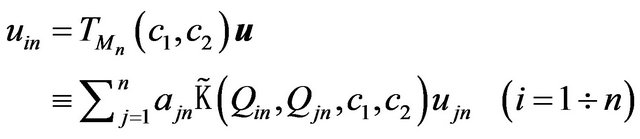 , (87)
, (87)
where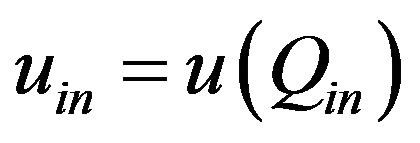 .
.
The presence of such values of parameters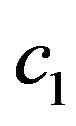 ,
, 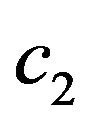 , which are the solutions of the equation
, which are the solutions of the equation
 , (88)
, (88)
is necessary condition of the existence different from zero solutions of (87). We consider (88) as the problem on finding the implicitly given function , reducing it to the Cauchy problem (82) and (83). Putting
, reducing it to the Cauchy problem (82) and (83). Putting 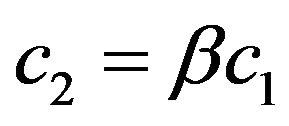 in (85), we shall consider the auxiliary oneparameter spectral problem
in (85), we shall consider the auxiliary oneparameter spectral problem
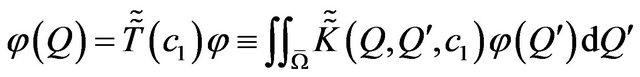 solutions of which we use as initial conditions in the Cauchy problem (83). Corresponding this equation SLAE has the form
solutions of which we use as initial conditions in the Cauchy problem (83). Corresponding this equation SLAE has the form
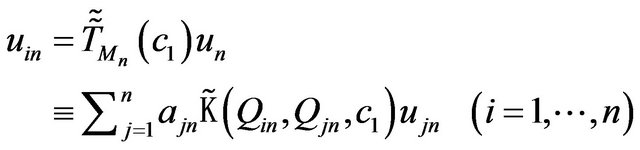 , (89)
, (89)
and the problem on finding the eigenvalues of this system is reduced to finding the roots of the equation
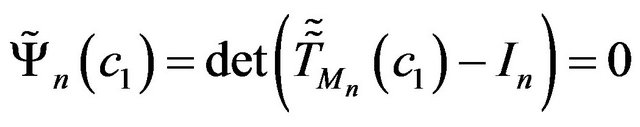 . For the numerical solution of the Cauchy problem (82) and (83) are used the Runge-Kutta and Adams methods.
. For the numerical solution of the Cauchy problem (82) and (83) are used the Runge-Kutta and Adams methods.
We shall present numerical examples of finding the solutions of (73) for two given amplitude DP’s. In Figures 3 and 4 are shown spectral lines of (73), corresponding the given DP 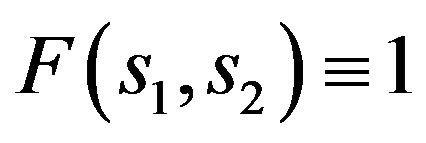 and given DP which is defined by the formula:
and given DP which is defined by the formula:

(90)
Note that to each point of the spectral lines given in these figures correspond the eigenfunctions of (73) with the characteristic properties for each line. For example, below are shown the eigenfunctions that correspond to points of intersection of the spectral lines 1 and 2 (Figures 3 and 4) with the beam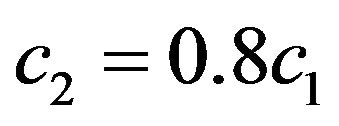 .
.
3.2.4. Variational Approach to Solution of the Nonlinear Spectral Problems
In [71,72] along with the implicit functions method a variational approach to solution of the nonlinear oneparameter and two-parameter spectral problems on finding the eigenvalues 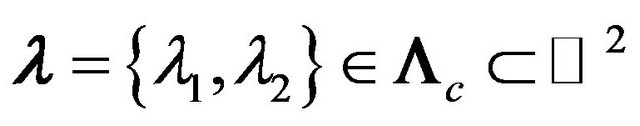 and eigenelements
and eigenelements 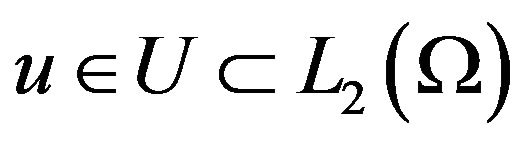 of equation
of equation
 (91)
(91)
in the real Hilbert space 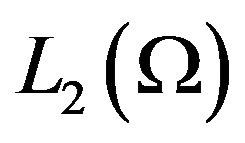 for the case when
for the case when 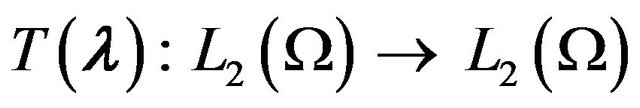 is a linear positive definite
is a linear positive definite

Figure 3. The possible branching lines of solutions of system of (65) for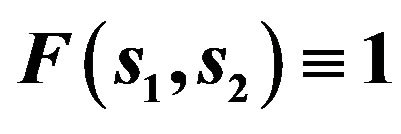 .
.
c2 c2 = c1

Figure 4. The possible branching lines of solutions of system of (65) for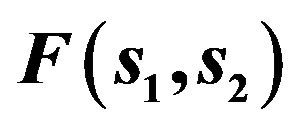 , which is defined by (90).
, which is defined by (90).
self-adjoint operator nonlinearly depending on the parameters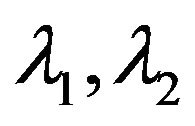 , is proposed. Variational problem is formulated as the problem on finding such values of parameter
, is proposed. Variational problem is formulated as the problem on finding such values of parameter 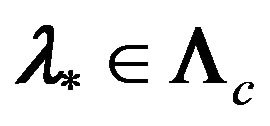 and such functions
and such functions 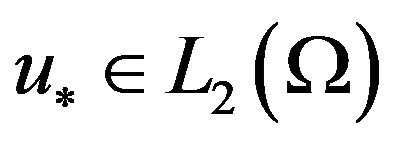 on which functional
on which functional
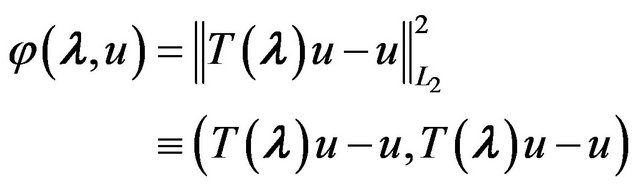 (92)
(92)
becomes minimum. The equivalence of the spectral problem (91) and put it in correspodence of variational problem (92) is proved. Based on the method of generalized coordinate descent iterative process for the numerical finding one of the eigenvalues and the corresponding eigenfunction of (91) is suggested. Local convergence is proved.
Example of use of a variational approach to finding the eigenvalues and eigenfunctions of (73) is shown in Figure 5 for 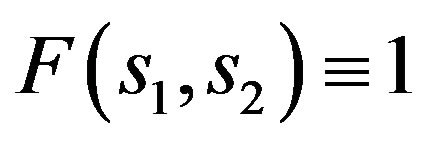 and in Figure 6 for the case when the function
and in Figure 6 for the case when the function 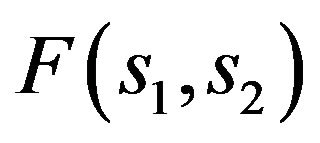 is defined by (90). Later on the eigenfunctions of (73), corresponding to eigenvalues belonging to curves 1, 3 illustrated in Figure 5(b) are shown. From the analysis of the figures we see that the eigenfunctions
is defined by (90). Later on the eigenfunctions of (73), corresponding to eigenvalues belonging to curves 1, 3 illustrated in Figure 5(b) are shown. From the analysis of the figures we see that the eigenfunctions 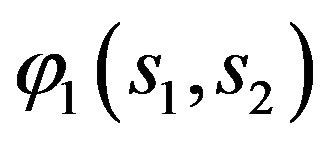 are odd by argument
are odd by argument 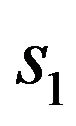 and functions
and functions 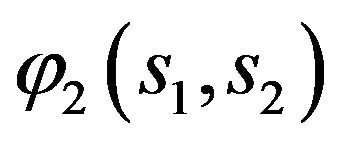 are odd by both arguments.
are odd by both arguments.
 (a)
(a) (b)
(b)
Figure 5. Normalized eigenfunctions of (73) corresponding to the eigenvalues: (а) (с1 = 3.14159393, с2 = 2.51327514); (b) (с1 = 3.64391021, с2 = 2.91512817).
 (a)
(a)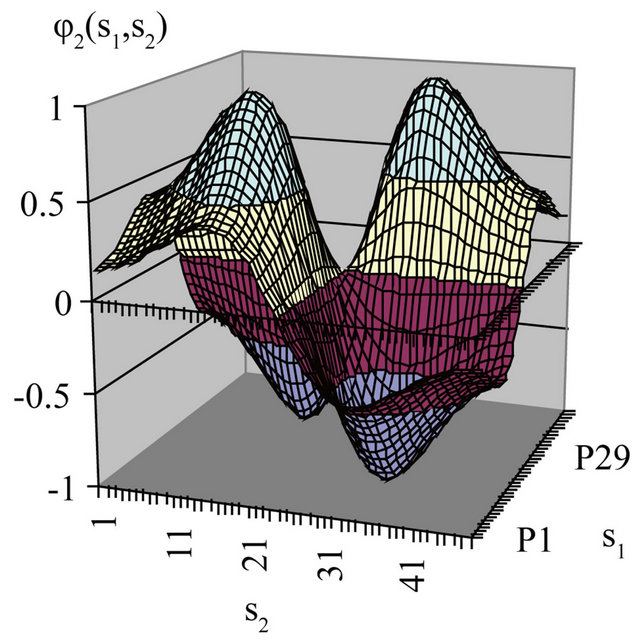 (b)
(b)
Figure 6. Normalized eigenfunctions of (73) corresponding to the eigenvalues: (a) (с1 = 3.43408813, с2 = 2.74727050); (b) (с1 = 4.18890991, с2 = 3.351127928).
Found by numerical method form and properties of eigenfunctions in the possible branching points are used to determine of the properties of branching-off in these points of solutions of nonlinear systems of (65).
3.3. About Branching of Solutions in the Case of a Flat Aperture
In [56,58,73,74] using the found branching lines and eigenfunctions, the analytical investigations of branching of the primary solution of the first type of (65) for the case when the the kernel 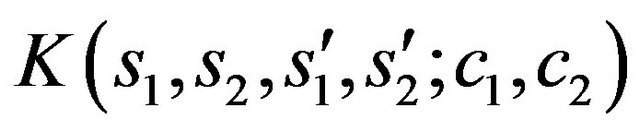 has the form (61), and the multiplicity of eigenvalues of the linear Equation (73) at the branching points
has the form (61), and the multiplicity of eigenvalues of the linear Equation (73) at the branching points 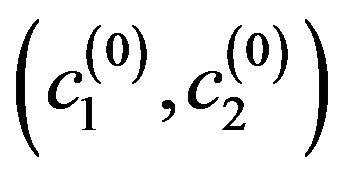 is two, are presented.
is two, are presented.
The study of solutions of (65) is realized on the beam 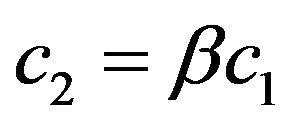 belonging to the domain
belonging to the domain . Let
. Let
 be eigenvalue of (73). We assign to parameter
be eigenvalue of (73). We assign to parameter  the small disturbance
the small disturbance
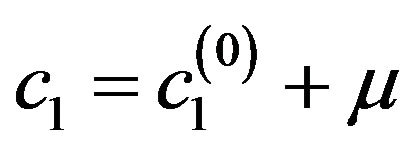 ,
, 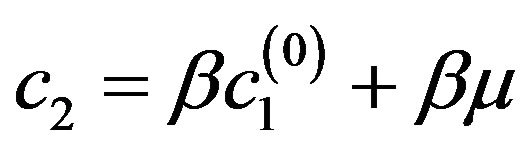 and consider the problem on finding all different from
and consider the problem on finding all different from  solutions of (65), which at
solutions of (65), which at 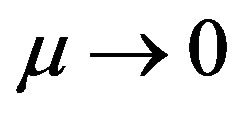 satisfy the conditions
satisfy the conditions
 ,
,
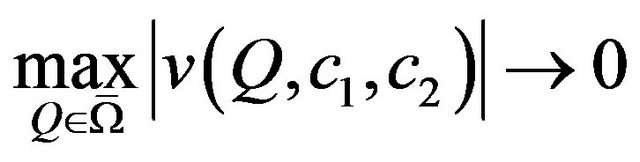 .
.
The system of (65) by means of expanding the integrand functions is reduced to the corresponding system of Lyapunov-Schmidt equations, similar to (71) and (72). Desired solutions are found in the form
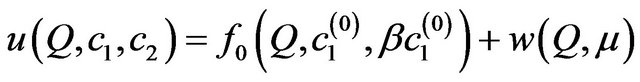 ,
,
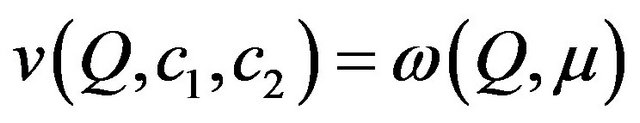 .
.
As a result we obtain [74] that at the points
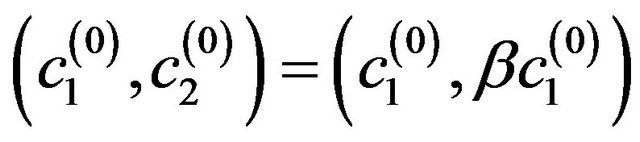 from the primary solution
from the primary solution
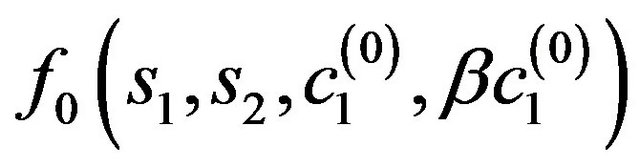 branch-off two complex-conjugate solutions having in the first approximation the form
branch-off two complex-conjugate solutions having in the first approximation the form
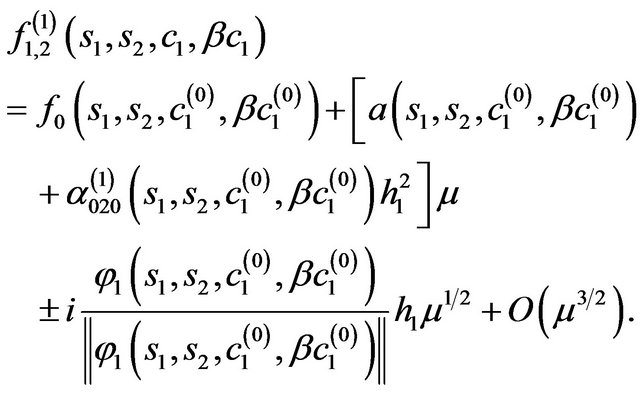 (93)
(93)
The imaginary part being determined by the properties of eigenfunctions . Functions
. Functions
 , obtained on the base of (93), determine the properties of the phase DP and APD of the field in aperture. The properties obtained in the first approximation of solutions agree with numerical results.
, obtained on the base of (93), determine the properties of the phase DP and APD of the field in aperture. The properties obtained in the first approximation of solutions agree with numerical results.
For example, in Figure 7 are shown the values of the functional 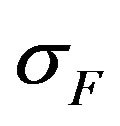 at
at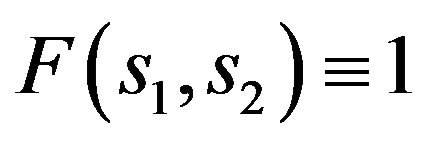 , which it takes on the primary (curve 1) and branching-off (curves 2, 3, 4) solutions on the beam
, which it takes on the primary (curve 1) and branching-off (curves 2, 3, 4) solutions on the beam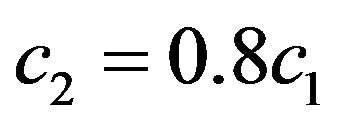 . Note, that on the segment
. Note, that on the segment 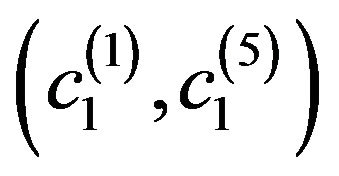 the branching-off solutions with an odd phase DP
the branching-off solutions with an odd phase DP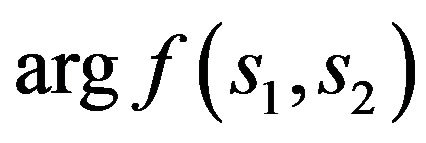 , to which the nonsymmetric amplitude-phase distribution of the field in aperture corresponds, are the most effective. On the segment
, to which the nonsymmetric amplitude-phase distribution of the field in aperture corresponds, are the most effective. On the segment 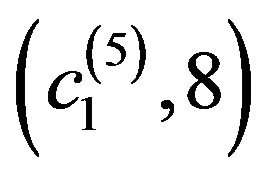 the most effective is the solution of 4 with properties
the most effective is the solution of 4 with properties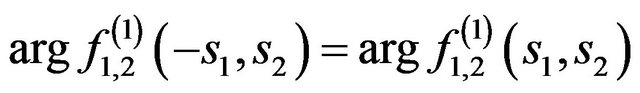 ,
,
 . The symmetric but complex APD of the field in aperture corresponds to it. From the analysis of Figure 7 follows that the same efficiency of the synthesis can be achieved on the branching-off solutions at smaller sizes of aperture and smaller values of parameters
. The symmetric but complex APD of the field in aperture corresponds to it. From the analysis of Figure 7 follows that the same efficiency of the synthesis can be achieved on the branching-off solutions at smaller sizes of aperture and smaller values of parameters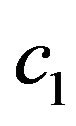 ,
, 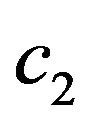 , than on the primary solution. The linear size of aperture can be decreased by the amount
, than on the primary solution. The linear size of aperture can be decreased by the amount 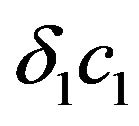 or
or  at realization of branching-off solution.
at realization of branching-off solution.
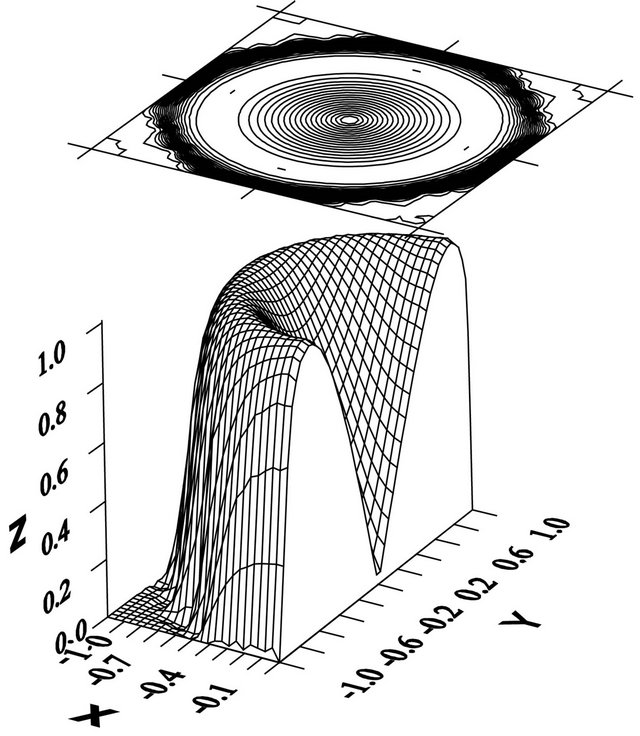
Numerical examples of synthesis of given funnelshaped amplitude DP defined in the domain 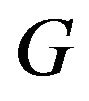 by (90), are given in Figures 8 and 9. The branching lines of solutions of (63) for this DP are shown in Figure 4. The given DP and optimum synthesized DP are presented in Figures 8(a) and (b), respectively, at
by (90), are given in Figures 8 and 9. The branching lines of solutions of (63) for this DP are shown in Figure 4. The given DP and optimum synthesized DP are presented in Figures 8(a) and (b), respectively, at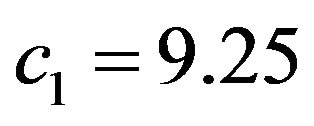 ,
, 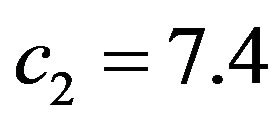 . The optimum amplitude distribution of the field in an aperture
. The optimum amplitude distribution of the field in an aperture , which creates given in Figure 8(b) the synthesized DP, is shown in Figure 9. From the analysis of these figures we see that the symmetric amplitude DP (Figure 8(b)) can be created by different distributions of the field in aperture of radiating system, including real and nonsymmetric distribution (Figure 9).
, which creates given in Figure 8(b) the synthesized DP, is shown in Figure 9. From the analysis of these figures we see that the symmetric amplitude DP (Figure 8(b)) can be created by different distributions of the field in aperture of radiating system, including real and nonsymmetric distribution (Figure 9).

Figure 7. The values of the functional 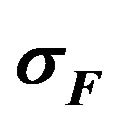 at
at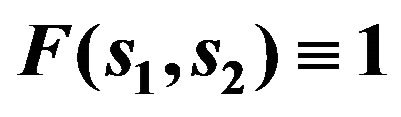 .
.
 (a)
(a)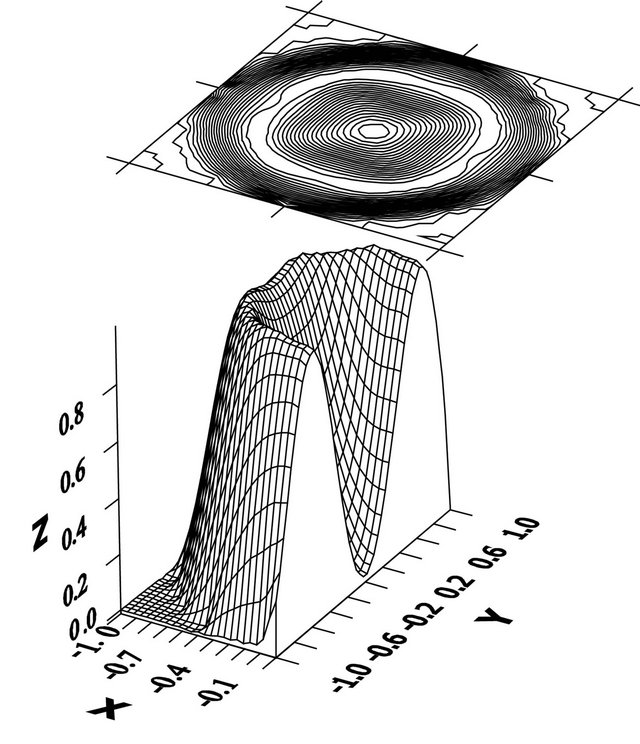 (b)
(b)
Figure 8. The prescribed (а) and synthesized (b) DP.

Figure 9. Amplitude distribution of field in aperture which creates DP given in Figure 8(b).
4. Synthesis of Discrete Radiating Systems— Antenna Arrays (AA)
The investigations of nonlinear synthesis problems of linear and planar antenna arrays (AA) according to the prescribed amplitude DP are presented partially in [7,24, 28-37]. In the basis of construction of mathematical models it is assumed [6,27] that the excitation of each radiator is characterized by a single complex number  - complex amplitude of excitation, the physical meaning of which depends on the type of radiating system. Taking into account the linearity of Maxwell’s equations, the complex amplitudes of excitation enter linearly in the expression for DP of array, that is
- complex amplitude of excitation, the physical meaning of which depends on the type of radiating system. Taking into account the linearity of Maxwell’s equations, the complex amplitudes of excitation enter linearly in the expression for DP of array, that is
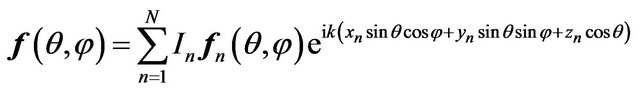 . (94)
. (94)
Here  is a vector DP of
is a vector DP of  -th radiator. Vector
-th radiator. Vector  is called the vector of excitation of array or vector of amplitude-phase distribution of currents in the array. Such formulation of DP of array is used in the synthesis problems with regard for mutual influence of radiators [27, 29,30]. Thus the problem on finding the functions
is called the vector of excitation of array or vector of amplitude-phase distribution of currents in the array. Such formulation of DP of array is used in the synthesis problems with regard for mutual influence of radiators [27, 29,30]. Thus the problem on finding the functions  is reduced to solution of the corresponding boundary problem of electrodynamics in multiply connected domains [2,4,39,40]. The method of integral equations [40,42] is used widely in such classes of problems. The synthesis method of antenna arrays with cylindrical dipoles with account of mutual influence is proposed in [29,34]. Analysis of nonuniqueness problem of solutions is studied there by means of computational experiments.
is reduced to solution of the corresponding boundary problem of electrodynamics in multiply connected domains [2,4,39,40]. The method of integral equations [40,42] is used widely in such classes of problems. The synthesis method of antenna arrays with cylindrical dipoles with account of mutual influence is proposed in [29,34]. Analysis of nonuniqueness problem of solutions is studied there by means of computational experiments.
In the problems of analysis and synthesis of antenna arrays with many elements is used simplified mathematical model of AA [5,6]. It is assumed [6] that AA consists of N identical and identically oriented in space radiators, and vector DP of radiators are identical for all emitters, i.e.
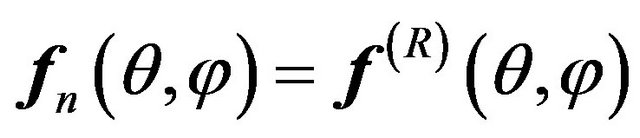 . Formula (94) for DP of flat AA takes the form
. Formula (94) for DP of flat AA takes the form
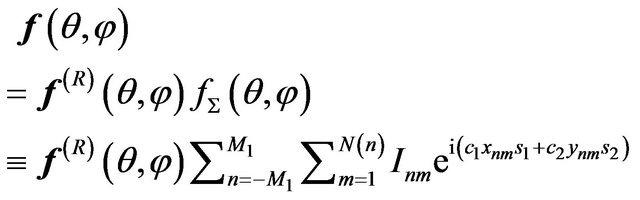 (95)
(95)
Here 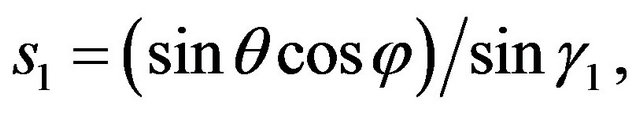
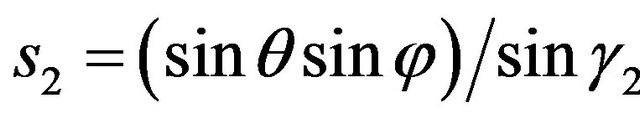 are the generalized angular coordinates,
are the generalized angular coordinates,
 ,
, 
are dimensionless numerical parameters characterizing the distance between the radiators and the domain (solid angle) G, in which the required amplitude DP 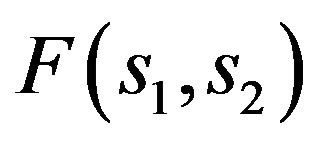 is given. Since in (95) only the second multiplier depends on the vector APD of excitation currents in the array:
is given. Since in (95) only the second multiplier depends on the vector APD of excitation currents in the array:
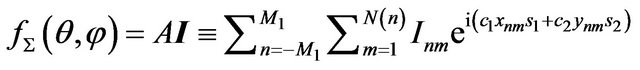 , (96)
, (96)
only the synthesis problem of factor of AA is considerd. Function 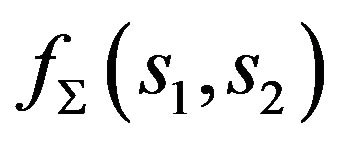 is
is  -periodic by argument
-periodic by argument 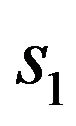 and
and  -periodic by
-periodic by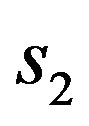 . We consider also (96) as the action of the operator
. We consider also (96) as the action of the operator  from a finite-dimensional space
from a finite-dimensional space 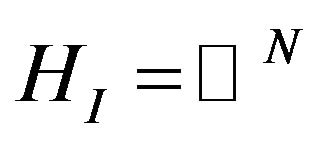 (
(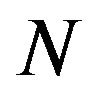 is number of radiators) into the finite-dimensional subspace of the space
is number of radiators) into the finite-dimensional subspace of the space 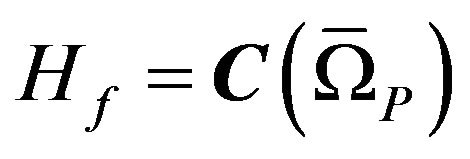 where
where 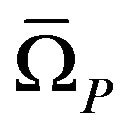 is the domain corresponding to the period of array. Let the amplitude DP
is the domain corresponding to the period of array. Let the amplitude DP 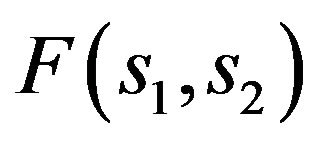 be given in the domain
be given in the domain 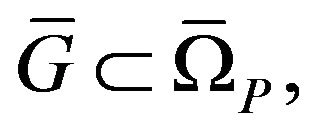 and on the set
and on the set  is identically equal to zero. The synthesis problem is to minimize the functional [35]
is identically equal to zero. The synthesis problem is to minimize the functional [35]
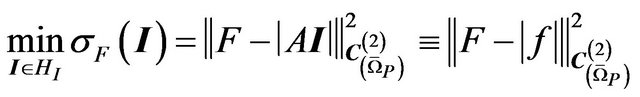 . (97)
. (97)
The basic of synthesis equations of multiplier of AA have the form
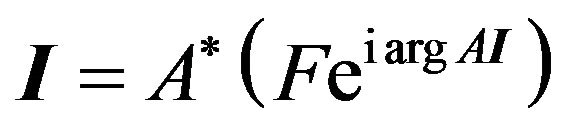 (98)
(98)
the equation concerning APD of currents in AA, where  is conjugate with
is conjugate with  operator, and
operator, and
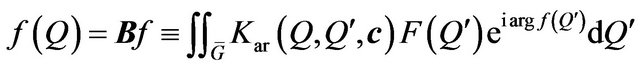 (99)
(99)
is equation concerning of synthesized DP. Here
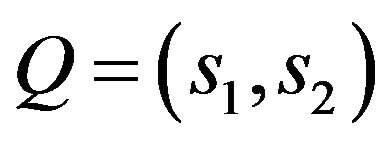 ,
, 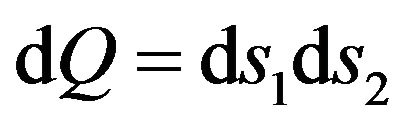 ,
,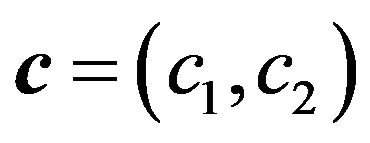 ;
; 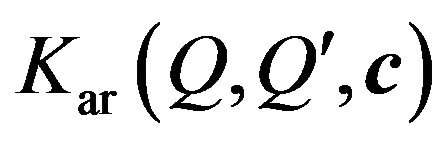 is the kernel the form of which depends on the distribution of elements in AA. In particular, in the case of a rectangular array with number of elements
is the kernel the form of which depends on the distribution of elements in AA. In particular, in the case of a rectangular array with number of elements
 the kernel
the kernel  is written as
is written as
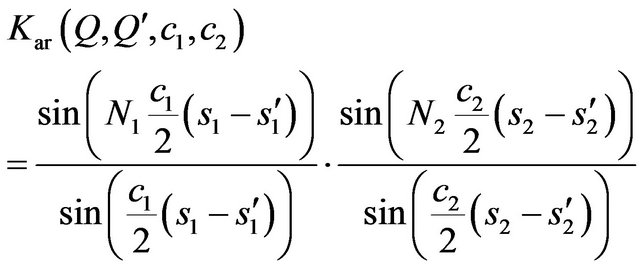 . (100)
. (100)
To find the possible branching lines of solutions of (99) a linear homogeneous integral equation

(101)
is obtained where  is a primary solution of (99).
is a primary solution of (99).
Note that the kernel 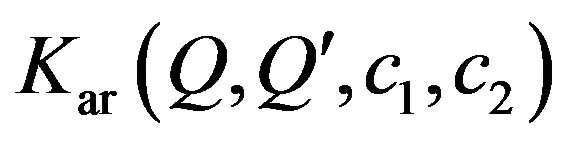 is degenerate. Consequently, Equation (101) is reduced to the corresponding homogeneous SLAE what in a special case of rectangular array has the form
is degenerate. Consequently, Equation (101) is reduced to the corresponding homogeneous SLAE what in a special case of rectangular array has the form
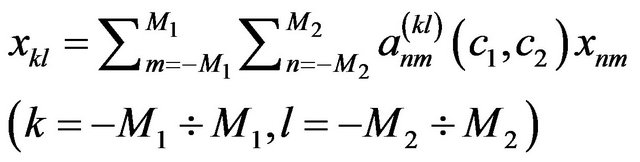 . (102)
. (102)
Coefficients of this system depend nonlinearly on the spectral parameters  and on the given amplitude DP. In [35,65] the conditions are determined and the existence theorem of connected components of the spectrum of (101) is proved. To find the spectral lines the implicit function method (82) and (83), is used.
and on the given amplitude DP. In [35,65] the conditions are determined and the existence theorem of connected components of the spectrum of (101) is proved. To find the spectral lines the implicit function method (82) and (83), is used.
Consider the numerical results of finding the solutions of the branching lines in the synthesis problems of a plane equidistant antenna array with  radiators for two given in the domain
radiators for two given in the domain 
amplitude DPs 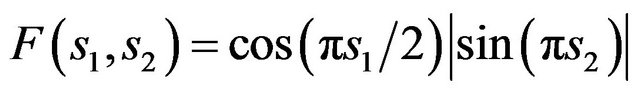 (Figure 10) and
(Figure 10) and 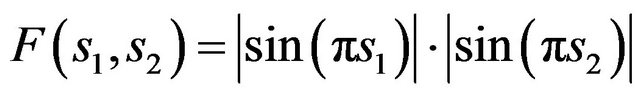 (Figure 11), which are obtained by solving of (101) and (102).
(Figure 11), which are obtained by solving of (101) and (102).
The prescribed and synthesized amplitude DPs (with phase DP odd by argument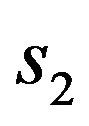 ) at
) at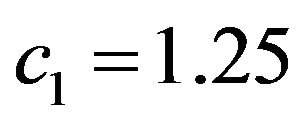 ,
,  , are shown in Figure 12 and 13, respectively. The amplitude and phase distributions of currents in the array of corresponding synthesized DP are given in Figure 14. From the analysis of this figure we see that nonsymmetric Y-direction distribution of currents in the array forms symmetrical amplitude DP.
, are shown in Figure 12 and 13, respectively. The amplitude and phase distributions of currents in the array of corresponding synthesized DP are given in Figure 14. From the analysis of this figure we see that nonsymmetric Y-direction distribution of currents in the array forms symmetrical amplitude DP.

Figure 10. The possible branching lines of solutions of (99) for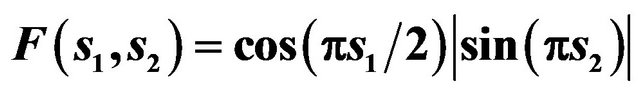 .
.

Figure 11. The possible branching lines of solutions of (99) for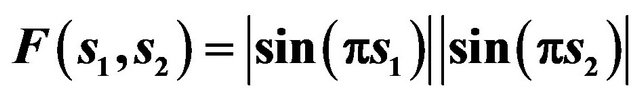 .
.
5. Numerical Methods of Solution of the Basic Synthesis Equations
The above results show that the nonlinear synthesis problems according to the prescribed amplitude DP and given energy DP have nonunique solutions. Application of the methods of branching theory of solutions to nonlinear integral equations allows to determine the quantity of existing solutions, to find solutions in the first approximation and to determine their quality characteristics. To find the complete solutions of these equations numerical methods [7,29,36,49,75] are applied. The defined properties of solutions obtained by analytical investigations make it possible to choose the initial approximation having the basic properties of the desired solutions and they are placed in certain neighborhoods of complete solu-
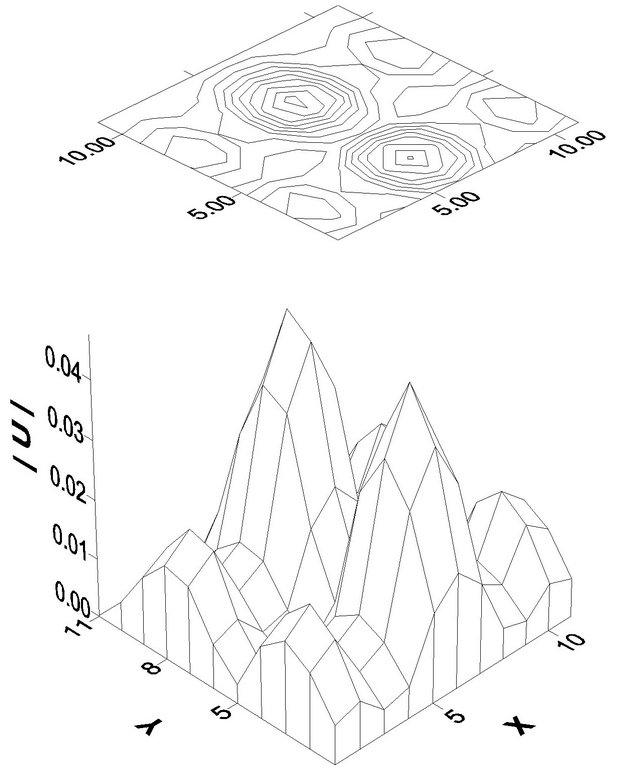 (a)
(a)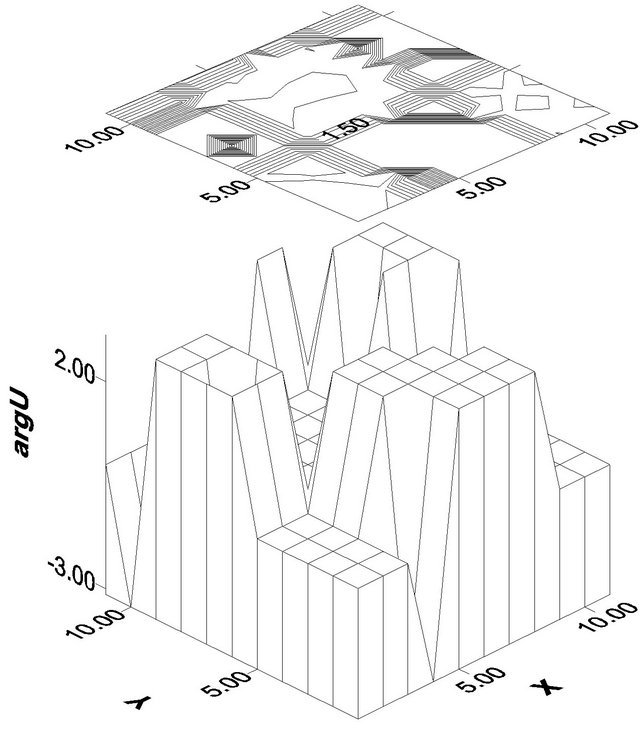 (b)
(b)
Figure 14. The optimal amplitude (a) and phase (b) distributions of currents in the array.
tions.
Conditionally the process of numerical solution of synthesis problem can be divided into two stages. The first of them is described partially above and it consists in finding the points (lines) of branching and determination of types of existings solutions depending on the value of physical parameters. The second stage consists in solving the basic synthesis equations by iterative methods.
5.1. Numerical Solution of Synthesis Equations Corresponding to Functional 
As an example of the scalar problem we consider iterative process of solving the equation of type (9), in the base of which we put the successive approximations method [7,75]
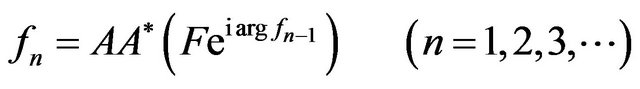 . (103)
. (103)
Obviously, the successive approximations method (103) is equivalent to the following iterative process
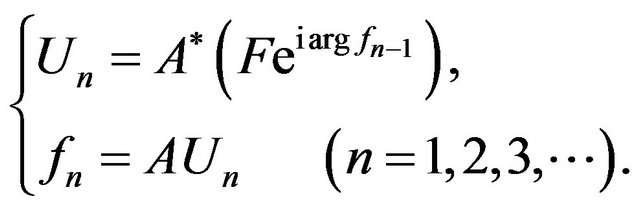 (104)
(104)
In [75] it is shown that the sequences 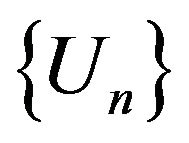 and
and 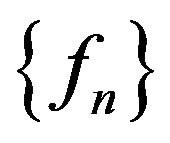 generated by iterative process (104), are relaxational for functional
generated by iterative process (104), are relaxational for functional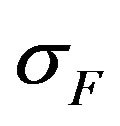 . Relaxation properties of (104) states Theorem 5.1. The sequence
. Relaxation properties of (104) states Theorem 5.1. The sequence  is generated by the iterative process (104), it is relaxation for functional
is generated by the iterative process (104), it is relaxation for functional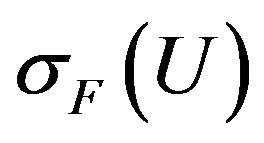 , and the values which it takes on
, and the values which it takes on 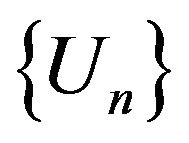 form a convergent numerical sequence
form a convergent numerical sequence .
.
Formulate also the properties of the operator  entering in (41) that complement the properties of 1˚ - 3˚ solutions of (41), presented in Section 3.1.
entering in (41) that complement the properties of 1˚ - 3˚ solutions of (41), presented in Section 3.1.
Theorem 5.2. Nonlinear operator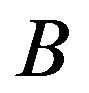 , defined by (41), acts in the space
, defined by (41), acts in the space 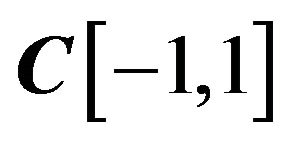 of continuous complex- valued functions, it is a compact and maps set
of continuous complex- valued functions, it is a compact and maps set 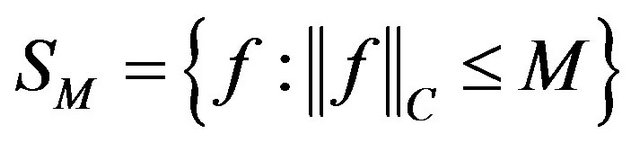 it into itself, where
it into itself, where
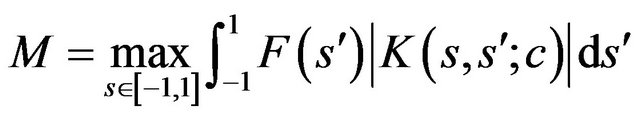 (105)
(105)
that is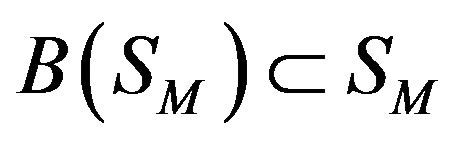 .
.
From the proved theorem follows, in particular, the following fact. Since the solutions of (41) are fixed points of the operator B, from the relation 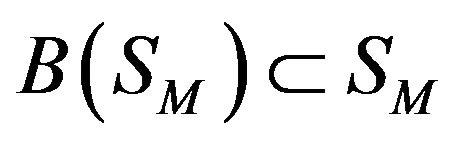 follows that all solutions of this equation belong to the set
follows that all solutions of this equation belong to the set . In addition, is valid [75]
. In addition, is valid [75]
Corollary 5.1. If the sequence 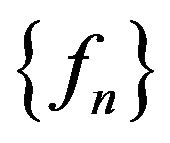 which is generated by the iterative process (104), is minimizing for the functional
which is generated by the iterative process (104), is minimizing for the functional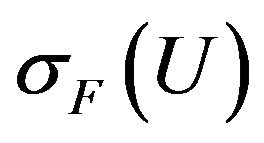 , then from
, then from 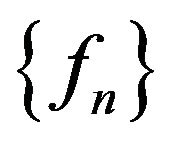 can be selected a subsequence
can be selected a subsequence 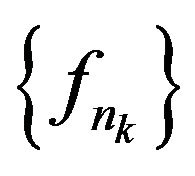 converging uniformly to the minimum point
converging uniformly to the minimum point 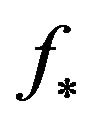 of the functional
of the functional .
.
Note that Theorem 5.2 and Corollary 5.1 are extended to the case of synthesis problem of a flat aperture with use of equation of the type (63).
5.2. Numerical Solution of Synthesis Equations Corresponding to Functional 
In the base of construction of iterative processes of solving the nonlinear operator equations of the type (12) and (13) we put implicit scheme of the successive approximations method [7,76]. In a general case, the iterative process of solution of (12) has the form
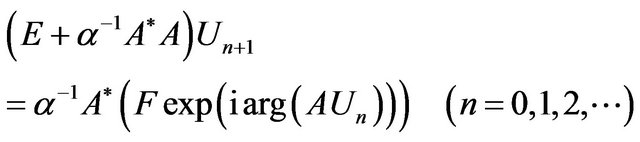 , (106)
, (106)
where 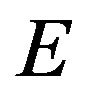 is an identity operator acting in the space
is an identity operator acting in the space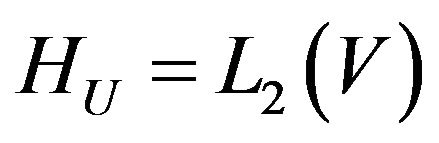 .
.
The implicit scheme of iteration process for (13) with respect to synthesized DP 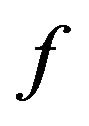 3 has the form similar to (106)
3 has the form similar to (106)
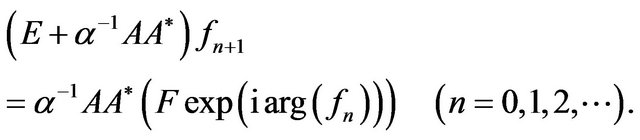 (107)
(107)
Note that the implicit schemes (106) and (107) are characterized by the fact that linear operator equation is solved on every iteration step. In addition the question of solvability of (106) and (107) appears, to which a positive answer gives a theorem about the solvability of the functional equation of the second kind of the type
 (108)
(108)
in the Banach space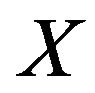 , where
, where  is a linear compact operator [69].
is a linear compact operator [69].
Theorem 5.3 [69]. In order that (108) have the solution at an arbitrary , it is necessary and sufficiently that homogeneous equation
, it is necessary and sufficiently that homogeneous equation  have a unique solution (obviously, that
have a unique solution (obviously, that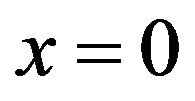 ).
).
For a sequence 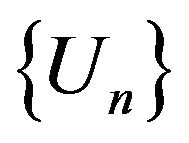 obtained by (106), is valid Theorem 5.4. Let
obtained by (106), is valid Theorem 5.4. Let 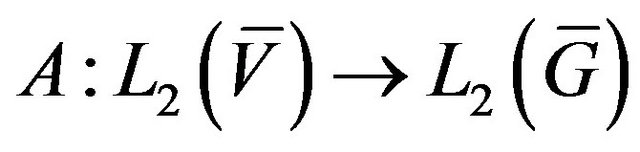 be a completely continuous operator,
be a completely continuous operator, 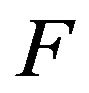 be a continuous real nonnegative function in
be a continuous real nonnegative function in 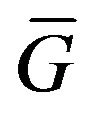 and at
and at  there exists the inverse operator
there exists the inverse operator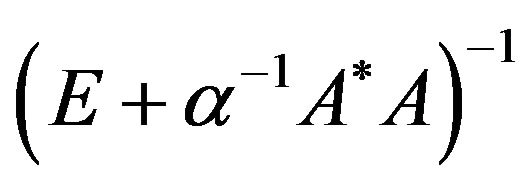 , in additionthe dimension of the space of zeros
, in additionthe dimension of the space of zeros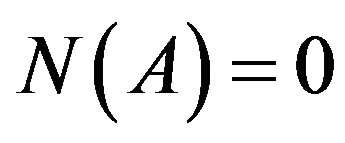 .
.
Then the sequence 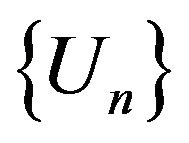 generated by the iterative process (106), is a minimizing for the functional
generated by the iterative process (106), is a minimizing for the functional
 (109)
(109)
in the space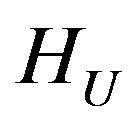 .
.
We denote the operator in right part of (106) as:
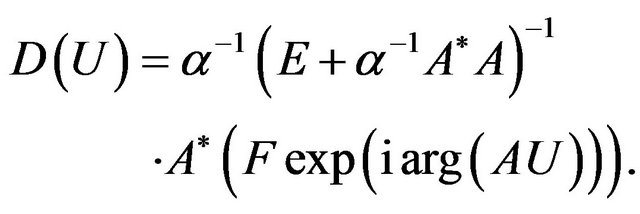 (110)
(110)
For the operator 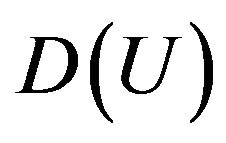 is valid Lemma 5.1. Let
is valid Lemma 5.1. Let 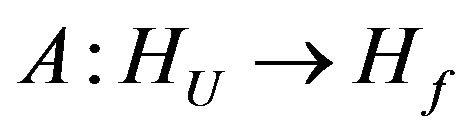 be a completely continuous operator. Then the operator
be a completely continuous operator. Then the operator  defined by (110), is compact and it transfers any bounded set
defined by (110), is compact and it transfers any bounded set 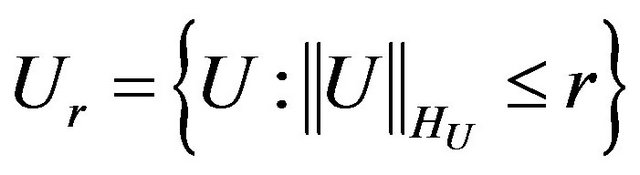 into its relatively compact part at
into its relatively compact part at
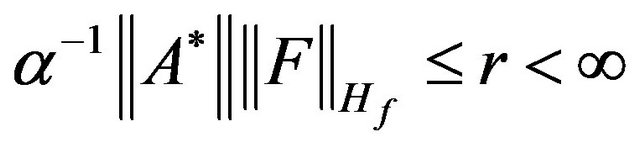 .
.
Thus, it is shown that there is true Corollary 5.2. If  is operator continuous in some neighborhood
is operator continuous in some neighborhood 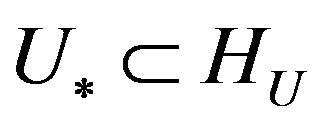 of the point
of the point , then from Theorem 5.2 and Lemma 5.1 follows that the subsequence
, then from Theorem 5.2 and Lemma 5.1 follows that the subsequence 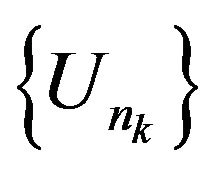 converges to some solution of (12) by the norm of the space
converges to some solution of (12) by the norm of the space 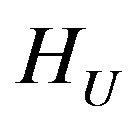 if
if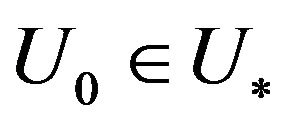 .
.
Dependent on the choice of initial approach the successive approximations (106) can converge to the solutions of various types [56-58].
5.3. Numerical Solution of Synthesis Problems with Use of the Energy Criterion 
First we shall consider the iterative process of solution the equation of type (34) in the Hilbertian space  under certain restrictions on the parameter
under certain restrictions on the parameter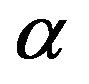 . This equation is written as
. This equation is written as
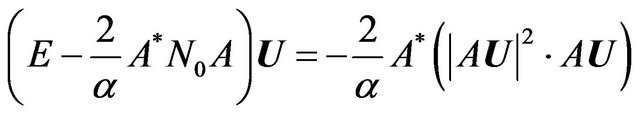 , (111)
, (111)
where  is an identity operator,
is an identity operator,
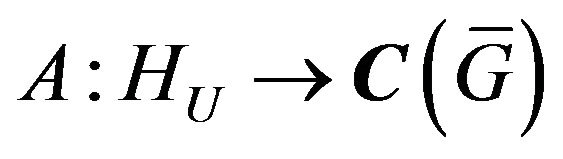 is completely continuous operator. We denote
is completely continuous operator. We denote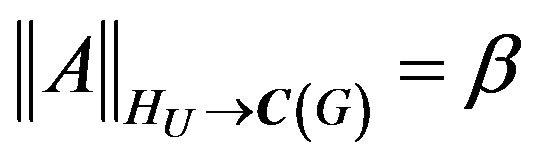 . Note that the scalar product and the corresponding norm
. Note that the scalar product and the corresponding norm  in the space
in the space 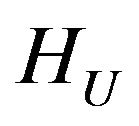 are defined by (14) and (15), and the Chebyshev
are defined by (14) and (15), and the Chebyshev 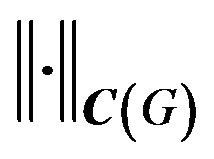 and mean-square
and mean-square  norms in the space
norms in the space  are introduced by Formulas (16)-(18).
are introduced by Formulas (16)-(18).
Henceforth we shall consider completion of the space
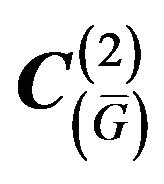 relatively to the norm
relatively to the norm 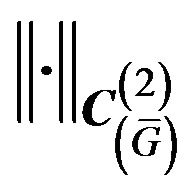 [14], which is the Banach space and coincides with the Hilbertian space
[14], which is the Banach space and coincides with the Hilbertian space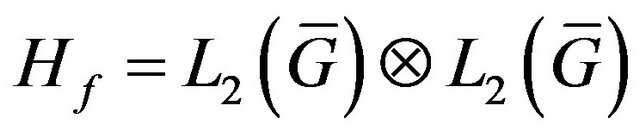 , the norm in which we shall denote by symbol
, the norm in which we shall denote by symbol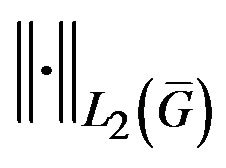 . We assume that
. We assume that 
is a completely continuous operator and in the space 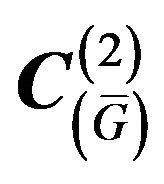 the domain of its values
the domain of its values 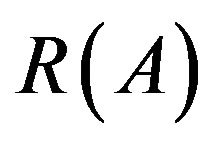 is a set of continuous functions.
is a set of continuous functions.
Taking into account the equality  we shall consider the expression
we shall consider the expression  in (111) as an operator of multiplication by the function
in (111) as an operator of multiplication by the function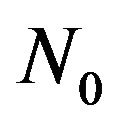 :
:
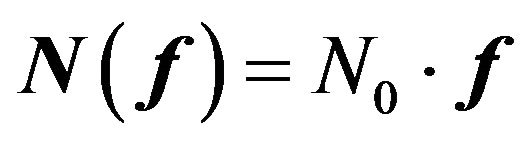 , (112)
, (112)
acting in the space 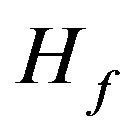 where
where 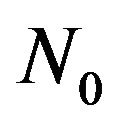 is real nonnegative continuous function on the compact
is real nonnegative continuous function on the compact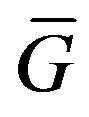 , in addition
, in addition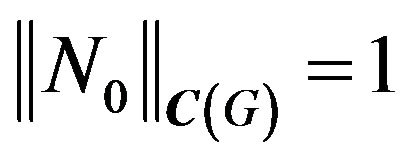 . Obviously, that (112) is a linear bounded operator, and
. Obviously, that (112) is a linear bounded operator, and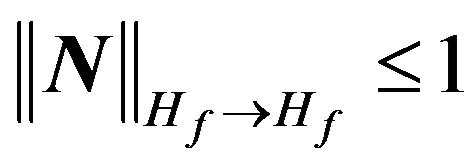 .
.
If , then there exists the inverse operator
, then there exists the inverse operator
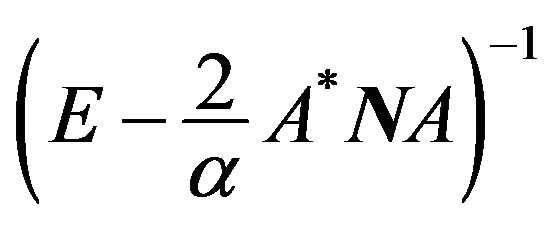 , the norm of which satisfies the inequality [14].
, the norm of which satisfies the inequality [14].
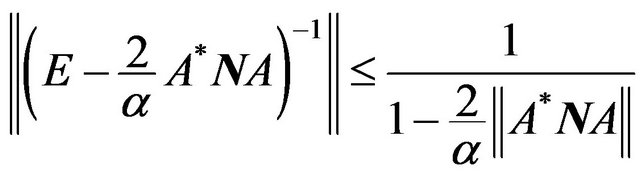 . (113)
. (113)
In this case, Equation (111) we shall write as
 . (114)
. (114)
Here we shall show that the solution of (114) can be obtained as a limit of successive approximations of the iterative process [61]:
 , (115)
, (115)
where 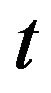 is some fixed number with the interval
is some fixed number with the interval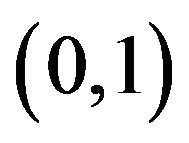 . In addition successive approximations can converges to different solutions of (114) depending on the choice of the initial approximation.
. In addition successive approximations can converges to different solutions of (114) depending on the choice of the initial approximation.
To determine the conditions and to justify convergence of (115), we shall use the Theorem 4.1 with [61, p. 68], according to which: if nonexpanding operator  converts a closed convex set
converts a closed convex set  of strictly convex Banach space
of strictly convex Banach space 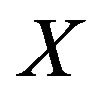 into its compact part, then successive approximations
into its compact part, then successive approximations
 where
where  is any fixed number from the interval
is any fixed number from the interval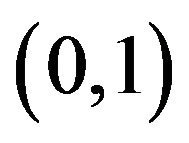 , converges to some solution of the equation
, converges to some solution of the equation 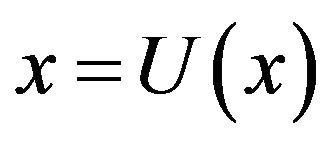 at some
at some .
.
Since the Hilbertian space 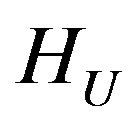 is strictly convex Banach space (see [61, p. 67]), then to satisfy of the conditions of this theorem concerning (114), it is sufficiently to show that a closed convex set
is strictly convex Banach space (see [61, p. 67]), then to satisfy of the conditions of this theorem concerning (114), it is sufficiently to show that a closed convex set 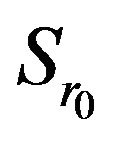 exists in the space
exists in the space , where the operator
, where the operator 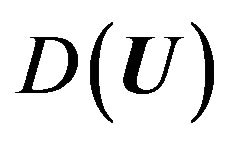 is nonexpanding and completely continuous. In addition there is such relation
is nonexpanding and completely continuous. In addition there is such relation
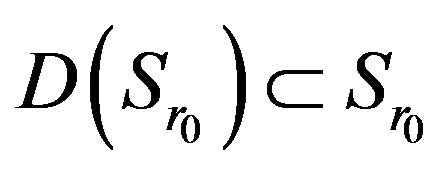 .
.
Satisfication of these conditions results from lemmas, proved in [7,49].
Lemma 5.2. Let 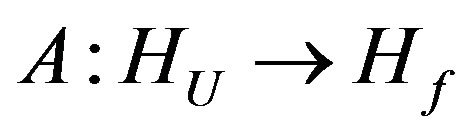 be a linear completely continuous operator and the domain of its values
be a linear completely continuous operator and the domain of its values 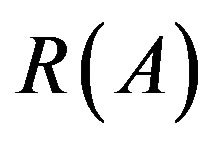 is a set of continuous functions,
is a set of continuous functions, . Then
. Then 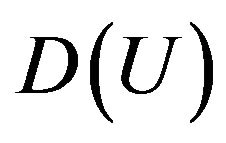 is a nonexpanding operator on
is a nonexpanding operator on
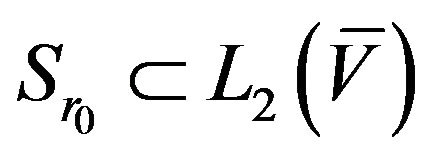 , where
, where
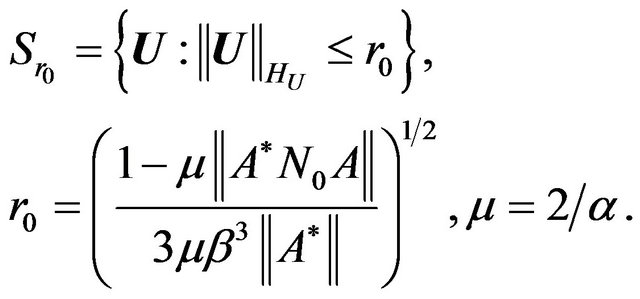 (116)
(116)
that is, for any 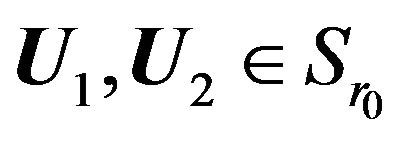 the inequality
the inequality
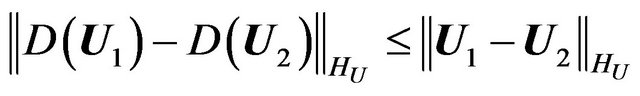 (117)
(117)
is satisfied.
Lemma 5.3. Let 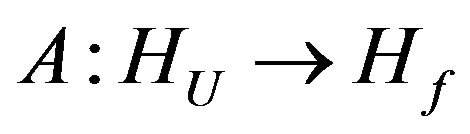 be a linear completely continuous operator and the domain of its values
be a linear completely continuous operator and the domain of its values  is a set of continuous functions,
is a set of continuous functions, . Then
. Then , defined by (114), is a completely continuous operator for which the relation
, defined by (114), is a completely continuous operator for which the relation
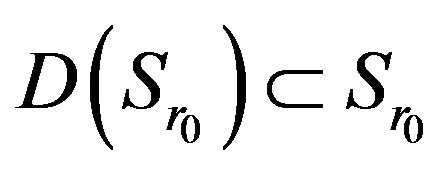 (
(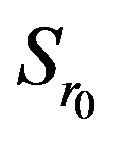 is a closed convex set, defined by
is a closed convex set, defined by
(116)), is satisfied.
5.4. Numerical Solution of Synthesis Problems with Optimization of Geometry of Radiating System
In this section we shall consider the synthesis problem of a flat aperture according to the prescribed amplitude DP for the case when the form of aperture and amplitudephase distribution of the field (currents) in it is optimized simultaneously, limiting by the case of linear polarization [25,26,77]. We shall consider a special case when the field in the aperture is linearly polarized along one of the coordinate axes, and DP has only one component. We introduce inside of aperture the polar coordinate system: ,
, . Let
. Let  be a function of the boundary of aperture
be a function of the boundary of aperture . Then DP
. Then DP 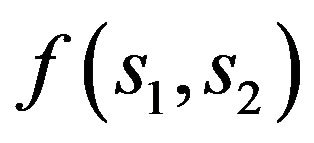 which is formed by amplitude-phase distribution of the field in the aperture
which is formed by amplitude-phase distribution of the field in the aperture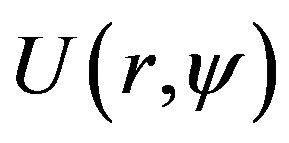 , is given by the formula [7,16]
, is given by the formula [7,16]
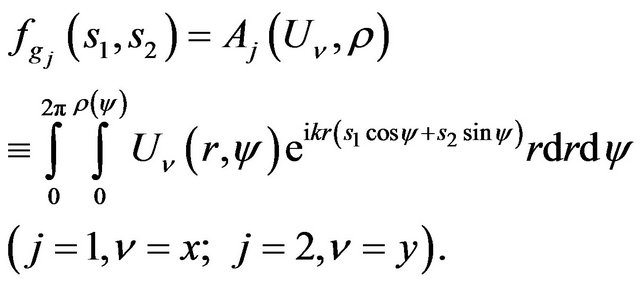 (118)
(118)
Later on we omit the index in definition of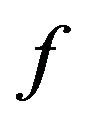 . Let the given amplitude DP
. Let the given amplitude DP 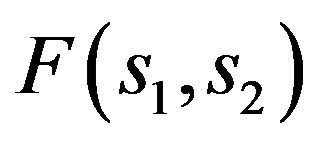 be different from identical zero in some limited closed domain
be different from identical zero in some limited closed domain 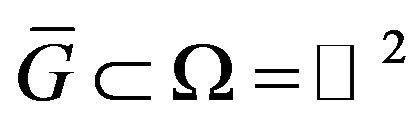 and it is identically equal to zero at
and it is identically equal to zero at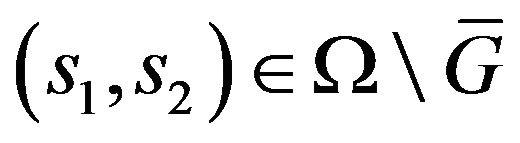 . The problem of simultaneous synthesis of the aperture shape
. The problem of simultaneous synthesis of the aperture shape  and amplitude-phase distribution of the field in it is considered as the problem on finding the functions
and amplitude-phase distribution of the field in it is considered as the problem on finding the functions 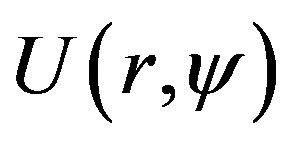 and
and 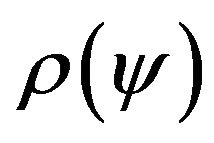 minimizing the functional
minimizing the functional
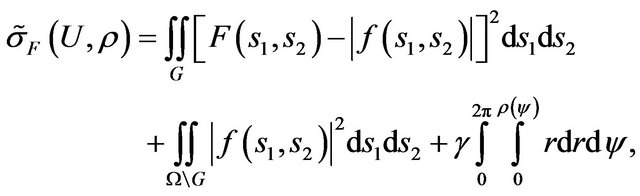 (119)
(119)
in which the first two summands describe the meansquare deviation of modules of given and synthesized DP’s in space , and the third one—imposes restrictions on the square of aperture
, and the third one—imposes restrictions on the square of aperture . We shall consider the parameter
. We shall consider the parameter 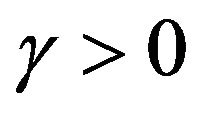 as a weight coefficient.
as a weight coefficient.
We introduce into consideration the following functional spaces: 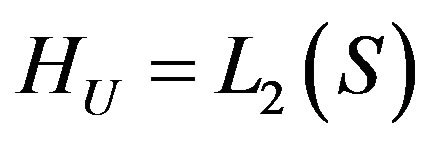 is a space of square integrable complex functions in the domain
is a space of square integrable complex functions in the domain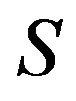 ,
,
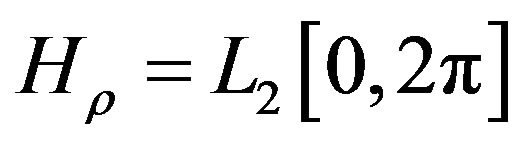 is a space of square integrable real functions on the segment
is a space of square integrable real functions on the segment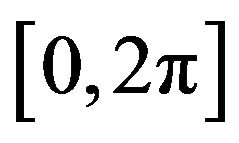 ,
, 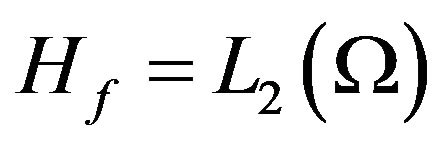 is a space of square integrable complex functions in the domain
is a space of square integrable complex functions in the domain . Scalar products and generated by it norms we shall introduce as follows:
. Scalar products and generated by it norms we shall introduce as follows:
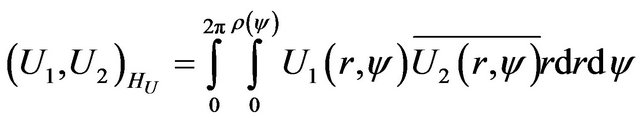 ,
,
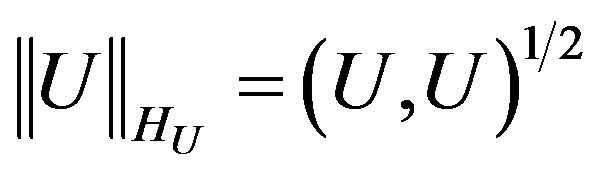 ,
,
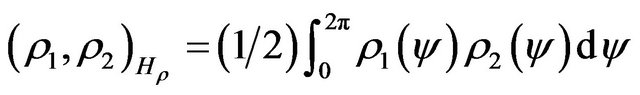 ,
,
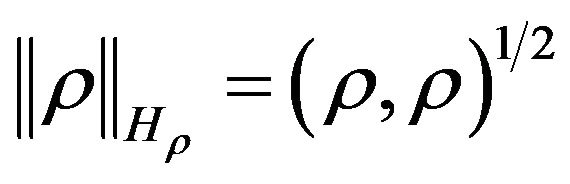 ,
,
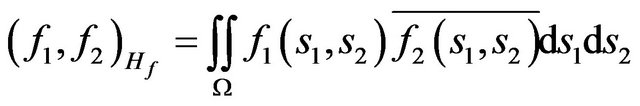 ,
,
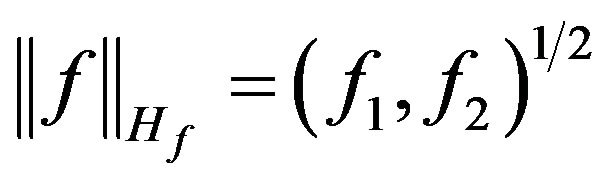 . (120)
. (120)
Taking into account the introduced norms, the last summand in (119) and Parseval’s equality have the form
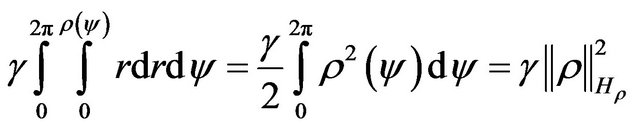 ,
,
 .
.
On this base the functional 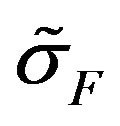 is presented as:
is presented as:
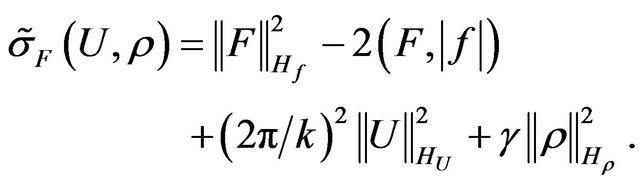 (121)
(121)
We shall consider the iterative process of numerical minimization of (121). In it base we shall put the ideas similar, as at minimization of functions of two variables by a coordinate descent method. Let 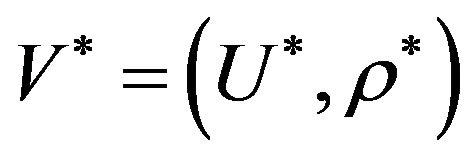 be a minimum point of the functional
be a minimum point of the functional 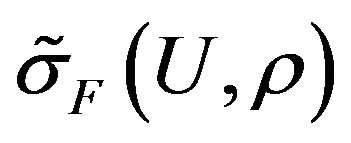 and
and
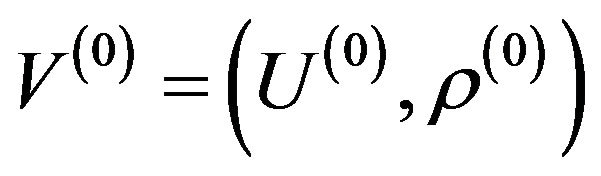 be an initial approximation chosen from some neighborhood of the point
be an initial approximation chosen from some neighborhood of the point . We shall denote by
. We shall denote by 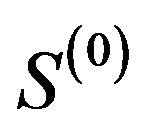 the initial shape of aperture, that is described by the function
the initial shape of aperture, that is described by the function . Substitute
. Substitute 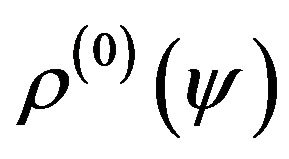 in (121) and consider its restriction in the space
in (121) and consider its restriction in the space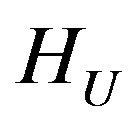 :
:
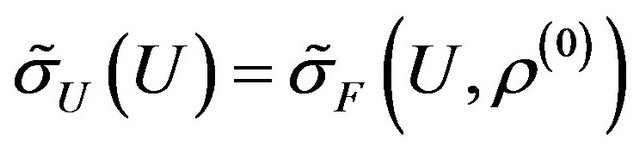 . (122)
. (122)
From the necessary condition of the functional minimum 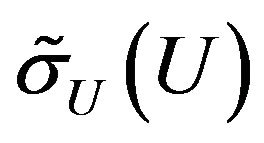 we obtain equation of type (9). Numerically we solve it by successive approximations method, given in pt. 5.1:
we obtain equation of type (9). Numerically we solve it by successive approximations method, given in pt. 5.1:
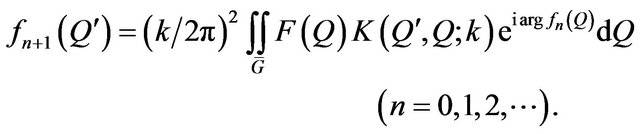 (123)
(123)
As a result, we find the function , and obtain the first approximation of the solution
, and obtain the first approximation of the solution 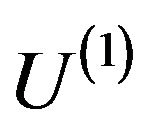 by the formula of type (10).
by the formula of type (10).
We shall pass to finding the function 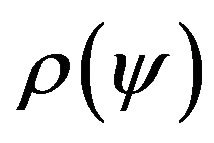 that describes the boundary of aperture
that describes the boundary of aperture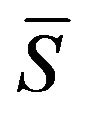 . We fix the function
. We fix the function  extending its analytically according to (10) to the plane
extending its analytically according to (10) to the plane  in (121), and consider the functional
in (121), and consider the functional
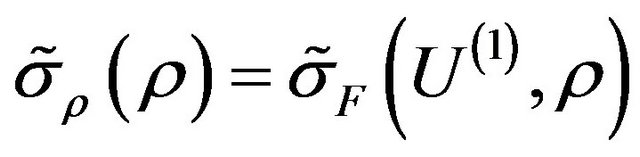 which depends only on the function
which depends only on the function . With the necessary minimum condition:
. With the necessary minimum condition:
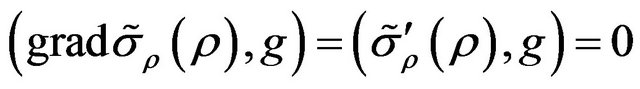 , where
, where
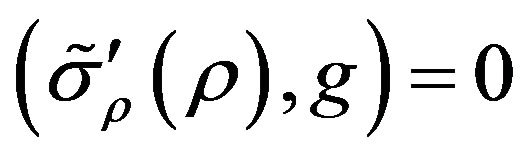 is an arbitrary element of the space
is an arbitrary element of the space , we obtain the equation
, we obtain the equation
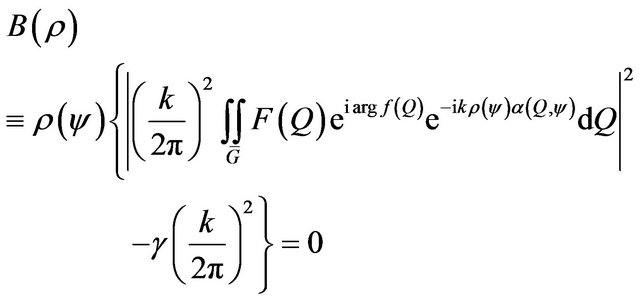 (124)
(124)
which is a nonlinear functional equation with respect to the function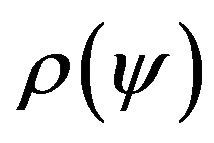 .
.
We shall find numerically solutions of (124), using the Newton-Kantorovich method [69]:
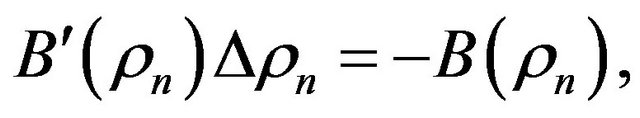 (125)
(125)
 , (126)
, (126)
where 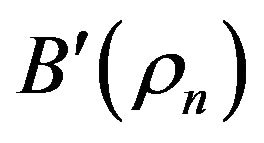 is the partial Frechet derivates of operator
is the partial Frechet derivates of operator  by the function
by the function . We assume that
. We assume that . Equation (125) is a linear integral equation of the form
. Equation (125) is a linear integral equation of the form
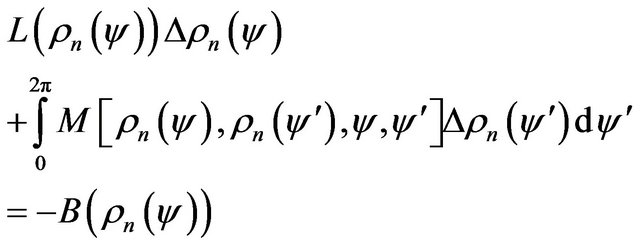 (127)
(127)
which 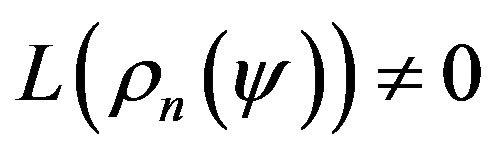 can be reduced to the Fredholm equation of the second kind at
can be reduced to the Fredholm equation of the second kind at . Solving (127) we find the first approximation for the function
. Solving (127) we find the first approximation for the function  that describes a boundary of aperture of the radiating system.
that describes a boundary of aperture of the radiating system.
Continuing finding in turn the approximations of functions 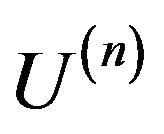 and
and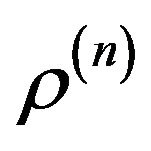 , we obtain the sequence
, we obtain the sequence
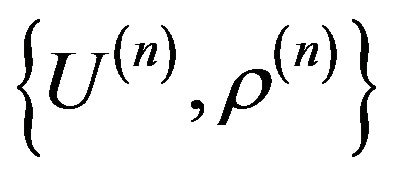 that is relaxational for (119). In more detail the problem of choice of initial approximations and justification of relaxation for functional
that is relaxational for (119). In more detail the problem of choice of initial approximations and justification of relaxation for functional 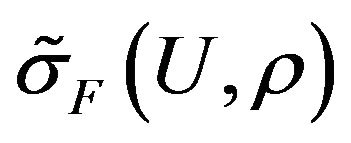 is given in [7,56,57].
is given in [7,56,57].
First we shall consider the numerical results of synthesis of flat aperture with optimization of its geometry. In Figures 15 and 16 the examples of synthesis of amplitude DPs, which in cross section have quasi-square and

Figure 15. Synthesis DP with square contour: (a) Synthesized DP with square contour; (b) The optimal shape of aperture.
quasi-triangular shapes, are given. The optimal shapes of apertures are given there too.
Note that the problems of such class arise, in particular, at the synthesis of contour DPs of fixed and variable forms for satellite antenna systems needed for uniform irradiation of a given territorial zone from the board of artificial satellite, where multi-beam antennas are used often [77- 82].
If multibeam antenna (MBA) has a radiating aperture of circular shape, and partial beams in the cross section have the shape of a circle and nonuniform distribution of radiated energy inside of the section, then on the junction of three neighboring rays with a circular cross section the so-called critical zones (Figure 17) with low level of radiated energy occur. One of the possible ways of solution of this problem is passage to alternative forms of apertures that on the base of the optimal APD will form rays that have rectangular, triangular or hexagonal shapes and close to constant (inside of contour) coefficient of directed action in rectangular cross section.
Obviously that on the base of such partial beams it is easy to synthesize given summary DP without critical

Figure 16. Synthesis of DP with triangular contour: (а) Synthesized DP with quasi-triangular contour; (b) Optimal shape of aperture.

Figure 17. Critical zones with low level of radiated energy.
zones. Below the results of synthesis of triangle-beam contour DP with partial beams with circular (Figure 18(a)) and quasi-rectangular (Figure 18(b)) contours are presented.
From the analysis of the figures we see that in the summary DP which is obtained on the base of quasisquare of contours, critical zones are absent, and variation of radiated energy inside of the contour does not exceed 2 dB.
 (a)
(a)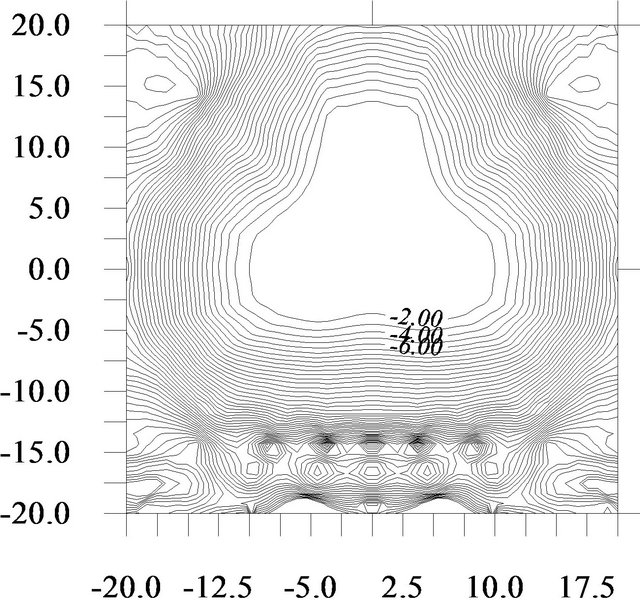 (b)
(b)
Figure 18. Synthesis of contour DP.
6. Conclusions
Note the main features and problems arising at investigations of othe class of problems reviewed in the article:
• The investigation of nonuniqueness and branching of existing solutions, which depend on the physical parameters of the problem is the main difficulty at solving this class of problems. As follows from the researches presented, in particular, for a special case in [7,13,16], when , the quality of existing solutions increases significantly with growth of parameters
, the quality of existing solutions increases significantly with growth of parameters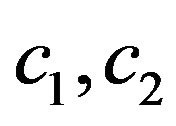 . However, to obtain the best approximation to the given amplitude DP
. However, to obtain the best approximation to the given amplitude DP 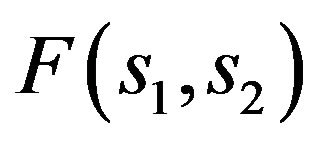 at relatively small values of the parameters
at relatively small values of the parameters 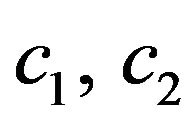 describing the sizes of aperture, allowing to confine by investigations of the first few branching points (lines), is essential in the synthesis problems of radiating systems.
describing the sizes of aperture, allowing to confine by investigations of the first few branching points (lines), is essential in the synthesis problems of radiating systems.
• At finding the solutions of (45) by the successive approximations method in the case of the even by both arguments (or one argument) functions 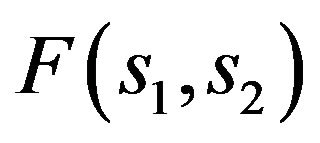 to obtain solution of certain type it is necessary to choose an initial approximation, which belongs to the corresponding invariant set of nonlinear operators
to obtain solution of certain type it is necessary to choose an initial approximation, which belongs to the corresponding invariant set of nonlinear operators  and
and .
.
• On the base of computational experiments it is revealed that the branching-off complex solutions, which exist at small sizes of aperture, increase the efficiency of synthesis within 20% - 40% compared with the real (primary) solutions. The presence of different by structure but identical by efficiency solutions (in the sense of value of the corresponding functional), provides for practice the possibility of choosing one of them that has a simpler physical realization. In addition, the branching-off solutions at conservation of the same efficiency which corresponds to real solutions allow to reduce the linear size of the aperture in the limits of 10 to 20 percent.
• The proposed numerical method of solution of nonlinear two-parameter spectral problems arising at investigation of nonlinear integral equations can be successfully applied, in particular, to solving the linear and nonlinear two-parameter spectral problems concerning matrix equations and ordinary differential equations of the second 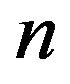 -th order with nonlinear occurrence of the spectral parameters into coefficients of equations and boundary conditions.
-th order with nonlinear occurrence of the spectral parameters into coefficients of equations and boundary conditions.
• A mathematical analogy between the synthesis problems of acoustic and electromagnetic antennas and synthesis problems of radio allows to use developed methods and numerical algorithms in the above sections of acoustics, radio physics and radio engineering.
• In mathematical aspect the synthesis problems of radiating systems formulated in paragraph 2, belong to problems of non-linear approximation of real finite functions by modules of one-dimensional or two-dimensional, or else discrete Fourier transforms [56,57]. In this connection, the above results can be directly applicable to solving the problems of mean-square approximation of nonnegative finite functions.
NOTES
2Definition 3.2 [68]. The sequance 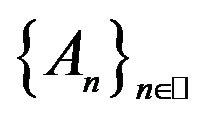 of operators
of operators 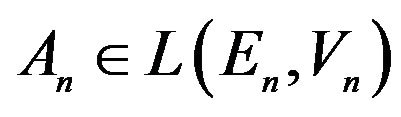 converges stably to
converges stably to , if
, if 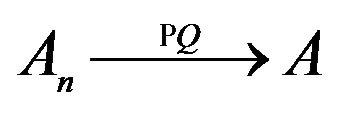
 and the following condition (stability condition) is valid:
and the following condition (stability condition) is valid: 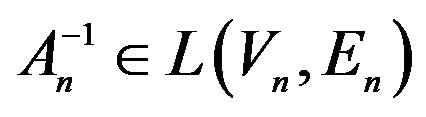 exists at all n, at that
exists at all n, at that 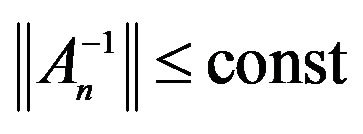
 .
.
3Comment 5.1. Since the set of continuous functions in the domain 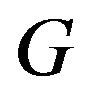 is a dense everywhere in the space
is a dense everywhere in the space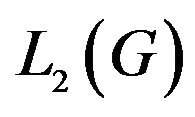 , and completion of space
, and completion of space 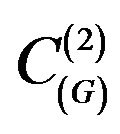 of continuous functions as the nor- malized space (with norm
of continuous functions as the nor- malized space (with norm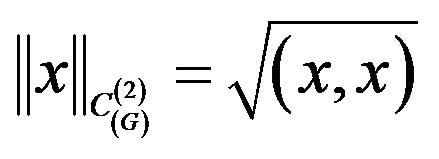 ), coincides with the Hilbertian space
), coincides with the Hilbertian space 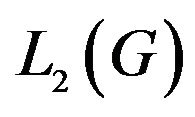 [14], justification of the convergence of (107) concerning equation of the type (22) can be considered in the Hilbertian space
[14], justification of the convergence of (107) concerning equation of the type (22) can be considered in the Hilbertian space 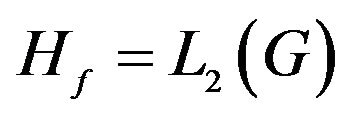 (
( or
or ).
).