Accurate Solution to the Gravitational Bending of Starlight by a Massive Object ()
1. Introduction
Gravitational deflection of starlight by a massive object such as the Sun, causing the light trajectory to bend from a straight line, has been an interesting topic for over three centuries [1] - [6] . Sir Isaac Newton first proposed the bending of light by gravity in his book on optics in the 1700s, by viewing light as a particle. J. von Soldner published his calculation in 1801 based on Newton’s classical theory, predicting a deflection angle of 0.87" for the Sun. A. Einstein also published a paper with the same result as Soldner using the equivalence principle in 1911 [2] , before he established the general theory of relativity in 1916 [3] .
It has been a main-stream understanding that, Newton’s classical theory of gravity yields a deflection angle of about 0.87" for light beam from a remote star passing near the surface of the Sun, and the deflection angle as calculated by Schwartzchild’s metric based on general relativity is 1.75", twice the value as obtained by the classical theory [1] [4] [5] . So far, light deflection by the gravity has been taken as one of the major evidences differentiating the theory of general relativity from the classical Newton’s law of gravity.
In order to demonstrate the theoretical predictions, an expedition led by Eddington during the total solar eclipse in 1919, reported the observation of light deflection with an angle consistent with general relativity [6] . There exist several potential ambiguities with the observation including the atmospheric turbulence, as well as the plasma deflection by the solar corona [7] [8] [9] [10] . Due to the uncertainties in observations using the visible light, which can be done only during a total solar eclipse, other techniques of measurements based on radio-frequency (RF) signal transmission have been developed, serving as an indirect evidence for light bending by measuring the time delay (or retardation) of RF signals transmitting between the Earth and other planets, stars, or spacecrafts [10] [11] [12] [13] . Recently, direct observations of background starlight deflected by a white dwarf star has been reported, and used to measure the mass of the star [4] .
Along with the successful explanation for the anomalous precession of the perihelion of Mercury, direct observations of light bending by gravity in the trajectory so as to compare the observed deflection angle with the theoretical results will be a strong supplement to fully appreciate the acclaimed theory of general relativity. Due to the profound nature of space-time curvature in the theory, calculations for the deflection angle by Schwartzchild’s metric based on general relativity require complicated mathematics [1] [5] , so far, only an approximated result has been obtained.
We shall present detail formulations with an exact solution for the trajectory of light from a remote background star grazing a massive object, without resorting to general relativity. We shall demonstrate that, the approximated result for the deflection angle obtained by Schwartzchild’s metric based on general relativity is valid only when the mass to radius ratio (
) is small, and the approximated result will deviate largely from the accurate value when the mass to radius ratio of the massive object is close to or larger than one.
2. Calculation
We start from Newton’s law of gravity. The gravitational force on a mass m0 from a central mass M is
, with G the gravitational constant, and r the distance between the two objects. Based on the mass-energy relation
and Plank’s principle of radiation quantization, light (or photons) of energy
will exhibit an effective mass of
, where c is the velocity of light, h is Plank’s constant. By solving the related orbital equation under proper boundary conditions, an exact deflection angle of
can be obtained, with k0 a constant related to the speed of light and the solar mass and the solar radius. Following is the detail derivation.
Assuming the origin O of polar coordinates is located at the centre of the massive object such as the Sun as illustrated in Figure 1, P(r, φ) is an arbitrary point in the light path, u = 1/r, under the centripetal force of Gm0M/r2, photons of energy m0c2 follow Binet’s orbital equation [14]
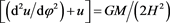 . (1)
. (1)
![]()
Figure 1. Schematic of the bending of the light beam from a remote background star. The light trajectory will be deflected on both sides as light passing near the surface of a massive object such as the Sun, with OQ parallel to the asymptotic line PE of the incoming light from a remote star. CD is the asymptotic line of the outcoming light from the Sun to the remote observer. The total deflection angle is 2α1.
where H is the angular momentum per unit mass,
, M is the mass of the Sun, and the photon mass m0 is not involved in the equation.
The general solution to the above equation is
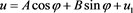 . (2)
. (2)
with
,
. Based on the boundary condition and asymptotic behavior at specific angles and positions, the constants A and B can be determined.
At the closest spot S from the light beam to the surface of the Sun, φ = π/2, r = R, with R the radius of the Sun, or the closest distance between the light beam and the center of the Sun, the orbital equation yields,
, and
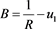 . (3)
. (3)
For the light beam traveling from a remote star towards the Sun, it has already been deflected before reaching the Sun. As a result, under the condition φ = π, r is not infinite (
). Only when φ is larger than π by a deflection angle α1, which is the angle between the line OQ and the X-axis, so that the asymptotic line PE tangential to the hyperbola of the light beam at the negative infinite distance (from the remote star) tends to be parallel to OQ, with
, then
, and u = 0, the orbital equation yields
. (4)
The same consideration also applies for the light beam travelling away from the Sun to the other side of infinite distance (such as the Earth). Under the condition φ = 0, r is not infinite (
), rather a finite value, only when φ is smaller than 0 by a deflection angle α1 with
, then
, and u = 0, the orbital equation yields
. (5)
Combining the above two conditions of Equation (4) and Equation (5),
, and
. (6)
The eccentricity of the hyperbola orbit is
, with E the total energy,
, and
. At the remote infinite distance, the gravitational potential energy is zero, and E = m0c2. At the closest spot S from the light beam to the Sun,
,
. So,
where
, which is a constant related to the speed of light, and the solar mass and the solar radius.
Solving the above quadratic equation we get,
, and
. (7)
The deflection angle α1 at one side of the Sun is
. (8)
The total deflection angle at both sides is
. (9)
This solution is analytically exact without simplification, with related assumptions for the photon energy of the form m0c2, and the gravitational force of the form Gm0M/r2.
Under the small angle approximation, with a small value of k0 for the Sun of about 10−6, which is much smaller than one, then
,
,
, the total deflection angle reduces to
. (10)
The approximated deflection angle of 4k0 is the same as given by general relativity based on Schwartzchild’s metric, and equal to 1.751" for the Sun. Most of the reported values for the deflection angle by the Sun are about 1.7" [1] [5] .
The above derivation procedure for the light trajectory is the same as solving Kepler’s orbital problem in the fundamental mechanics [14] , assuming a photon energy of m0c2. If the photon energy is taken as a classical particle of the form 1/2mc2, using the same boundary conditions and asymptotic behavior, the deflection angle becomes
, one fourth of the value of 4k0. And under no circumstances, a deflection angle of 2k0 could be obtained based on the classical gravitational theory as so far claimed by main-stream understandings, if the orbital equation is solved under the proper boundary conditions.
For nearly a century, it has been a widely accepted opinion that, the deflection angle based on the classical Newtonian theory is half the value as given by general relativity [1] [4] [5] , which is due to the inadequacy of Newtonian theory. In fact, this long-lasting understanding is a misunderstanding, the value of 2k0 previously obtained by Newton’s classical theory as calculated by Soldner and Einstein, as compared to the value of general relativity of 4k0 [1] [5] , is not due to the inadequacy of Newton’s theory, but due to minor errors during the calculation.
One of the errors during the conventional calculation based on the classical Newton’s theory is mistakenly ignoring one side of the deflection for incoming light from the remote star, resulting in half of the deflection angle, with another mistake of a wrong asymptotic behavior in the orbit, as shown in Figure 2. The mistake is obvious when the light beam is grazing the solar surface, in the conventional calculation based on classical theory, the incoming light will hit the surface, and will be blocked by the Sun. The conventional value obtained by the classical theory with a wrong deflection angle of 2k0 has nothing to do with the theory adopted. Even if a wrong form for the photon energy of 1/2mc2 is assumed, the corresponding deflection angle will be k0
![]()
Figure 2. Mistakenly assumed light path during traditional calculations based on the classical Newton’s theory. (a) Traditional calculations only considered half side of the deflection with an incorrect asymptotic condition. (b) Actual light path as the same as Figure 1, with the original undeflected light along the X-axis.
based on the classical theory.
A simple way to modify the mistakes in the conventional calculation based on the classical theory, is to multiply the deflection angle by a factor of two, resulting in a deflection angle of 4k0, which is the same as that obtained by general relativity. In fact, in the calculations based on general relativity, Schwartzchild’s metric also considered a multiplying factor of two.
The reason for the good agreement between the observations and the theoretical value of 4k0 as given by general relativity for light passing near the Sun, if the observations are reliable and other deflection mechanisms are properly excluded, is due to the specific parameters of the Sun. Based on the mass and the radius of the Sun,
, then
, the deflection angle of 4k0 as given by general relativity will be highly accurate.
For other stars or galaxies of much larger masses and smaller radii, with k0 close to one or even larger than one, the deflection angle of 4k0 as given by general relativity will deviate largely from the accurate value as given above. Observations of starlight deflected by a massive objects with a high density such as neutron stars, quasars, or black holes, can be used to test the above differences.
Since distortions of radio signals caused by the plasma fluctuations in the solar corona has been observed [7] [8] [9] [10] , as reflected by the time delay of radio signals, which may exhibit a similar order of magnitude as the expected gravitational deflection, the deflection angle observed by visible light during a solar eclipse may deviate from, and most likely larger than, the theoretical value.
3. Conclusion
In summary, the deflection angle of light from a remote star grazing a massive object has been derived with an exact solution by solving Binet’s orbital equation, based on the classical Newton’s law of gravity F = Gm0M/r2, with a photon energy in the form of m0c2. The present solution is more accurate than the result as given by general relativity based on Schwartzchild’s metric. As a key candidate for testing the effectiveness of general relativity, direct observations of light bending in the trajectory by the Sun with an accurate deflection angle, or preferably by other massive objects with a known mass and a larger mass to radius ratio, will continue to be a challenge for experimental studies.