Isolating a Minimum Radius of the Universe Consistent with the Production of at Least 1 Unit of Entropy, at the Start of Inflation ()
1. Introduction
We begin with the expression given in [1] [2] [3] , with F the free energy, and S the entropy, so that
 (1)
(1)
The end result is that we will approximate the entropy count as given by the last line of Equation (1) so that we can refer to an article in [4] for which there exists a critical Hubble parameter, 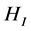 for which we have by [1] a
for which we have by [1] a  value that will be shown to have
value that will be shown to have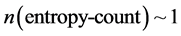 , with a radius of the universe of about 1000 times Planck length. Also, where if we have instead,
, with a radius of the universe of about 1000 times Planck length. Also, where if we have instead, 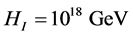 , we have
, we have 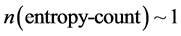 with a radius of the Universe of about one Planck length. After this is done, we will then comment upon the value of the square of the average inflaton value given by [5] . Where the square, of the inflaton, is given as follows, with a single inflaton given in Equation (2) as follows:
with a radius of the Universe of about one Planck length. After this is done, we will then comment upon the value of the square of the average inflaton value given by [5] . Where the square, of the inflaton, is given as follows, with a single inflaton given in Equation (2) as follows:
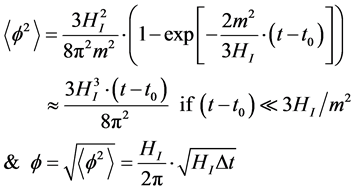 (2)
(2)
With the substitution of m as the mass of a graviton, as given in [6] , i.e. about 10^-62 grams, the inequality leading to a graviton mass induced behavior of the inflaton which we will comment upon fully while making use of 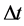 that is discussed in [7] [8] . In doing so, if one wants to be close to a Pre-Planckian length and time step, the preference would use
that is discussed in [7] [8] . In doing so, if one wants to be close to a Pre-Planckian length and time step, the preference would use , which then gets to the issue of interpretation of what to make of the following, from [9] , i.e. if
, which then gets to the issue of interpretation of what to make of the following, from [9] , i.e. if 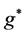 refers to initial degrees of freedom, then we will interpret several different cases for Equation (3) below, with different mass scale ideas in, and different initial temperature scenarios.
refers to initial degrees of freedom, then we will interpret several different cases for Equation (3) below, with different mass scale ideas in, and different initial temperature scenarios.
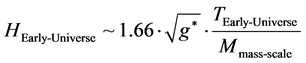 (3)
(3)
We will discuss all this and more in the subsequent analysis. Our final points will be using a comment from Rudin, as to outer measures [10] and its relationship to the causal structure brought up in [11] and [12] .
2. The Basic Analysis to Consider
What we are looking at first of all, is if Equation (1) is true, and Entropy is a counting algorithm, which is not so farfetched, then by use of [4] for entropy, and 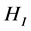 as well as [3] for
as well as [3] for 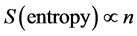 (particle count) then
(particle count) then
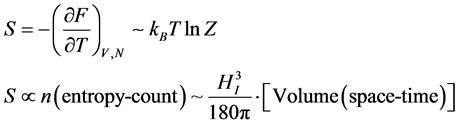 (4)
(4)
Then, we have that
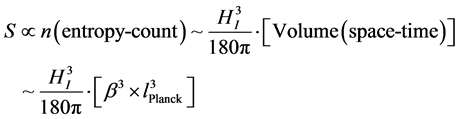 (5)
(5)
We then will pick the smallest possible entropy value of n as equal to 1. Then what we are looking at is
 (6)
(6)
We will look at two cases for our analysis, and the first one is with the [5] value of 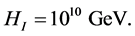
3. What If ? Consequences for Equation (6)
? Consequences for Equation (6)
Here we first normalize the ![]() with regards to the Planck Mass. The Planck Mass is [13]
with regards to the Planck Mass. The Planck Mass is [13]
![]() (7)
(7)
We will set c = 1 a, normalize the Planck mass to be = 1. If so then we write
![]() (8)
(8)
If so then, we will have Equation (6) rendered to be
![]() (9)
(9)
By inspection, it means in order to have Equation (6) of the order of magnitude of about 1, or less, we need to look at
![]() (10)
(10)
i.e. ![]() would be at least a billion times larger than
would be at least a billion times larger than![]() , in order to have Planck length of radii of the initial configuration of space time for at least 1 unit of entropy production. With the lower value of
, in order to have Planck length of radii of the initial configuration of space time for at least 1 unit of entropy production. With the lower value of ![]() as specified in [5] we would have then an initial radii of Planck length times one billion for about 1 unit of entropy production of our analysis.
as specified in [5] we would have then an initial radii of Planck length times one billion for about 1 unit of entropy production of our analysis.
4. Consequences of ![]() Instead of
Instead of ![]()
Going back to the Equation (3) it depends upon what we choose the Mass, in the denominator, to be, of which if it is Planck Mass, and we normalize that to 1, then we have at the boundary of about a Planck length for a 1 entropy value, i.e. one count of a primordial particle, but at an insanely high initial temperature, of the order of Planck temperature of about 1.417 × 1032 kelvin, or about 1.22 × 1019 GeV, for the given production of 1 unit of Planck mass. Note that Planck length is about, in simple units set about being 1.616229(38) × 10−35 m so this means that the radii of the universe even with
![]() (11)
(11)
5. Conclusion: Planck Radii in Length for Initial Configuration of Universe Could Lead to One Unit of Entropy Production. Consequences? Ultra High Temperatures. What Else?
What we would have to go back to, then would be to review the ideas given in the document about the Dowker Structure of space-time as given in [12] and that would place a premium upon also understanding the role of the formulation of a causal boundary, as given in [11] , where after this boundary, we would employ [11] after an initial radii of space-time, is traversed from an initial starting point given by what is written below.
![]() (12)
(12)
i.e. what we are asserting is that at Planck temperature, we are observing a convergence close to the value of where we may have the initiation of a Causal structure. If so, then is Entropy, initially created at the START pf causal structure, due to an opportune selection of a special unit of ![]() i.e. note that in [8] we did suggest that the formation of the arrow of time, so done, would be a precursor of entropy, i.e. our argument may in itself be a first principle proof that the arrow of time, as initially formed, is a precursor for at least 1 unit of entropy created, and that this would be commensurate with making sense of
i.e. note that in [8] we did suggest that the formation of the arrow of time, so done, would be a precursor of entropy, i.e. our argument may in itself be a first principle proof that the arrow of time, as initially formed, is a precursor for at least 1 unit of entropy created, and that this would be commensurate with making sense of
![]() (13)
(13)
i.e. if we satisfy Equation (11), Equation (12), Equation (13) in the case of
![]() , we are also asserting that the formation of an
, we are also asserting that the formation of an
Inflaton, according to [5] , is in our estimation simultaneous with the formation of causal structure as indicated by Equation (12), as well as giving more inputs into the Padmadabhan model we used in [8] for the inflaton, i.e. [14] , as well as the idea given by Corda as to the Gravity’s breath suggestion he made. The author is aware of which the author finds quite pleasing to contemplate [15] .
In doing so, in the formation of Causal structure, so long as it does not contravene the outer measure definition given in [10] and requirements linked toward getting Equation (11) satisfied, we are not in trouble, at least mathematically for the time being. We will be using the nonsingular approach pioneered by [16] and [17] and we should do our best to avoid problems in our analysis which may contradict the LIGO results of [18] and [19] [20] , especially if each single count of n, as referenced to entropy is in common with gravitons. Also, our analysis should be further refined to take into account [20] , which may be with initial doable instrument refinements. Even so, we also point to [21] as having relevance to early universe work in our future endeavors [22] .
Acknowledgements
This work is supported in part by National Nature Science Foundation of China Grant No. 11375279.