How a Minimum Time Step and Formation of Initial Causal Structure in Space-Time Is Linked to an Enormous Initial Cosmological Constant ()
1. Framing the Initial Inquiry
Volovik [1] derives in page 24 of his manuscript a description of a total vacuum energy via an integral over three-dimensional space
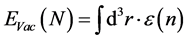 (1)
(1)
The integrand to be considered is, using a potential defined by 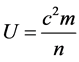 as
as
given by Volovik for weakly interacting Bose gas particles, as well as
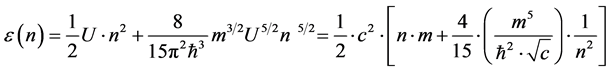 (2)
(2)
For the sake of argument, m, as given above, will be called the mass of a graviton, the given number, n, is a numerical count of gravitons in a small region of space, and afterwards, adaptations as to what this expression means in terms of entropy generation, will be subsequently raised. A simple graph of the 2nd term of Equation (2) with comparatively large m and with 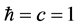 has the following qualitative behavior. Namely for
has the following qualitative behavior. Namely for
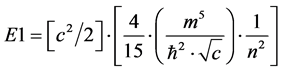 (3)
(3)
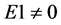 when n is very small, and
when n is very small, and 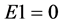 as
as 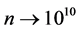 at the onset of inflation. This will tie in directly with a linkage between energy and entropy, as seen in the construction, looking at what Kolb [2] put in, i.e.
at the onset of inflation. This will tie in directly with a linkage between energy and entropy, as seen in the construction, looking at what Kolb [2] put in, i.e.
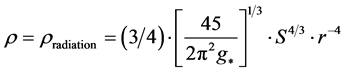 (4)
(4)
Here, the idea would be, to make the following equivalence, namely look at,
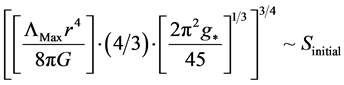 (5)
(5)
We furthermore, make the assumption of a minimum radius of
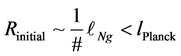 (6)
(6)
Equation (6) will be put as the minimum value of r, in Equation (5), where we have in this situation [3] [4]
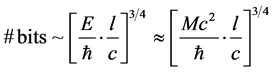 (7)
(7)
And if M is the total space-time energy mass, for initial condition and E1 is the main fluctuation in energy, we have to consider, if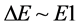 , as well as [3] [4]
, as well as [3] [4]
![]() (8)
(8)
Then what can be said about the inter relationship of graviton counts, and the onset of Causal structure?
2. Examination of the Minimum Time Step, in Pre-Planckian Space-Time as a Root of a Polynomial Equation
We initiate our work, citing [5] to the effect that we have a polynomial equation for the formation of a root finding procedure for![]() , namely if
, namely if
![]() (9)
(9)
From here, we then cited, in [5] , using [6] a criteria as to formation of entropy, i.e. if ![]() is an invariant cosmological “constant” and if Equation (10) holds, we can use the existence of nonzero initial entropy as the formation point of an arrow of time.
is an invariant cosmological “constant” and if Equation (10) holds, we can use the existence of nonzero initial entropy as the formation point of an arrow of time.
![]() (10)
(10)
This leads to the following, namely in [5] we make our treatment of the existence of causal structure, as given by writing its emergence as contingent upon having
![]() (11)
(11)
The rest of this article will be contingent upon making the following assumptions. FTR
![]() (12)
(12)
In short, our view is that the formation of a minimum time step, if it satisfies Equation (11) is a necessary and sufficient condition for the formation of an arrow of time; at the start of cosmological evolution we have a necessary and sufficient condition for the initiation of an arrow of time. With causal structure, along the lines of Dowker, as in [7] and given more detail by Equation (12) above as inputs into Equation (10) and Equation (11) i.e. Planck length is set equal to 1 and.
![]() (13)
(13)
i.e. the regime of where we have the initiation of causal structure, if allowed would be contingent upon the behavior of [5] [8] [9]
![]() (14)
(14)
i.e. the right hand side of Equation (14) is the square of the scale factor, which we assume is ~10^-110, due to [4] [10] , and an inflaton given by [4] [11] .
So, the question well will be leading up to is what does Equation (9), Equation (12), and Equation (13), tell us about graviton production, and the causal foundation condition stated at Equation (14)?
3. Conclusion, So What Is the Root of Our Approximation for a Time Step?
Here for the satisfying of Equation (14) is contingent upon ![]() as an initial event horizon, of our bubble of space-time being of the order of magnitude of Planck Length,
as an initial event horizon, of our bubble of space-time being of the order of magnitude of Planck Length,
![]() (15)
(15)
A convenient normalization would be to have
![]() (16)
(16)
If so then, Equation (14) would read as a causal formation transformation, we would give as
![]() (17)
(17)
And then we would have the following equation if we make the following further normalization, as to Planck Mass, and Graviton mass, namely Planck Mass ~2.17645e−5 grams, whereas M (graviton) ~2.1e−62 grams, i.e. If Planck Mass = 1 in normalization, then Mass (graviton) is 10^-57 that of a Planck mass, with Planck mass rescaled to 1 which affects our equations and their scaling.
![]() (18)
(18)
i.e. we would roughly have
![]() (19)
(19)
This outlines the enormity of the change from Pre-Planckian to Planckian physics. If this is true, it indicates the enormity of the Pre-Planckian to Planckian transformation. If we assume that ![]() remains invariant, it means that the contribution of the inflaton becomes almost infinitely larger i.e.
remains invariant, it means that the contribution of the inflaton becomes almost infinitely larger i.e. ![]() in size.
in size.
So, if we have
![]() (20)
(20)
and if ![]() So that we have
So that we have
![]() (21)
(21)
As
![]() (22)
(22)
Or more approximately as
![]() (23)
(23)
Now, set ![]()
![]() (24)
(24)
This is on the order of the Cosmological constant, as computed by [12] and Peskins, in [13] so that the Pre-Planckian Cosmological constant would have an enormous value on par with the Quantum field theory estimate of the Plancks constant, in Pre-Planckian space-time [12] [13] .
This so happens to be consistent with Equation (5) of our document. It also has some similarities with the ideas given in [14] .
Finally this should be seen in the light of [15] [16] [17] that establish a non linear electrodynamic treatments of space-time as not bound by initial singularities, which the author views as credible alternatives to space-time singularities and which lead to mathematical treatments as an alternative to [18] and the Penrose Singularity theorem.
Acknowledgements
This work is supported in part by National Nature Science Foundation of China Grant No. 11375279.