1. Introduction
Observation of neutrino oscillations between the three lepton flavour species, 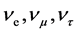 [1] [2] , means that at least two different mass eigenstates have non- vanishing mass. In particular one may mention the disappearance of solar neutrinos
[1] [2] , means that at least two different mass eigenstates have non- vanishing mass. In particular one may mention the disappearance of solar neutrinos 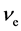 [3] as a first indication for transformation of flavour states together with
[3] as a first indication for transformation of flavour states together with 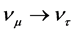 oscillation [4] [5] and
oscillation [4] [5] and 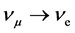 oscillation [6] [7] as spectacular confirmations. From the oscillations one infers mass differences between mass eigenstates. Now the task remains to determine the masses themselves. An experimental set-up, KATRIN [8] [9] [10] using tritium decay is undertaken in Karlsruhe, Germany with results for electron-based neutrinos expected in 20181.
oscillation [6] [7] as spectacular confirmations. From the oscillations one infers mass differences between mass eigenstates. Now the task remains to determine the masses themselves. An experimental set-up, KATRIN [8] [9] [10] using tritium decay is undertaken in Karlsruhe, Germany with results for electron-based neutrinos expected in 20181.
We suggest the electron-based anti-neutrino mass scale to originate in a slightly misaligned Higgs vacuum [11] [12] [13] [14] [15] occurring in the neutron beta decay
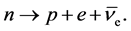 (1)
(1)
In our first scenario, we find
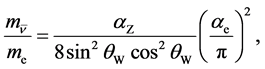 (2)
(2)
which yields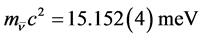 . In our second scenario we find
. In our second scenario we find
 (3)
(3)
with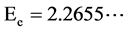 , which yields
, which yields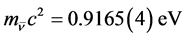 . The latter is below the limit 2 eV from tritium decay [2] but above the limit
. The latter is below the limit 2 eV from tritium decay [2] but above the limit 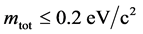 on the sum-total of stable neutrino masses from cosmological phenomenology [16] .
on the sum-total of stable neutrino masses from cosmological phenomenology [16] .
The first scenario value is comparable in order of magnitude with [2]
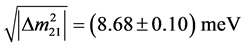 (4)
(4)
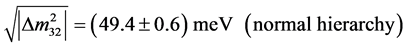
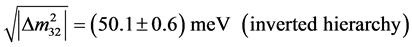
determined from the observed neutrino oscillations. The first scenario value at 15 meV positions itself intriguingly with respect to the Cyclotron Radiation Emission Spectroscopy technique of Project 8 [17] . Project 8 states a lower bound 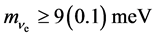 from neutrino oscillations, cf. the first equation in (4) and they expect their own sensitivity level to go down to
from neutrino oscillations, cf. the first equation in (4) and they expect their own sensitivity level to go down to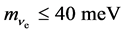 .
.
Neutrino oscillations are traditionally described by mixing between left handed flavour fields via a non-diagonal matrix U relating to left handed mass eigenstates [18]
 (5)
(5)
From the Pontecorvo-Maki-Nakagawa-Sakata mixing matrix U one gets “effective” flavour masses. For the anti-neutrino state created in the beta decay, one has [19]
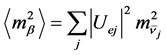 (6)
(6)
where the sum runs over the mass eigenstates![]() . It is not known whether
. It is not known whether
![]() ends at
ends at![]() .
.
We write only ![]() for the mass eigenstate in (2) and (3). In the discussion section we make a choice on hierarchy. For a three neutrino model in normal hierarchy we get from (6) our most probable mass value for the neutrino flavour generated in beta decay
for the mass eigenstate in (2) and (3). In the discussion section we make a choice on hierarchy. For a three neutrino model in normal hierarchy we get from (6) our most probable mass value for the neutrino flavour generated in beta decay
![]() (7)
(7)
2. Leptonic Sector
Both our scenarios set out from an intrinsic description of the electron, related to a similar description of the nucleon.
The value ![]() in the second scenario (3) is found from an electronic ground state on the intrinsic configuration space, the Lie group
in the second scenario (3) is found from an electronic ground state on the intrinsic configuration space, the Lie group ![]() with a hamil- tonian structure
with a hamil- tonian structure
![]() (8)
(8)
where ![]() is the energy scale and
is the energy scale and ![]() is the configuration variable. We assume the lowest neutrino mass eigenstate to be the ground state of a similar hamiltonian structure
is the configuration variable. We assume the lowest neutrino mass eigenstate to be the ground state of a similar hamiltonian structure
![]() (9)
(9)
The two Equations (8) and (9) share dimensionless eigenvalues for the ground state, i.e.
![]() (10)
(10)
where ![]() and
and![]() .
.
If we can solve (8) (and we can), all that is needed to determine ![]() is to fix
is to fix![]() . Below we shall present two different scenarios for the determination of
. Below we shall present two different scenarios for the determination of![]() .
.
3. The Leptonic Ground State
The particle data group notes that existing upper limits on neutrino masses imply very low masses of the order of one millionth of charged lepton ![]() and quark masses
and quark masses ![]()
![]() (11)
(11)
and they conclude [20] : “It is natural to suppose that the remarkable smallness of neutrino masses is related to the existence of a new fundamental mass scale in particle physics and thus to new physics beyond that predicted by the Standard Model”.
In the present work we suggest two mass scale scenarios. The new physics component offered in that connection is the idea of intrinsic configuration variables.
The configuration variables in (8) and (9) contain four dynamical variables from the four dimensions laid out by the four generators of![]() . Two of the generators are toroidal, i.e. diagonal
. Two of the generators are toroidal, i.e. diagonal ![]() matrices in a two-dimensional representation. We thus write
matrices in a two-dimensional representation. We thus write
![]() (12)
(12)
where ![]() are the two off-diagonal Pauli matrices
are the two off-diagonal Pauli matrices
![]() (13)
(13)
and the two diagonal generators
![]() (14)
(14)
are represented by
![]() (15)
(15)
The more common parametrization from using
![]() (16)
(16)
as diagonal ![]() generators is equivalent to the choice in (15) but does not match the polar decomposition of the Laplacian
generators is equivalent to the choice in (15) but does not match the polar decomposition of the Laplacian ![]() which we need in order to solve (8) and (9).
which we need in order to solve (8) and (9).
The wavefunction in (8) can be factorized in a torodial and an off-torus part
![]() (17)
(17)
in analogy with solving the Hydrogen atom in polar coordinates. The off- toroidal degrees of freedom can be integrated out to get for the measure-scaled toroidal wavefunction ![]()
![]() (18)
(18)
with the van de Monde determinant [21]
![]() (19)
(19)
and with potential
![]() (20)
(20)
Here the trace potential from (8) spells out as, see Figure 1
![]() (21)
(21)
with periodic parametric potentials [22]
![]() (22)
(22)
and the nominator ![]() in the centrifugal term is obtained by using
in the centrifugal term is obtained by using
![]() for states of spin s. The constant curvature [23] term 1/4 and the centrifugal term originate in the Laplacian [24]
for states of spin s. The constant curvature [23] term 1/4 and the centrifugal term originate in the Laplacian [24]
![]() (23)
(23)
where ![]() are dynamical toroidal eigenangles from the two eigenvalues
are dynamical toroidal eigenangles from the two eigenvalues ![]() of the configuration variable u.
of the configuration variable u.
The eigenvalue of the ground state in (8), respectively (18), can be lowered by allowing period doublings in the measure-scaled torodial wavefunction, see Figure 2. This is possible because of the periodic nature of the potential which opens for Bloch degrees of freedom like in solid state physics [25] . In order that the wavefunction remains single-valued on ![]() the Bloch phase factors are
the Bloch phase factors are
restricted to ![]() with
with![]() . For 4p-periodic states we expand R in (18)
. For 4p-periodic states we expand R in (18)
on Slater determinants [26]
![]() (24)
(24)
with half odd-integer![]() .
.
![]()
Figure 1. Parametric periodic potential, “egg-tray”. The periodicity in coordinate space represents the compact nature of the intrinsic configuration space of our description. The colour shading is only to enhance the 3D perception.
The electron rest energy ![]() is identified with the eigenvalue of the ground state
is identified with the eigenvalue of the ground state ![]() in (8). In other words,
in (8). In other words, ![]() is the dimensionless eigenvalue. We have determined
is the dimensionless eigenvalue. We have determined ![]() by a Rayleigh-Ritz method [27] with 3368 base functions of the type (24) which is at the limit of our computer programme. All the integrals needed in the Rayleigh-Ritz procedure can be solved analytically (see appendix C in [28] for a similar problem) which means that
by a Rayleigh-Ritz method [27] with 3368 base functions of the type (24) which is at the limit of our computer programme. All the integrals needed in the Rayleigh-Ritz procedure can be solved analytically (see appendix C in [28] for a similar problem) which means that ![]() can be determined with high accuracy. The potential (21) is shown in Figure 1 with a characteristic periodic structure originating in mapping to a real parameter space from the compact configuration space. An alternative basis to (24) can be constructed as Slater determinants from solutions to the one-dimensional equation
can be determined with high accuracy. The potential (21) is shown in Figure 1 with a characteristic periodic structure originating in mapping to a real parameter space from the compact configuration space. An alternative basis to (24) can be constructed as Slater determinants from solutions to the one-dimensional equation
![]() (25)
(25)
The two basis sets are both complete and yield the same spectrum as they should, but the integrals for the Rayleigh-Ritz solution based on parametric eigenfunctions from (25) can only be solved numerically. The reduced zone scheme for the lowest levels of (25) is shown in Figure 2. See e.g. [28] for more details on the parametric solutions.
4. Baryonic Sector
We have described the baryon spectrum by configurations on the Lie group ![]() with dynamics determined by a Kogut-Susskind-inspired structure [29] [30]
with dynamics determined by a Kogut-Susskind-inspired structure [29] [30]
![]() (26)
(26)
Here the configuration variable ![]() and
and ![]() is the energy scale corresponding to a length scale a which we took to be related to the classical electron radius
is the energy scale corresponding to a length scale a which we took to be related to the classical electron radius ![]() [31] [32] by the projective relation [30] , see Figure 3
[31] [32] by the projective relation [30] , see Figure 3
![]() (27)
(27)
This scale reproduces accurately the electron to neutron mass ratio
![]() (28)
(28)
with the dimensionless eigenvalue ![]() determined by solving (26). It also reproduces the
determined by solving (26). It also reproduces the ![]() and
and ![]() baryon spectrum with no missing resonance problem [33] . Flavour degrees of freedom are hidden in the Laplacian [24]
baryon spectrum with no missing resonance problem [33] . Flavour degrees of freedom are hidden in the Laplacian [24]
![]() (29)
(29)
where [21]
![]() (30)
(30)
and the off-diagonal generators fulfil
![]() (31)
(31)
Colour degrees of freedom are generated by the three ![]() s, intrinsic spin
s, intrinsic spin
degrees of freedom are generated by the three ![]() s with commutators like body-fixed coordinate angular momenta in nuclear physics [34] . The flavour degrees of freedom are contained in the three
s with commutators like body-fixed coordinate angular momenta in nuclear physics [34] . The flavour degrees of freedom are contained in the three ![]() s which connect the algebra. These mixing generators have a spectrum for
s which connect the algebra. These mixing generators have a spectrum for ![]() determined by the hypercharge quantum number y and the isospin three component quantum number
determined by the hypercharge quantum number y and the isospin three component quantum number ![]() [30]
[30]
![]() (32)
(32)
![]()
together with the spin quantum number s and the integer quantum number n which can be thought of as an intrinsic toroidal excitation number analogous to the radial quantum number in the case of the hydrogen atom in a polar decom- position like (29)
![]() (33)
(33)
where ![]() is the angular momentum operator. Compare (33) and (29) for the term “polar decomposition”.
is the angular momentum operator. Compare (33) and (29) for the term “polar decomposition”.
5. Electroweak Scale―The Higgs Connection
The transition from neutron to proton in (26) follows from a topological change in the wavefunction![]() . For the neutronic state the wavefunction has a 2p-periodicity when parametrized in the toroidal eigenangles
. For the neutronic state the wavefunction has a 2p-periodicity when parametrized in the toroidal eigenangles ![]() belonging to the three eigenvalues
belonging to the three eigenvalues ![]() of u whereas for the protonic state, the wavefunction has a slightly broken symmetry with respect to the potential, namely a 4p-periodicity expressed by the appearance of fractional Bloch phase factors
of u whereas for the protonic state, the wavefunction has a slightly broken symmetry with respect to the potential, namely a 4p-periodicity expressed by the appearance of fractional Bloch phase factors ![]() in the wavefunction. Such factors are allowed since the square of the wavefunction remains single-valued when extracted in parameter space, see also Bohr and Mottelson [35] for a note on doubling the angular domain for odd integer D-functions. The Bloch phase factors can lower the ground state eigen- value―provided a mechanism exists to open the relevant degrees of freedom. That mechanism is the Higgs mechanism and we connected the strong and electroweak sectors by the Ansatz [33]
in the wavefunction. Such factors are allowed since the square of the wavefunction remains single-valued when extracted in parameter space, see also Bohr and Mottelson [35] for a note on doubling the angular domain for odd integer D-functions. The Bloch phase factors can lower the ground state eigen- value―provided a mechanism exists to open the relevant degrees of freedom. That mechanism is the Higgs mechanism and we connected the strong and electroweak sectors by the Ansatz [33]
![]() (34)
(34)
with strong energy scale![]() , torodial colour angle field
, torodial colour angle field![]() , electroweak fine structure coupling
, electroweak fine structure coupling ![]() and Higgs field
and Higgs field![]() .
.
We can support this Ansatz by old time quantum mechanics arguments based on the minimum quantum of action, h. The length scale a introduced above can be used for a space projection
![]() (35)
(35)
and a time projection [36]
![]() (36)
(36)
A full shift of 2p in the angular time variable ![]() corresponds to an exterior period
corresponds to an exterior period ![]() determined by
determined by
![]() (37)
(37)
leading to a minimum action
![]() (38)
(38)
As Planck’s constant h is the minimum unit of action in the time-domain, we can use hc as a minimum unit of “action” in the space-domain, i.e. we have a minimum space action
![]() (39)
(39)
For the exchange with the Higgs field we need a measure for the level of interaction energy. We take it to be![]() , i.e. the electroweak fine structure coupling
, i.e. the electroweak fine structure coupling ![]() times the vacuum expectation value
times the vacuum expectation value ![]() of the Higgs field. Thus the minimum space action to determine
of the Higgs field. Thus the minimum space action to determine ![]() is
is
![]() (40)
(40)
Equating (39) and (40) we get
![]() (41)
(41)
With the time period ![]() from (37) and
from (37) and ![]() as in (26) we then
as in (26) we then
have
![]() (42)
(42)
This settles the electroweak scale v by
![]() (43)
(43)
corresponding to the standard model value [2] [33]
![]() (44)
(44)
See also arguments leading up to (58).
The 2p-shift behind (42) is what is needed for the topological change leading to the period doubling in the nucleonic wavefunction, see Figure 4. In this figure, the Higgs potential
![]() (45)
(45)
mimics the parametrized intrinsic potential. The 2p-shift in ![]() is accompanied
is accompanied
![]()
Figure 4. Higgs mechanism in neutron decay. The higgs potential (solid, blue) is structured by the intrinsic potential, either Wilson-inspired [37] (dotted, green) or Manton-inspired [38] (dashed, red), which are periodic in parameter space. Both parametric potentials yield the same value for the electroweak energy scale v, the Higgs mass ![]() and the quadric Higgs self-coupling
and the quadric Higgs self-coupling ![]() but only the Manton-inspired potential yields a satisfactory description of the baryon spectrum. The Manton-inspired potential expresses the euclidean measure folded onto the intrinsic configuration space [39] . Figure adapted from [40] .
but only the Manton-inspired potential yields a satisfactory description of the baryon spectrum. The Manton-inspired potential expresses the euclidean measure folded onto the intrinsic configuration space [39] . Figure adapted from [40] .
by a shift in the Higgs field from ![]() before the neutron decay to
before the neutron decay to ![]() after the neutron decay, see Figure 4. The parameters in the Higgs potential are
after the neutron decay, see Figure 4. The parameters in the Higgs potential are
![]() (46)
(46)
We revived the pionic Goldstone modes [41] by a slight vacuum misalignment in the Higgs mechanism with a misalignment angle ![]() determined by (see Figure 5)
determined by (see Figure 5)
![]() (47)
(47)
With the mass parameter ![]() in the Higgs potential (45) we obtained
in the Higgs potential (45) we obtained
the Higgs and pion masses determined by
![]() (48)
(48)
and
![]() (49)
(49)
by using the trailing
![]() (50)
(50)
from (42). The value for the pion mass can be improved by iterative determina- tion of the fine structure constant towards the pion mass scale.
We regret not seeing the connection (50) prior to the observation of the Higgs particle since it leads to a rather accurate value for the Higgs mass, see (48). Note however, that (46) also gives a prediction for the quadric Higgs self coupling
![]() (51)
(51)
which still remains to be tested by experiment together with our prediction [41]
![]() (52)
(52)
for the triple Higgs self-coupling. We here used the terminology of [42] for the mass and self-coupling terms of the Higgs particle field h
![]() (53)
(53)
expanded about a minimum of the Higgs potential [42]
![]() (54)
(54)
The standard model values are [42]
![]() (55)
(55)
where ![]() is the electroweak energy scale. The latter value is traditionally estimated from the Fermi constant in muon decay as [43]
is the electroweak energy scale. The latter value is traditionally estimated from the Fermi constant in muon decay as [43]
![]() (56)
(56)
On the other hand, from the vacuum expectation value ![]() at the minimum of the Higgs potential (54) one has
at the minimum of the Higgs potential (54) one has
![]() (57)
(57)
Since our v is based on the d to u quark transformation in the n to p decay, ![]() [44] is used, i.e. a quark mixing matrix element
[44] is used, i.e. a quark mixing matrix element ![]() is introduced
is introduced
![]() (58)
(58)
In total we get for Higgs self-couplings relative to the standard model
![]() (59)
(59)
![]()
which yields ![]() [2] and
[2] and![]() . Finally note that we actually announced the value 125.1 GeV for the Higgs mass [45] almost a year prior to the result 125.09 GeV from the combined ATLAS and CMS data [46] . Figure 6 shows the chronology.
. Finally note that we actually announced the value 125.1 GeV for the Higgs mass [45] almost a year prior to the result 125.09 GeV from the combined ATLAS and CMS data [46] . Figure 6 shows the chronology.
6. Neutrino Mass Scenario II
The scale ![]() in the leptonic sector is defined by the electron rest energy in (8) as
in the leptonic sector is defined by the electron rest energy in (8) as ![]() with the dimensionless eigenvalue
with the dimensionless eigenvalue ![]() of the period-doubled ground state of (18). Conservation of spin in the neutron decay requires the creation of the anti-electron neutrino. Thereby also the idea of lepton number conservation is introduced. As the (anti)-neutrino has no charge, we assume its creation to be mediated by neutral weak currents, i.e. the coupling
of the period-doubled ground state of (18). Conservation of spin in the neutron decay requires the creation of the anti-electron neutrino. Thereby also the idea of lepton number conservation is introduced. As the (anti)-neutrino has no charge, we assume its creation to be mediated by neutral weak currents, i.e. the coupling
![]() is replaced by
is replaced by ![]() [51] [52] , where the couplings
[51] [52] , where the couplings ![]() are
are
determined by ![]() and
and ![]() from the electroweak mixing angle
from the electroweak mixing angle![]() . To determine the neutrino energy scale
. To determine the neutrino energy scale ![]() we may suggest the misalignment factor
we may suggest the misalignment factor ![]() to enter a trailing
to enter a trailing
![]() (60)
(60)
analogous to (50) with the Higgs vacuum expectation value ![]() substituted by a residual electronic scale
substituted by a residual electronic scale![]() . From (60) we get for the neutrino mass
. From (60) we get for the neutrino mass
![]() (61)
(61)
Using (47) for the misalignment![]() , we have
, we have
![]() (62)
(62)
The strong scale ![]() contains the classical electron radius
contains the classical electron radius ![]() and can therefore be expressed as
and can therefore be expressed as
![]()
Figure 6. The chronology of experimental higgs mass values from the ATLAS collaboration (A) [47] [49] and the CMS collaboration (C) [48] [50] compared with our calculation (U) [45] . The last result shown is from the combined data by ATLAS and CMS at LHC run 1 (A + C) [46] .
![]() (63)
(63)
Inserting (63) in (62), using the identity
![]() (64)
(64)
and exploiting (10), we get
![]() (65)
(65)
This yields![]() . The uncertainty on
. The uncertainty on ![]() is estimated as
is estimated as![]() , i.e. of the order of the uncertainty on
, i.e. of the order of the uncertainty on ![]() corresponding to 0.022%.
corresponding to 0.022%.
7. Neutrino Mass Scenario I
Instead of the second order misalignment in the Higgs mechanism leading to the result ![]() in (65) from (60), we look in the present section for a first order misalignment but with a different length scale set by the proton and electron charges in space, i.e. the Bohr radius.
in (65) from (60), we look in the present section for a first order misalignment but with a different length scale set by the proton and electron charges in space, i.e. the Bohr radius.
Consider the classical electromagnetic field ![]() for a proton at rest [53]
for a proton at rest [53]
![]() (66)
(66)
where ![]() yields the Coulomb potential energy
yields the Coulomb potential energy
![]() (67)
(67)
for an electric charge ![]() at a distance
at a distance ![]() from the proton. Here we separated out the fine structure constant
from the proton. Here we separated out the fine structure constant ![]() in order to enter into a quan- tum regime. We reinterpret
in order to enter into a quan- tum regime. We reinterpret ![]() as a dimensionless coupling constant in quan- tum field theory. To set up the trailing in this scenario we make the substitu- tions
as a dimensionless coupling constant in quan- tum field theory. To set up the trailing in this scenario we make the substitu- tions
![]() (68)
(68)
to get ![]() of dimension energy at a characteristic length scale of the Bohr radius
of dimension energy at a characteristic length scale of the Bohr radius ![]()
![]() (69)
(69)
We use the Bohr radius [2] as a characteristic scale by imagining the creation of the anti-electron-neutrino to happen at a length scale given by the electro- magnetic interaction in space between the electric charges of the proton and electron created during the neutron decay. This assumption expresses the fact that all three particles ![]() and
and ![]() are created simultaneously in the neutron decay. Thus, the proton and the electron charges (together with their masses)― by defining the scale of the hydrogen atom corresponding to
are created simultaneously in the neutron decay. Thus, the proton and the electron charges (together with their masses)― by defining the scale of the hydrogen atom corresponding to![]() ―sets the scene for the projection of the intrinsic dynamics of the anti-electron-neutrino. If we accept (69) as a reasonable length scale, we get a trailing
―sets the scene for the projection of the intrinsic dynamics of the anti-electron-neutrino. If we accept (69) as a reasonable length scale, we get a trailing
![]() (70)
(70)
where the charged current coupling ![]() is substituted by the neutral charge
is substituted by the neutral charge
coupling ![]() [51] [52] and
[51] [52] and
![]() (71)
(71)
is the residual energy scale for neutrino mass creation. Thus the minimum space action exchange behind (70) is
![]() (72)
(72)
Like in (37), the characteristic time ![]() is determined by
is determined by
![]() (73)
(73)
which inserted in (72) gives (70). From (70) and (10) follows
![]() (74)
(74)
as stated in (2). With![]() ,
, ![]() ,
,
![]() and
and ![]() [2] this yields
[2] this yields
![]() as already mentioned. To observe a neutrino mass this small would require an improvement by one and a half order of magnitude from the sensitivity of the KATRIN experiment [8] but lies close to the sensitivity of the CRES technique [17] prospected in Project 8.
as already mentioned. To observe a neutrino mass this small would require an improvement by one and a half order of magnitude from the sensitivity of the KATRIN experiment [8] but lies close to the sensitivity of the CRES technique [17] prospected in Project 8.
8. Discussion
The second scenario with ![]() combined with the observed mass square differences (4) from neutrino oscillations means nearly degenerate neutrino mass eigenstates of the order of 1 eV. This is in conflict with cosmo- logical constraints [16] as mentioned in the introduction. For the first scenario we follow the interpretation implied by the Project 8 collaboration, that the lowest mass eigenstate should be of the order of
combined with the observed mass square differences (4) from neutrino oscillations means nearly degenerate neutrino mass eigenstates of the order of 1 eV. This is in conflict with cosmo- logical constraints [16] as mentioned in the introduction. For the first scenario we follow the interpretation implied by the Project 8 collaboration, that the lowest mass eigenstate should be of the order of![]() . We infer in normal hierarchy from (2) and (4)
. We infer in normal hierarchy from (2) and (4)
![]() (75)
(75)
![]()
![]()
This leads to a sum-total
![]() (76)
(76)
Using (6) with![]() ,
, ![]() and
and ![]() where
where![]() ,
, ![]() and
and ![]() [54] we infer
[54] we infer
![]() (77)
(77)
in accordance with what can be read off from figure 10 in ref. [55] correlating beta neutrino mass with cosmological constraints for the sum-total mass in (76) and in agreement with the disfavouring of inverted hierarchy in recent results from the NOνA neutrino oscillation experiment [56] . Note that the complex phase ![]() cancels out in the norm square of the matrix elements
cancels out in the norm square of the matrix elements ![]() in (6) as does possible Majorana phases.
in (6) as does possible Majorana phases.
9. Conclusion
We have investigated two possible scale scenarios for neutrino mass generation. Both scales relate to an intrinsic conception of the origin of the Higgs potential. This conception leads to slight discrepancies from standard model expectations in the quadric and triple Higgs self-couplings by having the d to u quark mixing matrix element as a factor in the electroweak energy scale v derived from neutron to proton decay. The foundation we have suggested is that of exchange of minimum quanta of action which can be used without knowing the detailed mechanisms behind the exchange between various degrees of freedom. We look forward to future accelerator experiments to test the Higgs self-couplings and to results from KATRIN and Project 8 to determine or constrain neutrino masses and possibly clarify the mechanisms behind neutrino mass generation.
Acknowledgements
I thank my colleagues H. G. Bohr and M. S. Jensen for co-work on the Higgs mass and H. G. Bohr for co-work on the pion mass. I thank both for showing interest in the intrinsic viewpoint and I thank the Technical University of Denmark for an inspiring working environment.
NOTES
![]()
1See the KATRIN homepage, http://www.kit.edu/kit/english/20624.php, where it reads: “Erste interessante Ergebnisse zur Neutrinomasse werden bereits für Mitte 2018 erwartet”. And further: “Die endgültige geplante Sensitivität erreicht KATRIN aber erst nach fünf Kalenderjahren Messzeit”, kes. 17.10.2016.