1. Introduction
During the latter part of the nineteenth century, Ludwig Boltzmann initiated the application of statistics to many-particle systems. He pursued this approach despite the strongly prevailing belief in a continuum structure of matter during that period. With the introduction of the ensemble concept by Willard Gibbs in 1902, the resulting statistical mechanics achieved several great successes, including the statistical definition of entropy and derivations of thermodynamics and fluid mechanics.
During the past century, the belief that quantum mechanics (QM) is the truly fundamental theory of nature has become overwhelmingly prevailing. On the basis of an enormous number of correct predictions, and apparently no incorrect ones, this belief continues to strengthen despite the puzzling fact that QM makes only statistical predictions. How can a statistical theory be fundamental? Any such theory must involve a statistical treatment of some number of underlying quantities.
None of the abovementioned approaches has been shown to apply to all classical systems. The principal goals of the work reported in this paper are to develop a statistical description of the nonrelativistic classical motions of the coordinates of any system, based on the probability continuity relation in the coordinate configuration space, and to investigate how close is that description to the nonrelativistic quantum mechanics of the system.
We pursue those goals as follows: In section 2, we consider a general non- relativistic classical system involving 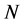 generalized (curvilinear or rectilinear) coordinates that define the
generalized (curvilinear or rectilinear) coordinates that define the 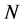 -dimensional configuration space (not the phase space) of the system. We note that if for any reason we wish to treat the system statistically, we may apply the continuity equation for the probability density and flux in that configuration space. Then we prove that this equation alone implies the existence of a statistical wave equation (SWE) that is exactly the same as the Schrödinger equation (SEQ) for the system, provided an unknown constant is set equal to
-dimensional configuration space (not the phase space) of the system. We note that if for any reason we wish to treat the system statistically, we may apply the continuity equation for the probability density and flux in that configuration space. Then we prove that this equation alone implies the existence of a statistical wave equation (SWE) that is exactly the same as the Schrödinger equation (SEQ) for the system, provided an unknown constant is set equal to  and two unknown functions are set equal to the physical potentials in the
and two unknown functions are set equal to the physical potentials in the 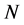 -space. The new results include an actual derivation of general “canonical quantization” and the operator Hamiltonian, as well as a derivation of nonrelativistic Lagrangian classical mechanics and the associated Newton’s laws of motion. Furthermore, we show that the quantitative solutions of the SWE must be exactly the same as those of the axiomatic SEQ for any given nonrelativistic system, but that some interpretations of these solutions must be different. In section 3, we provide analyses for three important illustrative examples, including particles with spin and systems of arbitrarily many identical particles. In sections 4 and 5, we offer a brief summary and discussion of our results, as well as a few conclusions.
-space. The new results include an actual derivation of general “canonical quantization” and the operator Hamiltonian, as well as a derivation of nonrelativistic Lagrangian classical mechanics and the associated Newton’s laws of motion. Furthermore, we show that the quantitative solutions of the SWE must be exactly the same as those of the axiomatic SEQ for any given nonrelativistic system, but that some interpretations of these solutions must be different. In section 3, we provide analyses for three important illustrative examples, including particles with spin and systems of arbitrarily many identical particles. In sections 4 and 5, we offer a brief summary and discussion of our results, as well as a few conclusions.
2. General Statistical Wave Equation
In this section we treat general nonrelativistic classical systems, which are invariably described in terms of 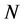 of generalized coordinates, where
of generalized coordinates, where 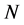 may be any integer
may be any integer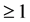 . For example, for a classical nonrelativistic system of
. For example, for a classical nonrelativistic system of 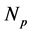 identical particles, each having only translational and rigid rotational degrees of freedom, the coordinates for each particle could be three Cartesian coordinates for the center-of-mass (CM) motion, and three Euler angles for the rigid rotational motion about the CM, or altogether
identical particles, each having only translational and rigid rotational degrees of freedom, the coordinates for each particle could be three Cartesian coordinates for the center-of-mass (CM) motion, and three Euler angles for the rigid rotational motion about the CM, or altogether  generalized coordinates that comprise the configuration space of the system.
generalized coordinates that comprise the configuration space of the system.
2.1. Generalized Coordinates for Nonrelativistic Classical Systems
We include this subsection to establish our notation, which is the notation used by Lichnerowicz [18] and Hartle [19] , simply extended to 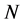 dimensions. We represent the generalized-coordinate manifold of a system under consideration by the set
dimensions. We represent the generalized-coordinate manifold of a system under consideration by the set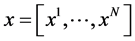 , where each coordinate
, where each coordinate 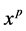 is an independent real continuous variable that may have any physical dimension and any range. A classical nonrelativistic system moves on a trajectory in this
is an independent real continuous variable that may have any physical dimension and any range. A classical nonrelativistic system moves on a trajectory in this 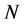 -space given by
-space given by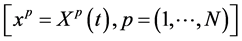 , where
, where 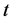 is the continuous time variable as read on a reference clock.
is the continuous time variable as read on a reference clock.
For such systems, the kinetic energy 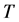 is always a positive definite quadratic form in the coordinate velocities
is always a positive definite quadratic form in the coordinate velocities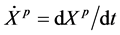 :
:
![]() (1)
(1)
where we use the extended Einstein summation convention that all repeated indices are summed over from 1 to![]() . Here,
. Here, ![]() is an overall mass para- meter that may be chosen at will, and
is an overall mass para- meter that may be chosen at will, and ![]() is the metric of the
is the metric of the ![]() -space, whereby the system configuration space is a Riemannian space. In general, off-diagonal
-space, whereby the system configuration space is a Riemannian space. In general, off-diagonal ![]() may be nonzero, so the coordinates may not be orthogonal. We use the coordinate basis vector approach to general tensor calculus [18] [19] [20] . That approach employs the covariant (subscripted) basis vectors
may be nonzero, so the coordinates may not be orthogonal. We use the coordinate basis vector approach to general tensor calculus [18] [19] [20] . That approach employs the covariant (subscripted) basis vectors ![]() and the contravariant (superscripted) basis vectors
and the contravariant (superscripted) basis vectors ![]() as dual sets of basis vectors for the linear vector space that is tangent to the configuration space. The generalized inner or dot products of these basis vectors are symmetric and are defined by
as dual sets of basis vectors for the linear vector space that is tangent to the configuration space. The generalized inner or dot products of these basis vectors are symmetric and are defined by
![]() (2)
(2)
where ![]() is the Kronecker delta, and the matrix with elements
is the Kronecker delta, and the matrix with elements ![]() is the inverse of the metric matrix that has elements
is the inverse of the metric matrix that has elements![]() . Any
. Any ![]() -vector field
-vector field ![]() may be written as a linear combination (LC) of either set of basis vectors:
may be written as a linear combination (LC) of either set of basis vectors:
![]() . The fields
. The fields ![]() are the (contra- variant, covariant) components of
are the (contra- variant, covariant) components of![]() . Indices may be raised or lowered with the metric:
. Indices may be raised or lowered with the metric:![]() ;
;![]() ; etc. Please see e.g. Chap. 20 of Hartle’s textbook [19] , esp. Table 20.1, for more details.
; etc. Please see e.g. Chap. 20 of Hartle’s textbook [19] , esp. Table 20.1, for more details.
2.2. Statistical Wave Equation
In treating classical motions statistically, one may always begin with the coor- dinate probability density. The fine-grained coordinate probability density in the ![]() -space is
-space is
![]()
where ![]() is the Dirac delta and
is the Dirac delta and ![]() is the magnitude of the determinant of the metric matrix. Note that the integral of
is the magnitude of the determinant of the metric matrix. Note that the integral of ![]() over all
over all ![]() -space is unity, since the volume element is
-space is unity, since the volume element is![]() . The corresponding fine-grained proba- bility current density is
. The corresponding fine-grained proba- bility current density is ![]() These quantities satisfy the
These quantities satisfy the ![]() -space continuity equation
-space continuity equation![]() ; this equation is necessary and sufficient to guarantee conservation of probability. The
; this equation is necessary and sufficient to guarantee conservation of probability. The ![]() -space vector gradient operator
-space vector gradient operator ![]() is defined [19] by
is defined [19] by
![]() (3)
(3)
where![]() .
.
These fine-grained probability densities are almost never useful in application, because it would be virtually impossible to solve for the detailed coordinate trajectories ![]() even if we knew all the force fields acting on every element of the system exactly, which we do not. What is needed are smooth densities that are continuous, bounded, and at least first order differentiable. Smooth densities have always been (tacitly) assumed to exist in all statistical treatments. In earlier work [21] [22] [23] [24] , we showed that the smoothing must be accomplished by an ensemble average over the global random variables associated with the classical statistical description of a system. The smooth coordinate probability density
even if we knew all the force fields acting on every element of the system exactly, which we do not. What is needed are smooth densities that are continuous, bounded, and at least first order differentiable. Smooth densities have always been (tacitly) assumed to exist in all statistical treatments. In earlier work [21] [22] [23] [24] , we showed that the smoothing must be accomplished by an ensemble average over the global random variables associated with the classical statistical description of a system. The smooth coordinate probability density ![]() satisfies the requirement that
satisfies the requirement that ![]() be equal to the proba- bility that the system coordinates are within the volume element
be equal to the proba- bility that the system coordinates are within the volume element ![]() around
around ![]() at time
at time![]() . Conservation of probability demands that the smooth densities
. Conservation of probability demands that the smooth densities ![]() and
and ![]() must also satisfy the continuity equation
must also satisfy the continuity equation
![]() (4)
(4)
Note that Equation (4) must be satisfied irrespective of what stochastic process is considered, e.g., Markovian or not, and independently of what kind of stochastic dynamics is considered, e.g., the Langevin equation, the Fokker- Planck equation, etc., and independently of what kind of position-velocity or position-momentum phase space treatment may be valid. Therefore, the statistical description of a system’s classical coordinates that evolves from just this conti- nuity equation will be incomplete, but still must be obeyed.
Now we proceed by following Collins’ method [13] (which mathematically is essentially Bohm’s approach in reverse order), but with our new generalization to the ![]() -dimensional metric configuration space required by an arbitrary nonrelativistic classical system. The first step is to define an
-dimensional metric configuration space required by an arbitrary nonrelativistic classical system. The first step is to define an ![]() -vector proba- bility flow velocity field
-vector proba- bility flow velocity field ![]() by writing
by writing
![]() (5)
(5)
Then ![]() is smooth since both
is smooth since both ![]() and
and ![]() are smooth by definition. (Note well that
are smooth by definition. (Note well that ![]() is not related directly to the underlying coordinate velocity com- ponents
is not related directly to the underlying coordinate velocity com- ponents![]() ; instead, it is analogous to a fluid flow velocity). This definition of
; instead, it is analogous to a fluid flow velocity). This definition of ![]() may always be made provided that
may always be made provided that ![]() is bounded everywhere, which is the case in any physical theory. Then, with no loss of generality, one may invoke the
is bounded everywhere, which is the case in any physical theory. Then, with no loss of generality, one may invoke the ![]() -space analog of Helmholtz’ theorem to express
-space analog of Helmholtz’ theorem to express ![]() as the sum of a gradient and another vector field that is not a gradient:
as the sum of a gradient and another vector field that is not a gradient:
![]() (6)
(6)
where ![]() is an unknown real-valued function that we require to be dimensionless, whereby
is an unknown real-valued function that we require to be dimensionless, whereby ![]() is an unknown real constant that has the physical dimension of angular momentum; and
is an unknown real constant that has the physical dimension of angular momentum; and ![]() is an unknown real-valued
is an unknown real-valued ![]() -vector field, not a gradient, having physical dimension velocity. (The methods of Gilson [12] and Collins [13] did not treat arbitrary curvilinear coordinates, and were not applied in general
-vector field, not a gradient, having physical dimension velocity. (The methods of Gilson [12] and Collins [13] did not treat arbitrary curvilinear coordinates, and were not applied in general ![]() -dimensional configuration spaces. Only Collins included the vector field
-dimensional configuration spaces. Only Collins included the vector field![]() , and then only in the 3-space of a single particle’s CM coordinates). The next step defines the complex-valued function
, and then only in the 3-space of a single particle’s CM coordinates). The next step defines the complex-valued function ![]() as
as
![]() (7)
(7)
This relation is known as the Madelung transform [17] ; it is usually applied to a given SEQ in a Euclidean 3-space, to obtain the Madelung/Bohm “hydrody- namical” equations, which did not include the non-gradient vector field![]() . Here, the transform is being used in reverse in a general metric
. Here, the transform is being used in reverse in a general metric ![]() -space. Note that
-space. Note that![]() , so
, so ![]() is well-defined and real
is well-defined and real ![]() if
if ![]() is smooth, e.g., not a product of Dirac deltas as is the fine-grained density. Equations (5)-(7) combine to yield
is smooth, e.g., not a product of Dirac deltas as is the fine-grained density. Equations (5)-(7) combine to yield
![]() (8)
(8)
![]() (9)
(9)
Then, requiring that the continuity Equation (4) be satisfied yields easily
![]() (10)
(10)
where ![]() is the operator
is the operator
![]() (11)
(11)
and ![]() is an unknown real-valued
is an unknown real-valued ![]() -scalar field having physical di- mension energy. Therefore, the equation that must be satisfied by
-scalar field having physical di- mension energy. Therefore, the equation that must be satisfied by ![]() is
is
![]() (12)
(12)
where ![]() is defined by
is defined by
![]() (13)
(13)
This ![]() -space SWE (12) has exactly the same form as the conventional SEQ for the system. Since the smoothed probability continuity Equation (4) is as discussed above an ensemble-averaged equation, then the SWE is an ensemble- averaged equation, and the eigenvalues of its Hamiltonian operator
-space SWE (12) has exactly the same form as the conventional SEQ for the system. Since the smoothed probability continuity Equation (4) is as discussed above an ensemble-averaged equation, then the SWE is an ensemble- averaged equation, and the eigenvalues of its Hamiltonian operator ![]() must be ensemble-averaged energies.
must be ensemble-averaged energies.
Note that we are not getting something for nothing: The quantities
![]() and
and ![]() must be real-valued and have the physical dimensions noted above, but are otherwise arbitrary. The
must be real-valued and have the physical dimensions noted above, but are otherwise arbitrary. The ![]() -space probability continuity equation merely guarantees that the SWE (12) must be obeyed for arbitrary functions
-space probability continuity equation merely guarantees that the SWE (12) must be obeyed for arbitrary functions ![]() and
and![]() . However, the meanings of
. However, the meanings of ![]() and
and ![]() are known a priori here (which was not the case during the original development and interpretation of the SEQ), whereby
are known a priori here (which was not the case during the original development and interpretation of the SEQ), whereby ![]() must satisfy the same continuity, integrability, boundedness, and boundary conditions that are imposed by postu- late on the conventional SEQ wavefunction for a system involving an
must satisfy the same continuity, integrability, boundedness, and boundary conditions that are imposed by postu- late on the conventional SEQ wavefunction for a system involving an ![]() -dimen- sional configuration space. Thus, for any system, the quantitative solutions of the SWE and SEQ must be identical, for given potentials
-dimen- sional configuration space. Thus, for any system, the quantitative solutions of the SWE and SEQ must be identical, for given potentials ![]() and
and![]() , if
, if![]() . Therefore, all typically quantum-mechanical relations, such as the uncertainty principle, also follow from the SWE, but some must be interpreted differently. We will discuss such differences in detail in later work.
. Therefore, all typically quantum-mechanical relations, such as the uncertainty principle, also follow from the SWE, but some must be interpreted differently. We will discuss such differences in detail in later work.
Of course, one can identify![]() ,
, ![]() ,
, ![]() , and
, and ![]() in Equation (12) by com- parison of its predictions with experimental results, or equivalently by comparison with the known SEQ. (It probably requires a complete cosmological model to predict the value of
in Equation (12) by com- parison of its predictions with experimental results, or equivalently by comparison with the known SEQ. (It probably requires a complete cosmological model to predict the value of![]() ). Several authors [7] [13] have provided arguments to identify
). Several authors [7] [13] have provided arguments to identify ![]() and
and ![]() for a single pointlike particle. One method that has been used for such a particle, but as far as we know not in the generalized-coordinate
for a single pointlike particle. One method that has been used for such a particle, but as far as we know not in the generalized-coordinate ![]() -space needed for more complex systems, is to require that Equation (12) yield the Hamilton-Jacobi equation in the classical (non-statistical) limit. This approach is quite simple. As is easily shown, (e.g. see Goedecke and Davis [25] for the 3-space version), substitution of Equation (7) into the SWE, Equation (12), yields two equations that must be satisfied. One is the probability continuity Equation (4) itself, while the other is
-space needed for more complex systems, is to require that Equation (12) yield the Hamilton-Jacobi equation in the classical (non-statistical) limit. This approach is quite simple. As is easily shown, (e.g. see Goedecke and Davis [25] for the 3-space version), substitution of Equation (7) into the SWE, Equation (12), yields two equations that must be satisfied. One is the probability continuity Equation (4) itself, while the other is
![]() (14)
(14)
If![]() , the last term on the left-hand side of this equation is the so-called quantum-mechanical potential (energy) [1] [2] , generalized to the
, the last term on the left-hand side of this equation is the so-called quantum-mechanical potential (energy) [1] [2] , generalized to the ![]() -space. If it is negligible, then this equation reduces to the classical limit, the Hamilton- Jacobi equation for Hamilton’s principal function
-space. If it is negligible, then this equation reduces to the classical limit, the Hamilton- Jacobi equation for Hamilton’s principal function ![]() for the
for the ![]() -space classical nonrelativistic system, with
-space classical nonrelativistic system, with ![]() and
and ![]() being the physical fields (elec- tromagnetic, gravitational, etc.) that appear in the classical
being the physical fields (elec- tromagnetic, gravitational, etc.) that appear in the classical ![]() -space Hamil- tonian of the system.
-space Hamil- tonian of the system.
These identifications and the above derivation of the SWE from the probability continuity relation actually provide a derivation of classical mechanics (CM) for any nonrelativistic Lagrangian system as well, since the Hamilton-Jacobi equation implies the existence of a Hamiltonian, a Lagrangian containing the kinetic energy and metric (Equation (1)), the Euler-Lagrange equations, and thereby Newton’s laws of motion, for arbitrarily chosen potentials ![]() and
and![]() . Note that the hydrodynamic form of the SEQ, identical to Equation (14) if
. Note that the hydrodynamic form of the SEQ, identical to Equation (14) if![]() , does not allow quite the same conclusion, because in conventional QM the SEQ is not derived from a more fundamental equation. Also note that although Lagrangian/ Hamiltonian CM follows from Hamilton’s principle, that principle is yet another postulate, in contrast to the manifestly essential conservation of probability used to derive the SWE.
, does not allow quite the same conclusion, because in conventional QM the SEQ is not derived from a more fundamental equation. Also note that although Lagrangian/ Hamiltonian CM follows from Hamilton’s principle, that principle is yet another postulate, in contrast to the manifestly essential conservation of probability used to derive the SWE.
Canonical quantization. We define the vector conjugate momentum operator
![]() (15)
(15)
Then the covariant components of ![]() follow from Equation (3):
follow from Equation (3):
![]() (16)
(16)
and the Hamiltonian operator of Equation (13) is
![]() (17)
(17)
Therefore, the general rule for obtaining the SWE for any nonrelativistic classical Lagrangian system is simply to write down the classical Hamiltonian and then replace the conjugate momentum ![]() -vector
-vector ![]() by
by![]() . This is exactly the standard “canonical quantization” rule, except for the unknown constant
. This is exactly the standard “canonical quantization” rule, except for the unknown constant ![]() replacing
replacing![]() . Note that the commutator
. Note that the commutator ![]() is predicted. Also note that the presence of the combination
is predicted. Also note that the presence of the combination ![]() in
in ![]() ensures that the
ensures that the ![]() -vector potential field
-vector potential field ![]() must have the same significance as the electromagnetic vector potential for a single electric monopole, that of a gauge field.
must have the same significance as the electromagnetic vector potential for a single electric monopole, that of a gauge field.
3. Examples
In this section, we consider three examples that should help clarify the gene- ralized-coordinate approach. One is a system of two spinless pointlike particles that may have different masses. Another is a system of arbitrarily many identical spinless pointlike particles with two-body central force instantaneous internal interactions. A third is a system of one nonrelativistic rigid rotator. In these examples, we put![]() , as implied by the general results above.
, as implied by the general results above.
3.1. Two Pointlike Particles
The designation “pointlike” does not mean that the particles are actual points; instead, it means that the model particles considered are allowed no coordinates other than their CM coordinates. In this example, let the masses be![]() , and choose three Cartesian coordinates for each particle’s CM location,
, and choose three Cartesian coordinates for each particle’s CM location, ![]() for particle 1,
for particle 1, ![]() for particle 2. Then the kinetic energy
for particle 2. Then the kinetic energy ![]() on the trajectory
on the trajectory ![]() is
is
![]() (18)
(18)
where the index ![]() ranges and sums from 1 to 3. From Equation (18), we may read off the diagonal 6-space metric:
ranges and sums from 1 to 3. From Equation (18), we may read off the diagonal 6-space metric:
![]() (19)
(19)
with other components zero. Since ![]() in general, and
in general, and ![]() for
for ![]() in this example, and zero otherwise, we have
in this example, and zero otherwise, we have
![]() (20)
(20)
where ![]() and
and ![]() are the Cartesian unit basis vectors in the 6-space.
are the Cartesian unit basis vectors in the 6-space.
For this example, we consider the unperturbed central force case, by choosing ![]() and
and ![]() in the classical Hamiltonian, where
in the classical Hamiltonian, where
![]()
is the distance between the particle CM’s. The classical Hamiltonian is
![]() , and
, and![]() . Thus, according to our general results in Section 2, the Hamiltonian operator in the statistical wave equation is
. Thus, according to our general results in Section 2, the Hamiltonian operator in the statistical wave equation is![]() . Therefore, that SWE is
. Therefore, that SWE is
![]() (21)
(21)
At this point, one may go to the conventional notation![]() , and then to the system CM and relative coordinates.
, and then to the system CM and relative coordinates.
One reason for choosing this particular example is that it is probably the simplest two-particle example of the general method derived in section 2. Another reason is to emphasize that what you get in the Hamiltonian operator in the derived SWE is exactly what you have included in the classical Hamiltonian. For example, it is clearly physically incorrect to choose ![]() and thus omit all incident and self radiation fields. It is fortunate that perturbation theory works well in some cases. It is also incorrect in principle to neglect retardation in two-body interactions, but that will be a negligible effect in cases involving slow motions of particles that remain close together.
and thus omit all incident and self radiation fields. It is fortunate that perturbation theory works well in some cases. It is also incorrect in principle to neglect retardation in two-body interactions, but that will be a negligible effect in cases involving slow motions of particles that remain close together.
3.2. Many Identical Pointlike Particles
Consider the extension of the two-particle system above to ![]() pointlike spinless particles interacting with each other via two-body central force potential energies involving their CM coordinates and also allowing external electro- magnetic fields. We let the particles be identical, each with electric charge
pointlike spinless particles interacting with each other via two-body central force potential energies involving their CM coordinates and also allowing external electro- magnetic fields. We let the particles be identical, each with electric charge![]() , mass
, mass![]() , and possibly other charges, and each with CM location but no other degrees of freedom. Then the classical nonrelativistic Lagrangian, Hamiltonian, and motion equations each involve
, and possibly other charges, and each with CM location but no other degrees of freedom. Then the classical nonrelativistic Lagrangian, Hamiltonian, and motion equations each involve ![]() coordinates,
coordinates,
![]() . The development in Section 2 yields the general statistical wave Equation (12) involving these
. The development in Section 2 yields the general statistical wave Equation (12) involving these ![]() coordinates. For this example, the metric may be chosen as the
coordinates. For this example, the metric may be chosen as the ![]() -space Kronecker delta metric,
-space Kronecker delta metric,
![]() , corresponding to three independent Cartesian coordinates for each particle CM. In order to achieve a familiar notation, we relabel the coordinates by letting
, corresponding to three independent Cartesian coordinates for each particle CM. In order to achieve a familiar notation, we relabel the coordinates by letting![]() , so that
, so that ![]() is a particle index and
is a particle index and ![]() is a Cartesian coordinate index. Then, by analogy with the previous example, the simplest nontrivial unperturbed classical Hamiltonian contains
is a Cartesian coordinate index. Then, by analogy with the previous example, the simplest nontrivial unperturbed classical Hamiltonian contains ![]() and
and
![]() (22)
(22)
where terms with ![]() are omitted from the double sum,
are omitted from the double sum,
![]() , and
, and ![]() is a two-body central force interaction energy that could involve not only the Coulomb repulsion but also other forces such as Yukawa interactions and gravity. If we allow given external electro- magnetic potentials
is a two-body central force interaction energy that could involve not only the Coulomb repulsion but also other forces such as Yukawa interactions and gravity. If we allow given external electro- magnetic potentials ![]() to perturb the system, then the Hamiltonian would include the terms
to perturb the system, then the Hamiltonian would include the terms
![]() (23)
(23)
where ![]() stands for
stands for![]() . The
. The ![]() -vector
-vector![]() , where
, where
![]() , the Cartesian unit basis vector, the same for all
, the Cartesian unit basis vector, the same for all![]() . Again we emphasize that the functions
. Again we emphasize that the functions ![]() and
and ![]() that appear in the Hamiltonian operator are exactly those that are chosen for inclusion in the classical Hamiltonian. This often-used example omits internal vector potentials and also neglects retardation and self-fields.
that appear in the Hamiltonian operator are exactly those that are chosen for inclusion in the classical Hamiltonian. This often-used example omits internal vector potentials and also neglects retardation and self-fields.
For the identical particles in this example, the total Hamiltonian is invariant under all pair interchanges of particle indices. This invariance leads immediately to the result that the total wavefunction solution of the general many-particle SWE must either change sign under each pair interchange, yielding Fermions, or not change sign, yielding Bosons. As discussed in detail by Schweber [26] , the set of all Schrödinger equations for ![]() identical particles is mathe- matically equivalent to the “second quantized” many-particle quantum field theory for Fermions or Bosons in occupation number space.
identical particles is mathe- matically equivalent to the “second quantized” many-particle quantum field theory for Fermions or Bosons in occupation number space.
3.3. Nonrelativistic Rigid Rotator
Many authors have considered classical spinning top models and their possible connections to quantum spin and magnetic moment, e.g. [27] - [37] . Their treatments either postulate the usual commutation rules for the Cartesian components of the spin operator in the non-rotating coordinate system, by analogy with the rules for orbital angular momentum, or postulate that the momenta conjugate to the Euler angles become operators equal to ![]() times derivatives with respect to to the angles, by analogy with conjugate translational momenta. In our approach, no such postulates are needed; we simply apply the general statistical description developed in section 2 to the nonrelativistic rotations of a rigid body described by three Euler angle coordinates, as shown below.
times derivatives with respect to to the angles, by analogy with conjugate translational momenta. In our approach, no such postulates are needed; we simply apply the general statistical description developed in section 2 to the nonrelativistic rotations of a rigid body described by three Euler angle coordinates, as shown below.
3.3.1. Euler Angles and Angular Velocity
We include this subsection to establish our notation and method. For a rigid rotator with a fixed CM, the coordinates are a set of Euler angles,
![]() . We adopt the set
. We adopt the set ![]() used by Arfken [38] , and called the “zyz” set [39] . (Altogether there are twelve sets of Euler angles; all yield the same general results found below). A general rotation of Cartesian coordinates from a non-rotating system with Cartesian unit basis vectors
used by Arfken [38] , and called the “zyz” set [39] . (Altogether there are twelve sets of Euler angles; all yield the same general results found below). A general rotation of Cartesian coordinates from a non-rotating system with Cartesian unit basis vectors ![]() to a rotating system with Cartesian unit basis vectors
to a rotating system with Cartesian unit basis vectors![]() , with the origins of both systems at the body center of mass, is obtained by the relation
, with the origins of both systems at the body center of mass, is obtained by the relation
![]() (24)
(24)
where the orthogonal matrices ![]() and
and ![]() are given by
are given by
![]() (25)
(25)
Thus, the complete rotation is specified by the orthogonal matrix
![]() .
.
The angular velocity 3-vector can be found from the relations defining rigidly rotating Cartesian coordinates,
![]() (26)
(26)
where × is the cross-product, and ![]() is the instantaneous angular velocity. Its Cartesian components
is the instantaneous angular velocity. Its Cartesian components ![]() in the non-rotating frame, and
in the non-rotating frame, and ![]() in the rotating frame, can be obtained using Equations (24)-(26). The results are
in the rotating frame, can be obtained using Equations (24)-(26). The results are
![]() (27)
(27)
where we have specified the time-dependent trajectories of the Euler angles by![]() . The matrices
. The matrices ![]() and
and ![]() are easily shown to be
are easily shown to be
![]() (28)
(28)
3.3.2. Model Rotator, Metric, and Conjugate Momenta
In this introductory work, we treat a very simple model rotator, a non-translating but freely rotating rigid extended symmetric object having only the attributes of mass![]() , three equal principal moments of inertia
, three equal principal moments of inertia![]() , and three Euler angle coordinates and the associated 3-vector angular velocity
, and three Euler angle coordinates and the associated 3-vector angular velocity ![]() about the fixed CM. The Lagrangian
about the fixed CM. The Lagrangian ![]() is the kinetic energy
is the kinetic energy
![]() (29)
(29)
The metric of the Euler angle 3-space is easily identified as
![]() . It is not diagonal, so these Euler angle coor- dinates are not orthogonal. We do not need the metric in what follows.
. It is not diagonal, so these Euler angle coor- dinates are not orthogonal. We do not need the metric in what follows.
We may define the conjugate momentum 3-vector by
![]() (30)
(30)
where ![]() is the intrinsic (spin) angular momentum about the CM, conjugate to
is the intrinsic (spin) angular momentum about the CM, conjugate to![]() . Then the Hamiltonian
. Then the Hamiltonian ![]() is simply
is simply
![]() (31)
(31)
The (angular) momenta conjugate to the angles are
![]() (32)
(32)
Contraction with ![]() and
and ![]() and comparison with Equation (30) yields
and comparison with Equation (30) yields
![]() (33)
(33)
where the ![]() are the (non-rotating system, rotating system) Cartesian components of the conjugate spin angular momentum 3-vector
are the (non-rotating system, rotating system) Cartesian components of the conjugate spin angular momentum 3-vector![]() .
.
3.3.3. Statistical Wave Equation and Spin Operators
The relevant SWE for any nonrelativistic system having three coordinates is the three-dimensional version of the general SWE (12). In this case, the fields ![]() and
and ![]() are zero, and the gradient operator in the Euler angle space is given by
are zero, and the gradient operator in the Euler angle space is given by
![]() (34)
(34)
where![]() . Therefore, the conjugate classical momenta must be re- placed by the operators
. Therefore, the conjugate classical momenta must be re- placed by the operators
![]() (35)
(35)
just as postulated by some of the authors mentioned above. Writing Equation (31) in summation notation and making these substitutions yields
![]() (36)
(36)
where, from Equations (33) and (35),
![]() (37)
(37)
It is not difficult to show that the operators ![]() and
and ![]() are Hermitian provided the coordinate probability density obeys periodic boundary conditions in the Euler angle space. Using Equations (28) and (37), it is easy to show that the spin operators
are Hermitian provided the coordinate probability density obeys periodic boundary conditions in the Euler angle space. Using Equations (28) and (37), it is easy to show that the spin operators ![]() satisfy the usual angular momentum commutation rules,
satisfy the usual angular momentum commutation rules,
![]() (38)
(38)
where ![]() is the completely antisymmetric Levi-Civita symbol. Equations (33) and (35) also yield the expressions
is the completely antisymmetric Levi-Civita symbol. Equations (33) and (35) also yield the expressions
![]() (39)
(39)
Equations (28) and (39) then yield easily
![]() (40)
(40)
Note the minus sign, compared to Equation (38). These “left-handed” commu- tation rules must be obeyed by the rotating system Cartesian components of![]() .
.
Note that![]() , Equation (31), has eigenvalues
, Equation (31), has eigenvalues![]() , where the spin
, where the spin![]() . Therefore, the energy required to produce a transition from
. Therefore, the energy required to produce a transition from ![]() to
to ![]() is
is![]() . Let
. Let![]() , where
, where ![]() is the approximate linear extension of the model rotator. For a nucleon, with
is the approximate linear extension of the model rotator. For a nucleon, with ![]() and
and ![]() fm,
fm, ![]() , so (unstable) spin-3/2 baryons should exist, and they do. However, for an electron, with
, so (unstable) spin-3/2 baryons should exist, and they do. However, for an electron, with ![]() and
and![]() ,
,![]() . One must conclude that creating a spin-3/2 lepton having
. One must conclude that creating a spin-3/2 lepton having ![]() is virtually impossible. Furthermore, any model of a charged object having semi-definite charge density, mass and intrinsic magnetic moment of the order of electronic values, and relevant linear extension
is virtually impossible. Furthermore, any model of a charged object having semi-definite charge density, mass and intrinsic magnetic moment of the order of electronic values, and relevant linear extension
![]() , rotating rigidly with angular speed
, rotating rigidly with angular speed![]() , and having spin angular momentum of order
, and having spin angular momentum of order![]() , predicts a linear surface speed
, predicts a linear surface speed ![]() [40] . There- fore, rotations and translations of electrons and probably other leptons must be treated relativistically, which is beyond the scope of this work. (See the Appendix for a simple illustrative relativistic rotator model).
[40] . There- fore, rotations and translations of electrons and probably other leptons must be treated relativistically, which is beyond the scope of this work. (See the Appendix for a simple illustrative relativistic rotator model).
In a paper to follow, we will derive several relevant detailed results for a charged nonrelativistically spinning top of arbitrary shape and structure immersed in a magnetic field, including the following: 1) The commutation rules of Equations (38) and (40) are unchanged, whereby the commuting operators ![]() still have the same simultaneous eigenfunctions, sometimes called the Wigner harmonics, with eigenvalues
still have the same simultaneous eigenfunctions, sometimes called the Wigner harmonics, with eigenvalues![]() ,
, ![]() ,
, ![]() , respectively, where
, respectively, where![]() , and independently,
, and independently, ![]() , in integer steps; 2) a general rigid rotator wavefunction may be a superposition of integer spin eigenstates only, or of half-odd-integer spin eigenstates only, but not both, whereby e.g. electromagnetic transitions from a half-odd-integer spin state to an integer spin state are forbidden; 3) In the presence of a constant uniform magnetic field, one obtains the expected spinor equations consisting of
, in integer steps; 2) a general rigid rotator wavefunction may be a superposition of integer spin eigenstates only, or of half-odd-integer spin eigenstates only, but not both, whereby e.g. electromagnetic transitions from a half-odd-integer spin state to an integer spin state are forbidden; 3) In the presence of a constant uniform magnetic field, one obtains the expected spinor equations consisting of ![]() coupled equations for each choice of
coupled equations for each choice of ![]() and
and![]() . For example, for
. For example, for![]() , and
, and ![]() either
either ![]() or
or![]() , one obtains two coupled equations that comprise the Pauli-Schrödinger equation, when written in matrix/spinor form; and 4) For an anisotropic rotator, the Hamiltonian eigenvalues may depend on
, one obtains two coupled equations that comprise the Pauli-Schrödinger equation, when written in matrix/spinor form; and 4) For an anisotropic rotator, the Hamiltonian eigenvalues may depend on ![]() and/or
and/or ![]() as well as on
as well as on![]() .
.
4. Summary, Discussion, and Conclusions
In this work, using a derivation from first principles with no approximations, we proved that any nonrelativistic classical physical system must obey a statistical wave equation (SWE) that has the same form and the same quantitative solu- tions as the Schrödinger equation (SEQ) for the system. In the non-statistical (“classical”) limit, the SWE yields a system Hamiltonian and Lagrangian and thus the Euler-Lagrange equations and Newton’s laws of motion for the system coordinates. The SWE also yields quantum spin and many-body quantum field theory for nonrelativistic systems. On the basis of these results, should we not conclude that the classical statistical theory (CST) developed in this work actually provides a derivation of nonrelativistic classical and quantum dynamics for all Lagrangian systems composed of massive particles?
Our answer to that question is “not yet, and maybe never”. In earlier work [21] [22] [23] [24] and in this work (see Section 2.2) we found that a classical statistical theory based on continuity equations does not allow the conventional QM interpretations of the same quantitative results. In particular, the SWE by itself does not provide a complete statistical description of any system. For example, restrictions on initial conditions may exist such that the system cannot be in a single excited state initially, but only in a mixture of excited states [23] [24] . Also, the SWE is an ensemble-averaged equation, so its quantized Ha- miltonian eigenvalues, the same as those of the SEQ, are ensemble-averaged energies; the actual energies are not quantized. Nevertheless, standard per- turbation theory applied to a perturbed SWE still yields the Einstein rule in- volving the differences of the unperturbed eigenvalues for the frequencies of the dominant transitions, as well as the conventional transition rules and pro- babilities. (Prediction of transition probabilities for spontaneous emission using either the SEQ or the SWE requires either quantized electromagnetic fields or the inclusion of a radiation reaction vector portential in the vector potential![]() ; please see below, and also see reference [24] for a detailed discussion of this feature).
; please see below, and also see reference [24] for a detailed discussion of this feature).
Detailed analysis of such profound interpretational differences is well beyond the scope of this introductory paper. Our results would require an ensemble interpretation of QM, as well as other re-interpretations; see e.g. work by Ballentine [41] [42] . Furthermore, all our derivations follow conventional logical paths, but in reverse. For example, in this work we started our derivation with classical systems that do have coordinate trajectories, and used the Madelung transform in reverse to obtain the SWE/SEQ. On the other hand, Erwin Schrödinger inferred his SEQ nearly a century ago; the Madelung transform was applied to the SEQ to obtain its full hydrodynamic form, Equation (14). How- ever, scientists are still discussing whether classical trajectories are compatible with conventional QM [43] .
The CST derived herein makes sense only if there are reasons why even a one-particle classical system might require a statistical treatment. One possible reason is the known fact that any classical system is continually bombarded by thermal and other highly fluctuating background radiation fields. One model background field used in Stochastic Electrodynamics [7] [8] is the electro- magnetic stochastic zero-point field (SZPF), which is a stochastic analog of the quantized electromagnetic field; see e.g. [21] . Up to a multiplicative adjustable constant, chosen to be![]() , the SZPF is the only stochastic electromagnetic free field having a rotation-invariant, translation-invariant, and Lorentz-invariant ensemble-averaged energy density spectrum. Postulating the presence of this field enabled Boyer [44] to derive the Planck spectrum without quantum as- sumptions, and also allowed classical statistical derivations of Casimir forces [45] . The presence of the SZPF also yields a phase space derivation that au- tomatically includes a radiation reaction vector potential in the SWE/SEQ, as well as a companion equation that restricts initial conditions, for the nonrelati- vistic charged harmonic oscillator [23] [24] . Together, these equations predict the correct (QM) transition rates, including those for spontaneous emission, without quantization of classical electromagnetic fields. The presence of the SZPF also provides a physical rationale for the interference phenomena predicted by the SWE/SEQ. All of these SED results are based on ensemble averages over the random amplitudes of the plane waves that comprise the SZPF.
, the SZPF is the only stochastic electromagnetic free field having a rotation-invariant, translation-invariant, and Lorentz-invariant ensemble-averaged energy density spectrum. Postulating the presence of this field enabled Boyer [44] to derive the Planck spectrum without quantum as- sumptions, and also allowed classical statistical derivations of Casimir forces [45] . The presence of the SZPF also yields a phase space derivation that au- tomatically includes a radiation reaction vector potential in the SWE/SEQ, as well as a companion equation that restricts initial conditions, for the nonrelati- vistic charged harmonic oscillator [23] [24] . Together, these equations predict the correct (QM) transition rates, including those for spontaneous emission, without quantization of classical electromagnetic fields. The presence of the SZPF also provides a physical rationale for the interference phenomena predicted by the SWE/SEQ. All of these SED results are based on ensemble averages over the random amplitudes of the plane waves that comprise the SZPF.
5. Conclusion
In conclusion: Before we are willing to conclude that the CST actually provides a derivation of a good part of modern physics, we feel that at least two things must be accomplished. One is a statistical treatment of relativistic classical systems, with a closer correspondence to our nonrelativistic treatment herein than our work reported in 2010 [25] . The other is a resolution of the interpretational differences between the CST and conventional QM. This latter accomplishment may require clever experiments that will take some time.
Acknowledgements
The author would like to thank Stephen Pate, Michael Engelhardt, and Stefan Zollner for helpful discussions and assistance in preparing the manuscript.
Appendix A: Relativistic Rotation
As mentioned above, one objection to a nonrelativistic extended spinning electron model having semidefinite charge density is that it seems to require tangential linear speeds ![]() that far exceed lightspeed
that far exceed lightspeed![]() . In this appendix we treat a simple model relativistically and show that then
. In this appendix we treat a simple model relativistically and show that then ![]() for all parameter choices. The model is a circular ring of radius
for all parameter choices. The model is a circular ring of radius ![]() with mass
with mass ![]() and charge
and charge ![]() uniformly distributed around the ring. Let the ring lie in the
uniformly distributed around the ring. Let the ring lie in the ![]() plane and be constrained to rotate about the
plane and be constrained to rotate about the ![]() -axis, its symmetry axis, with angular velocity
-axis, its symmetry axis, with angular velocity ![]() -component
-component![]() , where
, where ![]() is the relevant Euler angle. If one neglects/ignores the self magnetic field and there are no applied fields, the nonrelativistic expression for the
is the relevant Euler angle. If one neglects/ignores the self magnetic field and there are no applied fields, the nonrelativistic expression for the ![]() -component of the canonical spin angular momentum is simply
-component of the canonical spin angular momentum is simply![]() . If this expression must have magnitude
. If this expression must have magnitude![]() , one obtains
, one obtains![]() . Using the electron mass
. Using the electron mass ![]() and radius
and radius ![]() yields
yields![]() !
!
Evidently we should have used relativistic expressions for the momenta. For this model rotator, any infinitesimal ring segment of restmass ![]() has tangential linear momentum
has tangential linear momentum![]() , where
, where![]() . Therefore, in the absence of magnetic fields the spin angular momentum of the ring is
. Therefore, in the absence of magnetic fields the spin angular momentum of the ring is
![]() . For
. For![]() , one obtains
, one obtains![]() , whereby
, whereby
![]() . For the electron parameter values above,
. For the electron parameter values above, ![]() , whereby
, whereby![]() ! For baryon parameter values,
! For baryon parameter values, ![]() ,
, ![]() , one obtains
, one obtains![]() , which is essentially nonrelativistic.
, which is essentially nonrelativistic.
It is interesting to to evaluate the magnitude ![]() of the magnetic moment predicted by this electron model due to its intrinsic rotation only. Since
of the magnetic moment predicted by this electron model due to its intrinsic rotation only. Since![]() ,
, ![]() , at most
, at most ![]() times the correct value. This result supports the old idea that the electron magnetic moment may be almost entirely due to highly irregular relativistic translational motion (zitterbewegung) that could be induced by a stochastic field such as the SZPF.
times the correct value. This result supports the old idea that the electron magnetic moment may be almost entirely due to highly irregular relativistic translational motion (zitterbewegung) that could be induced by a stochastic field such as the SZPF.
![]()
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jmp@scirp.org