1. Introduction
Discovering the origin of the Klein-Gordon equation is an important step to solve the mysteries behind the laws of Physics, since it is a bit more than just an equation for spin-zero particles. It can be related to the Dirac equation and to some extent to higher spin theories as well as to the non-relativistic Schrödinger equation. Quantum Mechanics occupies a very unusual place among physical theories: it contains Classical Mechanics as a limiting case, yet it requires this limiting case for its own formulation (p. 3 in [9] ). This is in our view a clear hint towards a close relation between the two theories. Several derivations or interpretations of Quantum Mechanics start with the textbook axioms of Quantum Physics, but this is nonsense according to some authors [8] [10] . The results of this paper should help answer questions raised by the unexpected coexistence of Classical and Quantum Mechanics in some macroscopic topological insulators [11] .
In Section 2, we derive the Klein-Gordon equation for free fields in a curved space time from purely geometrical considerations. In Section 3, we introduce interactions of the scalar field with some vector potentials. In Section 4, we discuss our results and in Section 5 we give our conclusions.
2. Free Scalar Fields
The idea that the laws of Classical Mechanics may have a geometric origin is indeed very old. One may e.g. cite Lagrange (1736-1813) [12] :
Nous allons employer la théorie des fonctions dans la mécanique. Ici les fonctions se rapportent essentiellement au temps, que nous designerons par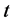 ; et comme la position d’un point dans l’espace dépend de trois coordonnées rectangulaires
; et comme la position d’un point dans l’espace dépend de trois coordonnées rectangulaires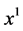 ,
, 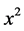 ,
, 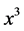 , ces coordonnées, dans les problèmes de mécanique, seront censées être fonctions de
, ces coordonnées, dans les problèmes de mécanique, seront censées être fonctions de . Ainsi on peut regarder la mécanique à quatre dimensions, et l’analyse mécanique comme une extension de l’analyse géométrique.
. Ainsi on peut regarder la mécanique à quatre dimensions, et l’analyse mécanique comme une extension de l’analyse géométrique.
This program has been fulfilled to some extent with the advent of Special Relativity and Generality. However it is not clear whether this picture should be extended to Quantum Mechanics. This is the aim of the present study.
First of all we assume that spacetime is a smooth four dimensional real Riemann manifold. Each spacetime point 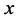 is labeled by four coordinates
is labeled by four coordinates
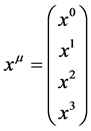 (1)
(1)
where 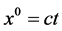 represents the time coordinate and
represents the time coordinate and 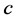 is a dimensional constant (e.g. the velocity of light in empty space),
is a dimensional constant (e.g. the velocity of light in empty space), 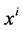 are spatial coordinates
are spatial coordinates
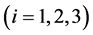 . The points of a curve are characterized by their distance
. The points of a curve are characterized by their distance 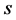 from the origin.
from the origin. 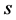 is defined as
is defined as
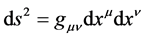 (2)
(2)
where  is the metric tensor. It can be used to evaluate scalar products and to rise as well as to lower the indices of four dimensional vectors. One defines to this purpose the inverse tensor
is the metric tensor. It can be used to evaluate scalar products and to rise as well as to lower the indices of four dimensional vectors. One defines to this purpose the inverse tensor 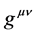 by the the relation
by the the relation
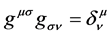 (3)
(3)
where 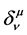 is the Kronecker delta symbol. It takes the value one for equal indices and zero otherwise. To obtain a real value of the curve length
is the Kronecker delta symbol. It takes the value one for equal indices and zero otherwise. To obtain a real value of the curve length ![]() we require
we require
![]() (4)
(4)
Instead of ![]() one may use the equally good parameter
one may use the equally good parameter ![]() (proper time) defined as
(proper time) defined as
![]() (5)
(5)
The velocity vector along the curve is defined as
![]() (6)
(6)
It yields by definition (2) the identity
![]() (7)
(7)
where
![]() (8)
(8)
We are now ready to study the variation of scalar field ![]() along a curve
along a curve![]() . A field is by convention a function of space and time.
. A field is by convention a function of space and time.
The total derivative of the scalar field ![]() yields
yields
![]() (9)
(9)
where ![]() is a partial derivative
is a partial derivative
![]() (10)
(10)
We use implicitly Einstein’s sum convention [13] .
Since ![]() transforms like a vector field we may define the auxiliary vector field
transforms like a vector field we may define the auxiliary vector field ![]() as
as
![]() (11)
(11)
where ![]() represents a dimensional constant. We use here the standard notations of Quantum Mechanics with purpose. One may apply the inverse metric tensor on
represents a dimensional constant. We use here the standard notations of Quantum Mechanics with purpose. One may apply the inverse metric tensor on ![]() to obtain the momentum field
to obtain the momentum field
![]() (12)
(12)
Equation (9) yields
![]() (13)
(13)
The expression ![]() represents the scalar product of two vector fields; it is therefore a scalar field by itself. It can in principle take any value. However a small miracle happens when the trajectory is chosen so that the velocity
represents the scalar product of two vector fields; it is therefore a scalar field by itself. It can in principle take any value. However a small miracle happens when the trajectory is chosen so that the velocity ![]() is parallel to the momentum
is parallel to the momentum![]() , it means
, it means
![]() (14)
(14)
where ![]() is a third scalar dimensional constant besides
is a third scalar dimensional constant besides ![]() and
and![]() . To make sense
. To make sense ![]() and
and ![]() must be real. Negative values of
must be real. Negative values of ![]() are in principle allowed. In the following we show that the scalar field
are in principle allowed. In the following we show that the scalar field ![]() will then obey the Klein Gordon equation that the path
will then obey the Klein Gordon equation that the path ![]() will obey at the same time the geodesic equation, further we will try to find the meaning of the classical trajectory
will obey at the same time the geodesic equation, further we will try to find the meaning of the classical trajectory ![]() for the wave function
for the wave function![]() .
.
Equations (6) (7) (14) yield
![]() (15)
(15)
![]() (16)
(16)
Equations (11) and (16) mean that the scalar field ![]() will obey the Klein-Gordon equation
will obey the Klein-Gordon equation
![]() (17)
(17)
for free particles if ![]() is constant in a Minkowski spacetime
is constant in a Minkowski spacetime
![]() (18)
(18)
To show (17) multiply Equation (16) with ![]() and use the definition (11). The Klein-Gordon equation is used to describe spinless particles. Notice that Dirac fields for spin-
and use the definition (11). The Klein-Gordon equation is used to describe spinless particles. Notice that Dirac fields for spin-![]() particle are also solutions of (17). Schrödinger wave functions are non-relativistic approximations for
particle are also solutions of (17). Schrödinger wave functions are non-relativistic approximations for![]() . We will not further discuss these well known facts. In more general cases multiply (16) with
. We will not further discuss these well known facts. In more general cases multiply (16) with ![]() from left and
from left and ![]() from rights, it yields
from rights, it yields
![]() (19)
(19)
One may try to use the left hand side of (19) as a Lagrangian density
![]() (20)
(20)
for the Klein-Gordon field. The action reads
![]() (21)
(21)
where
![]() (22)
(22)
It leads to the Klein Gordon equation
![]() (23)
(23)
in curved space times. Very often some extra terms containing the curvature scalar ![]() are arbitrarily added to Equation (23) in the literatur [14] .
are arbitrarily added to Equation (23) in the literatur [14] .
Unlike the usual derivations of Quantum Mechanics the geometrical path taken in this paper is inconsistent unless we give an equation for the classical trajectory as well. To do this recall that Equation (14) looks like Hamilton’s equation
![]() (24)
(24)
for which we already know the Hamiltonian
![]() (25)
(25)
and we determine the Lagrangian
![]() (26)
(26)
It yields the Euler-Lagrange equations
![]() (27)
(27)
where
![]() (28)
(28)
are Christoffel symbols [13] . They vanish in Minkowski space. Equation (26) may also be written without indices as
![]() (29)
(29)
This is a geodesic equation. It means that the curve ![]() is the shortest path between two of its points.
is the shortest path between two of its points.
Finally it is interesting to solve Equation (13). We find
![]() (30)
(30)
only the phase of the wave function ![]() changes along the field lines
changes along the field lines![]() . Remember
. Remember![]() . The intensity
. The intensity ![]() remains constant. This allows some kind of statistical interpretation of the wave function.
remains constant. This allows some kind of statistical interpretation of the wave function.
Equations (11) (14) (27) determine a set of lines (trajectories) that do not intersect and that are characterized by a probability which is the same at each of their points. This is clearly an addition to the standard interpretation of Quantum Mechanics.
3. Interactions
The simplest way to insert interactions of the Klein-Gordon field with external fields is given by the principle of minimal substitution:
![]() (31)
(31)
which means
![]() (32)
(32)
and
![]() (33)
(33)
we define the Lagrangian density for the Klein-Gordon equation
![]() (34)
(34)
and the action
![]() (35)
(35)
It yields Lagrange’s equations in Minkowski space (18)
![]() (36)
(36)
and
![]() (37)
(37)
in more general spacetimes.
The Hamiltonian for the classical trajectory is
![]() (38)
(38)
The Lagrangian reads
![]() (39)
(39)
It yields the Euler-Lagrange equations
![]() (40)
(40)
where
![]() (41)
(41)
is Maxwell’s field strength tensor. Equation (40) is postulated within Special Relativity and General Relativity as a generalization of Newton’s second law for the motion of a particle in the electromagnetic field![]() . Notice that we did not need at all use the point particle concept in order to derive (40) from pure Mathematics. Just as in the case of the free particle Equations (33) (40) yields a congruence of trajectories that have defined probabilities. Equations (13) (33) yield an additional contribution of the interaction to the phase of the wave function
. Notice that we did not need at all use the point particle concept in order to derive (40) from pure Mathematics. Just as in the case of the free particle Equations (33) (40) yields a congruence of trajectories that have defined probabilities. Equations (13) (33) yield an additional contribution of the interaction to the phase of the wave function
![]() (42)
(42)
Adding an arbitrary phase ![]() to (42) will correspond to a modification of the vector potential
to (42) will correspond to a modification of the vector potential
![]() (43)
(43)
in full agreement with gauge theory.
4. Discussion
It is generally accepted that Classical Mechanics is the limit of Schrödinger equation when![]() , that is when the action of the moving particles are much bigger than
, that is when the action of the moving particles are much bigger than![]() . This restricts the scope of Quantum Mechanics to microscopic systems. We have found the derivations of the Schrödinger equation not quite convincing. Therefore we have tried to find the origin of Quantum Mechanics in the mathematical properties of scalar functions defined over a spacetime endowed with a metric tensor
. This restricts the scope of Quantum Mechanics to microscopic systems. We have found the derivations of the Schrödinger equation not quite convincing. Therefore we have tried to find the origin of Quantum Mechanics in the mathematical properties of scalar functions defined over a spacetime endowed with a metric tensor ![]() that allows us to define the proper time
that allows us to define the proper time![]() .
.
Requiring the velocity ![]() to be parallel to the gradient
to be parallel to the gradient ![]() of the scalar field is the ultimate cause of fundamental equations of Classical and Quantum Mechanics. The rest mass plays the role of a (scalar) proportionality constant that can in principle take any real value. We have reinterpreted the relations (14) (33) as a Hamilton equations and we have calculated the equations of motion for classical trajectories. These are lines of constant intensity. Our work seems to give partial support to the standard probabilistic interpretation of Quantum Mechanics.
of the scalar field is the ultimate cause of fundamental equations of Classical and Quantum Mechanics. The rest mass plays the role of a (scalar) proportionality constant that can in principle take any real value. We have reinterpreted the relations (14) (33) as a Hamilton equations and we have calculated the equations of motion for classical trajectories. These are lines of constant intensity. Our work seems to give partial support to the standard probabilistic interpretation of Quantum Mechanics.
Trajectories have always been related to particles. They have been banned from Quantum Mechanics but we find here that they are intrinsic properties of the fields (wave functions) themselves. It means that Quantum Mechanics in its present status may indeed be somehow incomplete and we need to correct this. New interpretations of Quantum Mechanics and the uncertainty relations are therefore required.
There are some claims of observed macroscopic quantum effects e.g. topological insulators which exhibit a coexistence of Classical and Quantum Mechanics, in contradiction with textbook knowledge [11] . Our analysis shows however that Classical and Quantum Mechanics have the same mathematical origin. They are completely tied and It seems reasonable to expect that both should be valid all over the universe with practical limitations given by Heisenberg uncertainty relations and the experimental facilities. This is matter of further research.
5. Conclusion and Outlook
We have shown how the Klein-Gordon equations of Quantum Mechanics and relativistic Newton’s equations of Classical Physics can be simultaneously derived from the mathematical properties of scalar functions and not from physical principles and postulates. Since fermions obey the Dirac equation but also the Klein Gordon equation in Minkowski space, we may see why they behave just like other particles (bosons) in Classical Physics. We wish the same could happen in curved spacetimes [15] [16] , but this remains to be confirmed. There are big questions about particles: how do they inherit their properties (rest mass, energy-momentum, electric charge, classical trajectories etc.) from fields? Understanding the Mathematics behind the laws of Physics is not only thrilling but it is required in order to achieve a deeper understanding of nature. Geometry (Gravity) seems to play a decisive role in the selection of the fundamental laws of Physics.