Medium Term Load Forecasting for Jordan Electric Power System Using Particle Swarm Optimization Algorithm Based on Least Square Regression Methods ()
1. Introduction
MTLF is extremely important for energy suppliers and other participants in electric energy generation, transmission, distribution and markets. It helps make decisions, including decisions on purchasing and generating electric power system utilities. The main role of electric load forecasting in the electric system is to help the energy companies to plant the purchasing and generating of electric power needed. Load forecasting studies can be categorized based on forecasting period into three categories: short term load forecast (STLF) from one hour to a week, medium term load forecast (MTLF) from one week to a year and long term load forecast (LTLF) longer than one year [1] . These categories of forecasts are different as well, for example for a particular region it is possible to predict the next three days peak load with accuracy (1% - 2%), but it is impossible to predict the next year peak load with similar accuracy because we do not have weather observations [2] . MTLF is one of the most difficult problems in distribution power system planning and analysis [3] . There are many factors affecting the load forecasting such as historical load data, population growth and economic development. MTLF is not easy due to: firstly, because the load series is complex and shows vacillating behavior [4] ; secondly, there are many important variables that must be considered, including weather data. To determine the accuracy of MTLF, a comparison between the actual load taken by NEPCO and the approximation load calculated by LSRM and PSO algorithm must be achieved. To achieve a good forecasting prediction many approaches have to deal with programmed power network [5] . Accurate tracking of weekly demand and monthly peak demands is very important for the operation of any power system. MTLF is basically used to decide whether an extra power generation should be provided to meet the demand or not. The demand can be met by either increasing the generation, installing new generation units into service or by power exchange from neighboring countries. On the other hand, MTLF can also be used to decide whether the output of the running generation units should be decreased or stopped. In order to predict the electric load demand of a power system, it is important to investigate the load pattern, its response and the factors effect on the demand [4] . Two main challenges have a direct impact on the Jordan power operator center, the first one: obtaining optimal economic dispatch for electrical utilities and the second one is determining medium term unit commitment in order to maintain the system reliability. Therefore, there is a necessity to make a robust MTLF models as a first step for power system operation and planning based on LSRM and PSO optimization. The existing forecasting predictions of MTLF employed by National Electric Power Company (NEPCO) in Jordan are based on the educated guess assumptions which depend on gathering the electricity consumption of domestic, commercial, industrial, and public lighting sectors. The average error obtained by NEPCO was in the range from 8.2% to 12.8% in 2015, which is high. Therefore, it is necessary to have reliable model to predict the load for medium term periods [5] .
2. Forecasting Procedure
The MTLF procedure for the models can be viewed in Figure 1.
2.1. Data Source
Input variable selection, including: month type, peak load, average electrical de- mand, humidity and temperature data, and weather influences of previous time.
2.2. Historical Data
The monthly or weekly peak load demand data recorded from NEPCO for the years (2008-2014) taking into account external variables like holidays, weather and population growth.
2.3. Data Pre-Processing
It may be inevitable to have improperly recorded data and observation error.
Therefore the monthly and weekly reported data from NEPCO used to initialize the simulation results.
2.4. Simulation
In this part, the peak load forecasting output is simulated using Matlab.
2.5. Convergence Criteria
The stopping criterion is met when the parameters of PSO are achieving a global forecasting error within an efficient computation time. The convergence error must be less than 0.01% to make a sufficiently good fitness value.
2.6. Post Processing
The LSRM and PSO coefficients require calculations to prompt the desired forecasted load results.
2.7. Error Analysis
As characteristics of load changes, error observations become more significant for the forecasting process. LSE is used to improve the accuracy of these models.
3. Forecasting Methodology
Regression analysis is widely used in the analysis of data for any design. Regression models one of the most commonly used statistical analysis techniques in any research [6] . Typically, regression analysis is used to discover the relationships between a dependent variable and a set of independent variables based on a sample from input data [7] . We will study the method in the context of a regression problem, where the variation in one variable, called the response variable Y, can be partly explained by the variation in the other variables, called co-variables X. For example, variation in exam results Y are mainly caused by variation in abilities X of the students [8] . The least squares estimates used to minimize the error sum of squares:
(1)
where: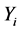
: Actual load value in MW for week or month,
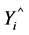: Predicted load value in MW for week or month,
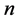: Number of samples (weeks or months).
3.1. Least Square Regression Methods
Regression analysis is the study of the action of the time series or process in the past and it is mathematical model, therefore the future behavior can be expected from it. In the forecasting process of medium term peak load, least squares regression methods are used by different relations between the input and output [9] .
3.1.1. Linear Regression
The medium term load forecasting of many business series such as, sales exports and production usually approximates a straight line. The simple linear regression method LRM model is designed to study the relationship between a pair of variables that appear in a data set. It is a model based on the linear relationship between the total demand y and month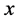 
as shown in Equations (2)-(4) [10] .
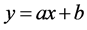(2)
where:
: The slope,
: The interception point at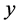 
axis.
The least squares criterion is used to generate the line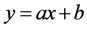 
that fits a set of n data points.
By using the least square error approach [10] ,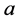 
and 
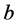coefficients can be given by:
(3)
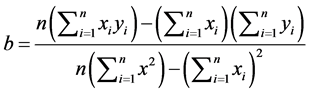(4)
where: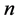
: The number of months which the forecasting is based on,
: The total load demand for all period for forecasting,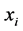
: The total sum of months.
When ![]()
and ![]()
coefficients are obtained, the load forecasting is performed by Equation (2.2).
3.1.2. Quadratic Regression
In this approach the parabolic function which is given in Equation (5) is used
![]()
(5)
After applying least square error we can find![]()
, ![]()
and ![]()
parameters in matrix form [10] .
![]()
(6)
When![]()
, ![]()
and ![]()
coefficients obtained the load forecasting is performed by Equation (5).
3.1.3. Exponential Regression
In this method the exponential function is obtained through Equations (8)-(15) to get Equation (7).
![]()
(7)
By writing the equation in logarithmic form, the equation becomes:
![]()
(8)
The properties of algorithms give
![]()
(9)
This expresses ![]()
as a linear function of ![]()
with slope.
![]()
(10)
![]()
(11)
Therefore, if we find the best line using ![]()
as A function the slope and intercept will be gives as linear regression, so that the coefficients ![]()
and A derives as linear equation.
![]()
(12)
![]()
(13)
After linearization, ![]()
and ![]()
coefficients are shown in Equations (12) and (13).
![]()
(14)
![]()
(15)
When ![]()
and ![]()
coefficients are obtained the load forecasting is performed by Equation (7) [10] .
3.2. Particle Swarm Optimization
A Particle swarm optimization PSO technique is used to find the optimal parameters for different forecasting methods. This algorithm is used to solve a wide class of complex optimization problems in engineering and science. Both linear and nonlinear models will be used in the system and the results will be obtained using PSO. Through the implementation of PSO all particles are kept as members of the population. The basic idea of the PSO is the mathematical modeling and simulation of the food searching activities of a swarm of birds in the multi- dimensional space where the optimal solution is sought. Each particle in the swarm is moved towards a point where it obtains optimal solution by the influence of its velocity. The velocity of a particle is affected by three factors; inertial momentum, cognitive and social [11] . The goal of PSO is to find the optimal variable values for a certain function. Each particle knows its optimal value (![]()
) and its velocity and position. Also, each particle knows the optimal value in the group (![]()
) among pbests. Each particle seeks to adjust its position using the current velocity and the distance obtained from the ![]()
and![]()
. Based on the above discussion, the mathematical model for PSO is represented as velocity update equation given by Equations (16)-(18).
![]()
(16)
![]()
(17)
where:
![]()
: The velocity of particle.
![]()
: The current position of particle.
![]()
and ![]()
are positive constants, used to pull each particle to ![]()
and![]()
.
![]()
and ![]()
are two randomly generated numbers with a range [0 1].
![]()
is the inertia weight and it keeps balance between exploration and exploitation.
![]()
(18)
![]()
: The initial weight.
![]()
: The final weight.
![]()
: The best particle position i achieved.
![]()
: The best position of all particles achieved.
![]()
: The iteration index.
In this work, PSO is employed to minimize the LSE between the real values and prediction values. To evaluate the forecasting process for each model, LSE error can be used.
3.3. Auto Regressive (AR) Model
The AR model was developed by Box and Jenkins in 1970 to analyze historical data that had relations within it. In this study, the parameters were obtained from NEPCO. The AR process utilizes the least squares (LS) method, and it is an analogous way to fit a model by minimizing the sum of square errors for estimating parameters. The LSE uses the normal equations to implement the polynomial system. The parameters can be solved by Matlab. The purpose of this study was to implement the discounted least squares method with direct smoothing for estimating autoregressive model parameters [12] .
The AR model structure is given by Equation (19)
![]()
(19)
![]()
: The parameters that are estimated using variants of the least-squares method.
![]()
: iddata object that contains the time-series data (one output channel).
![]()
: Random Error.
The parameters of ![]()
can be estimated by Equation (20).
![]()
(20)
![]()
: The coefficients for each order.
![]()
: Scalar that specifies the order of the model you want to estimate (the number of A parameters in the AR model).
![]()
: Random error.
4. Results and Discussions
Real peak loads are used in this study, so the electric peak loads in the years [2008-2014] have been founded for Jordan country. The data used are monthly and weekly peak loads recorded in the years [2008-2014]. This system of equation is solved using the proposed PSO algorithm to find the optimal coefficients for different forecasting models. Linear, quadratic, exponential and AR models are used in the system and the results obtained using PSO are compared with those of LSRM. A Matlab code was generated to execute the PSO Algorithm and LSRM Using the peak data of NEPCO grid. For PSO, all particles start at a random position in the range [0, 1] for each dimensions. The swarm size was limited to 250 particles. The selections of some parameters to carry out the procedures of the work successfully has great effect on the model, these parameters are maximum speed, inertia weight and acceleration constants. The most suitable values for maximum speed is set to be 2, ![]()
and ![]()
are 0.9 and 0.4, C1 and C2 are 2.
Key parameters of PSO algorithm used in this paper are presented in Table 1.
4.1. Case One: MTLF Based on Peak Load Data
Peak Loads of NEPCO recorded in the years [2008-2014] are used to estimate the coefficients of linear, quadratic and exponential models for MTLF. The inputs of these models are the number of weeks or months and the peak loads recorded in the years [2008-2014], whereas the output is the monthly or weekly peak loads predicted for the year 2015.
4.1.1. Monthly Forecasting
PSO and LSRM techniques are used to estimate models parameters. Horizon and the computed parameters are tabulated in Table 2.
Since the forecasting in this work is carried out on monthly bases, monthly least square error is performed and calculated by Equation (21). The equation used is given by:
![]()
(21)
![]()
Table 2. Monthly estimated coefficients based on LSRM and PSO.
The monthly forecasted peak loads based on the parameters of linear, quadratic and exponential models and monthly least square error are shown in Table 3.
It can be concluded from the tables that the results computed by PSO are more close to the peak load and have less error. In both approaches, the monthly peak load is increased continuously from January till December when using linear or exponential models. In quadratic model, the peak load is decreased continuously from January till June and increased from June till December. The forecasted monthly peak load using different models are shown in Figure 2.
It can be seen from the figure that the PSO and LSRM are close to each other. In each model the difference between LSRM and PSO is arranged from [10] [11] [12] MW. This difference make LSRM very close to the real peak load in April, May and October, otherwise the PSO achieves better estimation for the predicted peak load. The results show that the PSO model is more accurate than LSRM and moreover, it is closer to the real peak load data for the year 2015. The monthly error performed by LSRM and PSO algorithm is shown in Figure 3.
From Figure 3, it can be observed that the Error for 2015 with LSRM and PSO is arranged from 0.04% to 16.85%. The Error less than 10% for nine months in LSRM and PSO approaches. The average error in LSRM for linear model is 6.64%, for quadratic model is 6.40%, and for exponential is 7.41%. So it can be seen that the best represented model between the months and peak load in LSRM is the quadratic regression model. The average error in PSO for linear model is 6.47%, for quadratic model is 6.18%, and for exponential is 7.09%.
![]()
Table 3. Monthly morning peak loads for the year 2015 compared with the actual readings.
![]()
Figure 2. Monthly forecasted peak load using LSRM and PSO.
![]()
Figure 3. Monthly error associated with LSRM and PSO.
Therefore the best represented model between the months and peak load in PSO is the quadratic regression model.
4.1.2. Weekly Forecasting
Weekly real peak demands recorded in the years [2008-2014] are used in this section. The data set is used to establish an over determined system of equations. This system of equations is LSRM and PSO technique. The weekly real peak loads are used to find the coefficients for linear, quadratic and exponential models. PSO and LSRM techniques are used to estimate models parameters for the same time horizon and the computed parameters are tabulated in Table 4.
The forecasted loads based on the parameters of linear, quadratic and exponential models and weekly least square error are shown in Table 5.
It can be concluded from the tables that the error computed by PSO are less than LSRM. In linear and exponential models, the weekly prediction load is increased from the first week till last week of the year 2015. In quadratic model, the weekly prediction load has vertex point [minimum peak value] occurs at week number 26. The peak load demand expected using LSRM and PSO shown in Figure 4.
![]()
Table 4. Weekly estimated coefficients based on PSO and LSRM.
![]()
Table 5. Weekly peak loads for the year 2015 compared with the actual readings.
![]()
Figure 4. Weekly forecasted peak load using LSRM and PSO.
From Figure 4, it can be concluded that the PSO technique gives more accurate results than LSRM. In LSRM model, the prediction of the weekly peak load data gives results close to the real value in the weeks number 20, 24 and 44, otherwise the PSO technique represent the best model for all weeks in the year 2015. The weekly error performed by LSRM and PSO algorithm is shown in Figure 5.
From Figure 5, it can be seen that the error has minimum values for 20 weeks and maximum values for 10 weeks arranged from 0.0% to 15.99%. From average error point of view it is found that PSO method has produced better estimates than the LSRM and the quadratic model has the least error. Therefore, the best represented model between the weeks and peak load in LSRM and PSO is the quadratic regression model.
4.2. Case Two: MTLF Based on Weather Effect
Weather is the most important independent variable for MTLF. In this section, MTLF models used weather influence to predict the future peak load demand in terms of month and week. Various weather variables could be considered for MTLF. Temperature is the most commonly used for load predictors. The result of the previous section shows that there is a high positive correlation between temperature and peak load during summer and there is a negative correlation between temperature and peak load during winter. For these positive and negative correlations, LSRM used to predict the peak load in the hot and cold days. Because the relation between temperature and peak load is very complicated in nature and cannot be analyzed with ordinary mathematical models, the quadratic model used for data obtained in summer and winter seasons.
4.2.1. Monthly Forecasting
Peak loads of NEPCO are used to estimate the coefficients of quadratic model for MTLF in summer and winter season. Summer season extends from June till September; winter season extends from December till March. Long studies investigated that the changing of the temperature affects the peak load. The researches focused on the effect of the higher and lower temperatures on electricity
![]()
Figure 5. Weekly error associated with LSRM and PSO.
consumption using peak load data and temperature influence. The studies indicate that the impact of a one-degree in temperature higher than 25˚C, the peak load predicted will increase by 8 MW and a one-degree in temperature lower than 15˚C, the peak load predicted will increase by 6 MW [13] .
The inputs of this model is the number of months per each season and the peak loads recorded in the years [2008-2014], whereas the output is the monthly peak loads predicted for the year 2015 after taking the temperature effect by each season. PSO and LSRM techniques are used to estimate quadratic model parameters for winter and summer season. The quadratic parameters are tabulated in Table 6.
Table 7 represents the adjusted forecasted loads based on the parameters of quadratic model after taking the temperature effect by each season and monthly least square error.
It can be concluded from the table that in summer season, the peak load is increased continuously from June till August and decreased from August till
![]()
Table 6. Monthly estimated coefficients for LSRM and PSO based on temperature effect.
![]()
Table 7. Monthly forecasted peak load by quadratic model based on temperature effect.
September, while in winter season the peak load is increased continuously from December till January and decreased continuously from January till March. The forecasted monthly peak load using quadratic model and PSO algorithm based on temperature effect is shown in Figure 6.
It can be observed from Figure 6 that the results obtained by the PSO are very close to the real values and more accurate than the results obtained by LSRM. The prediction load obtained by LSRM is very close to the real peak load in January, April and October, otherwise the PSO made better estimation for the predicted peak load. Figure 7 is shown the monthly least square error based on temperature effect.
From Figure 7, it can be noticed that the error for 2015 with quadratic model and PSO algorithm is less than 5% for every month. The minimum error 0.0% is happened in November, while the maximum error 4.68% is happened in September. The average error in Quadratic model is 2.02% and in PSO algorithm is 1.73%. Therefore, the PSO approach gives the best represented model between the months and peak load based on temperature effect.
4.2.2. Weekly Forecasting
The historical and weather data for the period [2008-2014] are used for estimation the models parameters for winter and summer seasons. Data for the year
![]()
Figure 6. Monthly peak load using quadratic model based on temperature effect.
![]()
Figure 7. Monthly forecasting error using quadratic model based on temperature effect.
2015 are used for testing LSRM and PSO models. The inputs of this model is the number of weeks per each season, whereas the output is weekly peak loads predicted for the year 2015 after taking the temperature effect by each season. The quadratic parameters are tabulated in Table 8.
The weekly forecasted peak load using quadratic model and PSO algorithm based on temperature effect is shown in Figure 8.
From Figure 8, it can be noticed that the PSO results are very close to the real peak load data for the most weeks in the year 2015. The maximum peak loads in 2015 are happened in the weeks representing the summer and winter seasons, therefore the difference in values between real and prediction load data has the maximum in these weeks. The adjusted forecasted loads based on the parameters of quadratic model and weekly least square error are shown in Table 9.
It can be concluded from the table that in summer season, the peak load is increased continuously from the 22nd week till the 35th week and decreased from the 36th week till the 39th week (the weeks representing summer semester), while in winter season the peak load is increased continuously from the 48th week till the 3rd week and decreased continuously from the 4th week till the 12th week (the weeks representing the winter semester). The weekly least square error depends on the temperature effect is shown in Figure 9.
From Figure 9, it can be observed that the error has minimum values for 45 weeks and maximum values for 7 weeks arranged from 0.02% to 2.25%. The average error in Quadratic model is 2.20% and in PSO algorithm is 1.55%. From
![]()
Table 8. Weekly estimated coefficients for LSRM and PSO based on temperature effect.
![]()
Figure 8. Weekly peak load using quadratic model based on temperature effect.
![]()
Figure 9. Weekly forecasting error using quadratic model based on temperature effect.
![]()
Table 9. Weekly forecasted peak load by quadratic model based on temperature effect.
average error point of view it is found that PSO method has produced better estimation than the LSRM.
4.3. MTLF Using AR Model
In this paper, the autoregressive data were generated with order equal 13. Therefore, AR (13) was investigated and the forecasts of this model were started from the month [84 - 95] for monthly prediction and from the week [313 - 364] for weekly prediction (The months and weeks which are represented the year 2015. A Matlab code was used to generate the data and check the AR property. The results were evaluated by LSE to compare computing peak loads and accuracy of the two forecast basis, respectively.
4.3.1. Monthly Forecasting Using AR Model
Monthly real peak demands recorded in the years [2008-2014] are used to implement AR model and the real data for 2015 is used to test this model. The monthly AR model parameters which are estimated using variants of the least- squares method are given by the following equation.
![]()
(22)
The monthly forecasted loads based on the parameters of AR model and monthly least square error are shown in Table 10.
It can be concluded from the table that the error computed by AR model is high compared with other techniques. In February, March and May the AR model gives good results, otherwise the results gives unacceptable prediction of peak load data. By using Equation (19) in Matlab, The monthly forecasted peak load using AR model can be shown in Figure 10.
From Figure 10, it can be observed that the difference between the results obtained by AR model for monthly peak load and the real data is relatively high. This difference makes an average error high compared with the LSRM and PSO techniques used in previous section. The monthly least square error using AR model is shown in Figure 11.
From Figure 11, it can be observed that the error is very high shown in 6 months for the year 2015. The AR model gives the maximum error 17.96% in January while gives the minimum error 2.35% in March with an average error equal to 8.88% for this model.
![]()
Table 10. Monthly forecasted peak load using AR model.
![]()
Figure 11. Monthly forecasting error using AR model.
4.3.2. Weekly Forecasting Using AR Model
Weekly real peak demands recorded in the years [2008-2014] are used in this section. The data set is used to establish AR model. The weekly AR model parameters which are estimated using variants of the least-squares method are given by the following equation.
![]()
(23)
The weekly forecasted loads using AR model and weekly least square error are shown in Table 11.
It can be seen from the table that the results computed by AR have the least accuracy compared with LSRM and PSO. In AR model, the weekly prediction load has maximum value in the week number 6 for the year 2015, but it still has a big difference compared with real value shown in many weeks for this year. By using Equation (19) in Matlab, The weekly forecasted peak load using AR model can be shown in Figure 12.
From Figure 12, it can be noticed that the results obtained by AR have a big difference with the real peak load data for the most weeks in the year 2015, therefore the difference in values between real and prediction load data has maximum for this model. The weekly least square error using AR model is shown in Figure 13.
![]()
Table 11. Weekly forecasted peak load using AR model.
![]()
Figure 13. Weekly forecasting error using AR model.
From Figure 13, it can be observed that the error has minimum values for 10 weeks and maximum values for 25 weeks arranged from 0.2% to 18.99%. From average error point of view it is found that AR model has produced least estimates than the LSRM and PSO with an average error equal to 8.12%.
5. Conclusion
The particle swarm optimization PSO, least square regressive LSR and auto regressive AR methods are presented as MTLF techniques for Jordan electric power systems. This paper has presented approaches used for MTLF of electric loads: LSRM and PSO algorithm. The prediction is made either weekly or monthly based on historical peak load data and weather influence. Least square error (LSE) is introduced to evaluate the performance of the two models then compared these models with AR model and the educated guess assumptions currently used in NEPCO. The comparison between LSRM, PSO and AR models is made by using an average error and depicted by using tables and figures. A PSO algorithm is presented for optimal parameter estimation of MTLF in power system. The solution is implemented and tested using actual recorded data obtained from NEPCO. Real peak load data from NEPCO are used to validate the performance of these approaches; three different models for LSRM and PSO algorithm based on the peak load data and weather influence are used; the quadratic model provides the least errors for both monthly and weekly peak load compared with the linear and exponential models. The forecasted peak load resulted by using the PSO algorithm has been compared with that obtained with LSRM and AR models. From average error point of view, it is found that LSRM and PSO algorithm have produced better estimation than the AR model and current prediction assumptions used in NEPCO. The results are shown the average error for each model used. Two cases were obtained; forecasting depends on peak load data and forecasting depends on peak load data influenced by the weather
![]()
Table 12. The monthly and weekly average error for each model covered in this work (%).
effects. The average error for LSRM and PSO for the three models and forecasting using AR model are represented in Table 12.