1. Introduction
1.1. Introduction: Superrelativity before Black Hole Shock
Black Hole Shock, introducing my new concept of coordinate geometry, is my mathematical obsession now because a brilliant idea flashed like lightning into my brain after publication of my Superrelativity paper [1] . An explanation of Black Hole Shock’s history will help physics enthusiasts to comprehend my ideas and equations involved. Very radical ideas and equations flowed out in the fluid dynamics of Superrelativity that seemed impossible for me to surpass. More radical is my new physics paper named Black Hole Shock. Its coordinate system will surprise physicists.
1.2. Introduction: Open Journal of Fluid Dynamics Published Superrelativity
Recently, Open Journal of Fluid Dynamics published my Superrelativity paper that included exciting equations which were modifications of those by Navier, Stokes, Einstein, and Hawking. Such revolutionary equations inspire physicists to comprehend reality better. These revelatory equations, created to derive the Navier-Stokes Equations, for a possible Clay Mathematics Institute Millennium Prize, stirred attention from some inventors [2] . Creative UFT ideas had been eloquently put into fluid dynamics equations. What I achieved, though not ultimate perfection, was extremely difficult to achieve, and was revelatory for fluid dynamics enthusiasts. What I intend to do, in Black Hole Shock, is to improve those equations, or to progress from those equations. I want to reconsider my use of Schwarzschild’s method, and attempt to better understand quantum aspects of physics. Einstein’s relativity mathematics has always been my forte as I ignore Quantum Physics. The Klein-Gordon Equation and the Schrodinger’s Equation deserve mathematical impact from me.
1.3. Introduction: Reversibility or Irreversibility & Fallibility or Infallibility
The famous Schwarzschild’s equation inspired me to go mathematically creative; so did my search for irreversibility of events with time [3] [4] [5] [6] . 4-D and 3-D gave good results! Is Einstein fallible? Is Maxwell fallible? Maxwell’s Equations became eight Maxwell-Rodgers Equations to help us rethink the basic concepts of physics. I suspected that I used too many aspects in the Z of my Schwarzschild’s Equation. A fun guy, I love creating my own new coordinate systems for reversibility or irreversibility. Maxwell’s Equations have usually helped physicists, but they have also limited them because the equations are not 100% correct.
1.4. Introduction: Turbulence & Inexplicable Realities
Many years of fishing and watching rivers flow caused me to be thrilled by my discovery about why turbulence existed―something fascinating I had tried to explain when I was a child. Fun-loving surf-board riders really ride on waves, following equations in fluid dynamics. Waves permeate through our universe. The mathematics delved into physics is superb reality beyond full comprehension-genius mathematics not entirely understood by human geniuses. Albert Einstein and Stephen Hawking, despite their high IQs, could not be infallible about this extraordinary complexity of mathematical physics [7] . My difficult equations progressed due to scribbled nonsensical possibilities on thousands of pieces of papers that I screwed up and hurled at cockroaches. Physics can be funny, wild conjecture about the inexplicable realities of this universe. You and I, we are also inexplicable realities of this universe.
1.5. Introduction: Mysterious Navier-Stokes Equations
The famous Navier-Stokes Equations have been a mystery for 180 years because nobody has known how to derive those equations from basics. A solution to this mystery will advance fluid dynamics immensely [8] [9] . Superrelativity might be accepted as a prize-worthy solution. Fluid dynamics is very important for engineers, physiologists, cosmologists and you. Plants and animals, including humans, consist of fluids essential to sustain life. Fluid dynamics is about inanimate and animate existences. Fluid dynamic equations are more universal than many believe they are. Any unified field theory must provide the Navier-Stokes Equations. I did not realise that until I created Superrelativity as my attempt to win the Clay Mathematics Institute Millennium Prize for the derivation of the Navier-Stokes Equations.
1.6. Introduction: Gravito-Electro-Magnetic Waves
Superrelativity moves mathematically from my UFT equations into the Schwarz- schild’s metric equation, and then into the functional Navier-Stokes Equations of fluid dynamics [1] [8] [10] . Gravito-electro-magnetic waves were suggested in my previous UFT papers. Realise that I am a gravito-electro-magnetic mathematician, writing this physics paper for gravito-electro-magnetic you! But, for many years, I have considered gravito-electro-magnetism to be electro-magnetism with variable permittivity. Is it possible that mass is misunderstood? Does mass exist?
1.7. Introduction: Viscosity & Relativity
Viscosity is a mystery [11] . Brilliant physicists must judge whether my conception of viscosity is valid for the Millennium prize. My Superrelativity exponential equations are impressive wave equations appropriate for fluid dynamics. Four dimensions are easy because most physicists learnt about four dimensions. Four seems to be a magic number, but I hope it is not a tragic number that has led dimensional physics astray. Four dimensions were used by Albert Einstein, so physicists obsessively followed his example, and based their PhD papers on relativity mathematics. Are there more dimensions? Are there fewer dimensions? How many coordinates exist? Are humans intelligent enough to actually decipher the innate equations of this universe? Against the odds, be positive!
1.8. Introduction: Schwarzschild’s Metric Equation to Superrelativity
Relativity does not match reality because relativity does not include acceleration, relativity uses a constant velocity of light rather than a variable velocity, and relativity gives reversibility of events with time though irreversibility is what happens. Irreversibility is important in Superrelativity, as are the eight Maxwell-Rodgers Equations. A very significant fact is that light-rays are bent by both mass and charge. That fact implies that the Schwarzschild’s metric equation is appropriate for light going past a mass or a charge. This revelation was important for creation of my UFT ideas and Superrelativity. My expertise with advanced multi-massed equations enabled extremely long, multi- symbolled equations to develop in my brain and on paper. This lover of light needs to think more deeply about what bends lightrays because this might mean my Superrelativity equations need to be modified. No physics equation is ever perfect, just nearly perfect like its physics theorist.
1.9. Introduction: Expansion of Famous Physics Ideas
Some geniuses love my Superrelativity equations. My exciting exponential equations include aspects from the kinetic theory of gases. The variable velocity of light, that I use, can be constant if you imagine that. The struggle to describe reality inspired my expansion of famous ideas of Albert Einstein, Stephen Hawking, and other brilliant physicists [12] [13] . But I am not 100% satisfied, because satisfaction stops mathematical progression. Further, possible errors are my wild obsessions in my equations. To create a UFT, a person must be an obsessive-compulsive mathematician like me. Possibly crazy! Those wild obsessions excite me to create Black Hole Shock.
1.10. Introduction: Search for Simplistic Universal Structure
What I strived to achieve was to conglomerate very many physics ideas effectively into a simplistic universal structure [7] . My search for the unified field theory of physics had started this quest that never ends. Superrelativity contains a list of many preliminary physics papers of my original mathematics I wrote as my hobby. Richard Lawrence Norman inspired me to more effort by publishing them in Mind Magazine on the internet for free. Being an independent creative-thinker enabled me to follow any intellectual tangent I wanted to follow. All of my mathematics was original, but not all of my words, because I was a dyslexic mathematician. All I knew was equations. Sometimes, I think physicists do not place enough emphasis on the equations of physics. They are attempting to communicate too many difficult ideas to non-mathematical people who should become mathematical. In Superrelativity and now in Black Hole Shock, this calculus freak includes mathematics that only geniuses will really understand. You might not realise that I have attempted to lay the explanations out simply by using mathematical progressions.
1.11. Introduction: UFT Equations to Navier-Stokes Equations
Superrelativity followed as an attempt to put my UFT ideas into the Navier-Stokes Equations, but the layout is at a much higher academic standard. Fluid dynamics can be fun, and thinking about fluid dynamics helped me question relativity and improve my UFT mathematics [14] . My progression is from Einstein’s relativity to UFT to Superrelativity to this paper, Black Hole Shock. But, whenever I improve my equations and concepts, I am actually creating a better and better UFT. That also improves my fluid dynamics equations. I hope that dignitaries from Clay Mathematics Institute are reading Superrelativity and Black Hole Shock. I intend to create amazing equations in this paper that shrewd physics-enthusiasts should read, and have tattooed on their bodies.
1.12. Introduction: Turbulence & Kinetic Energy
Turbulence does not come from Einstein’s simple Special Relativity equations. Turbulence, caused by modifying his equations, is important to fluid dynamics and the whole universe. The modification, in Superrelativity, also superbly explains what kinetic energy is. In Black Hole Shock, I will think about turbulence and kinetic energy as I create new equations. Turbulence, kinetic energy, and acceleration are significant aspects of this universe’s mathematics.
1.13. Introduction: Exponential Energy Equation
Those turbulence and kinetic energy advancements were not my limit in superrelativity [1] . Unexpectedly, Rodgers’s Exponential Energy Equation appeared as an equational progression, my greatest mathematical creation so far. That exponential equation possesses an exquisite, symmetrical beauty attractive to a mathematician. Further, the exponential of turbulence meant that I had doubly-solved the turbulence problem. The exponential of turbulence produced more and more little turbulences. In fact, Rodgers’s Exponential Energy Equation is a succession of exponentials multiplied. These elaborate equations impress the mathematically-gifted, but Superrelativity equations simplify physics of our universe. My exponential equations are functional foundations for fluid dynamics. But, although I am very proud of Superrelativity, I am attempting to improve my equations in this new Black Hole Shock.
1.14. Introduction: Black Hole & Navier-Stokes Equations
Superrelativity’s Black Hole equations are interesting, but Superrelativity is mostly about mathematical possibilities for derivation of the mysterious Navier-Stokes Equations. The UFT I seek is never entirely unified because this universe is mathematically magnificent, very intriguing, and beyond human comprehension. The mathematics of this universe is like the skeleton of the human body. The body is greater than its skeleton, like the universe is greater than its mathematics that is innately and surprisingly great.
1.15. Introduction: Proud of Superrelativity
Superrelativity progressed my mathematical understanding in many ways. My sophisticated physics equations have inspired geniuses to congratulate me. Due to irreversibility of events with time, I can never rewrite that physics paper again, but I am very proud of my Superrelativity [1] [5] [6] . Those equations are why Black Hole Shock’s equations will be even better equations, and why I can pinpoint possible weaknesses in my thinking.
1.16. Introduction: Obsession Now Black Hole Shock
Black Hole Shock is my new obsession because, although I believed superrelativity was my intellectual perfection in physics, I experienced a dazzling inspiration, a quantum creative leap from my methodical, mathematical conjecture in Superrelativity. Publication, of my very inclusive paper, forced me to look at my equations from a myriad of paranoid perspectives. That obsessive-compulsive analysis led to two revolutionary revelations. Firstly, I introduced acceleration because acceleration does happen despite Einstein ignoring it. To my sense of mathematical symmetry, Klein-Gordon Equation and Schrodinger’s Equation both seem to be incomplete equations that can be improved. In Black Hole Shock, I want to reconsider my Superrelativity use of Schwarzs- child’s method, and attempt to better understand quantum aspects of physics. Einstein’s relativity mathematics has always been my forte as I ignored Quantum Physics that is extremely important. The Klein-Gordon Equation and the Schrodinger’s Equation deserve mathematical impact from me to improve Black Hole equations, Navier-Stokes equations, and Unified Field Theory equations. That explains my reasons for creation of Black Hole Shock.
1.17. Introduction: Unexpected Energy Equation
In Black Hole Shock, I will create an unexpected energy equation. In Albert Einstein’s Special Relativity and my Superrelativity, mass was the initial basic ingredient of our universe. Further, I try to understand why gravity affects both masses and lightrays, and what masses really are. This physics paper continues from my Superrelativity equations, but its equations include re-arrangements of formulae to enable better mathematics for our universe. Exponentials provide the most efficient, functional wave-equations for a systematic layout of a complicated, multi-particled system. Both simplicity and accuracy are important in physics. My equations will enable computer program input to solve complicated problems.
1.18. Introduction: Extraordinary Mathematics Innate
Physicists strive for answers to our many questions about this mysterious universe. Does dark energy exist to cause this universe to expand faster and faster? Does undetected dark matter exist? Why do Albert Einstein’s equations predict reversibility of events with time when it is impossible to reverse a rise in entropy? Why are physicists suggesting parallel universes? How can we pinpoint the age of this universe? A revelation of the extraordinary mathematics innate in this universe’s physics achieves much for humanity. The major equation will be evidence of the remarkable structure of everything physical in this universe. This equation will boost philosophical conjecture about how and why this universe exists, and how and why gravito-electro-magnetic we exist, or why electro-magnetic we exist. I hope for great exponential repercussions due to Black Hole Shock.
2. Materials and Methods
3. Results
Black Hole Shock goes beyond Superrelativity that goes beyond relativity. This paper Black Hole Shock gives new multi-coordinate, radial-3-dimensional geometries, and will surprise physicists. These complicated equations go far beyond constant velocity to include accelerations and accelerations of accelerations, to go to a universe Albert Einstein ignored. Black Hole Shock includes very good formulae for horizontal and vertical angular motions and their accelerations to help explain turbulences in fluids. This paper improves upon the Klein-Gordon Equation and the Schrodinger’s Equation to end confusing duality of a particle [15] [16] . This paper goes beyond Albert Einstein’s mass-energy equivalence equation to a more universal equation. This paper gives a better radius of a Black Hole, and a better Black Hole power radiation equation [17] [18] . Black Hole Shock gives elaborate equations for multi-particled systems, and those can be modified for use in fluid dynamics.
4. Discussions
4.1. Discussions: Maxwell-Rodgers Equations from Zero Relativity & Superrelativity
Here are my Maxwell-Rodgers Equations for particle a:
Eqn I:
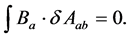
Eqn II:
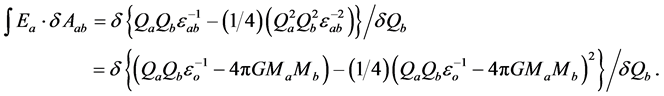
Eqn III:
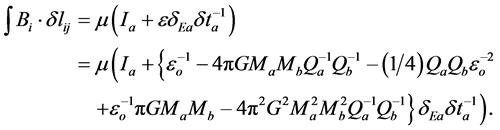
Eqn IV:
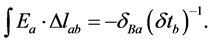
Extra Eqn V:
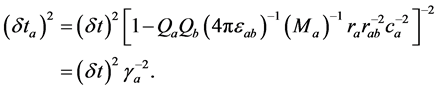
Extra Eqn VI:
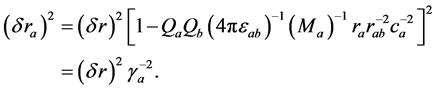
Extra Eqn VII:
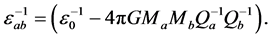
Extra Eqn VIII:
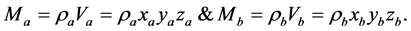
Maxwell’s Equations are not fully correct for many reasons. Appropriate mathematics would explain why attractive interactions become repulsive, and why repulsive interactions become attractive, at short radii if 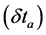 and
and 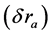 are modified. Light-rays are bent by gravity, but light-rays are also bent by a charge. Above, I unify Coulomb and gravitational interactions by introducing variable permittivity
are modified. Light-rays are bent by gravity, but light-rays are also bent by a charge. Above, I unify Coulomb and gravitational interactions by introducing variable permittivity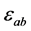 . In Zero Relativity, I improved Schwarzschild’s equations for
. In Zero Relativity, I improved Schwarzschild’s equations for  and
and  so they produced reversals in effects of gravity and charge interactions at very short distances. By modifying Maxwell’s Equations and adding four equations, in my unified physics paper Zero Relativity, Refinements to Maxwell’s Equations apply to a multi-particled system of charged particles. They use the centre-of-mass of the entire system as the reference point for distances involved in the equations. They include variables μ and ε rather than the constants
so they produced reversals in effects of gravity and charge interactions at very short distances. By modifying Maxwell’s Equations and adding four equations, in my unified physics paper Zero Relativity, Refinements to Maxwell’s Equations apply to a multi-particled system of charged particles. They use the centre-of-mass of the entire system as the reference point for distances involved in the equations. They include variables μ and ε rather than the constants 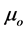 and
and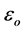 , because it is known that permeability and permittivity are variable. They predict a variable velocity-of-light that accords with the photon move at different velocities, and the velocity-of-light changing during history. They include separate equations for each of particle a & particle b. They use
, because it is known that permeability and permittivity are variable. They predict a variable velocity-of-light that accords with the photon move at different velocities, and the velocity-of-light changing during history. They include separate equations for each of particle a & particle b. They use

They include the gravitational components as in Schwarzschild’s equation to predict gravitational bending of the space-time continuum [19] [20] . They mathematically explain why particles with similar charges attract each other when at very short distances apart. They have different times for different charged particles. They include the fully correct rab between the particles. They mathematically explain why mass, like energy, is variable with charge. When I created the eight Maxwell-Rodgers Equations, I spent a lot of time and effort on their modification or creation. That does not mean that they are perfect. But they are very useful, thought-provoking equations. Some of them are not fully necessary for this Navier-Stokes paper. Intellectually delving into those basic equations has helped me understand topics to greater depth in this paper.
Zero Relativity’s and Superrelativity’s eight listed Maxwell-Rodgers Equations are not all perfectly correct. These meticulous attempts develop basic mathematical ideas that can help create advancements in mathematics and physics. These equations have stimulated other possibilities. Many of the equations include masses, but I suspect that dualities, including masses and wavelengths, should replace the masses [21] . My Maxwell-Rodgers Equations excite me to radiate new thoughts onto pieces of paper, then onto Black Hole Shock.
4.2. Discussions: Pressure Component in Fluids from Superrelativity
Fluids Are Like Gases. The interactions between atoms or molecules in fluids are similar to those in gases. From my Zero Relativity paper, I now copy and paste the following relevant section about my past conjectures:
Rodgers’s kinetic molecular theory of gases. Rodgers’s Theory of Gases is a development from the Kinetic Molecular Theory for Gases, and requires most of the latter assumptions. In Rodgers’s Theory of Gases: The interactions between molecules are not negligible. Relativistic effects are not negligible. Quantum mechanical effects are not negligible. The total volume of the individual gas molecules added up is not negligible compared to the volume of the container. Where pressure equals P, volume equals V, and v equals velocity, the Kinetic Molecular Theory of Gases gives that  decide to use
decide to use 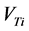 for total volume, and
for total volume, and ![]() for the volume of a molecule of mass
for the volume of a molecule of mass![]() . I introduce Kinetic Energy as K. For my system with variable velocity-of-light,
. I introduce Kinetic Energy as K. For my system with variable velocity-of-light,
![]() .
.
But,
![]() .
.
Energy density of the gas system is
![]() .
.
The mathematics pertaining to a Carnot engine is as follows:
![]()
These ideas about gas pressure have led to the pressure component in the equations of my Superrelativity paper.
My method for including the pressure component in Superrelativity is interesting, but I intend to use a better method for including the pressure component in Black Hole Shock.
4.3. Discussions: Rodgers’s Rectified Exponential Energy Equation
While creating this Black Hole Shock paper, I realised that there is a slight omission error in Rodgers’s Exponential Energy Equation of my Superrelativity paper. I rectified the error. Now, Rodgers’s Exponential Energy Equation is Superrelativity’s most impressive equation. This highlight equation will be modified more in this Black Hole Shock paper because its formulation can be improved. Enormous amounts of effort, to re-analyse equational components and to re-arrange them, especially to agree with Schrodinger, have produced other impressive equations that I include in this paper. I have concentrated on developing better geometries for particles in a volume.
4.4. Discussions: Four-Dimensional Frustration
Mathematicians, including physicists, often think in terms of four dimensions with co-ordinates x, y, z, and ict (where i2) = −1. This system sometimes frustrates physicists as it leads to confusing mathematics that seems erroneous in complicated physics equations about energies [4] [22] . A simpler system of three radial dimensions, that I created, makes physics calculations and comprehension much easier.
4.5. Discussions: Conventional Acceleration Equations
![]() (1)
(1)
In conventional ![]() geometry, mathematicians think:
geometry, mathematicians think:
![]() (2)
(2)
![]() . (3)
. (3)
![]() . (4)
. (4)
4.6. Discussions: Rodgers’s Hyperacceleration Geometry
![]() . (5)
. (5)
![]() . (6)
. (6)
![]() . (7)
. (7)
The components go beyond acceleration components of ![]() to
to ![]() as n goes to infinity.
as n goes to infinity.
4.7. Discussions: Einstein-Rodgers Relativity Equation from Superrelativity
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
If ![]() is approximately equal to
is approximately equal to![]() ,
,
![]() (12)
(12)
is approximately equal to![]() .
.
This gives a very good mathematical explanation of why kinetic energy exists. But the accelerations, by using![]() , and Schwarzschild’s effect, by using
, and Schwarzschild’s effect, by using![]() , must be included in those equations.
, must be included in those equations.
4.8. Discussions: Rodgers’s Basic Hyperacceleration Geometry
Say there are six vectors:
![]() (13)
(13)
![]() (14)
(14)
Here, ![]() is the horizontal angle, and
is the horizontal angle, and ![]() is the vertical angle, and
is the vertical angle, and
![]() (15)
(15)
4.9. Discussions: Questioning Duality
Up until now, in physics papers, I have proposed using mc2 as the basic ingredient of our universe when analysis is pertaining to energies. Thousands of hours of scribbling possibilities has often led me to accept that Albert Einstein, in his Relativity papers, and I, in my Superrelativity paper, have chosen the correct basic ingredient of this universe. Re-looking at The Time-Dependendent Schrodinger Equation has stressed the dual nature of the basic ingredient of this universe [23] [24] . Recently, I have communicated with C Peter O’Connor, physics theorist, and we both, separately, for many years, have believed that our universe is electromagnetic. I have attempted to take masses from my equations by re-arranging the Klein-Gordon Equation and Schrodinger’s Equation many times, but duality has remained until now [25] [26] . Inspired by agreement with C Peter O’Connor about an electromagnetic universe, I am attempting to re-arrange the Klein-Gordon Equation and Schrodinger’s Equation again.
4.10. Discussions: Klein-Gordon Equation
The Klein-Gordon Equation is
![]() (16)
(16)
4.11. Discussions: Schrodinger’s Equation
![]() (17)
(17)
From the Klein-Gordon Equation and the Schrodinger’s Equation, I created a better equation.
4.12. Discussions: Klein-Gordon-Schrodinger-Rodgers Equation
![]() (18)
(18)
With a constant mass, the equation can become this:
![]() (19)
(19)
With variable mass, the equation can become this:
![]() (20)
(20)
Note that
![]() . (21)
. (21)
4.13. Discussions: Simplifying Physics Equations
![]() (22)
(22)
becomes
![]() (23)
(23)
This equation indicates that mass can be eliminated from physics equations.
Albert Einstein’s ![]() can be improved to a new energy equation.
can be improved to a new energy equation.
4.14. Discussions: Einstein-Rodgers’s Mass-Wave-Energy4 Equivalence Equation
![]() (24)
(24)
where
![]() . (25)
. (25)
This can further include the horizontal angle and vertical angle.
4.15. Discussions: Einstein-Schwarzschild-Klein-Gordon-Schrodinger- Rodgers Mass-Hyperacceleraton Geometry
![]() (26)
(26)
Therefore,
![]() (27)
(27)
Here,
![]() (28)
(28)
where
![]() (29)
(29)
and
![]() . (30)
. (30)
Components for PV and kT can be introduced into my equation by heeding the Ideal Gas Law.
4.16. Discussions: Einstein-Schwarzschild-Klein-Gordon-Schrodinger- Rodgers Mass-Hyperacceleraton Equation
Of the possibilities with different powers, the following equation is the most accurate equation because it implies temperature to the radiation power’s power of four.
![]() (31)
(31)
4.17. Discussions: Black Hole Equations
In my SUPERRELATIVITY paper, I have proposed two very significant equations for total energy of a multi-massed system. I wanted to add to work about Black Holes that I, too pedantically, believing in variable velocity of light for 45 years, had always stated do not exist [27] [28] [29] . I realised that Stephen Hawking’s power equation might be extremely useful for mankind, and I wanted to contribute to his Stefan-Boltzmann- Schwarzschild-Hawking Black Hole Radiation Power Law and did put forward, in Superrelativity, my Stefan-Boltzmann-Schwarzschild-Hawking-Rodgers Black Hole Radiation Power Law that is an interesting attempt. With my new equations, I want to attempt this interesting Black Hole situation again.
Firstly, here are the equations leading to Stephen Hawking’s equation:
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]()
is the radius Stephen Hawking used.
![]()
is the power radiation equation Stephen Hawking attained.
Despite the complexity of Hawking’s power equation, it is a mathematical simplification that should include a more complicated equation for (T)4 including charge. Not merely an attractive mass, a black hole has an overall charge that impacts upon its surroundings.
4.18. Discussions: Black Hole Power Radiation Equation
For the Black Hole situation, the appropriate equation is as follows:
![]() (31)
(31)
![]() . (32)
. (32)
![]() (33)
(33)
![]() (34)
(34)
![]() (35)
(35)
with ![]() in this case.
in this case.
![]() . (36)
. (36)
4.19. Discussions: Improved Hawking-Rodgers Radius of a Black Hole
![]() (37)
(37)
4.20. Discussions: Einstein-Klein-Gordon-Schrodinger-Stefan- Boltzmann-Scwarzschild-Hawking-Rodgers Black Hole Radiation Equation
![]() (38)
(38)
4.21. Discussions: Mental To Experimental
In the future, experimental physicists can decide about the correctness of my theoretical, fundamental equations. These equations are possibilities that can lead to more and more possibilities that might be correct. My major hope is for a wonderful unification to end discrepancies in physics. Further, my equations are combining mainstream physics and fluid dynamics, especially the Navier-Stokes Equations, with relativity, quantum aspects, kinetic energy, turbulence, irreversibility, and acceleration. These papers are directed, as simply as possible, towards mathematics geniuses with theoretical physics knowledge. My purpose, for both Superrelativity and Black Hole Shock, is not to be popular, but to create correct equations in an extremely difficult area of intellectual conjecture. Most intelligent physics enthusiasts praise Superrelativity. More will praise Black Hole Shock because its mathematics reveals that mass need not be in physics equations.
4.22. Discussions: Implications for Fluid Dynamics of Einstein-Schwarzschild-Klein-Gordon-Schrodinger-Rodgers Mass-Hyperacceleraton Equation
![]() (39)
(39)
where![]() .
.
This equation, for a multi-massed system, is much more elaborate than but leads to the Navier-Stokes Equations. The equation comes from considering angular motions and accelerations, so can be used to explain turbulence. Further, it can be used to explain irreversibility of events with time.
5. Conclusion
Black Hole Shock is a revolutionary theoretical physics paper. The mysterious Navier-Stokes Equations, of my recent Superrelativity, confused me and inspired me to think more deeply. My physics papers have progressed towards a solution of difficult mathematical physics problems, especially a unified field theory of physics. That is extremely important for physics. The Clay Mathematics Institute requested, “Prove or give a counter-example of the following statement: In three space dimensions and time given an initial velocity field, there exists a vector velocity and a scalar pressure field that are both smooth and globally defined, which solve the Navier-Stokes Equations.” That contest has motivated me to create two unique physics papers, Superrelativity and Black Hole Shock that have raised interest in fluid dynamics. Because humans are mostly water, and are reliant on water for survival; fluid dynamics is extremely important. An enormous amount of effort went into creating mathematics of Superrelativity. After that effort, I was hallucinating extremely long equations. These led to five very significant equations:
(a) Klein-Gordon-Schrodinger-Rodgers Equation,
(b) Einstein-Rodgers’s Mass-Wave-Energy4 Equivalence Equation,
(c) Einstein-Schwarzschild-Klein-Gordon-Schrodinger-Rodgers Mass-Hyperaccele- raton Geometry,
(d) Einstein-Klein-Gordon-Schrodinger-Stefan-Boltzmann-Scwarzschild-Hawking- Rodgers Black Hole Radiation Equation,
(e) Improved Hawking-Rodgers Radius of a Black Hole.
In this paper, the equations are impressive, but what is the most impressive is mathematics that ends the concept of duality of a particle and shows everything is electro-magnetic. With these new equations, physics will take quantum leaps into the future.
Acknowledgements
Thanks to the following:
・ Journal Applied Mathematics and Physics for publishing my Black Hole Shock paper;
・ Open Journal of Fluid Dynamics for publishing my Superrelativity paper;
・ The Clay Mathematics Institute for offering prizes to inspire mathematicians;
・ The Royal Brisbane and Women’s Hospital that used chemotherapy to save me from serious cancer in 2013;
・ Schwarzschild, Einstein, Newton, Hawking, and other great creators of stimulating physics equations;
・ Internet’s Mind Magazine that published a succession of my papers;
・ Psychologists who assessed that I was extremely intelligent and kept it a secret as I requested;
・ Creators of internet intelligence tests for geniuses, because you helped me to escape from boredom;
・ Internet geniuses because communicating with you made me feel normal;
・ St Joseph’s College, Gregory Terrace, where I was a double-visioned, diabetic, dyslexic, dysphasic, epileptic non-reader;
・ All good friends and good relatives;
・ Physics enthusiasts who enjoy reading Superrelativity and Black Hole Shock;
・ Me because I strived very hard to create Black Hole Shock while experiencing traumatic events.