1. Introduction
The Standard Model (SM) of particle physics gives a coherent quantum-mechanical description of electromagnetic, weak and strong interactions based on fundamental constituents―quarks and leptons―interacting via force carriers―photons, W and Z bosons, and gluons. The SM is supported by two theoretical “pillars”: the gauge prin- ciple and the Higgs mechanism for particle mass generation. In the SM, where electro- weak symmetry is broken by the Higgs mechanism, the mass of a particle depends on its interaction with the Higgs field, a medium that permeates the universe. The photon and the gluon do not have such couplings, and so they remain massless. The SM predicts the existence of a neutral spin-0 particle associated with the Higgs field, but it does not predict its mass.
Whereas the gauge principle has been firmly established through precision electro- weak measurements, the Higgs mechanism is yet to be fully tested. A state decaying to several distinct final states was observed in 2012 at the CERN Large Hadron Collider (LHC) with a statistical significance of five standard deviations [1] [2] . The observed state has a mass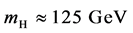 . Its production rate is consistent with the predicted rate for the SM Higgs boson. Furthermore, event yields in different production topolo- gies and different decay modes are self-consistent [3] .
. Its production rate is consistent with the predicted rate for the SM Higgs boson. Furthermore, event yields in different production topolo- gies and different decay modes are self-consistent [3] .
All of the couplings of the Higgs particle to gauge bosons and fermions are com- pletely determined in the SM in terms of electroweak coupling constants and fermion masses. In the SM, Higgs production and decay processes can be computed un- ambiguously in terms of the Higgs mass. Since the coupling of the Higgs boson to fermions and gauge bosons is proportional to the particle masses, the Higgs boson is produced in association with heavy particles and decays into the heaviest particles that are kinematically accessible.
The Higgs-boson mass affects the values of electroweak observables through radia- tive corrections. Many of the electroweak measurements obtained over the past three decades may be combined to provide a global test of consistency with the SM. The best constraint on 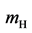 is obtained by making a global fit to the electroweak data. Such a fit strongly suggests that the most likely mass for the SM Higgs boson is just above the limit of 114.4 GeV set by direct searches at the LEP
is obtained by making a global fit to the electroweak data. Such a fit strongly suggests that the most likely mass for the SM Higgs boson is just above the limit of 114.4 GeV set by direct searches at the LEP  collider [4] . This is con- sistent with the value of the Higgs mass measured at LHC.
collider [4] . This is con- sistent with the value of the Higgs mass measured at LHC.
High-precision electroweak measurements, therefore, provide a natural complement to direct studies of the Higgs sector. All the measurements made at LEP and SLC could be repeated at the proposed facility using 90% polarized electron beams and at much higher luminosities [5] .
The rich set of final states in  and
and 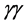 collisions at the proposed SLC-type facility would play an essential role in measuring the mass, spin, parity, two-photon width and trilinear self-coupling of the SM Higgs boson, as well as its couplings to fermions and gauge bosons. Such measurements require centre-of-mass (c.m.) energies
collisions at the proposed SLC-type facility would play an essential role in measuring the mass, spin, parity, two-photon width and trilinear self-coupling of the SM Higgs boson, as well as its couplings to fermions and gauge bosons. Such measurements require centre-of-mass (c.m.) energies , considerably exceeding those attainable at circular
, considerably exceeding those attainable at circular 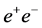 colliders.
colliders.
2. Single SM Higgs Production in 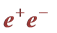 Annihilations
Annihilations
A particularly noteworthy feature of an 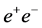 collider is that the Higgs boson can be detected in the Higgs-strahlung process (see Figure 1)
collider is that the Higgs boson can be detected in the Higgs-strahlung process (see Figure 1)
 (1)
(1)
even if it decays into invisible particles (e.g., the lightest neutralino of a supersymmetric model). In this case the signal manifests itself as a peak in the invariant mass distri- bution of the system which recoils against the lepton pair stemming from Z-boson decay. In Equation (1), ![]() is the Higgs coupling to the Z boson and
is the Higgs coupling to the Z boson and ![]() is the square of the c.m. energy.
is the square of the c.m. energy.
By exploiting the ![]() channel, the Higgs-strahlung cross-sections can be measured with a statistical error of about 2 percent for a Higgs-boson mass
channel, the Higgs-strahlung cross-sections can be measured with a statistical error of about 2 percent for a Higgs-boson mass
![]()
Figure 1. Centre-of-mass energy dependence of the cross-sections for SM Higgs-boson pro- duction in the Higgs-strahlung, W-fusion and Z-fusion processes [7] . Note that one has to measure separately the couplings HWW, HHH and Htt at ![]() in order to determine the corresponding SM loop contributions to the effective HZZ coupling.
in order to determine the corresponding SM loop contributions to the effective HZZ coupling.
![]() (see [6] and references therein). From the fits to the reconstructed mass spectra in the channels
(see [6] and references therein). From the fits to the reconstructed mass spectra in the channels ![]() and
and![]() , the Higgs-boson mass can be determined with an uncertainty of about 40 MeV for
, the Higgs-boson mass can be determined with an uncertainty of about 40 MeV for ![]() [6] .
[6] .
To determine the spin and parity of the SM Higgs boson in the Higgs-strahlung process, one can use the information on (1) the energy dependence of the Higgs-boson production cross-section just above the kinematic threshold, and (2) the angular distribution of the Z/H bosons. The best way to study the CP properties of the Higgs boson is by analyzing the spin correlation effects in the decay channel ![]() [6] .
[6] .
The Higgs-strahlung cross-section, which dominates at low c.m. energies, decreases with energy in proportion to![]() . In contrast, the cross-section for the W-fusion process (see Figure 1 and Figure 2)
. In contrast, the cross-section for the W-fusion process (see Figure 1 and Figure 2)
![]() (2)
(2)
increases with energy in proportion to![]() , and hence becomes more im- portant at energies
, and hence becomes more im- portant at energies ![]() In Equation (2),
In Equation (2), ![]() is the Higgs coupling to the W boson.
is the Higgs coupling to the W boson.
The Higgs-fermion couplings can be extracted by measuring the branching fractions of the Higgs boson. There are two methods to determine the Higgs branching fractions: (1) Measure the event rate in the Higgs-strahlung process for a given final-state configuration and then divide by the total cross-section; (2) Select a sample of unbiased events in the Higgs-strahlung recoil-mass peak and determine the fraction of events that correspond to a particular decay channel. See [6] and references therein for an estimate of the accuracy that can be achieved in such measurements.
For![]() , the total decay width of the Higgs boson,
, the total decay width of the Higgs boson, ![]() , can be determined indirectly by employing the relation between the total and partial decay widths for a given final state:
, can be determined indirectly by employing the relation between the total and partial decay widths for a given final state:
![]()
Figure 2. Centre-of-mass energy dependence of various cross-sections for single and double SM Higgs-boson production in ![]() annihilations [8] .
annihilations [8] .
![]() . (3)
. (3)
For instance, consider the decay![]() . One can directly measure the branching fraction
. One can directly measure the branching fraction![]() , determine the coupling HZZ in the process
, determine the coupling HZZ in the process![]() , relate the HZZ and HWW couplings (
, relate the HZZ and HWW couplings (![]() ), and then use the fact that
), and then use the fact that ![]() to obtain the partial width
to obtain the partial width ![]() from the information on the HWW coupling. The accuracy with which the determination of
from the information on the HWW coupling. The accuracy with which the determination of ![]() can be achieved for
can be achieved for ![]() is estimated in [6] .
is estimated in [6] .
3. Single SM and MSSM Higgs Production in ![]() Collisions
Collisions
Since photons couple directly to all fundamental fields carrying the electromagnetic current (leptons, quarks, W bosons, supersymmetric particles), ![]() collisions provide a comprehensive means of exploring virtually every aspect of the SM and its extensions (see [9] [10] and references therein).The cross-sections for production of charged-par- ticle pairs in
collisions provide a comprehensive means of exploring virtually every aspect of the SM and its extensions (see [9] [10] and references therein).The cross-sections for production of charged-par- ticle pairs in ![]() interactions are approximately an order of magnitude larger than in
interactions are approximately an order of magnitude larger than in ![]() annihilations. For some processes within and beyond the SM, the required c.m. energy is considerably lower in
annihilations. For some processes within and beyond the SM, the required c.m. energy is considerably lower in ![]() collisions than in
collisions than in ![]() or proton-proton interac- tions.
or proton-proton interac- tions.
In ![]() collisions, the Higgs boson is produced as a single resonance in a state of definite CP, which is perhaps the most important advantage over
collisions, the Higgs boson is produced as a single resonance in a state of definite CP, which is perhaps the most important advantage over ![]() annihilations, where this s-channel process is highly suppressed. At c.m. energies
annihilations, where this s-channel process is highly suppressed. At c.m. energies![]() , the effective cross-section for
, the effective cross-section for
![]() (4)
(4)
is at least a factor of four larger than any cross-section for Higgs production in ![]() annihilations. Moreover, the process
annihilations. Moreover, the process ![]() requires considerably higher c.m. energies than
requires considerably higher c.m. energies than![]() .
.
Any theoretical model based on the gauge principle must evoke spontaneous symmetry breaking. In the minimal supersymmetric extension of the Standard Model (MSSM), for instance, spontaneous electroweak symmetry breaking results in five physical Higgs-boson states: two neutral scalar fields ![]() and
and![]() , a pseudoscalar
, a pseudoscalar ![]() and two charged bosons
and two charged bosons![]() . In
. In ![]() annihilations, the heavy neutral MSSM Higgs bosons can be created only by associated production (
annihilations, the heavy neutral MSSM Higgs bosons can be created only by associated production (![]() ), whereas in
), whereas in ![]() collisions they are produced as single resonances (
collisions they are produced as single resonances (![]() ) with masses up to 80% of the initial
) with masses up to 80% of the initial ![]() collider energy [11] . For example, if their masses are around 500 GeV, then
collider energy [11] . For example, if their masses are around 500 GeV, then ![]() and
and ![]() could be produced either in pairs in
could be produced either in pairs in ![]() annihilations at
annihilations at![]() , or as single particles in
, or as single particles in ![]() collisions at
collisions at![]() .
.
The reaction![]() , which is related to
, which is related to![]() , proceeds through a “loop diagram” and receives contributions from all charged particles that couple to the photon and the Higgs boson. Thus, the two-photon width
, proceeds through a “loop diagram” and receives contributions from all charged particles that couple to the photon and the Higgs boson. Thus, the two-photon width ![]() is sensitive to the Higgs-top Yukawa coupling, as well as mass scales far beyond the energy of the
is sensitive to the Higgs-top Yukawa coupling, as well as mass scales far beyond the energy of the ![]() collision. Assuming that the branching ratio
collision. Assuming that the branching ratio ![]() can be measured to an accuracy of about 2% in the process
can be measured to an accuracy of about 2% in the process![]() , the
, the ![]() partial width can be determined with a similar precision by measuring the cross-section
partial width can be determined with a similar precision by measuring the cross-section
![]() . (5)
. (5)
Each of the decay modes![]() , WW can be measured in photon-photon collisions with a precision comparable to that expected from analyses based on
, WW can be measured in photon-photon collisions with a precision comparable to that expected from analyses based on ![]() data (see, e.g., [12] ).
data (see, e.g., [12] ).
High-energy photons can be produced by Compton-backscattering of laser light on electron beams. Both the energy spectrum and polarization of the backscattered photons depend strongly on the polarizations of the incident electrons and laser photons. The key advantage of using ![]() beams is that they can be polarized to a high degree, enabling one to tailor the photon energy distribution to one’s needs. In a
beams is that they can be polarized to a high degree, enabling one to tailor the photon energy distribution to one’s needs. In a ![]() collision, the possible helicities are 0 or 2. The Higgs boson is produced in the
collision, the possible helicities are 0 or 2. The Higgs boson is produced in the ![]() state, whereas the background processes
state, whereas the background processes ![]() are suppressed for this helicity configuration. The circular polarization of the photon beams is therefore an important asset, for it can be used both to enhance the signal and suppress the background.
are suppressed for this helicity configuration. The circular polarization of the photon beams is therefore an important asset, for it can be used both to enhance the signal and suppress the background.
The CP properties of any neutral Higgs boson that may be produced at a photon collider can be directly determined by controlling the polarizations of Compton- scattered photons [13] . A CP-even Higgs boson couples to the combination![]() , whereas a CP-odd Higgs boson couples to
, whereas a CP-odd Higgs boson couples to![]() , where
, where ![]() are polarization vectors of colliding photons and
are polarization vectors of colliding photons and ![]() is the momentum vector of one of the Compton- scattered photons. The scalar (pseudoscalar) Higgs boson couples to linearly polarized photons with a maximum strength if the polarization vectors are parallel (perpendi- cular).
is the momentum vector of one of the Compton- scattered photons. The scalar (pseudoscalar) Higgs boson couples to linearly polarized photons with a maximum strength if the polarization vectors are parallel (perpendi- cular).
The general amplitude for a CP-mixed state to couple to two photons can be expressed as
![]() (6)
(6)
where ![]() is the CP-even and
is the CP-even and ![]() the CP-odd contribution to the amplitude. If we denote the helicities of the two photons by
the CP-odd contribution to the amplitude. If we denote the helicities of the two photons by ![]() and
and![]() , with
, with![]() , then the above vector products read
, then the above vector products read ![]() and
and![]() . As shown in [13] , one can define three polarization asymmetries that yield an unambig- uous measure of CP-mixing. Note that it is necessary to have both linearly and circularly polarized photons in order to measure those asymmetries. In
. As shown in [13] , one can define three polarization asymmetries that yield an unambig- uous measure of CP-mixing. Note that it is necessary to have both linearly and circularly polarized photons in order to measure those asymmetries. In ![]() annihi- lations, it is possible to discriminate between CP-even and CP-odd neutral Higgs bosons, but would be difficult to detect small CP-violating effects (which contribute only at the one-loop level) for a dominantly CP-even component (which contributes at the tree level in
annihi- lations, it is possible to discriminate between CP-even and CP-odd neutral Higgs bosons, but would be difficult to detect small CP-violating effects (which contribute only at the one-loop level) for a dominantly CP-even component (which contributes at the tree level in ![]() collisions) [14] .
collisions) [14] .
A study of single Higgs-boson production in ![]() collisions via the hadronic content of the photon (resolved processes) was reported in [15] . Such contributions to
collisions via the hadronic content of the photon (resolved processes) was reported in [15] . Such contributions to ![]() are non-negligible. Resolved photon production of the heavy MSSM Higgs bosons
are non-negligible. Resolved photon production of the heavy MSSM Higgs bosons ![]() and
and ![]() would complement other measurements by probing particular regions of the SUSY parameter space [15] .
would complement other measurements by probing particular regions of the SUSY parameter space [15] .
To ascertain the physics potential of a ![]() collider, one must take into account the fact that the photons are not monochromatic [16] . As already mentioned, both the energy spectrum and polarization of the backscattered photons depend strongly on the polarizations of the incident electrons and photons. A longitudinal electron-beam polarization of 90% and a 100% circular polarization of laser photons are customarily assumed.
collider, one must take into account the fact that the photons are not monochromatic [16] . As already mentioned, both the energy spectrum and polarization of the backscattered photons depend strongly on the polarizations of the incident electrons and photons. A longitudinal electron-beam polarization of 90% and a 100% circular polarization of laser photons are customarily assumed.
4. Higgs-Pair Production in ![]() and
and ![]() Collisions
Collisions
It is well known that hadron colliders are not ideally suited for measuring the self- coupling of the Higgs boson if ![]() [17] . The potential of a future
[17] . The potential of a future ![]() collider for determining the HHH coupling has therefore been closely examined (see [18] - [23] ).
collider for determining the HHH coupling has therefore been closely examined (see [18] - [23] ).
The production of a pair of SM Higgs bosons in photon-photon collisions,
![]() (7)
(7)
which is related to the Higgs-boson decay into two photons, is due to W-boson and top-quark box and triangle loop diagrams. The total cross-section for ![]() in polarized photon-photon collisions, calculated at the leading one-loop order [24] as a function of the
in polarized photon-photon collisions, calculated at the leading one-loop order [24] as a function of the ![]() c.m. energy and for
c.m. energy and for ![]() between 115 and 150 GeV, is given in [18] . The cross-section calculated for equal photon helicities,
between 115 and 150 GeV, is given in [18] . The cross-section calculated for equal photon helicities, ![]() , rises sharply above the
, rises sharply above the ![]() threshold for different values of
threshold for different values of![]() , and has a peak value of about 0.4 fb at a
, and has a peak value of about 0.4 fb at a ![]() c.m. energy of 400 GeV. In contrast, the cross-section for opposite photon helicities,
c.m. energy of 400 GeV. In contrast, the cross-section for opposite photon helicities, ![]() , rises more slowly with energy because a pair of Higgs bosons is produced in a state with orbital angular momentum of at least
, rises more slowly with energy because a pair of Higgs bosons is produced in a state with orbital angular momentum of at least ![]() (see Figure 3).
(see Figure 3).
The cross-sections for equal photon helicities are of special interest, since only the ![]() amplitudes contain contributions with trilinear Higgs self-coupling. By adding to the SM Higgs potential
amplitudes contain contributions with trilinear Higgs self-coupling. By adding to the SM Higgs potential ![]() a gauge-invariant dimension-6 operator
a gauge-invariant dimension-6 operator![]() , one introduces a gauge-invariant anomalous trilinear Higgs coupling
, one introduces a gauge-invariant anomalous trilinear Higgs coupling ![]() [24] . For the reaction
[24] . For the reaction![]() , the only effect of such a coupling in the unitary gauge would be to
, the only effect of such a coupling in the unitary gauge would be to
replace the trilinear Higgs coupling of the SM, ![]() , by an anomalous Higgs self- coupling
, by an anomalous Higgs self- coupling![]() . The dimensionless anomalous coupling
. The dimensionless anomalous coupling ![]() is normalized so that
is normalized so that ![]() exactly cancels the SM HHH coupling. The cross-sections
exactly cancels the SM HHH coupling. The cross-sections ![]() for five values of
for five values of ![]() are shown in Figure 3.
are shown in Figure 3.
In an experiment to measure the trilinear Higgs self-coupling, the contribution from ![]() for opposite photon helicities represents an irreducible background. How- ever, this background is suppressed if one chooses a
for opposite photon helicities represents an irreducible background. How- ever, this background is suppressed if one chooses a ![]() c.m. energy below about 320 GeV.
c.m. energy below about 320 GeV.
The Feynman diagrams for the process ![]() are shown in [24] . New physics beyond the SM introduces additional complexity into the subtle interplay between the Higgs “pole amplitudes” and the top-quark and W-boson “box diagrams”:
are shown in [24] . New physics beyond the SM introduces additional complexity into the subtle interplay between the Higgs “pole amplitudes” and the top-quark and W-boson “box diagrams”:
![]() (8)
(8)
where ![]() is the trilinear Higgs self-coupling in the SM. From this expression we infer that the cross-section
is the trilinear Higgs self-coupling in the SM. From this expression we infer that the cross-section
![]() (9)
(9)
is a quadratic function of the coupling![]() .
.
The trilinear self-coupling of the Higgs boson can also be measured either in the so-called double Higgs-strahlung process
![]() (10)
(10)
or in the W-fusion reaction
![]() . (11)
. (11)
The total cross-section for pair production of 120-GeV Higgs bosons in ![]() colli- sions, calculated for unpolarized beams, are shown in Figure 4 for anomalous trilinear Higgs self-couplings
colli- sions, calculated for unpolarized beams, are shown in Figure 4 for anomalous trilinear Higgs self-couplings ![]() or
or![]() . If the electron beam is 100% polarized, the double Higgs-strahlung cross-section will stay approximately the same, while the W- fusion cross-section will be twice as large. From the plots in Figure 4 we infer that the SM double Higgs-strahlung cross-section exceeds 0.1 fb at 400 GeV for
. If the electron beam is 100% polarized, the double Higgs-strahlung cross-section will stay approximately the same, while the W- fusion cross-section will be twice as large. From the plots in Figure 4 we infer that the SM double Higgs-strahlung cross-section exceeds 0.1 fb at 400 GeV for![]() , and reaches a broad maximum of about 0.2 fb at a c.m. energy of 550 GeV. The SM cross-section for W-fusion stays below 0.1 fb for c.m. energies up to 1 TeV.
, and reaches a broad maximum of about 0.2 fb at a c.m. energy of 550 GeV. The SM cross-section for W-fusion stays below 0.1 fb for c.m. energies up to 1 TeV.
For![]() , and assuming a longitudinal electron-beam polarization of 90%, the maximum sensitivity to an anomalous trilinear Higgs self-coupling is achieved in the so-called double Higgs-strahlung process at a c.m. energy of about 500 GeV [18] . This is significantly higher than the optimal c.m. energy in
, and assuming a longitudinal electron-beam polarization of 90%, the maximum sensitivity to an anomalous trilinear Higgs self-coupling is achieved in the so-called double Higgs-strahlung process at a c.m. energy of about 500 GeV [18] . This is significantly higher than the optimal c.m. energy in ![]() collisions. In the W-fusion process, a similar sensitivity is attained at c.m. energies well above 500 GeV.
collisions. In the W-fusion process, a similar sensitivity is attained at c.m. energies well above 500 GeV.
Calculations show that the statistical sensitivity of ![]() to the Higgs self-coupling is maximal near the kinematic threshold for Higgs-pair production if
to the Higgs self-coupling is maximal near the kinematic threshold for Higgs-pair production if![]() , and is comparable with the sensitivities of
, and is comparable with the sensitivities of ![]() and
and ![]() to this coupl- ing for
to this coupl- ing for![]() , even if the integrated luminosity in
, even if the integrated luminosity in ![]() collisions is only one third of that in
collisions is only one third of that in ![]() annihilations [18] . The overall acceptance should, in principle, be considerably larger in the process
annihilations [18] . The overall acceptance should, in principle, be considerably larger in the process ![]() than in the reaction
than in the reaction ![]() due to the smaller final-state particle multiplicity.
due to the smaller final-state particle multiplicity.
Since the cross-section ![]() does not exceed 0.4 fb, it is essential to attain the highest possible luminosity, rather than energy, in order to measure the trilinear Higgs self-coupling. As shown in [18] , appropriate angular and invariant-mass cuts and a reliable
does not exceed 0.4 fb, it is essential to attain the highest possible luminosity, rather than energy, in order to measure the trilinear Higgs self-coupling. As shown in [18] , appropriate angular and invariant-mass cuts and a reliable ![]() -tagging algorithm are needed in order to suppress the dominant WW, ZZ and four-quark backgrounds well below the HH signal.
-tagging algorithm are needed in order to suppress the dominant WW, ZZ and four-quark backgrounds well below the HH signal.
The results of detailed feasibility studies for measuring Higgs-pair production in ![]() and
and ![]() collisions have been reported [25] [26] . It has been shown that the optimum
collisions have been reported [25] [26] . It has been shown that the optimum ![]() collision energy is around 270 GeV for a 120-GeV Higgs boson, and that the main backrounds at this energy are the processes
collision energy is around 270 GeV for a 120-GeV Higgs boson, and that the main backrounds at this energy are the processes![]() . The preliminary analysis described in [25] suggests that the process
. The preliminary analysis described in [25] suggests that the process ![]() could be observed with a statistical significance of about
could be observed with a statistical significance of about![]() , provided proper color-singlet clustering is used in jet reconstruction. The precision with which the trilinear Higgs self-coupling could be measured in the process
, provided proper color-singlet clustering is used in jet reconstruction. The precision with which the trilinear Higgs self-coupling could be measured in the process ![]() at
at ![]() and in the reaction
and in the reaction ![]() at
at ![]() is presented in [26] .
is presented in [26] .
5. The Proposed Facility
A schematic layout of the proposed SLC-type ![]() facility is shown in Figure 5. Damped and bunch-compressed electron and positron beams, accelerated by a single linear accelerator (linac), traverse two arcs of bending magnets in opposite directions and collide at an interaction point surrounded by a detector. The beams are then disposed of, and this machine cycle is repeated at a rate that depends on whether the linac is made of L-band or X-band accelerating structures. Using an optical free electron laser (FEL), high-energy photons for a
facility is shown in Figure 5. Damped and bunch-compressed electron and positron beams, accelerated by a single linear accelerator (linac), traverse two arcs of bending magnets in opposite directions and collide at an interaction point surrounded by a detector. The beams are then disposed of, and this machine cycle is repeated at a rate that depends on whether the linac is made of L-band or X-band accelerating structures. Using an optical free electron laser (FEL), high-energy photons for a ![]() collider are created by Compton backscattering of FEL photons on electrons prior to their collision.
collider are created by Compton backscattering of FEL photons on electrons prior to their collision.
With a crossing angle at the interaction point (IP), separate beam lines may be used to bring the disrupted beams to their respective dumps, thereby enabling post-IP diagnostics. It is also envisaged that a “bypass line” for low-energy beams would be employed to accumulate data at the Z resonance in the process![]() . These runs could be used to regularly calibrate the detector, fine-tune the accelerator and measure its luminosity.
. These runs could be used to regularly calibrate the detector, fine-tune the accelerator and measure its luminosity.
The proposed facility could be constructed in several stages, each with distinct physics objectives that require particular center-of-mass (c.m.) energies:
![]()
![]()
Figure 5. Schematic layout of the proposed SLC-type facility. A 350-GeV superconducting linac (with a focusing quadrupole in each cryomodule) could also be a part of the FCC injector chain.
For instance, the top-quark mass could be measured in the process ![]() at the pair-production threshold; one expects
at the pair-production threshold; one expects ![]() [27] .
[27] .
The linac at the proposed SLC-type facility would consist either of (1) high-gradient X-band cavities developed for CLIC and a corresponding klystron-based power source (a two-beam scheme could be implemented at a later stage); or (2) ILC-type supercon- ducting L-band cavities placed within cryogenic vessels and fed by multi-beam klystrons.
The 11.4 GHz X-band rf technology was originally developed at SLAC and KEK. The choice of this technology is motivated by the cost benefits of having relatively low rf energy per pulse and high accelerating gradients. A comprehensive review of the status of X-band accelerator technology is given in [28] . Since then, significant advances have been made in pulsed HV and rf power generation, high gradient acceleration and wakefield suppression. The ultimate design of rf cavities will depend on the outcome of the ongoing effort to develop 100 MeV/m X-band structures for a CLIC-type linear collider.
As proposed in [23] , a single X-band rf unit contains a modulator that drives a pair of 50 MW klystrons, each of which generates 1.6 μs rf pulses at 50 Hz. An rf compression system enhances the peak power of the klystrons by a factor of 3.75, and produces 245 ns pulses that match the accelerator structure requirements. The resulting 375 MW, 245 ns pulses feed seven 0.21m-long accelerator structures, producing a 85 (100) MV/m loaded (unloaded) gradient in each structure.
The current design for the International Linear Collider (ILC), based on the super- conducting technology originally developed at DESY, uses L-band (1.3 GHz) super- conducting niobium rf cavities that have average accelerating gradients of 31.5 MeV/m (see [29] and references therein). Nine cavities, each 1 m long, are mounted together in a string and assembled into a common low-temperature cryostat or cryomodule. Liquid helium is used to cool cavities to![]() .
.
An ILC-type main linac is composed of rf units, each of which is formed by three contiguous cryomodules containing 26 nine-cell cavities. Every unit has an rf source, which includes a pulse modulator, a 10 MW multi-beam klystron, and a waveguide system that distributes the power to the cavities. An ILC-type design offers some advantages over the X-band technology:
Wakefields are drastically reduced due to the large size of the rf cavities, which means that cavity alignment tolerances can be relaxed. This is crucial for an SLC-type facility, where both ![]() and
and ![]() bunches are alternately accelerated;
bunches are alternately accelerated;
Superconducting rf cavities can be loaded using a long rf pulse (1.5 ms) from a source with low peak rf power;
Wall-plug to beam’ power transfer efficiency is about twice that of X-band cavities;
The long rf pulse allows a long bunch train (~1 ms), with many bunches (~3000) and a relatively large bunch spacing (~300 ns). A trajectory correction (feedback) system within the train can therefore be used to bring the beams into collision.
However, in contrast to a compact, high-gradient X-band machine, a collider based on the current ILC-type design would be characterized by (a) low accelerating gradients; (b) two large damping rings with a total length of at least six kilometers, and (c) a technologically challenging cryogenic system that requires a number of surface cryo- genic plants.
An important feature of the proposed SLC-type facility is the possibility of using backscattered laser beams to produce high-energy ![]() collisions [16] . In order to attain maximum luminosity at a
collisions [16] . In order to attain maximum luminosity at a ![]() collider, every electron bunch in the accelerator should collide with a laser pulse of sufficient intensity for
collider, every electron bunch in the accelerator should collide with a laser pulse of sufficient intensity for ![]() of the electrons to undergo a Compton scattering. This requires a laser system with high average power, capable of producing pulses that would match the temporal spacing of electron bunches [23] .
of the electrons to undergo a Compton scattering. This requires a laser system with high average power, capable of producing pulses that would match the temporal spacing of electron bunches [23] .
These requirements could be satisfied by an optical free electron laser (FEL) [30] . The radiation produced by an FEL has a variable wavelength, and is fully polarized either circularly or linearly depending on whether the undulator is helical or planar, respectively. The wavelength ![]() of FEL radiation is determined by
of FEL radiation is determined by![]() , where
, where ![]() is the Lorentz factor of the electron beam with energy E and
is the Lorentz factor of the electron beam with energy E and ![]() is the periodic length of the undulator. To produce photon pulses of required intensity, suitable high-intensity, low-emittance rf guns have to be developed [31] .
is the periodic length of the undulator. To produce photon pulses of required intensity, suitable high-intensity, low-emittance rf guns have to be developed [31] .
Assuming that the mean number of Compton interactions of an electron in a laser pulse (the Compton conversion probability) is 1, the conversion coefficient
![]()
where ![]() is the number of electrons in a “bunch” and
is the number of electrons in a “bunch” and ![]() is the number of scattered photons. The luminosity of a gamma-gamma collider is then
is the number of scattered photons. The luminosity of a gamma-gamma collider is then
![]() (12)
(12)
where ![]() is the geometric luminosity at a conventional two-linac collider:
is the geometric luminosity at a conventional two-linac collider:
![]() . (13)
. (13)
In this expression, ![]() are the horizontal and vertical beta functions, respectively,
are the horizontal and vertical beta functions, respectively, ![]() are the normalized transverse beam emittances,
are the normalized transverse beam emittances, ![]() is the number of bunches per rf pulse,
is the number of bunches per rf pulse, ![]() is the pulse repetition rate,
is the pulse repetition rate, ![]() is the c.m. energy, and
is the c.m. energy, and ![]() is the beam power.
is the beam power.
There are ![]() electron or positron bunches in each arc of an SLC-type facility. If its repetition rate is twice that of a conventional two-linac collider, so that roughly the same wall-plug power is used, the two machines would have the same luminosity (see Equation (13)).
electron or positron bunches in each arc of an SLC-type facility. If its repetition rate is twice that of a conventional two-linac collider, so that roughly the same wall-plug power is used, the two machines would have the same luminosity (see Equation (13)).
The energy loss per turn due to synchrotron radiation (SR) in a storage ring is given by
![]() (14)
(14)
where![]() , E [GeV] is the beam energy,
, E [GeV] is the beam energy, ![]() is the effective bending radius,
is the effective bending radius, ![]() is the beam path length, and
is the beam path length, and![]() . For
. For ![]() and
and![]() , the expression on the left yields
, the expression on the left yields ![]() per half turn; for
per half turn; for ![]() and the same radius,
and the same radius, ![]() per half turn. If there are no accelerating structures in the arcs, the linac energy must be increased, e.g., from
per half turn. If there are no accelerating structures in the arcs, the linac energy must be increased, e.g., from ![]() to
to ![]() in order to attain
in order to attain![]() .
.
The critical energy of SR photons, ![]() , is approximately 8 MeV for
, is approximately 8 MeV for ![]() and
and![]() . The energy spread in an electron beam due to SR is given by
. The energy spread in an electron beam due to SR is given by
![]() (15)
(15)
where ![]() is the Lorentz factor of the beam,
is the Lorentz factor of the beam, ![]() , and
, and ![]() is the bending radius. For
is the bending radius. For ![]() and
and![]() , Equation (15) yields
, Equation (15) yields ![]() (cf. Figure 6). For
(cf. Figure 6). For ![]() a preliminary calculation indicates that the growth of the horizontal beam emittance in the bending arcs would not exceed the value at KEK’s ATF damping ring (see Figure 7).
a preliminary calculation indicates that the growth of the horizontal beam emittance in the bending arcs would not exceed the value at KEK’s ATF damping ring (see Figure 7).
In contrast to ILC or CLIC, an SLC-type collider would have a single bunch compression system and a short beam transfer line connecting the damping rings with the entrance to the main linac (see Figure 5). A 350-GeV superconducting L-band linac at the proposed facility may form, together with a 3-TeV energy booster, the injector
![]()
Figure 6. Energy spread in an electron beam traversing an arc with an effective bending radius![]() . To produce this plot, a lattice of combined-function FODO cells was used as an input to K. Oide’s SAD tracking code. Credit: D. Zhou, KEK.
. To produce this plot, a lattice of combined-function FODO cells was used as an input to K. Oide’s SAD tracking code. Credit: D. Zhou, KEK.
![]()
Figure 7. Energy dependence of the growth of the horizontal electron beam emittance in an arc with an effective bending radius![]() . To produce this plot, a lattice of combined-function FODO cells was used as an input to K. Oide’s SAD tracking code. Credit: D. Zhou, KEK.
. To produce this plot, a lattice of combined-function FODO cells was used as an input to K. Oide’s SAD tracking code. Credit: D. Zhou, KEK.
chain for a proton collider in the FCC tunnel (e.g., the linac could replace the chain LINAC4 → PSB → PS → SPS at CERN).
6. Concluding Remarks
It is proposed to place the arcs of an SLC-type facility inside the 100 km long tunnel of a Future Circular Collider (FCC). Electron and positron beams, accelerated in a single X-band or L-band linac, would traverse the arcs of bending magnets in opposite directions (see Figure 5) and collide at c.m. energies considerably exceeding those attainable at circular ![]() colliders. Using an optical free-electron laser (FEL), the SLC-type facility could be converted into a
colliders. Using an optical free-electron laser (FEL), the SLC-type facility could be converted into a ![]() collider. Large savings in construction cost could be achieved if the crossing angle and the beam dump are exactly the same for the operation of the SLC-type facility in the
collider. Large savings in construction cost could be achieved if the crossing angle and the beam dump are exactly the same for the operation of the SLC-type facility in the ![]() and
and ![]() collision modes.
collision modes.
The proposed ![]() collider could be built in several stages, each with distinct physics objectives that require particular c.m. energies (see Sections 2-5). The following unique features of the proposed facility are particularly noteworthy:
collider could be built in several stages, each with distinct physics objectives that require particular c.m. energies (see Sections 2-5). The following unique features of the proposed facility are particularly noteworthy:
The maximum luminosity at a circular ![]() collider is severely constrained by beamstrahlung effects at high energies; also, it is very difficult to achieve a high degree of beam polarization [32] . This is not the case at an SLC-type facility, where luminosity is proportional to beam energy and the electron beam polarization can reach about 90%. The availability of polarized beams is essential for some important precision measurements in
collider is severely constrained by beamstrahlung effects at high energies; also, it is very difficult to achieve a high degree of beam polarization [32] . This is not the case at an SLC-type facility, where luminosity is proportional to beam energy and the electron beam polarization can reach about 90%. The availability of polarized beams is essential for some important precision measurements in ![]() and
and ![]() collisions [33] .
collisions [33] .
It is straightforward to convert an SLC-type facility into a high-luminosity ![]() collider with highly polarized beams. This considerably increases its physics potential (see below).
collider with highly polarized beams. This considerably increases its physics potential (see below).
A 350-GeV superconducting L-band linac at the proposed facility may form, together with a 3-TeV energy booster, the injector chain for a 100-TeV proton collider in the FCC tunnel. The L-band linac could also be used to produce high-intensity neutrino, kaon and muon beams for fixed-target experiments, as well as X-ray FEL photons for applications in material science and medicine [34] .
If electron or positron bunches, accelerated by the L-band linac at the proposed facility, are brought into collision with the 50-TeV FCC proton beams, the whole accelerator complex could serve also as a source of deep-inelastic ![]() interactions [35] . Such interactions would yield valuable information on the quark-gluon content of the proton, which is crucial for precision measurements at the FCC hadron collider. The physics potential of an
interactions [35] . Such interactions would yield valuable information on the quark-gluon content of the proton, which is crucial for precision measurements at the FCC hadron collider. The physics potential of an ![]() collider is discussed, e.g., in [36] .
collider is discussed, e.g., in [36] .
The rich set of final states in ![]() and
and ![]() collisions at the proposed SLC-type facility would play an essential role in measuring the mass, spin, parity, two-photon width and trilinear self-coupling of the SM Higgs boson, as well as its couplings to fermions and gauge bosons. Such measurements require c.m. energies considerably exceeding those attainable at circular
collisions at the proposed SLC-type facility would play an essential role in measuring the mass, spin, parity, two-photon width and trilinear self-coupling of the SM Higgs boson, as well as its couplings to fermions and gauge bosons. Such measurements require c.m. energies considerably exceeding those attainable at circular ![]() colliders. For instance, one has to measure separately the couplings HWW, HHH and Htt at
colliders. For instance, one has to measure separately the couplings HWW, HHH and Htt at ![]() in order to determine the corresponding SM loop contributions to the effective HZZ coupling (see Sections 2-5 and, e.g., [37] ).
in order to determine the corresponding SM loop contributions to the effective HZZ coupling (see Sections 2-5 and, e.g., [37] ).
For some processes within and beyond the SM, the required c.m. energy is con- siderably lower in ![]() collisions than in
collisions than in ![]() or proton-proton interactions. For example, the heavy neutral MSSM Higgs bosons can be created in
or proton-proton interactions. For example, the heavy neutral MSSM Higgs bosons can be created in ![]() annihilations only by associated production (
annihilations only by associated production (![]() ), whereas in
), whereas in ![]() collisions they are produced as single resonances (
collisions they are produced as single resonances (![]() ) with masses up to 80% of the initial
) with masses up to 80% of the initial ![]() collider energy.
collider energy.
Both the energy spectrum and polarization of the backscattered photons at a ![]() collider depend strongly on the polarizations of the incident electrons and laser photons. The circular polarization of the photon beams is an important asset, for it can be used both to enhance the signal and suppress the background. The CP properties of any neutral Higgs boson produced at a photon collider can be directly determined by controlling the polarizations of Compton-scattered photons.
collider depend strongly on the polarizations of the incident electrons and laser photons. The circular polarization of the photon beams is an important asset, for it can be used both to enhance the signal and suppress the background. The CP properties of any neutral Higgs boson produced at a photon collider can be directly determined by controlling the polarizations of Compton-scattered photons.
Acknowledgements
I would like to thank I. Ginzburg, T. Higo, A. Wolski and K. Yokoya for valuable comments and suggestions concerning various aspects of this proposal. I am especially grateful to K. Oide and D. Zhou for helping me estimate some relevant beam properties at the proposed facility.