The Zhou’s Method for Solving the Euler Equidimensional Equation ()
1. Introduction
We know that when the coefficients 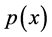 and
and 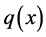 are analytic functions on a given domain, then the equation
are analytic functions on a given domain, then the equation 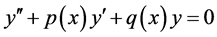 has analytic fundamental solution. We want to study equations with coefficients p and q having singularities, for this reason we study in this paper with one of the simplest cases, Euler’s equidimen- sional equation. This is an important problem because many differential equations in physical sciences have coefficients with singularities [3] . One of the special features of the equidimensional equation is that order of each derivative is equal to the power of the independent variable. This means that this type of equations can be reduced to linear equation with constant coefficient by using a change of the form
has analytic fundamental solution. We want to study equations with coefficients p and q having singularities, for this reason we study in this paper with one of the simplest cases, Euler’s equidimen- sional equation. This is an important problem because many differential equations in physical sciences have coefficients with singularities [3] . One of the special features of the equidimensional equation is that order of each derivative is equal to the power of the independent variable. This means that this type of equations can be reduced to linear equation with constant coefficient by using a change of the form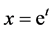 .
.
Many numerical methods were developed for this type of equations, specifically on Euler’s equations such that Laplace transform method and Adomian method [4] . The method proposed in this paper was first established by Zhou to solve problems in electric circuits analysis. In this work, the differential transformation method is applied to solver the Euler equidimensional equations and to illustrate this method, several equations of this type are solved [5] [6] .
2. The Euler Equidimensional Equation
A Euler equidimensional equation is a differential equation of the form
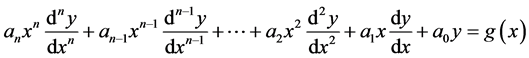 (1)
(1)
where 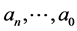 are constants and
are constants and 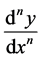 is an n-th derivative of the function
is an n-th derivative of the function 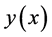
and 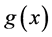 is a continuous function.
is a continuous function.
Now, we consider a second order differential equation (homogeneous Euler equidi- mensional) of the form
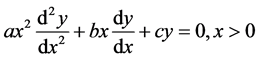 (2)
(2)
The solution can be obtained by using the change of variables
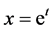 (3)
(3)
where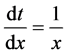 . In fact, for
. In fact, for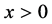 , we introduce
, we introduce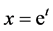 , therefore
, therefore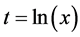 . Then, the
. Then, the
first and second derivatives of 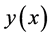 are related by the chain rule,
are related by the chain rule,
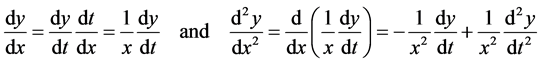 (4)
(4)
Now, substituting (4) in (2) yields a second order differential equation with constant coefficients, i.e.,
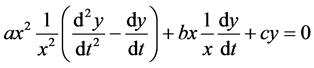
![]()
![]() (5)
(5)
Equation (5) can be solved using the characteristic polynomial
![]() (6)
(6)
where roots are ![]() and
and ![]() which give the general solution but depending on the type of roots it has, i.e.,
which give the general solution but depending on the type of roots it has, i.e.,
a) If![]() , real or complex, then the general solution of the Equation (2) is given by
, real or complex, then the general solution of the Equation (2) is given by
![]()
b) If![]() , then the general solution of the Equation (2) is given by
, then the general solution of the Equation (2) is given by
![]()
3. The Zhou’s Method or DTM
Differential transformation method (DTM) of the function ![]() is defined as
is defined as
![]() (7)
(7)
In (7), we have that ![]() is the original function and
is the original function and ![]() is the transformed function. The inverse differential transformation is defined as
is the transformed function. The inverse differential transformation is defined as
![]() (8)
(8)
but in real applications, function ![]() is expressed by a finite series and Equation (8) can be written as
is expressed by a finite series and Equation (8) can be written as
![]() (9)
(9)
which implies that
![]()
is negligibly small where n is decided by the convergence of natural frequency in this study.
The following theorems that can be deduced from Equations (7) and (9) and the proofs are available in [4] [5] [6] .
Theorem 1 If![]() , then
, then![]() .
.
Theorem 2 If![]() , then
, then ![]() with
with ![]() constant.
constant.
Theorem 3 If![]() , then
, then![]() .
.
Theorem 4 If![]() , then
, then![]() .
.
Theorem 5 If![]() , then
, then![]() , where
, where
![]()
Theorem 6 (Cárdenas, P). If![]() , then
, then
![]()
with![]() .
.
4. Numerical Results
To illustrate the ability of the Zhou’s method [2] [7] for the Euler equidimensional equation, the next problem is provided and the results reveal that this method is very effective.
Example 1 (Homogeneous case). To begin, we consider the initial value problem
![]() (10)
(10)
Using the substitution (3) and (4), the IVP (10) is transformed to a second order differential equation with constant coefficients, i.e.,
![]()
![]()
![]() (11)
(11)
Now, of the initial conditions we have that as![]() , then
, then ![]() and therefore
and therefore ![]() and
and![]() . So, the new IVP is given by
. So, the new IVP is given by
![]() (12)
(12)
The exact solution of the problem (12) is![]() . Taking the differential transformation of this problem we obtain
. Taking the differential transformation of this problem we obtain
![]()
or
![]() (13)
(13)
where ![]() and
and![]() . Therefore, the recurrence Equation (13) gives:
. Therefore, the recurrence Equation (13) gives:
・ ![]() ,
,
![]()
・ ![]() ,
,
![]()
・ ![]() ,
,
![]()
Therefore, using (9), the closed form of the solution can be easily written as
![]() (14)
(14)
but since![]() , then we obtain (see Figure 1)
, then we obtain (see Figure 1)
![]()
![]()
Figure 1. The Zhou’s method vs. exact solution.
Example 2 (Non-homogeneous case). We consider the following IVP
![]() (15)
(15)
Then, problem (15) is transformed to a second order differential equation with con- stant coefficient by using (3) and (4), i.e.,
![]()
![]()
![]() (16)
(16)
We know that of the initial conditions ![]() and therefore
and therefore![]() , so we obtain
, so we obtain ![]() and
and![]() . Then, the IVP is given by
. Then, the IVP is given by
![]() (17)
(17)
The exact solution of the problem (15) is![]() . Now, the DTM of (17) is
. Now, the DTM of (17) is
![]()
or
![]() (18)
(18)
with ![]() and
and![]() . So, the recurrence Equation (18) gives:
. So, the recurrence Equation (18) gives:
・ ![]() ,
,
![]()
・ ![]() ,
,
![]()
・ ![]() ,
,
![]()
・ ![]() ,
,
![]()
Therefore, using (9), the closed form of the solution can be easily written as
![]() (19)
(19)
But since![]() , then we obtain (see Figure 2)
, then we obtain (see Figure 2)
![]()
Example 3 (Third order Euler’s equation). Consider the following IVP
![]() (20)
(20)
Now, to find ![]() we use the chain rule. In fact we obtain
we use the chain rule. In fact we obtain
![]()
Figure 2. The Zhou’s method vs. exact solution.
![]() (21)
(21)
Therefore, using (3), (4) and (21) we have
![]()
![]()
![]() (22)
(22)
Now, as in the previous example ![]() and then
and then![]() . So, the new initial con- ditions are given by
. So, the new initial con- ditions are given by ![]() and
and![]() . Using (7) we find that
. Using (7) we find that
![]() and
and![]() . Therefore, we obtain the IVP
. Therefore, we obtain the IVP
![]() (23)
(23)
Applying DTM to (23) we obtain
![]()
or
![]() (24)
(24)
So, the recurrence equation (24) gives:
・ ![]() ,
,
![]()
・ ![]() ,
,
![]()
・ ![]() ,
,
![]()
Therefore, using (9), the closed form of the solution can be easily written as
![]()
Figure 3. The Zhou’s method vs. exact solution.
![]() (25)
(25)
But since![]() , then we obtain (see Figure 3)
, then we obtain (see Figure 3)
![]()
5. Conclusion
In this paper, we presented the definition and handling of one-dimensional differential transformation method or Zhou’s method. Using the substitutions (3) and (4), Euler’s equidimensional equations were transformed to a second and third order differential equations with constant coefficients, next using DTM these equations were transformed into algebraic equations (iterative equations). The new scheme obtained by using the Zhou’s method yields an analytical solution in the form of a rapidly convergent series. This method makes the solution procedure much more attractive. The figures [4] [5] and [6] clearly show the high efficiency of DTM with the three examples proposed.
Acknowledgements
Foremost, we would like to express my sincere gratitude to the Department of Mathematics of the Universidad Tecnológica de Pereira and group GEDNOL for the support in this work. In the same way, we would like to express sincere thanks to the anonymous reviewers for their positive and constructive comments towards the improvement of the article.