Nuclear Magnetic Resonance Study of Water-Polymer Interactions and Self-Diffusion of Water in Polymer Films ()
1. Introduction
A fundamental understanding of the ingress of water into copolymer/polymer composites and its effect on the polymer properties is essential [1] - [12] . This impacts the performance in polymer formulations [3] [5] - [7] [9] . The properties and applications of copolymer materials and polymer films in the presence of water have been investigated extensively using several techniques including NMR-methods [6] [8] - [12] . NMR has been used to estimate the amount of water as well as water self-diffusion in porous polymer materials [6] [9] [10] [12] . Different parts of the pore structure can be probed through the partial immobility of the liquid in pores. NMR diffusion is a very useful technique for studying the translational motion in the liquid state on the micrometer length scale [9] [13] - [15] . The translational motion of water in a porous medium is affected by the restriction geometry and this approval has been used to determine the surface to volume ratio, pore size, and tortuosity of porous materials [15] - [18] . The method has also been applied to natural biopolymers and other materials as well [18] - [22] .
Water is known to interact strongly with a variety of polymeric materials having polar functional groups [1] [6] - [9] and both reversible and irreversible effects are known to occur [3] [5] [6] [11] . Short-term water exposure tends to give rise to reversible effects such as plasticization of the matrix, while longer-term exposures may lead to irreversible chemical changes in the system. An understanding of the nature of these processes is important in the design of composite structures having enhanced moisture resistance [2] [6] [8] [10] - [12] .
The properties of films prepared from polymer dispersions are influenced by a drying or film formation process [1] [6] [9] [10] . When polymers are processed from solvent, an initially homogeneous solution passes through a series of aggregated states prior to the formation of a homogenous film that is insoluble in water. Different types of solvent molecules could be distinguished in these partly dried films, e.g., in the polymer/solvent interface and also solvent inside the swollen polymer [1] [2] [6] . The formation of films from polymer solutions is still something of a mystery and there is little fundamental understanding about how molecular level interactions can lead to the specific properties of the films [9] [10] . A diffusion behavior at interfacial layers is not clear too. These interfacial phenomena impact performance in polymer formulation and have a technology importance in industry materials based on random copolymers. A major factor is the copolymer composition (e.g., hydrophobic moiety and weak polyacid) [14] [15] which influences the removal of solvent at film formation. Another essential question is how the dried film interacts with water [6] [9] - [12] .
Molecular mobility and self-diffusion of water in the films based on copolymers of butyl methacrylate (BMA) and methacrylic acid (MAA) have not been studied extensively despite technological importance. The important question to be answered is how the films from random copolymer solutions are penetrated by water [9] .
The present work focuses on the studies of the water dynamics in films formed from the BMA/MAA random copolymer solutions with different mole% of BMA. This research describes how special NMR techniques (1H NMR relaxation and PFG NMR) can be used to obtain such information. The work investigates also the molecular mobility and self-diffusion of water in fully dried films that have been swollen in H2O.
2. Experimental Materials and Methods
2.1. Materials
The polymer materials under this study have been described in details in early publications [9] [14] [15] . Originally random copolymers BMA/MAA were in solutions (31% - 32% solids) in isopropanol (IPA)-(CH3)2CHOH (with BMA mole% = 100; 90; 60). The polymer solutions were dried under vacuum for 24 hrs at 40˚C in order to remove solvent. Then 13C CP/MAS NMR spectra have been registered for identification of the polymers and confirmation of their structure. For NMR analysis dried copolymers were dissolved in deuterated chloroform. The IPA used in the work was purchased from Aldrich.
2.2. Preparation of Films: Experimental Conditions
The films were formed from BMA/MAA copolymer/IPA solutions (32% polymer concentration). The required amounts of polymer solution were subsequently transferred into PTFE or PET dishes. The samples were drying on an open bench at room temperature (22˚C), for 5 - 6 days. The subsequent 1H NMR spectra showed only a broad resonance line of solid-like signal. The dried films were immersed in distilled water for a period of 47 - 50 days. In some characterized experiments the time for water exposure was equal to 6 hrs, 18 hrs, 32 hrs and 6 days. The samples (films saturated with H2O) were removed from the vial with water, their surfaces dried with a soft paper tissue, and then placed into a 5 mm NMR tubes. Figure 1 shows the pictures of films under study (with and without water) obtained using optical microscopy (a film with water is opaque and a film without water is clear).
To detect the ingress of the water into the copolymer films and to identify the nature of the macromolecular interactions the 1H NMR spectra as well NMR-relaxation times and self-diffusion coefficients were measured. The thickness of the polymer films was between 0.8 and 1.2 mm.
![]()
Figure 1. The pictures of BMA/MAA 90/10 films (with and without water). The samples examined by an optical microscope (top left, right; bottom left). Top left (dried film; clear), top right (the film with water; opaque (white)), bottom left (film partly filled with water).
2.3. Gravimetric Analysis
After the NMR experiments all the films were dried to constant weight (W0). During water sorption the samples were removed periodically from the water vial, dried of excess of water and weighed (W1). The water uptake Wup was calculated according to Equation (1):
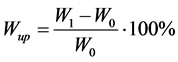. (1)
The samples were weighed both before and after the NMR-experiments. In the water evaporation study samples were left inside a thermostat oven (at 50˚C) for 24 hrs. Constant weight and NMR spectrum additionally testified that all water is gone at drying. The masses of water in the film were calculated then.
2.4. CRYO-SEM Examination of Hydrated Films
Samples were removed from water and quickly frozen using a liquid nitrogen-cooled specimen stub. Using the Gatan Alto cryo-system, the samples were then plunged into further liquid nitrogen, evacuated and transferred to a cryo-preparation chamber. The samples were fractured, etched (by raising the temperature to −95˚C in order to sublime off a small quantity of water), sputtered and mounted onto a cold stage in the Hitachi S4500 SEM. Secondary electron imaging was carried out at an acceleration voltage of 10 kV. Further film samples were fractured at room temperature then dried, sputtered and examined in routine fashion on the same instrument.
2.5. NMR-Spectra
The copolymers (dried films) before immersion in water were characterized by 1H NMR. In control experiments the films were dissolved in deuterated chloroform. 13C CP/MAS NMR spectra for solid samples were obtained at the Bruker DSX 300 NMR spectrometer (field 7.046 T) using 7-mm rotor with rotor frequency of 7000 Hz at room temperature.
Figure 2 shows a typical 13C CP/MAS NMR spectrum of the dried copolymer film (mole% BMA = 80). The resonance signals characterised polymer groups were as follows: ~15 ppm―CH3?C; ~20 ppm―CH3?CH2?(CH3 in the C4H9 BMA-unit); ~30 ppm―CH2?CH2?; ~45 ppm―C?CH2?C?(CH2 in main copolymer chain); ~55 ppm― C?; ~65 ppm―OCH2; ~177 - 185 ppm―CO.
2.6. Free Induction Decay (FID) and NMR-Relaxation Times
All the NMR measurements of FIDs and spin-spin (T2) relaxation times were performed on a Bruker DSX 300 NMR spectrometer (at a proton resonance frequency of 300 MHz)
When the sample is placed in a magnetic field B0 the macroscopic magnetization M of the sample is related to the number of spins NI and the absolute temperature T through Equation (2) [13] [16] - [18] :
. (2)
![]()
Figure 2. 13C CP/MAS NMR spectrum of the BMA/MAA 80/20 copolymer dried film. Signals at ~118 and ~238 ppm are spinning sidebands. T = 298 K, frequency for 13C is 75.43 MHz.
Here gI is the gyromagnetic ratio for nuclei with spin I, NI is a number of spins I, T is the absolute temperature, h is Planck’s constant, kB is Boltzmann’s constant, and I is the spin quantum number of the observed nucleus. The proportionality constant 
is known as the magnetic susceptibility of the medium. The free induction decay (FID) signal, S(t) disappears with the characteristic time constant T*2. Static dipolar interactions for spins residing in solid environments cause a rapid decay of the FID, and T*2 is on the order of 0.010 ms. The dipolar interaction is averaged to zero in liquids, and T*2 is between 1 ms and 1 s. From Equation (2), it is evident that it is possible to determine the number of spins within a sample from the initial signal strength S0 which measures magnetization M at time t = 0. After application of a radio frequency pulse, the receiver is unable to acquire a signal from the sample for a time of ~0.005 to 0.010 ms due to interfering signals from the electronic circuits and the probe material. Signal acquisition starts after a delay, the receiver dead time [16] [17] . This time is quite negligible in the quantitative measurements for polymer-water system because of the long T*2 for liquid. In the case of solids, it is necessary to extrapolate the signal to zero time to obtain the correct value of S0 and, thus, 1H content.
Depending on the line shape, the damping of the FID has a certain functional form. For most cases NMR peaks are Lorentzian and/or Gaussian line shapes [13] [16] [17] [23] . If the line shape of the mobile protons is expected to be Lorentzian this gives for the FID the exponential function:
. (3)
For the Gaussian shape spectra the FID signal should be expressed by Equation 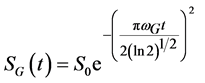(4):
. (4)
Here wL and wG are the Lorentzian and Gaussian widths at half height of the peaks in the frequency domain. Normally Equation (3) and Equation (4) are characteristics for liquids and solids respectively, although combinations can also take place (e.g., a Gaussian broadening of an inherently liquid-like signal) [19] [20] [23] .
Figure 3 shows typical FIDs for the dried copolymer films. The decay consisting of two clearly discernible parts, a fast decaying component (solid-like) and slower decaying component (liquid-like), could be decomposed using published equations [17] [24] . The total time domain signal is the sum of the signals from these both parts. The solid like part of the FID was described by a combination of a sinc function and Gaussian broadening [16] [17] :
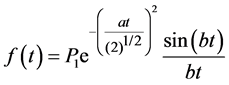. (5)
Here P1 is the signal intensity of the solid like part FID curve at t = 0. The parameters of a and b are used in the equation for the second moment М2= a2 + b2/3 [16] [23] - [25] .
The slow relaxing component has been fitted as a two exponential function or as a Voight line-shape function [9] [24] [25] , that has both Lorentzian and Gaussian functions:
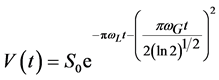(6)
where S0 is the signal intensity at t = 0; wL and wG―Lorentz and Gauss widths of the NMR-spectra at half of the peak height in frequency scale. We observed that fitting the slow relaxing component of the FID-curve was better with two exponential functions than by Voight function. For the data fitting the population of the slowest relaxing component (T2 = 0.10 - 0.15 ms) was about 1% - 2% that could be neglected during the calculation of M2-values and the T2 for fast relaxing component. The correlation times associated with this T2-value of slowest exponential component were in the range of tc = (0.6 − 3.0) ´ 10−6 s.
![]()
Figure 3. Typical FIDs (normalized per maximum) in dried BMA/MAA copolymer films: mole% BMA = 100 (curve 1) and 60 (curve 2). T = 298 K, frequency for 1H is 300 MHz.
The molecular correlation times in the parts of polymer films could be estimated according to the case when a distribution P(τ) of the correlation times of segmental motion was considered to be connected to the experimental transverse magnetization decay curve F2(t) of polymer protons according to Equation (7) [24] [26] :
. (7)
The relationship between the spin-spin relaxation time T2p of polymer protons, the second moment М2, the correlation time τc and the spectrometer operating frequency ω0 is presenting by the Equation (8) [17] [24] [25] :
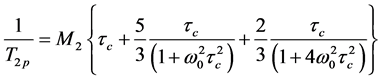. (8)
In calculations (8) we have used the average value M2 = (10 ± 2) ´ 109 s−2 measured for the films with different BMA mole%. The segmental mobility in the polymer films depended on the time of drying process and thickness of the film. For example, for the film with thickness of about 0.4 - 0.8 mm only proton fraction of 1% - 3% had correlation times tc ~ 1 ´ 10−6с.
The intensity of the slow relaxing component of the FID in the films swollen in water was larger than fast one. In one particular example (BMA/MAA 60/40 film) circa 57% of all protons were associated with the slowest relaxing component (T*2 ~ 0.142 - 0.150 ms).
The large difference in decay rates between the signals originating from liquids and solids makes the FID analysis a powerful tool in the study of water in the pores of solid polymers. By deliberately setting the receiver dead time to a value 3T*2 for the solid, it is possible to isolate the signal from the liquid. The amount of liquid in pores could be estimated then on a relative scale. The signal arising from a solid proton-containing material can be used to make an absolute determination of the amount of pore water, expressed as mass liquid/mass dry solid mliq/msol, if the proton density of the solid is known. The use of this approach to determine water content relies on the assumption that the liquid does not contribute to the solid-like signal (or this influence is negligible) and vice versa. In any case, the system was also analysed by gravimetric data.
Water in differing physical environments is generally characterized by different transverse relaxation time T2. The Carr-Purcell-Meiboom-Gill (CPMG) experiment, 90˚x − (tcp ? 180˚y ? tcp)n, [15] - [17] is a powerful method to quantify the relative proportions of water with different values of T2. The method has been applied to polymer films swollen in water. T2 is shortened from the bulk value by interaction with the walls of the pore film. For a compartmentalized system, the CPMG decay curve is given by Equation (7) [17] [24] , in which P(τ) is the probability density P(T2), t = 2ntcp is the time after the 90˚ pulse, n is the number of echoes, and tcp is the pulse spacing between 90˚ and 180˚ pulses in the CPMG sequence. An analysis of the experimental data with P(T2) deconvolution is conducted using in-house MatLab® programs. In many porous systems T2 is proportional to the pore radius [13] [17] [22] . Then P(T2) can be reinterpreted as a radius distribution [13] [22] .
2.7. Pulsed Field Gradient (PFG) NMR
All the PFG NMR experiments were performed on a Bruker DSX 300 NMR spectrometer (at working frequency of 300 MHz for 1H) equipped with a Bruker diff 30 probe. The pulsed-field-gradient stimulated-echo sequence was used [13] [17] [19] [20] . The three 90˚ pulses produce a stimulated spin-echo at time 2t1 + t2 (where t1 is the time between the first and second 90˚ pulses and t2 is the time between the second and third pulses). The magnetic field gradient of amplitude G (with duration d = 1 ms) was varied linearly between zero and maximum value of 1 T/m in 16 or 32 steps. For films with low water content (small value of self-diffusion coefficient) the gradient value of Gm = 10 T/m has been used. Self-diffusion coefficients were calculated using a non-linear least squares fitting procedure of echo attenuation data.
The field gradient was calibrated using the same gradient sequence but with a sample of water (diffusion experiments in doped water (MnCl2) which has a diffusion coefficient of (2.36 ± 0.03) ´ 10−9 m2/s at 25˚C). The value t1 was 2.54 msin all diffusion experiments. According to the Stejskal-Tanner relationship [16] [17] [19] [22] the echo amplitude depends on the gradient factor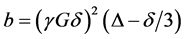 
and the experimental parameters t1 and t2 as in Equation 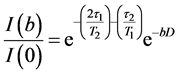(9):
. (9)
Here g is the gyromagnetic ratio for protons = 267.51 ´ 106 rad.T−1s−1, D is the time between the leading edges of the gradient pulses and is the effective diffusion time. Because of the homogeneity of the main magnetic field, any constant background gradient can be neglected. Diffusion coefficients, D, were determined from the decay of the signal intensity I(b)/I(0) plotted versus b using a least-squares fit to the slope in a semi- logarithmic plot [15] [18] [19] . In systems where free diffusion occurs, the echo attenuation is given by the term 
in Equation (9). A single exponential decay is observed only in the case of non-restricted diffusion, while in many systems where significant deviations occur from this linear form, the data may be interpreted as the effects of restricted diffusion [13] [17] [22] [24] . For a molecule moving in an isotropic and homogeneous medium (in the absence of chemical exchange), the measured diffusion coefficient is independent of the experimental diffusion time, Δ. However, for a molecule diffusing within a restricted geometry, the displacement along the direction of the applied field gradient will be a function of Δ, D, and the size and shape of the restriction geometry [16] [20] [22] . As Δ becomes larger, a fraction of the molecules will be affected by the boundary of the sphere and the measured diffusion coefficient (Dapp) will appear to be time dependent [13] - [16] . When Δ becomes very long, such that the displacement of the confined molecule is restricted by the boundary of the sphere, the measured displacement, and hence the measured diffusion coefficient, becomes independent of Δ and depends only on the size of the sphere. For unrestricted diffusion D is independent of Δ and the mean square displacement 
of the diffusion species obeys the Einstein equation:
. (10)
Thus, for normal, free diffusion
2> is proportional to D. However when diffusion barriers exist and the diffusion is restricted, the mean square displacement
increases with less than the first power of the diffusion time [17] [20] :
![]()
. (11)
Then the apparent self-diffusion coefficient depends on D as Dapp ~ Dk−1. In the case of completely restricted diffusion k = 0 and ![]()
does not increase when the diffusion time increases (independent onD), and Dapp ~ 1/D. The spin-echo attenuation in this case reflects the dimension of the restriction geometry [13] [15] [22] .
3. Results and Discussion
3.1. 1H NMR Spectra and T2 Studies of the Swollen Films
Figure 4 shows the typical spectra for the dried polymer film (mole% BMA = 100) and for the same film swollen in water (bottom). The spectrum of dried film contains wide complex peak that characterises the residual protons of solvent with low mobility in dried sample (these are the humps at ~1 - 2 and ~4 ppm from CH3 and CH2 groups). This is confirmed by the published data [9] which showed how 1H NMR spectrum of isopropanol in copolymer solution changed during drying process and film formation. For the swollen film the spectrum (Figure 4, bottom) shows the narrow peaks. The protons in swollen film are more mobile than those in the dried polymer film as
![]()
Figure 4. 1H NMR spectra for the dried BMA/MAA 100/0 copolymer film (top spectrum) and for the same film swollen in H2O during 18 hrs (bottom spectrum). T=298 K, frequency for 1H is 300 MHz.
expected. The signal at ~1 - 2 ppm belongs to the CH3?groups of residual IPA and a broad signal around ~4 ppm belongs to OH peak of water overlapped with CH and OH peaks of IPA (in original IPA solution they are at ~4 and ~5 ppm respectively [14] [15] ). In swollen film IPA (CH3) peak became narrower as a mobility of residual IPA is larger in the presence of water in film. A description of the peak ~4 ppm as H2O signal has been confirmed by additional experiments with drying a film as well as by swelling a film in D2O. In particular, the intensity of this peak (at 4 ppm) in 1H NMR spectrum of swollen poly-BMA film decreased with drying the film swollen in H2O. For a film swollen in D2O there was no 4 ppm peak of protons from OH group.
Figure 5 shows the experimental 1H NMR spectra for a dry BMA/MAA copolymer (mole% BMA = 60) film and for the same film swollen in water. It can be seen that after water exposure there is a large portion of mobile protons in the swollen film (a signal of OH protons at ~4.8 ppm). The peak at ~1.2 - 1.5 ppm was associated with residual solvent in the film. A water signal was sensitive to mole % BMA in swollen film. In particular, a comparative study of water exposure for the BMA/MAA 60/40 and 100/0 films shows that first is more sensitive to water uptake and the intensity of their mobile components is larger. For example, after 6 hrs water exposure the copolymer film with mole% BMA = 60 had ~60% of mobile protons associated with slowest relaxing T2- component. The BMA/MAA copolymer film with BMA mole% = 100 after 6 hrs water exposure had considerably less intensity (~30%) of slowest T2-component. This is a direct consequence of the change in hydrophilic/hydrophobic ratios of the polymer [9] .
![]()
Figure 5. 1HNMR spectra for the dry BMA/MAA 60/40 copolymer film (diamond) and for the film swollen in water during 48 hrs (blue triangle). T=298 K, frequency for 1H is 300 MHz.
According to published data [27] [28] , the effect of water uptake into the copolymers and plasticization depends on the fraction of hydrophobic domains in the polymer chain. In particular, Ghi et al. [27] [28] showed that the rate of diffusion of water into a copolymer, as well as the amount of equilibrium water which can be absorbed by the polymer matrix, is dependent on the nature of the monomers present and their molar ratios. These results have been obtained using NMR imaging on a series of hydrohyethyl methacrylate (HEMA), copolymers with tetrahydrofurfuryl methacrylate (THFMA) [28] .
The estimation of the correlation times as characteristics of molecular mobility of water in the copolymer films can be obtained by following expressions [17] [29] [30] :
![]()
![]()
. (12)
Here С = 2.5 ´ 1010 s−2 is a constant of dipole-dipole binding for water molecules, ω0―Larmor resonance frequency for the protons, R2w―spin-spin relaxation rate for the protons of water (at room temperature R2w ~ 0.5 s−1) [17] [30] . η. is the fraction of bound water (ratio of number of water molecules bounded to the surface of rigid polymer to all water molecules). At low water concentration (~10wt % or less), it is assumed that η~1 [30] (at low water concentration all water molecules are bounded to the surface of polymer matrix) in order to calculate the correlation times using the equations (12). Although this model has a single correlation time, it is helpful to investigate the role of water mobility inside the film. This approach had proved to be successful in several publications [17] [25] [29] [30] . We have found that the correlation times τс for water molecules in the polymer films after 6 hrs water exposure were equal to tc = (3.8 ± 0.3) ´ 10−7 s (mole% BMA = 60) and tc = (4.1 ± 0.3) ´ 10−7 s (mole% BMA = 100). Water content of these films after 6 hrs water exposure was in the range 3% - 4%. A tendency was discovered for the copolymer films under study: the volume-averaged water mobility decreased with increasing hydrophobic content of the polymers. Data for wet biopolymers at comparable moisture conditions (5% - 7% or less) obtained similar values of tc [29] [30] . These correlation times correspond to tightly bound water because those motions are only slightly faster than the motion of most mobile protons in dry polymer films. This dynamic behaviour of water in the polymer matrix could be changed by increasing water exposure time [2] [6] [10] - [12] or variable proportion of BMA/MAA monomers [9] .
The dynamics of water molecules inside the film depends on the chemical surrounding. Water is a non-solvent for BMA but it is a solvent for MAA-units [9] [14] [15] . When more water molecules penetrate into the film the NMR signal becomes more intensive (Figure 5) and the transverse relaxation rate of the water is much slower. For longer exposure times of BMA/MAA films in water (>6 hrs) faster molecular motions could be detected for the water in the film matrix. In this way, the mobility of water molecules in a matrix can also be investigated by CPMG-sequence. For example, 12 hrs water exposure of the BMA/MAA copolymer films (mole% BMA = 60 and 80) resulted in following T2-data. For both types of copolymer films the CPMG-curves were fitted to two exponential components. With the aid of Equation (12) the fast relaxing component has been characterized by correlation times of tc = (0.42 − 0.74) ´ 10−8 s and the slow relaxing component resulted intc = (1.2 − 1.6) ´ 10−10 s. The last tc values seems are comparable with published values tc (~1 ´ 10−10 s) for water adsorbed in natural polymers (collagen, gelatine) at water content ~12% - 20% [29] [30] . It shows that the slow relaxing water component has common nature and usually is considered as interface water one or the component characterizing water in pores of microstructure of polymer (natural or synthetic) network.
In other example (the BMA/MAA 90/10 polymer film with water content = 8.4 wt%) a CPMG decay curve has been fitted to the sum of two components with ![]()
(population = 83%) and ![]()
(population = 17%). This supposes that the water component with the larger ![]()
values could be associated with water protons in the large pores and holes, and a component with smaller ![]()
is supposed to explain a mobility of water in the smaller size pores.
3.2. Self-Diffusion of Water in the Swollen Films
The self-diffusion of water molecules in the polymer matrix of swollen films in current study has been investigated according to PFG NMR approaches [9] [17] . A typical dependence of self-diffusion constants on diffusion time for the BMA/MAA film with molar ratio = 90/10 is shown in Figure 6. Diffusion is quasi-restricted, i.e., a value of diffusion constant D depended on the diffusion time D as Dapp ~ Dk−1 with k < 1 [16] [18] [20] [31] .
In a continuous medium, with an arbitrary permeability p and a barrier spacing a, Tanner and Stejskal for the long time-scale limit (![]()
) obtained the expressions of the echo attenuation function for diffusion within reflecting spherical boundaries [31] - [34] :
![]()
(13a)
![]()
. (13b)
According to Tanner’s approach, in the spherical-boundary system the apparent diffusion coefficient is a2/5D [17] [33] . This presents the mean square distance diffused by the molecules of water, 2a2/5, divided by 2Δ [31] . The Δ-dependency of Dapp in the film with water (Figure 6) may be due to the restriction of water diffusion by a film structure.
For short D-values, Tanner considers [32] - [34] the apparent diffusion coefficient as the free diffusion coefficient D0. When Δ is increased, the apparent diffusion coefficient decreases and it approaches asymptotic value, Dasym, which depends on permeability p and barrier spacing a according to [17] [34] :
![]()
Figure 6. The diffusion constants of water in the BMA/MAA 90/10 film with water content of 7.4% (after 50 days in water) as a function of diffusion time with a fit to a restricted diffusion model: D = mDk−1 (where k < 1, and m is a constant). k = 0.213. T = 298 K, frequency for 1H is 300 MHz.
![]()
. (14)
Using the procedure undertaken by Tanner [32] - [34] for the data of Figure 6 a restricted diffusion length a ≈ 0.61 µm and permeability p ≈ 2.6 ´ 10−9 m/s have been obtained. Applying Tanner’s model and procedure to the experimental D-data on BMA/ MAA 90/10 film with water content of 8% resulted in comparable values: a ≈ 0.54 µm and permeability p ≈ 2.72 ´ 10−9 m/s.
For the film prepared from pure poly BMA (mole% BMA = 100) and swollen in water during 18 hrs the diffusion is again restricted, i.e., apparent diffusion coefficient of water Dapp depends on the diffusion time D as Dapp ~ Dk−1 with k < 1 [9] [15] [17] . Following the approach presented above the size of the restriction a≈0.85 µm has been estimated.
It is worth to mention that the confinement theory does not accurately represent the actual geometry if there is more than one barrier in this range [33] [34] . These barriers are caused by the surface of pores within the film. Concerning the estimation of Dasym the measured values of D did not become absolute constant with increasing D in spite of long diffusion times [19] [20] [22] [31] [32] . The uncertainty in the calculation of p is increased by the assumption that the samples from two particular films have the same physical parameters. In addition to this an exchange between different diffusion components needs to be taken into account. The apparent self-diffusion coefficient Dapp is a function of diffusion time. The diffusion experiments for the film samples with comparable water content showed the data that the average sizes of pores copolymer films are in the range of 0.5 - 1.0 µm. The two exponential fit to the CPMG curves could be alternatively associated with pores of two sizes (small and large pores). A rough estimation for the pore sizes could be made from T2-CPMG-data [6] [35] [36] .
The transverse relaxation time in a spherical pore is given by exponential decay with a relaxation time T2 = (T2s/λ).(a/3) [35] . Here T2s is the surface relaxation time, λ is the thickness of the surface layer which is taken to be order of 3 Å, and a is the pore size. For other pore geometries, the proportionality constant (a/3) may be slightly different (e.g., a/2 for cylinders) [35] . A surface relaxation time is estimated roughly as 60 - 100 µs [35] . With these data the fitted values of T2 for the polymer films (e.g., using relaxationT2-component for BMA/MAA 90/10 film) have been converted into pore size giving a = 0.8 - 1.2 µm. This value is reasonable and in line with the estimate from the diffusion data mentioned above. CRYO-SEM data for the 90/10 BMA/MAA copolymer film are presented in Figure 7. The micrographs illustrate that film samples contain spherical pores, typically around 1 µm in diameter. This is in good agreement with value estimated from diffusion and relaxation data. As it is seen from Figure 7 there is a distribution of pore sizes indeed: from small (~0.5 µm) to large (~2 µm) pores.
4. Conclusion
NMR relaxation and PFG NMR techniques have been demonstrated to be the useful tools for the characterization of diffusion of water into butyl methacrylate and methacrylic acid copolymer films. Water-concentration distributions were directly observable and FID and T2 experiments performed at various molar BMA/MAA ratios and immersion experiments gave useful information about molecular mobility of the system
![]()
![]()
Figure 7. The micrographs (two different scales: top―all marked range is 10 µm for 10 tics; bottom―a range is 5 µm for the 10 tics) from Cryo-SEM examination of hydrated copolymer 90/10 BMA/MAA film.
and water inside the films. The strong increase in water absorption and water molecular mobility was observed after increasing the immersion water time or in increasing the hydrophilic monomer MAA fraction in the copolymer film. The PFG NMR experiments showed that the echo attenuation function depended on the diffusion time. The diffusion constants decreased with increasing the diffusion time implying that the motion is restricted. The data obtained have been discussed using physical models for diffusion of water in polymer materials. The results are rationalized in terms of structure of the studied samples. Water inside the swollen film is trapped in restricted confinement. The sizes of pores inside the film have been estimated as a = 0.6 - 1.0 µm. Diffusion coefficients of water in swollen BMA/MAA films were well characterized by restricted diffusion theory and the Tanner and Stejskal model for a spherical-boundary problem and the size of the restriction. It is shown that transverse relaxation yields information about the distribution of water in the pores. The volume-averaged water mobility for the copolymer with large mole% BMA is lower than that in copolymer with low mole% BMA.
Acknowledgements
The authors thank Dr. Martin Murrey.